Parallel flow of immiscible liquids in a microreactor: modeling and experimental study

Abstract

Two-phase parallel flow can be utilized in microreactor engineering for performing reactions and extractions, and also for achieving efficient phase separation at the exit of the microreactor. Typical laminar flow at the microscale allows two phases to flow in parallel without mixing, allowing highly controlled conditions for a specific chemical process. Since the liquid with the higher viscosity has a tendency to occupy a larger fraction of the microchannel, the position of the interface can be controlled through the adjustment of flow rates. The prediction of the position of the interface is important for microreactor design and operation and requires the solution of the governing equations of fluid mechanics. In this work, the theoretical description for two-phase parallel flow, based on the Navier–Stokes equations in three dimensions was expressed with a mathematical model and validated with experimental observations. The movement of the interface was achieved through the adjustment of fluid properties according to the position of the central streamlines. The predicted position of the interface was in good agreement with experimental data. A correlation for the flow rate ratio required for positioning the interface in the middle of the channel for various viscosity ratios was proposed, as well as a correlation for the prediction of the parallel to slug transition for a water/n-hexane system.

1 Introduction

Liquid–liquid and other multiphase reactions in microchemical systems, including nitration, extraction, and emulsification are common processes applied in a broad range of application areas (Zhao et al. 2006). Knowledge of the hydrodynamics in a microreactor is of essential value when dealing with operational parameter determination, or for the set-up of a reaction or extraction process. Being able to predict the position of the interfacial border (and by that the required flow ratios) means you can quickly asses the suitability of a chosen two-phase system for specific work. Flow profiles in a microreactor depend on many parameters including linear velocities, fluid properties, and microchannel geometry and material. The flow is typically laminar; when the system is two-phasic the interfacial borders are distinct and organized.

Some characterization of the flow can made with dimensional analysis. The capillary number (Ca = μv/γ) is a dimensionless number describing the ratio of viscous forces to surface tension acting across the interface between two immiscible liquids, where μ is the viscosity, v the characteristic velocity, and γ is the interfacial tension between two fluid phases. It is one of the most important numbers at the microscale, where viscous and surface tension forces are dominant. This holds true when the capillary number is less than approximately 10⁻⁵. Slug flow is normally formed at higher values of surface tension, where the interfacial area tends to be as small as possible. Parallel flow is more common at higher flow rates, where the inertial forces take over. For stable parallel flow, an aspect ratio of width/depth of at least 4 is favorable (Pohar and Plazl 2008), and Zhao et al. (2006) reported parallel flow in a 600 μm wide and 300 μm deep channel. There have been some reports that the transition from droplet regime to parallel flows cannot be described in terms of capillary numbers (Guillot and Colin 2005).

Due to the small dimensions, the flow regime is typically laminar, although turbulence can also be achieved under very high flow rate conditions (Pohar and Plazl 2008). The Reynolds number (Re = ρvD _h/μ) describes the ratio of inertial to viscous forces, where D _h is the hydraulic diameter and ρ is the fluid density. The critical Reynolds number (transition to turbulence) has been shown to be comparable to macro scale at width to depth channel aspect ratios close to unity. Lowering of the critical Reynolds number has been reported by many researches, although it is likely that this is a consequence of higher wall roughness effects on the fluid flow at the microscale, especially notable at higher microchannel aspect ratios (Pohar and Plazl 2008).

The dimensionless Bond number (Bo = ΔρgD ²_h /γ) is a measure of the importance of gravitational forces compared to surface tension forces, where Δρ is the density difference of the two phases, g is the gravitational acceleration, and γ is the interfacial tension. When the characteristic length is sufficiently small, the Bond number is low and gravitational effects are negligible.

Another dimensionless number that is frequently used to analyze fluid flows with an interface in between is the Weber number (We = ρv ² D _h/γ). It is a measure of the relative importance of the fluids’ inertia compared to its interfacial tension. Zhao et al. (2006) performed a detailed study on the flow patterns in a microchannel. Six well defined patterns were observed after a T-junction and superficial Weber numbers were used to predict flow patterns.

In a work by Žnidaršič-Plazl and Plazl (2007), steroid extraction was performed in a microreactor utilizing two-phase parallel flow. It was displayed how two immiscible fluids can flow next to each other without turbulent mixing, giving efficient phase separation at the exit of the microreactor. Furthermore, it was pointed out that when two immiscible fluids with different viscosities are pumped into the system at the same flow rates, the fluid with the higher viscosity moves slowly compared to the other fluid and therefore occupies a greater fraction of the channel. In order to keep the interface position in the center, the flow rates of both phases can be adjusted. In the work, stable parallel flow was obtained for the whole 33.4 cm length of the microchannel. In another work (Žnidaršič-Plazl and Plazl 2009), water/n-hexane two phase parallel flow was used for ester synthesis in the same microreactor configuration. It was shown that the interface position moves towards the n-hexane phase, if the same flow rates are used for both phases. Consequently, water occupies a larger fraction of the channel. By adjusting the flow rates to a ratio of 1:3 (water to n-hexane), the position of the interface moved to the center and the developed velocity profile was calculated with the experimental observation of the ratio of flow rates required.

Aljbour et al. (2009) published a work on two-phase parallel flow. They used a microchannel with two inlets and two outlets to carry out two-phase catalytic phase transfer reactions with phase separation at the exit of the microchannel. The organic phase could be separated completely from one outlet and a part of the aqueous phase (containing one of the reactants in excess) was separated purely and could be reused. Zhao et al. (2006) recognized parallel flow for being an effective way to perform solvent extraction or purification, which is a key operation in analytical processing. Lu et al. (2011) acknowledged parallel laminar flow for being an effective platform for enhanced mass transfer, for simultaneous preservation of separate phases, for fast phase equilibrium or diffusivity determination with trace chemical consumption, and for continuous, efficient and even multi-stage industrial extraction techniques. Münchow et al. (2007) utilized parallel flow for electrophoretic partitioning of proteins and Guillot et al. (2008) developed a method to perform automated rheological measurements on a microfluidic chip. They also numerically calculated the steady-state developed velocity profiles for two-phase parallel flow and Galambos and Forster (1998) used an analytical solution of simplified Navier–Stokes equations to obtain the velocity profile at steady-state and to predict the position of the interface of developed flow. Similarly, Hitt and Macken (2004) predicted the fully developed interfacial location downstream of a convergence of identical microchannels.

In this computational fluid dynamics study, the Navier–Stokes equations for incompressible flows in primitive variables in terms of the pressure and velocity were solved in three dimensions at steady-state conditions. The adjustment of fluid properties (density and viscosity) according to the position of the central streamlines was achieved in an iterative process, thus illustrating the movement of the interface position. The results of mathematical modeling were validated with experiments.

2 Materials and methods

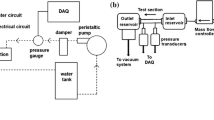
The microreactor system used for the experiments was obtained from Micronit Microfluidis (The Netherlands). Three microreactors were experimented on, all with 2 inlet and 1 outlet channels and a 3 cm long central channel (Fig. 1a). The channels were of rectangular shape. The depth and width of the first were 50 and 220 μm, respectively, the second 50 and 440 μm, and the third 100 and 1000 μm. The corresponding hydraulic diameters were 81.5, 89.8, and 181.8 μm. The angle between the inlet channels was 45°, but they joined together in parallel at the junction. The microreactors were made from borosilicate glass and were optically transparent which allowed for flow observation. They were fitted into a stainless steel housing with inlet and outlet tubing. High pressure syringe pumps (Harvard Apparatus, USA) with stainless steel syringes assured well defined, continuous, and uninterrupted flow.

Fig. 1

The microreactor with 2 inlets and a 220 μm × 50 μm central microchannel used for experimentation (a); parallel flow of the organic and water phase in the central channel; x is the vertical and y is the horizontal dimension (b)

The contact angle between water, n-hexane, and borosilicate glass was assessed by taking photos of the two fluids inside a borosilicate test tube and analyzing them with computer graphics software.

Deionized water and n-hexane were pumped through the microreactors with flow rates ranging from 1 to 400 μl/min and at various flow ratios ranging from 1 to 6. A microscope and a camera were used for flow visualization and computer graphic software for analysis of the interface position. The conditions required for parallel flow were studied. Additionally, dodecane/water parallel flow was investigated for the determination of the flow rate ratio required for positioning the interface in the middle of the channel. The experiments were conducted at room temperature (25°C).

The viscosities and densities of the fluids in question were taken from literature and are presented in Table 1. The interfacial tension between n-hexane and water is 51.1 mN/m.

Table 1 Fluid properties used for the simulations

2.1 Method of solution

The Navier–Stokes equations are nonlinear partial differential equations describing the motion of a viscous fluid. For Newtonian incompressible fluids at steady-state, the equations written in Cartesian coordinates for three spatial dimensions in differential form are comprised of three momentum equations for each spatial direction (Eq. 1), and the continuity equation (Eq. 2):

$$ \rho \left( {u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} + w\frac{\partial u}{\partial z}} \right) = - \frac{\partial p}{\partial x} + \mu \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{{\partial^{2} u}}{{\partial z^{2} }}} \right) + \rho g_{x} $$

$$ \rho \left( {u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} + w\frac{\partial v}{\partial z}} \right) = - \frac{\partial p}{\partial y} + \mu \left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }} + \frac{{\partial^{2} v}}{{\partial z^{2} }}} \right) $$

$$ \rho \left( {u\frac{\partial w}{\partial x} + v\frac{\partial w}{\partial y} + w\frac{\partial w}{\partial z}} \right) = - \frac{\partial p}{\partial z} + \mu \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }} + \frac{{\partial^{2} w}}{{\partial z^{2} }}} \right) $$

(1)

$$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0 $$

(2)

where ρ is the fluid density, μ is the dynamic viscosity, p is the pressure, u, v, and w are linear velocities corresponding to x, y, and z directions. g _x is the gravitational acceleration (9.81 m/s²), with the gravitational force acting only in the x direction (depth).

The equations can be simplified to describe a fully developed Poiseuille-type flow, with the interface in the middle of the microchannel, considering steady parallel flow and neglecting compressibility and gravitational forces (Žnidaršič-Plazl and Plazl 2007, 2009). The x-momentum equations therefore read:

$$ 0 = - \frac{\partial P}{\partial z} + \mu_{\text{w}} \left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right) $$

(3)

$$ 0 = - \frac{\partial P}{\partial z} + \mu_{\text{h}} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) $$

(4)

with no-slip boundary conditions at the walls and:

$$ \mu_{\text{w}} \frac{{\partial v({W \mathord{\left/ {\vphantom {W 2}} \right. \kern-\nulldelimiterspace} 2},x)}}{\partial y} = \mu_{\text{h}} \frac{{\partial v({W \mathord{\left/ {\vphantom {W 2}} \right. \kern-\nulldelimiterspace} 2},x)}}{\partial y};\,0 < x < L $$

(5)

at the interface, where z is in the direction of convection and x and y planes are perpendicular. μ _w is the dynamic viscosity of the water phase, μ _h is the dynamic viscosity of the n-hexane phase, v is the z-dimensional linear velocity in the water phase, and u is the z-dimensional linear velocity in the n-hexane phase. W represents the microchannel width and L the length. For the calculation, the experimental observation of the ratio of flow rates required to position the interface in the middle is needed.

In this work, the full Navier–Stokes equations for incompressible flows in primitive variables in terms of the pressure and velocity were solved on a collocated grid using a finite difference domain discretization (Eqs. 1–2). Because there is no direct link for the pressure between the continuity and momentum equations, a mathematical procedure was applied for the coupling of velocities and pressure, specifically the introduction of artificial compressibility into the continuity (Andreson 1995). The artificial compressibility method for solving three dimensional steady incompressible viscous flows was compared to pressure-based methods in an article by Tamamidis et al. (1996). Their results showed that both methods are capable of producing results in reasonable agreement with experimental data and that predictions from pressure-based methods compare only slightly more favorably with measurements and well-resolved computations than the artificial compressibility method. The method was chosen due to the simple implementation of the code to three dimensions. Although the results were calculated for a steady-state problem, due to numerical consideration, a pseudo-transient scheme was incorporated. The artificial compressibility equation is:

$$ \frac{\partial p}{\partial t} + \frac{1}{\tau }\left( {\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z}} \right) = 0 $$

(6)

where τ is the artificial compressibility.

In the limit t → ∞, as steady-state is approached, the artificial compressibility equation is transformed into the incompressible continuity equation. Consequently, a pressure field, which assures a divergence-free flow, is generated. An implicit scheme was used and the adjustment of fluid properties (density and viscosity) according to the position of the central streamlines was achieved in an iterative process.

Before the main calculation, in order to obtain an approximate pressure field and decrease the time needed to satisfy continuity, the pressure field was predicted in such way, that it linearly decreased form an initial value at the entrance to zero at the exit, and was uniform in the depth and width dimensions. Subsequently, only the z-directional velocity was calculated. The average outlet velocity was compared to the inlet velocity, and the initial value for the pressure drop was corrected by the same factor of proportion. This was repeated until the error between the inlet average velocity and the outlet average velocity was satisfactory. This predicted pressure field was then used for further refinement.

The no-slip boundary condition was used at the walls, which assumes zero velocity of the fluid immediately at the surface. The Neumann boundary condition was used at the microchannel exit, where the velocity profile had already been developed. The two phases came in parallel into the central channel from the inlet channels. The two flows were therefore already developed and of parabolic shape at the entrance into the central channel. The flow fields of the two phases at the entrance were calculated by Eqs. 3–4 and used as the initial Dirichlet condition.

Surface tension effects were not taken under consideration. If surface tension is not sufficiently strong, its effects can be neglected for the simulations of parallel flow, since otherwise it would cause the curving of the interface, which would consequently lead to annular or slug flow. The Young–Laplace equation is:

$$ \Updelta p = \gamma \left( {\frac{1}{{R_{1} }} + \frac{1}{{R_{2} }}} \right) $$

(7)

where R ₁ and R ₂ are the radii of curvature. For very large values of R ₁ and R ₂, where the interfacial surface is almost flat (as is the case with parallel flow), Δp is approximately 0. The assumption of a planar fluid interface formed in steady, converging microchannel flows has already been made by Galambos and Forster (1998) and Hitt and Macken (2004). In this work, the assumption was also made through experimental observation and contact angle measurement.

The finite difference discretization of the first order velocity and pressure derivatives was backward in space, while the first derivatives of the artificial compressibility equation were forward in space. This type of discretization was found to be the most stable for the selected collocated grid. The whole system of mutually dependent equations was transformed into matrix form and was solved with gauss elimination and iterated until the pressure field satisfied the continuity equation. The code was written and simulated with in Matlab. The calculations were computationally intensive due to the large amount of grid points being processed at once, due to the three dimensional nature of the problem. A two-dimensional analysis would not be appropriate since the width to depth aspect ratios (required for parallel flow) are high. Due to the no-slip boundary condition, the parabolic shape of the velocity profile in a two-dimensional space would be formed between the left and right wall. That would only be applicable for a microchannel, which would be (almost) infinitely deep.

3 Results and discussion

The contact angle of water in the water/n-hexane/borosilicate glass system was determined to be 53°. Figure 1b illustrates the accurate representation of the curvature of the interface inside the microchannel, for the case of the microchannel with the smallest width to depth aspect ratio of 4.4. The assumption of a planar interface is presumed to be reasonable since the maximum span of the interface represents only 2.5% of the channel width. For the other two microreactors (width to depth: 8.8 and 10), this value is even lower.

Dimensional analysis of all data for all microreactors showed that the Reynolds numbers ranged from 0.2 to 60, which means that the flow was fully laminar and well below the critical Reynolds number. For such high aspect ratios of the three microreactors’ channels, and for the same smooth microchannels as used in our previous study on laminar to turbulent transition (Pohar and Plazl 2008), we would expect it to be around Re _c = 410. Since the Reynolds numbers were not Re ≪ 1, the simplification of the governing equations to those for Stokes flow would not be appropriate.

It is generally believed that gravity does not influence fluid flow at the microscale. When the interfacial forces dominate over gravity, the Bond number is <1 (Kashid and Kiwi-Minsker 2011). According to Cheng and Wu (2006), the effect of gravity can be neglected when the Bond number is less than 0.05. Hibara et al. (2001) showed that interfacial tension has a much larger effect on the interface than gravity inside microchannels. The Bond numbers in this work were 4.4 × 10⁻⁴ (220 μm × 50 μm channel), 5.3 × 10⁻⁴ (440 μm × 50 μm channel), and 2.2 × 10⁻³ (1000 μm × 100 μm channel), which means that gravity is surpassed by surface tension. The effect of gravity is therefore insignificant for any microreactor or interface orientation.

In the 220 μm × 50 μm Y-shaped microchannel, two flow regimes were observed: slug flow and parallel flow. Figure 2 shows the flow map of n-hexane/water, showing the conditions for the two regimes, along with the conditions for parallel flow, with the interface positioned in the middle of the channel. Parallel flow was also achieved at the flow rates of n-hexane and water of 45 and 36; 50 and 42; and 100 and 80 μl/min (not shown on graph), and these values were also used for the construction of the parallel to slug flow transition line. The determined linear function, indicating the lowest average n-hexane velocity (at the inlet to the central channel) required for parallel flow, as a function of the average inlet velocity of water is: v _h = 0.69·v _w + 0.005 m/s (valid for average water velocities of more than 0.003 m/s). v _h and v _w are the average velocities (in m/s) of n-hexane and water, respectively. Parallel flow with the interface in the middle of the channel was attained at a 1:2.5 water to n-hexane flow rate ratio.

Fig. 2

The flow map of n-hexane/water in the Y-shaped 220 μm × 50 μm rectangular microchannel. The primary axes show the average inlet velocities into the central channel, while the secondary axes show the corresponding flow rates

Due to the complexity of two-phase flow in microchannels, which is influenced by the net result of interactions among surface tension, liquid inertia, and liquid viscous forces, along with wall adhesion effects (contact angle and surface roughness), there are no generic boundaries regarding the dimensionless numbers characterizing fluid flow.

Water wets the glass surface much better than n-hexane so n-hexane is the dispersed phase and as such forms slugs inside the continuous water phase. At water flow rates of 1–4 μl/min, parallel flow was observed at the n-hexane flow rate of 10 μl/min or higher. High n-hexane inertia prevented surface tension from curving the interface and forming slugs, elongating the interface in the flow direction. Kashid et al. (2011) stated that for parallel flow, the shear force is dominant over the surface tension force. The capillary number for n-hexane (calculated using the average velocity of n-hexane) indicating the parallel to slug transition in this region is 1.7 × 10⁻⁴.

At higher water flow rates of more than 4 μl/min, the transition to slug flow is dependent on the velocity ratio between the two phases. Higher flow rates of water require higher flow rates of n-hexane. If the flow rate of water is too high, the shear stress at the interface will contribute to its curving which will, along with the interfacial tension, cause slug flow.

No specific correlation to Weber numbers was found for the parallel to slug flow transition, which is not a direct effect of the flow rate ratio requirement. Parallel flow was achieved at Weber numbers as low as 4.4 × 10⁻⁴ for water and 1.2 × 10⁻³ for n-hexane (calculated from the average velocities of each phase).

For the parallel flow simulations, a grid of 20 × 24 × 30 (depth, width, length) was proven to be satisfactory for the simulations and provided results of high resolution. There was no observed difference in the calculations if the mesh was refined. The solutions of the model were three spatial velocities u, v, and w at each position of the grid and a pressure field. The overall flow field (designated uvw) is a description of the velocity of the fluid at a given position and can be calculated from the three velocity components:

$$ uvw = \sqrt {u^{2} + v^{2} + w^{2} } $$

(8)

After analysis of the experimental interface positions, it was found that they were at equivalent distances for all three microreactors for all flow aspect ratios, so the results were combined. Photos taken under the microscope revealed that steady-state conditions had been met. Highly accurate syringe pumps with stainless steel syringes provided precise, steady flow with no disturbances.

The simulations are presented for the 220 μm wide (W) and 50 μm deep (H) channel. Simulations with the other two microchannel geometries showed identical results with identical interface positions and are therefore not presented. The results of the simulations for the whole length of the channel (3 cm) were stable and showed immediate movement of the interface. The calculations for the entrance region were therefore done to show the movement in detail.

Figures 3, 4, 5, and 6 show the results of the model simulation and the photo taken under the microscope for the water/n-hexane system at identical flow rates of 25 μl/min on each syringe pump. All simulation images, which display the planes inside the microchannel, have the planes positioned at 1/2 depth, 1/4 length, 1/2 length, and 3/4 length, and all images are presented along with the boundary conditions. The simulations were done to the distance of 660 μm (L), which was enough for the flow to stabilize.

Fig. 3

Results of the simulation of the water/n-hexane system at identical flow rates of 25 μl/min for the 220 μm × 50 μm channel. a Velocity fields at the inlet. The left peak is the velocity of water (Re = 5) and the right is the velocity of n-hexane (Re = 12). b The stabilized field further along the microchannel

Fig. 4

Results of the simulation of the water/n-hexane system at identical flow rates of 25 μl/min for the 220 μm × 50 μm channel. The images show the pressure (a) and the v velocity field (b)

Fig. 5

Results of the simulation of the water/n-hexane system at identical flow rates of 25 μl/min for the 220 μm × 50 μm channel. The images show the velocity field, interface position (left) and an experimental photo for comparison (right). Water is left of the interface and n-hexane is on the right

Fig. 6

Results of the simulation of the water/n-hexane system at flow rates of 10 μl/min (water) and 25 μl/min (n-hexane) for the 220 μm × 50 μm channel. a Velocity fields at the inlet. The left peak is the velocity of water (Re = 2) and the right is the velocity of n-hexane (Re = 12). b The stabilized field further along the microchannel

Figure 3 shows the velocity profile immediately at the merging of inlet channels and further along the channel where the flow stabilizes. In Fig. 3a the velocities are the same (this is also the Dirichlet initial boundary condition); due to the movement of the interface to the right, the resulting velocity profile has a high peak at the center of n-hexane flow (on the right side).

The pressure field is presented in Fig. 4a. It can be seen that the pressure drops from some value at the beginning to zero at the end. Higher transverse fluid movements (changing of flow direction) give higher pressure differences at the areas of movement, which can be seen in the image; in the simulations where the movement was more intense this could be even more clearly visible. Apart from the initial transverse pressure variation, the pressure drop is exactly linear in the rest of the channel. In Fig. 4b the v component of the velocity can be seen. At the merging of the channels we can see the movement of the fluid towards the right, towards n-hexane. Further along the channel the flow stabilizes and there is no movement of fluid in this dimension (velocity is zero).

The middle of the two centerline streamlines in Fig. 5a represents the two fluids’ interface. Although the flow rates of the fluids are the same, there is movement of the flow towards the less viscous phase, namely n-hexane. The velocity of n-hexane is therefore adequately higher since the volumetric flow rate stays the same. Figure 5b shows the good agreement with the photo, taken under the microscope.

Figures 6, 7, and 8 show the results for the flow rates set to 10 μl/min (water) and 25 μl/min (n-hexane), giving a fluid flow ratio of 2.5 (n-hexane to water), in an effort to move the interface to the center.

Fig. 7

Results of the simulation of the water/n-hexane system at the flow rates of 10 μl/min (water) and 25 μl/min (n-hexane), for the 220 μm × 50 μm channel. The images show the pressure (a) and the v velocity field (b)

Fig. 8

Results of the simulation of the water/n-hexane system at the flow rates of 10 μl/min (water) and 25 μl/min (n-hexane), for the 220 μm × 50 μm channel. The images show the velocity field, interface position (left) and an experimental photo for comparison (right)

Figure 6a, b shows the velocity profile immediately at the merging of inlet channels and further along the channel where the flow stabilized. In Fig. 6a the much higher velocity of n-hexane entering the channel can be seen. Further along the microchannel (Fig. 6b) the flows merge. The much higher velocity of n-hexane prevents water from expanding into the other half of the channel. The maximum linear velocity slightly decreases, due to the shift towards the center.

In Fig. 7a the pressure field can be seen. Since there is no major movement of the fluid, apart from that to the center, the pressure mostly linearly decreases towards zero at the exit. Figure 7b shows the v velocity component. The picture shows the movement of the fluid to the center, where the velocity was initially zero. The red color represents positive velocity (in the right direction), while the blue color show negative velocity—in the other direction, also towards the center. When the flow stabilizes, there is zero movement in that direction.

The comparison with the experiment is presented in Fig. 8. The interface is present in between the two middle streamlines on the left picture. The 1:2.5 ratio of flow rates positioned the interface in the middle of the channel. The much higher velocity of the n-hexane phase can be observed.

While decreasing the n-hexane/water ratio to less than 2/3 (higher water flow rate), slug flow of n-hexane began since it could not exit the inlet channel until enough pressure built up to force the flow in. The theoretical values for parallel flow were nonetheless calculated. In Fig. 9 the results of all three microreactors are presented, since they yielded equivalent results. At higher n-hexane/water ratios, discrepancies between the model and experimental points can be seen. It seems that the model does not move the position of the phase border as much as water does in reality. It is felt that very drastic conditions (flow ratio of more than 5) are a lot harder to simulate with such a complex set of equations, but could possibly be done with other numerical methods, perhaps the lattice Boltzmann method. Apart from that, the majority of the results showed very good agreement. Comparing the results to the previous work of Žnidaršič-Plazl and Plazl (2009) where the ratio of 1:3 (water to n-hexane) was reported for positioning the interface in the middle with the model, it can be seen that the model and the experimental data also shows good agreement with the ratio of the channel occupied by water being 0.48.

Fig. 9

The ratio of the channel occupied by water in terms of the flow rate ratio (n-hexane to water)

An ionic liquid/n-heptane system was also considered due to the high difference in viscosities of the two liquids. The experiments were done in a previous work (Pohar et al. 2009), where parallel flow with phase separation at the exit of the microreactor was achieved by adjusting the ratio of flow rates of n-heptane and the ionic liquid to 45:1 (45 and 1 μl/min). The ionic liquid used was [bmpyr][dca] with a viscosity of 33.6 mPas, and the viscosity of n-heptane was 0.386 mPas. The developed model successfully predicted the position of the interface, which was reported in the published article, and can be seen in Fig. 10.

Fig. 10

Ionic liquid/n-heptane parallel flow at the 45:1 ratio of flow rates (n-heptane/IL) for a 220 μm × 100 μm channel

The ratio of flow rates, required for positioning the interface in the middle of the channel, as a function of the viscosity ratio is shown in Fig. 11. The flow rate ratio for dodecane/water was experimentally determined to be 0.77 (dodecane to water). Additional values were taken from previous work: 2.1 for ethyl acetate/water (Žnidaršič-Plazl and Plazl 2007) and 45 for [bmpyr][dca]/n-heptane (Pohar et al. 2009). For a 1:1 viscosity ratio, a 1:1 flow rate ratio was used. The inverse values of the flow rate ratios and viscosity ratios were also calculated and plotted in Fig. 11. All experimental values were confirmed with the mathematical model.

Fig. 11

The ratio of flow rates, required for positioning the interface in the middle of the channel, as a function of the viscosity ratio

The proposed correlation for the flow rate ratio required for positioning the interface in the middle of the channel obtained by nonlinear regression analysis:

$$ \frac{{\Phi_{1} }}{{\Phi_{2} }} = \left( {\frac{{\eta_{1} }}{{\eta_{2} }}} \right)^{ - 0.76} $$

(9)

where Φ ₁ is the flow rate of one phase and Φ ₂ is the flow rate of the other phase. The correlation is valid under parallel flow conditions, and is more accurate for lower viscosity ratios.

4 Conclusions

A three dimensional numerical simulation of the position of the interface of two-phase parallel flow inside a microreactor was performed. A nonphysical time dependent term was added to the continuity equation, where time only plays the role of iteration with no physical significance. Fluid properties were adjusted according to the movement of the centerline streamlines in all three dimensions, thus simulating the two fluids. The simulations give a detailed description of the velocity distribution inside the two-phase flow microreactor, and through visualization can give us a better understanding of fluid movement, all of the velocity components and pressure. The developed model is valid for Newtonian incompressible fluids at steady-state, for smooth channel walls, and under parallel flow conditions. The parallel flow conditions for a water/n-hexane system were displayed in Fig. 2 and a correlation for the lowest average n-hexane velocity required for parallel flow, as a function of the average inlet velocity of water was proposed.

Furthermore, a correlation for the flow rate ratio required for positioning the interface in the middle of the channel for various viscosity ratios was proposed.

Channel geometry had no effect on the results with the three microreactor configurations experimented on, which was also proven with the model. This is another reference to the fact that surface tension for the n-hexane water system at parallel flow effects had no significant effect. Gravity had no effect on the microfluidic two-phase flow. No movement of the fluid with the higher density below the lower was noticeable. Simulations at higher length scales clearly showed that particular movement. The position of the interface between two Newtonian fluids was the same with various flow rates, as long as the ratio between then remained constant, which was also noted by Guillot et al. (2008).

In this microfluidic computational fluid dynamics study, the results provided by the numerical simulation for the chosen water/n-hexane two-phase system showed good agreement with the photographs of the position of the two-fluid interface taken under the microscope under parallel flow conditions. Discrepancies were observed at higher n-hexane/water ratios, but high ratios are not preferable for practical work with reactions or extractions and are computationally unstable. The calculations of the velocity field can also be used for the modeling of reaction–diffusion dynamics in a two-phase parallel flow reactor. If the alterations due to the reaction/extraction process would affect the fluids’ properties, the solution could be easily integrated in the iteration process of the model.