1 Introduction

Microfluidic channels are integral components of a Lab-on-a-Chip devices. Transport of biomolecules, particles, or chemicals of interest within these microchannels is an important requirement which has been achieved by several traditional or conventional pumping mechanisms. However, in most of the mechanisms till date, pumping has been actuated by external actuations, which are an additional burden on the system. Most commonly, transport is obtained with pressure-driven flow by actuating a mechanical pump. However, due to large surface forces at micro-scale, a very high pressure drop is required for the transport of the working fluid. Hence, non-mechanical pumping approaches like electrokinetic and electromagnetic pumping have been introduced (Nguyen and Werely 2003; Narayan et al. 2005). Commencement of such flows requires external equipments to actuate electrical and magnetic fields, which in turn requires additional complex fabricating steps for the device. In such cases, external microscopic actuators and connectors with electromechanical interface restrict the flexibility of devices. Moreover, electroviscous effects have to be included with other significant effects (Phan et al. 2009). Attempts are being made to establish flow without any external means, i.e., autonomous flow. The fluid transport can be achieved by controlling channel geometries, surface chemistry, and physical properties of the fluid like surface tension. Such pumping approach is widely termed as autonomous or passive pumping which would be an ideal mechanism of transport for microfluidic devices (Juncker et al. 2002; Zimmermann et al. 2007). As the size of the device decreases, the large surface to volume ratio makes surface forces dominant, particularly the force due to capillarity-induced pressure is very high as compared to other forces (Eijkel and van den Berg 2006). Attempts are also being made to pump the fluid with capillary flow in closed end nanochannels (Radiom et al. 2010; Phan et al. 2010). Hence, the use of surface forces to transport the liquid with capillary action is becoming a popular option in microfluidic devices (Walker and Beebe 2002) and have attracted special attention at micro (Waghmare and Mitra 2010a, b, c), meso (Zhang 2011; Diotallevi et al. 2009), and molecular level (Dimitrov et al. 2007).

Theoretical understanding of capillarity has been conducted over the past century. Through the theoretical investigations, temporal variation in the position of the flow front along the length of the capillary is predicted. The position of the flow front from the capillary inlet is generally termed as penetration depth. Two distinct modeling approaches are reported in the literature. In the first approach, the closed form expression for the transient variation in the penetration depth is proposed which is similar to Washburn approach (Washburn 1921). Whereas, in the second approach, the differential equation in terms of penetration depth is obtained which encompasses all possible forces present during the penetration of the flow front (Levin et al. 1976). The penetration depth with the first approach is predicted without considering the viscous and inertial effects and therefore to include such effects, the second approach has been developed (Levin et al. 1980). Further, the final governing equation for the capillary penetration is obtained by applying differential (Levin et al. 1980) or integral (Dreyer et al. 1993) momentum equation. Washburn (1921) has reported the close form solution for the entrance length, which emphasizes that the steady state velocity assumption is a valid assumption for capillary flow analysis. A microscopic energy balance is used by Newman (1968) and Szekely et al. (1971), as opposed to the quasi-steady state approximation of Washburn (1921) and they have claimed that the Washburn approach (Washburn 1921) can not be used for short capillary transport. Further, Saha and Mitra (2009b) demonstrated numerically and experimentally (Saha et al. 2009) that Washburn prediction deviates for micro-scale geometries. Moreover, Saha and Mitra (2009a) have performed the numerical simulation of capillary filling process in a pillared microfluidic geometry and reported that variation in the capillary filling length does not follow the Washburn equation. Dreyer et al. (1994) have also quantified the capillary flow behavior according to the penetration depth variations with respect to the time. In such analysis, the governing equation for penetration depth is obtained by balancing various forces viz., the entrance pressure force, the surface or the pressure force at the interface, the viscous and the gravity forces with the inertial and transient terms in the momentum equation. The viscous force, inertial, and convective terms in the momentum equation depend on the velocity profile across the channel. Whereas, other forces are function of the fluid properties, as reported in a recent modeling effort (Waghmare and Mitra 2010a, b, c). In such analysis, the velocity dependent terms are determined by assuming a fully developed, i.e., parabolic velocity profile across the channel.

The assumption of the parabolic velocity profile is a valid assumption for steady state conditions. In case of the transient flow, several researchers have used the assumption of parabolic velocity profile (Washburn 1921; Levin et al. 1976, 1980; Dreyer et al. 1993, 1994; Newman 1968; Szekely et al. 1971; Chakraborty 2007) in their analyses. But this assumption is only valid for a high viscous fluid or very low Reynolds number flow which may not be true in all cases (Bhattacharya and Gurung 2010). Hence, it is important to adopt a different approach for capillary flow analysis to rectify this discrepancy. This can be achieved by considering the transient velocity profile derived from transient momentum equation. This transient velocity profile not only satisfies the transient integral momentum equation but also accounts for the time dependent term in the velocity profile. The equation which governs the capillary transport consist of two types of terms: velocity-dependent and velocity-independent terms. The velocity-dependent terms can be determined using transient velocity profile and further transient effects can be analyzed by comparing the results with the steady state velocity profile.

The velocity-independent terms in the momentum equation are force terms except the viscous force viz.; pressure forces at the inlet of the microchannel and at the air-fluid interface. The pressure field at the air–fluid interface can be calculated using Young–Laplace equation. On the other hand, Levin et al. (1976) proposed the pressure field at the inlet of the microchannel, different from the common notation of an atmospheric pressure typically applied at the entrance of the microchannel. In their study, they have proposed the pressure field expression for circular capillary. Several researchers have extended this circular capillary expression for non-circular capillaries with equivalent radius assumption. The equivalent radius assumption may not be applicable for a wide range of microchannel aspect ratios. This literature suggest that there is a lack of a pressure field expression for rectangular microchannels, which is a more common geometry based on microfabrication techniques for microfluidic devices. The authors have attempted to propose a pressure field expression at the entrance of a parallel plate arrangement (Waghmare and Mitra 2010a, b, c). The pressure field expression is developed by assuming the length of the plate is much longer than the gap between two plates, but in microfluidics applications such assumption may not be universally valid. Further, the capillary transport analysis with such modified pressure field for a rectangular microchannel is also not available in the literature. Therefore, it is necessary to determine the appropriate pressure field at the entrance of the rectangular microchannel and the effect of such pressure field expression on the capillary flow analysis needs to be studied, which is performed in the later part of this study.

A generalized non-dimensional equation for capillary transport can be obtained by calculating the velocity dependent and independent, i.e., appropriate force terms. In the upcoming section, the theoretical model for capillary transport with transient velocity profile is presented. Further, a generalized non-dimensional equation with steady state and transient velocity profiles is derived and solved numerically to investigate the effect of transient velocity profile. An appropriate pressure field expression at the entrance of the rectangular microchannel is also derived in the later part of this study. Finally, the effect of such pressure field on the capillary transport is also analyzed. Hence, the analysis presented here is a comprehensive one, which provides a greater understanding of capillary transport in rectangular microchannels.

2 Mathematical modeling

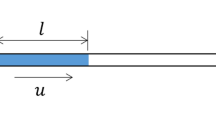
In most of the capillary flow analysis, the integral momentum equation for deformable fluid control volume along the microchannel is used (Levin et al. 1976, 1980; Dreyer et al. 1993, 1994). The integral momentum equation for the fluid transport in the microchannel of width 2B and depth 2W, as shown in Fig 1, can be written as,

$$ \sum F_{z}=\frac{\partial}{\partial t}\int\limits_{0}^{h}\int\limits_{-W}^{W}\int\limits_{-B}^{B}{\rho v_{z} {\rm d}x{\rm d}y{\rm d}z}+\int\limits_{-W}^{W}\int\limits_{-B}^{B}{{v_{z}}(-\rho v_{z}){\rm d}x{\rm d}y} $$
(1)
Fig. 1
figure 1

Schematic of microchannel of width 2B and depth 2W considered for the theoretical modeling of capillary transport

Full size image

Here, ρ is the density of the fluid, v z is the velocity of the capillary across the channel, and h is the penetration depth or movement of the fluid flow front in the capillary. This momentum equation governs the transient response of the capillary front movement along z-axis, which is termed as penetration depth in this analysis. Here, ∑F z is the summation of all forces acting on the fluid under consideration viz., viscous \((F_{\rm v}),\) gravity \((F_{\rm g} =4\rho ghBW),\) pressure forces at the flow front \((F_{\rm {pf}})\), and at the inlet \((F_{\rm {pi}}),\) as illustrated here:

$$ \sum F_{z}={\underbrace{F_{\rm v}}_{\rm{velocity\,dependent}}} +{\underbrace{F_{\rm g}+F_{\rm {pf}}+F_{\rm {pi}}}_{\rm {velocity\,independent}}} $$
(2)

Transient and convective terms in Eq. 1 and the viscous force term in Eq. 2 can be determined by using the velocity profile, v z across the channel. For simplicity, fully developed Poiseuille flow is assumed in the literature (Washburn 1921; Levin et al. 1976, 1980; Dreyer et al. 1993, 1994; Newman 1968; Szekely et al. 1971; Chakraborty 2007; Waghmare and Mitra 2010a, b, c), neglecting the change in the velocity profile at the entrance region and at the flow front. This introduces an inconsistency due to the fact that the fully developed velocity profile assumption is valid only for steady flow systems (Bhattacharya and Gurung 2010). Thus, a developing, i.e., transient velocity profile instead of a developed velocity profile needs to be considered for the analysis. This can be achieved by considering the transient momentum equation in the direction of the flow with pressure drop \({\rm d}p/{\rm d}z\) as depicted here,

$$ \rho\frac{\partial v_{z}}{\partial t}=\mu\frac{\partial^{2} v_{z}}{\partial x^2}+\frac{{\rm d}p}{{\rm d}z} $$
(3)

where μ is the viscosity of the fluid. The velocity in Eq. 3 can be decoupled in the following manner (Keh and Tseng 2001),

$$ v_{z}(x,t)={v_{z}}_\infty(x)+{v_{z}}_t(x,t)$$
(4)

here, \({v_{z}}_\infty(x)\) is the velocity field at steady state, which can be written as (White 2006),

$$ {v_{z}}_\infty(x)=\frac{B^2}{2\mu}\frac{{\rm d}p}{{\rm d}z}\left[1-\left(\frac{x}{B}\right)^{2}\right] $$
(5)

The transient component of the velocity can be obtained from following equation using boundary conditions of no slip and maximum velocity at wall and center, respectively with zero velocity as an initial condition (Keh and Tseng 2001),

$$ \rho \frac{\partial {v_{z}}_{t}}{\partial t}=\mu \frac{\partial^{2} {v_{z}}_{t}}{\partial x^{2}} $$
(6)

The method of separation of variable is used to obtain the solution of Eq. 6 and is given as,

$$ {v_{z}}_{t}(x,t)=2\sum\limits_{n=1}^{\infty}(-1)^{n}\left[\frac{1}{B\mu\lambda_{n}^{3}}\frac{{\rm d}p}{{\rm d}z} \right]\cos(\lambda_{n} x) \exp(-\nu \lambda_{n}^{2}t) $$
(7)

where \(\lambda_{n}=\frac{(2n-1)\pi}{2B}\) and ν is the kinematic viscosity of the fluid. Hence, the transient fluid velocity profile v z (x, t) can be obtained by combining Eqs. 5 and 7.

$$ {v_{z}}(x,t)= \left\{\sum_{n=1}^{\infty}(-1)^n\frac{1}{B\mu}\left(\frac{2}{\lambda_n^3}\right)\cos(\lambda_{n} x) \exp(-\nu \lambda_{n}^{2} t) +\frac{1}{2\mu}\left(B^{2}-x^{2}\right)\right\}\frac{{\rm d}p}{{\rm d}z} $$
(8)

The average velocity across the channel can be expressed as,

$${v_{z}}(t)_{\rm {avg}}=\frac{B^{2}}{3\mu}{\left[1-\sum_{n=1}^{\infty}\frac{96}{(2n-1)^{4}\pi^{4}} \exp\left[-\frac{(2n-1)^{2}\pi^{2} \nu t }{4B^{2}}\right]\right]}\frac{{\rm d}p}{{\rm d}z} $$
(9)

As done for other capillary flow models (Newman 1968), the pressure drop term in Eq. 8 is replaced by the average velocity so that the velocity profile is obtained in terms of the penetration depth,

$$ \begin{aligned}{v_{z}}(x,t) = \frac{B^{2}}{2\mu}\alpha_{1}\left\{\sum\limits_{n=1}^{\infty}(-1)^{n}\left[\frac{4}{(B\lambda_{n})^{3}}\right]\cos(\lambda_{n} x)\exp(-\nu \lambda_{n}^{2}t)+\left(1-\frac{x^2}{B^2}\right)\right\}\times \left\{\frac{1}{\alpha_{1}{\left[1-\sum_{n=1}^{\infty}\beta_{1}\exp\left(-\lambda_{n}^{2} \nu t \right)\right]}}\right\}\frac{{\rm d}h}{{\rm d}t}\\ \end{aligned} $$
(10)

where

$$ \alpha_{1}=\frac{\left[{\left(\phi\right)^{4}-4\exp{-\frac{\phi^{2}t}{3}}}\right]} {\left[{\left(\phi\right)^{4}-6\exp{-\frac{\phi^{2}t}{3}}}\right]}$$
(11)

and ϕ = λ n B. The velocity dependent terms of the governing equation for capillary transport can be derived with transient velocity profile provided in Eq. 11. Pressure forces at the fluid-air interface within the microchannel and at the inlet of the microchannels can be determined by using respective pressure field distributions at the interface and at the inlet of microchannel. Young–Laplace equation (Washburn 1921) with the fluid surface tension, σ and equilibrium angle, θ is used to determine the pressure at the interface. The radii of curvature for Young–Laplace equation are as \(B/\cos\theta\) and W, respectively. The concept of pressure force at the entrance of the capillary was first proposed by Levin et al. (1976). However, they have reported the pressure field expression at the entrance of circular capillaries and several researcher have extended this circular capillary expression to parallel plate configuration with a simplified assumption. For parallel plate configuration, the pressure field is investigated by assuming a hemispherical control volume and the radius of the hemisphere is determined from the projected cross sectional area at the capillary entrance. The derived pressure field in such case, as used by several other researchers for rectangular capillaries like flow of liquid coolant (Dreyer et al. 1994), alcohol (Xiao et al. 2006), nanoparticulate slurry (Marwadi et al. 2008), and blood (Chakraborty 2007), can be written as,

$$ p(o,t)= p_{\rm {atm}}- \left\{ 1.11\rho \sqrt{BW} \frac{{\rm d}^2h}{{\rm d}t^2} +1.58 \rho \left(\frac{{\rm d}h}{{\rm d}t}\right)^{2}+\frac{1.772\mu}{\sqrt{BW}}\frac{{\rm d}h}{{\rm d}t}\right\} $$
(12)

To emphasize and analyze the effect of transient velocity profile, in this part of analysis the pressure field expression from existing literature (i.e., Eq. 12) is used to determine the pressure force at the entrance of the microchannel. An appropriate pressure field expression for rectangular microchannel and the importance of such accurate pressure field expression are presented in the later part of this study. Finally, one can rewrite the momentum equation Eq. 1 incorporating the relevant forces, transient and convective terms, where the transient velocity profile is used for calculating the velocity dependent terms. Further, the non-dimensional analysis is performed which results in a generalized non-dimensional governing equation for capillary flow in microchannel which can be written as (Waghmare and Mitra 2010a, b, c),

$$ (h^{*}+C_{1})\frac{{\rm d}^{2}h^{*}}{{{\rm d}t^{*}}^{2}}+C_{2}\left(\frac{{\rm d}h^{*}}{{\rm d}t^{*}}\right)^{2} +\left(C_{3}+C_{4}h^{*}\right)\frac{{\rm d}h^{*}}{{\rm d}t^{*}}+C_{5}h^{*}+C_{6}=0 $$
(13)

The non-dimensional time (t *) and the penetration depth(h *) which are defined with respect to the characteristic time, \(t_{0}=\frac{\rho\left(2B \right)^{2}}{12\mu}\) and the characteristic length h 0 = 2B, respectively. Table 1 depicts the different constants of Eq. 13 for an evolving capillary transport. All coefficients are the function of the velocity profile. In non-dimensional analysis, two non-dimensional numbers are obtained, i.e., Bond number (Bo) and Ohnesorge number (Oh). The Ohnesorge number \(\left({\rm {Oh}}=\frac{\mu}{\sqrt{2B\rho\sigma}}\right)\) represents the ratio of viscous to surface tension force, the Bond number \(\left( {\rm {Bo}}=\frac{\rho g (2B^{2})}{\sigma}\right)\) dictates the ratio of gravity to surface tension force and another non-dimensional parameter, i.e., γ (=B/W) is the aspect ratio of the microchannel, defined as the ratio of width to depth of the microchannel.

Table 1 Constants of the generalized non-dimensional governing equation for a capillary flow in a rectangular microchannel with a developing velocity profile
Full size table

3 Effect of developing velocity profile in capillary transport

It is important to analyze the importance of such transience in velocity during the capillary transport. The variation in the penetration depth with the steady sate and unsteady state velocity profile are presented in Figs. 2 and 3. The bottom left inset of Fig. 2 shows penetration depth variations at the beginning of the transport and the attainment of the equilibrium penetration depth is shown in the upper right inset. The equilibrium penetration depth is the length along the microchannel for which the flow front attains a zero velocity. In this analysis, the development of velocity profile from unsteady to steady state is accounted with a developing, i.e., transient velocity profile. At the beginning of the channel filling process, the velocity is undeveloped, therefore, the magnitude of the penetration depth is smaller than the penetration depth with the developed velocity profile. The lower bottom inset of Fig. 2 suggests that within the first 10 ms, there is a difference of 5 mm in the penetration depth, which has important implications in terms of controlling chemical reactions, antigen-antibody binding, and other bio-MEMS applications. As the flow front approaches toward the equilibrium penetration depth, the transient velocity profile attains the steady state and the quantitative difference in the penetration depth is negligible as depicted in the upper right inset of the Fig. 2.

Fig. 2
figure 2

Transient response of penetration depth with fully developed (steady state) and developing (unsteady) velocity profile. The corresponding dimensional time and penetration depth are presented on the top and left axis, respectively. The bottom left inset shows the enlarge view of the penetration depth variations at the beginning of the transport and the variations in the penetration depth during the attainment of the equilibrium penetration depth is presented in the upper right inset

Full size image
Fig. 3
figure 3

Transient response in the difference in the penetration depths with fully developed (steady state) and developing (unsteady) velocity profile under different conditions. a Penetration depth variations for fluid with Bo = 0.01 and b Oh = 0.05

Full size image

The effect of transient velocity profile with the change in the fluid properties is depicted in Fig. 3. For a highly dense and viscous fluid, the effect of transience in the velocity profile is qualitatively same as observed in the previous case. Figure 3a shows the penetration depth variation with highly dense (Bo = 0.01) fluid whereas, similar variations are observed for highly viscous fluid in Fig. 3b. The inset of both the figures shows the enlarged views of the penetration depths with two velocity profiles. The equilibrium penetration depth with a high density fluid is smaller than penetration depth with high viscous fluid. In case of high viscous fluid, a longer time is required to attain the same equilibrium penetration as compared to the case shown in Fig. 2. It is important to quantify the difference in penetration depths, even though it may seem to be small, due to the transience in the velocity profiles. Therefore, the difference in the penetration depths with developed and developing velocity profiles for the same time instant is calculated and the percentage change in the penetration depth is presented in Fig. 4. In this particular case study, the comparison in penetration depths of previous three cases (Figs. 2, 3) is presented. The enlarged view in the inset shows that the penetration depth with transient velocity profile deviates up to 16% from the penetration depth value with steady state velocity profile. The boundary layer formation is the effect of no slip at the wall which propagates across the channel and the rate of propagation is decided by the physical properties of fluid, particularly the fluid viscosity. As the viscosity of fluid increases, the boundary layer thickness also increases, which results in the retardation of flow within the boundary layer. The density has an opposite effect (Schlichting 1968). It is observed that for a high viscosity fluid, the percentage difference in the penetration depth is lower (8%) as compared to the difference with high density fluid (16%). Thus, it can be concluded that the fully developed velocity profile assumption needs to be used carefully in the capillary analysis. It is stated in the literature that (Bhattacharya and Gurung 2010), the approximation of steady state velocity is a valid assumption for low Reynolds number flows like a creeping flow. Also literature suggests that the surface driven flow can be considered as a creeping flow and hence the simplified fully developed velocity profile can describe the velocity field across the microchannel in case of a capillary transport. Here, the quantified difference in penetration depth due to such assumption is presented and observed that at the beginning of the capillary transport the transience in the velocity plays a significant role. At micro-scale, such effects need to be considered carefully before designing microfluidic devices particularly for devices, with capillary transport.

Fig. 4
figure 4

Transient response in the difference in the penetration depths with fully developed (steady state) and developing (unsteady) velocity profile under different conditions

Full size image

As mentioned earlier, apart from the velocity profile across the microchannel, the pressure field at the inlet of the microchannel is another aspect, which has been considered with some degree of approximation in the existing literature. It is necessary to derive the appropriate pressure field at the entrance of a rectangular microchannel. Therefore, in the next section, the pressure field for a rectangular microchannel is derived. Moreover, the penetration depth with the proposed and approximated pressure field from literature is compared to analyze the importance of the proposed pressure field.

4 Pressure field at the entrance of the microchannel

As explained in Sect. 2 , the force at the capillary entrance is calculated using the pressure field at the entrance of the capillary. Levin et al. (1976) reported that the pressure at the entrance of the microchannel is different than the atmospheric pressure. A separate control volume, as shown in Fig. 5, at the entrance of the capillary, in addition to the deformable control volume along the microchannel, has been considered for the derivation of the pressure field. A well defined control volume at the entrance, such as a hemispherical fluid volume shown in Fig. 5a, within a large volume of a fluid in contact with capillary is responsible for defining the pressure field at the inlet. For a circular capillary, Levin et al. (1976) has taken a hemispherical control volume of radius equal to that of the capillary. The velocity components in the hemispherical control volumes are determined and further the momentum balance to the fluid flow in the control volume is applied to calculate the pressure field.

Fig. 5
figure 5

The fluid volume from infinite reservoir considered as control volume for pressure field expression analysis. a The control volume considered for circular capillary, b the appropriate control volume for parallel plate arrangement and for rectangular microchannel, and c the appropriate control volume. Arrow shows the direction of the fluid flow from the reservoir into the microchannel

Full size image

The classical expression proposed for circular capillary has been extended by several researchers for capillaries of different geometries like, parallel plates (Dreyer et al. 1993). In parallel plate arrangement, a hemispherical control volume in the reservoir is assumed, as done by Levin et al. (1976). The radius of this hemisphere is calculated by equating the projected area of hemisphere to the cross sectional area at the entrance of the parallel plates (Dreyer et al. 1993). Several other researchers have adopted this concept of equivalent radius and performed the capillary flow analysis in rectangular microchannels (Dreyer et al. 1994; Xiao et al. 2006; Marwadi et al. 2008; Chakraborty 2007). The concept of equivalent radius with an assumption of hemispherical control volume is not a realistic representation of the entrance region in non-circular geometries. For high aspect ratio channels (width < < depth), the region for the fluid volume or the appropriate control volume for the analysis can not be considered as a hemisphere. For non-circular geometries, e.g., rectangular microchannels, a separate shape for the control volume needs to be considered. For the parallel plate arrangement, authors have earlier derived the pressure field expression which only depends on the gap between the two plates and is independent of the depth of the plates (Waghmare and Mitra 2010a, b, c). It is necessary to derive the appropriate expression for pressure field with an appropriate control volume at the entrance of non-circular microchannels. In the upcoming section, the appropriate control volume is considered and the pressure field at the entrance of non-circular microchannel is derived.

4.1 Pressure field at the entrance of non-circular microchannels

Figure 5 shows a representative control volume for different capillary geometries (circular, parallel plate, and rectangular), which acts as a fluid source mimicking a sink flow at the microchannel entrance. Further, the same control volume is used for the derivation of the entrance pressure field expression. In the literature, for a circular capillary a hemispherical control volume is assumed (Levin et al. 1976), and for parallel plate arrangements, the semicylindrical control volume is considered (Waghmare and Mitra 2010a, b, c), as shown in Fig. 5a and b, respectively. It is also assumed that the control volume at the entrance of capillary aligns with the microchannel at the entrance. In case of rectangular microchannels, neither the hemispherical nor the semicylindrical control volume is an appropriate control volume for the analysis. The hemispherical control volume represents the axi-symmetric sink flow at the entrance whereas, in case of semicylindrical shape (Fig. 5b), the flow along the length of a semicylinder is considered. Further, in case of a semicylindrical control volume, the fluid volume contained at the two ends of the semicircular cylinder is neglected. This might be a valid assumption for very high aspect ratio microchannels, where the microchannel can be treated as parallel plates for the analysis. But for moderate aspect ratio microchannels, like rectangular microchannels, which are generally used in microfluidic applications, the fluid volumes at the two ends of the semicircular cylinder need to be incorporated. Hence, it is necessary to consider a different shape for the control volume representing rectangular microchannels. Therefore, to account such effects, the combination of the cylindrical and the spherical control volumes, as depicted in Fig. 5c, is considered as an appropriate control volume for the analysis. For the rectangular microchannel of aspect ratio γ, which is the ratio of width to depth of the microchannel, the control volume shown in Fig. 5c is an appropriate control volume. A cylindrical and a spherical co-ordinate system with origin O c and O s, respectively, are considered for cylindrical and spherical regions. One can determine the radial velocity in the corresponding regions by applying the continuity equation to the control volumes. The origin O c of cylindrical region coincides with the origin of the microchannel at the inlet plane. It is assumed that v r is the radial velocity components for both the coordinates.

As mentioned earlier, \(\frac{{\rm d}h}{{\rm d}t}\) is the penetration rate along the microchannel. The flux of volume in the direction of the capillary flow from the reservoir can be calculated using continuity equation as follow,

$$ v_{\rm {rc}} r_{\rm c}\pi l_{\rm c}+2\pi {v_{\rm r}}_{\rm s} r_{\rm s}^{2}=-4BW\frac{{\rm d}h}{{\rm d}t} $$
(14)

Here, l c represents the length of cylindrical control volume. In this analysis, the subscripts c and s are used to represent the cylindrical and spherical regions. From Eq. 14, one can deduce the radial velocity component from cylindrical and spherical regions as,

$$ {v_{\rm r}}_{\rm s}=-\frac{2BW}{\pi r_{\rm s}^{2}}\frac{{\rm d}h}{{\rm d}t}-\frac{{v_{\rm r}}_{\rm c} r_{\rm c} l_{\rm c}}{2r_{\rm s}^{2}} $$
(15)
$$ {v_{\rm r}}_{\rm c}=-\frac{4BW}{\pi r_{\rm c} l_{\rm c}}\frac{{\rm d}h}{{\rm d}t}-\frac{2{v_{\rm r}}_{\rm s} r_{\rm s}^{2}}{r_{\rm c} l_{\rm c}} $$
(16)

Now, the pressure field in the radial direction can be determined using the momentum equation in the radial direction. The momentum equation can be written as,

$$ \rho \left\{ \frac{\partial {v_{\rm r}}_{\rm c}}{\partial t} \right\} =-\frac{\partial p}{\partial r_{\rm c}}+\mu\left\{\frac{\partial }{\partial r_{\rm c}}\left(\frac{1}{r_{\rm c}}\frac{\partial}{\partial r_{\rm c}}\left[r_{\rm c} v_{r_{\rm c}}\right] \right) \right\} .$$
(17)

Using Eq. 16, the pressure field in the cylindrical region of the control volume can be expressed as,

$$ p(r_{\rm c},t)=p_{\rm {atm}}-\frac{4\rho B W}{\pi l_{\rm c}}\left(\ln \frac{r_{\infty}}{r_{\rm c}}\right)\frac{{\rm d}^{2}h}{{\rm d}t^{2}} $$
(18)

Here, \(r_{\infty}\) is the radial distance far away from the inlet of the microchannel outside the cylindrical region where, the pressure p(r c, t) approaches to atmospheric pressure p atm and capillary force becomes negligible. Following the same approach, the pressure field for the two end regions, i.e., for the spherical domain is given by,

$$ p(r_{\rm s},t)=p_{\rm {atm}}-\frac{2BW\rho}{\pi r_{\rm s}}\frac{{\rm d}^{2}h}{{\rm d}t^{2}} $$
(19)

The velocity field within the control volume is unknown which is necessary to determine the pressure field at the entrance of the microchannel. Such velocity field can be computed by considering the momentum balance which suggests that the rate of change of total momentum in the control volume is equal to the combination of the net momentum flux and forces acting on the surface of the control volume.

Two major forces are acting on the control volume shown in Fig. 5c; the first one is along the surface of the entire control volume and another one is at the inlet of the microchannel. These forces are determined by calculating the momentum flux and rate of change of momentum within the control volume. Forces acting along the surface at r c = B and r s = B in the direction of capillary flow can be determined by using the stress tensor in the radial direction. The forces on both the surfaces are calculated separately. Using Eqs. 16 and 18, the stress tensor along the surface of cylindrical region in the radial direction is,

$$ \sigma_{r_{\rm c},r_{\rm c}}|_{r_{\rm c}=B} =-p_{\rm {atm}}+\frac{2\rho B }{\pi (1-\gamma) }\left(\ln \frac{R_{\infty}}{B}\right)\frac{{\rm d}^{2}h}{{\rm d}t^{2}}+\frac{4\mu}{\pi B }\frac{{\rm d}h}{{\rm d}t} $$
(20)

Similarly, using Eqs. 15 and 19, the stress tensor for the spherical region is

$$ \sigma_{r_{\rm s},r_{\rm s}}|_{r_{\rm s}=B} =-p_{\rm {atm}}+\frac{2\rho W}{\pi }\frac{{\rm d}^{2}h}{{\rm d}t^{2}}+\left(\frac{8\mu}{\pi B}\right)\frac{(2-\gamma)}{\gamma }\frac{{\rm d}h}{{\rm d}t} $$
(21)

From Eqs. 20 and 21, the total force acting on the surface of the control volume in the direction of the capillary transport is

$$ \begin{aligned} F_{r=B} = \left[2\pi B^{2}+ 4 BW(1-\gamma)\right]p_{0} -4\rho B^{2} W\left[1-\frac{2 }{\pi} \ln \frac{R_\infty}{B} \right] \frac{{\rm d}^{2}h}{{\rm d}t^{2}} -16\mu W\left[ (2-\gamma)+\frac{(1-\gamma) }{\pi} \right]\frac{{\rm d}h}{{\rm d}t} \end{aligned} $$
(22)

The other force acting in the direction of the capillary transport from the same control volume is the force at the inlet of the microchannel, i.e., at the plane z = 0. This can be calculated as,

$$ F_{z=0}=-\int\limits_{-W}^{W}\int\limits_{-B}^{B}p(0,t){\rm d}x{\rm d}y $$
(23)

The total rate of change of momentum within the control volume can be calculated with the instantaneous acceleration within the system. It is difficult to determine the instantaneous acceleration within the system, therefore, the mean of accelerations at the curvature of control volume and at the inlet of the microchannel are calculated.

The rate of change of momentum is the product of the mass of the control volume and the total acceleration across the control volume (Levin et al. 1976). The total acceleration can be determined by calculating the acceleration flux within the control volume and the volume flux along the microchannel.

The total acceleration flux at r = B is,

$$ 4BW\frac{{\rm d}h}{{\rm d}t} \left\{ \left[\frac{1}{\pi}+\frac{4}{\pi^{2}} \right]\frac{{\rm d}^{2}h}{{\rm d}t^{2}} +\left[\frac{4(2-\gamma)}{B\pi^{2}} -\frac{8(1-\gamma)}{\pi^{3} \gamma W} \right]\left(\frac{{\rm d}h}{{\rm d}t}\right)^{2}\right\} $$
(24)

which is the combination of acceleration flux at r c = B and r s = B. The volume flux along the rectangular microchannel can be given as, \(4BW\frac{{\rm d}h}{{\rm d}t}.\)

Using the expression Eq. 24 and in conjunction with the volume flux along the rectangular microchannel, the mean acceleration at r = B can be written as,

$$ a_{{\rm {mean}}_{r=B}}= \left[\frac{1}{\pi}+\frac{4}{\pi^{2}} \right]\frac{{\rm d}^{2}h}{{\rm d}t^{2}} +\left[\frac{4(2-\gamma)}{B\pi^{2}} -\frac{8(1-\gamma)}{\pi^{3} \gamma W} \right]\left(\frac{{\rm d}h}{{\rm d}t}\right)^{2} $$
(25)

Similarly, the mean acceleration at the entrance of the microchannel is (Levin et al. 1976),

$$ a_{{\rm {mean}}_{z=0}}= \frac{6}{5}\frac{{\rm d}^{2}h}{{\rm d}t^{2}} $$
(26)

The mean acceleration of the control volume can be determined by the calculating the average of the mean accelerations over r = B and z = 0. Therefore, the rate of change of total momentum can be expressed as,

$$ 2\pi \rho B^{2}W\left[\frac{2\gamma+6 (\gamma-1)}{3}\right]\left\{\left[\frac{1}{2\pi}+\frac{1}{\pi^2}+\frac{6}{5} \right]\frac{{\rm d}^2h}{{\rm d}t^2} +\left[\frac{4(2-\gamma)}{B\pi^2 } +\frac{4 (1-\gamma)}{\pi^{3} \gamma W} \right]\left(\frac{{\rm d}h}{{\rm d}t}\right)^{2} \right\} $$
(27)

One also needs to find out the total momentum flux across the surface of the control volume. The momentum flux across the curvature is the combination of the flux across the cylindrical and the spherical regions, which can be written as:

$$ {\dot{M}}_{r=B}=\frac{4\rho B^{2}}{\pi} \left[1+\frac{4(1-\gamma)}{\gamma \pi}\right]\left(\frac{{\rm d}h}{{\rm d}t}\right)^{2} $$
(28)

Equation 28 shows the momentum flux across the curvature. The momentum flux at the microchannel entrance (z = 0) is given by (Levin et al. 1976),

$${\dot{M}}_{z=0}=\frac{24\rho B W}{5}\left(\frac{{\rm d}h}{{\rm d}t}\right)^{2} $$
(29)

Finally, one can write the momentum balance for the control volume using Eqs. 22, 23, 25, 27–29 and by rearranging the terms, the pressure field expression for rectangular microchannel is

$$ \begin{aligned} p(0,t) =p_{\rm{atm}} -\rho B \left\{\left[\frac{4\gamma+3 (1-\gamma)}{24}\right] \left\{ \pi\left[\frac{1}{2\pi}+\frac{2 }{\pi^{2}} +\frac{6}{10}\right]\right\} +\left[1-\frac{2 }{\pi} \ln \frac{R_\infty}{B} \right] \right\}\frac{{\rm d}^{2}h}{{\rm d}t^{2}} +\rho\left\{\left[\frac{4(1-\gamma)}{\pi^2} -\frac{6}{5}\right] -\left[\frac{4\gamma+3 (1-\gamma)}{6}\right] \left[\frac{(2-\gamma)}{2\pi} -\frac{ (1-\gamma)}{\pi^2} \right]\right\}\left(\frac{{\rm d}h}{{\rm d}t}\right)^{2}-\frac{4\mu} {B}\left[ (2-\gamma)+\frac{(1-\gamma) }{\pi} \right]\frac{{\rm d}h}{{\rm d}t}\\ \end{aligned} $$
(30)

In Eq. 30 by substituting γ = 1, one can readily find the pressure field at the inlet of a square capillary, which can be written as,

$$ p(0,t) =p_{\rm{atm}} -\rho B \left\{ \frac{13}{12}+\frac{1}{3\pi} +\frac{\pi}{10}\right\} \frac{{\rm d}^{2}h}{{\rm d}t^{2}} -\rho\left\{\frac{6}{5} +\frac{1}{3\pi} \right\}\left(\frac{{\rm d}h}{{\rm d}t}\right)^{2} -\frac{4\mu} {B}\frac{{\rm d}h}{{\rm d}t} $$
(31)

Another limiting case is when the length of the channel is very large compare to its width, i.e., \(\gamma \rightarrow 0, \) for which the pressure field can be written as,

$$ \begin{aligned} p(0,t)&= p_{\rm{atm}} -\left\{\frac{1}{4\pi} +\frac{3\pi}{40}-\frac{15}{16}+\frac{2}{\pi} \ln \frac{R_\infty}{B} \right\} \frac{{\rm d}^{2}h}{{\rm d}t^{2}}\\ &\quad-\rho\left\{\frac{9}{2\pi^{2}} -\frac{6}{5} -\frac{1}{2\pi} \right\} \left(\frac{{\rm d}h}{{\rm d}t}\right)^2 -4\left[ 2+\frac{1}{\pi} \right]\frac{\mu}{B}\frac{{\rm d}h}{{\rm d}t} \end{aligned} $$
(32)

One can re-derive the governing equation Eq. 13 with the proposed pressure field as presented in Eq. 30 instead of Eq. 12. It is necessary to perform the analysis to understand the effect of pressure field on the capillary transport. Therefore, in the upcoming section the penetration depth with the pressure field from the literature is compared with the penetration depth calculated using the proposed pressure field.

5 Effect of appropriate pressure field in the capillary transport

Figure 6 shows the variation in the penetration depth with the pressure field from the literature and with the newly proposed pressure field expression. As mentioned earlier, the pressure field expression for rectangular microchannel from literature has been extended from circular capillary expression with an equivalent radius assumption. Hence in Fig. 5c, the penetration depth obtained using the pressure field from the literature is labeled as the pressure field with equivalent radius. For higher aspect ratio microchannels, the length of the cylindrical region (Fig. 5c) is much longer than the radius of the spherical region, therefore, the fluid volume entering through the spherical region is negligible as compared to the fluid volume entering through the cylindrical region.

Fig. 6
figure 6

The comparison of variations in the penetration depth with equivalent radius and with recently proposed pressure field expressions. a shows the comparison of penetration depth for γ = 0.05 with the corresponding difference in the penetration depth where b shows the comparison for γ  = 0.9

Full size image

Figure 6a shows the variations in the penetration depths for γ = 0.05 which represents the microchannel of very small width as compared to its depth. For such arrangements, it is observed that there is a negligible difference between the penetration depths with two different pressure fields. In such cases, the flow from cylindrical region of control volume plays significant role compared to the flow from the spherical region of the control volume, therefore, the difference in the penetration depth is negligible. In case of lower aspect ratio microchannels, where the width is comparable with the depth of microchannel, the fluid volume entering from the ends of semicylindrical volumes, i.e., from the spherical regions along with that from cylindrical region can not be neglected. The penetration depth under such condition is depicted in Fig. 6b. The penetration depth with proposed pressure field is significantly different than the penetration depth with pressure field from the literature. During the filling of the microchannel, the magnitude of the penetration depth with the proposed pressure field is less than the penetration depth with the pressure field from literature for the same time instant, which can be attributed to the additional fluid mass from the spherical regions. It is observed that pressure field from the literature over predicts the penetration depth. Thus, the proposed pressure field expression is an appropriate pressure field expression for the analysis of capillary flow in rectangular microchannel, which is applicable for a wide range of aspect ratios of the microchannel.

6 Conclusion

In traditional capillary flow analysis, the velocity across the microchannel and the pressure field at the microchannel entrance are considered with the simplified assumptions. In this study, these assumptions are revisited and modifications in these assumptions are presented. Initially, the analysis emphasize on the nature of the velocity profile across the microchannel. For inherently transient capillary flow analysis, the steady state velocity profile is used in the literature. In this study, the transient developing velocity profile instead of fully developed velocity profile is used to investigate the effect of transience in the velocity profile. The non-dimensional governing equation for penetration depth, i.e., flow front movement along the microchannel due to capillary with the transient velocity profile is derived. Further, the penetration depth with the proposed velocity profile is compared with the penetration depth for steady state velocity profile. While deriving the governing equation, different forces like, gravity, viscous, and pressure forces acting on the fluid volume are considered. In general, the pressure force acting at the entrance of the microchannel is deduced from the pressure field expression at the microchannel inlet. In the past studies, for rectangular microchannels, the circular capillary expression is adopted with an equivalent radius assumption. This assumption may not be valid for all cases. An appropriate pressure field for rectangular microchannels is proposed and compared with the pressure field from literature. From the theoretical analysis following important conclusions can be made:

  • In capillary flow analysis, transience in the velocity profile need to be considered at the beginning of the transport. The difference in the penetration depth is observed at the beginning of the filling process whereas, this difference is negligible as flow becomes developed or steady state flow.

  • For a high density and viscous fluid, transient effect is observed at the beginning of the filling of the microchannel.

  • Transience effect is more for high density fluid than high viscosity fluid.

  • The flow front progression with the proposed pressure field is slower than the flow front progression with the approximated pressure field from the literature.

  • For lower aspect ratio microchannels, where typically the rectangular microchannel geometries approaches toward the square microchannel, it is important to consider the proposed pressure field.