Output pressure and efficiency of electrokinetic pumping of non-Newtonian fluids

Abstract

Theoretical expressions of the flow rate, output pressure and thermodynamic efficiency of electrokinetic pumping of non-Newtonian fluids through cylindrical and slit microchannels are reported. Calculations are carried out in the framework of continuum fluid mechanics. The constitutive model of Ostwald-de Waele (power law) is used to express the fluid shear stress in terms of the velocity gradient. The resulting equations of flow rate and electric current are nonlinear functions of the electric potential and pressure gradients. The fact that the microstructure of non-Newtonian fluids is altered at solid–liquid interfaces is taken into account. In the case of fluids with wall depletion, both the output pressure and efficiency are found to be several times higher than that obtained with simple electrolytes under the same experimental conditions. Apart from potential applications in electrokinetic pumps, these predictions are of interest for the design of microfluidic devices that manipulate non-Newtonian fluids such as polymer solutions and colloidal suspensions. From a more fundamental point of view, the paper discusses a relevant example of nonlinear electrokinetics.

1 Introduction

Electro-osmotic flow (EOF) is a well known mechanism to transport fluids through microchannels (Probstein 1989; Hunter 1992; Li 2004). It requires the presence of electrostatic charges at the solid–liquid interface, with the associated counterions in solution that form the electric double layer (EDL). When an electric potential difference ΔV is imposed, the electric forces acting on excess ions in the EDL give rise to a plug-like velocity profile. In electrokinetic pumps, the system works against a hydrodynamic load, for example due to unequal fluid height Δh in reservoirs (Fig. 1a), where the adverse pressure ΔP induces a back flow. The overall flow rate Q results from the linear combination of the forward EOF and the backward pressure-driven flow (PDF). Indeed, electrokinetic pumping is a subject of intense research at present motivated by applications in microfluidic systems (Chen and Santiago 2002; Brask et al. 2003; Min et al. 2004; Griffiths and Nilson 2005; Xuan and Li 2006; Wang et al. 2006; Edwards IV et al. 2007; Seibel et al. 2008). A comprehensive review on electrokinetic pumps has been recently published (Wang et al. 2009), and the comparison to other micropumps is also available (Laser and Santiago 2004; Iverson and Garimella 2008).

Fig. 1

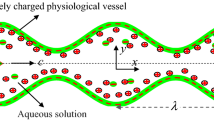
Highly schematic representation of a an elementary electrokinetic pump consisting of a microchannel with a negatively charged interface, connected to fluid reservoirs and a DC power source; b slit and cylindrical microchannels with geometrical dimensions and the coordinate system used in calculations

All the papers indicated above, and references therein, deal with Newtonian fluids (generally aqueous solutions of simple electrolytes), the viscosity of which is a constant coefficient μ. Hence Q is linear with both ΔV and ΔP. In the case of non-Newtonian fluids like polymer solutions, the viscosity η is a function of the velocity gradient developed in the microchannel. As a consequence, Q is nonlinear with ΔV and/or ΔP (Berli and Olivares 2008; Olivares et al. 2009) and additional contributions involving ΔVΔP also arise (Afonso et al. 2009). This is a crucial aspect for the design and operation of microfluidic devices, thus several authors are currently studying the electrokinetic flow of non-Newtonian fluids in microchannels (Zimmerman et al. 2006; Das and Chakraborty 2006; Chakraborty 2007; Park and Lee 2008; Zhao et al. 2008; Berli and Olivares 2008; Tang et al. 2009; Afonso et al. 2009; Olivares et al. 2009).

In particular, the use of non-Newtonian fluids in electrokinetic pumps has been claimed in a patent (Phillip 2006), where it is suggested that the output pressure can be substantially increased in relation to simple electrolyte solutions. Nevertheless, to the author’s knowledge, the subject has not been treated theoretically in the open literature so far. This is precisely the objective of the present work, which discusses the flow rate, output pressure and thermodynamic efficiency attained when typical non-Newtonian fluids are electrokinetically pumped through single microchannels. For the purposes, the paper is organized as follows: Sect. 2 presents the governing equations of the fluid dynamic problem, Sect. 3 describes analytical expressions of the flow rate and electric current, Sect. 4 discusses the maximum flow rate and output pressure, Sect. 5 shows the validation of the model against experimental data, Sect. 6 analyzes the thermodynamic efficiency and finally Sect. 7 outlines the main conclusions.

2 Theoretical framework

2.1 Non-Newtonian fluid dynamics

The electrokinetic flow of non-Newtonian fluids is studied here in the framework of continuum fluid mechanics. Axisymmetric and plane-symmetric flows are considered, which develop in cylindrical and slit microchannels, respectively (Fig. 1b). The fluid velocity is established in the axial direction y, and varies in the transverse direction x, which is normally accomplished in slim microchannels. The steady state flow of incompressible fluids is governed by the y-component of the momentum balance Equation (Bird et al. 1987; Probstein 1989; Hunter 1992):

$$ 0 = -\,{\frac{\partial P}{\partial y}} + {\frac{1}{{x^{m} }}}{\frac{{\partial (x^{m} \sigma_{xy} )}}{\partial x}} - \rho_{\text{e}} {\frac{\partial V}{\partial y}}, $$

(1)

with m = 0 for slits and m = 1 for cylinders. In this expression, $\sigma_{xy}$ is the shear component of the stress tensor and ${{\partial P} \mathord{\left/ {\vphantom {{\partial P} {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}} = {{\partial (p - \rho g_{y} y)} \mathord{\left/ {\vphantom {{\partial (p - \rho g_{y} y)} {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}$ is the total pressure gradient, where p is the isotropic pressure, ρ is the fluid density and g _y is the y-component of gravitational acceleration. The last term on the right hand side (RHS) of Eq. 1 represents the contribution of electric forces to the fluid momentum, where $\rho_{\text{e}}$ is the local charge density of the fluid and $- \partial V/\partial y$ is the externally applied electric field. According to the standard electrokinetic model (Probstein 1989; Hunter 1992; Li 2004), $\rho_{\text{e}}$ is related to the EDL potential ψ(x) through Poisson equation, $\nabla^{2} \psi = - {{\rho_{\text{e}} } \mathord{\left/ {\vphantom {{\rho_{\text{e}} } \varepsilon }} \right. \kern-\nulldelimiterspace} \varepsilon }$, where ε is the electrical permittivity of the medium. Temperature is assumed to be uniform throughout the flow domain, which requires negligible Joule effect in microchannels.

In order to determine the fluid velocity $u_{y} (x)$ from Eq. 1, a constitutive relationship for the shear stress $\sigma_{xy}$ in terms of the fluid velocity gradient $\dot{\gamma }_{xy} = {{\partial u_{y} } \mathord{\left/ {\vphantom {{\partial u_{y} } {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}$ must be adopted. The simplest model is the empirical law of Newton, $\sigma_{xy} = \mu \dot{\gamma }_{xy} ,$ where the viscosity μ is a constant coefficient. The present work deals with non-Newtonian fluids subjected to steady state, isothermal, fully developed, unidirectional, shear flows, in the geometries of Fig. 1b. Under these conditions, possible elastic effects are irrelevant (see Park and Lee 2008 for square microchannels), and the dominant influence is the variation of the viscosity with the shear rate $\dot{\gamma } = \left| {\dot{\gamma }_{xy} } \right|$ (Bird et al. 1987; Hunter 1992). Therefore one may introduce $\sigma_{xy} = \eta (\dot{\gamma })\dot{\gamma }_{xy}$, where the function $\eta (\dot{\gamma })$ describes the non-Newtonian viscosity of inelastic fluids.

2.2 Fluid viscosity model

The constitutive model of Ostwald-de Waele is

$$ \eta (\dot{\gamma }) = \beta \dot{\gamma }^{\alpha - 1} , $$

(2)

where α is the flow behaviour index and β is the consistency parameter (Bird et al. 1987; Hunter 1992). This model is known as power law (PL) because of the relation between $\eta$ and $\dot{\gamma }$. Accordingly, fluids that satisfy the model in a certain range of $\dot{\gamma }$ are called PL fluids. Values of α < 1 indicate shear-thinning behaviour: $\eta$ decreases with $\dot{\gamma }$, the most common response observed in polymeric fluids at relatively high values of $\dot{\gamma }$, as those developed in microchannels. Values α > 1 indicates shear-thickening behaviour: $\eta$ increases with $\dot{\gamma }$, which is rather unusual. When α = 1, the Newton law is recovered with β ≡ μ. Figure 2 presents typical viscosity curves in a log–log plot, where the slope is α − 1, and the intercept at $\dot{\gamma } = 1\;{\text{s}}^{ - 1}$ is β.

Fig. 2

Viscosity as a function of shear rate for PL fluids. Full lines are the prediction of Eq. 2. Symbols are experimental data (adapted from Olivares et al. 2009) of an aqueous solution of 1% carboxymethyl cellulose at pH 7 and 25°C. The dashed line represents the solvent, which is an aqueous solution of 15-mM phosphoric acid

Non-Newtonian fluids to be used in electrokinetic pumps are mainly polymer solutions (Phillip 2006). These fluids are constituted by a background electrolyte solution, hereafter named the “solvent”, and a certain concentration of dissolved polymers. Thus parameters α and β depend on polymer concentration, ionic strength, pH, and temperature. In any case, the viscosity of polymer solutions is higher than that of the solvent (an example is included in Fig. 2).

Finally it is worth noting that the PL model may lose validity at the extremes of very low and very high shear rates. In Fig. 2, for example, if the curve with α = 0.8 represents an aqueous polymer solution, it should not be extrapolated to $\dot{\gamma } > 10^{5} \,{\text{s}}^{ - 1}$, where viscosities would be lower than that of water: the actual viscosity curve eventually decreases the slope and becomes parallel to the dashed line.

2.3 Dimensions involved

Non-Newtonian behaviour appears in complex fluids such as polymer solutions and colloidal suspensions, which contain discrete entities in the nano-scale, namely macromolecules and colloidal particles, respectively. In order to satisfy the hypothesis of continuum medium, the channel cross-sectional size needs to be much larger than the size of these entities. This condition is normally attained in microchannels with d > 10 μm. On the other hand, for the ionic concentrations normally used in experiments, the EDL thickness is κ ⁻¹ < 10 nm. Thus one may reasonably assume κd ≫ 1 to simplify the treatment of the EDL potential. Given these assumptions, the electrokinetic flow equations reported below are addressed to channels with depths micrometric or larger (they do not apply to nanochannels).

3 Electrokinetic flow

3.1 Newtonian fluids

The equations for simple electrolyte solutions are outlined first as a reference. Calculations can be found in classical papers considering slits (Burgreen and Nakache 1964) and cylindrical channels (Rice and Whitehead 1965), as well as in recent works related to microfluidics (Xuan and Li 2004; Berli 2007; Wang et al. 2009). For relatively thin EDL, the flow rate Q and electric current I are, respectively,

$$ Q = -\,{\frac{{A_{m} d^{2} \Updelta P}}{(1 + m)(3 + m)\mu l}} + {\frac{{A_{m} \varepsilon \zeta \Updelta V}}{\mu l}}, $$

(3)

$$ I = {\frac{{A_{m} \varepsilon \zeta \Updelta P}}{\mu l}} - {\frac{{A_{m} s\Updelta V}}{l}}, $$

(4)

where $A_{m}$ is the cross-sectional area of the channel, being $A_{0} = 2wd$ for slits, and $A_{1} = \pi \,d^{2}$ for cylindrical channels (Fig. 1b). The first term on the RHS of Eq. 3 represents the PDF, where ${{\Updelta}}P = P_{\text{out}} - P_{\text{in}}$ is the pressure difference between microchannel ends (Fig. 1a). The second term represents the EOF, where ${{\Updelta}}V = V_{\text{out}} - V_{\text{in}}$ is the applied potential difference, and ζ is the value of the EDL potential at the interface. One should note that the flow is established in the positive y-direction of the capillary (Fig. 1a) if ζ < 0 and ΔV < 0, or vice versa, while ΔP ≥ 0 (backpressure).

Equation 4 shows that the transport of electricity in the flow domain also has two main contributions. The first term on the RHS of Eq. 4 involves the convective transport of excess ions in the EDL due to the PDF, which is denominated streaming current. The second term, where s is the electrical conductivity of the bulk, accounts for the motion of ions under the action of the applied electric field, which is denominated conductive current. Furthermore, the first term of Eq. 4 divided by ΔP (streaming coefficient) coincides with the second term of Eq. 3 divided by ΔV (electro-osmotic coefficient), thus satisfying Onsager reciprocal relations for electrokinetic phenomena (de Groot 1951).

3.2 PL fluids

The derivation of Q and I from Eqs. 1 and 2 is depicted in the Appendix. Analytical solutions cannot be obtained straightforwardly for arbitrary values of the exponent α and EDL potential ψ. Nevertheless, for relatively thin EDL (κd ≫ 1), the following expressions are found,

$$ Q = -\,{\frac{{A_{m} d}}{(2 + m + 1 /\alpha )}}\left[ {{\frac{d\Updelta P}{(1 + m)\beta l}}} \right]^{1 /\alpha } + {\frac{{A_{m} \alpha }}{{\kappa^{1 - 1 /\alpha } }}}\left( {{\frac{\varepsilon \zeta \Updelta V}{\beta l}}} \right)^{1 /\alpha } , $$

(5)

$$ I = {\frac{{A_{m} (1 + m)\varepsilon \zeta }}{d}}\left[ {{\frac{d\Updelta P}{(1 + m)\beta l}}} \right]^{1 /\alpha } - {\frac{{A_{m} s\Updelta V}}{l}}. $$

(6)

It is worth to mention that the thin EDL approximation is more suitable for shear-thinning fluids than for Newtonian fluids. In fact, PL fluids with α < 1 favour the formation of the plug-like flow profile associated to EOF, because the fluid viscosity decreases significantly in the interfacial zone where $\dot{\gamma }$ is high (Zhao et al. 2008; Tang et al. 2009; Olivares et al. 2009).

Equation 5 shows that both PDF and EOF are nonlinear due to the $\dot{\gamma }$-dependence of the viscosity. One should note that the numerical value of ζΔV must be positive in this equation: the EOF is established in the positive y-direction of the capillary for either negatively charged surfaces under positive electric field (Fig. 1a), or positively charged surfaces under negative electric field.

According to Eq. 6, the streaming current exhibits nonlinear effects as well. In addition, the first term of Eq. 6 divided by ΔP (streaming coefficient) differs from the second term of Eq. 5 divided by ΔV (electro-osmotic coefficient), meaning that Onsager reciprocal relations for electrokinetic phenomena (de Groot 1951) are not satisfied in PL fluids. Indeed, these coefficients are equal only if α = 1. In this particular case, Eqs. 5 and 6 correspond to Eqs. 3 and 4, respectively. This last observation also shows the consistency of calculations in the Appendix.

3.3 PL fluids with wall depletion

As mentioned above, fluids presenting non-Newtonian behaviour necessarily contain discrete entities in their microstructure, for instance macromolecules of relatively high molecular weight, whose radius of gyration can be several tenths of nanometers. At the same time, electroosmosis takes place in the region of the EDL that extends a distance κ ⁻¹ from the wall, which is normally lower than 10 nm. This is important to note because Eqs. 5 and 6 implicitly assume that fluid properties are uniform throughout the flow field, including the interfacial region. Nevertheless, due to the interaction between macromolecules and the channel surface, the concentration is altered in the proximity of channel walls (de Gennes 1987). If the interaction is attractive, polymers adsorb onto the wall and electroosmosis is significantly affected (further discussions on this aspect are given in Olivares et al. 2009). On the other hand, if the interaction is repulsive, polymers are depleted from the wall, hence the interfacial region contains the solvent of the polymer solution only. The thickness δ of the depletion layer is of the order of the radius of gyration of macromolecules (Tuinier and Taniguchi 2005) or colloidal particles (Barnes 1995). Therefore, since κ ⁻¹ < δ, electro-osmotic and streaming effects are confined to the depletion layer, and the transport equations result (Berli and Olivares 2008),

$$ Q = -\,{\frac{{A_{m} d(1 - \delta /d)^{2 + m + 1 /\alpha } }}{(2 + m + 1 /\alpha )}}\left[ {{\frac{d\Updelta P}{(1 + m)\beta l}}} \right]^{1 /\alpha } - {\frac{{A_{m} d^{2} \left[ {1 - (1 - \delta /d)^{3 + m} } \right]\Updelta P}}{(1 + m)(3 + m)\mu l}} + {\frac{{A_{m} \varepsilon \zeta \Updelta V}}{\mu l}}, $$

(7)

$$ I = {\frac{{A_{m} \varepsilon \zeta \Updelta P}}{\mu l}} - {\frac{{A_{m} s\Updelta V}}{l}}. $$

(8)

Equation 7 shows that the PDF has two components: the first (nonlinear) term comes from the bulk PL fluid, while the second (linear) term is due to the layer of solvent adjacent to the wall, with thickness δ and Newtonian viscosity μ. This term vanishes when $\delta \to 0$. On the other hand, if hypothetically $\delta \to d$, meaning that there are no discrete entities in solution, the first term vanishes and one recovers Eq. 3.

Equation 8 indicates that the electric current is linear with both ΔP and ΔV. Further, Onsager reciprocity is satisfied in Eqs. 7 and 8, because the streaming coefficients is equal to the electro-osmotic one $\left( {{{A_{m} \varepsilon \zeta } \mathord{\left/ {\vphantom {{A_{m} \varepsilon \zeta } {\mu l}}} \right. \kern-\nulldelimiterspace} {\mu l}}} \right)$ regardless of the values of α and δ/d.

4 Analysis of the flow rate and output pressure

4.1 Newtonian fluids

The maximum flow rate is reached when the backpressure is null (ΔP = 0), hence it is given by the second term on the RHS of Eq. 3,

$$ Q_{\max }^{{({\text{S}})}} = {\frac{{A_{m} \varepsilon \zeta \Updelta V}}{\mu l}}, $$

(9)

where the superscript S stands for solvent. In contrast, the maximum output pressure is reached when the flow rate is null (Q = 0). In this case Eq. 3 yields,

$$ {{\Updelta}}P_{\max }^{{({\text{S}})}} = {\frac{(1 + m)(3 + m)\varepsilon \zeta \Updelta V}{{d^{2} }}}. $$

(10)

It is worth to remark that this expression is valid for κd ≫ 1, hence the possibility of increasing the maximum pressure by decreasing d is limited.

The relationship between Q and ΔP, the so-called pump curve, is usually written in a condensed form by combining Eqs. 3, 9 and 10 (Chen and Santiago 2002; Min et al. 2004; Wang et al. 2006; Edwards IV et al. 2007; Wang et al. 2009); that is,

$$ {\frac{Q}{{Q_{\max }^{{({\text{S}})}} }}} = 1 - {\frac{{{{\Updelta}}P}}{{{{\Updelta}}P_{\max }^{{({\text{S}})}} }}}. $$

(11)

This expression emphasizes the linear response of Newtonian fluids.

4.2 PL fluids

Figure 3 presents the curves Q vs ΔP predicted by Eq. 5, for a given ΔV, and typical values of d, ζ and κ ⁻¹. It is observed that the maximum flow rate (intercept at ΔP = 0) is lower than that of the solvent, since the EOF is inversely proportional to the bulk viscosity. This is better observed in the following expression extracted from Eq. 5,

$$ Q_{\max }^{{({\text{PL}})}} = {\frac{{A_{m} \alpha }}{{\kappa^{1 - 1 /\alpha } }}}\left( {{\frac{{\varepsilon \zeta {{\Updelta}}V}}{\beta l}}} \right)^{1 /\alpha } . $$

(12)

Fig. 3

Flow rate as a function of pressure gradient for PL fluids in cylindrical microchannels (Eq. 5). Parameter values used in calculations are ε = 7.1 × 10⁻¹⁰ C²/Nm²; ζ = −50 mV; κ ⁻¹ = 1 nm; d = 50 μm; ΔV/l = −1 kV/m. The dashed line represents an aqueous electrolyte solution (Eq. 3) under the same experimental conditions

More details on the EOF of PL fluids are reported elsewhere (Olivares et al. 2009).

Figure 3 also shows that large values of the maximum output pressure (intercept at Q = 0) are predicted for α < 1. From Eq. 5,

$$ {{\Updelta}}P_{\max }^{{({\text{PL}})}} = {\frac{{(1 + m)(2 + m + 1 /\alpha )^{\alpha } \alpha^{\alpha } (\kappa d)^{1 - \alpha } \varepsilon \zeta \Updelta V}}{{d^{2} }}}, $$

(13)

which is plotted in Fig. 4. The maximum pressure is linear with the applied field, but strongly depends on the character of the fluid: high pressure values can be attained with shear-thinning fluids, while shear-thickening fluids yield pressures lower than that obtained with the solvent.

Fig. 4

Maximum pressure gradient as a function of the applied electric field for PL fluids in cylindrical microchannels (Eq. 13). Parameter values are those reported in the legend of Fig. 3. The dashed line represents an aqueous electrolyte solution (Eq. 10) under the same experimental conditions

A relevant detail of Eq. 13 is that, if α < 1, the maximum pressure may be improved by increasing κd (relatively thin EDL). This factor contributes to increase the value of $\dot{\gamma }$ at the wall, which in turn lowers the viscosity in the interfacial zone, thus favouring the EOF and increasing the output pressure. The opposite is expected if α > 1, since the viscosity in the interfacial region is enhanced, which diminishes the EOF.

From Eqs. 5, 12 and 13, the condensed pump curve results,

$$ {\frac{Q}{{Q_{\max }^{{({\text{PL}})}} }}} = 1 - \left( {{\frac{{{{\Updelta}}P}}{{{{\Updelta}}P_{\max }^{{({\text{PL}})}} }}}} \right)^{1 /\alpha } , $$

(14)

which comprises the nonlinear response of PL fluids in electrokinetic pumping. The linear pump curve of simple electrolytes (Eq. 11) is recovered when α = 1.

4.3 PL fluids with wall depletion

Figure 5 presents the curves Q vs ΔP predicted by Eq. 7, for a given ΔV. The limit δ/d ≪ 1 is considered for the sake of simplicity. It is observed that the maximum flow rate coincides with that of the solvent, because the EOF is determined solely by the viscosity of the depletion layer. In fact, from Eq. 7 one has,

$$ Q_{\max }^{{({\text{WD}})}} = {\frac{{A_{m} \varepsilon \zeta {{\Updelta}}V}}{\mu l}} = Q_{\max }^{{({\text{S}})}} , $$

(15)

where the superscript WD is included to indicate wall depletion.

Fig. 5

Flow rate as a function of pressure gradient for PL fluids with wall depletion in cylindrical microchannels (Eq. 7 with δ/d ≪ 1). Parameter values used in calculations are ε = 7.1 × 10⁻¹⁰ C²/Nm²; ζ = −50 mV; d = 50 μm; ΔV/l = −1 kV/m. The dashed line represents an aqueous electrolyte solution (Eq. 3) under the same experimental conditions

Figure 5 also shows that the maximum pressure is always higher than that of the solvent, independently on the character of the fluid (shear-thinning/thickening). Setting Q = 0 and δ/d ≪ 1 in Eq. 7 yields,

$$ {{\Updelta}}P_{\max }^{{({\text{WD}})}} = {\frac{{(1 + m)(2 + m + 1 /\alpha )^{\alpha } \beta l}}{{d^{1 + \alpha } }}}\left( {{\frac{\varepsilon \zeta \Updelta V}{\mu l}}} \right)^{\alpha } . $$

(16)

Figure 6 illustrates the nonlinear dependence of the maximum pressure with the applied field in PL fluids with wall depletion. Another interesting feature of Eq. 16 is that the output pressure is proportional to the consistency parameter β, which measures the bulk viscosity at low shear rates (more precisely at $\dot{\gamma } = 1\;{\text{s}}^{ - 1}$). In addition, Fig. 6 shows how the maximum pressure increases with α. Therefore, the larger the viscosity of the polymer solution, the larger the output pressure, provided there is polymer depletion at the wall. The curve with α = 1 indicates that the increase of the output pressure takes place even if the polymer solution is Newtonian, which differs from the case of fluids with uniform polymer concentration (Fig. 4).

Fig. 6

Maximum pressure gradient as a function of the applied electric field for PL fluids with wall depletion in cylindrical microchannels (Eq. 16). Parameter values are those reported in the legend of Fig. 5. The dashed line represents an aqueous electrolyte solution (Eq. 10) under the same experimental conditions

From Eqs. 7, 15 and 16, the condensed pump curve is,

$$ {\frac{Q}{{Q_{\max }^{{({\text{WD}})}} }}} = 1 - \left( {{\frac{\Updelta P}{{{{\Updelta}}P_{\max }^{{({\text{WD}})}} }}}} \right)^{1 /\alpha } , $$

(17)

which presents the same fashion of Eq. 14, although with different maximum values.

5 Comparison with experimental data

In this section, model predictions are validated with the sole set of experimental data found in the literature: Phillip (2006) reported the maximum pressure obtained with aqueous solutions of 8.33-mM polyacrylic acid (molecular weight 42 kD) at pH 8.2 in silica capillaries. The background electrolyte (solvent) of this polymeric fluid was an aqueous solution of 10-mM TRIS and 5-mM acetic acid at pH 8.2. Capillary dimensions were d = 10 μm and l = 5 cm. Data are plotted in Fig. 7. The maximum pressure attained with the solvent is described by Eq. 10, with ζ = −80 mV, which was determined as a fitting parameter (dashed line in Fig. 7). This value of ζ is characteristic for silica surfaces at that pH.

Fig. 7

Maximum pressure as a function of the applied potential difference. Symbols are experimental data (adapted from Phillip 2006) of an aqueous solution of polyacrylic acid, and the respective solvent (see text for details; Sect. 5). Lines are the prediction of the model proposed here, with m = 1; d = 10 μm; l = 5 cm; ε = 7.1 × 10⁻¹⁰ C²/Nm²; ζ = −80 mV; μ = 1 mPas; α = 0.38 and β = 380 mPas^α

It is clear in Fig. 7 that the maximum pressure of the polymer solution is several times higher than that attained with the solvent, and presents a nonlinear relation with ΔV. According to the discussions given above, the trend of the curve suggests strong shear-thinning behaviour and wall depletion (compare to Fig. 6). In fact, polyacrylic acid solutions, customarily known as carbopol, behave as PL fluids in a wide range of shear rates (see, for instance, Lin and Ko 1995). Polymer depletion at the walls is also expected, taking into account that both macromolecules and the silica surface are negatively charged at pH 8.2. For these reasons, experimental data are successfully fitted to Eq. 16 with α = 0.38 and β ≈ 380 mPas^α (solid line in Fig. 7). These values are quite reasonable for the system under study (Lin and Ko 1995).

It should be also mentioned that at high polymer concentrations, and certain conditions of pH and ionic strength, carbopol solutions may present a yield stress of the order of 10 Pa. For these cases, the PL model with a yield stress parameter is normally used to represent the viscosity, which is known as Herschel–Bulkley model (Bird et al. 1987). This approach is required in fluid dynamic problems where shear rates are very low (e.g. Dubash and Frigaard 2007). In contrast, relatively high values of $\dot{\gamma }$ are involved in the electrokinetic pumping through microchannels (Fig. 2), particularly in the system under consideration, where pressures exceed 10⁴ Pa (Fig. 7). Hence potential effects of a yield stress are irrelevant in this case, and the simple PL model appears to be appropriate.

It is worth to stress that experimental data of electrokinetic pumping of non-Newtonian fluids are well predicted and rationalized by the modelling carried out in this work. The energetic efficiency is considered next to conclude the analysis.

6 Analysis of the efficiency

6.1 Newtonian fluids

The thermodynamic efficiency of electrokinetic pumps is defined as the ratio of the useful mechanical power to the electrical power consumption (Morrison Jr and Oesterle 1965; Min et al. 2004; Griffiths and Nilson 2005; Xuan and Li 2006),

$$ \chi = {\frac{{Q{{\Updelta}}P}}{{I( - {{\Updelta}}V)}}}. $$

(18)

Introducing Eqs. 3 and 4, and reordering yields,

$$ \chi = {\frac{{1 - {{{{\Updelta}}P} \mathord{\left/ {\vphantom {{{{\Updelta}}P} {{{\Updelta}}P_{\max }^{{({\text{S}})}} }}} \right. \kern-\nulldelimiterspace} {{{\Updelta}}P_{\max }^{{({\text{S}})}} }}}}{{{{\mu s{{\Updelta}}V} \mathord{\left/ {\vphantom {{\mu s{{\Updelta}}V} {(\varepsilon \zeta {{\Updelta}}P) - 1}}} \right. \kern-\nulldelimiterspace} {(\varepsilon \zeta {{\Updelta}}P) - 1}}}}} $$

(19)

In the denominator of this equation, the first term is higher than 10⁵ for ordinary values of the parameters, meaning that the streaming current is negligible in comparison with the conductive current of the bulk. Thus the maximum efficiency for a given ΔV is reached at ${{\Updelta}}P = {{{{\Updelta}}P_{\max }^{{({\text{S}})}} } \mathord{\left/ {\vphantom {{{{\Updelta}}P_{\max }^{{({\text{S}})}} } 2}} \right. \kern-\nulldelimiterspace} 2}$ and $Q = {{Q_{\max }^{{({\text{S}})}} } \mathord{\left/ {\vphantom {{Q_{\max }^{{({\text{S}})}} } 2}} \right. \kern-\nulldelimiterspace} 2}$ (Chen and Santiago 2002; Min et al. 2004; Wang et al. 2006), and may be expressed as follows,

$$ \chi_{\max }^{{({\text{S}})}} = {\frac{{{{\Updelta}}P_{\max }^{{({\text{S}})}} Q_{\max }^{{({\text{S}})}} }}{{4{{A_{m} s{{\Updelta}}V^{2} } \mathord{\left/ {\vphantom {{A_{m} s{{\Updelta}}V^{2} } l}} \right. \kern-\nulldelimiterspace} l}}}}. $$

(20)

One should note that $\chi_{\max }^{{({\text{S}})}}$ is actually independent of ΔV (see Eqs. 9 and 10).

6.2 PL fluids

Following Eq. 18, the efficiency of PL fluids is calculated by using Eqs. 5 and 6, which yields

$$ \chi = {\frac{{1 - \left( {{{{{\Updelta}}P} \mathord{\left/ {\vphantom {{{{\Updelta}}P} {{{\Updelta}}P_{\max }^{{({\text{PL}})}} }}} \right. \kern-\nulldelimiterspace} {{{\Updelta}}P_{\max }^{{({\text{PL}})}} }}} \right)^{1 /\alpha } }}{{{\frac{{\kappa^{1 - 1 /\alpha } }}{\alpha }}\left\{ {{\frac{{s{{\Updelta}}V^{2} }}{{l{{\Updelta}}P}}}\left( {{\frac{\beta l}{{\varepsilon \zeta {{\Updelta}}V}}}} \right)^{1 /\alpha } - \left[ {{\frac{{(1 + m)\varepsilon \zeta {{\Updelta}}V}}{{d{{\Updelta}}P}}}} \right]^{1 - 1 /\alpha } } \right\}}}}. $$

(21)

In the denominator of Eq. 21, the first term of the sum is much higher than the second one, which equals 1 for α = 1. Thus the contribution of streaming effects to the current may be neglected. Under these conditions, the maximum efficiency $\chi_{\max }^{{({\text{PL}})}}$ for a given ΔV is reached at ${{\Updelta}}P = {{{{\Updelta}}P_{\max }^{{({\text{PL)}}}} } \mathord{\left/ {\vphantom {{{{\Updelta}}P_{\max }^{{({\text{PL)}}}} } {(1 + 1 /\alpha )^{\alpha } }}} \right. \kern-\nulldelimiterspace} {(1 + 1 /\alpha )^{\alpha } }}$ and $Q = {{Q_{\max }^{{({\text{PL}})}} } \mathord{\left/ {\vphantom {{Q_{\max }^{{({\text{PL}})}} } {(1 + \alpha )}}} \right. \kern-\nulldelimiterspace} {(1 + \alpha )}}.$ Writing $\chi_{\max }^{{({\text{PL}})}}$ relative to the solvent results,

$$ {\frac{{\chi_{\max }^{{({\text{PL}})}} }}{{\chi_{\max }^{{({\text{S}})}} }}} = {\frac{4}{{(1 + 1 /\alpha )^{\alpha } (1 + \alpha )}}}{\frac{{{{\Updelta}}P_{\max }^{{({\text{PL}})}} }}{{{{\Updelta}}P_{\max }^{{({\text{S}})}} }}}{\frac{{Q_{\max }^{{({\text{PL}})}} }}{{Q_{\max }^{{({\text{S}})}} }}}. $$

(22)

The prediction of this Equation is illustrated in Fig. 8. It is observed that the maximum efficiency of PL fluids depends on ΔV, is generally lower than that of the solvent, and strongly decreases with the viscosity of the bulk fluid. In the case of α > 1, both ratios ${{{{\Updelta}}P_{\max }^{{({\text{PL}})}} } \mathord{\left/ {\vphantom {{{{\Updelta}}P_{\max }^{{({\text{PL}})}} } {{{\Updelta}}P_{\max }^{{({\text{S}})}} }}} \right. \kern-\nulldelimiterspace} {{{\Updelta}}P_{\max }^{{({\text{S}})}} }}$ and ${{Q_{\max }^{{({\text{PL}})}} } \mathord{\left/ {\vphantom {{Q_{\max }^{{({\text{PL}})}} } {Q_{\max }^{{({\text{S}})}} }}} \right. \kern-\nulldelimiterspace} {Q_{\max }^{{({\text{S}})}} }}$ are lower than 1. In the case of α < 1, ${{\Updelta P_{\max }^{{({\text{PL}})}} } \mathord{\left/ {\vphantom {{\Updelta P_{\max }^{{({\text{PL}})}} } {\Updelta P_{\max }^{{({\text{S}})}} }}} \right. \kern-\nulldelimiterspace} {\Updelta P_{\max }^{{({\text{S}})}} }} > \;1$ (Fig. 4), but these pressures are not enough to counterbalance the relatively low flow rates $\left( {{{Q_{\max }^{{({\text{PL}})}} } \mathord{\left/ {\vphantom {{Q_{\max }^{{({\text{PL}})}} } {Q_{\max }^{{({\text{S}})}} < 1}}} \right. \kern-\nulldelimiterspace} {Q_{\max }^{{({\text{S}})}} < 1}}} \right)$, and the overall result is a loss of efficiency in relation to simple electrolytes.

Fig. 8

Maximum efficiency, relative to that of the solvent, as a function of the applied electric field for PL fluids in cylindrical microchannels (Eq. 22). Parameter values are those reported in the legend of Fig. 3

In the predictions of Fig. 8 there are certain viscosity values that allow ${{\chi_{\max }^{{({\text{PL}})}} } \mathord{\left/ {\vphantom {{\chi_{\max }^{{({\text{PL}})}} } {\chi_{\max }^{{({\text{S}})}} }}} \right. \kern-\nulldelimiterspace} {\chi_{\max }^{{({\text{S}})}} }} > 1$, for example α = 0.8, β = 10 mPas^α. However, in these limiting cases one has to take care of the validity of PL model, as discussed in Sect. 2.2.

6.3 PL fluids with wall depletion

Introducing Eqs. 7 and 8 into Eq. 18 yields,

$$ \chi = {\frac{{1 - \left( {{{{{\Updelta}}P} \mathord{\left/ {\vphantom {{{{\Updelta}}P} {{{\Updelta}}P_{\max }^{{({\text{WD}})}} }}} \right. \kern-\nulldelimiterspace} {{{\Updelta}}P_{\max }^{{({\text{WD}})}} }}} \right)^{1 /\alpha } }}{{{{\mu s{{\Updelta}}V} \mathord{\left/ {\vphantom {{\mu s{{\Updelta}}V} {(\varepsilon \zeta {{\Updelta}}P)}}} \right. \kern-\nulldelimiterspace} {(\varepsilon \zeta {{\Updelta}}P)}} - 1}}}. $$

(23)

If streaming effects are neglected, as before, the maximum efficiency is reached at ${{\Updelta}}P = {{{{\Updelta}}P_{\max }^{{({\text{WD}})}} } \mathord{\left/ {\vphantom {{{{\Updelta}}P_{\max }^{{({\text{WD}})}} } {(1 + 1 /\alpha )^{\alpha } }}} \right. \kern-\nulldelimiterspace} {(1 + 1 /\alpha )^{\alpha } }}$ and $Q = {{Q_{\max }^{{({\text{WD}})}} } \mathord{\left/ {\vphantom {{Q_{\max }^{{({\text{WD}})}} } {(1 + \alpha )}}} \right. \kern-\nulldelimiterspace} {(1 + \alpha )}}.$ Further,

$$ {\frac{{\chi_{\max }^{{({\text{WD}})}} }}{{\chi_{\max }^{{({\text{S}})}} }}} = {\frac{4}{{(1 + 1 /\alpha )^{\alpha } (1 + \alpha )}}}{\frac{{{{\Updelta}}P_{\max }^{{({\text{WD}})}} }}{{{{\Updelta}}P_{\max }^{{({\text{S}})}} }}}. $$

(24)

The prediction of Eq. 24 is illustrated in Fig. 9, where one observes that the maximum efficiency depends on ΔV, is always higher than that of the solvent, and strongly increases with the viscosity of the bulk fluid. In fact, in polymer solutions with wall depletion, high output pressures are induced by the central part of the flow (${{{{\Updelta}}P_{\max }^{{({\text{WD}})}} } \mathord{\left/ {\vphantom {{{{\Updelta}}P_{\max }^{{({\text{WD}})}} } {{{\Updelta}}P_{\max }^{{({\text{S}})}} > 1}}} \right. \kern-\nulldelimiterspace} {{{\Updelta}}P_{\max }^{{({\text{S}})}} > 1}}$; Figs. 6 and 7), while the flow rate is defined by the interfacial layer of solvent $\left( {Q_{\max }^{{({\text{WD}})}} = Q_{\max }^{{({\text{S}})}} } \right)$. The overall result is a substantial gain of efficiency in relation to simple electrolytes.

Fig. 9

Maximum efficiency, relative to that of the solvent, as a function of the applied electric field for PL fluids with wall depletion in cylindrical microchannels (Eq. 24). Parameter values are those reported in the legend of Fig. 5

7 Concluding remarks

A theoretical analysis of electrokinetic pumping of non-Newtonian fluids through single microchannels is presented. Analytical expressions of the flow rate, output pressure and thermodynamic efficiency are reported, which comprise a new contribution to the fields of electrokinetics and microfluidics.

In the case of polymer solutions with uniform concentration in the interfacial region, the output pressure may be higher than that of the solvent, however with a considerably loss of efficiency. In contrast, if wall depletion takes place, the output pressure may be several times higher than that of the solvent, with a proportional gain of efficiency. Because of the assumptions made in modelling, these predictions are applicable to channels with depths larger than 10 μm, approximately (not to nanochannels). But precisely, an advantage of using non-Newtonian fluids is that good pumping performances can be reached with relatively large channel diameters and/or low electric fields.

Apart from potential applications in electrokinetic pumps, results reported here are of interest for the design and operation of microfluidic devices that manipulate macromolecular solutions and colloidal suspensions. From the fundamental point of view, one observes that non-Newtonian fluids lead to striking nonlinear electrokinetic effects that encourage further research.

Appendix: Flow rate and electric current of PL fluids with relatively thin EDL

The velocity profile $u_{y} (x)$ of PL fluids is derived from Eq. 1, after including $\sigma_{xy} = \eta (\dot{\gamma })\dot{\gamma }_{xy}$, with $\eta (\dot{\gamma })\,$ from Eq. 2, i.e.

$$ 0 = - {\frac{\partial P}{\partial y}} + {\frac{\beta }{{x^{m} }}}{\frac{\partial }{\partial x}}\left( {x^{m} \left| {{\frac{{\partial u_{y} }}{\partial x}}} \right|^{\alpha - 1} {\frac{{\partial u_{y} }}{\partial x}}} \right) + {\frac{\varepsilon }{{x^{m} }}}{\frac{\partial }{\partial x}}\left( {x^{m} {\frac{\partial \psi }{\partial x}}} \right){\frac{\partial V}{\partial y}}, $$

(25)

where m = 0 for slits and m = 1 for cylindrical microchannels. The boundary conditions associated to the flow domains of Fig. 1b are written as follows,

$$ x = 0,\,\,\,\,\partial u_{y} /\partial x = 0,\,\,\,\partial \psi /\partial x = 0; $$

(26)

$$ x = d,\,\,\,u_{y} = 0,\,\,\,\,\psi = \zeta . $$

(27)

Analytic expressions $u_{y} (x)$ cannot be found for arbitrary values of the exponent α and functions $\psi (x)$. In order to inspect the form of the solutions, the particular case of α = 1/2 is considered here. Further, as mentioned in Sect. 2.3, κd ≫ 1 is assumed to simplify the calculations of $\psi (x)$. This condition implies both a roughly flat EDL and that EDL potentials from opposite sides of the channel do not interfere each other. Thus the Debye–Hückel approximation yields,

$$ \psi (x) = \zeta \,{\text{e}}^{ - \kappa (d - x)} , $$

(28)

which is valid for |ζ| < 50 mV at room temperature (Hunter 1992). Finally, introducing Eq. 28 into Eq. 25, setting m = 1, integrating twice, and using boundary conditions (Eqs. 26 and 27) yields,

$$ \begin{gathered} u_{y} (x) = - \left( {{\frac{1}{\beta }}{\frac{\partial P}{\partial y}}} \right)^{2} {\frac{{d^{3} }}{12}}\left[ {1 - \left( {{\frac{x}{d}}} \right)^{3} } \right] + \left( {{\frac{\varepsilon \zeta }{\beta }}{\frac{\partial V}{\partial y}}} \right)^{2} {\frac{1}{2\lambda }}\left[ {1 - {\text{e}}^{ - 2\kappa (d - x)} } \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + {\frac{\varepsilon \zeta }{\beta }}{\frac{\partial V}{\partial y}}{\frac{\partial P}{\partial y}}(d - x){\text{e}}^{ - \kappa (d - x)} . \hfill \\ \end{gathered} $$

(29)

In comparison with the electrokinetic flow of Newtonian fluids, Eq. 29 presents an extra contribution to the fluid velocity that involves the coupling of electric potential and pressure gradients (see also Afonso et al. 2009). The flow rate Q is obtained by integrating Eq. 29 in the cross-sectional area of the channel:

$$ \begin{gathered} Q = \pi d^{2} \left\{ { - {\frac{{d^{3} }}{20}}\left( {{\frac{1}{\beta }}{\frac{\partial P}{\partial y}}} \right)^{2} } \right. + {\frac{\kappa }{2}}\left( {{\frac{\varepsilon \zeta }{\beta }}{\frac{\partial V}{\partial y}}} \right)^{2} \left[ {1 - {\frac{1}{\kappa d}} + {\frac{1}{2}}\left( {{\frac{1}{\kappa d}}} \right)^{2} \left( {1 - {\text{e}}^{ - 2\kappa d} } \right)} \right] \hfill \\ \,\,\,\,\,\,\,\,\,\left. { + \left( {{\frac{1}{\kappa d}}} \right)^{2} {\frac{2\varepsilon \zeta }{\beta }}{\frac{\partial V}{\partial y}}{\frac{\partial P}{\partial y}}\left[ {1 + {\text{e}}^{ - \kappa d} - {\frac{2}{\kappa d}}\left( {1 - {\text{e}}^{ - \kappa d} } \right)} \right]} \right\} \hfill \\ \end{gathered} $$

(30)

In this expression one observes that the extra term is of the order of (κd)⁻², hence it vanishes quickly when κd ≫ 1. Therefore, if this contribution is neglected right before the second integration of Eq. 25, then one may operate analytically with arbitrary values of α, and the resulting expression of Q(ΔP, ΔV) is that given in Sect. 3.2.

Concerning the electric current, two main contributions are considered, namely streaming current I _ΔP and conductive current I _ΔV . The first one is due to the PDF, and is modelled as follows. If κd ≫ 1, the streaming effect is confined to a thin layer adjacent to the wall, hence the current density per unit width of the (locally flat) interface is $\varepsilon \zeta \dot{\gamma }$, provided $\dot{\gamma }$ is uniform in the EDL (Hunter 1992). As a first approximation, one may consider that the value of $\dot{\gamma }$ at the wall holds up to a distance around κ ⁻¹ into the fluid (Hunter 1992). For PDF of PL fluids in the flow geometries of Fig. 1b, the wall shear rate is (Bird et al. 1987),

$$ \left. {\dot{\gamma }} \right|_{x = d} = \left[ {{\frac{{d{{\Updelta}}P}}{(1 + m)\beta l}}} \right]^{1 /\alpha } , $$

(31)

with ${{\Updelta}}P \ge 0$. Given the symmetry of the flow domains under study, and assuming uniform ζ-potential, the streaming current results,

$$ I_{{{{\Updelta}}P}} = {\frac{{A_{m} (1 + m)\varepsilon \zeta }}{d}}\left[ {{\frac{{d{{\Updelta}}P}}{(1 + m)\beta l}}} \right]^{1 /\alpha } . $$

(32)

On the other hand, the conductive current is obtained by integrating the bulk current density $- s{{{{\Updelta}}V} \mathord{\left/ {\vphantom {{{{\Updelta}}V} l}} \right. \kern-\nulldelimiterspace} l}$ in the cross-sectional area of the channel, where s is the electric conductivity of the solution:

$$ I_{{{{\Updelta}}V}} = - {\frac{{A_{m} s{{\Updelta}}V}}{l}}. $$

(33)

Finally, adding Eqs. 32 and 33 yields the expression I(ΔP, ΔV) reported in Sect. 3.2. As discussed above, additional terms involving the coupling of electric potential and pressure gradients are neglected. Possible effects of the Stern layer conductance are also disregarded under the circumstances (e.g. Davidson and Xuan 2008).