1 Introduction

Nonspherical particles are currently being considered for a wide range of applications including: electronic devices (Appell 2002; Evoy et al. 2004; Beckman et al. 2005; Park et al. 2004); wave guides (Greytak et al. 2005); construction of photonic crystals (Liddell and Summers 2004); and biological, sensing, separation, or lab-on-a-chip systems (Patolsky et al. 2006a, b; Hamers et al. 2006; Reich et al. 2003; Stone et al. 2004; Hughes 2000). In certain cases, controlled transport and manipulation of single particles may be useful or necessary. One means of transporting particles in suspension is to use an electric field and drive the particle motion by dielectrophoresis or electrophoresis. Dielectrophoresis is often favored as a means to exert control over particle motion due to the possibility of solely exerting forces on the particles in the system. However, common applications such as sensing or chemical reactions at the particle surface may benefit from the increased particle–fluid contact possible when both the particle and fluid are in motion. Given the commonplace nature of geometric features such as corners and turns in microfluidic systems, the two goals of the present study are: (1) to determine the fundamental effect of a 90° corner on the motion of an individual cylindrical particle under standard DC electrophoresis, and (2) to determine whether or not a geometric feature, in this case a corner, within a microfluidic system may be used as a passive control element as part of a larger system.

In an electrophoretic system, the ionic concentration of the suspending medium has a large effect on the properties of the system since it controls the thickness of the electrical double layer. The electrical double layer is a layer of ions of charge opposite to that of the channel or particle surface that create a small charged region near the surface. The higher the ionic concentration of the solution the thinner the electrical double layer. The Debye length, κ, is used as an inverse measurement of the thickness of the electrical double layer. A particle dimension, a, is commonly used to nondimensionalize the Debye length. Thus, a system with thin electrical double layers would be represented by a value of κa ≫ 1 as is the case in this study due to the prevalence of practical situations that meet this criteria. A variety of previous studies exist which examine the fundamental electrophoretic motion of spheres (Keh and Anderson 1985; Yariv and Brenner 2002, 2003; Ye et al. 2005) and cylinders (Ye et al. 2002; Liu et al. 2004; Davison and Sharp 2006) in straight channels where the channel boundaries affect the motion of the particle. A cylindrical particle translating horizontally through a straight channel has been shown to move in an oscillatory manner in both vertical displacement and angle, with the nature of the motion dependent on the initial position and angle of the particle (Davison and Sharp 2007). Previous work with corners and junctions in microfluidic systems have largely focused on fluid-only systems (Slentz et al. 2002; Zimmerman et al. 2006). Thamida and Chang (2002) examined the aggregation of small (< 1% of the channel width) colloidal particles at the corner of a microfluidic junction. More pertinently, Ye and Li (2004) studied the motion of a large spherical particle (40% of the channel width) as it moved electrophoretically through a 90° corner as part of a T-junction. However, since the particle was a sphere, no emphasis was placed on the rotation of the particle as it passed through the corner region. For the motion of a cylindrical particle, both the trajectory of the particle center and the angle of the particle are critical to describing the electrophoretic motion. The effect of various system parameters on these two motion components is categorized as having minimal or significant impact and is detailed herein.

2 Problem definition

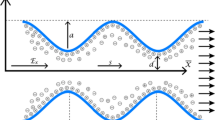
The current investigation seeks to determine the trajectory of a cylindrical particle as it moves through a 90° corner under the influence of electrophoresis. Figure 1a shows the modeled two-dimensional system in a typical initial position as well as geometrical descriptors of the problem. The channel consists of two sections with a length of L and width b joined into a 90° corner, with the inlet, Γin, and outlet, Γout, leading to reservoirs open to the atmosphere (no pressure gradient through the channel). A small radius (a/2) is applied to the corners where the channel sections meet in order to eliminate the numerical singularity that would exist at a sharp corner. The channel, outside of the particle and thin electrical double layers on the surfaces, is filled with an incompressible, Newtonian fluid which makes up the computational domain, Ω. The particle has a total length of l, with hemispherical ends of radius a. The boundary of the particle and electrical double layer is designated by Γ p , while the boundary of the channel walls is denoted by Γ w . The electrical field, E x , is applied from the inlet to the outlet causing the fluid flow to proceed in the same direction due to the uniform and negative zeta potential, ζ w , of the channel walls. The distribution of electric field in the channel, without the presence of a particle, is shown in Fig. 1b. The Reynolds number of the system can be calculated based on the particle motion and length scale yielding a value of 4 × 10−5 or the fluid velocity and channel width which gives 2 × 10−4. The Stokes equations are used to model the fluid motion due to the low Reynolds number of the modeled system. Since the particle has a uniform zeta potential, ζ p , that is greater in magnitude than the channel walls (ζ w /ζ p  < 1) the particle will move from Γout to Γin. The importance of Brownian motion can be estimated by a Peclet number defined as the ratio between the electrophoretic velocity, U ep, and the translational Brownian diffusion, D Brownian, \(\hbox{Pe}=\frac{a U_{\rm ep}}{D_{\rm Brownian}}\) (Probstein 2003; Wilson et al. 2000), where a is the particle radius. For simplicity in calculating the Peclet number, the cylindrical particle is replaced by a sphere with an equivalent volume which yields a Peclet number of Pe = 460. This indicates that Brownian translation is much less significant than the electrophoretic motion and so Brownian motion is neglected in the following analysis. Within the current system, various parameters are theorized to have an effect on the motion of the cylindrical particle. The zeta potential ratio (γ), channel width (b), particle aspect ratio (l/a), initial particle angle (θ0), and initial vertical position in the channel (Y 0) will be varied to determine the effect on the electrophoretic motion of the cylindrical particle.

Fig. 1
figure 1

a Diagram of cylindrical particle at initial position in channel with relevant dimensions and variables. The origin of the coordinate system used lies at the intersection of the channel centerlines and is indicated by the X, Y axes in the figure. Unstructured triangular mesh of computational domain included to illustrate increase in mesh density around the particle. b Diagram of the distribution of electric field, with electric field lines, present in the channel without a particle present. Shading indicates strength of the electric field, with lighter colors (e.g., at the inner corner) designating a stronger field

Full size image

3 Equation set and numerical method

The trajectory of the cylindrical particle is determined by simultaneously solving the equations for the electrical field, fluid flow, and particle motion. The equations presented are nondimensionalized by the particle radius, a, the applied electrical voltage, ϕ0, and the electrophoretic velocity of the particle in an unbounded channel, \(U_{\infty}=\frac{\varepsilon \varepsilon_0 \zeta_p}{\mu} \frac{\phi_0}{a},\) where ɛɛ0 is the fluid dielectric constant times the permittivity of a vacuum and μ is the fluid viscosity. These quantities are used to form the nondimensional position, velocity, pressure, and electric potential by allowing \({\mathbf {x}}=a {\mathbf {x}}^*, {\mathbf {u}} = U_{\infty} {\mathbf {u}}^*, p = \frac{\mu U_{\infty}}{a}p^*,\) and ϕ = ϕ0 ϕ*, respectively,where all starred quantities are nondimensional. In using the thin electrical double layer approximation, the fluid boundary conditions are simplified to a slip velocity equal to the electroosmotic velocity due to the zeta potential of the surface (Keh and Anderson 1985). On the channel walls, this results in a velocity boundary condition

$${{\mathbf{u}}}^* = \gamma({{\mathbf{I}}} - {{\mathbf{nn}}}) \cdot \nabla^* \phi^* \, \hbox{on} \, \Gamma_w $$
(1)

where the velocity, u*, depends upon the ratio of zeta potentials, γ = ζ w /ζ p , and the gradient of the electrical potential, ϕ*, at the surface. This velocity condition also exists at the particle surface but must also include the motion of the particle surface

$${{\mathbf{u}}}^* = {{\mathbf{U}}}_p^* + \omega_p^* \times ({{\mathbf{x}}}_p^*-{{\mathbf{X}}}_p^*)+({{\mathbf{I}}} - {{\mathbf{nn}}}) \cdot \nabla^* \phi^* \quad \hbox {on}\, \Gamma_p. $$
(2)

The translational velocity vector, U p *, rotational velocity, ω p *, position vector of the particle surface, x p , and position vector of the particle center, X p , combine to give the motion of the particle which adds to the electroosmotic fluid velocity to yield the surface velocity boundary condition. These boundary conditions are used with the Stokes equations to solve for the fluid flow

$$\nabla^* \cdot {{\mathbf{u}}}^* = 0 \quad \hbox{in}\, \Omega$$
(3)
$${\nabla^*}^2 {{\mathbf{u}}}^*+\nabla^* p^* =0 \quad \hbox{in}\, \Omega$$
(4)

where p is the pressure.

The electrical potential, ϕ*, is governed by Laplace’s equation

$${\nabla^*}^2\phi^*=0 \quad \hbox{in} \, \Omega $$
(5)

as well as the applied voltage between the inlet and outlet and insulating particle and channel surfaces

$$\phi^* = 1 \quad \hbox{on} \, \Gamma_{\rm in}, \quad \phi^*=0 \quad \hbox{on}\,\Gamma_{\rm out}$$
(6)
$$ {{\mathbf{n}}} \cdot \nabla^* \phi^* = 0 \quad \hbox{on} \, \Gamma_w \, \hbox{and} \, \Gamma_p.$$
(7)

Here n represents a unit normal vector pointing from the particle or channel surface into the fluid domain.

The motion of the particle is determined by solving Newton’s 2nd law for the velocity of the particle from the force and torque exerted by the fluid system. The force and torque exerted on the particle are found by integrating the surface stress tensor over the surface of the particle

$${{\mathbf{F}}}^*=m^* \frac{\hbox{d} {{\mathbf{U}}}_p^*}{\hbox{d}t^*} =\int \sigma^* \cdot {{\mathbf{n}}} \hbox{d} \Gamma_p^*$$
(8)
$${{\mathbf{T}}}^*=I^* \frac{\hbox{d} \omega_p^*}{\hbox{d}t^*}=\int ({{\mathbf{x}}}_p^*-{{\mathbf{X}}}_p^*) \times (\sigma^* \cdot {{\mathbf{n}}})\hbox{d}\Gamma_p^*. $$
(9)

The surface stress tensor arises from the interaction of the fluid motion and the particle surface and is defined as

$$\sigma^* =-p^* {{\mathbf{I}}} + [\nabla^{*}{{\mathbf{u}}}^{*} + (\nabla^{*} {{\mathbf{u}}}^{*})^{T}].$$
(10)

The quantities (force, torque, stress tensor, mass, moment of inertia, and time, respectively) used to solve for the particle motion are nondimensionalized as above: F = μU ∞ a F*, T = μU ∞ a 2 T*, \(\sigma=\frac{\mu U_{\infty}} {a} \sigma^*, \, m=\frac{\mu a^2}{U_{\infty}} m^*, \, I=\frac{\mu a^4} {U_{\infty}}I^*, \, \hbox{and} \, t= \frac{a}{U_{\infty}}t^*.\)

The system of equations is solved using a commercial finite element package, Comsol Multiphysics (Comsol, Inc.; Burlington, MA, USA). The current results are based upon two dimensional models, representing the central plane of either a cylindrical or square channel, due to limitations of computer resources. A previous comparison between two and three dimensional results showed that the three dimensional results were more accurate (0.5 vs. 4%) in comparison to other published results (Davison and Sharp 2006). However the two dimensional results demonstrated the same trends in the motion of the particle and so are used herein with confidence that the behavior seen is a good representation of what would be expected in three dimensions. The computational domain, Ω, is meshed with unstructured triangles. As seen in Fig. 1a, the mesh density is increased around the particle due to the more complicated motion in that region. The particle is initially at rest, though the electric field and subsequent motion are established instantaneously once the model begins. At each time step, the system of equations for the electric field and fluid motion is solved directly. An iteration scheme is used to solve the ordinary differential equations for the particle motion, the forces and torques present at the particle surface. Additional second order elements are added to the variable set and used to solve for the particle surface stress tensor. These additional variables are used instead of differentiating the velocity components of the solution in order to increase the accuracy of the solution. Once the particle motion has been solved for, the particle is moved by deforming the mesh according to an arbitrary Langrangian–Eulerian (ALE) scheme. After the mesh deforms to a designated point of decreased quality, a new geometry is created on which a new mesh is applied and the process repeated to model large particle motions.

4 Results and discussion

As indicated earlier, the equation system is nondimensionalized and as such the results are presented nondimensionally. The constants are chosen to model a system whose dimensions are based upon a particle radius, a = 1.5 μm and aqueous fluid properties. The base particle has an aspect ratio of l/a = 6 and moves through a channel with a width of b/a = 10 and horizontal and vertical segments of L/a = 25. To determine the effect of the corner on the electrophoretic motion of the particle, transient simulations were run exploring the effect of varying the zeta potential ratio, channel width, particle aspect ratio, initial angle of the particle, and initial vertical position of the particle on the motion of the particle. Typical results include a trajectory plot of the position of the center of the particle graphed against nondimesional X* and Y* coordinates (X* = X/a, Y* = Y/a). The angle of the particle is presented against the nondimensional time elapsed. The angle is given in degrees for ease of interpretation, but is calculated in nondimensional radians. The results obtained are assembled based on the impact of the parameter on the particle motion.

4.1 Parameters with minimal impact on particle motion

4.1.1 Effect of zeta potential ratio

The zeta potential of the channel walls was varied to produce cases with γ = 0.375 and 0.75. The aspect ratio of the particle was held at l/a = 6, the channel width was b = 10, and the initial angle of the particle was θ0 = 0°. The results of these tests are presented in Fig. 2. The trajectories for the two cases are presented in Fig. 2a, and indicate that the cylindrical particle travels an identical path for the zeta potential ratios tested. Likewise, Fig. 2b includes the angle of the two particles against time and demonstrates the two cases have the same angular behavior to within ±1°, but over two different time scales. This behavior is also clear in the trajectories plot (Fig. 2a), because each successive data symbol is given for five nondimensional time units of motion. Changing the zeta potential ratio (γ) of the system changes the ratio of the fluid and particle velocities, which are in opposite directions for 0 < γ < 1. By increasing γ, the fluid velocity was increased in the direction opposite to the particle motion resulting in a lower particle velocity. The change in γ did not alter the effect of the corner geometry on the cylindrical particle as the only differentiating characteristic is the time scale of the motion.

Fig. 2
figure 2

Effect of the zeta potential ratio, γ, on the motion of a cylindrical particle with l/a = 6, b = 10, and θ0 = 45°. a Trajectories of the particles with zeta potential ratios of γ = 0.375 and 0.75. The channel boundaries are included for reference. Data symbols are given for every 5 nondimensional units of time. b Change in the angle (degrees) of the particle as a function of time

Full size image

4.1.2 Effect of channel width

A particle with an aspect ratio of l/a = 6, zeta potential ratio of γ = 0.375, and initial angle of θ0 = 0° was modeled in channels with widths of b = 6, 10, and 15. Figure 3 contains the trajectories and angular time histories of these cases. The particles are shown, in Fig. 3a, to travel the same path in the horizontal and vertical sections of the channels, with the only variations in trajectories in the corner region. The physical shape of the channel leads to this result, as the channel geometries sketched in Fig. 3a indicate that the larger the channel width the larger the radius of the trajectory in the corner. Another result present in the trajectory plot is that the particle translates slower in a channel with smaller width. The influence of boundaries on the translation of particles is a balance of two competing effects, one which increases the particle and fluid velocities and the other which decreases particle velocity. Specifically, for smaller separations the electric field is increased between an insulating particle and insulating walls resulting in increased particle and fluid velocities, and the hydrodynamic drag caused by the wall on the particle is also increased which decreases particle velocity (Davison and Sharp 2006). In this case, the increase in drag is dominant resulting in slower translation of the particle as the channel width is decreased. This change in translational velocity is indicated by the symbols in the trajectory plot which are five nondimensional time units apart, and Fig. 3b where the particle angle is plotted against nondimensional time. As expected, the angle of the particle increases substantially as the particle passes through the corner region, this increase occurs earlier the larger the channel width. Essentially, as is shown in Fig. 3a, the particle cuts across the corner (and rotates) sooner because the corner occurs at a more negative value of X* in a larger channel. Within the system modeled, the angle of the particle reaches a larger value as the channel width is decreased. As the particle exits the corner, its angle is around 50°–60°, and the ends of the cylinder interact with the wall in differing amounts depending on the channel width. As the channel width is reduced, the interaction is increased leading to greater hydrodynamic drag on the ends which yields a greater torque on the particle. This trend is evident in Fig. 3b where the particles in smaller channels rotate to angles closer to 90° (vertical) than the larger channels.

Fig. 3
figure 3

Effect of the channel width on the motion of a cylindrical particle with l/a = 6, γ = 0.375, and θ0 = 0°. a Trajectories of the particles for channels with widths of b = 6, 10, and 15 units. The channel boundaries corresponding to each data curve are included in the matching line type. Data symbols are given for every 5 nondimensional units of time. b Change in the angle (degrees) of the particle as a function of time

Full size image

4.1.3 Effect of aspect ratio

To determine the effect of the particle aspect ratio, the length (l) of the particle was varied to produce aspect ratios of l/a = 2 (sphere), 4, 6, and 8. The particle motion was simulated through a channel with a width of b = 10, a zeta potential ratio of γ = 0.375, and initial angle of θ0 = 0°. The trajectories and angular motion are presented in Fig. 4. The trajectories show that the particles travel nearly the same path through the channel. In the vertical section, there is some differentiation among the paths with longer particles trending toward the right hand wall (+X* direction), but the change in position is small, less than two particle radii. The trajectory plot also indicates that longer particles translate at a reduced velocity, due to increased fluid drag along their larger surface areas. The motion of the spherical case (l/a = 2) is substantively similar to the trajectory of a sphere in a T-junction under an equivalent electric field presented in Ye and Li (2004). In the angle plot, Fig. 4b, the spherical particle only experiences torque, and therefore a change in angle, in the corner region where the electric and fluid fields are not uniform around the sphere. For the remainder of the cases, the ends of longer particles are closer to the channel walls which leads to increased torque on the particle and leads to the larger angles indicated.

Fig. 4
figure 4

Effect of the aspect ratio of a cylindrical particle with b = 10, γ = 0.375, and θ0 = 0°. a Trajectories of particles with aspect ratios of l/a = 2 (sphere), 4, 6, and 8. The channel boundaries are included for reference. Data symbols are given for every 5 nondimensional units of time. b Change in the angle (degrees) of the particle as a function of time

Full size image

4.2 Parameters of significant impact on particle motion

4.2.1 Effect of initial angle

The initial angle (to the horizontal) of the particle was varied from θ0 = 90° to −75°, which covers the complete range of angles since θ = 90° = −90°, while holding the particle aspect ratio of l/a = 6, channel width of b = 10, and zeta potential ratio of γ = 0.375 fixed. For clarity, the results of selected values of initial angle are presented in Fig. 5. The trajectory plot in Fig. 5a demonstrates that there is a difference in trajectory as a function of initial angle. The cases for θ0 = 0° and 90° translate down the center of the horizontal section of the channel, which follows from symmetry of the electric and fluid fields. The cases with positive initial angles translate upwards in the Y* direction, while the negative initial angle cases translate downwards in the −Y* direction. This correlates to earlier work on translation in a straight channel in which the flow around an angled particle causes it to translate in the direction its leading edge is translating (Davison and Sharp 2007). This previous observation also explains the trajectory of the particles in the vertical section. The two cases with negative initial angle move from right to left (−X* direction) across the vertical section. After the corner, the leading edge of these particles is oriented toward the −X* + Y* quadrant, leading to an observed translation in the −X* + Y* direction. Similarly, the positive initial angle particles are oriented toward the + X* + Y* quadrant (after the corner), but at an angle closer to vertical so the motion in the + X* direction is not as pronounced. The trajectory plot also indicates that the particle moves slower as its angle is increased as a result of the increased drag from a larger area exposed to the flow (Davison and Sharp 2007).

Fig. 5
figure 5

Effect of the initial angle of a cylindrical particle with l/a = 6, b = 10, and γ = 0.375. a Trajectories of particles with initial angles of θ0 = 90°, 60°, 30°, 0°, −30°, and −60°. The channel boundaries are included for reference. Data symbols are given for every 5 nondimensional units of time. b Change in the angle (degrees) of the particle as a function of time. Dashed lines indicate θ = 90° and −90° which is when a particle would be aligned with the vertical centerline

Full size image

The angular motion of the particle is shown in Fig. 5b. It is clear that there exist two distinct rotational motions through the corner region, for these cases. With an initial angle of θ0 = 0° to 60° the particle rotates toward a larger value of θ as the particle moves through the corner, and all the cases end at a value of θ around 70°. The cases of θ0 = −30° and −60° pass through the corner while rotating to a more negative value of θ and finish around −60°. The corner is influencing all the cases to trend toward an alignment with the vertical channel, an angle of 90° or −90°. To clarify, the absolute value of the angle the particle makes to the vertical direction, θ′ is plotted in Fig. 6a. The value of θ′ is found by defining θ′ = 90° − |θ|. The plot of θ′ demonstrates that the initial angle to the vertical is reduced by passing the particles around the corner. The initial spread of 90° is reduced to 29.9° at the end of the current computational domain. The change in θ′ is presented visually in Fig. 6b, where the initial angular positions of the particle cases are shown in diagram (i) and the final positions in diagram (ii). Each particle retains its shading from (i) to (ii) in Fig. 6b. The reduction in angle is very promising as it demonstrates a corner geometry could be a possible means to passively exert control over the particle orientation. However, this positive control element comes with restrictions. The angle reduction neither continues to improve nor remains constant if the motion is allowed to continue in a straight channel. Previous studies have shown that an angled cylindrical particle moving electrophoretically through a straight channel will oscillate in angle and position perpendicular to the channel axis (Davison and Sharp 2007). This restricts the positive aspects of this control element to near the channel lengths investigated herein, namely around 25 particle radii from the corner.

Fig. 6
figure 6

Description of the change in angle of cylindrical particles after passing through a 90° corner. a Change in absolute value of angle (degrees) with respect to the vertical direction, θ′ = 90 − |θ|. b Diagrams of the initial and final angular positions of the cylindrical particles. The shading designates a specific particle’s initial and final angular positions

Full size image

4.2.2 Characteristic motion through corner

In Fig. 5b, there seems to be two distinct classes of motion through the corner among the selected cases for that plot. When all cases are examined, it is clear that there are actually three distinct classes of angular motion through the corner, the two classes noted from Fig. 5b and a third borderline class. Figure 7a shows the angular motion of every case of initial angle modeled, and the division into the three classes of motion. The motion designated as Class I consists of particles with initial angles from θ0 = −10° to 90° which tend to increase in angle by moving through the corner. These particles have angles of θ f = 60° to 90° (to the horizontal) at the end of the modeled motion. In Fig. 7b, the Class I motion is demonstrated by a series of images from the motion of the θ0 = 45° case. Class II consists of particles with initial angles from θ0 = −20° to −75° that tend toward more negative angles through the corner. Final angles of θ f = −40° to −80° are seen in these cases. A series of images from the θ0 = −45° case illustrate this motion in Fig. 7b. Finally, the θ0 = −15° motion is the borderline case labeled as Class III and depicted in the final series of images in Fig. 7b. The behavior seen is a result of the electric field present in the corner of the channel. The curve of the electric field lines around the corner causes a region of higher electric field near the inner corner, with a corresponding drop in electric field near the outer corner, as shown in Fig. 1b. In electrokinetic flow, the magnitude of the electric field determines the magnitude of the velocity. As a particle undergoing Class I motion approaches the corner, its positive angle nearly aligns the particle with the electric fields lines resulting in the entire particle being moved around the corner following the electric field lines. This is contrasted by Class II motion where the negative angle of the particle means that the trailing edge is in the higher electric field and is made to move faster than the other end, rotating the particle to nearly −90° and becoming the new leading edge. Class III motion acts similarly, where the trailing edge is accelerated through the corner, but only to the point where the particle is nearly horizontal upon exit from the corner.

Fig. 7
figure 7

Description of the three characteristic motions of a cylindrical particle through a 90° corner. a Change in the angle (degrees) of the particles as a function of time. Particles with initial angles from θ0 = −10° to 90° make up the type of motion designated as Class I. Particles with initial angles from θ0 = −20° to −75° make up the type of motion designated as Class II. The bordering case is that of a particle with an initial angle of θ0 = −15° and designated as Class III. b Representative diagrams showing the three classes of motions of a cylindrical particle as it travels around a 90° corner. The particle is initially located in the center of the channel, five nondimensional units from Γout at angles of 45°, −45°, and −15° to the horizontal. An image is presented at the initial location and then once every six nondimensional time units until the particle center reaches five nondimensional units from Γin

Full size image

4.2.3 Effect of initial position

The initial vertical position in the channel was varied by one nondimensional unit up and down to determine the effect on the motion of a particle with an aspect ratio of l/a = 6, channel width of b = 10, zeta potential ratio of γ = 0.375, and initial angle of θ0 = 0°. The trajectory and angle plots are presented in Fig. 8. Due to the added computational complexity of having a particle closer to the walls, the particles were started from a position of X 0* = −10 instead of X 0* = −25. Figure 8a shows that the trajectories of the particles are dependent on their initial position, with the particles maintaining the same order in the channel in the vertical section as initially present. All three cases seem to be translating a small amount in the + X* direction, as would be inferred from the positive angles of the particles, leading to a reduced horizontal separation compared to the initial vertical separation. The varying proximity to the inner corner is evident in the varied velocities through the corner. The Y 0* = + 1 case translates with the greatest velocity through the corner since it is nearest the high electric field region. Oppositely, the Y 0* = −1 case is the furthest away and translates the slowest. The angular motion in Fig. 8b, demonstrates the effect of the walls on the rotation of the particles. The Y 0* = −1 case exits the corner and is located closer to the right wall which results in greater torque on the particle and a larger angle compared to the Y 0* = 0 case. The different shape of the Y 0* = +1 case is a result of the interaction of the trailing edge of the particle to the high electric field region of the inner corner. Here the trailing edge is accelerated, causing the angle of the particle to decrease until the particle leaves the corner region and the boundary induces the increase in angle seen of the remainder of the angular plot.

Fig. 8
figure 8

Effect of the initial position of a cylindrical particle with l/a = 6, b = 10, γ = 0.375, and θ0 = 0°. a Trajectories of particles with initial positions of Y 0* = 1, 0, and −1 units. Particles started from X 0* = −10 instead of X 0* = −25 due to increased computational difficulties with particles passing closer to the corner. The channel boundaries are included for reference. Data symbols are given for every 5 nondimensional units of time. b Change in the angle (degrees) of the particle as a function of time

Full size image

5 Summary

The transient motion of a cylindrical particle under electrophoresis was modeled as the particle moves through a 90° corner. One goal of the paper was to investigate various parameters and geometries of the system to fundamentally determine the effect on the motion of a cylindrical particle. The trajectories of the particles were simulated numerically using a deformable mesh to capture the particle motion. Changing the zeta potential of the system changed the particle velocity, but did not effect the trajectory or angle of the particle. Likewise, alterations in the channel width and particle aspect ratio had minimal effects on the trajectories of the particles. The initial angle and initial vertical position of the particle were found to have significant effects on the particle motion. The initial angle causes a variation in particle trajectory of a few particle radii, and causes three distinct classes of angular motion through the corner region. Likewise, the initial position affects the paths of the particles and the angles of the particles as they move through the corner. It is evident that there is some potential for using a corner region as a passive control element as part of a larger microfluidic system. Particles passing through the corner with an initial distribution of angles to the vertical of 90°, exited the corner with a difference of angle of less than 30°. However, this effect is limited to the region immediately surrounding the corner suggesting that to be useful it would have to be used in close succession with other control elements.