Introduction and Purpose

Malaria is the most nagging parasitic infection affecting humans, accounting for an estimated 300–500 million cases of malaria worldwide with 90% of annual cases reported in sub-Saharan Africa (Reiter 2008). A recent resurgence of malaria in the East African highlands involves multiple factors, ranging from climate and land use change, to drug resistance, variable disease control efforts and other socio-demographic factors (Patz et al. 2002; Pascual et al. 2006). Malaria epidemics have long been reported to occur among vulnerable populations where immunity is often non-existent or poorly developed. It is estimated that epidemic malaria causes between 12% and 25% of estimated annual worldwide malaria deaths, including up to 50% of mortality in persons less than 15 years of age (Thomson et al. 2005).

Malaria is an extremely climate-sensitive disease (Rogers and Randolph 2000) common in the tropics, (Patz and Olson 2006), but also reported in mild-to-cold climates (Hulden and Hulden 2009). Large epidemics of malaria elsewhere have been associated with climate anomalies, such as in Colombia, the Indian subcontinent, and Uganda (Bouma and van der Kaay 1996). Rainfall and temperature are the main climate factors that influence malaria transmission. Rainfall provides conducive site conditions for mosquito breeding, while humidity and temperature together affect mosquito survival (Poveda et al. 2001). Warmer temperatures shorten the mosquito life cycle, thereby increasing its population (Patz et al. 2005; Patz and Olson 2006). High temperature shortens the development time of vector-borne pathogens, accelerates vector life cycle and also decreases the incubation period of the parasite; and combined with favourable climatic conditions, the population of carrier mosquitoes increases (Kovats and Martens 2000; Atul and Nettleman 2005; Naqvi 2009; Huang et al. 2011).

Empirical studies have linked rainfall anomalies (Connor et al. 1999; Lindblade et al. 1999; Githeko and Ndegwa 2001; Thomson et al. 2005; Nkomo et al. 2006) and warmer temperatures (Pascual et al 2006; Paaijmans et al. 2010; Ngomane and de Jager 2012; Siraj et al 2014) to correspond with concomitant increases in malaria incidences. However, other studies have included other variables such as humidity and vegetation (Haque et al. 2010; Alemu et al. 2011; Lunde et al. 2013a, b). Other factors, e.g. social and economic factors—population and migration—also play a significant role (Haines et al. 2000; van Lieshout et al. 2004). Moreover, a combination of mutating malaria parasites, resource constrains and weak health systems implies low adaptive capacity (Kovats and Haines 2005). Moreover, a combination of mutating malaria parasites, resource constrains and weak health systems, alongside drug resistance and land use patterns, implies low adaptive capacity and increase in malaria (Kovats and Haines 2005; Harrus and Baneth 2005; Pascual et al. 2006; IOM 2008; Relman et al. 2008).

Mordecai et al. (2013) conclude that as temperature increases due to climate change, vector control will likely become more important, difficult and expensive in temperate areas, but some war areas may simply become too hot to support malaria. Ebi et al. (2005) assert that Zimbabwean highlands will become climatologically favourable to malaria by 2050.

A trade-off exits between fast parasite development and high mosquito mortality at temperature and rainfall ranges above or below optimum, such that high temperature does not always increase transmission. Although temperature shortens mosquito life cycle with optimal transmission occurring at 25°C (Lunde et al. 2013a, b, Mordecai et al., 2013), at very high temperatures, above 28°C, or low temperatures, below 16°C, the cycle cannot occur or become incomplete, and transmission declines dramatically (Mordecai et al., 2013, Zucker, 1996; Williams et al., 1999).

South Africa has a warm climate, and much of the country experiences average annual temperatures of above 17°C (DST 2010). Summer season begins in August and ends in April. In Limpopo Province, average annual temperature is about 22°C, with the highest temperatures, about 25°C, recorded between December and January, while the lowest is felt in July, about 15°C (Tshiala et al; 2011). Malaria transmission is distinctly seasonal and limited to warm and rainy summer months. Case notifications generally increase from November, peak in late March to May, and then decline by the end of June. Craig et al. (2004) report that, in South Africa, the average seasonal pattern in malaria incidence follows periodicity in rainfall and temperature with a 3–4 months lag. Although we find this lag time rather long, elsewhere, the response time is not uniform. One plausible explanation to this is that lag time itself could be temperature sensitive because of the temperature-sensitive development rate of larval mosquitoes and extrinsic incubation period of the parasite. In the East African Highlands for example, Zhou et al. (2004) finds a 1–2 and 2–5 month lag for minimum and maximum temperature, respectively, while Briet et al. (2008) and Hashizume et al. (2009) report rainfall lag time of 0–3 and 2–3 months for Sri Lanka and Kenya, respectively.

Malaria is endemic in the low-altitude areas of South Africa at the border with Mozambique and Zimbabwe. Specifically, transmission is prevalent in three provinces: KwaZulu-Natal, Limpopo, and Mpumalanga province (Sharp et al. 1998; Gerritsen et al. 2008; Ngomane and de Jager 2012; Kondo et al. 2002). Limpopo Province (Approximately 22–25°S, 27–32°E) lies in the low-altitude area pre-disposed to malaria due to warm conditions. The occurrence of malaria cases in the province has been reported to be highly dependent on seasons (Bouma and van der Kaay 1996). Interventions through the malaria control programme in South Africa rely heavily on the intermittent use of indoor residual spraying in periods shortly after heavy rains when malaria cases tend to rise. This programme continues despite no empirical evidence that rainfall drives malaria in the province. Therefore, there is a need to establish the relative importance of rainfall and temperature in malaria transmission for effective malaria control. It is important to understand the relative importance, strengths, and direction of causality of climate-malaria drivers, as well as the role of rainfall and temperature as it relates to malaria dynamics in the short and long run. This is central in enhancing malaria’s control policy measures and informing the design of malaria’s early warning systems. Due to the fact that climate change by itself will increase vulnerability (Bohle et al. 1994; van Lieshout et al. 2004), target planning is necessitated by careful consideration of all factors.

Despite reported reduction in malaria trends in South Africa through a combination of various social, economic, and policy efforts (Blumberg and Frean 2007), the impact of recent climate change on malaria incidence remains poorly understood. Little is written about climate impacts on malaria in Limpopo Province. While Shewmake (2008) does not mention malaria in a study of household vulnerability to climate change, Gerritsen et al. (2008), on the other hand, provide only an overview of seasonal malaria incidence and mortality, and detect trends over time and places in the province.

This study uses Spatio-temporal, correlation, and econometric approaches (unit root tests and causality tests) to achieve the above aims. The spatial method examines the distribution of malaria at the district level within the province, while Pearson Correlation determines the direction and strength of the linear relationship between malaria with the meteorological variables. The econometric approach is applied to (1) validate and examine the intrinsic characteristics (stationarity) of malaria cases, rainfall, and temperature; (2) test the direction and relative strength of causation; and (3) ascertain the short-run and long-run equilibrium relationship of the variables. The strength of econometric methods lies in their ability to distinctively separate the effects of correlation from those that are related to causality, thereby eliminating the common fallacy that correlation implies causation. Causality is tested using the standard Granger Causality Test.

Conceptual Framework

The conceptual framework for this study advances a multiple-factor explanation for malaria, ranging from climate and land use change, to drug resistance, variable disease control efforts, and other socio-demographic factors. Figure 1 below illustrates a simplified, non-detailed interrelationship. This study looks at the climate-malaria interrelationship.

Figure 1
figure 1

Malaria-environment nexus

Full size image

Methods

Data and Sources

Monthly average rainfall and temperature along with the number of malaria cases from January 1998 to July 2007 are used. Climate data were obtained from the South Africa Weather Services, while malaria data were obtained from South African Department of Health and Malaria control Centre in Tzaneen, captured through passive and active surveillance systems. Details of the methods on how this data were collected can be obtained from Gerritsen et al. (2008).

Description of Methods

Spatio-Temporal and Correlation

The spatial distributions of malaria at municipality and district levels were mapped using the inverse distance weighted (IDW) interpolation routine in ArcGIS. The IDW routine assumes that each measured point has a local influence that diminishes with distance e.g. in Baltas (2007). It gives greater weights to points closest to the prediction location, and the weights diminish as a function of distance. Malaria records for the various municipalities were spatially weighted and aggregated at the district level (Fig. 2). Weighted points at the centroid of each district were then interpolated using the IDW following (Jorgensen et al. 2010; Messina et al. 2011; Hanafi-Bojd et al. 2012). Given seasonalised climate variables, a linear relationship between temperature, rainfall, and malaria cases can be derived from the Pearson Correlation coefficients as reported by Wilks (1995). The linear relationship between temperature and malaria cases with the influence of precipitation can be determined as a partial correlation (Panofsky and Brier (1968) and Mardia et al. (1979).

Figure 2
figure 2

Ten-year municipal and district spatial distribution of malaria in Limpopo Province

Full size image

Econometric Approaches

Causality

In order to determine causality, Granger (1969) proposed a time series data-based approach. Intuitively, the standard Granger causality test examines whether past changes in one variable, y, help explain current changes in another variable, x, over and above the information provided by the lagged values of x. If not, then one concludes that “y does not Granger-cause x”. To determine whether causality runs in the opposite direction, from x to y, one basically repeats the experiment, but with the variables interchanged. The null hypothesis that y does not Granger-cause x is rejected if the coefficients in the equation are jointly significant based on the standard F test.

There are three different types of situations in which a Granger causality test can be applied and four possible feasible outcomes. The situations are (i) a simple Granger causality test with two variables and their lags, (ii) a multivariate Granger causality test with more than two variables, and (iii) Granger causality in a Vector Autoregression (VAR) framework (VAR is an econometric model used to capture the linear interdependencies among multiple time series). For the purposes of this study, we focus on the second situation (multivariate Granger causality) since we have three variables: malaria cases, rainfall, and temperature. The four feasible outcomes are (1) independence; here, neither malaria cases, rainfall, nor temperature, Granger-cause each other; (2) unidirectional Granger causality where rainfall or temperature independently Granger-causes malaria cases, but not the other way round; (3) unidirectional Granger causality where malaria cases cause rainfall or temperature independently, but not vice versa; and (4) bi-directional (or feedback) causality where malaria cases, rainfall, and temperature Granger-cause each other. Theoretically, it is expected that rainfall and temperature influence malaria cases. A bi-directional causality is expected between rainfall and temperature. We do not expect malaria cases to cause rainfall or temperature.

Stationarity (Unit Root) Test

As a requirement for time series analysis, this paper first studies the univariate characteristics (stationarity) of rainfall, temperature, and malaria cases in this study using the standard Augmented Dickey–Fuller (ADF) (Dickey and Fuller 1981) and Kwiatkowski, Phillips, Schmidt and Shin (KPSS) tests (Kwiatkowski et al. 1992). Stationarity is a process where the parameters of the process do not change with time, i.e. the mean, variance, and autocorrelations are constant in time, while the non-stationary variable is otherwise. A non-stationary variable can be transformed into a stationary process by either adjusting for trends or including a time index as an independent variable in the regression. Sometimes de-trending and inclusion of a time index may not be sufficient to make the series stationary due to the possibility that statistics for changes in the series between periods and seasons are constant, in which case, the data are differenced. Differencing implies transforming the variables into a series of period to period and/or season to season differences. A stationary series is denoted as I (0) but when the series is differenced once, it is said to be integrated to order one, i.e. I (1) and a twice difference is I (2).

In econometrics, testing for stationarity is an indispensable requirement for two main reasons. First, without stationarity tests, it is not possible to obtain any meaningful sample statistics such as means, variances, and correlations with other variables. Secondly, stationarity tests provide important clues in the search for an appropriate methodology and forecasting model. Although it is known from the literature that combining stationary variables with non-stationary variables in a regression model yields spurious (non-sensical) results and, therefore, an unreliable outcome (Komen and Kapunda 2006; Gupta and Komen 2009), models now exist that regresses both stationary and non-stationary data. The recourse lies in the recently developed Autoregressive Distributed Lag (ARDL)-Wald (Bounds) test framework by Pesaran and Shin (1999).

Autoregressive Distributed Lag (ARDL)–Bounds Test Model

The ARDL methodology is applicable in testing causation and long-term relationship in cases where not all variables are integrated to the same order. Cointegration (long-run relationship) is a situation where two or more series are non-stationary, but a linear combination of them is stationary. The advantage of using the ARDL–Bounds test in testing cointegration is that while the conventional cointegration method estimates the long-run relationships within the context of a system of equations, the ARDL method employs only a single reduced form equation (Pesaran and Shin 1999). Most importantly, the ARDL framework avoids the larger number of specifications to be made in the standard cointegration test, such as decisions regarding the number of endogenous and exogenous variables to be included, the treatment of deterministic elements, as well as the optimal number of lags to be specified (Duasa 2007). The procedure can be applied irrespective of whether the regressors are stationary or non-stationary, or mutually cointegrated (Pesaran et al. 2001).

Model Specification

The ARDL specification takes the following form:

$$ \Delta \ln {\text{mala}}_{t} = \upgamma + \sum\limits_{i = 0}^{\upeta } {\upalpha_{i} \Delta \ln {\text{rain}}_{t - i} + \sum\limits_{i = 0}^{\upeta } {\updelta_{i} \Delta \ln {\text{temp}}_{t - i} + \sum\limits_{i - 1}^{\upeta } {\uppi_{i} \Delta \ln {\text{mala}}_{t - i} } + } } \upbeta_{1} \ln {\text{rain}}_{t - 1} + \upbeta_{2} \ln {\text{temp}}_{t - 1} + \upbeta_{3} \ln {\text{mala}}_{t - 1} + \upepsilon_{t - 1}, $$
(1)

where ln mala is the natural logarithm of malaria cases; ln rain is the natural logarithm; ln temp is the natural logarithm; Δ denotes the first difference operator; η is the optimal lag length; β1, β2, and β3 are the long-run coefficients; αi δi and ϖi represents the short-run dynamics; and ɛ is the random disturbance term.

The F test is performed on null hypothesis (H0) of no long-run relationship among variables (estimation of Eq. (1)) which are tested against an alternative hypothesis (H1), as presented below:

$$ \begin{aligned} {\text{H}}_{0} = \upbeta_{1} = \upbeta_{2} = \upbeta_{3} = 0 \\ {\text{H}}_{1} = \upbeta_{1} \ne \upbeta_{2} \ne \upbeta_{3} \ne 0\\ \end{aligned}. $$

The absence of a long-run equilibrium relationship between the variables coincides with zero coefficients for ln rain t−1, ln temp t−1, and ln mala t−1. A rejection of H0 implies that we have a long-run relationship.

The ARDL estimation proceeds in two steps. First is the estimation of Eq. (1) by ordinary least squares in order to establish the existence of a long-run linear relationship. Once cointegration is confirmed, the second step is to estimate the long-run coefficients (Eq. 2).

$$ \ln {\text{mala}}_{t} = \upgamma_{1} + \sum\limits_{i = 0}^{\upeta } {\upalpha_{1i} \ln {\text{rain}}_{{_{t - i} }} + \sum\limits_{i = 0}^{\upeta } {\updelta_{1i} \ln {\text{temp}}_{t - i} + \sum\limits_{i - 1}^{\upeta } {\uppi_{1i} \ln {\text{mala}}_{t - i} + } } \upepsilon_{t - 1} } $$
(2)

The investigation of the long-run relationship using the ARDL approach involves the estimation of Eq. (2), through an unrestricted error correction model (UECM). Since specification assumes that the disturbances are serially uncorrelated, the choice of appropriate lag order is important (Sultan 2010). The appropriate lag length in the ARDL model is selected by either Akaike Information Criterion or the Schwarz Bayesian criterion (SBC). The lag length that minimises SBC is selected. The unrestricted model is then estimated and progressively reduced, eliminating the statistically insignificant coefficients, and reformulating the lag structure where appropriate, to achieve orthogonality. The unrestricted ECM minimises the possibility of estimating spurious relations, while retaining the long-run information, suitable for economic interpretation (Greenidge et al. 2009). A battery of diagnostic tests can then be used to check the performance of the UECM (Akinboade et al. 2008; Hendry et al. 1984 in Sultan 2010).

The short-run dynamics is derived from the ARDL specification, Eq. (3), by constructing and error correction model (ECM), Eq. (4):

$$ \Delta \ln {\text{mala}}_{t} = \upgamma_{2} + \sum\limits_{i = 0}^{\upeta } {\upalpha_{2i} \Delta {\text{ln rain}}_{t - i} \, + \,\sum\limits_{i = 0}^{\upeta } {\updelta_{2i} \Delta {\text{ln temp}}_{t - i} + \sum\limits_{i - 1}^{\upeta } {\uppi_{2i} \Delta {\text{ln mala}}_{t - i} + } \sigma {\text{ECM}}_{t - 1} + \upepsilon_{t - 1} } }, $$
(3)

where ECM is the error correction term, defined as

$$ {\text{ECM}}_{t} = \ln {\text{mala}}_{t} - \upgamma_{1} - \sum\limits_{i = 0}^{\upeta } {\upalpha_{1i} \ln {\text{rain}}_{t - i} - \sum\limits_{i = 0}^{\upeta } {\updelta_{1i} {\text{ ln temp}}_{t - i} + \sum\limits_{i - 1}^{\upeta } {\uppi_{1i} {\text{ln mala}}_{t - i} } } }. $$
(4)

All coefficients of the short-run equation are coefficients relating to the short-run dynamics of the model’s convergence to equilibrium, and σ represents the speed of adjustment.

The F test is used to test the existence of long-run relationship.

The asymptotic distribution of the obtained F statistic is nonstandard regardless of the degree of integration of the variables. This, however, depends on whether (1) the variables included in the ARDL model are I (0) or I (1), (2) the number of regressors, (3) the model contains an intercept and/or a trend, and (4) the sample size. Two sets of critical F values, representing the lower bound and the upper bound, have been provided by Pesaran and Shin (1999) for large samples. Narayan (2004) presents the critical F values for sample size ranging from 30 to 80. If the computed F statistic for a chosen level of significance lies outside the critical bounds, a conclusive decision can be made regarding the cointegration of the regressors. If the statistic is higher than the upper bound, the null hypothesis of no cointegration can be rejected, and the next step is to estimate the ARDL ECM where the short-run and long-run elasticities may be determined (Narayan 2004; Pesaran and Shin 1999 in Sultan 2010).

Computed and critical bounds of the F Statistic are provided by Pesaran et al. (2001). The F statistics should lie outside the bounds for a long-run relationship to exist, but for short-run relationship, the coefficient of the ECM should be negative and statistically significant.

Results

Spatio-Temporal and Correlation Results

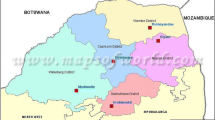
The number of malaria cases at the district level shows that malaria is high in the Mopani and Vhembe districts throughout the study period of analysis, 1998–2007. The Vhembe district consistently shows more malaria cases. In the Mopani district on the other hand, malaria cases appear to be erratic, as shown on the maps. The overall trend shows that, whereas there were fewer cases in 1998, this was followed by a slight increase from 1999 to 2006. Very few cases were reported in Capricorn, Waterberg, and Greater Sekhukhune.

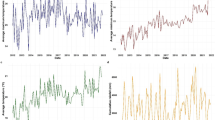
Figure 3 shows a scatter plot for rainfall and temperature with malaria cases. More observations are scattered away from the fitted line in the first panel (rainfall) than in the second panel (temperature). This indicates a high positive correlation with temperature than rainfall with an R 2 of 57.8%.

Figure 3
figure 3

Correlation of rainfall and temperature with malaria—a graphical outlook

Full size image

Figure 4 illustrates the trend relationship between average rainfall and average temperature in relation to malaria cases.

Figure 4
figure 4

Plot for average rainfall, average temperature, and malaria cases

Full size image

This reveals a very strong positive correlation between rainfall and temperature with malaria cases, although higher rainfall does not increase malaria cases significantly (e.g. 1999, 2001, and 2005). An increase in temperature is, however, consistent with an increase in malaria cases. The actual influence is further validated by statistics using the cross-correlation method. This study finds a strong positive correlation of climate variables to malaria cases, with temperature exhibiting a stronger influence as compared to rainfall. The coefficients for temperature and rainfall are found to be 0.5212 and 0.2810, respectively.

Results for Causal Relationships

Table 1 presents Granger causality test results.

Table 1 Causal Relationships.
Full size table

Rainfall Versus Malaria Cases

We find a unidirectional causality from rainfall to malaria cases. For 117 observations, at a 5% significance level, the computed F statistic is equal to 3.89071 with P = 0.0232 implies that the null hypothesis that rainfall does not granger-cause malaria is rejected. Rainfall, therefore, influences malaria but reverse is not true. We do not reject the null hypothesis that malaria granger-causes rainfall since the F statistic equal to 1.44730 with P = 0.2396.

Temperature Versus Malaria Cases

We also find a unidirectional causality from temperature to malaria cases. The computed F statistic is 20.0805 with P < 0.001 implying that reject the null hypothesis that temperature does not granger-cause malaria cases while from malaria cases to temperature, the F statistic is 0.07211 with P = 0.9305, implying malaria cases does not granger-cause temperature.

Temperature Versus Rainfall

This study finds a bi-directional causality between temperature and rainfall at 1% level of significance. The F statistics for the causation from temperature to rainfall and from rainfall to temperature are 19.80 and 17.14, respectively, with P < 0.001, in both cases meaning that rainfall influences temperature and vice versa.

Stationarity (Unit Root) Results

Table 2 shows a summary of the stationarity test.

Table 2 Unit Root Test Results.
Full size table

The results indicate that malaria and rainfall follow an autoregressive process with a unit root as the null hypothesis is rejected for these variables, while for temperature, the null hypothesis for existence of a unit root could not be rejected, implying that rainfall and malaria cases are stationary, while temperature is non-stationary.

ARDL Results

Short-Run and Long-Run Results

These are results of estimating Eq. (1). This stationarity test result pointed to ARDL–Bounds Test as the appropriate methodology for analysis of the analysis of the short-run (in this case, variation within months) and long-run (variation in years) dynamics of rainfall and temperature as they relate to malaria. UECM results are summarised in Table 3, following similar procedure by Hendry et al. (1984) and Akinboade et al. (2008).

Table 3 Unrestricted Error Correction Model.
Full size table

The model passes all basic time series tests. There is no autocorrelation or serial correlation, and no omitted variables; variance is homogeneous and residuals are normally distributed as confirmed by Durbin Watson statistic, Ramsey RESET test, Breusch–Godfrey LM, White’s test, and Jarque–Bera test. The R 2 for the UECM is 50%, which indicates a relatively good and satisfactory fit in this case. The appropriate lag length automatically selected by SBC is 3. Empirical studies report non-uniform lag time for malarial response to climatic variation. There seems to be an average malaria response within 3 months from the onset of the rainy season. Briet et al. (2008) report rainfall lag time of 0–3 months, while Hashizume et al. (2009) report 2–3 months. Regarding temperature, Zhou et al. (2004) find minimum and maximum temperature lag time to be between 1–2 and 2–5 months, respectively.

Bounds test (cointegration) results are presented in Table 4.

Table 4 Cointegration Properties.
Full size table

The F statistic is outside the critical bounds (8.29 lies outside 4.35top and 3.23bottom). We therefore reject the null hypothesis of no cointegration at a 5% significance level and conclude that a long-run relationship (cointegration) exists between malaria and the climatic variables.

The long-run relationship is reported in Table 5, while the short-run results are reported in Table 6.

Table 5 Long-Run Relationship Between Malaria Cases with Rainfall and Temperature.
Full size table
Table 6 Short-Run Relationship Between Malaria Cases with Rainfall and Temperature.
Full size table

In both short- and long-run instances, temperature maintains a very high level of significance: 4.784184 (0.0000) and 4.557185 (0.0000); while rainfall is low in both: 0.263281 (0.1509) and 0.373873 (0.2648).

Discussion

We report GIS results of five districts (Capricorn, Greater Sekhukhune, Mopani, Waterberg, and Vhembe) in Limpopo Province. The Vhembe district consistently shows more malaria cases, while very few cases were reported in Capricorn, Waterberg, and Greater Sekhukhune throughout the period of analysis. In the Mopani district, malaria cases appear to be erratic. Spatial differences could be explained by socio-economic reasons, migration, malaria control programmes, and even climate change. Understanding the differences in spatial distribution and areas burdened is crucial for targeted control measures.

In this study, rainfall and temperature are positively correlated with malaria, while temperature shows a stronger influence as compared to rainfall. We find the correlation coefficient of temperature and rainfall to be 0.5212 and 0.2810, respectively. Positive correlation between malaria and climate variables has been reported elsewhere. Rainfall: Huang et al. (2011); for Tibet: Briet et al. (2008), for Sri Lanka. Rainfall and temperature: Craig et al. (2004); Githeko and Ndegwa (2001) studies on Kenyan Highlands in Eastern Africa. Rainfall, temperature, humidity and vegetation cover: Haque et al. (2010) for Bangladesh. In Ghana, a positive correlation was found to exist between malaria and climate elements (Nkomo et al. 2006). The strength of the effect seems to flow from humidity to temperature and rainfall. This result is consistent with Huang et al. (2011), who found the correlation coefficients for Tibet to be 0.518 and 0.348 for temperature and rainfall, respectively, concluding that temperature had a greater influence on malaria.

Regardless of the greater influence of temperature, warming and rainfall would create the conditions for malaria vectors to thrive (Epstein et al. 1997), boost the population of disease-carrying mosquitos, and result in increased malaria epidemics (Lindsay and Martens 1998; Nkomo et al. 2006). Increases in temperature generally accelerate vector life cycles and also decrease the incubation period of the parasite (Kovats and Martens 2000; Huang et al. 2011). However, at a very high temperature, the mosquito life cycle cannot be completed and transmission cannot occur (Zucker 1996; Williams et al. 1999). It is interesting to observe a strong influence of temperature on malaria transmission in Limpopo; Ngomane and de Jager (2012), however, have reported rainfall as the main driver in the neighbouring Mpumalanga Province.

The limitations of this study relate to the fact that temperatures in the study area are limited to a range on the curve where it is linear. Also, the study did not show whether year to year variations in malaria were driven by year to year variability in temperature/precipitation. This will be the focus of the forthcoming paper.

Conclusion

This paper has utilised spatial, correlation methods as well as bound testing approach to cointegration developed within an ARDL framework to test spatial malaria distribution at district level, test the strength of correlation, and determine the existence of a long-run equilibrium relationship between climatic variables with malaria. There is strong evidence that climate influences malaria significantly both in the short and long run. We find that malaria pressure varies in different districts. We recommend (1) a study to ascertain the thresholds of temperature and rainfall under which malaria cases are probable; (2) the development and enhancement of early warning systems for malaria at the district level; (3) strengthening collaboration, partnership, and response integration with other principle sectors, such as meteorological departments; and finally (4) long-term public health planning to combat malaria as a part of the key functions of the public health systems.