Introduction

As the frequency and intensity of heavy rainfall increase with the changing climate, extreme rainfall events, which are characterized by short duration and high intensity, become one of the major triggers of shallow landslides and debris flows, in Korea and other countries (Chou et al. 2012; Wu et al. 2011; Dahal et al. 2009; Pradhan and Kim 2015; Tsuchida et al. 2015; Vasu et al. 2016; Kumar et al. 2017; Wu 2017). Extreme rainfall-induced landslides are powerful and can cause enormous damage and catastrophic fatalities. In Korea, shallow landslides induced by extreme rainfall events have, in recent decades, caused severe damage to property, economic losses, and casualties (National Institute for Disaster Prevention 2009; Park et al. 2013; Oh and Park 2014). Therefore, a process for recognizing landslide-prone areas and evaluating the landslide hazard caused by extreme rainfall is badly needed.

Landslide hazard is defined as the probability of a potentially damaging landslide occurrence in a specific period of time and in a given area (Varnes 1984; van Westen et al. 2006). It means that in the process of assessing landslide hazards, one has to predict “where” a landslide may occur (spatial probability) and “when” it may occur (temporal probability). Landslide susceptibility is the likelihood of a landslide occurring in an area. It depends on local terrain conditions and estimates “where” landslides are likely to occur (Guzzetti et al. 2005; Reichenbach et al. 2018). Various approaches have been developed, and extensively published, for the spatial assessment of landslide susceptibility. Compared with susceptibility analysis, only limited research has sought to estimate the temporal probability of landslide occurrence (Guzzetti et al. 2005, 2006; Corominas and Moya 2008; Zêzere et al. 2008; Jaiswal and van Westen 2009; Jaiswal et al. 2010, 2011; Das et al. 2011; Martha et al. 2013; Tien Bui et al. 2013; Afungang and Bateira 2016; Vasu et al. 2016; Dikshit et al. 2020). Two main approaches have been commonly used to assess the temporal probability of the future occurrence of landslides: the physically based method (or geomechanical approach) and statistical analysis of past landslide events (Corominas and Moya 2008; Corominas et al. 2014). The physically based method considers the present slope conditions and evaluates landslide potential using stability analysis and numerical modeling. This approach may also couple the slope stability analysis with hydrological models to estimate the effect of rainfall on slope stability. It has been applied to regional-scale analyses of rainfall-induced shallow landslide susceptibility with simplified hydrological methods in a GIS platform (Crosta and Frattini 2003; Godt et al. 2008; Park et al. 2013; Chen and Zhang 2014; Corominas et al. 2014; Lee and Park 2016; Salciarini et al. 2017; Gutiérrez-Martín 2020). In addition, a probabilistic approach has been used to properly deal with uncertainties in the geotechnical and hydrological input parameters, caused by the limited and incomplete information common in a regional study. However, the deterministic approach does not easily accommodate such uncertainties especially when large spatial datasets must be obtained and processed (Park et al. 2013; Rossi et al. 2013; Raia et al. 2014; Lee and Park 2016; Chae et al. 2017; Salciarini et al. 2017). In the evaluation of temporal probability using a physically based model, the computational demands increase significantly when applied in a dynamic time-dependent modeling framework, especially in a broad study area where high-resolution DEM and time-variant rainfall patterns are used in the modeling. These extremely high computational requirements bring forth the reluctance to use the physically based models for temporal probability estimation over large areas (Rossi et al. 2013; Vasu et al. 2016; Canli et al. 2018a, b).

Statistical analysis of historical landslide records covering a long time span support estimation of the temporal probability of landslide occurrence (Brabb 1985; Guzzetti et al. 2002, 2005, 2006; Jaiswal et al. 2011; Das et al. 2011; Motamedi and Liang 2014). In this approach, the return periods of landslide events are determined from the historical landslide records, and then, the expected frequency of future landslides is obtained. Using historical data such as a multi-temporal landslide inventory, the annual probability of landslide events and the exceedance probability, which is the probability of occurrence of one or more landslides at any given time, can be calculated. The statistics involved in the approach are simple, and results are easy to implement (Jaiswal et al. 2010). However, it is quite difficult to acquire sufficiently complete multi-temporal landslide inventories for long time spans at a regional scale. In addition, because this approach is based on the historical recurrences of landslides, it is only valid for repetitive landslide conditions and is not appropriate for the prediction of unique events (Guzzetti et al. 1999; Cascini et al. 2005).

Therefore, an alternative indirect method, using the frequency of landslide triggers (such as extreme rainfall), has been suggested to estimate the temporal probability of landslides. In this approach, the temporal probability of a landslide triggering rainfall event is considered to also be the temporal probability of landslide occurrence. The advantage of this approach is that it does not require a complete multi-temporal landslide inventory because the return period of the landslides is assumed to be that of the rainfall, which can be evaluated from historical rainfall records. In this approach, a reliable relationship between rainfall and the occurrence of landslides, which is a rainfall threshold, needs to be established (Jaiswal and van Westen 2009; Jaiswal et al. 2010). The rainfall threshold is the minimum amount or duration of rainfall required to trigger landslides. Determination of the rainfall thresholds for landslide occurrence is a basic and prerequisite step for the evaluation of exceedance probability. Various methods have been proposed to determine rainfall thresholds; these tend to be either process based (physical) or empirically based (historical) (Corominas 2000; Crosta and Frattini 2001; Aleotti 2004; Wieczorek and Glade 2005; Guzzetti et al. 2007). Process-based models use a physical slope model coupled with a hydrological model to calculate the rainfall amount needed to trigger slope failures, and hence the anticipated location and time of landslides. On the other hand, empirical rainfall thresholds are defined by analysis of past rainfall events that have resulted in landslides. Recently, automated methods have been used to determine empirical rainfall thresholds for shallow landslide initiation (Vessia et al. 2014, 2016; Melillo et al. 2015), while geostatistical tools have been used to evalaute map-based empirical rainfall thresholds (Vessia et al. 2020).

Once the rainfall threshold is determined, the probability that a rainfall event will exceed the threshold can be obtained (Chleborad et al. 2006). Subsequently, the exceedance probability of rainfall events is evaluated using binomial or Poisson distribution models. However, this approach also requires the assumption that recurrent rainfall events trigger landslides. Thus, the mean recurrence interval, which is a required parameter for the evaluation of the exceedance probability using either the binomial or Poisson distribution model, should be estimated using the historical rainfall recurrence records for periods between landslide triggering events. In addition, the threshold for landslide initiation can be estimated using the correlation between rainfall events and recurrent landslide events. However, in areas where historical data are limited, for example, where an initial landslide event or a nonrecurrent landslide event has occurred under extreme rainfall, it is difficult to estimate either the mean recurrence interval or the rainfall threshold. Consequently, it is impossible to obtain the temporal probability of future landslide occurrence in such an area.

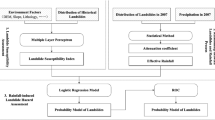
The main objective of this study was to assess the temporal probability of future landslide occurrence for a study area with limited historic landslide records. The Jinbu area, the study area of this research, experienced a large number of landslides, under extreme rainfall, in 2006. However, there are no landslide records from before or after the 2006 events. Therefore, a multi-temporal landslide inventory is not available in this area, and there are no records of recurrent landslide triggering rainfall events. Consequently, the previously mentioned approach to temporal probability is not appropriate for this study area. This study, therefore, developed a new approach to assessment of the temporal probability of future landslide occurrence using the limited rainfall records and landslide inventory. In particular, extreme value theory, which is commonly used for the analysis of extreme events, was used to evaluate the temporal probability of the future landslide occurrence. Then, the spatial probability of landslide was evaluated using a multi-layer perceptron; the temporal probability was then integrated with this spatial probability in order to estimate landslide hazard.

Study area and landslide inventory

To apply the proposed approach to a practical situation, a study area in Jinbu, Gangwon-do, Korea, was selected (Fig. 1). This area experienced a great number of landslides related to an extreme rainfall event on July 14–16, 2006. The study area lies between 37° 34′ 42.93″ and 37° 39′ 16.01″ north latitude, and between 128° 29′ 9.73″ and 128° 36′ 35.95″ east longitude. The total area is 64.74 km2, and the extents are 10.81 km east–west and 8.6 km south–north. The altitude of the study area is between 495 m and 1385 m above sea level, and more than 78% of it is mountainous terrain.

Fig. 1
figure 1

The study area

Full size image

Geologically, this area is based on Precambrian biotite gneiss, which is exposed in the southwest and on which discontinuous Jeongseon limestone and Nokan series sandstone are located. There has been an extensive intrusion of Jurassic Imgye granite, widely distributed in the study area, with deposits of quaternary alluvium along the streams and in lowlands (Geological Society of Korea 1962) (Fig. 2).

Fig. 2
figure 2

Geological map of the study area

Full size image

In this study, landslide inventory data were obtained and used for the spatial landslide susceptibility analysis. Because the study area is too large for a complete field survey, landslide locations were determined using aerial photographs with 0.5-m resolution, taken before and after the landslides. Related information is available in the authors’ prior research (Park et al. 2013). Based on these photographs, a point vector layer was constructed by digitizing the landslide locations. A total of 1035 landslide locations were digitized, and a landslide inventory map was compiled (Fig. 1).

To evaluate the temporal probability of landslide occurrence using rainfall event records, hourly rainfall data, from 1986 to 2018, were obtained from the Sangjinburi rainfall station, which is located at 37° 39′ 32″ north and 128° 34′ 41″ east (Fig. 1). This is the closest and most representative station in the area where the rainfall-induced landslides occurred. The hourly rainfall data are available via the Water Resources Management Information System of South Korea (http://wamis.go.kr/wkw/rf_dubrfobs.aspx). In addition to gauge-based rainfall data, satellite-derived rainfall data can also be used to analyze rainfall triggered landslides (Guzzetti et al. 2008; Posner and Georgakakos 2015; Robbins 2016; Segoni et al. 2018). To compare the gauge-based rainfall data with the satellite-derived rainfall data, we obtained the Tropical Rainfall Measurement Mission (TRMM) Multi-satellite Precipitation Analysis (TMPA, Huffman et al. 2007) 3B42 version 7 rainfall product with fine temporal and spatial scales (3-hourly and 0.25°×0.25°) from 1998 to 2018. TRMM data are available from the Goddard Earth Sciences Data and Information Services Center (GES DISC) (https://disc.gsfc.nasa.gov/datasets/ TRMM_3B42 _7/summary).

Temporal probability of landslide occurrence

Determination of rainfall threshold

The most commonly used empirical threshold in previous temporal probability evaluations is the rainfall intensity–duration threshold (Zêzere et al. 2004; Chleborad et al. 2006; Corominas and Moya 2008; Brunetti et al. 2010; Segoni et al. 2014, 2018; Afungang and Bateira 2016; Bogaard and Greco 2018). However, the intensity–duration threshold requires extensive rainfall records and landslide occurrence data with high-quality and temporal resolution, which were not available in this study area, or many other areas. Therefore, an antecedent threshold has been adopted for evaluation of temporal probability in several studies (Jaiswal and van Westen 2009; Jaiswal et al. 2010; Tien Bui et al. 2013; Afungang and Bateira 2016; Dikshit et al. 2020). An antecedent threshold is based on the amount of antecedent rainfall, which is relatively simple to measure over a large area. This approach was employed here because the study area has experienced only one landslide occurrence by an extreme rainfall event, in 2006, and consequently, sufficient rainfall and landslide data are not available. However, it is difficult to determine the number of days that should be used when using an antecedent rainfall threshold (Guzzetti et al. 2007). Because landslides have different types and geological conditions, the number of antecedent days for the rainfall threshold may appropriately range from 3 days for shallow landslides to 30 days for deep landslides (Kim et al. 1992; Aleotti 2004; Zêzere et al. 2004; Chleborad et al. 2006; Jaiswal and van Westen 2009; Tien Bui et al. 2013). Based on previous landslide studies in Korea (Kim et al. 1992; Yoo et al. 2012; Lee et al. 2015), as well as in other countries (Dahal and Hasegawa 2008; Jaiswal and van Westen 2009; Shou and Yang 2015), and because the landslides in the study area were mostly shallow, a 3-day (72-h) antecedent rainfall threshold was used in this study.

In the Jinbu area, landslides occurred sporadically during the heavy rainstorm of July 14–16, 2006, resulting in seven deaths (National Institute for Disaster Prevention 2006). Figure 3 shows the hourly rainfall time series for July 12–16, 2006 from Sangjinburi rainfall station in the study area. A rainfall event of 90 mm/h, which is the maximum rainfall intensity during the overall observation period, occurred on 15 July at the time when the most casualties were incurred. Therefore, a rainfall event of 90 mm/h is considered a key trigger of initial landslide occurrence. In addition, based on the government report on the landslide events in 2006 (National Institute for Disaster Prevention 2006), the 72-h rainfall event preceding the landslides totaled 430 mm (blue line in Fig. 3).

Fig. 3
figure 3

Hourly rainfall records in the study area in the period July 12–17, 2006

Full size image

Estimation of the temporal probability of rainfall-induced landslides

Estimation of exceedance probability, using the Poisson distribution model, is one of the most commonly used methods to calculate the temporal probability of landslide occurrence (Coe et al. 2000; Crovelli 2000; Guzzetti et al. 2005; Romeo et al. 2006; Jaiswal and van Westen 2009; Jaiswal et al. 2010; Tien Bui et al. 2013; Afungang and Bateira 2016). The exceedance probability, using the Poisson distribution, was evaluated using

$$ P\left\{N(t)\ge 1\right\}=1-{e}^{-\lambda t}=1-{e}^{-t/\mu }, $$
(1)

where N(t) is the number of landslides, in t years, whose probability is being estimated; λt is the expected number of landslide occurrences over t years, and μ (=1/λ) is the anticipated mean recurrence interval.

However, if landslides have only occurred once so far in an area or there are insufficient historical rainfall records, it is difficult to apply this approach. In these circumstances, it is not feasible to determine the mean recurrence interval of landslide triggering rainfall events (or threshold exceedance). Therefore, a new approach is necessary to estimate the temporal probability of future landslide occurrence in an area where no recurrent landslide triggering rainfall event has ever been recorded.

Extreme value analysis enables inferences about future probabilities of extreme event occurrences based on past observations (El Adlouni et al. 2007). Therefore, it has been widely used for engineering design and risk management related to hydrological extreme events such as heavy rainfall and flooding. The block maxima approach, one of the techniques used for extreme value analysis, consists of modeling a sequence of maximum values obtained from blocks (periods) of equal length. If the period is a year, the annual maximum (AM) event data are used. Under the assumption that the maximum values are stationary, independent, and identically distributed, they follow a generalized extreme value (GEV) distribution (see Coles et al. (2001) for more details). The GEV distribution is classified into three types: extreme value type I (Gumbel distribution), extreme value type II (Fréchet distribution), and extreme value type III (Weibull distribution). The cumulative density function (CDF) for the GEV is

$$ {F}_{\mathrm{GEV}}(x)=\exp \left[-{\left(1-k\frac{x-u}{\alpha }\ \right)}^{\frac{1}{k}}\right], $$
(2)

where u, α, and k are the location, scale, and shape parameters, respectively. The three cases are (1) for k = 0, the extreme value type I distribution, (2) for k < 0, extreme value type II distribution, and (3) for k > 0, extreme value type III distribution (Chow et al. 1988). In all three cases, α is greater than zero.

The Gumbel (extreme value type I) distribution has been used for extreme value analysis of heavy rainfall events to estimate the temporal probability of rainfall-induced landslides (Finlay et al. 1997; Zêzere et al. 2008; Frattini et al. 2010; Jaiswal et al. 2011; Nefeslioglu et al. 2011; Martha et al. 2013; Lee et al. 2015; Afungang and Bateira 2016). In addition, the Gumbel distribution is recommended for estimation of the occurrence frequency and magnitude of extreme rainfall events in Korea (ME 2019). However, while previous studies have used the Gumbel distribution to evaluate rainfall return periods or probabilities of maximum daily rainfall events, the Gumbel distribution has not been used to evaluate the temporal probability of landslide occurrence. This study used the Gumbel distribution to evaluate the temporal probability that one or more rainfall events, which exceed the rainfall threshold, will occur during a specified time. Unlike the Poisson distribution, the Gumbel distribution does not require the mean recurrence interval, normally obtained from historical rainfall records. This is an advantage when the exceedance probability must be evaluated in an area with limited data on rainfall and landslides. The CDF of the Gumbel distribution is given by

$$ {F}_{\mathrm{GUM}}(x)=\exp \left\{-\exp \left(-\frac{x-u}{\alpha}\right)\right\}\kern0.5em -\infty <x<\infty, $$
(3)

where u and α (>0) are location and scale parameters, respectively. Then, the exceedance probability (p) of a certain rainfall event in a given year can be calculated by

$$ p=1-{F}_{\mathrm{GUM}}(x)=1-\exp \left\{-\exp \left(-\frac{x-u}{\alpha}\right)\right\}. $$
(4)

To determine the exceedance probability using the Gumbel distribution, the location and scale parameters must be estimated. Several methods estimate the statistical parameters of a probability distribution, including the method of moments (Wallis et al. 1974; Jaiswal et al. 2011; Martha et al. 2013), the method of maximum likelihood, and the method of probability-weighted moments (PWM) (or L-moments). The PWM method (Greenwood et al. 1979), in particular, provides efficient and computationally convenient estimates, even for small samples (Hosking 1990). In addition, the L-moments method, which is defined as linear combinations of PWMs, is widely used to estimate the parameters of various probability distributions, including the GEV and Gumbel distributions because parameter estimates based on L-moments are unbiased and less sensitive to outliers and observational errors than other conventional methods (Hosking and Wallis 1997; Rao and Hameed 2000; Gubareva and Gartsman 2010; Drissia et al. 2019). Therefore, the L-moments method was employed to estimate the parameters of the Gumbel distribution.

The first and second population L-moments are defined by the first and second population PWMs (b0 and b1) of the Gumbel distribution as follows (Hosking and Wallis 1997):

$$ {\lambda}_1={b}_0=u+\gamma \alpha, $$
(5)
$$ {\lambda}_2=2{b}_1-{b}_0=\alpha \cdotp \mathit{\ln}2, $$
(6)

where γ is Euler’s constant (=0.577215 …). Then, the L-moment estimators, \( \hat{\alpha} \) and \( \hat{u} \), of the Gumbel distribution can be derived from Eqs. (5) and (6).

$$ \hat{\alpha}=\left(2{\hat{b}}_1-{\hat{b}}_0\right)/\mathit{\ln}2, $$
(7)
$$ \hat{u}={\hat{b}}_0-\gamma \hat{\alpha}, $$
(8)

where the r-th sample PWM, \( {\hat{b}}_r \), can be obtained by (Hosking et al. 1985)

$$ {\hat{b}}_r={n}^{-1}{\sum}_{j=r+1}^n\frac{\left(j-1\right)\left(j-2\right)\cdots \left(j-r\right)}{\left(n-1\right)\left(n-2\right)\cdots \left(n-r\right)}{x}_{j:n}\kern0.5em \mathrm{for}\kern0.5em r>0, $$
(9)

and x1 : n ≤ x2 : n ≤ ⋯xn : n are the ordered AM rainfall series xi (i = 1, 2, ⋯, n) where n is the sample size. Note that \( {\hat{b}}_0 \) is the sample mean (\( \frac{1}{n}{\sum}_{i=1}^n{x}_i \)).

The value of AM (annual maximum) rainfall event for the i-th year (xi) is given by the largest rainfall event, within a specific duration that occurred in that year. Since the duration of the rainfall threshold was determined as 72-h in “Determination of rainfall threshold” section, Gumbel distribution modeling was performed using the 72-h AM rainfall series. To determine the 72-h AM rainfall event value, a moving window procedure was used with hourly rainfall observations. For each year, all 72-h rainfall event values were extracted by moving the 72-h window on an hourly basis. The AM rainfall event for that year was set to the largest extracted value. Figure 4 presents the 72-h AM rainfall series obtained both from hourly observations at Sangjinburi rainfall station (n = 33 years) and from the 3-hourly TRMM gridded data (n = 21 years). The 72-h AM rainfall series from the station (black solid line) and from TRMM data (blue dotted line) show a similar pattern. In particular, the gauged and TRMM AM values in 2006, the year of the first landslide occurrence in the study area, are almost the same and have the largest value over the entire observation period. However, since the rainfall data from the rainfall station have a longer time span and a higher sampling rate, the temporal probability analysis was carried out using these gauge-based rainfall data. Using these data, sample PWMs were calculated as shown in Table 1. Based on Eqs. (7) and (8), the location and scale parameters were estimated as \( \hat{\mu} \) = 157.772 and \( \hat{\sigma} \) = 75.258, respectively. The exceedance probability of the determined rainfall threshold (xTh = 430 mm) was calculated as p = 0.0265.

Fig. 4
figure 4

72-h annual maximum rainfall events at Sangjinburi rainfall station (1986–2018)

Full size image
Table 1 72-h annual maximum rainfall series and its sample PWMs at Sangjinburi rainfall station (n = 33)
Full size table

From this, the probability of experiencing at least one extreme event, greater than the threshold, over N years, Pr(N), can be calculated as follows:

$$ \mathit{\Pr}(N)={\sum}_{t=1}^N{\left(1-p\right)}^{t-1}p=1-{\left(1-p\right)}^N. $$
(10)

The concept of the Pr(N) is referred to as “risk of failure” defined by Yen (1970). It is described in most introductory textbooks and recommended as an essential metric for assessing the actual probability of an extreme event during a given period (Serinaldi 2015; Serinaldi and Kilsby 2015). In this study, we assumed that extreme rainfall events over the rainfall threshold xTh lead to landslide occurrences. Then, the concept of the Pr(N) was employed to calculate the temporal probability of landslide occurrences. The probability of experiencing at least one extreme rainfall event greater than xTh in N years, PrGUM(xTh, N), can be defined by substituting Eq. (4) into Eq. (10):

$$ {\mathit{\Pr}}_{\mathrm{GUM}}\left({x}_{Th},N\right)=1-{\left\{{F}_{\mathrm{GUM}}\left({x}_{Th}\right)\right\}}^N. $$
(11)

Figure 5 illustrates the temporal probability of landslide occurrences for N = 1, 2, 5, 10, 20, 50, 100, 150, 200 years in the study area. Because the graph of PrGUM(xTh, N) moves rightward as N increases, for a certain rainfall threshold, the temporal probability of landslide occurrences increases with N. The temporal probabilities of landslide occurrences for the determined rainfall threshold (xTh = 430 mm) are presented in Table 2. As an example, the temporal probability of landslide occurrences during any 1 year is equal to the exceedance probability of the rainfall threshold (p = 0.0265).

Fig. 5
figure 5

Temporal landslide probabilities for different time periods (1 year 0.027, 2 years 0.052, 5 years 0.126, 10 years 0.236, 20 years 0.416, 50 years 0.739, 100 years 0.932, 150 years 0.982, and 200 years 0.995)

Full size image
Table 2 Temporal probabilities, in the study area, of rainfall-induced landslide occurrences over period N
Full size table

Landslide susceptibility analysis

Landslide susceptibility analysis (or spatial probability analysis) estimates the potential for a landslide by considering landslide inducing factors (or conditioning factors) and analyzing the spatial distribution of these factors (Chae et al. 2017). However, landslide susceptibility assessment is not straightforward because the occurrence of landslide is controlled by diverse spatial conditioning factors, including geology, topography, and vegetation. Several assessment approaches have been suggested. Among them, data-driven landslide susceptibility analysis has been widely used and evaluates the statistical relationships between the locations of landslides and the landslide inducing factors. However, because the relationship between the independent variables (landslide affecting factors) and a dependent variable (landslide occurrence) is often complex and nonlinear, it is not easy to determine the relationship through simple statistical analysis. Therefore, various machine learning approaches, such as neurofuzzy methods, support vector machines, evidential belief functions, and artificial neural networks, have been developed to evaluate the susceptibility of landslide occurrence. Multi-layer perceptron (MLP) neural networks, a type of artificial neural network (ANN), have been applied successfully and efficiently in landslide prediction (Gomez and Kavzoglu 2005; Zare et al. 2013; Pham et al. 2017). MLP is a feedforward back error propagation neural network with one or more hidden layers between the input layers and output layers. It has several advantages including that the distribution of training dataset is not dependent on pre-assumptions, no decision is required about the relative importance of input factors, and most input factors are selected based on weightings adjustment during the training process (Gardner and Dorling 1998). In addition, ANN can process input data with different measurement scales and units, such as continuous, categorical, and binary data, a significant advantage for landslide susceptibility analysis (Garrett 1994).

Spatial database construction

For the susceptibility analysis, various digital maps were used to construct a spatial database including the following landslide conditioning factors (Table 3): elevation, slope angle, slope aspect, planform curvature, profile curvature, standard curvature, stream power index (SPI), topographic wetness index (TWI), specific catchment area (SCA), geology, forest type, forest density, timber age, timber diameter, soil series, soil texture, soil sub-texture, soil drainage, soil thickness, and land use. In total, 20 factors were used in the analysis. The relevant digital maps are listed in Table 3, and they are available at different scales and formats in the Korean archives. After acquisition from several governmental institutes, the digital maps were converted into grid-based raster layers with 10-m resolution to create thematic maps for analysis.

Table 3 The landslide conditioning factors used in this study
Full size table

The geomorphological database of the study area was based on a 1:5000 scale digital topographic map, provided by the National Geographic Information Institute. The contour polyline vector layer, including elevation attributes, was extracted from the digital map. A TIN (triangulated irregular network) was generated from the contour layer and converted into a grid-based raster layer as a digital elevation model (DEM). The DEM was used to compute the geomorphological factors (Fig. 6a–i): elevation, slope angle, slope aspect, standard curvature, profile curvature, planform curvature, SCA, TWI, and SPI. SCA, defined as the area of land upslope of a width of the contour, is commonly used to describe complex terrain when analyzing water flow on hill slopes (Tretkoff 2011). The TWI is a runoff-based model that describes the relationship between the water inclination that accumulates in any location and the gravitational force inclination in the stream that accumulates down the slope (Althuwaynee et al. 2014). The SPI is the erosive power of the water flow based on an assumption that the discharge is proportional to the SCA. This factor predicts erosion along the slope of the profile’s convexity and deposition in the profile’s concavity. Among the other factors, curvature refers to the curvature of a line formed by intersecting the ground surface and a plane (horizontal or vertical). Profile curvature is parallel to the direction of the slope angle and indicates the direction of the slope. It affects the acceleration and deceleration of flow through the surface, and associates with erosion and deposition of slope material. Planform curvature is perpendicular to the slope and affects the convergence and divergence of flow on the surface. Standard curvature is a combination of profile and planform curvature. Using these factors, it is possible to understand the flow from the surface when rainfall occurs (Yilmaz et al. 2012; Chen et al. 2017).

Fig. 6
figure 6figure 6figure 6

Thematic maps of landslide conditioning factors: a slope, b elevation, c aspect, d standard curvature, e profile curvature, f planform curvature, g specific catchment area, h topographic wetness index, i stream power index, j forest type, k timber diameter, l timber age, m forest density, n soil series, o soil texture, p soil sub-texture, q soil drainage, r soil thickness, and s land use

Full size image

The geological data (Fig. 2) were derived from a 1:50,000 scale digital geological map provided by the Korea Institute of Geoscience and Mineral Resources. Forest-related data drew on the Korea Forest Service’s 1:25,000 digital forest map. Forest type, timber diameter, timber age, and forest density were isolated as thematic maps (Fig. 6j–m). Based on the 1:25,000 digital soil map provided by the National Institute of Agricultural Sciences, the soil series maps—texture, sub-texture, drainage, and thickness—were derived (Fig. 6n–r). Finally, the land use map (Fig. 6s) was based on the 1:5000 digital land cover map provided by the Ministry of Environment.

Evaluation of landslide susceptibility using a multi-layer perceptron

Machine learning is related to pattern recognition and computational learning techniques in artificial intelligence, a subfield of computer science. Neural networks, one of the machine learning approaches, have been used successfully for classification and prediction in various problem domains (Paliwal and Kumar 2009), and MLP is the most widely used neural network architecture for classification or regression problems (Yilmaz and Kaynar 2011). MLP uses a neural network of at least three node layers: input, hidden, and output. Input layers are the landslide inducing factors, regarded as independent variables, and the output layer has a result classified as either a landslide or nonlandslide class. The hidden layers are the classifying layers that transform inputs into outputs (Pham et al. 2017). The hidden layer computes the expected output through nonlinear activation functions and determines the difference from the actual output in the training dataset (feedforward propagation). Using the differences, the number of layers and nodes in hidden layer is adjusted. Each node is a neuron that uses its nonlinear activation function to distinguish data that are not linearly separable, or separable by a hyperplane (Cybenko 1989; Khalil Alsmadi et al. 2009). In the MLP, the connection weights between the input neuron and the hidden neurons as well as between the hidden neurons and the outputs are initialized and then trained using a backpropagation algorithm. There are two steps in the training, i.e., feedforward and backpropagation (Tien Bui et al. 2016): (i) in the feedforward, the input is propagated forward through the layers resulting in a response at the output layer. The output response values are compared with actual values, and the differences are assessed; (ii) in the backpropagation, the connection weights are updated to minimize the differences. In this study, the weights were calculated using rectified linear unit (ReLU) activation functions, the most commonly used activation function in neural networks. The goal of MLP is to derive a model that minimizes the difference between the actual and estimated values. In this study, we set the number of times the model repeats the learning (epoch) as 1000 and the rate at which to approach the minimum target error (learning rate) as 0.005.

First, it was necessary to preprocess the data for machine learning. The database of the study area, including landslide locations and landslide conditioning factors, was reconstructed to a landslide inventory map and thematic maps of conditioning factors using ArcGIS and Python. The grid pixels in the landslide inventory map were divided into two classes: landslide pixels and nonlandslide pixels (Tien Bui et al. 2016). A grid cell where a landslide has occurred is assigned “1,” and a cell without the landslide is assigned “0.” The landslide dataset was combined with the attribute data of the conditioning factors and used in training the MLP model and then to calculate the probability of landslide occurrence. The landslide susceptibility analysis results are expressed in terms of the probability of occurrence, which ranged from “0” (landslide less likely to occur) to “100%” (landslide more likely to occur). In general, because the number of landslide pixels is very small compared with the total number of pixels in the study area, the amount of landslide occurrence data is smaller than the amount of nonlandslide data. This study had 647,433 pixels, but the number of landslide pixels was only 1035. Consequently, the data were significantly unbalanced. This data unbalance can cause serious errors in the analysis. Specifically, the evaluated probability values in all pixels of the study area can converge to “0,” which meant that the entire study area would be classified as stable. Therefore, nonlandslide data representing just one or two times the number of landslide pixels should be selected to overcome the data unbalance problem described in previous studies (Pradhan 2013; Pham et al. 2016; Chen et al. 2018). In this case, we trained the model using the same number of the nonlandslide and landslide pixels selected randomly. The randomly selected dataset was partitioned into two subsets as training and test datasets. Training data were used to build the model while test data were used to validate the model and evaluate its accuracy. In this process, the test data should be different from those that trained the model (Chung and Fabbri 2008; Pradhan and Lee 2010). However, no mathematical rule to determine the relative partitioning of these subsets exists (Pham et al. 2017). In this study, 70% of the data were used for training the network, and the rest were used to test the final MLP model, as previous studies have suggested (Tien Bui et al. 2016; Chen et al. 2017). A confusion matrix was used to evaluate the performance of the prediction model using the test data. Finally, the remaining data, which were not used for training or testing of the prediction model, were used to evaluate the spatial probability of landslide susceptibility throughout the study area. Figure 7 shows the resulting landslide susceptibility map. A receiver operating characteristics (ROC) graph and its area under the graph (AUC) were used to verify the accuracy of the susceptibility map by comparing actual landslide locations with the analysis results (Fig. 8). The AUC value of the landslide susceptibility map in this study was 79.33%.

Fig. 7
figure 7

Landslide susceptibility map obtained using MLP

Full size image
Fig. 8
figure 8

ROC (receiver operating characteristics) graph. (AUC: area under the curve)

Full size image

Landslide hazard assessment

The landslide hazard in the study area was then computed by multiplying the temporal probability of landslide occurrence, derived using the Gumbel distribution, with the landslide susceptibility obtained using MLP. To compare landslide hazards for different time periods, nine future time periods (1, 2, 5, 10, 20, 50, 100, 150, 200 years) were used, as described in “Estimation of the temporal probability of rainfall-induced landslides” section. The hazard assessments for the different periods are given in Table 4, which shows that the calculated hazard values for most pixels of the study area for 1, 2, and 5-year periods were less than 0.3 (30%). In each of the relatively short periods (1, 2, 5, 10, and 20 years), the hazard values of all pixels were less than 0.5 (50%). This is because the mean AM rainfall value is much smaller than the landslide rainfall trigger threshold. Statistical analysis of the time-series rainfall data for 33 years (from 1986 to 2018) showed that the mean AM rainfall amount was 201.2 mm/72 h. However, the landslide trigger rainfall in 2006 was 430 mm/72 h, and this was used as the threshold for the temporal probability analysis. Consequently, the temporal probabilities for the five periods (1, 2, 5, 10, 20 years) were very small, and so, the hazard values were also generally small for these periods. In contrast, the evaluated hazard values in the area were much higher for time periods greater than 50 years. That is, the proportion of hazard values greater than 0.5 (50%) in the study area increased from 23.22% over 50 years to 45.8% over 200 years, which means that the landslide hazard is greater when longer periods are considered, as is evident in the landslide hazard maps for 20, 50, 100, 200-year periods (Fig. 9). For presentation purpose, only four landslide hazard maps for 20, 50, 100, 200-year periods are shown in Fig. 9.

Table 4 Landslide hazard value proportions (%) for different time periods
Full size table
Fig. 9
figure 9

Examples of landslide hazard maps for four different periods: a 20 years, b 50 years, c 100 years, and d 200 years

Full size image

Discussion and conclusions

In this study, we developed an approach that can be applied in an area where the landslide inventory and landslide triggering rainfall events data are incomplete or where a nonrepetitive landslide event has occurred. This approach allowed us to estimate the temporal probability of landslide occurrence in an area where a multi-temporal landslide inventory and historical rainfall records for repetitive landslides were incomplete. The study area had experienced landslide occurrence just once, in 2006, which means that the recurrent rates of landslide or triggering rainfall events could not be determined. Instead, this study evaluated temporal probability using the extreme value analysis. Extreme value analysis has been widely used for hydrological extreme events such as heavy rainfall. To evaluate the future probability of extreme event occurrence (e.g., extreme rainfall) based on extreme value theory, the Gumbel (extreme value type I) distribution was applied to the available time series rainfall data to estimate the probability of extreme events over several future time periods. This probability was then, indirectly, considered as the temporal probability of extreme rainfall-induced landslides.

The described approach was applied to the study area, which had experienced a large number of landslides following extreme rainfall in 2006. Based on previous landslide studies and rainfall records in the study area, a 3-day (72-h) antecedent rainfall threshold was adopted and estimated as 430 mm. AM values, for each 72-h period, were calculated using a moving window and hourly rainfall records from 1986 to 2018. Then, using the AM data, the location and scale parameters of the Gumbel distribution were found to be 157.77 and 75.25, respectively. Subsequently, the rainfall threshold’s exceedance probability for any year was calculated as 0.0265. From this, the probabilities of at least one extreme event, greater than the threshold, over 1, 2, 5, 10, 100, 150, and 200 years were 0.0265, 0.0523, 0.1257, 0.2355, 0.4156, 0.7389, 0.9318, 0.9822, and 0.9954, respectively.

The temporal probability of landslide occurrence was then combined with the spatial probability of landslides to determine landslide hazard. The landslide susceptibility map was constructed after MLP modeling in which 20 conditioning factors and the landslide inventory were used to analyze the relationship between landslide locations and conditioning factors. The MLP was trained through backpropagation, the most frequently used neural network method. Validation showed a prediction accuracy of 79.3%. Landslide hazard maps were then obtained by integrating the temporal probability of landslides with the landslide susceptibility maps.

The proposed approach improves on previous studies. Determination of the exceedance probability of a rainfall threshold has previously depended on frequency analysis of past repetitive events, with a Poisson distribution. However, when the historical data for repetitive events are limited or there is only one landslide event, as in our study area, temporal probability cannot be estimated using the previous approach. In this case, the Gumbel distribution can be used for temporal probability evaluation provided continuous time-series rainfall data are available in the area. Thus, the proposed approach can be used even if a Poisson model cannot be adopted. Several previous studies have adopted the Gumbel model, but they did not use it to evaluate the temporal probability of a landslide. The previous studies utilized the Gumbel distribution to calculate the return period of extreme rainfall events or to evaluate the probability of daily rainfall occurrence. The developed approach, on the other hand, was able to estimate the temporal probability of landslide occurrence using the Gumbel model by adopting extreme value theory.

Our approach also has some limitations. The importance of the spatial variability of rainfall is well recognized in landslide studies. However, precise prediction of rainfall across an area is difficult when there are few available rainfall gauges. Therefore, the simplified approach to determining the rainfall amount for a certain region was utilized with single rain gauge near a specified landslide site or the selected rain gauge as representative locations for a predefined region (Chiang and Chang 2009; Canli et al. 2018a; b). In this study, we used rainfall records obtained from only one rainfall station (Sangjinburi) to evaluate the temporal probability of landslide triggering rainfall. Sangjinburi is the station closest to the landslide locations, and best represents rainfall conditions in the study area. Consequently, we could not consider spatial variation of rainfall. If there is no representative rainfall station, or the rainfall record is too short to conduct the extreme value analysis, satellite-based rainfall data, such as TRMM, can be used to estimate the temporal probability of landslide occurrences. In fact, gauged data and TRMM data produced differences in the temporal probabilities of rainfall-induced landslide occurrences of less than 3% for all the analysis period. Therefore, when the gauge-based rainfall data are not available, TRMM rainfall data can be a viable alternative.

In addition, this approach considered stationary rainfall data, which means that the conditions of rainfall and its essential statistical characteristics (e.g., mean and variance of the probability distribution) are invariant with respect to time. Consequently, the Gumbel distribution used in this analysis is also based on the stationary condition. However, as IPCC (2014) pointed out, global warming is expected to lead to a greater frequency and magnitude of heavy precipitation. This means that the stationary rainfall assumption will not be valid. Recently, in the field of hydrology, nonstationary approaches have been suggested for most hydrological processes including rainfall. Because the probability distribution parameters will change with the time due to climate change, we need a different approach that can analyze nonstationary rainfall time series data.