Introduction

Back analysis for shear strength parameters of a failed slope is a practical and widely used strategy in remedial design or stability evaluation of the analogous slopes (Duncan et al. 2014). The failed slope can be regarded as a large-scale in situ experiment. When the slope failed, the factor of safety (FS) equals unity at the time of failure, and portions of actual slip surface can be obtained. The back calculated parameters incorporate all the in situ information are therefore more representative than the parameters obtained from laboratory test.

Generally, back analysis methods can be divided into two categories, i.e., deterministic methods and probabilistic methods. Deterministic methods try to find a set of certain values satisfying the observed information. For example, Wesley and Leelaratnam (2001) and Jiang and Yamagami (2006, 2008) and Gao (2016) implemented deterministic back analysis of the shear strength parameters by fully utilizing the information of FS and location of observed slip surface. Deterministic back analysis methods are simple and easy to implement. However, these methods can only provide a single set of parameters and are limited in providing confidence intervals on parameters. In contrast, probabilistic back analysis methods based on Bayes’ theorem try to obtain the posterior distribution of shear strength parameters by incorporating the uncertainty of obtained information. They can derive both mean and variance of shear strength parameters. Therefore, the information provided by probabilistic methods is more fruitful than that of deterministic methods. Due to the merit of probabilistic back analysis methods, they are becoming popular in recent years. For example, Zhang et al. (2009) developed an optimization method by spreadsheet and analytically sensitivity analysis method for probabilistic back analysis of Shek Kip Mei landslide in HongKong and Congress Street Cut landslide in Chicago. Zhang et al. (2010) implemented probabilistic back analysis of shear strength parameters of a hypothetical landslide based on Bayes’ theorem and solved the results by Markov chain Monte Carlo simulation method (MCMC). Zhao et al. (2016) applied first-order reliability method and Monte Carlo simulation to back calculate the shear strength parameters of Zhuquedong landslide. Sun et al. (2019) adopted Bayesian methods for back analysis of the geo-mechanical parameters of high rock slopes using multi-type monitoring data.

However, in previous studies about probabilistic back analysis of shear strength parameters of landslides (Zhang et al. 2009, 2010; Wang et al. 2013; Zhao et al. 2016; Jahanfar et al. 2017), it is assumed that the actual slip surface is fully known and fixed. Only the information of FS being unity is used. This strategy may not be always reasonable. Because when the back calculated values are used to search for the critical slip surface, the obtained slip surface may be very different from the observed actual slip surface. In this case, the back calculated values are not reliable. More reliable back calculated parameters should simultaneously satisfy two conditions (Deschamps and Yankey 2006; Jiang and Yamagami 2006, 2008; Duncan et al. 2014): (1) the FS at the time of failure should be close to unity; (2) the back calculated critical slip surface should be consistent with the actual slip surface. Therefore, to obtain reliable parameters, the probabilistic back analysis should incorporate the observed slip surface information.

The determination of the slip surface of a failed slope is quite challenging since the slip surface is buried in displaced materials. The slip surface is usually speculated by curve fitting via a limited number of observations such as the crown of landslide and portions of slip surface exposed by drilling and trench. Obviously, the speculated slip surface is uncertain because the existence of measurement errors and blunders caused by empirical judgment of engineers and the different curve fitting techniques. Different slip surfaces will result in different back analysis results. Therefore, in probabilistic back analyses of shear strength parameters, the uncertainty of slip surface should also be considered.

This paper proposes a probabilistic framework for the back analysis of shear strength parameters of landslides based on Bayes’ theorem. Unlike the traditional probabilistic back analysis methods, the proposed method considered the uncertainty of slip surface. The MCMC method is used to solve the posterior distribution of shear strength parameters. The slope stability analysis model for calculating FS and critical slip surface suffers high computation cost. To improve its computational efficiency, an extreme learning machine (ELM)-based response function is applied. Given a set of shear strength parameters, the corresponding FS and critical slip surface can be accurately predicted by the ELM-based response surface function. The proposed and traditional methods are first compared using a synthetic slope for which the actual shear strength parameters and slip surface are known. Then, the effects of prior distribution of shear strength parameters on back analyzed results are studied. Finally, the effectiveness of the proposed method is further verified by a practical landslide.

Methodology

Probabilistic back analysis by Bayesian updating

For a 2-dimension landslide composed of n layers of soil, it can be assumed that its FS is unity at the time of failure, and the coordinates of m scatters on the actual slip surface can also be observed by landslide site survey. These observations are hereafter called measurements. Let Y = {FS, x1, y1, …, xm, ym} represents a (2 m + 1)-vector of measurements, where the x and y are the horizontal and vertical coordinate of scatters, respectively. The measurements can be simulated by the following formulation:

$$ Y=f\left(\uptheta \right)+E $$
(1)

where θ = {c1, ϕ1, …, cn, ϕn} is a 2n-vector representing the shear strength parameters (cohesion c and internal friction angle ϕ) of n layers of soil in Mohr–Coulomb failure criterion. The f(θ) is a model for predicting FS and location of critical slip surface. The E = {εFS, εx1, εy1, …, εxm, εym} is a (2 m + 1)-vector representing the total error of measurements and predictive model.

The shear strength parameters θ of slope materials are usually uncertain, and their probability distribution can be obtained by regional statistics or multiple experiments. In Bayesian formalism, this distribution is called prior distribution, and the back analysis of θ refers to update the distribution of θ by calculating conditional probability of θ given the measurements. The conditional probability of θ is called posterior distribution and can be defined by the following formulation (Vrugt 2016):

$$ p\left(\uptheta |\mathrm{Y}\right)\propto p\left(\uptheta \right)L\left(\uptheta |\mathrm{Y}\right) $$
(2)

where p(θ) and p(θ|Y) denote the prior and posterior probability density function of θ, respectively. L(θ|Y) represents likelihood function.

Assume that the total error E is normally distributed, i.e., E~N (με, σε2), where με and σε are mean and standard deviation of total error. The likelihood function L(θ|Y) can be written as (Vrugt 2016):

$$ L\left(\uptheta |\mathrm{Y}\right)={\prod}_{i=1}^{\left(2m+1\right)}\frac{1}{\sqrt{2\pi }{\sigma}_i}\exp \left[-\frac{1}{2}{\left(\frac{y_i-f\left(\theta \right)-{\upmu}_i}{\sigma_i}\right)}^2\right] $$
(3)

For numerical stability and algebraic simplicity, it is recommended to use log-likelihood (Vrugt 2016), i.e., the logarithm of Eq. (3):

$$ \log \left(L\left(\uptheta |\mathrm{Y}\right)\right)=-\frac{\left(2m+1\right)}{2}\log \left(2\pi \right)-{\sum}_{i=1}^{\left(2m+1\right)}\left\{\log \left({\sigma}_i\right)\right\}-\frac{1}{2}{\sum}_{i=1}^{\left(2m+1\right)}{\left(\frac{y_i-f\left(\theta \right)-{\upmu}_i}{\sigma_i}\right)}^2 $$
(4)

Once the likelihood function L(θ|Y) and the prior distribution p(θ) of shear strength parameters are defined, the posterior distribution of θ can be derived. Since the models for predicting FS and critical slip surface are often nonlinear, the traditional analytical means or analytical approximation may not perform well in deriving the posterior distribution of θ. In this case, the MCMC sample method is more applicable and preferred. In this method, the random samples of a Markov chain will be either accepted or rejected by a random decision rule (Kelly and Huang 2015). After the algorithm is stable, the posterior distribution of θ can be obtained by counting the accepted samples along the Markov chain.

The MCMC method is widely used in parameter calibration. In this paper, the differential evolution adaptive metropolis (DREAM) algorithm (Vrugt 2016) is applied for implementing MCMC simulation. The DREAM algorithm is a multi-chain MCMC simulation algorithm which performs outstanding in sampling efficiency on complex, high-dimensional and multi-modal posterior distributions (Vrugt 2016). Generally, when the MCMC simulation satisfies the convergence index \( \hat{R} \) which is less than or equal to 1.2 (i.e., \( \hat{R} \)≤ 1.2) for each random variable, and the acceptance rate is greater than 15%, it indicates that the MCMC simulation achieves convergence and acceptable performance. The DREAM algorithm is implemented in MATLAB, and it can be treated as a “black box.” Although a thorough understanding of mathematical modeling algorithms is always advantageous, it is not a prerequisite for engineers to use the “black box” (Li et al. 2016). Geotechnical practitioners only need to focus on slope stability analysis. The DREAM will automatically obtain the posterior distribution given the prior distribution, predictive model, measurements, and errors distribution. This allows engineers to use the DREAM without being compromised by the complicated algorithms. A thorough explanation of DREAM appears in (Vrugt 2016), and interested readers are referred to this publication for further details.

Predictive model

In this paper, the program Slide (version 6.007, © 1998–2010 Rocscience, Inc.) is selected as the predictive model to calculate the FS and the critical slip surface on given shear strength parameters. An interface program for Slide using MATLAB (version R2017a, © 1984–2017 The MathWorks, Inc.) is used to call Slide as a module for automatically building and running the slope stability analysis model and extracting the calculation results. However, although the interface program is computationally efficient, the calculation process of Slide is still time consuming when the chain of MCMC is long. Thus, to further improve computational efficiency, a response surface function is constructed to approximate the relationship between inputs (i.e., shear strength parameters) and outputs (i.e., FS and critical slip surface). Since the inputs are the 2n-vector θ, and the outputs are the (2 m + 1)-vector Y, the response surface model must be multi-output. The artificial neural networks can address the multi-output problems well. Among the artificial neural networks, the ELM is considered to be a neural network that can always yield satisfactory performance with an extremely high learning speed (Wang et al. 2019). Therefore, the ELM model is selected as the response surface function.

ELM is a new machine learning algorithm for single-hidden-layer feedforward neural networks (SLFNs) proposed by Huang et al. (2006). In ELM, the input weights and hidden biases are randomly chosen, and the output weights are analytically determined. Compared to conventional neural networks, ELMs overcome many limitations, such as overtraining, local minima, and high computational burdens. For N arbitrary distinct samples (θi, Yi), a standard SLFN with K hidden nodes (K ≤ N) and an activation function g(θ) can be expressed by the following equation (Huang et al. 2006):

$$ {\sum}_{i=1}^K{\beta}_ig\left({w}_i\ast {\theta}_j+{b}_i\right)={o}_j,\kern0.5em j=1,\cdots, N $$
(5)

where wi is the weight vector connecting the ith hidden neuron and the input nodes, βi is the weight vector connecting the ith hidden neuron and the output nodes, oj is the jth output vector of the SLFN, and bi is the bias of the ith hidden neuron.

The above N equations can be compactly written as follows (Huang et al. 2006):

$$ \mathrm{H}\beta =\mathrm{O} $$
(6)

where H and O are the hidden layer output matrix and the output matrix of SLFNs, respectively. To minimize the cost function ||O-Y||, the output weights β can be simply constructed by finding the least squares solution to the linear system Hβ = Y, as expressed by the following equation (Huang et al. 2006):

$$ \hat{\beta}={\mathrm{H}}^{+}\mathrm{Y} $$
(7)

where H+ is the Moore-Penrose generalized inverse of matrix H.

Steps of probabilistic back analysis

The whole process of Bayesian back analysis can be divided into the following four steps: (1) parameter initialization; (2) sample generation; (3) response surface construction; (4) Bayesian updating. Fig. 1 shows the flowchart of Bayesian back analysis. The details are described as follows:

  1. 1)

    Parameter initialization

    Before the Bayesian back analysis, the prior distribution type, mean, standard deviation (or coefficient of variation) and correlation coefficient of the shear strength parameters, and the distribution of total error need to be determined. Furthermore, in DREAM algorithm, the number of shear strength parameters, Markov chains, and generations of each chains should also be determined.

  2. 2)

    Sample generation

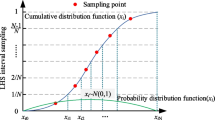
    Based on the prior distribution of shear strength parameters, the range of each parameter can be determined. Then, the Latin hypercube sampling (LHS) method is applied to uniformly generate N pairs of shear strength parameter samples within their ranges. These samples will be transferred to the MATLAB interface program of Slide to calculate their corresponding FS and critical slip surface. After all the samples are calculated, an inputs-outputs dataset containing N pairs {θ, Y} can be obtained.

  3. 3)

    Response surface construction

    Step (2) will be repeated twice to obtain two inputs-outputs datasets, one for the training set for ELM training and the other for the testing set to test the performance of trained ELM. The coefficient of determination (R2) between actual and predicted values is used for evaluating the performance of ELM. When the ELM performs well in testing set, the trained ELM can be used as a predictive model instead of the program Slide.

  4. 4)

    Likelihood function construction

    When Steps 1–3 are finished, given the measurements, the log-likelihood function can be built based on Eq. (4).

  5. 5)

    Bayesian updating

    The DREAM algorithm will sample the posterior distribution of shear strength parameters based on the prior distribution and log-likelihood function. When the DREAM algorithm reaches convergence, the posterior distribution of shear strength parameters can be obtained.

Fig. 1
figure 1

Flowchart of Bayesian back analysis for shear strength parameters of landslide

Full size image

Method verification

A synthetic homogeneous slope is used to verify the proposed method. In this slope, the actual shear strength parameters, FS, and slip surface location are known. The traditional probabilistic back analysis and the proposed method are compared with test whether the two methods can obtain the actual shear strength values.

Slope setting

Figure 2 shows the slope geometry. The height and slope angle are 12.25 m and 26.56°, respectively. The actual shear strength parameters are set to c = 12 kPa and ϕ=12°. The shear strength parameters, i.e., θ = {c, ϕ}, are considered as uncertain variables. Although the c and ϕ are typically lognormal distributions, in some cases, the distributions of c and ϕ are suggested to follow the normal distribution (Zhang et al. 2009; Zhao et al. 2016; Jahanfar et al. 2017). For briefness and practicality, the prior distributions of c and ϕ are assumed to follow the normal distribution. It is first assumed that c and ϕ are statistically independent, and then different negative correlation coefficients between c and ϕ are applied to study the effect of the correlation on the results. The prior mean of c and ϕ is set to 14 kPa and 12°, respectively. The coefficient of variation (COV) of c and ϕ is set to 0.20 and 0.15, respectively according to Zhang et al. (2010). The unit weight of slope material is set to 18 kN/m3. Table 1 lists the assumed actual shear strength parameters and their prior distributions.

Fig. 2
figure 2

Geometry of the homogeneous soil slope

Full size image
Table 1 Assumed actual shear strength parameters and their prior distributions
Full size table

In practical, the rigorous simplified method of Morgenstern-Price, which satisfies all three equilibrium conditions, is a commonly used slope stability analysis method in engineering and Zhang et al. (2010) also used this method for probability back analysis. Therefore, the Morgenstern-Price method is selected as the slope stability method. The actual FS calculated by this method is 1.0. This paper focuses on the effect of slip surface uncertainty on probabilistic back analysis. During the back analysis, the stability analysis method is fixed. Therefore, others rigorous methods, such as Spencer and Janbu method, can also be used for back analysis with no harm to the performance of the proposed framework and to the aim of the work. However, it should be noted that the method selected for back analysis should be consistent with the method used for remedial design or stability evaluation of the analogous slopes. This is to prevent an additional source of uncertainty arising from the inconsistency in the slope stability methods, because Spencer, Janbu, and Morgenstern-Price will provide different answers for FS although their results are very close.

The red dashed line in Fig. 2 denotes the actual slip surface corresponding to the actual shear strength parameter in Table 1. It is located by the auto refine search option for non-circular surfaces embedded in the program Slide. The work process of auto refine search method can be found in the web-help file of the program Slide (Rocscience 2010). The points A, B, and C in Fig. 2 represent the measurements of actual slip surface location, i.e., entry, exit, and slip point uncovered by drilling, respectively. All measurements are summarized in Table 2. These measurements will be used for updating the distributions of shear strength parameters.

Table 2 Information of measurements
Full size table

Case setting

To study the effect of slip surface uncertainty on the results of Bayesian back analysis, eight cases listing in Table 3 are investigated. The traditional method adopting fixed slip surface is firstly studied. Then, by gradually adding the number of measurements, the effect of slip surface uncertainty on the back analyzed parameters is studied.

Table 3 Case conditions for Bayesian back analysis
Full size table

For a real-world case, Christian et al. (1994) reported that the model uncertainty of the simplified method of Bishop follows a normal distribution with a mean of 0.05 and a standard deviation of 0.07. The results of the Morgenstern-Price method are usually similar to those of the Bishop simplified method. Therefore, it is assumed that the model uncertainty of the Morgenstern-Price method follows the same distribution as the Bishop method. Since this is a synthetic slope, the known actual FS and slip surface are obtained by the simplified method of Morgenstern-Price, which is consistent with the predictive model in back analysis. Therefore, the predictive model is assumed to be unbiased. The standard deviation of predictive model error for FS is assumed to be 0.07.

For the proposed method, the measurement errors must be input by the analyst. In literatures on the probabilistic back analysis (Kelly and Huang 2015; Huang et al. 2016; Sun et al. 2019), the measurement errors are commonly assumed to be normally distributed, unbiased, independent, and homogeneous. Therefore, in this paper, the measurement errors of the slip surface also follow this common assumption. There is little guidance in the literature about what magnitude of measurement errors of slip surface to specify. However, it should be noted that the measured capacities are of little value if the analyst has not assessed the measurements accuracy. The selection of measurement errors requires a degree of subjectivity because they depend on factors such as the skill of the measurer and interpretation of measurement results (Huang et al. 2016). It is physically plausible to assume that the measurement accuracy of the slip surface location does not exceed 1 m. Therefore, five different standard deviations of measurement errors are applied, i.e., 0.9 m, 0.7 m, 0.5 m, 0.3 m, and 0.1 m, to study the influence of measurement error of slip surface on back analyzed parameters.

Calculation process

The number of Markov chains and generations of each chains is set to 3 and 3000, respectively. The range of c and ϕ is set to [2, 45] and [2, 25], respectively. The LHS method is used to generate two data sets within parameters range for ELM training and testing. The training set contains 1000 samples, and the testing set contains 100 samples. Figure 3 shows the calculated critical slip surface samples and FS in training set and testing set. Each slip surface is represented by a polyline with 26 scatters, and any point on the slip surface can be obtained by one-dimensional linear interpolation. Thus, one pair of shear strength parameters {c, ϕ} corresponding to 53 (53 = 1 + 2 × 26) outputs. The ELM is used to construct the response surface function between the 2 inputs and 53 outputs.

Fig. 3
figure 3

Critical slip surface samples calculated by Slide in training set and testing set (the color of slip surface represents its FS)

Full size image

Based on the training data set, the number of hidden nodes of ELM is determined to 42 by 100-fold cross-validation. Then, the trained ELM is tested on the testing set. Figure 4 shows the predicted results in testing set. As shown in Fig. 4, the predicted and calculated values are almost coincident. The R2 is 0.99998 for FS prediction, and the mean R2 is 0.9977 and 0.9976 for x-coordinates and y-coordinates of slip surface prediction, respectively. It indicates that the ELM model exhibits excellent prediction accuracy and can be used as a response surface function to replace the time-consuming program Slide. There may be other ANNs that can achieve the same or higher accuracy as the ELM model. However, the ELM model has fully met the research needs of this paper. Therefore, other ANN-based response surface models are not applied. The DREAM algorithm is implemented for each case to solve the posterior distribution of c and ϕ. Figure 5 shows the evolution of convergence estimator \( \hat{R} \) and acceptance rate in the considered eight cases. As shown in Fig. 5, after about 2000 function evaluations, each DREAM run satisfies the convergence estimator threshold of \( \hat{R} \)≤ 1.2, and the acceptance rate is greater than 15%, indicating that the chosen number of Markov chains is reasonable and each DREAM run achieves convergence and acceptable performance.

Fig. 4
figure 4

Comparison between calculated values and predicted values. a FS. b x-coordinate. c y-coordinate

Full size image
Fig. 5
figure 5

Evolution of convergence estimator \( \hat{R} \) and acceptance rate in the eight cases

Full size image

Numerical results

Figure 6 shows the solved posterior distribution of each case under different measurement errors. Hereafter, the word “accuracy” denotes the proximity of the posterior mean of shear strength parameters to the actual value. The closer the posterior mean is to the actual value, the higher the accuracy. As shown in Fig. 6, in cases 1 and 2, the accuracy of posterior mean is the lowest. The posterior mean is far from the actual value (i.e., c = 12 kPa, ϕ=12°), and the posterior COV of c and ϕ is only slightly smaller than that of their prior. It indicates that Bayesian back analysis with fixed slip surface or using only FS information is unreliable. In cases 3–5, although the posterior mean is closer to the actual value compared with cases 1 and 2, the posterior COVs are high, indicating that using only the slip surface information in the Bayesian back analysis cannot obtain reliable results neither.

Fig. 6
figure 6

Posterior distribution of the eight cases. a Posterior μc. b Posterior μϕ. c Posterior COV of c. d Posterior COV of ϕ. e Posterior ρc,ϕ

Full size image

In cases 6–8, both FS information and slip surface information are considered in Bayesian back analysis. Compared with cases 1–5, the accuracy of posterior mean in cases 6–8 is significantly higher, and the posterior COVs are significantly less. It indicates that Bayesian back analysis comprehensively considering the information of FS and slip surface can yield satisfactory results. By gradually adding the information of slip surface, the posterior mean tends to close to the actual value, and the posterior COVs decrease. However, the change of posterior mean and COVs is small. For example, the posterior distribution of case 6 is basically same to that of case 8. It indicates that although the more the slip surface location information, the better the back analysis result, for this homogeneous slope, only using the information of slip surface entry and FS can still obtain satisfactory results. With the measurement errors of slip surface increase, the accuracy of posterior mean decreases and the posterior COVs increase, indicating that the measurement errors of slip surface have large effect on the results of Bayesian back analysis, and the smaller the measurement error, the higher the back calculated results accuracy.

From the previous analysis, it can be acknowledged that the traditional Bayesian back analysis with fixed slip surface may be unreliable. There are multiple combinations of shear strength parameters satisfy the condition of FS = 1. Traditional method does not consider the prior information of slip surface, which may cause the back calculated results fail to satisfy the condition that the back calculated critical slip surface should be consistent with the actual slip surface. In this condition, the back calculated parameters are inaccurate. In contrast, Bayesian back analysis considering both FS and slip surface location information can yield good results. Therefore, the slip surface uncertainty should be considered in Bayesian back analysis.

Effect of prior distribution

The prior distribution of parameters such as prior mean, COV, and correlation coefficient may affect the back analyzed results. In this section, the effect of prior distribution of parameters on Bayesian back analysis with fixed slip surface (case 1) and Bayesian back analysis considering slip surface uncertainty (case 6) are studied. In case 6, the measurement error of slip surface is set to 0.1 m. The reason for choosing case 6 as the base case is because it is more applicable, which can obtain satisfactory results by using only simple information of FS and slip surface entry. Table 4 shows the parameters setting of prior distribution.

Table 4 Parameters setting of prior distributions
Full size table

Fixed slip surface

Figure 7 shows the change of posterior distributions of parameters with varying prior distributions of parameters in the case of Bayesian back analysis with fixed slip surface. As shown in Fig. 7, all the posterior ρc,ϕ lie between − 0.5 and − 0.8 indicating that the posterior c and ϕ are highly negatively correlated when the slip surface is fixed in Bayesian back analysis.

Fig. 7
figure 7

Effect of prior distribution on Bayesian back analysis with fixed slip surface. a Effect of prior μc. b Effect of prior μϕ. c Effect of prior COV of c. d Effect of prior COV of ϕ. e Effect of prior ρc,ϕ

Full size image

Figure 7a, b shows that the posterior μc and μϕ basically increase linearly with the linear increase of the corresponding prior μc and μϕ. The average rate of change is defined as the slope of the secant line between the start point and the last point of curves in Fig. 7a, b, and it is used to quantify the sensitivity of posterior mean to prior mean. In Fig. 7a, the average rate of change of posterior μc and μϕ is 0.68 and − 0.26 (°/kPa), respectively. In Fig. 7b, the average rate of change of posterior μc and μϕ is − 0.60 (kPa/°) and 0.65, respectively. It indicates that the prior μc and μϕ have significant effects on posterior μc and μϕ. The posterior ρc,ϕ and COV of c and ϕ do not change much with the change of prior μc and μϕ, indicating prior μc and μϕ have small effects on posterior ρc,ϕ and posterior COV of c and ϕ.

In Fig. 7c–e, the posterior parameters basically remain stable when varying the prior COV and correlation coefficient. Changes in prior coefficient ρc,ϕ and COV of c and ϕ only slightly affect the changes in the corresponding posterior parameters. It indicates that the effects of prior COV and ρc,ϕ on posterior parameters are small.

The previous analysis indicates that in the case of Bayesian back analysis with fixed slip surface, the prior mean of c and ϕ have significant effects on back analyzed results, and the prior COV and ρc,ϕ have small effect on back analyzed results.

Further analysis of Fig. 7a, b shows that when the ratio of prior μc to μϕ is equal to or close to the ratio of actual c to ϕ, the posterior μc and μϕ are close to the actual values. For example, in Fig. 7a, when the prior μc equals 10 kPa, i.e., the ratio of prior μc to μϕ equals 10 kPa/10° = 1 (kPa/°), the posteriorμc and μϕ at this time are closest to the actual values. The same phenomenon can be observed when the prior μϕ equals 14° in Fig. 7b. It indicates that when the slip surface is fixed, the back calculated results are reliable only when the prior μc/μϕ ratio is close to or equal to the actual c/ϕ ratio. The reasons may be explained in the followings.

Jiang and Yamagami (2006, 2008) and Duncan et al. (2014) noted that for a simple homogeneous slope with a certain geometry, unit weight and pore water pressure distribution, the location of critical slip surface is related only to c/tanϕ, i.e., the closer the ratio c/tanϕ of two pairs c and ϕ, the closer their corresponding critical slip surface positions are. In this paper, the ratio of actual c to tanϕ is 12/tan12 ≈56.46. The corresponding ratio are 56.71 and 56.15 when the prior μc and μϕ are equal to 10 kPa and 14° in Fig. 7a, b, respectively. At this time, the ratio of prior μc to tan(μϕ) is very close to the ratio of actual c to tanϕ, indicating that the fixed slip surface is very close to the back calculated critical slip surface. In other words, the back analysis model innately satisfies the condition that the fixed slip surface is consistent with the back calculated critical slip surface. In this condition, a reliable back analysis result can be obtained by using only the information of FS = 1.

Considering slip surface uncertainty

Figure 8 shows the change in posterior parameters over the change of prior parameters in the case of Bayesian back analysis considering slip surface uncertainty. In Fig. 8a, b, the posterior μc and μϕ slightly increase with the increase of the corresponding prior μc and μϕ. In Fig. 8a, the average rate of change of posterior μc and μϕ is 0.12 and − 0.10 (°/kPa), respectively. In Fig. 8b, the average rate of change of posterior μc and μϕ is − 0.22 (kPa/°) and 0.21, respectively. These values are obviously less than that of Fig. 7a, b, indicating that the effects of prior μc and μϕ on posterior μc and μϕ are small. The posterior ρc,ϕ and COVs of c and ϕ basically remain stable when varying the prior μc and μϕ, indicating the effects of prior μc and μϕ on posterior ρc,ϕ and COVs of c and ϕ are also small.

Fig. 8
figure 8

Effect of prior parameters on Bayesian back analysis considering slip surface uncertainty. a Effect of prior μc. b Effect of prior μϕ. c Effect of prior COV of c. d Effect of prior COV of ϕ. e Effect of prior ρc,ϕ

Full size image

Figure 8c–e shows that the posterior parameters basically remain stable and are not sensitive to the change in the prior COVs and the correlation coefficient. It indicates that the prior COVs and ρc,ϕ have small effect on posterior parameters.

The previous analysis indicates that in the case of Bayesian back analysis considering slip surface uncertainty, the prior distributions of shear strength parameters have small effect on back analyzed results.

Case study

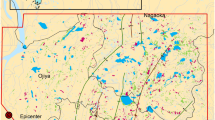
The Northolt landslide in Londay clay (Skempton 1964) is used to validate the effectiveness of the proposed method in actual landslides. This landslide occurred in 1955, 19 years after the excavation was made. The geometry, piezometric line, and portions of the slip surface exposed in trenches are shown in Fig. 9, which are reproduced from (Skempton 1964). The unit weight of London clay is 18.8 kN/m3. The peak strengths are c = 15.3 kPa and ϕ=20°, respectively, and the residual strengths are c = 0.0 kPa and ϕ=16°, respectively.

Fig. 9
figure 9

Geometry of Northolt landslide (reproduced from (Skempton 1964))

Full size image

In Bayesian back analysis, the prior mean of c and ϕ is set to equals peak strengths since the peak strengths are easier to obtain than residual strengths in practical. The variability and correlation coefficient of these variables were not reported in (Skempton 1964). According to the previous analysis, the prior COVs and ρc,ϕ have small effect on posterior parameters. Thus, the prior COVs and ρc,ϕ of Northolt landslide are set to equals that of the synthetic homogeneous slope, i.e., the COVs of c and ϕ are 0.2 and 0.15, respectively, and the ρc,ϕ equals 0. For briefness and practicality, the normal distribution is adopted. The Morgenstern-Price method is used to calculate the FS. Since the Northolt landslide is a real case, the Morgenstern-Price method uncertainty for FS including model bias and variance should be considered. According to Zhang et al. (2010), the model uncertainty of Morgenstern and Price method is assumed to follow normal distribution, and the model bias and variance are 0.05 and 0.07, respectively. Eight points (represented by small green circles in Fig. 9) are selected as the measurements of observed slip surface. In Fig. 9, the maximum vertical distance between the circular slip surface made by (Skempton 1964) and the observed slip surface is about 0.5 m. Therefore, the standard deviation of measurement error of the slip surface is assumed to be 0.5 m.

The sampling range of c and ϕ is [0, 20] and [10, 25], respectively. There are 1000 training sets, and 100 test sets are generated to train and test the ELM response surface function. The number of hidden nodes of ELM is determined to 38. The test results show that the R2 is 0.99988 for FS prediction, and the mean R2 is 0.9973 and 0.9965 for x-coordinates and y-coordinates of the slip surface prediction, respectively. The results of Bayesian back analysis are shown in Fig. 10. The posterior mean μc and μϕ are 2.75 kPa and 19.69°, respectively. The posterior standard deviation of c and ϕ is 0.65 and 1.56, respectively, and the posterior ρc,ϕ is − 0.26. The posterior mean lies between the peak strength and the residual strength, which verifies the feasibility and effectiveness of the proposed method.

Fig. 10
figure 10

Posterior density of c and ϕ

Full size image

Discussion

In previous studies about Bayesian back analysis of shear strength parameters of landslides, the slip surface uncertainty was always ignored. Researchers assumed that the actual slip surface is completely known and only used FS = 1 as the target in back analysis. The reliability of back calculated results is questionable. Because for a fixed slip surface, there are multiple combinations of shear strength parameters satisfy FS = 1, and the back calculated results may be only a local optimal solution. The results in this paper show that the traditional Bayesian back analysis generates results significantly deviating from the actual values and is sensitive to the prior mean of shear strength parameters. The results are reliable only when the prior μc/tan (μϕ) ratio is close to or equal to the ratio of actual values. In practical, however, the actual ratio of shear strength parameters is not known, so it is difficult to ensure if the ratio of the prior μc to μϕ is consistent with the ratio of actual values.

The limitations of this study are as follows: (1) the slope is a single-layer homogeneous slope, and the spatial variability of shear strength parameters is ignored. Further research considering the multi-layer soil and the spatial variability of shear strength parameters in Bayesian back analysis of landslides is currently undertaken. (2) The slip surface is basically circular. The landslide with non-circular slip surface is not fully investigated. The measurement error of slip surface is not available in the literature, and it is assumed to be normally distributed, independent, and homogeneous. Further research is needed to address this issue. (3) The case when the prior distributions of c and ϕ follow the lognormal distribution is not considered. (4) The calculation process is complicated, which may not facilitate practical application. Future research is needed to simplify the calculation process.

Conclusion

Back analysis is an effective technique to obtain the shear strength parameters of landslide. At present, most studies about Bayesian back analysis of shear strength parameters neglect the slip surface uncertainty. To fill this gap, this paper proposes a Bayesian back analysis method of landslides considering slip surface uncertainty. A hypothetic simple homogeneous slope case and a practical landslide are used to test the proposed method. Results show that the traditional Bayesian back analysis neglecting slip surface uncertainty is sensitive to the prior mean of shear strength parameters. By considering the slip surface uncertainty in Bayesian back analysis, the results are reliable and close to the actual values, whilst less affected by the prior distributions of shear strength parameters. The measurement error of slip surface has a certain influence on the results of the proposed method and should be minimized in practical engineering applications. This study highlights the importance of slip surface uncertainty on the reliability of Bayesian back analysis.