Introduction

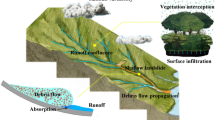
Debris flows are among the most common natural disasters in mountainous areas and have devastating impacts on structures, residents, and other elements at risk (Adhikari and Koshimizu 2005; Allen et al. 2016). Earthquakes and heavy rainfalls are two factors that can significantly increase the frequency of debris flow (Huang and Li 2009; Tang et al. 2009). For example, the recurrence time of debris flows in Taiwan decreased from 5 years to 2 years after the 1999 Chi-Chi earthquake, and the threshold values of relevant indexes (e.g. rainfall intensity, and critical accumulated precipitation) necessary to initiate debris flows decreased to less than one third the pre-earthquake values (Lin et al. 2004). Field investigations of earthquake-affected areas have found that a large number of loose materials are generated from slope failures triggered by earthquakes, and these materials could easily erode to contribute to debris flows in gullies (Sato and Harp 2009). Debris flows triggered by heavy rainfalls are generated by runoff or mobilized by a landslide. The development process for debris flow, shown in Fig. 1, can be described as follows: (i) rainfalls affect slope stability due to rainwater infiltration, ultimately resulting in slope failure; (ii) under sufficiently high rainfall intensities or slope surface saturation, runoffs are generated via microsurface ponding; (iii) loose materials from slope failures or the channel surface mix with runoffs, which finally form a debris flow. Runoff-generated debris flow, compared with landslide-generated debris flow, is mainly composed of the last two stages. The occurrence of an earthquake can generate loose materials within a very short period due to breaking of the slope, substantially shortening the time needed for stage i to occur and providing more source materials to promote stage iii. Hence, under heavy rainfalls, runoff-generated debris flows have more potential for occurrence than landslide-generated debris flow.

Fig. 1
figure 1

Simplified schematic diagram of a common debris flow development, and the possible influence of an earthquake

Full size image

Over the past decades, debris flows have been studied in detail to understand the initial conditions, propagation mechanisms, and risk assessments. Most research on the initial conditions of debris flows has been focused on the determination of material sources (Bardou et al. 2007). As a typical solid–fluid mixture flow, debris flows can obtain the solid phase from slope failure and surface sediments and the fluid phase from rainwater and snowmelt (Decaulne et al. 2005; Wieczorek and Glade 2005). Several models have been presented to describe this process, which mainly focuses on debris flows initiated by the mobilization of landslides (Iverson et al. 1997). Since large amounts of loose materials are generated after an earthquake, runoff-generated debris flows are more likely to occur by the entrainment of a large quantity of debris materials into runoff (Coe et al. 2008). For example, the debris flows in Wenjia gully (Sichuan Province, China) after the 2008 Wenchuan earthquake were formed by the following sequence of events: runoff, erosion, collapse, engulfment, and debris flow (Ni et al. 2012). Such a triggering mechanism, initially stressed by laboratory experiments (Gregoretti 2000), has also been shown by field investigations around the world in different environments (Kean et al. 2013; Ma et al. 2018). The debris flows after triggering can dramatically grow in volume due to the entrainment of debris materials during propagation; therefore, these debris flows are very dangerous as they cause high socio-economic impacts (Gregoretti et al. 2018). Such debris flows differ from those initiated by the mobilization of landslides (Berti and Simoni 2005) and are poorly understood. Moreover, debris flow propagation is influenced by terrain and flow properties (e.g. solid components, density, and viscosity) that relate to the initial conditions of the debris flow (Wang et al. 2018). Some behaviours can also make debris flow propagation more complex, such as entrainment (Iverson et al. 2011), solid–fluid interactions (Chen et al. 2014), phase separation (Pudasaini and Fischer 2016b), and dilatancy (Iverson and George 2014). According to field investigations and experiments, these behaviours can substantially alter the characteristics of debris flows (e.g. impact force, velocity, and volume) and should be considered under the actual condition. With the continuous development of simulation technologies, a numerical modelling for quantitative risk assessments of debris flows has shown improved availability and versatility (Luna et al. 2014; Ouyang et al. 2015). One of the most critical problems with the application of such models is the validity of a numerical model, which should be determined by application to actual cases. Several models can effectively describe debris flow propagation (Pudasaini 2012; Ouyang et al. 2015), but only a few have coupled these processes with the initiation conditions of debris flows. Individually studying debris flow processes may lead to unignorable errors in risk assessments, given that processes such as infiltration, runoff, entrainment, and flow properties influence one another. From this point of view, some integrated models were presented in recent years. Bout et al. (2018) integrated the Pudasaini (2012) two-phase solid–fluid equations in a catchment model for flash floods, debris flows, and shallow slope failures. Zhou et al. (2019) studied the possible clusters of debris flow in Hongkong Island under extreme rainfall conditions by using a two-step analysis procedure that includes slop failure and debris flow propagation. However, these models focused on the landslide-generated debris flow. By focusing on the post-wildfire debris flow, McGuire et al. (2017) combined a numerical model to simulate the transition from clear water flow to debris flow for investigating the initiation of runoff-generated debris flows. The formation of runoff in burned watersheds gets easier compared with that in unburned conditions, due to a lack of rainfall interception and fire-induced increase in the soil water repellency (Staley et al. 2012). Increases in solid erodibility and sediment supply (e.g. ashes) also reduce the difficulty of erosion and sediment transport. Wei et al. (2018) highlighted the correlation among rainfall, hydrological processes, and debris flow by exploring the effect of runoff behaviour (e.g. peak flow discharge) on the occurrence of channelized debris flow with two different modelling approaches. Gregoretti et al. (2019) studied the behaviour of runoff-generated debris flows that occurred at Cancia, by simulating the flow propagation under the conditions of with and without entrainment. However, these studies treat debris flow as a single-phase flow and do not consider the interaction between solid and fluid phases and their effect on debris flow propagation.

Given the existing gaps in debris flow modelling, the objective of this study is to develop an integrated model to describe the entire evolution process of runoff-generated debris flows. In this model, the debris flow characteristics are determined from a combination of initial conditions, evolution mechanisms, and entrainment effects. Rainfall infiltration into the slope and runoff generation are coupled and estimated using the tridiagonal matrix algorithm (TDMA) to solve the three-dimensional Richards’ equation and the finite volume method (FVM) to solve the two-dimensional shallow water equations. Two-phase depth-averaged equations proposed by Pudasaini (2012) are applied to simulate debris flows. Two experimental cases and a real case were modelled to test the validity of the presented model. In addition, analyses of key factors that influence the evolution process of debris flows were performed.

Model framework

The evolution process of a runoff-generated debris flow is similar to the normal process, as shown in Fig. 2. Based on the description in the “Introduction” section, the evolution process was refined into three stages for our model: (i) Rainfall–runoff: Although this stage could lead to slope failure, intense and prolonged rainfalls are generally required to provide sufficient water to infiltrate and degrade the inner structure of the slope, as is sufficient time for fracture development. By contrast, runoff generation, which is also caused during this stage, may occur more readily due to the low threshold requirements of rainfall and formation time; (ii) Entrainment of debris material into a runoff with the formation of a solid–liquid surge: Runoff expands itself by converging tributaries and spreads outward while travelling downstream. Meanwhile, runoff entrains materials loosened by earthquake-induced slope failure and gradually becomes a hyperconcentrated flow, which is a flow state between water and debris flows (Pierson and Scott 1985; Costa 1988); (iii) Debris flow routing: Hyperconcentrated flow transitions into a debris flow and increases in scale through continuous entrainment of loose materials (De Haas and Van Woerkom 2016; Pudasaini and Fischer 2016a). A detailed flow chart of this debris flow evolution process, as well as the numerical models and calculation methods adopted to describe each stage in this study, is presented in Fig. 2.

Fig. 2
figure 2

Detailed flow chart of the debris flow evolution process, along with the numerical models and corresponding calculation methods applied in this study

Full size image

Stage i: Richards’ equation and TDMA scheme

The governing equation for stage i is Richard’s equation, which represents a combination of Darcy’s law and the mass conservation law and effectively describes saturated–unsaturated flows in porous media (Warrick et al. 1990; Furman 2008). We assume a constant water mass density and a non-deformed porous medium which gives the following flow equation (Kavetski et al. 2001):

$$ \frac{\partial \theta }{\partial t}=\nabla \left(D\left(\theta \right)\nabla \theta \right)-\frac{\partial K\left(\theta \right)}{\partial z} $$
(1)

where t is the time, θ is the soil moisture content, D is the hydraulic diffusivity tensor, z is the upward positive vertical coordinate, and K is the hydraulic conductivity tensor. Of note, the values of D and K are influenced by moisture content and soil properties and differ somewhat by location for slopes with nonuniform soil properties (Pachepsky et al. 2003). For simplicity, the slope studied here was assumed to consist of homogenous soil, although complex soil properties may be more realistic for a natural slope. To solve governing Eq. 1, two types of boundary conditions (BCs), Dirichlet BCs and Neumann BCs, are necessary:

$$ {\displaystyle \begin{array}{l}\mathrm{Dirichlet}\kern0.3em \mathrm{BC}:\kern1.2em \left\{\begin{array}{l}\theta ={\theta}_{\mathrm{s}}\\ {}\theta ={\theta}_{\mathrm{m}}\end{array}\right.\\ {}\\ {}\mathrm{Neumann}\kern0.3em \mathrm{BC}:\kern1.2em \left\{\begin{array}{l}-D\left(\theta \right)\nabla \theta +K\left(\theta \right)=I(t)\\ {}-D\left(\theta \right)\nabla \theta +K\left(\theta \right)=0\end{array}\right.\kern0.2em \end{array}} $$
(2)

where θm and θs are the initial and given moisture contents, respectively, and I is the infiltration rate. The upper boundary changes depending upon the amount of rainfall and the moisture content of surface soil. Initially, the infiltration capacity of surface soil is higher than the amount of rainfall if the soil is dry, meaning that the actual infiltration rate equals the rainfall rate, and almost no runoffs are generated. Some special effects, such as evaporation and chemical reactions, are neglected. With continued rainwater seepage, the infiltration capacity of surface soil decreases, which could result in the generation of runoff when the infiltration rate is less than that of the rainfall. Until this point, Neumann BCs are applied. Once the surface soil reaches saturation, most of the rainfall contributes to the runoff. At this point, Dirichlet BCs are applied. No flow boundary (a Neumann BC) is applied at the lateral boundaries of the slope; thus, only the upper and lower surfaces have flow exchange. Here, Eq. 1 applies only to a non-deformed and uniform soil and does not consider some complex factors such as soil sorptivity and soil wettability, although these factors may have a notable influence on infiltration.

Since Eq. 1 is a three-dimensional quasi-linear diffusion equation and solved with BCs that change over time and require a robust numerical method. From this perspective, as a fully implicit scheme for discretizing each axial component, the TDMA scheme for solving the tridiagonal matrix and the alternating direction implicit (ADI) scheme for improving stability are coupled (Hsueh et al. 1999). This coupled method has second-order accuracy in both time and space.

Stage ii: shallow water equations and FVM scheme

One of the more widely used approaches for describing the propagation of runoff is that of shallow water equations, which can be obtained by simplifying the Navier–Stokes equations owing to the special disparity of the length scales (H/L < <1, where H is the typical depth and L is the typical topography-parallel length) of runoffs (Bradford and Sanders 2002; Bouchut et al. 2003). By coupling the shallow water equations with those describing the evolution of bed topography and sediment mass conservation, the complete system of mass and momentum conservation equations is written as follows (Cao et al. 2004):

$$ {\displaystyle \begin{array}{l}\frac{\partial h}{\partial t}+\frac{\partial (hu)}{\partial x}+\frac{\partial (hv)}{\partial y}=R(t)-I(t)+\left({E}_{\mathrm{r}}-{D}_{\mathrm{r}}\right){\left(1-p\right)}^{-1}\\ {}\frac{\partial (hu)}{\partial t}+\frac{\partial \left(h{u}^2+0.5g{h}^2\right)}{\partial x}+\frac{\partial \left( hu v\right)}{\partial y}\\ {}\begin{array}{l}\kern2.5em =- gh\frac{\partial {z}_{\mathrm{b}}}{\partial x}- gh{S}_{fx}-0.5\left({\rho}_{\mathrm{s}}-{\rho}_{\mathrm{f}}\right){\rho}^{-1}g{h}^2\frac{\partial c}{\partial x}-\left({\rho}_0-\rho \right){\rho}^{-1}\left({E}_{\mathrm{r}}-{D}_{\mathrm{r}}\right)u{\left(1-p\right)}^{-1}\\ {}\frac{\partial (hv)}{\partial t}+\frac{\partial \left( hu v\right)}{\partial x}+\frac{\partial \left(h{v}^2+0.5g{h}^2\right)}{\partial y}\\ {}\begin{array}{l}\kern2.5em =- gh\frac{\partial {z}_{\mathrm{b}}}{\partial y}- gh{S}_{fy}-0.5\left({\rho}_{\mathrm{s}}-{\rho}_{\mathrm{f}}\right){\rho}^{-1}g{h}^2\frac{\partial c}{\partial y}-\left({\rho}_0-\rho \right){\rho}^{-1}\left({E}_{\mathrm{r}}-{D}_{\mathrm{r}}\right)v{\left(1-p\right)}^{-1}\\ {}\begin{array}{l}\frac{\partial (hc)}{\partial t}+\frac{\partial \left( hu c\right)}{\partial x}+\frac{\partial \left( hv c\right)}{\partial y}={E}_{\mathrm{r}}-{D}_{\mathrm{r}}\\ {}\frac{\partial {z}_{\mathrm{b}}}{\partial t}=-\left({E}_{\mathrm{r}}-{D}_{\mathrm{r}}\right){\left(1-p\right)}^{-1}\end{array}\end{array}\end{array}\end{array}} $$
(3)

where h is the flow depth; R is the rainfall intensity; u and v are the depth-averaged velocity components in the x and y directions, respectively; c is the depth-averaged concentration of the volumetric sediment; ρ is the water–sediment mixture density, ρ = ρf(1 − c) + ρsc, in which ρs is the sediment density and ρf is the water density; g is the gravitational acceleration; ρb is the density of the bed, ρb = ρs(1 − p) + ρfθ, where p is the bed sediment porosity, p = θs. The friction slopes Sfx and Sfy in the x and y directions are written as Sfx = nb2u(u2 + v2)1/2/h4/3 and Sfy = nb2v(u2 + v2)1/2/h4/3, respectively; nb is the Manning friction coefficient; zb is the slope surface; Er and Dr are the entrainment and deposition rates at the interface between the bed surface and water column, respectively. The first formula in Eq. 3 represents mass conservation for the sediment–water mixture. The second and third formulas in Eq. 3 represent momentum conservation in x and y directions, respectively. The terms on its right-hand side relate to bed topography, friction loss, spatial variations in sediment concentration, and momentum transfer induced by sediment exchange between the erodible bed and the flow. Formula four links the local variation in bed elevation to erosion accumulated or removed at the bottom. Several empirical formulas have been proposed for determining the deposition and entrainment rates (Cao 1999; Li and Duffy 2011). For deposition and entrainment of non-cohesive sediment, we apply the following relationship (Cao 1999):

$$ {\displaystyle \begin{array}{l}{D}_{\mathrm{r}}=\omega {\left(1-{C}_{\mathrm{a}}\right)}^m{C}_{\mathrm{a}}\\ {}{E}_{\mathrm{r}}=160{R_{\mathrm{m}}}^{-0.8}\left(1-p\right){\alpha}_{\mathrm{c}}^{-1}d\left(\alpha -{\alpha}_{\mathrm{c}}\right){U}_{\infty }{h}^{-1}\end{array}} $$
(4)

where Ca is the near-bed volumetric sediment concentration, Ca = cmin(2, (1 − p)/c) (Cao et al. 2004); ω is the settling velocity of a single particle in tranquil water, ω = [(36υ/d)2 + 7.5ρsgd–36υ/d]0.5/2.8; υ is the water kinematic viscosity and d is the grain diameter of bed sediment; m is an exponent that indicates the effects of hindered settling caused by high sediment concentrations; Rm = d(sgd)0.5υ − 1, in which s = ρs/ρf − 1 is the submerged specific gravity of sediment; α is the Shields parameter, α = Vm2/(sgd), where Vm = [gh(Sfx2 + Sfy2)]1/2 is the friction velocity (Li and Duffy 2011); αc is the critical Shields parameter for initiation of sediment movement and Er = 0 if α < αc; and U∞ is the free runoff, U∞ = 7(u2 + v2)0.5/6. For the entrainment of cohesive sediment, we apply the following relationship (Izumi and Parker 2000):

$$ {E}_{\mathrm{r}}=\delta {\left(\sqrt{u^2+{v}^2}{u}_{\mathrm{c}}^{-1}-1\right)}^{\zeta } $$
(5)

where ζ is an exponent with a value typically ranging from 1 to 2; δ is a coefficient that indicates the ease with which sediment is eroded, and uc is a threshold entrainment flow velocity. Several advantages of Eqs. 4 and 5 include their ease of implementation in a model and their ability to represent physical processes (cf. Simpson and Castelltort 2006). First, the sediment load is treated as a single-mode because it is difficult to distinguish individual bedload and suspended load components when both exist in nature. Second, bed surface evolution depends on the relative flux between entrainment and deposition for any given flow conditions, and no other assumptions are required. Third, the entrainment and deposition fluxes are governed by different physics and can be readily modified by incorporating transport models or new data for studying different applications. However, the shallow water model assumes that the velocity profile of flow in the vertical direction is uniform, which results in some vertical change (e.g. turbulence) of runoff going unreflected. This model also assumes that the eroded materials are uniformly distributed in the flow; thus, it is not suitable for the flow with bedload transport.

To solve Eq. 3, a well-balanced FVM is applied to preserve steady state when discretizing the flux and source terms (Audusse et al. 2004), and a modified HLLC Riemann approximate solver is applied to prevent nonphysical flux when managing the discontinuous problem at the grid-cell interface (Liang and Borthwick 2009). This numerical scheme can achieve second-order accuracy in both time and space with the application of operator-splitting and interface reconstruction techniques (Liu and He, 2016). Alternative, widely used, and successful computational tool adopt high-resolution finite difference method (FDM) (Pudasaini and Hutter 2007; Mergili et al. 2017). In comparison with FDM, FVM can more easily satisfy the integral conservation of physical quantity under the coarse grid condition, making it suitable for simulating a case with a large computational domain while keeping high efficiency.

Stage iii: two-phase equations and FVM scheme

As mentioned above, a transitional process exists between water flow and debris flow. Currently, the state of flow is typically defined as either rheological method or suspended sediment concentration method (Rickenmann 1991; Pierson 2005). The rheological method divides flow type in terms of flow behaviour (e.g. Newtonian fluid or non-Newtonian fluid to distinguish water flow from hyperconcentrated flow) (Qian et al. 1980) and yield strength (e.g. at least 60 Pa to distinguish hyperconcentrated flow from debris flow) (Pierson and Costa 1987). Regarding the suspended sediment concentration method, many authors have applied certain boundary values to divide flow type. For example, Beverage and Culbertson (1964) suggested that hyperconcentrated flow should have a suspended sediment concentration of at least 20 vol.% and not more than 60 vol.%. Although these studies provide some useful approaches to define flow type, a precise and comprehensive definition has remained elusive. Generally, the type of flow change is reflected in its properties, such as bulk density, volume, and viscosity. As one of the most important properties of a fluid, viscosity normally increases with increasing sediment concentration, sometimes to a dramatic degree. From this perspective, we consider that the values of the flow properties, such as viscosity, vary spatiotemporally and are influenced by suspended sediment concentration, which could evolve with fluid–solid relative motion (Pudasaini and Fischer 2016b) or entrainment (Egashira et al. 2001). By considering these effects, expressions of viscosity should be replaced by the apparent viscosity (Ishii and Mishima 1984; Brown and Lawler 2003). Therefore, the relationship between the pure fluid viscosity μc and apparent viscous coefficient μf proposed by Mooney and Hermonat (1955) is used here. This relation correlates well with the “average sphere curve” proposed by Rutgers (1962) and can be expressed as

$$ \ln \left(\frac{\mu_{\mathrm{f}}}{\mu_{\mathrm{c}}}\right)=\frac{2.5{\alpha}_{\mathrm{s}}}{1-1.4{\alpha}_{\mathrm{s}}} $$
(6)

where αs is the solid volumetric fraction. Notably, the concentration range for the relationship between μc and μf is approximately 0–0.5. Beyond this concentration range, the flow is so viscous that the apparent viscosity coefficient is considered constant at 0.0645 (Huebl and Steinwendtner 2000).

Since debris flow is defined as a typical solid–fluid mixture flow, several models have been developed to describe its propagation by including different behaviours (Pudasaini 2012; Iverson and George 2014). However, debris flow propagation is highly complex and challenging to simulate using a single model that involves all behaviours. Here, solid–fluid interaction and entrainment are involved, and these two behaviours could have a significant influence on debris flow propagation. To simulate flow propagation, a generalized two-phase depth-averaged model modified from Pudasaini (2012) is applied. This model consists of mass and momentum balance equations for each phase. It describes momentum transfer more comprehensively, as reflected in the considerations of Coulomb plasticity for solid-phase, non-Newtonian viscous fluid stress, buoyancy, and generalized drag forces. Some additional terms are added in the model to consider the role of precipitation, frictional resistance, and erosion in flow propagation. This approach allows for smooth transitions between nonviscous flow, and debris flow states and solves the interactions between distinct flow types automatically. A standard and well-structured conservation equation of the model including erosion can be written as

$$ {\displaystyle \begin{array}{l}\frac{\partial \left({\alpha}_{\mathrm{s}}h\right)}{\partial t}+\frac{\partial \left({\alpha}_{\mathrm{s}}h{u}_{\mathrm{s}}\right)}{\partial x}+\frac{\partial \left({\alpha}_{\mathrm{s}}h{v}_{\mathrm{s}}\right)}{\partial y}={E}_{\mathrm{s}}\\ {}\frac{\partial \left({\alpha}_{\mathrm{s}}h{u}_{\mathrm{s}}\right)}{\partial t}+\frac{\partial \left({\alpha}_{\mathrm{s}}h\left({u}_{\mathrm{s}}^2+0.5{\beta}_{x\mathrm{s}}h\right)\right)}{\partial x}+\frac{\partial \left({\alpha}_{\mathrm{s}}h{u}_{\mathrm{s}}{v}_{\mathrm{s}}\right)}{\partial y}\\ {}\begin{array}{c}={u}_{\mathrm{s}}^b{E}_{\mathrm{s}}+h\left[{\alpha}_{\mathrm{s}}\left({g}_x-\frac{u_{\mathrm{s}}}{\left|{u}_{\mathrm{s}}\right|}{p}_{\mathrm{b}\mathrm{s}}\tan {\varphi}_{\mathrm{b}\mathrm{ed}}-\varepsilon {p}_{\mathrm{b}\mathrm{s}}\frac{\partial {z}_{\mathrm{b}}}{\partial x}\right)-\varepsilon {\alpha}_{\mathrm{s}}\gamma {p}_{\mathrm{b}\mathrm{f}}\left(\frac{\partial h}{\partial x}+\frac{\partial {z}_{\mathrm{b}}}{\partial x}\right)+{C}_{\mathrm{D}}\left({u}_{\mathrm{f}}-{u}_{\mathrm{s}}\right){\left|{u}_{\mathrm{f}}-{u}_{\mathrm{s}}\right|}^{J-1}\right]\\ {}\begin{array}{l}\frac{\partial \left({\alpha}_{\mathrm{s}}h{v}_{\mathrm{s}}\right)}{\partial t}+\frac{\partial \left({\alpha}_{\mathrm{s}}h{u}_{\mathrm{s}}{v}_{\mathrm{s}}\right)}{\partial x}+\frac{\partial \left({\alpha}_{\mathrm{s}}h\left({v}_{\mathrm{s}}^2+0.5{\beta}_{y\mathrm{s}}h\right)\right)}{\partial y}\\ {}={v}_{\mathrm{s}}^b{E}_{\mathrm{s}}+h\left[{\alpha}_{\mathrm{s}}\left({g}_y-\frac{v_{\mathrm{s}}}{\left|{u}_{\mathrm{s}}\right|}{p}_{\mathrm{b}\mathrm{s}}\tan {\varphi}_{\mathrm{b}\mathrm{ed}}-\varepsilon {p}_{\mathrm{b}\mathrm{s}}\frac{\partial {z}_{\mathrm{b}}}{\partial y}\right)-\varepsilon {\alpha}_{\mathrm{s}}\gamma {p}_{\mathrm{b}\mathrm{f}}\left(\frac{\partial h}{\partial y}+\frac{\partial {z}_{\mathrm{b}}}{\partial y}\right)+{C}_{\mathrm{D}}\left({v}_{\mathrm{f}}-{v}_{\mathrm{s}}\right){\left|{u}_{\mathrm{f}}-{u}_{\mathrm{s}}\right|}^{J-1}\right]\end{array}\end{array}\end{array}} $$
(7)
$$ {\displaystyle \begin{array}{l}\frac{\partial \left({\alpha}_{\mathrm{f}}h\right)}{\partial t}+\frac{\partial \left({\alpha}_{\mathrm{f}}h{u}_{\mathrm{f}}\right)}{\partial x}+\frac{\partial \left({\alpha}_{\mathrm{f}}h{v}_{\mathrm{f}}\right)}{\partial y}={E}_{\mathrm{f}}+R(t)\\ {}\frac{\partial \left({\alpha}_{\mathrm{f}}h{u}_{\mathrm{f}}\right)}{\partial t}+\frac{\partial \left({\alpha}_{\mathrm{f}}h\left({u}_{\mathrm{f}}^2+0.5{\beta}_{x\mathrm{f}}{h}^2\right)\right)}{\partial x}+\frac{\partial \left({\alpha}_{\mathrm{f}}h{u}_{\mathrm{f}}{v}_{\mathrm{f}}\right)}{\partial y}\\ {}\begin{array}{l}={u}_{\mathrm{f}}^b{E}_{\mathrm{f}}-{u}_{\mathrm{f}}R(t)+h{\alpha}_{\mathrm{f}}{g}_x-h{\alpha}_{\mathrm{f}}\varepsilon \left[\frac{1}{2}{p}_{\mathrm{b}\mathrm{f}}\frac{h}{\alpha_{\mathrm{f}}}\frac{\partial {\alpha}_{\mathrm{s}}}{\partial x}+{p}_{\mathrm{b}\mathrm{f}}\frac{\partial {z}_{\mathrm{b}}}{\partial x}-\frac{1}{\alpha_{\mathrm{f}}{N}_{\mathrm{R}}}\left(2\frac{\partial^2{u}_{\mathrm{f}}}{\partial {x}^2}+\frac{\partial }{\partial y}\left(\frac{\partial {v}_{\mathrm{f}}}{\partial x}+\frac{\partial {u}_{\mathrm{f}}}{\partial y}\right)-\frac{\chi {u}_{\mathrm{f}}}{\varepsilon^2{h}^2}\right)\right]\\ {}\kern1.5em -h{\alpha}_{\mathrm{f}}\varepsilon \left[\frac{1}{\alpha_{\mathrm{f}}{N}_{\mathrm{R}\mathrm{A}}}\left(2\frac{\partial }{\partial x}\left(\frac{\partial {\alpha}_{\mathrm{s}}}{\partial x}\left({u}_{\mathrm{f}}-{u}_{\mathrm{s}}\right)\right)+\frac{\partial }{\partial y}\left(\frac{\partial {\alpha}_{\mathrm{s}}}{\partial x}\left({v}_{\mathrm{f}}-{v}_{\mathrm{s}}\right)\right)+\frac{\partial {\alpha}_{\mathrm{s}}}{\partial y}\left({u}_{\mathrm{f}}-{u}_{\mathrm{s}}\right)\right)-\frac{\xi {\alpha}_{\mathrm{s}}\left({u}_{\mathrm{f}}-{u}_{\mathrm{s}}\right)}{\varepsilon^2{\alpha}_{\mathrm{f}}{N}_{\mathrm{R}\mathrm{A}}{h}^2}\right]\\ {}\begin{array}{l}\kern1.5em -h\left[\frac{1}{\gamma }{C}_{\mathrm{D}}\left({u}_{\mathrm{f}}-{u}_{\mathrm{s}}\right){\left|{u}_{\mathrm{f}}-{u}_{\mathrm{s}}\right|}^{J-1}+{\alpha}_{\mathrm{f}}{g}_z\frac{n_{\mathrm{b}}^2}{h^{4/3}}{u}_{\mathrm{f}}\left|{u}_{\mathrm{f}}\right|\right]\\ {}\frac{\partial \left({\alpha}_{\mathrm{f}}h{v}_{\mathrm{f}}\right)}{\partial t}+\frac{\partial \left({\alpha}_{\mathrm{f}}h{u}_{\mathrm{f}}{v}_{\mathrm{f}}\right)}{\partial x}+\frac{\partial \left({\alpha}_{\mathrm{f}}h{v}_{\mathrm{f}}^2+0.5\varepsilon {g}_z{\alpha}_{\mathrm{f}}{h}^2\right)}{\partial y}\\ {}\begin{array}{l}={v}_{\mathrm{f}}^b{E}_{\mathrm{f}}-{v}_{\mathrm{f}}R(t)+h{\alpha}_{\mathrm{f}}{g}_y-h{\alpha}_{\mathrm{f}}\varepsilon \left[\frac{1}{2}{p}_{\mathrm{b}\mathrm{f}}\frac{h}{\alpha_{\mathrm{f}}}\frac{\partial {\alpha}_{\mathrm{s}}}{\partial y}+{p}_{\mathrm{b}\mathrm{f}}\frac{\partial {z}_{\mathrm{b}}}{\partial y}-\frac{1}{\alpha_{\mathrm{f}}{N}_{\mathrm{R}}}\left(2\frac{\partial^2{v}_{\mathrm{f}}}{\partial {y}^2}+\frac{\partial }{\partial x}\left(\frac{\partial {u}_{\mathrm{f}}}{\partial y}+\frac{\partial {v}_{\mathrm{f}}}{\partial x}\right)-\frac{\chi {v}_{\mathrm{f}}}{\varepsilon^2{h}^2}\right)\right]\\ {}\begin{array}{l}\kern1.25em -h{\alpha}_{\mathrm{f}}\varepsilon \left[\frac{1}{\alpha_{\mathrm{f}}{N}_{\mathrm{R}\mathrm{A}}}\left(2\frac{\partial }{\partial y}\left(\frac{\partial {\alpha}_{\mathrm{s}}}{\partial y}\left({v}_{\mathrm{f}}-{v}_{\mathrm{s}}\right)\right)+\frac{\partial }{\partial x}\left(\frac{\partial {\alpha}_{\mathrm{s}}}{\partial y}\left({u}_{\mathrm{f}}-{u}_{\mathrm{s}}\right)\right)+\frac{\partial {\alpha}_{\mathrm{s}}}{\partial x}\left({v}_{\mathrm{f}}-{v}_{\mathrm{s}}\right)\right)-\frac{\xi {\alpha}_{\mathrm{s}}\left({v}_{\mathrm{f}}-{v}_{\mathrm{s}}\right)}{\varepsilon^2{\alpha}_{\mathrm{f}}{N}_{\mathrm{R}\mathrm{A}}{h}^2}\right]\\ {}\kern1em -h\left[\frac{1}{\gamma }{C}_{\mathrm{D}}\left({v}_{\mathrm{f}}-{v}_{\mathrm{s}}\right){\left|{u}_{\mathrm{f}}-{u}_{\mathrm{s}}\right|}^{J-1}+{\alpha}_{\mathrm{f}}{g}_z\frac{n_{\mathrm{b}}^2}{h^{4/3}}{v}_{\mathrm{f}}\left|{u}_{\mathrm{f}}\right|\right]\end{array}\end{array}\end{array}\end{array}\end{array}} $$
(8)
$$ \frac{\partial {z}_b}{\partial t}=-E=-\left({E}_s+{E}_f\right) $$
(9)

where αf denotes the volumetric fraction for the fluid phase, αf = 1 − αs; us = (us, vs) and uf = (uf, vf) are the velocities for the solid and fluid phases, respectively; γ = ρf/ρs is the density ratio; the aspect ratio ε is expressed as ε = H/L; (gx, gy, and gz) are the gravity acceleration components and can be included in the gradients of the basal topography (Fischer et al. 2012); usb = (usb, vsb) and ufb = (ufb, vfb) are the erosion velocities for the solid and fluid phases at the bottom boundary, respectively, which are associated with the erosion drift coefficients and the mean flow velocities (Pudasaini and Fischer 2016a). pbf and pbs are the effective fluid and solid pressures at the base; Es = (1 − p)E and Ef = pE (or θE) are the solid and fluid entrainment rates, respectively, in which E is the total entrainment rate. φbed is the Coulomb friction angle of the basal surface; the dimensionless variables NR and NRA are expressed as NR = ρfH(gL)0.5/(αfμf) and NRA = ρfH(gL)0.5/(Aμf), where A is the mobility of the fluid at the interface (Kattel et al. 2016); the parameter ξ takes into account different distributions of αs; χ is a shape factor that includes vertical shearing of fluid velocity; J = 1 or 2 represents linear (laminar-type) or quadratic (turbulent-type) drag; CD is the generalized drag coefficient. The terms ufR(t) and vfR(t) in the momentum equations of the fluid phase are to include the mass from precipitation into the debris material directly. It assumes that the added mass obtains kinetic energy from flow to have velocity instantaneously. Some other parameters involved in the above model equations are as follows:

$$ {\displaystyle \begin{array}{l}{\beta}_{x\mathrm{s}}=\varepsilon {k}_x{p}_{\mathrm{bs}},{\beta}_{y\mathrm{s}}=\varepsilon {k}_y{p}_{\mathrm{bs}},{\beta}_{x\mathrm{f}}={\beta}_{y\mathrm{f}}=\varepsilon {p}_{\mathrm{bf}},{p}_{\mathrm{bs}}=\left(1-\gamma \right){p}_{\mathrm{bf}},{p}_{\mathrm{bf}}=-{g}_z,\\ {}{C}_{\mathrm{D}}=\frac{\alpha_{\mathrm{s}}{\alpha}_{\mathrm{f}}\left(1-\gamma \right)}{{\left[\varepsilon {V}_{\mathrm{T}}\left\{ PF\left({R}_{\mathrm{e}\mathrm{p}}\right)+\left(1-P\right)G\left({R}_{\mathrm{e}\mathrm{p}}\right)\right\}\right]}^J},F=\frac{\gamma }{180}{\left(\frac{\alpha_{\mathrm{f}}}{\alpha_{\mathrm{s}}}\right)}^3{R}_{\mathrm{e}\mathrm{p}},G={\alpha}_{\mathrm{f}}^{M_{\mathrm{e}}-1},{R}_{\mathrm{e}\mathrm{p}}=\frac{\rho_{\mathrm{f}}d{V}_{\mathrm{T}}}{\alpha_{\mathrm{f}}{\mu}_{\mathrm{f}}}.\end{array}} $$
(10)

where kx and ky is the earth pressure coefficient for describing the state of stress when a material element deforms (Gray et al. 1999); VT is the terminal velocity of a particle falling in a fluid; P is a parameter which combines the solid-like (G) and fluid-like drag (F) contributions to flow resistance; the value of Me varies from approximately 4.65 to 2.4 as the Reynolds number increases from zero to infinity (Pitman and Le 2005). In summary, Eqs. 7 and 8 represent the mass conservation and momentum conservation of the solid and fluid phases, respectively, and each of them consists of three formulas. The first formulas in Eqs. 7 and 8 represent the mass conservation of the solid and fluid phases, respectively. The second and third formulas in Eq. 7 represent the momentum conservation of the solid phase in the x and y directions, with terms on the right-hand side indicating the effects of erosion, gravity, friction loss, bed topography, buoyancy force, and drag force, respectively. Similarly, the terms on the right-hand side of momentum conservation formulas in Eq. 8 for the fluid phase stand for the effects of erosion, rainwater, gravity, fluid pressure, bed topography, viscous force, friction loss, and drag force, respectively. Equation 9 links the local variation in bed elevation to erosion removed on the bottom. Similar to the shallow water model, the two-phase model also cannot reflect the vertical change of debris flow since it is derived based on the depth-averaged theory. Besides, for the case of debris flow involving large rock, this model is not suitable because the motion feature of large rock is quite different from that of the fluid phase.

During debris flow propagation, the flow dynamic characteristics and evolution of basal sediment beds can be significantly influenced by entrainment. For instance, due to the difference in the solid volume fraction between the bed and debris flow, the particle concentration of the flow body constantly varies by eroding dense/dilute material. In the past few years, several entrainment rate formulas that greatly improve our understanding of this process have been proposed (Pitman et al. 2003; McDougall and Hungr 2005; Iverson and Ouyang 2015). Researchers have recently agreed that pore pressure is a key factor that influences the entrainment dynamic process (Iverson et al. 2011; Luna et al. 2012). It is further agreed that, by ignoring the dilation effect due to the density difference between the debris flow and sediment materials, the entrainment rate formula satisfies the boundary jump conditions (Iverson and Ouyang 2015). The corresponding formula can be expressed as

$$ E=-\frac{\partial {z}_{\mathrm{b}}}{\partial t}=\frac{\tau_{\mathrm{b}}-{\tau}_{\mathrm{r}}}{\rho_{\ast}\sqrt{u_{\ast}^2+{v}_{\ast}^2}} $$
(11)

where u* = αsus + αfuf and v* = αsvs + αfvf are the phase-averaged variables; ρ* = αsρs + αfρf is the mixture density of debris flow; the total basal shear traction τb is considered to be a combination of the solid and fluid shear stresses, τb = αsτbs + αfτbf (Liu and He 2017), in which the solid shear stress τbs = (ρs − ρf)gzhtanφbed and the fluid shear stress τbf = ρfgznb2uf|uf|/h1/3. This form highlights the effect of volume fraction on basal shear stress while considering the leading role of each phase in flow propagation under different conditions. τr = co + ρ*(1–η)gzhtanφbin is the sediment shear resistance from the erodible bed, φbin and co are the internal friction angle and cohesion of the bed material, respectively; η is the pore pressure ratio that indicates the degree of liquefaction of the bed material (Medina et al. 2008). The value of η ranges from 0 (dry avalanche) to 1 (fully liquefied state), and the typically measured values of experimental debris flows are between 0.5 and 0.8 (Reid et al. 2011). Because of the complex evolutionary process of pore pressure during debris flow propagation, the value of η is assumed to be constant for simplicity. The two-phase model is solved following the same calculation procedure as applied to stage ii given in the “Stage ii: shallow water equations and FVM scheme” section.

Models interaction

The above three models are linked together by their input or output variables. For example, soil water content θ and residual rainwater on the surface R − I are obtained by solving Richard’s equation and are treated as input variables h = R − I and p = θ needed by shallow water equations. Runoff depth h and solid volume fraction c are obtained by solving shallow water equations and are treated as input variables αs = c, αf = (1 − c), p = θ, hs = hc, and hf = h(1 − c) needed to solve the two-phase equations. A global coordinate system with the z-axis paralleling the gravitational direction was adopted, supporting the use of the original topography data in the form of a digital elevation model (DEM) to construct the digital terrain directly. However, two problems need to be addressed for such a process implementation. First, the determination of the using condition of the two-phase model is pivotal to make the simulation process reasonable. Typically, the volume fractions of solid grains and intergranular liquid constituting debris flow approximate 30–70% (Iverson 2005). For most numerical cases of debris flows, the value of the solid volume fraction is also no less than 30% (Pudasaini 2012; George and Iverson 2014). Based on previous studies, a minimum solid volume fraction value for use in the two-phase model is set as 20%, which indicates that the two-phase model can also be applied to model hyperconcentrated flow. Below this value shallow water model is adopted. Second, how to handle the transition between the last two stages is important since the flow could consist of runoff and debris flow. Here, we solve this problem by handling the interface flux of calculating cell based on FVM. As an example, the variables change due to the flux difference between two adjacent cells. Depending on the flow type in the cell being runoff or debris flow, the fluxes are calculated by using the shallow water model and two-phase model, respectively.

Model application and discussion

Rainwater infiltration: soil column experiment

The validity of the subsurface model with the presented method was tested against an experiment performed by Yang et al. (1985). This experiment measured the behaviours of one-dimensional flows through unsaturated sandy loam soil under Dirichlet and Neumann BCs. The experimental setup consisted of a Perspex column filled with sandy loam soil and a control device that could apply different BCs at the upper boundary of the column. For the sandy loam soil, the initial moisture content, hydraulic diffusivity, and hydraulic conductivity were measured as θm = 0.025, D = 278.3θ8.05 cm2/min, and K = 1.42θ10.24 cm/min, respectively. Two cases of upper BCs were set as constant rainfall intensity input R = 0.02427 cm/min for 180 min and constant moisture content input θs = 0.4 for 150 min. The lower BC was set as θ = θm, indicating that deep soil maintained a constant moisture content. The time interval (TI) and grid spacing (GS) used for the calculation were 1 s and 0.1 cm, respectively. Comparisons of numerical results and experimental data are shown in Fig. 3. Our model produced soil moisture distribution curves very similar to those of the experimental data (Fig. 3). TI and GS are two key factors that affect the calculation accuracy. Here, we set calculation error = (θcl − θex)/θex × 100% (where θcl and θex are the numerical and experimental data, respectively), and the simulations performed with smaller and larger time steps from TI = 0.1 s to TI = 10 s showed little difference from the curve shown in Fig. 3a, indicating that the applied method can be adapted to changes in temporal scale while maintaining desired calculation accuracy when the subsurface model is coupled with a surface model that has an ever-changing TI. Besides, slight differences existed between the simulations performed with different GSs from 0.05 to 1 cm (Fig. 3a). Overall, the calculation accuracy was higher when using a smaller GS; however, an appropriate choice of GS was made in the following numerical tests according to the situation to improve the calculation efficiency while maintaining the calculation accuracy.

Fig. 3
figure 3

Comparisons of the numerical results and experimental data derived from Yang et al. (1985) for one-dimensional rainwater infiltration test under conditions of a constant moisture content input and b constant rainfall intensity input

Full size image

Runoff propagation: V-catchment experiment

A V-catchment test proposed by Di Giammarco et al. (1996) was simulated to assess whether the proposed surface model could effectively reproduce water dynamics. The results were compared with other results presented by Di Giammarco et al. (1996), Vander Kwaak (1999), and Li and Duffy (2011). The setup of V-catchment numerical experiment consisted of two 1000 × 800-m inclined planes, with a slope of 5% along each width and 2% along each length. A 20-m-wide and 1-m-deep channel was located at the bottom to carry the water towards the sole outlet of the domain (Fig. 4a). The Manning roughness coefficients for the plane and channel were set to 0.015 and 0.15 s/m1/3, respectively. A constant and uniform rainfall rate of R = 3 × 10−6 m/s was applied for 90 min on the surface, which had a dry state initially. Wall BCs were imposed on all sides of the surface, except the channel outlet, where a free BC was applied. The total simulation time was 180 min. The result of the hydrograph using a grid size of 10 × 10 m is shown in Fig. 4b. The simulation agreed well with the results from previous studies. Initially, the V-catchment test was designed only to validate and discuss runoff models; however, to introduce the interaction between subsurface and runoffs, a 1-m-deep subsurface domain was also added for this study (see Fig. 4a). This domain was parallel to the surface and maintained the same geometry and parameters as the original setting. The other parameters were GS = 1 cm, θm = 0.28, θs = 0.4, D = 10.25(θ/θs)8.05 cm2/min, K = 0.037(θ/θs)3.5 cm/min, and R = 0.0509 cm/min. The total simulation time was 360 min. The results of the hydrograph are shown in Fig. 4c. When considering the effect of infiltration, the flow discharge could change dramatically, which could further influence the formation of debris flows.

Fig. 4
figure 4

Simulation of a V-catchment numerical test proposed by Di Giammarco et al. (1996). a The numerical experimental settings. b Comparison of simulated flow discharge with other numerical results from Di Giammarco et al. (1996), VanderKwaak (1999), and Li and Duffy (2011). c Results of flow discharge under conditions of surface only, with infiltration case A and with infiltration case B. Infiltration cases A and B differ in terms of the lower boundary setting, in which case A assumes that soil remained saturated after rainfall and case B assumes that soil became unsaturated after rainfall if it could not get enough water

Full size image

Unsaturated soil becomes saturated with rainfall infiltration and returns to the unsaturated state after rainfall stops if moisture transfer is maintained and there is no enough water supply from the surface. Therefore, two cases were performed with different lower BCs to investigate the effects of this process. Case A assumed that soil remained saturated after rainfall, where − D(θ)▽θ + K(θ) = 0 (under rainfall) and θ = θs (after rainfall). Case B assumed that soil became unsaturated after rainfall if it could not get enough water, where − D(θ)▽θ + K(θ) = 0 (under rainfall) and θ = θm (after rainfall). The results showed marked differences in flow discharge between the two cases (Fig. 4c), indicating that we need to consider case B, where soil absorbs runoff (or ponding) to maintain its moisture content after rainfall, resulting in the reduction of runoff discharge. However, it may be more evident in the case that the runoff has a low speed or surface soil has a strong infiltration capacity (which is unlikely).

The debris flow event of 2010 in Hongchun gully

Finally, the described integrated model is applied to model the formation and propagation processes of the gully debris flow caused by heavy rainfalls on 14 August 2010 in the Hongchun catchment, northwestern Sichuan, China. The catchment is located on the left bank of Minjiang River and has an area of 5.35 km2, a channel length of 3.55 km, and a relative height difference of 1288.4 m (Tang et al. 2011). The average gradients on both sides of the gully reach 35%, and this steep terrain provides a favourable condition for flow propagation. The bedrock in this area mainly consists of Sinian pyroclastic rock, Triassic sandstone, highly fractured and weathered granitic rocks, and Carboniferous limestone. The total volume of the loosely deposited materials in Hongchun catchment increased to 350 × 104 m3 after the 2008 Wenchuan earthquake, and the new loose deposits had blocked the drainage channel (Xu et al. 2012). From 17:00 on 12 August to 2:00 on 14 August 2010, a rainstorm occurred in the Hongchun catchment, and the total cumulative rainfall over the 33 h period reached 162.1 mm (Tang et al. 2011). This rainfall event triggered many channelized debris flows instantaneously with some eyewitnesses claiming that the debris flows started around 03:00 and ended at 04:30 on 14 August 2010. A total volume of about 40 × 104 m3 of debris materials was carried from the valley into the Minjiang River plain, forming a natural debris dam (Li et al. 2013). According to the field investigation, the debris flow was initiated from the erosive channel rills of the landslide deposits in the upper reaches of the gully, and the runoff of water from the intense rainfall eroded the loose sediment materials to move downstream (Tang et al. 2011). One of the most important features of this event is that a landslide dam formed at 1080 m altitude after the earthquake blocked the gully and played a decisive role in debris flow formation and propagation (Fig. 5a). While the landslide dam resulted in a barrier lake that continuously expanded with the collection of runoff from the upstream catchment, these landslide dams were getting saturated, and unstable under the effect of rainfall. Once the overtopping occurred, the dam materials eroded fast and mixed with runoff to form massive debris flow (Le 2014). The downstream gully was heavily eroded by the outburst debris flow, with an average height of 6–10 m (reaching more than 20 m in some places) (Li et al. 2013).

Fig. 5
figure 5

Data describing the Hongchun catchment in Yingxiu, Sichuan, China: a remote sensing image, in which the coloured areas represent the source of the landslides that formed a dam in gully after earthquake (Huang and Tang 2017), b digital terrain based on high-performance unmanned aerial vehicle photogrammetry, and c hourly and cumulative rainfall from 17:00 on 12 August to 09:00 on 14 August 2010

Full size image

Additional input data were obtained, including terrain data, rainfall intensity, soil properties, and deposit properties to support the simulation. We consider a 2-m grid post-event terrain data for the simulation (Fig. 5b) that is modified from the high-resolution DEMs (with a resolution of 0.5 m) obtained by using Unmanned Aerial Vehicle photogrammetry. As suggested by Boreggio et al. (2018), the quality of DEMs has a great influence on the outcome of the debris flow routing models. Therefore, two ways are applied to modify the DEMs in this study, including data interpolation and grid coarsening for increasing data availability and improving calculation efficiency, respectively. According to the field survey, the landslide dam was approximately 150 m in length along the gully with a height of 10 to 40 m and a volume of approximately 6.5 × 105 m3 (Tang et al. 2011). Records of the hourly and cumulative rainfall from 17:00 on 12 August to 09:00 on 14 August 2010 were obtained from a nearby observation station located approximately 600 m from the debris flow alluvial fan with an elevation of 880 m asl, as shown in Fig. 5c (Xu et al. 2012). The rainfall frequency was high from 12:00 on 13 August to 12:00 on 14 August, with a total of 116.3 mm of accumulated rainfall. Unfortunately, no data were available concerning soil properties within the study area. Field investigation shows that the soil in northwestern Sichuan is mainly composed of purple soils at a regional scale. Therefore, some empirical formulas for diffusion and conductivity (D and K, respectively) of this type of soil obtained from laboratory experiments were used (Zhang et al. 1992). The deposits mostly originated from the landslide and rockfalls caused by the earthquake and consisted of granitic rocks, gravel soil, and small amounts of sand, and thus, a value of 2700 kg/m3 for soil density was used. Measured internal frictional angle in the study area ranges from 30 to 45° (Ouyang et al. 2015), and hence, an intermediate value of 35° was applied for the simulation. According to Xu et al. (2012), about 200 × 104 m3 of loose deposits formed before the earthquake and 150 × 104 m3 new loose deposits formed during the earthquake are distributed in both the main and tributary gullies of catchment, and part of them were all eroded by debris flow, making it difficult to obtain the depth distribution of deposits from DEM data. Based on the maximum erosion depth measured from the field, a depth of 30 m for deposits is applied for the simulation. This operation does not influence the simulation results and is only for preventing excessive erosion. Moreover, as suggested by Mergili et al. (2018), the values of some parameters (e.g. entrainment coefficient of cohesive sediment, δ) are adjusted in a trial-and-error procedure until empirical adequacy is reached. An overview of the required parameters for the model is provided in Table 1. In addition, an open BC was imposed on both sides of the study area for flows.

Table 1 The data used in the model, their values, and sources
Full size table

The evolution process of runoff-generated debris flow is presented, with observed uniform rainfall applied to the whole area (from 16:00 on 13 August to 06:00 on 14 August). The soil infiltration process was simulated from before the flow, and the transition moment for the infiltration process to shallow water flow is shown in Fig. 6a. During this stage, the soil moisture content changed with the rainfall intensity. When the rainfall intensity increased beyond the soil infiltration capacity, rainwater residue is produced at the surface. In contrast, the soil moisture content at the surface decreased because of the underground transition of rainwater (Fig. 6b). It can be found that the rainwater residue was produced in the key period between 21:00 and 23:00, on 13 August. After that, tributaries were formed and further collected into runoffs along the steep terrain. Figure 7 shows the simulated flow patterns and corresponding flow velocity at different moments. Initially, a few deposited materials started to be eroded by the runoff and were transported downstream. At this stage, the ability of the flow to carry deposited materials was weak because the flux and velocity of the flow were small. Due to the obstruction of the landslide dam located in the channel, a small barrier lake formed gradually with additional water from the upstream of the catchment (Fig. 7b). Persistent rainfall and additional water from the upstream of the channel raised the water level of the barrier lake. Once the water level was higher than the landslide dam, flood overtopping occurred and resulted in water erosion (Fig. 7c). However, the simulated time of dam break is 4 am, 14 August, which is later than the actual time of 3 am. This difference is attributed to parameter errors such as soil hydraulic diffusivity and dam shape. With continuous erosion of the dam breach, the scale enlarged, and the flow flux sharply increased. As the erosion ability of the debris flow was enhanced, more loose sediment materials were eroded. Therefore, the eroded area was mainly located in the lower parts of the main gully (Fig. 7e), and the maximum erosion depth was 18.4 m. The simulated erosion amount of bed materials in the lower parts of the main gully and the maximum flow flux in gully entrance are 47 × 104 m3 and 319.7 m3/s, respectively, and are near to the values of 43.22 × 104 m3 and 286.59 m3/s calculated by Gan et al. (2012). When the debris flow enters a flat area, it spreads not only downstream but also to either side and finally piles up in the gully entrance and blocks the Minjiang River (Fig. 7d). Meanwhile, some of the debris flow propagated along the river channel. The final solid volume fraction of debris flow, as shown in Fig. 7f, is a viscous flow formed by large quantities of deposits. The simulated results show that the evolution process of debris flow is consistent with the field investigation performed by Tang et al. (2011) and Le (2014).

Fig. 6
figure 6

Transition moment for the infiltration process to shallow water flow: a the evolution of rainwater residue under rainfall condition and b the evolution of water content along with the soil depth

Full size image
Fig. 7
figure 7figure 7

Simulation of the evolution process of the Hongchun runoff-generated debris flow; the left and right columns in (a–d) represent flow depth and flow velocity at different times, respectively; the colour columns in e and f represent the erosion depth and solid volume fraction of debris flow, respectively

Full size image

Since the runoff-generated debris flows mainly enlarge its scales by involving bed sediments along the channel, the liquefaction degree of sediments could play an important role in this process. Therefore, their values of η are applied to the simulations for investigating the effect of η on entrainment and debris flow routing. Figure 8 shows the flow flux histories of the event from the recording point located at the gully entrance by considering the different degree of liquefaction. For similar conditions, it can be found that the flow discharge is proportional to the liquefaction degree of sediments and offers an alternate explanation on why the debris flow is easy to occur during heavy rainfalls. With persistent rainfalls, the sediments absorb water until they become saturated. When the flow passes the saturated sediments, rapid loading by the weight of flow causes the liquefaction of the sediments. The excess pore water pressure generated within the sediments reduces the shear resistance of the sediments. More materials will be eroded by flow, to form debris flow or enlarge the scale of debris flow. Another interesting finding from the numerical results is that the time to peak flux of debris flow. As mentioned above, the 2010 Hongchun debris flow had a distinct characteristic of outburst enlargement due to the landslide dam that blocked the channel. The simulations show that the dam enlarged faster with a large value of sediment liquefaction degree resulting in a large flow discharge. Thus, the flow with a large discharge could have a strong ability to involve the downstream bed sediments. For the dam with a small value of sediment liquefaction degree, its breaking time is extended, resulting in a slow release of the water in the barrier lake. As a result, the erosion ability of the flow with a small discharge is reduced, and resulting peak flux at gully entrance is also small.

Fig. 8
figure 8

Simulated flow flux histories over time from the recording point located at the gully entrance for different pore pressure ratios of the bed material (η)

Full size image

Conclusions

In this study, we present a coupled model to describe the runoff-generated debris flow by dividing its evolution process into three stages: rainfall infiltration, runoff, and debris flow propagation. Each of these stages evolves with specific characteristics during their development and requires different simulating models. Our proposed model integrates Richards’ equations, shallow water equations, and two-phase equations to simulate these three stages, respectively. From the first stage to the second, soil saturation and rainfall intensity are the two main influencing factors. From the second stage to the third, entrainment is the major factor influencing the state of runoff. The application of these physically based multi-hazard models allows for the simulation of the whole debris flow formation process. We validated the feasibility of the proposed model using several experimental cases. In addition, the model was applied to the 2010 debris flow event in the Hongchun catchment to show how runoff-generated flow transforms from a water flow to a debris flow under the effect of entrainment. The results suggest that the prediction of hazard and risk assessment can be made using a model that integrates the behaviours of each stage of debris flow evolution.

The purpose of the proposed model is not the accurate prediction of debris flows for hazard and risk assessments but rather to provide a foundation for ultimately achieving this goal. It focuses on runoff-generated debris flows which occur under the conditions of heavy rainfall and enough loose deposits exist in gully. For other type of debris flow (e.g. debris flow transformed from landslide), this approach is not appropriate because the landslide motion is different with runoff and debris flow and the key factors influencing their evolution are also different. Currently, a lack of available data and physical mechanism investigations limits the prediction of debris flow hazards. Although the developed model describes all relevant processes, including some key influencing factors, it is still too simple to cover the full evolution process of debris flows. Even though the proposed model concentrates more on the whole evolution process of runoff-generated debris flow from formation to propagation, its advantage in terms of mechanics is not significant compared with the existing models with particular focus on debris flow propagation. For example, the D-CLAW by the US Geological Survey (USGS) considered some fundamental mechanics such as pore pressure (Iverson et al. 2011) and dilatancy (Iverson and George 2014; George and Iverson 2014), which can successfully explain motion features of debris flow. Thus, more works are needed to improve the proposed model in terms of mechanics. Besides, a single set of parameters as a simple way to represent the whole study area is used in the model, which results in the loss of accuracy. The characteristics, e.g. soil properties at different parts of study area, are actually not the same and using more realistic parameters will help to improve the simulation results. It is also necessary to strengthen the collection of field data in future work.