Introduction

Landslides cause grave losses of life and property every year around the world. Some of those landslides can enter reservoirs and generate large water waves. Because of their catastrophic consequences, landslide-generated waves (LGWs) have been considered to be one of the most important secondary hazards induced by landslides (Petley 2010). According to Yavari-Ramshe and Ataie-Ashtiani (2016), because of the energy trap, flood potential of LGW hazards is particularly hazardous in a restricted water body like a reservoir.

As it happened in the Vajont reservoir, Italy, in 1963 (Quecedo et al. 2004a, b), the impulsive waves with significant wave amplitude could overtop a dam, flood downstream areas, and cause important damages to both lives and properties in reservoir regions. Therefore, due to the high frequency and great destructive consequences of impulsive waves in reservoir areas (Dai et al. 2004; Gabl et al. 2015; Huang et al. 2009; Miyagi et al. 2011; Wang et al. 2016), it is of paramount importance to evaluate the LGW risk to design effective mitigation measures.

During past decades, many researchers have studied the mechanism of LGW hazard. The numerous research methods that have been employed to assess the risk of LGWs can be classified into four general categories: laboratory model tests, analytical solutions, empirical relationships, and numerical simulations.

In order to investigate the relation between the landslide properties (i.e., impact velocity, volume, density, geometry, etc.) and wave characteristics (i.e., wave amplitude, wave height, period, etc.), many experiments have been performed. Laboratory tests regarding LGWs started with Noda (1970) who carried out a laboratory study for both horizontal and vertical subaerial landslides with a solid block and summarized four patterns for landslide-generated waves as (i) non-linear oscillatory, (ii) transition, (iii) solitary like, and (iv) dissipative transient bores. A laboratory study using steel boxes as slide masses was conducted by Kamphuis and Bowering (1970). They concluded that the most significant factors affecting the generated waves are the slide volume and the Froude number at the impact. Huber and Hager (1997) modeled granular mass sliding into a water tank and found that the wave run-up mainly depends on a non-dimensional landslide volume. Walder et al. (2003) investigated LGWs in a regular flume, focusing on wave properties in the near field. From their scaling analysis, the near-field wave properties are mainly controlled by the non-dimensional landslide volume per unit width, the non-dimensional submerged time of motion, and the non-dimensional vertical impact speed. Carvalho and Carmo (2007) carried out a laboratory study to investigate the generation and propagation of LGWs and their impact on downstream water banks. In their study, a series of waves were generated by fallings of calcareous blocks and the wave heights were measured by five gauges. The experimental data show that the maximum positive wave amplitude has a strong dependence on the mass (volume) of the sliding mass and the initial water level. Furthermore, a wide range of laboratory tests for impulsive waves caused by both rigid and deformable slide masses was performed by Ataie-Ashtiani and Nik-Khah (2008) in a rectangular flume (2.5 m wide, 1.8 m deep, and 25 m long). As a result, an empirical equation for the impulse wave amplitude and the period was proposed. The experimental models presented by Huang et al. (2014) involved two common types of slopes in the Three Gorges Reservoir: a rigid rock falling into the water and a granular cluster sliding into the water. Based on 74 different experiments, Huang et al. (2014) developed two dimensionless equations for the estimation of the primary wave maximum amplitude which were then successfully verified for both two failure types. In general, laboratory experiments provide a first approximation to study the general behavior of both landslides and generated waves. This technique is considered to be a powerful tool for investigating LGWs; although, due to the drawbacks of preparation time and economical cost, laboratory model tests are limited to simple considerations rather than practical cases where complex topography and different material parameters need to be considered.

Besides the experiments, empirical equations based on either field data or numerical tests are intensively applied for estimating LGW properties. Based on a catalog of LGW events, Oppikofer et al. (2018) developed semi-empirical relationships which link wave run-up with distance from landslide impact and landslide volume. According to the proposed equation, run-up decreases with distance obeying a power law. Ataie-Ashtiani and Najafi-Jilani (2006) applied a higher order Boussinesq model to study the sensitivity of the amplitude of impulsive waves to the landslide geometry and kinematics. They proposed a simple engineering estimation method which can facilitate the prediction of the generated wave amplitude in reservoir areas. The available analytical solutions are usually based on some simplifying assumptions (Noda 1970; Renzi and Sammarco 2016; Sammarco and Renzi 2008). Therefore, those methods are not able to cope with the wave generation process where complex geometries and material characteristics are involved.

In numerical simulation of LGWs, mathematical formulations play a fundamental role. According to their complexity and accuracy, mathematical formulations can be classified into four types as (i) shallow water equations (SWEs), (ii) Boussinesq-type equations (BWEs), (iii) potential flow equations (PFEs), and (iv) full Navier–Stokes equations (NSEs) (Yavari-Ramshe and Ataie-Ashtiani 2016). NSEs have a full dispersion and strong coupling between different phases by utilizing an appropriate surface tracking technique. Nevertheless, the computer cost dramatically grows when considering full dispersive equations such that their application is generally restricted (Wanget al. 2016; Xie et al. 2014). BWEs and PFEs provide a good balance between computer cost and accuracy while most of the existing models consider rigid landslides or treat the sliding mass as a moving boundary. In practical problems, the application of SWEs results in a reasonable compromise between accuracy and computational cost. Therefore, even though other formulations can cover more complex aspects in LGWs, SWEs are still widely adopted by researchers and engineers. To take into account the slide propagation pattern and deformations, two-layer flow models have been extensively used by researchers and engineers (Bouchut et al. 2008; Liu et al. 2018; Ma et al. 2015; Macías et al. 2015; Majd and Sanders 2014; Pastor et al. 2009a, b; Yavari-Ramshe and Ataie-Ashtiani 2015).

Two-layer models generally consist of (i) a layer of water and (ii) a layer of deformable mass entering the water body which lays below the water. SWEs are solved in both layers interacting through their interface. The landslide is generally described as a fluidized mass.

Various alternative numerical models have been proposed to solve the related mathematical formulations over the past years. Particularly, because of being Lagrangian and “mesh-free,” SPH is considered to be one of the most appropriate methods for surface tracking. As a consequence, it has been extensively used by a large number of researchers to reproduce the process of LGWs (Ataie-Ashtiani and Jilani 2007; Gotoh and Sakai 2006; Heller et al. 2016; Monaghan and Kos 1999; Panizzo and Dalrymple 2005; Pastor et al. 2009a, b; Tatiana Capone et al. 2010).

The application of SPH for LGWs started with the pioneering work of Monaghan and Kos (2000) who utilized SPH to follow the formation of solitary waves and compared their results with the experiment. The possibility of extending the SPH technique to more general configurations was also discussed in their work. With the advancing of the SPH technique, more improved methods have been introduced: Ataie-Ashtiani and Shobeyri (2008) applied an incompressible SPH (I-SPH) method to simulate a submerged rigid wedge sliding along an inclined surface. The results were in a good agreement with the experimental data. Gomez-Gesteira et al. (2012) applied the open-source SPH code SPHysics to simulate the impact of a three-dimensional (3D) rock sliding into a reservoir. The results provided information on the movement of the block and the generated waves with time.

The SPH approach was also used by Viroulet et al. (2013) to conduct two numerical experiments including a vertical sinking box and a two-dimensional (2D) wedge sliding down an inclined plane. Their results agreed reasonably well with a two-phase finite-volume model. More recently, Wang et al. (2016) conducted a prototype-scaled experiment to take into account the topography effect. A 3-D SPH numerical simulation corresponding to the physical model was then implemented to investigate the details of impulsive waves, such as wave amplitude, wave run-up, and wave arrival time.

Although, 3D SPH models have been widely and successfully applied to analyze the LGW problems, some drawbacks still exist. The major one is the heavy computational cost for a real-scale problem. Therefore, the applications are usually either restricted to a reduced region of interest or involve simplified assumptions regarding the interaction of the different phases or the properties of the sliding materials, i.e., considering a rigid mass.

It is important to notice that in large-scale problems, it is necessary to apply boundary conditions of absorbing and prescribed incoming wave types. Details about such boundary treatment methods along with depth-integrated models can be seen in the work of Lastiwka et al. (2005), Peraire et al. (1986), Quecedo et al. (2004a, b), and Vacondio et al. (2012).

In the present study, the two-layer SPH model proposed by Pastor et al. (2009b) is improved by implementing an absorbing boundary condition and then tested against two available cases: (i) a numerical test conducted by Bouchut, et al. (2008) and (ii) an experiment performed by Fritz et al. (2001) for the LGW event of Lituya Bay, Alaska. Then, the extended model is applied to predict impulse waves generated by the Halaowo landslide, in China, in order to help designing effective protection plans.

The paper is organized as follow: In the “Two-later model” section, the SPH model is described. The rheological models are introduced in the “Rheological models” section. Then, the “An absorbing boundary condition for deep-integrated SPH models” section is devoted to present the absorbing boundary conditions implemented in the model. In the “Proposed benchmarks for assessing model accuracy” section, a series of numerical tests are performed and analyzed, in order to provide insight on the model predicting capabilities, including the boundary conditions. Finally, the validated model is utilized to predict the LGWs in the Xiangjiaba Reservoir, China.

Two-layer model

Mathematical model

The purpose of this section is to present the two-layer, depth-integrated model which will be used to model waves generated by landslides. We will start with the case of a single fluid, where the balance equations are given by:

  1. (a)

    Balance of mass

$$ \frac{d\rho}{d t}+\rho \operatorname {div}\ v=0 $$
(1)
  1. (b)

    Balance of linear momentum

$$ \rho \frac{dv}{dt}=\operatorname{div}\ \sigma +\rho b $$
(2)

where ρ is the density, vthe velocity, σ the total stresses, and b the body forces (gravity).

These equations can be complemented with a suitable rheological law linking displacements (or velocities) to strains (or rate of strains) as well as boundary and initial conditions.

Since a large amount of computer memory and high computational effort are required to solve real 3D problems, in practical engineering, depth-integrated models have been used extensively by many researchers because they present an excellent compromise between computational cost and accuracy.

Depth-integrated models have been used to model landslide propagation since the 1D Lagrangian model proposed by Savage and Hutter (1991). Since then, it has been extended to more general conditions by Gray et al. (1999), Hutter and Koch (1991), and Hutter et al. (1993) and has been employed by many researchers including Laigle and Coussot (1997), McDougall and Hungr (2004), Pastor et al. (2009a, b), Pastor et al. (2002), Pastor et al. (2017), Pudasaini and Hutter (2007), and Quecedo et al. (2004b). It is worth mentioning the textbook by Pudasaini and Hutter (2007) where the limitations of the depth-integrated models are presented and discussed.

The balance of mass and momentum equations can be integrated along x3 using the reference system given in Fig. 1. In this system, Z denotes the elevation of the bottom surface, h the flowing depth, and \( \overline{v} \) the averaged flow velocity, along x1 and x2, the over bar referring to depth integration.

Fig. 1
figure 1

Reference system, coordinates and notation

Full size image

We will define the “quasi-material derivative” as:

$$ \frac{\overline{d}}{dt}=\frac{\partial }{\partial t}+{\overline{v}}_j\frac{\partial }{\partial {x}_j}\kern0.84em j=1,2 $$
(3)

Depth-integrated models are based on Leibniz’s rule:

$$ {\int}_a^b\frac{\partial }{\partial s}F\left(r,s\right)\; dr=\frac{\partial }{\partial s}{\int}_a^bF\left(r,s\right)\; dr-F\left(b,s\right)\;\frac{\partial b}{\partial s}+F\left(a,s\right)\;\frac{\partial a}{\partial s} $$
(4)

The depth-integrated equations for both fluidized solid and water can be derived in the same way as a single fluid. Considering the situation sketched in Fig. 3, the balance equations of the sliding mass and the water can be integrated from Z to Z + hs, and Z + hs to Z + hs + hw, respectively. As indicated by Pastor et al. (2009b), the equations turn out to be:

  1. (a)

    balance of mass

$$ \frac{d{h}_{\mathrm{s}}}{dt}+{h}_{\mathrm{s}}\frac{\partial {{\overline{v}}_i}^{\left(\mathrm{s}\right)}}{\partial {x}_i}=0,\frac{d{h}_{\mathrm{w}}}{dt}+{h}_{\mathrm{w}}\frac{\partial {{\overline{v}}_i}^{\left(\mathrm{w}\right)}}{\partial {x}_i}=0 $$
(5)
  1. (b)

    balance of momentum

$$ {h}_{\mathrm{w}}\frac{d\;{\overline{v}}^{\left(\mathrm{w}\right)}}{dt}=\operatorname{grad}\left(\frac{1}{2}{g}_3{b}_3{h}_{\mathrm{w}}^2\right)+{g}_3{h}_{\mathrm{w}}\operatorname{grad}\;\left(Z+{h}_{\mathrm{s}}\right)+\frac{1}{\rho_{\mathrm{w}}}{\tau}_{\mathrm{i}}^{\mathrm{w}/\mathrm{s}} $$
(6)
$$ {\displaystyle \begin{array}{l}{h}_{\mathrm{s}}\frac{d\;{\overline{v}}^{\left(\mathrm{s}\right)}}{dt}=\operatorname{grad}\left(\frac{1}{2}{g}_3{h}_{\mathrm{s}}^2\right)+{g}_3{h}_{\mathrm{s}}\operatorname{grad}\;Z-\frac{1}{\rho_{\mathrm{s}}}{\tau}_{\mathrm{i}}^{\mathrm{w}/\mathrm{s}}\\ {}\kern2.879999em +\frac{1}{\rho_{\mathrm{w}}}{\tau}_{\mathrm{B}}-\frac{\rho_{\mathrm{w}}}{\rho_{\mathrm{s}}}{g}_3{h}_{\mathrm{s}}\operatorname{grad}\;{h}_w\end{array}} $$
(7)

where d/dt is the “quasi material derivative” defined in Eq. (3), h is depth, \( \overline{v} \) the depth-averaged velocity, Zthe elevation of terrain, ρ the density, g3 the gravity force along axis X3, τBthe friction between soil and basal surface, and τi the interface friction. Super indices(s) and (w) refers to soil and water, respectively. Please note that the terms describing the interaction between layers are

$$ {\displaystyle \begin{array}{l}\mathrm{solid}\to \mathrm{water}\ \mathrm{interaction}:\kern0.36em -{g}_3{h}_{\mathrm{w}}\operatorname{grad}\;\left(Z+{h}_{\mathrm{s}}\right)+\frac{1}{\rho_{\mathrm{w}}}{\tau}_{\mathrm{i}}^{\mathrm{w}/\mathrm{s}}\\ {}\mathrm{water}\to \mathrm{solid}\ \mathrm{interaction}:\kern0.5em -\frac{\rho_{\mathrm{w}}}{\rho_{\mathrm{s}}}{g}_3{h}_{\mathrm{s}}\operatorname{grad}\;{h}_{\mathrm{w}}-\frac{1}{\rho_{\mathrm{s}}}{\tau}_{\mathrm{i}}^{\mathrm{w}/\mathrm{s}}\end{array}} $$
(8)

In the proposed model, we have neglected both mass exchanges and the friction at the solid-water interface; Fig. 2 illustrates the different interactions taking place in the model. In this figure, I, J, and K represent the number of the SPH particles. The support domain of the kernel W is defined by the positive integer k usually taken as 2 and the smoothing length h.

Fig. 2
figure 2

Interactions of the soil and water particles in the SPH model

Full size image

Moreover, we have used the super indices B, A, and O which correspond to the bottom, the interface between soil and water and the free surface, as depicted in Fig. 3.

Fig. 3
figure 3

Landslide entering a reservoir

Full size image

Numerical model

The balance equations introduced in the previous section have been discretized using the SPH technique, where continuum media is represented by a set of particles. Therefore, any physical variable can be approximated by the surrounding values. Regarding the development of the method, it was proposed by Lucy (1977) for astrophysical problems and then exported to other research areas like hydrodynamics (Monaghan and Kos 1999; Vacondio et al. 2013), avalanche propagation (Manzanal et al. 2016; McDougall and Hungr 2004; Rodriguez-Paz and Bonet 2005), and flow through porous media (Zhu and Fox 2001).

SPH is based on the identity

$$ \phi (x)=\underset{\varOmega }{\int}\phi \left(x\hbox{'}\right)\;\delta \left(x\hbox{'}-x\right) dx\hbox{'} $$
(9)

where δ(x '  − x) is the Dirac’s delta function centered atx.

The delta function can be approximated by a weighting function W(x, h ) fulfilling

$$ \underset{h\to 0}{\lim }W\left(x\hbox{'}-x,\underset{\_}{h}\right)=\delta (x) $$
(10)

where \( \underset{\_}{h} \) is a parameter describing its decay.

The function ϕ(x) is approximated by

$$ \left\langle \phi (x)\right\rangle =\underset{\varOmega }{\int}\phi \left(x\hbox{'}\right)W\left(x\hbox{'}-x,\underset{\_}{h}\right) dx\hbox{'} $$
(11)

In the framework of SPH formulations, several kernels have been proposed in the past. Here, we will use the cubic spline kernel proposed by Monaghan and Gingold (1983) and Monaghan (1985).

Concerning the integral representation of the derivatives in SPH, they are given by:

$$ \left\langle {\phi}^{\prime },\left(,x,\right)\right\rangle =\underset{\varOmega }{\int}\phi \hbox{'}\left(x\hbox{'}\right)W\left(x\hbox{'}-x,\underset{\_}{h}\right) dx\hbox{'} $$
(12)

from where, and taking into account that the kernel has compact support, it results in:

$$ \left\langle \phi \hbox{'}(x)\right\rangle =-\underset{\varOmega }{\int}\phi \left(x\hbox{'}\right)W\hbox{'}\left(x\hbox{'}-x,\underset{\_}{h}\right) dx\hbox{'} $$
(13)

Differential operators of interest like the gradient of a scalar function, the divergence of a vector-valued function and the divergence of a tensor-valued function, are approximated as:

$$ {\displaystyle \begin{array}{l}\left\langle \operatorname{grad}\phi (x)\right\rangle =-{\int}_{\varOmega}\phi \left(x\hbox{'}\right)\;\frac{1}{h}W\hbox{'}\frac{x\hbox{'}-x}{r} d\varOmega \kern0.5em \mathrm{with}\kern0.5em r=\mid x\hbox{'}-x\mid \\ {}\left\langle \operatorname{div}\ u(x)\right\rangle =-{\int}_{\varOmega }u\left(x\hbox{'}\right) \operatorname {grad}\ Wd\varOmega =-{\int}_{\varOmega}\frac{1}{h}W\hbox{'}\frac{u\left(x\hbox{'}\right).\left(x\hbox{'}-x\right)}{r} d\varOmega \\ {}\left\langle \operatorname{div}\ \sigma (x)\right\rangle =-{\int}_{\varOmega}\sigma .\operatorname{grad}\ Wd\varOmega =-{\int}_{\varOmega}\frac{1}{h}W\hbox{'}\frac{\sigma .\left(x\hbox{'}-x\right)}{r} d\varOmega \end{array}} $$
(14)

where ϕ(x) is a scalar function, u(x) a vector-valued function, σ(x) a tensor-valued function, Ω an open bounded domain, W the kernel function, and h the smoothing length.

We will introduce a set of particles or nodes labeled with indexes K = 1...N. Of course, the level of approximation will depend on how these nodes are spaced in the domain. Therefore, as usual, those zones with large gradients require larger number of nodes.

Considering the approximation of a function, as the information concerning the function is only available at the set of N nodes, the integral could be evaluated by using a numerical integration technique:

$$ {\phi}_I={\left\langle \phi \left({x}_I\right)\right\rangle}_h=\sum \limits_{J=1}^N\phi \left({x}_J\right)W\left({x}_J-{x}_I,\underset{\_}{h}\right){\varOmega}_J $$
(15)

where we have used the sub-index “\( \underset{\_}{h} \)” to denote the discrete approximation. The weights of the integration formula are ΩJ = mJ/ρJ, with ΩJ, mJ, and ρJ being the volume, mass, and densities associated with node J.

If we consider that the kernel function has local support, i.e., it is zero when the sum extends only to the set of Nh points, we can write:

$$ {\phi}_I={\left\langle \phi \left({x}_I\right)\right\rangle}_h=\sum \limits_{J=1}^{Nh}\phi \left({x}_J\right)W\left({x}_J-{x}_I,\underset{\_}{h}\right){\varOmega}_J $$
(16)

which is the approximation in SPH. In the case we choose the function ϕ to represent the density, we will obtain:

$$ {\rho}_I=\sum \limits_{J=1}^{Nh}{\rho}_J{W}_{IJ}\;\frac{m_J}{\rho_J}=\sum \limits_{J=1}^n{W}_{IJ}\;{m}_J $$
(17)

with \( {W}_{IJ}=W\left({x}_J-{x}_I,\underset{\_}{h}\right) \)

If the 2D area associated to a node I is ΩI, we will introduce a fictitious volume mI with dimensions L3associated with this node:

$$ {m}_I={\varOmega}_I{h}_I $$
(18)

From here, we can discretize the balance of mass Eq. (5) which is exactly the same for both soil and water as:

$$ \frac{\overline{d}{h}_I}{dt}=-{h}_I\sum \limits_J\frac{m_J}{h_J}{v}_{IJ}^T.\operatorname{grad}\;{W}_{IJ} $$
(19)

where we have introduced vIJ = vI − vJ.

Next, we will consider the balance of momentum Eqs. (6) and (7) for both layers. They are those obtained for the single-phase fluid except for the additional terms which are given for the water and fluidized soil, respectively. Hence, the SPH discretized equations consist of two parts, the common part and the correction terms.

The common part is:

$$ {\displaystyle \begin{array}{l}\frac{\overline{d}}{dt}{\overline{v}}_I=-\sum \limits_J{m}_J\frac{p_I+{p}_J}{h_I{h}_J}\operatorname{grad}\;{W}_{IJ}+\frac{1}{\rho}\sum \limits_J{m}_J\frac{\sigma_I+{\sigma}_J}{h_I{h}_J}\operatorname{grad}\;{W}_{IJ}+b\\ {}\kern2.04em +\frac{1}{\rho {h}_I}\mid {N}^B\mid {t}_I^B\end{array}} $$
(20)

or

$$ {\displaystyle \begin{array}{l}\frac{\overline{d}}{dt}{\overline{v}}_I=-\sum \limits_J{m}_J\left(\frac{p_I}{h_I^2}+\frac{p_J}{h_J^2}\right)\operatorname{grad}\;{W}_{IJ}\\ {}\kern1.8em +\frac{1}{\rho}\sum \limits_J{m}_J\left(\frac{\sigma_I}{h_I^2}+\frac{\sigma_J}{h_J^2}\right)\operatorname{grad}\;{W}_{IJ}+b+\frac{1}{\rho {h}_I}\mid {N}^B\mid {t}_I^B\end{array}} $$
(21)

which applies for both water and fluidized soil. The correction terms are:

  1. (a)

    For water

$$ +\frac{1}{\rho_{\mathrm{w}}}{\tau}_{\mathrm{i}}^{\mathrm{w}/\mathrm{s}}+{b}_3{h}_{\mathrm{w}}\frac{\partial {h}_{\mathrm{s}}}{\partial {x}_i}\kern1.32em \left(\mathrm{water}\right) $$
(22)
  1. (b)

    For soil

$$ +\frac{1}{\rho_{\mathrm{s}}}{\tau}_{\mathrm{i}}^{\mathrm{s}/\mathrm{w}}+{b}_3\frac{\rho_{\mathrm{w}}}{\rho_{\mathrm{s}}}{h}_{\mathrm{s}}\;\frac{\partial {h}_{\mathrm{w}}}{\partial {x}_i}\kern0.6em \left(\mathrm{fluidized}\ \mathrm{soil}\right) $$
(23)

Rheological models

After integrating the balance of mass and momentum equations, the vertical structure of the flow and internal stresses result on boundary terms which characterize shear stresses on both the interfaces (top and bottom) for each layer should be described.

During the computations, at a given time step, the height of the flow and the averaged velocities for both layers are known. In order to retrieve the shear stress, the most common approach is assuming that the current basal stress is the same as that in an infinite landslide (where the main assumptions are steady flow, no variations along the velocity direction, and the velocity only depends on the X3 coordinate).

Basal shear stresses can then be obtained for a variety of 3D rheological models incorporating friction, viscosity, and cohesion.

For instance, in a viscous frictional fluid, where viscosity is quadratic, the basal shear stress is given by:

$$ {\tau}_b={\sigma}_3^{\prime}\tan \varphi +\frac{25}{4}{\mu}_{CF}\frac{{\overline{v}}^2}{h^2} $$
(24)

where \( {\sigma}_3^{\prime } \) is the effective vertical stress at the bottom, and μCF the quadratic viscosity.

For cohesive-viscous materials, Bingham model includes two material parameters, the yield stress below which the material does not flow, and the viscosity. The expression for the Bingham model is written as:

$$ \tau ={\tau}_y+\mu \left(\frac{\partial {v}_1}{\partial {x}_3}\right) $$
(25)

where τy is cohesion and μ is viscosity. Concerning the bottom friction, it can be related to the depth-averaged velocity using the following expression:

$$ \overline{v}=\frac{\tau_bh}{6\mu }{\left(1-\frac{\tau_y}{\tau_b}\right)}^2\left(2+\frac{\tau_y}{\tau_b}\right) $$
(26)

In order to obtain the basal shear stress, the roots of this third-order polynomial have to be obtained at every material node and time step. A possible approximation was proposed by Pastor et al. (2004). It consists of obtaining the root of the second-order polynomial which is the best approximation in the Chebyshev polynomials of the third-order one. It consists on obtaining the best second-order polynomial approximating a third-order one.

There are some other effective factors which are not considered in this study including landslide permeability to water, landslide-water interfacial friction, and also landslide-bottom frictional interactions.

An absorbing boundary condition for depth-integrated SPH models

As mentioned in the previous section, absorbing boundary conditions have been frequently applied to depth-integrated problems (Lastiwka et al. 2005; Peraire et al. 1986; Quecedo et al. 2004b). The method we apply here is based on the concepts of characteristic lines and Riemann invariants, and is described in detail by Vacondio et al. (2012).

The initial step to impose the boundary conditions depends on the Froude number:

$$ F=\frac{\mid \overline{v}\mid }{\sqrt{gh}} $$
(27)

When the Froude number is higher than 1, and the fluid is exiting the domain, both the height and the averaged velocity of the outflow particles will be set equal to the inner domain quantities.

In the case of subcritical flow, only one condition of either velocity or height value is prescribed and the remaining will be determined by using the Riemann invariants:

$$ {\displaystyle \begin{array}{l}{R}^{(1)}=2\sqrt{gh}+\overline{v}\\ {}{R}^{(2)}=2\sqrt{gh}-\overline{v}\end{array}} $$
(28)

characterizing the waves leaving and entering the domain.

In order to describe the boundary condition explained above, we will start with the definition of the influenced zone based on boundary particles.

As shown in Fig. 4, when a particle enters the active zone which is defined by boundary particles and their influence length, it will be marked as an active particle in the SPH code, and the absorbing boundary conditions algorithm will be applied as follows:

  1. (i)

    First of all, we obtain values of the unknowns at time n + 1 without applying any boundary condition, obtaining the “star” values \( {h}_{\ast}^{n+1} \)and \( {v}_{\ast}^{n+1} \). Then, we obtain the incoming and outgoing Riemann invariants as

Fig. 4
figure 4

Absorbing boundary condition along arbitrary geometries

Full size image
$$ {\displaystyle \begin{array}{l}{R}_{\ast}^{(1)}=2\sqrt{g{h}_{\ast}^{n+1}}+{\overline{v}}_{\ast}^{n+1}\\ {}{R}_{\ast}^{(2)}=2\sqrt{g{h}_{\ast}^{n+1}}-{\overline{v}}_{\ast}^{n+1}\end{array}} $$
(29)
  1. (ii)

    At time n + 1, we assume that the new Riemann invariants will be such that:

    • The outgoing Riemann invariant will be the same obtained in the “star” state.

    • The incoming Riemann invariant will be that of the still water at infinity, where the undisturbed water level is denoted \( {h}_{\ast}^{n+1} \).

Therefore, we can write

$$ {\displaystyle \begin{array}{l}{R}_{n+1}^{(1)}=2\sqrt{g{h}^{\mathrm{n}+1}}+{\overline{v}}^{\mathrm{n}+1}=2\sqrt{g{h}_{\ast}^{n+1}}+{\overline{v}}_{\ast}^{n+1}\\ {}{R}_{n+1}^{(2)}=2\sqrt{g{h}^{\mathrm{n}+1}}-{\overline{v}}^{\mathrm{n}+1}=2\sqrt{g{h}_{\infty}^{n+1}}\end{array}} $$
(30)

from where we obtain immediately the values of water height and velocity at time n + 1 as

$$ {\displaystyle \begin{array}{l}{h}^{n+1}=\frac{1}{16g}{\left(2\sqrt{g{h}_{\ast}^{n+1}}+2\sqrt{g{h}_{\infty }}-{\overline{v}}_{\ast}^{n+1}\right)}^2\\ {}{\overline{v}}^{n+1}=\frac{1}{2}\left(2\sqrt{g{h}_{\infty }}-2\sqrt{g{h}_{\ast}^{n+1}}+{\overline{v}}_{\ast}^{n+1}\right)\end{array}} $$
(31)

For instance, if an activated particle has an initial state of \( {h}_{\ast}^{n+1}=1.2\ \mathrm{m} \), \( {\overline{v}}_{\ast}^{n+1}=1\ \mathrm{m}/\mathrm{s} \) and the height at infinity is set as \( {h}_{\infty}^{n+1}=1\ \mathrm{m} \). Therefore, the averaged velocity and height at time n + 1 can be obtained by employing Eq. (31) which results in \( {h}_{\ast}^{n+1}=0.94\ \mathrm{m} \), \( {\overline{v}}^{n+1}=0.5\ \mathrm{m}/\mathrm{s} \).

Accordingly, the absorbing boundary condition is based on Riemann invariants which characterize magnitudes exiting or entering the domain, respectively. The magnitudes of averaged velocity and height are firstly obtained at time n + 1 without any boundary treatment. Then, the Riemann invariants of the outgoing wave are estimated using these values. Finally, with the velocity assumption for the reflected wave, it is possible to obtain the velocity and height of all active particles at the next time step.

Proposed benchmarks for assessing model accuracy

This section is devoted to assessing the proposed model’s accuracy using some benchmark tests available in the literature.

First, we will consider the test described by Bouchut et al. (2008) where a landslide impinges a water body. The second benchmark is the Lituya Bay impulse wave generated by a landslide, which was modeled in the laboratory (Fritz 2001; Fritz et al. 2009). In order to verify the quality of the proposed boundary algorithm, we use a modified geometry of Lituya Bay, by replacing the opposite slope by an absorbing boundary.

Landslide impinging a lake

This numerical test is devoted to simulating the waves caused by a subaerial landslide slipping into the water. The final deposit configuration is described and compared with the existing result from Bouchut et al. (2008). In this case, both the physical model and the coefficients are adopted from Bouchut et al. (2008) where the simulation is implemented in a 10-m long rectangular channel. The basal elevation of this test is defined as:

$$ b(x)=\Big\{{\displaystyle \begin{array}{cc}1-\frac{x}{5},& \mathrm{if}\kern0.5em 0\le x\le 5,\\ {}0,& \mathrm{otherwise}.\end{array}} $$
(32)

The initial conditions set for both soil and water are as follows:

$$ {h}_s(x)=\Big\{{\displaystyle \begin{array}{cc}\left(0.7-b(x)\right)/{\cos}^2\theta, & \mathrm{if}\kern0.5em 1.5\le x\le 2.5,\\ {}0,& \mathrm{otherwise}.\end{array}} $$
(33)

And

$$ {h}_w(x)=\Big\{{\displaystyle \begin{array}{cc}\left(0.4-b(x)\right)/{\cos}^2\theta, & \mathrm{if}\kern0.5em 3\le x\le 5,\\ {}0.4,& \mathrm{otherwise}.\end{array}} $$
(34)

The computation domain is depicted in Fig. 5a. It is modeled using 300 soil particles with a spacing of 0.0033 m and 350 particles of water with a spacing of 0.02 m. The boundary condition on the right border is considered absorbing and modeled using the boundary condition proposed in the previous section.

Fig. 5
figure 5

Time histories of the water surface and landslide predicted by the present model compared with the values from Bouchut et al. (2008)

Full size image

Besides, other parameters like the ratio of densities r (the ratio of the density of water and soil) are set to be 0.2 and the frictional angle δ0 is adopted as 10°, while the angle of the plane is 11.31°. This setup can ensure the sliding mass will slide down and deposit over the flat part of the bottom.

Figure 5 presents a sequence of the landslide impact compared with the results of Bouchut et al. (2008). Since the slope angle is higher than the frictional angle, the granular mass is unstable and starts to move from the stationary state (see Fig. 5(a)). At about 0.5 s, the front of the landslide contacts the water body and a shock is induced by the impact of the sliding mass. From here, with the interaction between the water, the landslide, and the bottom surface, the landslide material gradually comes to a stop at the toe of the slope (see Fig. 5b–e). Concerning the impulsive wave, it propagates toward the open boundary after generation. As it can be observed in Fig. 5d, when the wave reaches the open boundary, no conspicuous oscillations appear which means the absorbing boundary prevents the appearance of spurious reflected waves on the boundary. The final steady-state situation for both of the deposited material and the free surface of the lake is shown in Fig. 5 (f). It can be observed that the results obtained from the proposed model are consistent with the results of Bouchut et al. (2008) with minor differences. The maximum runout distance and the maximum wave height 3 s after the impact between the present numerical results and the results of Bouchut et al. (2008) are compared in Table 1. As it can be observed in Table 1, the maximum water wave heights for numerical and experimental results at t = 3.0 s are in a good agreement with a relative error of less than 1%. The predicted value of maximum landslide runout distance is about 6.7% larger than the experimental value. Additionally, the edge of the deposit mass in the work of Bouchut et al. (2008) seems to be steeper than the current results. This phenomenon can be interpreted as the smoothing effect of SPH at the boundaries of the considering domain. Special treatments like normalization may help to handle such non-continuum regions.

Table 1 Comparison of present results with the results of Bouchut et al. (2008)
Full size table

Lituya impulse wave event

In 1958, an earthquake-triggered subaerial landslide with an estimated volume of 30.6 million m3 slid into the Gilbert Inlet located at the head of Lituya Bay, Alaska. The landslide and the generated impact wave have been described by Fritz (2001) and Fritz et al. (2009). According to the in-situ evidence, the wave ran up to an elevation of 524 m at the opposite slope in the Gilbert Inlet. This giant wave is considered to be the highest wave run-up in recorded history. Therefore, it has received attention from many researchers, e.g., Mao et al. (2017), Pastor et al. (2009b), and Quecedo et al. (2004a). Among them, the physical model built by Fritz et al. (2009) has been frequently selected as a benchmark to check the performance of the numerical procedures in the simulation of impulsive waves.

Figure 6 a illustrates the simplified inlet model employed by Fritz et al. (2001). The model was reproduced in a rectangular prismatic channel with a scale of 1:675. The landslide mass was modeled by an artificial granular material with a bulk density of 1.61 t/m 3and a porosity of 39%. According to Fritz et al. (2009), the dynamic basal friction angle was chosen as 24°. It is also worth noting that the lateral spreading of the generated wave was assumed to be small by considering the topographic layout of the Gilbert Inlet. Consequently, the wave run-up heights were approximated by a two-dimensional physical model in Fritz’s experiment.

Fig. 6
figure 6

a, b Simplified geometry (from Fritz (2001)) and the numerical model of the Gilbert Inlet in Lituya Bay, Alaska

Full size image

In our simulation (see Fig. 6b), the entire boundary is considered an impermeable wall, the sliding mass and the water are modeled by 300 and 400 particles, respectively.

Figure 7 presents the evolution of the impulsive waves generated by the landslide in Gilbert according to the proposed model. As we can observe in Fig. 7a, part of the landslide mass has entered the water at t = 10s, and the wave has been generated at the near field. Subsequently, at t = 20s, the landslide and the waves arrive at the opposite bank and start to move uphill (Fig. 7b). After the water wave reaches the maximum run-up, it starts moving backwards which causes the oscillations of the water body (Fig. 7c–e). Finally, the landslide mass stops sliding along the bottom and eventually deposits. The stationary state is presented in Fig. 7f. Also, it should be noted that in some parts of the sequence, the water layer has a sharp edge, for instance, parts (c), (d), and (e). The reason is that plotting of the results was done by transferring information from the SPH particles to a temporal mesh used in the postprocessor.

Fig. 7
figure 7

Evolution of the Lituya landslide simulated by the presented model

Full size image

The numerical results are compared with experimental data of Fritz (2009) in Table 2. The comparison includes slide velocity at impact, maximum wave height, time for maximum wave, etc. As it can be observed from the table, the maximum wave heights, maximum wave run-up, and wave velocity are underestimated by the numerical model while the occurrence time of the maximum wave is overestimated. In the test, the wave height includes the air cavity which is generated by the fast impinging of the landslide to water. However, in the proposed depth-integrated model, the influence of the air is assumed to be small and neglected. By employing an analogous two-layer model to simulate tsunami waves, Ma et al. (2015) found the wave heights were overestimated by the presented model compared with the measure results in a three-dimensional LGW experiment. They summarized three possible reasons to explain the overprediction, one of these reasons is that the formation of air cavity during landslide impact is not captured. As the air intrusion reduces the water energy and perhaps its velocity and height, the neglect of air could result in greater wave heights. Regarding the Lituya case, the impact velocity of the landslides mass (about 110 m/s) is much higher than the test performed by Ma et al. (2015) which is about 4.54 m/s. Therefore, the formation of the generated waves in Lituya is mainly controlled by the brunt of the landslides. As stated in the theoretical part of the two-layer model, the generated waves are undervalued due to the neglect of landslide-water interfacial friction in the depth-integrated framework of this study. Consequently, the underestimation of the impact effect probably results in lower wave heights when the impact velocity is relatively high, even though the neglect of air could overestimate the calculated values of LGW heights. Figure 8 presents the spatial distribution of the SPH particles when the maximum wave run-up occurs.

Table 2 Comparison between experimental and computed results in the Lituya landslide
Full size table
Fig. 8
figure 8

Distribution of the landslide and water particles when the impulse wave reaches the maximum run-up (t = 38.3 s)

Full size image

Furthermore, in order to explore the presented boundary method, an artificial boundary is applied to substitute the right-hand slope in the case of Lituya, see Fig. 9, case A. There, the reference case is obtained by replacing the opposite slope with a horizontal plane (case B). Therefore, the results from these two scenarios should be consistent if the proposed boundary method works effectively. In both cases, the parameters are the same as the previous simulation except the frictional angle which has been increased to 31° for the purpose of avoiding the influence of the sliding mass hitting the new boundary.

Fig. 9
figure 9

The initial situations of two cases and the location of the monitoring point

Full size image

Figure 10 provides the sequence of the water surfaces and the landslide deformations in both cases.

Fig. 10
figure 10

Comparison of the evolution of landslide and water surface between case A and case B

Full size image

The time history of the water surface fluctuations at the monitoring points estimated by the model, including both with and without applying absorbing boundary conditions, is presented in Fig. 11. Since they are in a good agreement, it can be said that the presented boundary algorithm is able to reproduce open boundaries in real cases.

Fig. 11
figure 11

Time histories of the water surface fluctuations at the monitoring point in case A and B, respectively

Full size image

A case study: Halaowo landslide and its generated waves

In this section, the proposed two-layer model is applied to simulate a potential landslide case and its impulse waves. The simulation includes the whole process of a landslide-generated wave event.

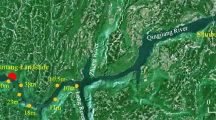
The Xiangjiaba hydropower station is a significant component of the Chinese mega-project “the west to east electricity transmission project.” It is also the last large-scale hydropower station in the lower reaches of the Jinsha River, southwestern China, as shown in Fig. 12. The hydropower project considers the water level to be located between two limiting values, 370 m and 380 m. The total reservoir capacity is 5.153 billion m3 with an active reservoir capacity of 0.09 billion m3. By cooperating with other hydroelectric projects, the Xiangjiaba hydropower station plays a key role in the regulation of the cascade power stations on the Jinshan River. Once the water level of the impounded water started to increase, seepage through the slope-affected pore water pressures decreased its stability and caused its failure. In the banks of the mainstream and the main tributaries of the reservoir area, more than 47 potential landslides and 37 collapsed deposits have been detected. Halaowo slope (over 7 × 106 m3) is one of the unstable slopes, located 18 km upstream of Xiangjiaba hydropower station (Fig. 12). Once the landslide is triggered and impacts the river, the impulsive waves generated will seriously threaten the dam body, shoreline properties, and lives.

Fig. 12
figure 12

The location of Xiangjiaba Hydropower Station and Halaowo Slope

Full size image

The topographic map of the Halaowo slope and the river channel are depicted in Fig. 13. As it can be observed, the slope is located at a bend of the Jinsha River. The computational domain for the simulations is also shown in Fig. 13. Inside the computational domain, eleven gauging points are selected to explore the generated wave characteristics. In addition, the aforementioned absorbing boundary is employed at the two borders of the water.

Fig. 13
figure 13

Terrain of Xiangjiaba Reservoir area with the location of the Halaowo landslide, absorbing boundaries and monitoring points

Full size image

Figure 14 shows the details of the established model including the terrain mesh and SPH particles for soil and water, respectively. According to the geological report and the study from Mao et al. (2017), the landslide mass is assumed to be a Bingham-type fluid with a yield stress τy = 1 kPa and a viscosity μ = 50 Pa. s.

Fig. 14
figure 14

Water and soil particles over the topography model (blue for water and gray for soil)

Full size image

The numerical simulations extend up to 220 s. According to the initial state (see Fig. 15a), a part of the sliding mass is under the water, and therefore, the investigated event could be classified as a semi-submerged landslide (SSL). After 20 s, a large portion of the landslide mass has moved into the water and started to propagate along both the original siding and the channel directions. Subsequently, at 40 s, the landslide reaches the opposite slope and gradually stops, which means the primary kinetic energy of the landslide has been transferred to the water.

Fig. 15
figure 15

Model predictions for the propagation of the Halaowo landslide (includes wave heights and the landslide particles)

Full size image

Eleven gauging points are selected to describe the behavior of the impulsive waves. The evolution of the water surface at those points is depicted in Figs. 16, 17, 18, and 19. It can be observed that most of them have a waveform which is composed of two major wave crests followed by a gradual decay.

Fig. 16
figure 16

Time history of the water surface at the cross-section 1 (including point L-1, C-1, and R-1)

Full size image
Fig. 17
figure 17

Time history of the water surface at the cross-section 2 (including point L0, C0, and R0)

Full size image
Fig. 18
figure 18

Time history of the water surface at the cross-section 3 (including point L1, C1, andR1)

Full size image
Fig. 19
figure 19

Time history of the water surface points close to computational borders (including point C-2, C2)

Full size image

Figure 19 shows the time history of the water surfaces at points C-2 (2.3 km away from the landslide source) and C2 (2.2 km away from the landslide source). As these points are close to the boundary and no significant oscillations appear, it suggests that the proposed boundary method is working well and can be utilized in real LGW cases. The wave amplitudes of sections 1, 2, and 3 are also presented in Figs. 16, 17, and 18, respectively. We can see in the graphs how the wave amplitudes of section 1 are relatively greater than those in section 3. Both sections 1 and 3 are located at approximately the same distance of 1.15 km from the landslide location. Although, the expansion of the river in section 1 can accelerate the energy dissipation of the waves. Besides, the dominant direction of the sliding slope is toward section 1 resulting in a larger wave height in this section than section 3.

According to the numerical simulations, the maximum wave height in the stream channel is 34 m and occurs at the control point located near the landslide trigger zone (see Fig. 20). Along the opposite shoreline with respect to the slope, the maximum run-up reaches a height of 42.75 m. After the landslide impacts into the water body, the impulsive waves start to propagate in the waterway and their amplitudes drop gradually. In order to investigate the wave run-up on the opposite slope, cross-section 2 (location can be seen in Fig. 13) is chosen along the sliding direction where the maximum wave run-up appears. The interactions between the water surface fluctuations and the landslide deformations on the typical section at several time steps have been plotted in Fig. 21.

Fig. 20
figure 20

Distribution of the maximum height of waves (m)

Full size image
Fig. 21
figure 21

Landslide profiles and water level elevations predicted by the presented model at cross-section 2

Full size image

Conclusions

In this study, a two-layer depth-integrated SPH model is applied to reproduce the whole process of landslide-induced waves. For the purpose of dealing with complex topography in practical events, which extend to large regions, an absorbing boundary condition has been implemented in the proposed numerical model. The model is validated by simulating two benchmark problems, including a numerical test available in the literature and the LGW experiment for the Lituya Bay impulsive waves event.

For the Lituya Bay case, the landslide-generated waves are also modeled for a modified Lituya basin which allows verification of the open boundary condition.

After validation, the model is applied to simulate the potential impulsive waves generated by Halaowo landslide in the Jinsha river area, China. The simultaneous interactions between the water body and the landslide are investigated, which also demonstrate the ability of the proposed model in dealing with impulsive wave hazards in reservoir areas. Moreover, the comprehensive results including the maximum wave amplitude, wave run-up on the opposite slope, and wave arrival time show that the model can be used to predict the potential hazard and mitigate future impulsive wave disasters in the reservoir areas.