Introduction

Debris flows are natural phenomena that frequently occur in mountainous areas as a consequence of intense rainfalls (Iverson 1997) that can cause serious damage to buildings, infrastructures, and, at worst, to human beings (Takahashi 2014).

Prevention measures to reduce the risk associated to debris flows may not be possible because interventions at the detachment zone may be too expensive or difficult to be technically feasible; in those cases, it is important to install early warning systems (Lacasse and Nadim 2009). These can be based on continuous monitoring systems (Frigerio et al. 2014) or on identifying triggering thresholds of key parameters (Guzzetti et al. 2008; Capparelli and Versace 2011) that predict an event with sufficient advance notice to be able to set off an alarm signaling evacuation procedures (Bossi et al. 2015a, b). Being able to predict the debris flow behavior and its run-out path are, in any case, the basic requirements for all early warning systems as they make it possible to identify potential hazards to people and property and to plan appropriate emergency procedures.

Over recent decades, researchers have developed several numerical debris flow forecasting models to improve understanding of their behavior and to identify areas at risk. These models generally integrate the small-scale shallow equations for a single-phase approach outlined in the Smoothed Particle Hydro dynamic method (Liu and Liu 2010) or the Discrete Element method (Cleary and Prakash 2004), adopting Bingham, Voellmy, or Coulomb rheological laws to describe the evolving geometry of a finite mass of granular material and offering different options to simulate various conditions and processes coupled with propagation (Pirulli and Pastor 2012). Two‐phase debris flow models have also been recently proposed (Pudasaini et al. 2005).

Even if these models have found wide approval within the circles of environmental scientists and have already been applied to successfully describe artificial debris flows (Cola et al. 2013) as well as real events (Revellino et al. 2004; Quan Luna et al. 2011; Wu et al. 2013), accurately predicting future propagation events is still problematic in view of the difficulty in obtaining accurate knowledge of the site’s geometry and reliable information about suitable parameters to utilize depending on the rheological model or integration approach being adopted.

Until now, researchers have concentrated their efforts on using back analysis to calibrate their models for phenomena that have already taken place; this has been done to attain the best parameter combination in order to reproduce one or more characteristics of debris flow events that have already occurred. Bertolo and Wieczorek (2005), for example, compared the simulated values of the flow rate and the run-out distances of a debris flow front with documented ones of debris flows that occurred in the Yosemite Valley (CA, USA); Pirulli and Sorbino (2008) compared the heights of deposited soil in some positions and the overall distance covered by flows affecting two sites in Sothern Italy; Revellino et al. (2004) analyzed the total run-out distance, the estimated velocity at some points along the path, and the thickness and distribution of debris deposits for 17 debris flows that occurred in the Campania area between 1998 and 1999. Of course, values obtained from back analysis unequivocally depend on the correspondence of the simulated values with real in situ measurements. In the past, researchers often had only a few measures of the valley’s configuration before and after the events at their disposal, but the availability of advanced, detailed technologies is presently reducing errors connected with reproduced geometry. In many of the documented cases of flow-like analysis, the calibration procedure is performed manually. Since no automatic procedure exists, it cannot be considered completely objective because each individual could obtain different parameter sets.

Parameter calibration is, of course, a problematic phase in developing numerical modeling, and some strategies have already been utilized by other research fields to overcome this subjective process (e.g., Robinson and Wastald 1987; Eckhardt and Arnold 2001). Some attempts have likewise already been made to use automatic procedures for parameter calibrations for landslide analysis: Schädler et al. (2015), for example, proposed an inverse identification approach associated with a back analysis procedure to establish the constitutive parameters of a viscous-elasto-plastic finite element model used to reproduce displacement evolution over time with regard to the Corvara landslide in Italy. To the authors’ knowledge, similar attempts have not yet been made for debris flow phenomena.

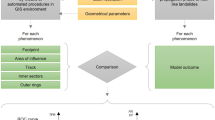
This paper proposes an automatic procedure that identifies the best set of parameters to model debris flow propagation. Belonging to the group known as data assimilation models, the method proposed was applied to find the best set of rheological properties for the GeoFlow–SPH code developed by Pastor and coworkers (Pastor et al. 2008, 2014). The procedure was applied to reproduce the debris flow that took place in the Rotolon basin (Vicenza, Italy) in November 2010.

A specific procedure aiming to consider all pertinent information needed to obtain a more complete, predictive calibration was developed.

Study event

The Rotolon catchment

The Rotolon catchment is located in the Vicentine Prealps, on the South-eastern flank of the Little Dolomites group in the uppermost portion of the Agno river valley. It lies under the jurisdiction of the municipality of Recoaro Terme (NE of Italy) situated at the border with the Trento province (Fig. 1).

Fig. 1
figure 1

Location of the Rotolon landslide in the Upper Agno Valley

Full size image

The instability phenomena studied here concern the mountain portion of the Rotolon stream that is about 5 km long and moves from an altitude of about 1350 m a.s.l. (the maximum altitude in its basin is 1942 m a.s.l. of Lovaraste Peak) to about 450 m a.s.l. where the 17 m high Georgetti dam was constructed in the twenties to protect the small town of Recoaro Terme from flooding.

From a geomorphological point of view, the Rotolon Mountain can be ideally subdivided into two segments: an upper part between 1350 and 850 m of elevation (bed slope around 30 %) and a lower one having a medium slope of less than 10 %. At the junction of the two portions, there is a 5 m high hydraulic weir and, immediately after, the injection of a small lateral stream, specifically the Agno of Campogrosso, which is generally dry and holds water only during exceptional rain events.

The path of the stream flows by a variety of formations (Barbieri et al. 1980; De Zanche and Mietto 1981). The mountain peaks are constituted by sub-horizontally bedded, intensely fractured, mainly dolomitic limestones (Dolomia Principale, Mt. Spitz Limestone, Calcareous at Trinodosus, Recoaro Limestone) typical of the South Alpine Domain and appearing in succession moving from west to east. It is important to note that the passage from the Dolomia Principale to Mt. Spitz Limestone is clearly indicated by the presence of a relatively thin layer of Raibl Formation, a sequence of conglomerates, sandstones, marls, and dolomitic evaporates showing a discontinuous level of easily alterable and erodible rhyolitic-dacitic porphyrities at the bottom.

The Werfen Formation can be found at the base of the dolomitic stratigraphic succession consisting of a varied sequence of sandstone and siltstone that outcrops near the confluence with the Campogrosso creek, just before the 5 m high weir. Along the lower portion, the torrent moves through extremely thick talus and alluvial deposits up to the final area where the outcrops of fillade metamorphic rocks can be observed on the left-hand side.

As reported and confirmed by local popular, religious, and administrative reports, instability processes, such as slope failures in the upper portion and consequent debris flows, have threatened the basin for centuries (Trivelli 1991). Many mainly hydraulic-forest interventions were carried out between the two world wars and in the period between 1985 and 1990, just after the occurrence of an important landslide followed by a large secondary debris flow. Those works mitigated the superficial erosion of the lateral slopes along the stream and prevented many flooding events, but they were unable to stabilize the large landslides still active at the head of the Rotolon creek.

Many countermeasure structures exist in the second segment: long stone walls protect the lateral slope of the bed and several inclined flow deflectors or hydraulic weirs have been realized over the years to keep the water flow at the center of the bed; two bridges, i.e., the Parlati and Luna bridges, cross the stream and connect the small hamlets located in the valley. There is a lateral basin upstream of the villages that was created after the intense debris flow that took place in 1985 to contain the transported material.

The debris flows that took place in 2009 and 2010

Two important debris flows occurred in May 2009 and November 2010 after the detachment of about 50,000 and 330,000 m3, respectively, at the head of the creek. In approximately 10 min, the first debris flow reached the Parlati and Turcati villages, damaging some hydraulic weirs and forming a lateral watercourse weld deposits up to 5 m high. The second one flowed close to the Parlati village, obstructing a bridge and flooding a public road: at that time, the inclusion of fresh water from the Agno of Campogrosso creek facilitated the flow. Fortunately, there were no fatalities in either of these cases.

After the 2009 event and just before the second debris flow, the Regional Territorial Service performed a LiDAR survey of the area and repeated it immediately after the 2010 event. The comparison between the two derived Digital Terrain Models (DTMs) (Fig. 2) provides a precise map of the flooded and erosion/deposition areas along the stream (Bossi et al. 2015a, 2015b) and makes it possible to calibrate a run-out model.

Fig. 2
figure 2

Map of deposited and eroded material obtained from the DoD analysis

Full size image

Some erosive zones were highlighted by the sliding movement: the detachment area in the upper part with an erosion depth of up to 27 m and others along the path where the velocity of the flow or the geometry and the mechanical properties of the bed allowed excavations.

The basal topography and the initial volume of the sliding mass were defined and used in the GeoFlow-SPH code on the basis of these data.

Propagation model

The GeoFlow-SPH designed by Pastor et al. (2008; 2014) is a model that has been developed over the last 25 years to analyze flow-like landslide propagation. Just as other models, i.e., DAN3D (McDougall and Hungr 2004, 2005) or RASH3D (Pirulli 2005), it is based on the shallow-water wave theory: the hypothesis is that in these processes, the average depths of the moving mass are small in comparison with its length and width. This makes it possible to simplify the 3D propagation model by integrating the velocity distribution along the vertical axis and substituting a vertical column of soil with a mass sliding along with an average moving rate. The resulting 2D depth-integrated model presents an excellent combination of accuracy and simplicity, providing important information about propagation, such as the velocity or depth of the flow along the path.

An integration of the 2D model is then obtained using the Smooth Particle Hydrodynamic (SPH) approach (Monaghan 1992; Liu and Liu 2003), a Lagrangian method in which the interaction among the columns is controlled by a kernel-type function (Pastor et al. 2008).

The vertical integration of the velocity profile of the GeoFlow-SPH is carried out taking into account the following hypotheses:

  • the material is considered an “equivalent fluid” governed by simple rheological relationships (Bingham, Voellmy, or Coulomb law) which can vary along the path according to the superficial material that is encountered;

  • the model considers strain-dependent, non-hydrostatic, anisotropic internal stresses due to the 3D deformation of material with internal shear strength and the centripetal acceleration due to path curvature;

  • the model simulates mass and momentum transfer due to entrainment and makes it possible to consider corresponding variations in flow rheology.

According to Pastor et al. (2014), it is better to consider the rheological law proposed by Voellmy (1955) in debris flows in which granular particles have high mobility and the drag forces due to the capillary contacts are important. This law includes, in the original frictional relation for shear strength, a component taking into account energy dissipation due to the flow turbulences strictly depending on the velocity. The shear strength relationship proposed by Voellmy is:

$$ \tau =\rho g\frac{v^2}{\xi }+\rho gh\kern0.5em \cos \theta \kern0.5em \tan \delta $$
(1)

in which the basal friction coefficient (tan δ) and the turbulence coefficient (ξ) represent the frictional and collisional components of dissipation.

As underlined by Sosio et al. (2008), some typical value ranges for rheological parameters can be found in the literature: they suggest that values between 0.05 and 0.25 be used for the basal friction coefficient and between 200 and 1000 m/s2 for the turbulence coefficient, depending on the flow type needing to be simulated.

It has, moreover, been underlined that the GeoFlow-SPH model makes it possible to have different values for the internal friction coefficient of a given soil (tanϕ) and the basal one (tanδ) in view of the fact that the debris composing the mass may have different compositions and frictional properties with regard to the material forming the river bed.

The GeoFlow-SPH also makes it possible to take into account the soil entrainment due to streambed erosion which plays a fundamental role in many flow-like landslides. Among several empirical formulas providing an estimation of erosion for depth-integrated models (Pirulli and Pastor 2012), GeoFlow-SPH adopts the Hungr erosion law (Hungr 1995) according to which the erosion rate increases in proportion to the flow depth according to the equation:

$$ \frac{dm}{ds}={E}_s\rho h $$
(2)

where m is the engaged mass per unit footprint area (units kg/m2), s is the distance along the flow path, h is the flow depth, ρ is the soil density (units kg/m3), and E s (units m−1) is the displacement erosion rate, the so-called average growth rate, which represents the bed-normal depth eroded per unit flow depth and unit longitudinal displacement. The growth rate, different from the time-dependent erosion rate e r (units m/s), is assumed to be independent of the flow velocity and is related to the erosion rate e r by:

$$ {e}_r={E}_sh\overline{v} $$
(3)

where \( \overline{v} \) is the depth-averaged flow velocity (Hungr 1995).

Despite the empirical nature of the Hungr erosion law, its physical basis is that the stress conditions leading to bed failure and entrainment are related to the total bed-normal stress and thus to the flow depth. The term E s is related to the variation of flow volume by the logarithmic relationship:

$$ {E}_s=\frac{ \ln \left(\frac{V_{\mathrm{fin}}}{V_0}\right)}{d} $$
(4)

where V 0 and V fin are the landslide volumes before and after propagation and d is the erosion path.

Summarizing, it is necessary to define four parameters to apply GeoFlow-SPH, three related to the rheological law and one to the erosion law. These parameters can assume different values along the propagation path.

It is important to remember that the GeoFlow-SPH is still being improved by its authors and the version being utilized in this study offers the possibility to use different values for the frictional and erosional parameters (δ and E) along the path; the turbulence and inner kinematical friction coefficients (ξ and ϕ) have, instead, fixed values. Even if this can be considered a limitation to modeling, for the purpose of the study, which was to develop an automatic calibration procedure more than to calibrate parameters, this was not considered a problem.

Ensemble smoothing

The calibration procedure developed by this project employs an Ensemble Smoother (ES) or data assimilation algorithm to provide improved estimations of geotechnical parameters. The ES is a Bayesian data assimilation method which, by minimizing the variance of the estimation error, merges “prior” information from a theoretical system, i.e., the propagation model, with field data collected from the real phenomena in order to produce a corrected “posterior” estimate. In our case, the ES algorithm assimilates the prior information with the deposited soil heights determined by the comparison of pre- and post-event LiDAR surveys.

It follows a two-step forecast-update process: the forecast process is obtained using a Monte Carlo simulation of the system state, while the update, or correction, of the prior information takes place when available measurements are assimilated by applying a specific filter to the forecast model results.

Monte Carlo forecast and performance indices

In view of the proliferation over recent decades of the number and types of climatic and environmental models, interest in formulations that produce more accurate and precise estimates of variables of interest has increased. Using an advanced model in which the result is influenced by numerous parameters (being n p the parameter number), the Monte Carlo analysis makes it possible to perform in an automatic way a large number of simulations, each carried out using an independent initial parameter set obtained by a random selection of values on the basis of a statistical distribution assigned to each parameter.

It is essential then to define statistical errors or performance indices which can be used to compare model-produced estimates with reliable independent information or reference data.

Statistical comparisons of model estimates or predictions (y t with t = 1, 2…, n) with matched measurements (\( \widehat{y_t} \) with t = 1, 2…, n) continue to be the most basic means of assessing a model’s performance. Since individual model-prediction errors are usually defined as \( e{}_t={y}_t-\widehat{y_t} \), the average model-estimation error associated to an analysis obtained with the parameter set ϑ can be generically expressed as:

$$ e\left(\vartheta \right)={\left[\frac{1}{n}{\displaystyle {\sum}_{t=1}^n\left|{y}_t\left(\vartheta \right)-\right.}\widehat{y_t}\left|{}^{\tau}\right.\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$b$}\right.} $$
(5)

where b ≠ 0 and τ ≥ 0 are two coefficients and y t  (ϑ) expresses the values y t obtained using the parameter set ϑ.

The most simple relation, assessed with b = 1 and τ = 1, gives the average error or Mean Absolute Error (MAE), according to:

$$ \mathrm{M}\mathrm{A}\mathrm{E}=\frac{1}{n}{\displaystyle {\sum}_{t=1}^n\left|{y}_t\left(\vartheta \right)-\widehat{y_t}\left|=\frac{1}{n}\right.\right.}{\displaystyle {\sum}_{t=1}^n\left|{e}_t\right|} $$
(6)

in which the absolute value of individual error is adopted in order to remove the error sign influence from the computation.

Another commonly defined index is the Root Mean Square Error (RMSE) which is derived from Eq. 5 with b = n and τ = 2. It is formulated as:

$$ \mathrm{RMSE}={\left[\frac{1}{n}{\displaystyle {\sum}_{t=1}^n{\left|{y}_t\left(\vartheta \right)-\widehat{y_t}\right|}^2}\right]}^{1/2}={\left[\frac{1}{n}{\displaystyle {\sum}_{t=1}^n{\left|{e}_t\right|}^2}\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} $$
(7)

where, again, the stated rationale for squaring each e t is to avoid the influence of the error sign. In this case, each error influences the total error in proportion to its square: as a result, large errors have a relatively greater influence on the RMSE with respect to smaller ones, meaning that the RMSE grows as the error is concentrated within a decreasing number of increasingly large individual errors.

The MAE and RMSE have the same units as the variable of interest, but they do reflect the relative error size. To deal with this problem, the Mean Absolute Percentage Error (MAPE) is defined as:

$$ \mathrm{MAPE}=\frac{100}{n}{\displaystyle {\sum}_{t=1}^n\frac{\left|{y}_t\left(\vartheta \right)-\widehat{y_t}\right|}{\widehat{y_t}}} $$
(8)

In this way, MAPE makes it possible to compare forecasts of different series in different scales.

When a Monte Carlo forecast approach is used, evaluation of these indices makes it possible to identify which out of all the simulations carried out is the best one.

Update step or data assimilation phase

The estimated variables (y t (ϑ) with t = 1, 2…, n) obtained with n sim simulations according to the Monte Carlo analysis compose the forecast ensemble U prior [n u  × n sim], being n u  = n hs + n p : generally, the ith column in the U prior matrix lists the n hs model variables y t (ϑ) estimated with the ith simulation and, below, the values of the n p model parameters adopted to perform the same simulation. The forecast ensemble should be corrected or updated using n obs field measurement data and the data assimilation algorithm. In general, n obs and n hs can be different. In this case, we decided to extract the values to be compared \( \widehat{y_t} \) corresponding to the same positions. Basically, it means that in the following, the symbol n will express the number of measured data as well as the number of data obtained from each simulation. We adopted the Kalman filter for the assimilation procedure (Baù et al. 2015; Evensen 2003) having the follow formulation:

$$ {U}_{\mathrm{post}}={U}_{\mathrm{prior}}+{K}_t\cdot \left({D}_t-H\cdot {U}_{\mathrm{prior}}\right) $$
(9)

where:

  • U post [n u  × n sim] is the updated ensemble.

  • H [n × n sim] is a matrix that maps measurement locations into the grid domain so that the product H ⋅ U prior indicates model results at measurement locations. As explained above, the nodes chosen for the comparison between simulated and observed values are the same. Consequently, the matrix H simplifies by becoming identity one.

  • D t [n × n sim] is a matrix that holds the perturbed measurement data using an ensemble of Gaussian noises, stored in a matrix E [n × n sim] representing the measurement random error. If the measurements are error-free, all n sim columns of D t are equal to the data.

At the right-hand side of Eq. 9, the residual D t  − H ⋅ U prior defines the deviation between the forecasted state and the true state at the measurement locations. This residual forms the basis for correcting the forecast ensemble. The degree of this correction depends upon the uncertainty of both the forecast ensemble and the measurement data, which is contained in the Kalman gain matrix K t [n u  × n]:

$$ {K}_t=C\kern0.5em {H}^T{\left(H\kern0.5em C\kern0.5em {H}^T+R\right)}^{-1} $$
(10)

where C [n u  × n u ] is the forecast error covariance matrix, and R [n × n] is the measurement error covariance matrix. These two matrices are defined as:

$$ C=\frac{\left({U}_{\mathrm{prior}}-\overline{U}\right){\left({U}_{\mathrm{prior}}-\overline{U}\right)}^T}{n_{\mathrm{sim}}-1} $$
(11)
$$ R=\frac{E\kern0.5em {E}^T}{n_{\mathrm{sim}}-1} $$
(12)

where each column of Ū [n u  × n sim] holds the average value of the ensemble for each node height distribution. Thus, the matrices C and R contain the spread of the model values and the measurement values, respectively.

As explained by Baù et al. (2015), if the spread of the measurement values is small compared to the spread of the model values, the residual between the modeled and measured values is weighted more heavily in correcting the model value so that it is closer to the measurement one. In fact, the matrix K t assumes the value of 1, so the prior matrix will be strongly updated. Conversely, if the spread of the measurements is large with respect to the spread of the model values, then the residual receives little weight in correcting the model value, which remains similar to the forecast estimate: the Kalman matrix approaches zero value, so the posterior results remain equal to the prior ones.

As an additional observation, it is interesting to note that the reversal operation contained in the calculation of K t requires special conditions. In fact, if the matrix U prior is excessively rectangular, the reversal of the residue in Eq. 9 will lead to a nearly singular matrix, thus compromising the success of the algorithm. In particular, the more the forecast ensemble is square, the better the filter applied will converge into a reliable solution. It was for this reason that it was decided to perform 1000 simulations, equal to the number of data to compare.

A final explanation aims to clarify what exactly the updated matrix contains. The lower 8 lines of the U post represent the corrected values of the parameters obtained by the filter. It is possible to plot their normal distributions and to compare them with the prior ones, as extracted by the Monte Carlo procedure. The upper part of the updated matrix contains the results of the application of the Kalman algorithm. The values there are not obtained from the propagation model, so their distribution only emphasizes how efficient the filter was in carrying out its work.

Application of data assimilation analysis

Selection of input data

Preliminary analyses carried out by Cola et al. (2014) have shown that the debris flow that occurred in the Rotolon catchment in 2010 could not be well simulated assuming a unique value for each parameter, and it was clear that the parameter values depending on the distance from the triggering zone needed to be varied.

As a result, in order to apply the data assimilation procedure, the basin was subdivided into six zones with limits identified according to specific elevations (Table 1). It should be noted that the zone extensions are very different because the limits were chosen subdividing the run-out length in homogeneous parts with respect to the erosion/deposition behavior of the debris flow resulting from the preliminary analysis by Cola et al. (2014).

Table 1 Limit elevations and rheological parameters assumed in the various zones
Full size table

The mean value of rheological parameters was estimated using values indicated in the literature (Pirulli and Sorbino 2008; Bertolo and Wieczorek 2005) and the preliminary results obtained by Cola et al. (2014): the latter authors, for example, showed that the basal friction coefficient decreases along the path of the debris flow, probably due to an increase in the fluidity of the material or to an arrest due to large boulders blocking the path as the bed slope decreased.

The internal friction angle ϕ and the turbulence coefficient ξ were assumed constant for all the zones, because, as already explained, the current version of the GeoFlow-SPH does not allow different values for them: in particular, the internal friction angle ϕ is assumed equal to 30° (tanϕ = 0.6), the minus value for the critical angle of a granular soil, the value commonly adopted for describing debris and rock flow (Sosio et al. 2008); the turbulence coefficient ξ was chosen equal to 700 m/s2, that is, a reliable value within the range of 100 and 1000 m/s2, as was suggested by Pirulli and Sorbino (2008).

Other suggestions about the ξ value were also made by Sosio et al. (2008) who indicated a range of 450–1000 m/s2 for rock avalanches and a range of 200–500 m/s2 for debris flows: the use of a unique value for ξ might contrast with the nature of the phenomenon studied, which could be more similar to a rock avalanche in the detaching upper area when, after covering a part of its trip and receiving water from lateral tributaries, it assumes the characteristics of a debris flow. The use of a constant parameter equal to 700 m/s2 seems in any case to be a compromise with values reported in the literature that would be compensated by assuming a normal distribution with a wide standard deviation.

The basal friction coefficient tanδ could be defined differently for each zone and it is reasonable to think that, along the river, both the debris flow and the bed material reduce their grain-size composition and, consequently, the basal friction angle is reduced as the flow proceeds downstream. In particular, Cola et al. obtained a good reproduction of the event assuming tanδ equal to 0.41 (δ = 22.3°) and 0.02 (δ = 1.1°), respectively, in the portions upstream and downstream the conjunction with the rio Campogrosso. Based on these observations, here we assumed four different mean values of δ: two different values for the first and the sixth zones and two other values for the second and third zones and for the fourth and fifth zones, respectively. The standard deviation was chosen proportionally to the mean value: for example, the basal friction coefficient in the first area, which has a mean value of 0.41, is associated with a relatively wide standard deviation of 0.03, while, on the contrary, the basal friction angle in the fourth zone has a smaller variation range because it was important to be sure that negative values were not included in the parameter set.

The mean value of the erosion parameter in the various zones was chosen on the basis of the DTM of difference (DoD) analysis: the E s value was assigned equal to 3·10−4, 8·10−5, or zero if the comparison between pre- and post-DTMs in a zone prevalently showed erosion, both erosion and deposition or prevalently deposition, respectively.

Table 1 summarizes the mean value and the standard deviation assigned to each zone for the forecast phase. There are eight rheological parameters: four values of the basal friction angles, two values of the erosion coefficients, one of the internal friction angles, and one of the turbulence coefficients.

In order to underline the role and the importance of each parameter, a sensitivity analysis was carried out before the data assimilation procedure was applied. This step is extremely useful to uncover to what extent an inaccurate choice of a parameter can affect model results.

Reference data and measurement error

In order to apply the calibration procedure, two other important issues needed to be solved: one regards the selection of the reference values to analyze the likelihood between simulated and measured values, the other the error associated to the reference data.

First of all, to make the calibration as complete as possible, it is appropriate to consider the highest number of values possible out of all those that are available. Each simulation with GeoFlow-SPH produces more or less 15,000 data referring to the heights of deposited soil along the river at the end of the debris flow propagation (in the following briefly indicated as soil height or h s ); in the same way, the comparison between pre- and post-DTMs could supply a large amount of data, such as a million and half of values.

On the other hand, to be correctly applied, the Kalman procedure requires the number of simulations to be comparable to the number of measurements being compared.

In view of the fact that the computational cost of each simulation is approximately an hour, in order to procure a sufficiently representative sample, we decided to limit the number of comparison data to 1000. The procedure would thus produce 1000 simulations (n sim = 1000), and from each of them, it will take 1000 values of soil heights to compose the upper part of the forecast ensemble U prior.

Once the number of data is fixed, another important issue is that of selecting the data which must describe the phenomenon as accurately as possible in all the source and deposition areas. For this reason, the talweg and two parallel polylines 15 m away from the talweg were identified on the DoD. The variables used for the comparison were the soil height in a selected number of nodes belonging to the polylines. In this way, the talweg represents the longitudinal section of the landslide and the data along it take into account the total propagation of the debris flow, while information along the parallel polylines would take into account the mass spreading along the path. Altogether, there are about 4000 nodes on the three polylines, but, again, only 1000 nodes were selected in a random way out of the 4000 nodes that were available, obtaining the n reference data to compose the vector of the reference heights.

As previously described, the ES algorithm needs to assign the normal distribution of error associated to LiDAR data in order to produce matrix E [n × n sim] and the error distribution affects the final result in a significant manner: a large error would lead to information that is not sufficiently precise for parameter optimization, but, conversely, if the error assigned is too small, the expectation to provide sufficiently precise information could be excessive and the optimization algorithm may not provide reliable parameters.

In our case, no information about the Gaussian distribution of error of the LiDAR data was available: as a result, we set the error of each derived DTM to 0.2 m, a typical value of airborne LiDAR surfaces (Cavalli and Tarolli 2011). The propagated error was consequently assumed constant in the DTM of difference (DoD) analysis (Bossi et al., 2015a) and equal to ±0.28 m. In the last part of the paper, a further analysis evaluating the influence of this parameter is presented together with some of our comments.

Finally, the procedure was performed extracting 1000 values from the normal distribution of each rheological parameter, defining 1000 combinations of parameters and performing the corresponding simulations. At the end of each simulation, the results were elaborated and 1000 data values were extracted from as many nodes. The final matrix has 1000 columns, one for each simulation, and 1000 rows, one for each node. The U prior matrix is the result of concatenation of this matrix [1000 × 1000] with the random parameters used for the simulations.

Model sensitivity

As mentioned in the “Selection of input data” section, in order to underline the importance of each parameter, the results of a sensitivity analysis are presented. Once a variation range for each parameter was chosen, eight series of seven simulations were developed in which only one parameter at a time was modified: a total 56 simulations were carried out, as outlined in Table 2. The central column contains the values that remained the same during the variation of one parameter.

Table 2 Values of rheological parameters assumed in the sensitivity analysis
Full size table

It should be noted that the values assumed for friction and turbulence coefficients differ for a constant quantity depending on the value of the parameter, while the erosion coefficient values vary according to a geometrical series in one order of magnitude.

In the bar plot of Fig. 3, the range of variation of the MAE, RMSE, and MAPE errors calculated for the seven simulations of each series is summarized. The horizontal line joins the error values obtained with the central combination of parameters. It is obvious that the larger the error variation is in function of a parameter variation, the larger is the influence of that parameter. Figure 3 shows, for example, that the internal friction coefficient tanϕ has a secondary role because MAPE varies only between 25 and 30.6 %. On the contrary, all the basal friction angles, in particular, the first three, are fundamental for the calibration process: in fact, small variations in their value cause significant fluctuations in the error. The influence of the erosion and turbulence coefficients is likewise very strong.

Fig. 3
figure 3

MAE (a), RMSE (b), and MAPE (c) of the analyses performed to evaluate the model’s sensitivity

Full size image

It is also interesting to observe that the performance indices were calculated for all the nodes of the simulation, and not only the 1000 nodes chosen for the subsequent application of the Kalman filter. This was done in order to evaluate the totality of the phenomenon that was simulated compared to real values.

A clarification must be made concerning calculation of the percentage error. The nodes that have a deposit or erosion in the simulation solutions are compared with the relative measurements. However, if an in situ observed value proves null, division by zero in formulating MAPE introduces serious problems. To overcome this situation, it was decided to exclude all nodes that have null measures or not null simulated values from the calculation of MAPE: of course, the mean value of error is calculated correcting the total number of compared data.

In our opinion, the best representative formula of error is the percentage one, because it weighs any difference in function of the respective measure. For this reason, in the following analysis, we decided to refer only to this error formulation.

Data assimilation analysis

Prior results

To obtain the prior ensemble U prior, 1000 simulations were performed with the parameter sets extracted from the parameter Gaussian distribution using the Monte Carlo procedure, and then the soil height values in correspondence to 1000 points belonging to the three reference polylines were pulled out, as described in the “Reference data and measurement error” section. The extracted soil heights are plotted in Fig. 4 forming three longitudinal profiles, each of which composed of 333 node values.

Fig. 4
figure 4

Soil height obtained with the 1000 GeoFlow-SPH forecast analyses of the nodes composing the talweg line (a) and the two parallel polylines (b, c)

Full size image

The colored lines represent the results of all the simulations, while the thick black lines indicate the DoD measurements of the same nodes. Here we see that the prior solutions are quite spread out, which is an effect on the input parameter variances originally chosen. It is in any case important that all the measurement lines are included in the range of the simulation results: in this way, the statistical algorithm that is applied later can give good results.

A first assessment of these analyses can be obtained by means of the distribution obtained for the percentage error. The minimum MAPE of all the simulations is 16.2 % while the mean and maximum values are 40.9 and 68.9 %, respectively.

The soil heights in the reference nodes from each simulation form a vector 1000 long. By adding the combination of parameters used for the simulation to it, the vector becomes 1008 long. Assembling all of these vectors permits us to build the prior [1008 × 1000] matrix.

Posterior results

The most important part of the calibration process regards the stage during which the Kalman filter is applied. As has already been described, it takes the prior matrix U prior and restitutes an updated matrix U post containing the corrected values. The Kalman filter was first applied with a measurement error set at ±28 cm which corresponds, as explained above, to the propagated error of the DoD analysis.

The upper part of this matrix expresses the performance of the algorithm applied: a reduction in the variety of the prior data underlines the fact that the posterior results are more similar to reality than the prior ones.

The lower part of the updated matrix can be compared with the lower part of the prior matrix. In particular, Fig. 5 compares the frequency distribution of each parameter that was obtained from the prior and post matrices, a comparison which give us some information about the parameter values to be used and about the relevance of each parameter for the model. The more the algorithm reduces the variance of the normal distribution of a parameter, the more important and better defined it will be.

Fig. 5
figure 5

Frequency distribution of the rheological parameters in input and output from the data assimilation analysis of the three procedure steps. (a) tanf; (b) tand1; (c) tand2; (d) tand3; (e) tand4; (f) x; (g) E1; (h) E2

Full size image

As the sensitivity analysis previously suggested, the most important parameters are the basal friction angles: for each of these, the filter furnishes a better frequency distribution with respect to the input one. The internal friction angle carries out a secondary role since its frequency curve seems less restricted after the filter has been applied. The same can be said about the turbulence parameter even if the analysis indicates that the mean value is much smaller with respect to the input one.

A final consideration concerns the filter’s indication about the erosion parameter: even if the mean value of E 1 introduced into the analysis was greater than E 2, its final value is one order of magnitude minor than the input one and minor than the E 2.

The mean values of the updated parameters are reported in Table 3. It is very interesting to compare the results of the simulation performed using these values as input with the measurements, as outlined in Fig. 6. The correspondence between the total run-out of debris flow in situ and in the model is very good, and the soil height distribution along the stream is also well described by the numerical model, even if the model seems to overestimate the deposition in the lower portion of the basin and, on the contrary, to underestimate the soil height in the upper part.

Table 3 Mean of the updated parameters after the first Kalman filter was implemented
Full size table
Fig. 6
figure 6

Comparison between the deposition and erosion maps of the data measured (a) and of the data before (b) and after the Kalman filter was applied (c, d)

Full size image

The second Kalman filter application

The last step of the procedure consists in carrying out 1000 new simulations with the parameters obtained using the Monte Carlo procedure from the updated frequency distribution and then once again applying the Kaman filter. The same steps as those adopted previously should be used; even in this case, it is possible to plot the soil height profiles along the reference polylines (Fig. 4).

The spread of the soil height profiles is lower than the one in the first analyses (Fig. 4). In fact, the orange lines remain closer to the line of the observed values (black line) than do the previous ones (yellow lines).

As before, the application of the Kalman algorithm provides a new updated matrix and new frequency distributions of parameters are obtained and compared with the input frequency distributions (Fig. 5). With the second application of the Kaman algorithm, some distributions maintain the same mean value and further reduce the variance, as occurred for tanδ 3 (Fig. 5d), while, on the contrary, for other distributions, as in the case of the turbulence (Fig. 5f), the algorithm gives new corrections even with regard to the mean value. It is necessary to clarify that the statistical filter applied considers each parameter as a number and does not take into account its physical meaning. This is the reason why the second application of the Kalman filter gives a negative value for the erosion coefficient E 1 (Fig. 5g). We have interpreted this result as meaning that we need to set a null value of erosion in the areas where we entered E 1.

Again, in Fig. 6d, the soil heights of the DoD are compared with the heights obtained with a new simulation performed setting the average value of the updated normal distribution for each parameter. The MAPE of this last result reached the value of 26.9 % (Table 4).

Table 4 Percentage errors of the simulation obtained with the user-defined parameter set and the two obtained with the simulations using the parameter set suggested by the Kalman filter
Full size table

Discussion of results

Comparison among errors

Some initial comments can be made about the comparison of the distribution of the performance index defined in Eq. 8, i.e., the MAPE. Figure 7 presents the comparison between the distribution of the percentage errors for the prior and post simulations, i.e., the simulations carried out with parameters extracted from the updated frequency distribution.

Fig. 7
figure 7

Normal distribution of the percentage errors of the first 1000 simulations compared with the normal distribution of the simulation after the Kalman filter was applied

Full size image

It is evident that the Kalman algorithm produces an important improvement in the distribution of the MAPE displayed here but also of other performance indices. Even if the lowest values of the three errors for the updated group of simulations did not decrease, a significant reduction in the highest and mean values was observed. The improvement of the MAPE, which fell from 40.9 to 28.3 %, is particularly evident (Table 5).

Table 5 Percentage errors of the prior 1000 simulations compared with the 1000 ones obtained after the first Kalman filter was implemented
Full size table

After the second application of the Kalman algorithm, we could also compare the performance indices of the third group of simulations, i.e., those carried out with parameters extracted using the frequency distribution suggested by the second Kalman filter.

As shown in the Table 4, the best MAPE obtained from the first simulation reached the value of 36.9 %. After the first application of the filter, we obtained a MAPE of 33.9 % from the simulation developed. At the end, after a new improvement procedure was implemented, we attained a MAPE of 26.9 %.

The effect of measurement error

The algorithm makes it necessary to make some assumptions about the distribution of errors affecting the reference data. As has been explained before, the propagated error of the DoD was set at a constant value but it may also be interesting to evaluate how the error value influences the optimization process results. In fact, if the assumed reference data are sufficiently descriptive of the debris flow and the model is really able to reproduce the phenomena, the posterior results should be stable regardless of error values.

To verify this condition, the Kalman algorithm was applied ten times to the same prior matrix adopting error values varying from 10 cm to 1 m in a logarithmic way: the boxplot of Fig. 8 summarizes distribution indicated by the filter for each parameter plotted versus the assumed error value and compares them with the forecast boxplot representing the normal distribution of the same parameter assumed at the beginning of the procedure. On each box, the central thick mark indicates the median value, the box edges the 25th and 75th percentiles respectively and the whiskers the 2.7σ ÷ 99.3σ range, σ being the standard deviation of the normal distribution of each parameter. The model sensitivity to the error value is represented by the filter’s ability to reduce the variance of the parameter distribution and to supply a unique mean value regardless of the assumed error.

Fig. 8
figure 8

Boxplots of the results using different values for the measurements error for each parameter after the Kalman filter was applied. (a) tanf1; (b) tand2, tand2, tand3 and tand4; (c) x; (d) E1 and E2

Full size image

All the posterior boxplots are more precise than the forecast distribution since in all cases the standard deviation is reduced, confirming that is algorithm is working well. Moreover, the results of Fig. 8 are consistent with those already obtained by the sensitivity analysis outlined in the “Model sensitivity” section. In fact, the error value does not change the posterior values of the basal friction angles (tanδ) and this confirms that these parameters have a strong influence on model calibration. Similar reasoning is appropriate for the erosion parameter in the lower part of basin E 2, but not for the erosion coefficient in the upper part of E 1 which has a mean value in output that is strongly dependent on the definition of the measurement error. Even this result confirms what was obtained in the previous sensitivity analysis.

Finally, modifications in the definition of error also produced different output values for the turbulence and internal friction parameters, but, after the filter was applied, their variance was reduced to a lesser extent with respect to the other parameters. This result can be justified by a variety of explanations. On the one hand, the internal friction angle seems to play a secondary role for the model because the model shows a greater tolerance in relating this parameter to the reference data. On the other, in view of the fact that the turbulence coefficient is extremely important for model calibration, it would probably be better to define different parameters for different zones. This consideration is made in the effort to explain the very different values for the turbulence coefficient that are found in the literature. In this way, it is probable that the values found in the literature in the future will be in better agreement with the real behavior of debris flows.

Conclusion

Models analyzing debris flow propagation are usually calibrated by comparing in a subjective way the predicted and measured lengths of the flow or heights of deposited soil in some particular sections. This procedure is, however, likely to be inaccurate if it is based on inappropriate performance indicators and may be further complicated by the fact that different combinations of values often lead to similar results.

The procedure proposed here, based on a data assimilation algorithm and the systematic use of performance indices, can be a useful tool because it presents some evident advantages, including the following ones:

  • it is applied starting from a large number of possible parameter combinations obtained extracting values in a random manner from reliable statistical distributions;

  • the comparison takes into account the totality of deposits along the debris flow path;

  • the evaluation is carried out using indices that are not affected by subjective interpretation;

  • it may be implemented in an automatic code in order to easily repeat its application numerous times and analyzing the effects of different initial assumptions;

  • it can be improved by including other rheological parameters or the most probable distribution of error in measurements.

It is also important to indicate critical points that need to be checked for the correct application of a similar calibration procedure. The most important are the following:

  • a large number of simulations have high computational costs depending on the time required to perform a single propagation analysis. At the same time, being able to simultaneously perform more than one simulation, depending on the number of processors that are available, may significantly reduce the computational time;

  • the choice of the performance index is extremely important since not all error formulations are sufficiently representative and reliable;

  • identifying the nodes to be considered for the Kalman filter application is an important step to converge to an optimal solution.

Some comments can also be made about the application of the data assimilation to the specific case history presented here. First of all, the subdivision of the basin into different portions with different parameters proved to be a good strategy that could be improved if it were possible to use different parameters and not just the basal friction angle.

In this case, the erosion evaluated using the Hungr formula resulted limited and the calibration of the representative parameters in the upper part of the basin did not furnish a reliable value, probably due to the minor relevance of the phenomena.

The basal friction angle, the turbulence coefficient, and the erosion rate in the lower basin are the most significant rheological parameters that must be carefully selected in order to reach a proper reproduction of the Rotolon debris flow.

The turbulence coefficient seems to play an ambiguous role: while in sensitivity analysis, the degree of uncertainty of this parameter seems to be important, with the data assimilation application its effect appears partially weaker. Moreover, this parameter is not stable with changing the distribution of errors affecting the reference data, so it could be concluded that the calibration of this parameter is not really important for the model. On the other hand, the discrepancies found applying different analyses were not completely understood and they may be partially explained with the fact that, in our model, the turbulence coefficient cannot change along the topography (as for other parameters like basal friction which results more “flexible”) or with different soil heights. Moreover, it was calibrated on the base of soil height measurements while the turbulence terms mainly influence flow velocity (Hürlimann et al. 2008).

These facts probably limits the achievement of the best possible calibration, which may be improved in the future incorporating the variability of this coefficient in the code and the possibility of a combined use of kinematic data in the assimilation procedure.

Finally, even if turbulence and friction coefficients have opposing influences on the model results, the assimilation of such a large number of data allow us to understand, which sets among all the combinations that lead to similar results.