Introduction

Hyrcania is located south of the Caspian Sea. It was one of the most fertile provinces of the ancient Persian Empire. In addition to fertility, the region is famous for its scenic beauty. Most of Hyrcania is in current Iran and Turkmenistan. In Iran, it covers approximately 50,000 km2 in the provinces of Gilan, Mazandaran, and Golestan. Good productivity is due to humid temperate climate and fertile soil. Intensive human settlement of the lower elevations as early as AD 1100 left large portions of the lowlands deforested, after these areas were converted to agricultural, residential, and industrial uses (Sefidi et al. 2011).

Oriental beech (Fagus orientalis Lipsky) is often the dominant species in the northern temperate forests of Hyrcania. Beech forests are mixed with Carpinus betulus, Alnus subcurdate, Acer velutinum, and other species. The forests are mostly uneven-aged and broad-leaved but conifers such as Taxus baccata and Cupressus sp. appear on some sites. The stands are often spatially heterogeneous with large variation in tree size (Marvie-Mohadjer 2012).

Recent awareness of the biological diversity of forests and interest in non-wood forest benefits has led to the demand of preserving the existing uneven-aged stand structures (Calama et al. 2008). Uneven-aged management is currently a topical issue also in Iran where even-aged forestry is being criticized due to its negative impacts on landscape and biodiversity. Recent studies suggest that in regions where trees grow slowly, uneven-aged continuous cover management may be more profitable than even-aged plantation forestry (Tahvonen 2009, 2011; Pukkala et al. 2010; Tahvonen et al. 2010).

Forests are long-living dynamic biological systems that are continuously changing. These changes need to be projected in order to produce useful information for decision making. Growth and yield models that describe forest dynamics (growth, mortality, and reproduction) have been widely used in forest management for predicting future yields and exploring management alternatives (Burkhart 1990; Vanclay 1994; Rößiger et al. 2011). Predicting future forest growth and yield under different management scenarios is a key element of sustainable forest management (Kimmins 1990, 1997; Peng 1999; Griess and Knoke 2013; Pretzsch et al. 2013). Pukkala et al. (2009) suggest that individual-tree models may be the most suitable approach to modeling the dynamics of uneven-sized stands. Trasobares et al. (2004) concluded that individual-tree model is the best model type for describing the dynamics of the uneven-aged mixed pine forests of northeast Spain. According to Vanclay (1994), the required model set in this approach consists of diameter increment, mortality, and recruitment models. Although uneven-aged and multilayer stands commonly exist in Iran, systematic uneven-aged forest management is rare. The growth of uneven-aged forests in the Caspian region has been studied earlier (e.g., Heshmatol Vaezin et al. 2008; Eslami and Hasani 2011) but there are no growth and yield models for uneven-aged stands that can be used in simulation and numerical optimization.

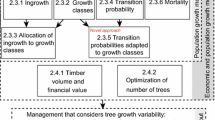
Due to changes in forest usage and demands by the public for more near-nature forest management and greater forest diversity (Lähde et al. 1999), development of models for uneven-aged forestry has become more and more urgent. This study developed models for diameter increment, tree height, tree survival, and ingrowth in the uneven-aged hardwood forests of Hyrcania. The models were used in simulation and optimization, to find stand structures that would maximize timber yields or economic profitability. Gradual conversion of different stand structures from the current state toward the optimal one was optimized for four different initial stands: young even-aged, mature even-aged, uneven-aged, and two-storied stand.

Materials and methods

Data collection

Data for modeling were collected in Gorazbon, which is one of the eight sections of the Kheyrud forest. The forests of the Gorazbon section are naturally regenerated and they have developed almost without human interference. The Kheyrud forest covers 80 km2 near the port city of Nowshahr. The elevation varies from 10 to 2,200 m above sea level. The soils are characterized by karst topography and the most common soil type is calsisols (Forest management project of Gorazbon Section 2009).

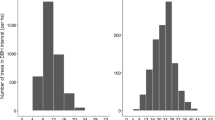
For modeling tree growth, survival, and ingrowth, 258 circular fixed area plots of 0.1 hectares were systematically placed on a rectangular grid of 150 × 200 m across the Gorazbon section. Due to steep slopes that are facing north, the directions of the grid axes were set north–south and east–west, allowing the surveyors to walk along contours. Slope correction was applied to plot radii (which were measured along soil surface), so as to obtain horizontal plot areas of exactly 0.1 ha.

The diameters of all trees with dbh at least 7 cm were measured before the growing season of 2003 and again after the growing season of 2012. Ten-year diameter increment was obtained as the difference between the two measurements. Plot center was marked with a pole in the first measurement, and breast height (1.3 m from ground) was marked to each stem with paint. Trees were numbered, and the number was painted on the stem. Diameters were measured in the same direction in both measurements (2003 and 2012). New ingrowth trees (trees that passed the 7-cm diameter threshold) were also measured in 2012. It was also recorded whether a tree was living or dead. The height of the tree closest to plot center and the height of the largest tree of the plot were also measured.

Growth and yield modeling

The data were used to fit the following set of models that enable the simulation of stand development:

  • Individual-tree diameter increment model.

  • Individual-tree survival model.

  • Individual-tree height model.

  • Ingrowth model.

The total number of observations (surviving trees) available for modeling diameter increment was 6,962 with the following species composition (number of dead trees in parenthesis): F. orientalis 2,360 (196), C. betulus 3,296 (371), Quercus castaneifolia 356 (12), A. subcurdate 324 (17), Parrotia persica 11 (0), A. velutinum 277 (3), Acer compesrte 202 (6), Tilia begonifolia 108 (2), Ulmus glabra 24 (11), and other species 4 (1). The number of observations available for survival modeling was 7,581 (both surviving and dead trees), and 525 pairs of dbh and height were available for modeling tree height (F. orientalis 229, C. betulus 196, Q. castaneifolia 20, A. subcurdate 34, A. velutinum 25, A. compesrte 5, T. begonifolia 9, and U. glabra 6 observations). The stand basal area and number of trees per hectare varied widely among the plots (Table 1). Tree diameter ranged from 7 to 188 cm. The 10-year diameter increment was 0–10 cm for the majority of trees, but there were a few growths less than zero or more than 10 cm. The reason for these exceptional growths was the fact that diameter increment was obtained as the difference between two diameter measurements, both of which included some measurement errors due to the irregular shape and large size of the trees.

Table 1 Characteristics of the data set used for diameter increment modeling
Full size table

Logistic model fitted with binary logistic regression analysis was used to model the probability of survival. Nonlinear mixed-effects modeling was used in height and diameter increment modeling. The predictors used in survival and increment modeling described the influence of tree size, competition, and species. A common model was fitted for all species, using indicator variables to account for any species effects. Competition was described by stand basal area and basal area in larger trees. Competition variables were not included in the tree height model since they would result in instantaneous (and illogical) changes in predicted tree height in simulated thinning treatments. Correlation of observations within a plot was taken into account by allowing a random plot factor in the models for diameter increment and tree height.

The current volume models of the region (Forest management project of Gorazbon Section 2009) are presented in the form of tables. The tabular models were converted into equations to improve the usability of the models in computer-based simulation and optimization. Equation models were fitted for total stem volume and for the proportions of different timber assortments. The current timber assortments of the region and their unit prices are shown in Table 2.

Table 2 Timber assortments and their stumpage prices in the study area
Full size table

Problem formulation for numerical optimization

Three sets of optimizations were conducted. The first set optimized the steady-state post-cutting diameter distribution described by right-truncated Weibull function. These optimizations were done for pure stands of F. orientalis, C. betulus, and Q. castaneifolia. Sustainable yield, i.e., non-declining periodical harvest, was maximized. There is no initial stand in this problem formulation. Instead, the initial post-cutting diameter distribution is optimized. A stand corresponding to a tested distribution is generated, after which its growth is simulated for a cutting cycle, i.e., until the next cutting. This cutting returns the frequencies of diameter classes to their initial levels. The removal is calculated from the differences of pre- and post-thinning frequencies of trees in different diameter classes. If the post-thinning frequency of some diameter class is smaller than its initial frequency, i.e., ingrowth is insufficient, the solution is penalized, preventing the selection of unsustainable stand structures.

The diameter distributions were described by the total number of trees per hectare with dbh > 7 cm (N), maximum diameter retained in cutting (Dmax), and a two-parameter Weibull function (Bailey and Dell 1973):

$$f(d) = \left( \frac{c}{b} \right)\left( \frac{d}{b} \right)^{c - 1} \exp \left[ {- \left( \frac{d}{b} \right)^{c} } \right]$$
(1)

where d is diameter, f(d) is frequency of diameter d, b is a location parameter, and c is a shape parameter. The use of Weibull function instead of the frequencies of diameter classes greatly decreased the number of optimized variables (Bare and Opalach 1987). The optimized variables were only four in number, namely N, Dmax and parameters b and c of the Weibull function. Previous research indicates that, in steady-state optimization, the use of Weibull parameters with N and Dmax produces equally good optima as optimizing the frequencies or spline-smoothed frequencies of diameter classes (Pukkala et al. 2010). Tahvonen (2011) obtained about 10 % lower net present values when using Weibull parameters instead of frequencies of diameter classes but Tahvonen did not report whether Dmax was one of the optimized variables. Using Dmax as a truncation diameter of the post-cutting diameter, distribution has strong impact on the optimization results (Pukkala et al. 2010).

When producing an initial stand corresponding to a certain set of optimized variables, frequencies were calculated from the Weibull function at 2-mm intervals for diameter range 7–Dmax cm. The obtained frequencies were scaled to give a total number of trees per hectare equal to N. Then, survival and growth of trees were simulated to the end of the cutting cycle, using a 10-year time step and the models developed in this study (“Models” section). Survival was simulated in the deterministic way, by multiplying the frequencies of trees by their survival probabilities. The cutting reduced the frequencies of trees in each 5-cm diameter class to their initial levels.

In the second set of optimizations, the sequence of post-cutting diameter distributions was optimized for pure F. orientalis in four different initial stands with a constraint that the diameter distribution must reach a pre-defined target distribution in a certain number of cuttings. The target distribution was an investment-efficient steady-state distribution (Bare and Opalach 1987), which maximizes the net present value (Eq. 2). The objective function of the conversion problems was also net present value, calculated with 1–3 % discount rates. The post-cutting distributions of five consecutive cuttings in years 0, 40, 80, 120, and 160 were optimized with the constraint that the predefined target distribution must be reached in the 6th cutting in year 200. The total length of the conversion period was set, so that it was possible to reach the target distribution in all initial stands during the conversion period.

Each post-cutting distribution was described by the total number of remaining trees per hectare, maximum retained diameter, and Weibull parameters b and c. In the conversion cuttings of years 0–160, the Weibull distribution was considered as a cutting limit, which means that excess was removed but deficit was not penalized. In the 6th cutting (year 200), any deficit compared to the target distribution was penalized, i.e., the target distribution had to be achieved exactly. The number of optimized decision variables was 5 × 4 = 20 (N 0, N 40,…, N 160, Dmax0,…, Dmax160, b 0,…, b 160, c 0,…, c 160).

In the third set of optimizations, the steady-state distribution was optimized simultaneously with the conversion cuttings. The steady-state distribution had to be reached in the 6th cutting. Now, the number of optimized decision variables was 6 × 4 = 24. Net present value with discounting rates 1, 2, and 3 % was maximized. The net incomes of the first six cuttings were discounted to the present and summed. Then, the periodic income of the steady-state forest was calculated by simulating one additional period. This income was converted to the net present value of an infinite series of periodic net incomes, which was discounted to the present and added to the net present value of the conversion cuttings.

Four different initial stand structures were used in the second and third set of optimizations: young even-aged stand, mature even-aged stand, uneven-aged stand, and two-storied stand. The so-called investment-efficient steady-state stand structure was also solved for comparison, using the same discount rates. In these optimizations, such a diameter distribution was searched, which maximizes the following formula (Chang 1981; Bare and Opalach 1987):

$$NPV_{T} = \frac{{N_{T} }}{{(1 + i)^{T} - 1}} - C_{T}$$
(2)

where N T is the net income obtained regularly at T-year intervals (€ ha−1), T is the length of the cutting cycle (years), and C T is the value of the initial investment (€ ha−1). The value of initial investment was calculated as the stumpage value of trees in the post-cutting stand. This problem formulation does not use any initial stand as the starting point. The purpose was to compare the investment-efficient distributions to the optimal ending distributions of different initial stands and to have an idea of the usability of the investment-efficient optimum as an overall target distribution. The optimization method used for all problems was evolution strategy optimization (Bayer and Schwefel 2002; Pukkala 2009).

Results

Models

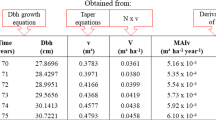
The model fitted for diameter increment is as follows:

$$id_{ij} = { \exp }\left( \begin{gathered} - 0. 8 8 2 4 { } + u_{j} + 0. 4 3 4 3 {\text{ln}}\left( {d_{ij} } \right) \, - 0. 1 9 8 7\left( {d_{ij} / 100} \right)^{ 2} -\,0.00 3 1BAL_{ij} + 0. 5 8 6 1Fagus \hfill \\ +\, 0. 4 3 9 6Carpinus + 0. 8 20 2Quercus + 0. 6 9 40Alnus + 0. 7 4 7 5AcerVelutinum \hfill \\ +\, 0. 6 7 9 6AcerCompestre + 0. 6 5 3 5Tilia \hfill \\ \end{gathered} \right) \, + e_{ij}$$
(3)

where id ij is the 10-year diameter increment of tree i of plot j (cm), u j  ~ N(0, σ 2 u ) is a random plot factor, d is diameter at breast height (cm), BAL is basal area in larger trees (m2ha−1), and e ij  ~ N(0, σ 2 e ) is residual. Fagus and Carpinus are indicator variables for different species (e.g., Fagus = 1 if species is F. orientalis and 0 otherwise). The standard deviation of the random plot factor is 0.068, and the standard deviation of residual is 3.68 cm. The model and Fig. 1 show that, in the uneven-aged hardwood stands of Hyrcania, diameter increment increases as a function of dbh, until 105 cm, after which increment begins to decrease. Of the two main species of the region (F. orientalis and C. betulus), F. orientalis grows faster. Q. castaneifolia has the fastest diameter increment of the analyzed species (Fig. 1). Increasing competition (BAL) decreases diameter increment.

Fig. 1
figure 1

Diameter increment as a function of dbh and species according to the model developed in this study. In the diagram, basal area in larger trees (BAL) is assumed to decrease from 35 to 0 when dbh increases from 5 to 180 cm

Full size image

No significant species influences were found in tree height modeling. The best fit was obtained for the following simple model:

$$h_{ij} = { 1}. 3 { } + d_{ij}^{ 2. 3 3 6} /\left( {0. 70 5+ 0. 3 60d_{ij} } \right)^{ 2} + {\text{ e}}_{ij}$$
(4)

where h ij the height of tree i of plot j, d ij is the diameter (dbh) of the same tree (cm), and e ij  ~ N(0, σ 2 e ) is residual. The plot effect was not significant and it was therefore not included in the model. The standard deviation of the residual is 5.49 m. The model explains only 68.4 % of the variation in measured tree height, suggesting that there is much variation in stem taper among the trees of Hyrcanian hardwood forests (Fig. 2).

Fig. 2
figure 2

Measured (dots) and modeled (line) relationship between dbh and tree height

Full size image

The following logistic function was fitted for the probability of survival:

$$s_{ij} = \frac{1}{{1 + \exp [- (1.282 + 0.954\ln (d_{ij} ) - 0.023d_{ij} - 0.116BAL_{ij} /\sqrt {d_{ij} + 1} - 0.438Carpinus)]}}$$
(5)

where s ij is the probability that tree i of plot j survives for 10 years, d is dbh (cm), and BAL is basal area in larger trees (m2 ha−1). The model shows that trees with dbh between 20 and 100 cm survive best (Fig. 3). Increasing competition (BAL) decreases survival, and C. betulus has a slightly lower survival rate than the other species. The percentage of correct predictions within modeling data was 91.8 (if 0.5 is used as the threshold probability), and the Nagelkerke R2 statistics was 0.082. The area under the receiver operating characteristic curve (see, e.g., Pukkala et al. 2009) was 0.702, which indicates a fair performance.

Fig. 3
figure 3

Probability to survive for 10 years as a function of diameter (dbh). In the diagram, basal area in larger trees (BAL) is assumed to decrease from 35 to 0 when dbh increases from 5 to 180 cm

Full size image

No model could be fitted for ingrowth, due to its high variation that was not related to stand basal area, mean tree size, species composition, or any other available stand characteristic. The average ingrowth rate, i.e., the number of trees that will pass the 7-cm diameter limit during a 10-year period, was 16 trees per hectare, distributed among different species as shown in Table 3. The mean diameter of the ingrowth trees at the end of the 10-year period was 10.6 cm.

Table 3 Mean 10-year ingrowth of different species in the modeling data
Full size table

The simplest way to predict and simulate ingrowth is to use the mean values for all stands. However, this is not biologically justified since ingrowth should eventually start to decrease with increasing stand basal area. It can also be assumed that regeneration would be low with very low stand basal area, due to the lack of seed trees and increased competition by bushes, herbs, and grass. This would result in decreased ingrowth. Therefore, another ingrowth model was manually adjusted to the data (Fig. 4):

$$IN_{j} = { \exp }\left( { 2. 7 5+ 0. 2 {\text{ln}}\left( {G_{j} } \right) - 0.00 5G_{j} } \right)$$
(6)

where IN j is the 10-year ingrowth of plot j (trees per hectares, which pass the 7-cm diameter limit) and G j is stand basal area (m2 ha−1). This model was used in the optimizations of this study.

Fig. 4
figure 4

Observed ingrowth of the study plots (dots) and a manually adjusted model (line)

Full size image

The official tariff tables (volume tables) of Gorazbon section (Forest management project of Gorazbon Section 2009) were converted into the following volume functions:

$$Fagus\,orientalis:v = \, 0.000 1000\;d^{ 2. 50 3}$$
(7)
$$Carpinus \, betulus:v = \, 0.0000 9 9 9d^{ 2. 4 70}$$
(8)
$${\text{Other species}}:v = \, 0.000 2 9 9 6d^{ 2. 2 7 3}$$
(9)

where v is stem volume (m3) and d is dbh (cm).

A set of models was developed for estimating the proportions of different timber assortments as a function of dbh (Fig. 5). The models are based on the official tariff tables for F. orientalis. The set of models consists of regression models for three logit-transformed proportions (y 1, y 2, and y 3; Eqs. 10, 15, and 17) and four constant proportions (Eqs. 13, 14, 19, and 20). First, the proportion of saw log (L1 + L2 + L3 + W4) is obtained from

$$y_{ 1} = \, - 8. 2 9 6+ 2. 4 4 5 {\text{ln}}\left( d \right)$$
(10)
$${\text{pLog }} = { \exp }\left( {y_{ 1} } \right)/\left( { 1+ { \exp }\left( {y_{ 1} } \right)} \right)$$
(11)

where pLog is the proportion of log of the total stem volume and d is dbh (cm). The proportions of B1 and B2 (pB1, pB2) are calculated as:

$${\text{p}}\left( {{\text{B1}} + {\text{B2}}} \right) \, = { 1} - {\text{pLog}}$$
(12)
$${\text{pB1 }} = \, 0. 4 4 {\text{ p}}\left( {{\text{B1}} + {\text{B2}}} \right)$$
(13)
$${\text{pB2 }} = \, 0. 5 6 {\text{ p}}\left( {{\text{B1}} + {\text{B2}}} \right)$$
(14)
Fig. 5
figure 5

Proportions of different timber assortments as a function of diameter at breast height

Full size image

The proportion of W4 of the total log volume (pW4ofLog) is:

$$ y_{ 2} = { 3}. 5 6 8 { } - 1. 10 8 {\text{ ln}}\left( {{d}} \right) $$
(15)
$${\text{pW4}}\,{\text{of}}\,{\text{Log }} = { \exp }\left( {y_{ 2} } \right)/\left( { 1+ { \exp }\left( {y_{ 2} } \right)} \right)$$
(16)

The proportion of W4 of the total stem volume can now be calculated as pW4 = pLog × pW4 of Log. The proportion of L3 of the total volume of L1, L2, and L3 (pL3 of L123) is:

$$ y_{ 3} = { 5}. 5 6 7 - 1. 2 8 7 {\text{ ln}}\left( {{d}} \right)$$
(17)
$${\text{pL3}}\,{\text{of}}\,{\text{L123 }} = { \exp }\left( {y_{ 3} } \right)/\left( { 1+ { \exp }\left( {y_{ 3} } \right)} \right)$$
(18)

The proportion of L3 of the total stem volume can now be calculated as pL3 = pLog × (1 − pW4ofLog) × pL3ofL123. Finally, the proportions of L1 and L2 are as follows

$${\text{pL1 }} = \, 0. 40 \, \times {\text{ pLog }} \times \, \left( { 1- {\text{pW4}}\,{\text{of}}\,{\text{Log}}} \right) \, \times \, \left( { 1- {\text{pL3}}\,{\text{of}}\,{\text{L123}}} \right)$$
(19)
$${\text{pL2 }} = \, 0. 60 \, \times {\text{ pLog }} \times \, \left( { 1 - {\text{pW4}}\,{\text{of}}\,{\text{Log}}} \right) \, \times \, \left( { 1 - {\text{pL3}}\,{\text{of}}\,{\text{L123}}} \right)$$
(20)

Optimal stand structure for maximum sustained yield

The first set of optimizations found such steady-state post-cutting diameter distributions that maximize the mean annual harvest. Optimizations were done for F. orientalis stands with 10, 20,…, 70 year cutting cycles, whereas 30 and 40 years were used for C. betulus and Q. castaneifolia. It was assumed that the stands are pure, one-species stands, and the ingrowth obtained from Eq. 6 was assumed to be of the same species.

The steady-state stand structures that maximize wood production are descending diameter distributions typical to uneven-aged management (Fig. 6). The main difference between the three analyzed species is that the largest retained trees are clearly larger in Fagus and Quercus stands (100 cm) as compared to Carpinus (85 cm). The maximum sustainable yield is about 4.8 m3 ha−1 a−1 for F. orientalis, 2.2 m3 ha−1 a−1for C. betulus, and 6.5 m3 ha−1 a−1 for Q. castaneifolia (Table 4). Since the removed trees are very large, most of the removed volume belongs to the log assortments (L1, L2, L3, and W4). If the cutting cycle is 30 or 40 years, the number of trees removed per hectare varies from 20 to 40, depending on species and cutting interval. Removed volume ranges from 68 (Carpinus, 30-year cutting cycle) to 260 m3 ha−1 (Quercus, 40-year cycle).

Fig. 6
figure 6

Optimal pre- and post-thinning steady-state diameter distribution for uneven-aged F. orientalis, C. betulus, and Q. castaneifolia forests when wood production is maximized with 30-year cutting cycle

Full size image
Table 4 Characteristics of the steady-state post-cutting stand when wood production is maximized with 30- or 40-year cutting cycle
Full size table

The pre-cutting basal area increases and the post-cutting basal area tends to decrease when cutting interval increases (Fig. 7). The main influence of cutting interval is that the diameters of the largest trees of the pre-thinning stand increase with increasing cutting interval. Another difference is that the diameter distribution (both before and after cutting) becomes slightly more uniform when cutting interval increases.

Fig. 7
figure 7

Effect of cutting interval on the optimal pre- and post-cutting basal area in F. orientalis

Full size image

Optimal conversion to investment-efficient target distribution

The second set of optimizations optimized the sequence of five post-cutting diameter distributions for different initial stands with the constraint that the remaining distribution after the sixth cutting should coincide with a predetermined steady-state distribution, which is equal to the investment-efficient optimum solved with 1 % discount rate. Four initial stands were analyzed: young even-aged, mature even-aged, uneven-aged, and two-storied stand. All calculations were made for pure F. orientalis stands. Net present value with 1 % discount rate was maximized, taking into account also the net present value of the steady-state stand that was reached in the sixth cutting.

The optimal sequences of post-cutting diameter distributions of Fig. 8 show how cuttings gradually convert the diameter distributions into the descending target distribution. The change in stand structure is not only because of cuttings but ingrowth and unequal growth rate of different tree sizes (widening of the diameter distribution) are also important elements. Since there is no removal in the first cutting (in year zero) except very little in the mature even-aged stand, the first post-cutting distribution also indicates the initial stand structure.

Fig. 8
figure 8

Optimal sequence of post-cutting diameter distributions for four initial stands when the target distribution is not optimized and net present value is maximized with 1 % discount rate

Full size image

The conversion cuttings started immediately in the mature even-aged stand but the first cutting in year zero was very light (Fig. 9). Uneven-aged and two-storied stands were cut for the first time in the second possible cutting year, 40 years since the start, whereas the young even-aged stand was cut for the first time in year 80. Typically, cuttings 4 and 5 (years 120 and 160) had the highest removals. The more there were large trees in the initial stand, the higher were the optimal removals of the first cuttings.

Fig. 9
figure 9

Removals of the conversion cuttings (C1–C6) for four initial stand structures

Full size image

The mean annual removal of the conversion period was highest in the uneven-aged initial stand, although its initial volume was clearly lower than in the mature even-aged stand (Table 5). In fact, the removed volume was nearly the same in the young and mature even-aged initial stands, although the latter had initially 171 cubic meters more per hectare to remove. The mature even-aged stand had a clearly lower volume growth during the conversion period than the other initial stands. The uneven-aged initial stand produced most wood during the conversion period, followed by the two-storied and young even-aged stands. The net present value of the cuttings, including the conversion period and the subsequent steady-state management, is largest for the mature even-aged stand and lowest for the young even-aged stand (Table 5). This is because of the strong influence of early cuttings on discounted revenues.

Table 5 Characteristics describing the conversion of four initial stands into a pre-defined uneven-aged steady-state stand
Full size table

Optimal conversion when ending distribution is optimized simultaneously

The third set of optimizations was similar to the second one, except that the final steady-state post-cutting distribution was optimized simultaneously with the conversion cuttings. Six conversion cuttings at 40-year intervals were allowed, and the sixth post-cutting distribution was to be followed to infinity. The sixth distribution had to be sustainable, which means that when the post-cutting stand was left to grow for 40 years, there had to be enough trees in all diameter classes. Net present value with 1 % discount rate was maximized.

Now, the final steady-state diameter distributions are different for different initial stands (Figs. 10, 11). The overall shape is decreasing number of trees toward larger diameter classes. The maximum diameter of the post-cutting steady-state stand is only 64 cm for the mature even-aged stand, which is clearly less than the 85–90 cm obtained for the other initial stands (Table 6; Fig. 11). The difference is partly due to the fact that, since small trees are missing from the mature initial stand, the conversion period (200 years) is too short for reaching such a continuous distribution in which the largest trees would be 85–90 cm in dbh. In the mature even-aged stand, all trees of the initial stand need to be replaced by new ingrowth to remove the gap from the diameter distribution. All the other stands can utilize initial trees as a part of the ending distribution. The diagrams for the uneven-aged stand in Fig. 10 show that the largest remaining trees are smaller in the first conversion cutting, only about 55 cm, after which the maximum retained diameter is gradually increased to 89 cm. The basal areas of the steady-state post-cutting stands range from 18.6 m2 ha−1 (mature even-aged stand) to 30.7 m2 ha−1 (uneven-aged stand).

Fig. 10
figure 10

Optimal sequence of post-cutting diameter distributions for four initial stands when the ending steady-state distribution is optimized simultaneously with the conversion distributions

Full size image
Fig. 11
figure 11

Effect of initial stand structure on the steady-state diameter distribution at the end of 200-year conversion period. The investment-efficient distribution maximizes Eq. 2 with 1 % discount rate and 40-year cutting cycle

Full size image
Table 6 Characteristics calculated for the conversion of four initial stands into uneven-aged steady-state stand
Full size table

No trees were removed immediately except a negligible volume (4.5 m3 ha−1) from the mature initial stand (Fig. 12, 1 %). The second cutting (year 40) was conducted only in the even-aged mature stand and uneven-aged stand. Cuttings 3–6 were conducted in all four initial stands. The mean annual removed volume of the conversion period was 4.67–4.98 m3 ha−1 (Table 6). The mean annual volume increment during the conversion period ranged from 4.5 (mature even-aged stand) to 5.5 m3 ha−1 (young even-aged stand). The periodical removal of the ending steady-state stand is lower for the mature even-aged stands than for the other initial structures (Fig. 12, 1 % discount rate, C7).

Fig. 12
figure 12

Removals of the conversion cuttings for four initial stand structures with three different discount rates

Full size image

Effect of discount rate on optimal conversion

The same optimizations as described in the previous subsection were repeated with 2 and 3 % discount rates, to see the influence of discount rate on economically optimal forest management. For comparison, the investment-efficient distributions were also directly optimized, by maximizing Eq. 2.

The effect of discount rate on the temporal distribution of removals is very clear (Fig. 12): the higher is the discount rate, the earlier and heavier are the cuttings. With 1 % discount rate, almost nothing is cut in year 0 and little in year 40. With 3 % discount rate, the removals of cuttings 1 and 2 are high, whereas cuttings 3–5 are light and sometimes skipped. In the mature even-aged stand, most of the total removal of the whole conversion period (cuttings 1–6 together) is to be removed immediately. The total removal of the conversion period is the lower the higher is the discount rate.

With all discount rates, the steady-state distributions are different for different initial stands and they are also different than suggested by the investment-efficient optima. However, the effect of discount rate is stronger than the effect of initial stand or type of optimization. The main effect between the investment-efficient optima and the other ones is that the maximum post-cutting diameter is smaller in the investment-efficient optima (Fig. 11 shows the results for 1 % discount rate). The maximum retained diameter and the post-cutting basal area get smaller with increasing discount rate (Fig. 13). The optimal steady-state diameter distributions for 1 % discount rate are reasonably near those distributions that maximize wood production. Maximizing NPV with 2 % discount rate resulted in steady-state forests where wood production is 2.3–4 m3 ha−1 a−1, but with 3 % discount rate, the steady-state forest would produce only 0.7–1.5 m3 ha−1 a−1. Maximizing net present value with high discount rate is therefore detrimental to wood production.

Fig. 13
figure 13

Basal area of the investment-efficient stand and in the ending steady-state forest for four different initial stands

Full size image

Discussion

The Hyrcanian forests have multiple functions such as wood production, amenities, biodiversity conservation, and soil protection. Therefore, uneven-aged management is looked for in these multipurpose forests. So far, lack of tools for uneven-aged continuous cover management has delayed the start of scientific and efficient uneven-aged management, based on analytical numerical optimization. The current study was conducted to alleviate this problem. The study developed models that can be used in Hyrcania to simulate stand development in alternative uneven-aged management schedules. The model set also enables managers to find optimal stand structures for maximal sustained wood production or economic profit.

The models and calculations of this study suggest that the volume production of uneven-aged Hyrcanian hardwood forests is usually 2.2–7 m3 ha−1 a−1. This is well in line with earlier studies, which report growth rates of 2–8 m3 ha−1 (Farahmand 2012) or 2.2–8.3 m3 ha−1 (Lohmander and Mohammadi-Limaei 2008). Some authors suggest that uneven-aged management may be difficult in the Caspian hardwood forests (Heshmatol Vaezin et al. 2008), while other studies (Lohmander and Mohammadi-Limaei 2008) assume that uneven-aged management is a feasible option. Our models and analyses show that uneven-aged management is feasible and sustainable, although ingrowth is low, only 1–2 trees per hectare and year. Because the number of trees that are removed in a cutting is also low, 20–40 trees per hectare every 30–40 years, the ingrowth is sufficient to replace the removed trees. However, better ingrowth would have a significant positive effect on productivity and it would also affect the optimal stand structure. If ingrowth rate is doubled, sustainable volume production would increase by 50 % in F. orientalis forests and about 100 % in C. betulus forests. Therefore, one of the key factors for improved productivity of the uneven-aged Hyrcanian forests is better recruitment and ingrowth.

Rather long cutting intervals, 40 years, were used in most analyses to guarantee that a reasonable number of trees per hectare can be harvested in every cutting. Using a 30-year cutting cycle had improved the net present value only by 0.2–2.9 % when maximized with 2 % discount rate, as compared to the 40-year cycle. Wood production was also insensitive to the length of cutting cycle; the mean annual harvest of pure F. orientalis stands ranged from 4.7 to 5.1 m3 ha−1 a−1 when the yield was maximized with 10- to 70-year cutting cycles. Optimization results also justify the use of a long cutting cycle since some of the possible cuttings were skipped even with the 40-year interval. In forestry practice, the cutting cycle could and should be varied according to the entry cost of harvesting, using for instance 30 years in easily accessible places and longer than 40-year intervals on remote areas.

Although the volume growth of the Hyrcanian forests is rather low for a temperate region, the mean annual incomes from timber sales are substantial, usually 850–1,000 USD/ha in F. orientalis, due to very high value of timber. The exceptionally high price is due to monopolistic timber markets and the current political situation of Iran. Maximizing net present value with discount rates higher than 1 % would result in significant reductions in wood production, income, and stand density, compared to the current situation or management that maximizes wood production.

The weakest part of the model set is the ingrowth sub-model but also the survival and diameter increment models would benefit from larger empirical datasets. Because of the erratic nature of mortality, regeneration, and ingrowth, larger data sets or larger plot sizes are needed to discern the effect of stand structure on ingrowth and survival. Since no significant relationships were found in ingrowth modeling, a plausible model was manually adjusted to the data. No site factors were included in any of the models. Slope, elevation, and aspect were not significant predictors, most probably because the data were collected from a limited area. Soil variables were not assessed and they were therefore not available for modeling. Further improvement of the models would need additional plots measured from different sites and maybe larger plot sizes to reduce variation in observed ingrowth.

Of the models developed in this study, the height model was not used in the simulations and optimizations because tree height was not a predictor in the used volume models. However, if taper models or improved volume functions using both dbh and height as predictors are developed for the region in the future, there would be a need to calculate also the height development of trees. A height increment model would be a better option for this purpose than a static dbh–height model. Since trees are slender in dense stand, using tree height as the second predictor in volume models may have a significant effect of the results.

The economic calculations of this study showed that the optimal steady-state structure depends on initial stand structure and discount rate when the length of the conversion period is fixed. The first result agrees with those of Mitchie (1985). The main difference between initial stands was that the mature even-aged stand had a narrower diameter distribution than the other initial stands (Fig. 11). The dependence of steady-state structure on initial stand conditions is unfortunate for practical management since there is no single target distribution that should be pursued in all forests. This problem has been tried to solve by optimizing the investment-efficient stand structure, which does not depend on initial stand structure. Unfortunately, using this distribution as the target may be questionable since, according to some authors, the problem formulation lacks a sound theoretical basis (Getz and Haight 1989; Tahvonen 2011). However, the influence of initial stand on the steady-state distribution should disappear when longer conversion periods are used (Haight 1985; Tahvonen 2011).The influence of initial stand structure on the steady-sate diameter distribution was small compared to the effect of discount rate.

The study confirms earlier findings that investment-efficient optima differ from the ending stand structures of conversion problems (Haight 1985). The main systematic difference between the investment-efficient and the other distributions is that the maximum retained diameter is smaller in the investment-efficient optima. Using the investment-efficient distribution as the target distribution reduced net present value (calculated with 1 % discount rate) by 0.6 % (uneven-aged initial stand) to 5.6 % (mature even-aged initial stand) when compared to optimizing the ending distribution simultaneously with conversion cuttings. Also, Haight and Getz (1987) found that the use of fixed target distribution decreases net present value because a fixed target distribution is an additional constraint of the optimization problem. The investment-efficient stand would produce a NPV of 68,316 USD/ha (1 % discount rate), which is close to the NPVs of the uneven-aged and two-storied initial stands.

As found, e.g., by Chang and Gadow (2010), the amount of residual growing stock is very sensitive to discount rate. In pure F. orientalis forests, the post-cutting basal area of the steady-state stand should be about 20–30, 10–15, or 5 m2 ha−1, respectively, when the discount rate is 1, 2, or 3 % and the cutting cycle is 40 years. The maximum retained diameter is 85–90 cm with 1 % discount rate, 50–65 cm with 2 % rate, and 42–52 cm with 3 % rate. When wood production is maximized, the post-cutting basal area should be about 30–35 m2 ha−1 in F. orientalis forests and the maximum retained diameter should be 80–100 cm if cutting cycle is 30–40 years.

Management schedules that maximize net present value with higher discount rates (especially 3 % or more) are exploitive from the wood production point of view since they lead to very strong immediate cuttings and reduced wood production in the longer term. Taking into account the multiple functions of the forests, these schedules may not be regarded as acceptable. Although the used discount rate should depend on the capital markets, a good compromise between economic profitability, wood production, and environmental services provided by the forests would be to follow those schedules that maximize economic profitability with 1 % discount rate. Another option would be to use a higher rate—if the market rate is higher—and add constraints to the problem formulation that guarantee a continuous presence of large trees and a sufficient growing stock volume. Most probably, the results would be rather similar to those obtained in this study for 1 % discount rate.

This study optimized the management of pure, one-species stands. Optimizing the management of species mixtures would be straightforward: the single post-cutting distribution is replaced by a set of species-specific distributions (e.g., Pukkala et al. 2012). However, the models presented in this study may not describe reliably enough the potential species interactions of the Hyrcanian forests with a consequence that optimizations for mixed stands should wait for improved models (Liang et al. 2005). Species interactions are most likely to occur in ingrowth (Pukkala et al. 2013) since some species are more shade-tolerant than others and therefore may gradually replace shade-intolerant pioneer species. Also, tree survival may depend significantly on the species composition of the stand (Griess et al. 2012). The gradual species succession in the natural stand dynamics should be taken into account when developing improved models for the mixed hardwood forests of Hyrcania. Optimizing cutting intervals simultaneously with cutting intensity or amount of residual growing stock (Chang 1981; Chang and Gadow 2010) would also be straightforward; the number of years since previous cutting (or start) needs to be added to the set of variables that define each cutting event. However, some caution is required since the time step of the growth models is 10 years. The entry cost of cutting needs to be taken into account when cutting interval is optimized. Another improvement would be to integrate timber price variation in the optimization (Lohmander 2007; Pukkala and Kellomäki 2012).