Introduction

As trees in a stand grow, they occupy an increasing amount of space, meaning that the gaps between trees are eventually filled and individuals begin to interfere with each other’s access to resources, such as light, water, and nutrients (Silvertown and Doust 1993; Silvertown and Charlesworth 2001). Such interference or competition within the stand alters both the patterns of biomass allocation and the yield and reproductive output of plants, inducing density-dependent mortality or self-thinning (Harper 1977; Weiner et al. 1990; Weiner and Thomas 1992).

Yoda et al. (1963) found that once a stand had reached its maximum or full density, mortality occurred in such a way that

$$ m = K\rho^{ - \alpha } $$
(1)

where m is the mean dry mass per plant (g), ρ is the stand density (m−2) (i.e., the number of plants per unit area), K is a constant (g m−2α) that varies among species, and α has been reported in various studies as having a value of approximately 3/2 for a wide range of species (e.g., White 1980; Westoby 1984; Zeide 1987). Having reached its maximum density, a stand is considered to follow the 3/2 power law of self-thinning (Yoda et al. 1963; White and Harper 1970), otherwise known as the self-thinning rule (Westoby 1984), although controversy exists regarding its degree of generality (Weller 1987a, b; Zeide 1987; Lonsdale 1990).

Weller (1987a) argued that the slope of the self-thinning line can depart from –3/2, although many data sets are consistent with the form of Eq. 1. Furthermore, Weller (1987b) proposed an allometric model that predicts that the slope of the self-thinning line varies with plant shape and biomass density, reflecting the degree of biomass packing within a stand of plants (Duarte and Kalff 1987, 1990; Lillie et al. 1997; Scrosati 2000; Verkerk 2005). Plant shape and biomass density have been reported to have an important influence on the slope of the self-thinning line (Lonsdale and Watkinson 1983; Norberg 1988; Weller 1989); however, few of the reports that consider plant shape and biomass density are based on experimental data. Although Osawa and Allen (1993), Kikuzawa (1999), and Xue et al. (1999) demonstrated the relationship between biomass density and tree size (or stand density) based on observations of forest stands, their results have no theoretical basis and the obtained relationships vary among different forest stands.

Therefore, the aim of the present paper is to theoretically model changes in biomass density with stand development and to analyze mathematically the interrelationships among biomass density, plant shape, such as the ratio of stem height to diameter, and self-thinning using experimental data for dense populations of hinoki cypress (Chamaecyparis obtusa (Sieb. et Zucc.) Endl.) seedlings (Ogawa et al. 1989, 1990; Ogawa 2001, 2003, 2005a).

Materials and methods

Data sources

This study makes use of data for first- (Ogawa et al. 1989, 1990) and second-year (Ogawa 2001, 2003, 2005a) hinoki cypress [Chamaecyparis obtusa (Sieb. et Zucc.) Endl.] seedlings grown in the Midorigaoka Nursery of the Gifu District Forest Office at Minokamo, Gifu Prefecture, Central Japan. The following experiments were conducted for the first- and second-year seedlings.

For the first-year seedlings, seeds were sown in March 1984 and germination was largely complete by June 1984. The first sampling was made on April 1984 from a seedbed 1 m wide and 80 m long. Twelve samplings were made at semi-monthly intervals from May through October 1984, and five samplings were made at monthly intervals from November 1984 through March 1985. For the second-year seedlings, seeds were sown in March 1989, and seedlings were sampled monthly from April 1990 to March 1991, giving 12 sample measurements.

At each sampling time, 100 (for the first-year) or 50 seedlings (for the second-year) were randomly harvested from the seedbed. To avoid edge effects in the crowded population, no seedlings near the periphery of the seedbed (within approximately 15 cm of the edge) were sampled.

At each harvest, the seedling height and clear bole length of the sampled seedlings were measured to determine the crown depth. For only the second-year seedlings, the stem diameter at the crown base was also measured. The seedlings were then divided into leaves, stems, and roots. The aboveground parts (i.e., leaves and stems) were used for measurements. The leaves and stems of the sampled seedlings were oven-dried at 85°C for 24 h, transferred to desiccators, cooled, and then weighed.

To examine the change in seedling density over time, a 0.5 m × 2 m (for the first-year) or 0.5 m × 1 m (for the second-year) subplot was established within the seedbed. The initial number of live seedlings in the subplot was counted, and at each harvest period the dead seedlings were counted and removed.

Modeling of the changes in biomass density with stand development

Following Kira and Shidei (1967), the biomass density d (g m−3) is defined as

$$ d = {\frac{y}{h}} = {\frac{m\rho }{h}} $$
(2)

where y, h, m, and ρ are shoot biomass per unit area (g m−2), average seedling height (m), average shoot mass (g), and stand density (m−2), respectively. It is assumed that

$$ h \propto m^{\theta } $$
(3)

where the allometric exponent θ represents the degree of allocation of resources to height growth (Weller 1987b). If θ is equal to 1/3, growth is isotropic with increasing shoot mass because the dimensions of the units on both sides of Eq. 3 are equal to (length).

The following relationship is derived from Eqs. 2 and 3:

$$ d \propto {\frac{m\rho }{{m^{\theta } }}} = m^{1 - \theta } \rho $$
(4)

Consider the following cases of stand development and the associated expressions of biomass density d.

Case 1

Early stage of stand development during which self-thinning does not occur; that is, ρ = const.

In this case, Eq. 4 is rewritten as

$$ d \propto m^{1 - \theta } $$
(5)

because d is able to increase with stand development, θ < 1.

Case 2

Stage during which self-thinning occurs; that is, ρ = ρ(t) ≠ const.

In this case, Eq. 4 is rewritten as

$$ d \propto m^{1 - \theta } \rho (t) $$
(6)

In the special case that the 3/2 power law of self-thinning (Yoda et al. 1963) is held, we have \( m \propto \rho (t)^{{ - {\frac{3}{2}}}} ; \) therefore, d is expressed as

$$ d \propto \rho (t)^{{ - {\frac{1}{2}} + {\frac{3}{2}}\theta }} $$
(7)

For \( \theta = {\frac{1}{3}}, \) Eq. 7 dictates that d = const.

In the present analysis, the coefficients of curvilinear equations were determined by the least-square method on log-transformed data, whereas the coefficients of nonlinear equations were determined using a statistical analysis software package (KaleidaGraph Version 4.02, Synergy Software, Pennsylvania, USA).

Results

Application of the model

3/2 power law

When density-dependent mortality starts to occur, the trajectories of shoot biomass and stand density begin to curve to the left in Fig. 1a (Perry 1994); therefore, the following mathematical model (Ogawa 2005a, b) was applied to the time-trajectory shoot biomass y (g m−2) and stand density ρ (m−2) using logarithmic coordinates:

Fig. 1
figure 1

a Relationship between shoot biomass y and stand density ρ. Circles first-year seedlings, squares second-year seedlings. The regression curve is given by Eq. 8, where the coefficient of determination (r 2) is 0.869. b Relationship between mean seedling height h and mean shoot mass m. Symbols are the same as those in Fig. 1a. The linear line and smooth curve are given by Eqs. 3 (r 2 = 0.982) and 10 (r 2 = 0.988), respectively. c Relationship between shoot biomass density d and mean shoot mass m. Symbols are the same as those in Fig. 1a. The regression lines are given by Eq. 5 for the first-year seedlings and d = const for the second-year seedlings

Full size image
$$ y = K\rho^{ - \alpha + 1} \left( {1 - \left( {{\frac{\rho }{{\rho_{0} }}}} \right)^{n} } \right)^{l} $$
(8)

where K, ρ 0, α, n, and l are coefficients whose values were calculated for the second year as 80,711 g m−2α, 1504.1 m−2, 1.515, 0.0741, and 0.0105, respectively.

The y–ρ trajectory produced by Eq. 8, when plotted on a log y:log ρ graph, indicates that shoot biomass increases during the early stages of stand development but that no change in density occurs, as indicated by the vertical line at ρ = ρ0 (Case 1). The trajectory then begins to curve towards the left-hand side of the graph, indicating a reduction in stand density (Case 2). Following this decreasing trend, the time trajectory becomes asymptotic, approaching the following power law relationship at the stand’s maximum or full density:

$$ y = K\rho^{ - \alpha + 1} $$
(9)

Dividing both sides of Eq. 9 by ρ leads to the relationship between mean shoot mass and density described in Eq. 1. The value of 1.515, which is close to 3/2, can be regarded as evidence that the 3/2 power law of self-thinning is applicable in this case (Yoda et al. 1963).

Allometric relationship between mean seedling height and mean shoot mass

In the first year, when self-thinning did not occur (Case 1), the allometric relationship between mean seedling height h and mean shoot mass m in Eq. 3 could be fitted by a single straight line on logarithmic coordinates (Fig. 1b). In the second year, however, when self-thinning occurred (Case 2), the h–m relationship was approximated by the following equation:

$$ {\frac{1}{h}} = {\frac{1}{{a_{1} m^{{b_{1} }} }}} + {\frac{1}{{a_{2} m^{{b_{2} }} }}} $$
(10)

where a 1, b 1, a 2, and b 2 are coefficients whose values were estimated to be 17.11 \( {\text{m}}\,{\text{g}}^{{ - b_{1} }} , \) 3.954, 0.3529 \( {\text{m}}\,{\text{g}}^{{ - b_{2} }} , \) and 0.3249, the curve in Eq. 10 gradually approaches the two allometries of \( h = a_{1} m^{{ - b_{1} }} \) and \( h = a_{2} m^{{ - b_{2} }} \) for small and large values of m, respectively. The estimation of b 1 and b 2 values leads to the interpretation that during the period when small m values were recorded, when b 1 nearly equals to 4.0, the mean seedling height shows a rapid increase with mean shoot mass, whereas during period with large m values, when b 2 nearly equals to 1/3, growth is isotropic with increasing shoot mass. The assumption of h–m allometry in Eq. 3 is therefore reasonable for the latter part of the second year as well as the first year. The value of the allometric coefficient b 2 is close to 1/3 in Eq. 10, indicating that the value of θ in the h–m allometry of Eq. 3 approached 1/3 with ongoing stand development.

Relationship between biomass density and mean shoot mass

In the first year, when self-thinning did not occur (Case 1), the relationship between biomass density d (g m−3) and mean shoot mass m (g) was formulated according to Eq. 5 (Fig. 1c). In the second year, when self-thinning occurred (Case 2), the value of b 2 (Eq. 10) or θ (Eq. 3) in h–m allometry approached 1/3 with continued stand development, and the self-thinning exponent α in Eqs. 8 or 9 was close to 3/2. Consequently, biomass density d was constant irrespective of mean shoot mass m (Fig. 1c).

The combined results obtained for the first and second years indicate that biomass density increases according to a power function with mean shoot mass, reaching a constant level when self-thinning occurs. This trend implies the existence of an upper limit at which organic matter is fully packed within a given unit volume of forest (Kikuzawa 1999).

Leaf biomass density

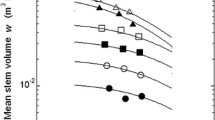
By dividing shoots into leaf and stem components, their changing biomass densities with ongoing stand development were examined for the second-year seedlings (Fig. 2a). The stem biomass density increased with increasing mean shoot mass (r = 0.9647, P < 0.001). This fact indicates the process of wood accumulation specific to woody species. In contrast, the leaf biomass density was largely constant (r = 0.06138, P = 0.801).

Fig. 2
figure 2

a Relationships between mean shoot mass and leaf (circles) and stem (squares) biomasses for second-year seedlings. b Relationship between leaf biomass on a crown depth basis and mean shoot mass for second-year seedlings. c Dependence of crown depth on mean shoot mass for second-year seedlings

Full size image

Because leaves are attached to that part of the stem above the crown base, the leaf biomass density on a crown depth basis (defined as the ratio of leaf mass to crown depth) is shown in relation to stand development (Fig. 2b). The leaf biomass density on a crown depth basis showed a significant increase with increasing mean shoot mass. Because the relationship between crown depth and mean shoot mass is asymptotic (Fig. 2c), it is concluded that the crowns of individuals overlap to a greater degree and aboveground competition is more intense with continued stand development.

Plant form

Figure 3a shows the allometric relationship between mean shoot mass m (g) and mean stem diameter D (cm) for the second-year seedlings. The allometry was fitted by a power function:

Fig. 3
figure 3

a Allometry of mean shoot mass m to mean stem diameter at the crown base D for second-year seedlings. The regression line represents Eq. 11 (r 2 = 0.966). b Relationship between the height:diameter ratio h/D and mean stem diameter at the crown base D for second-year seedlings. The smooth curve represents eq. 13

Full size image
$$ m = \eta D^{q} $$
(11)

where η and q are coefficients with values of 237.7 g cm−q and 3.086 for the stem diameter at the crown base, respectively, and 67.47 g cm−q and 2.446 for the stem diameter at 10% of seedling height.

Combining this allometry (Eq. 11) and the h–m relationship (Eq. 10) leads to an h–D relation of

$$ {\frac{1}{h}} = {\frac{1}{{a_{1} \eta^{{b_{1} }} D^{{b_{1} q}} }}} + {\frac{1}{{a_{2} \eta^{{b_{2} }} D^{{b_{2} q}} }}} $$
(12)

The following equation indicates that h/D (m cm−1), a simple measure of plant shape or slenderness index (Weiner and Thomas 1992), is dependent on the seedling size:

$$ {\frac{1}{h/D}} = {\frac{1}{{a_{1} \eta^{{b_{1} }} D^{{b_{1} q - 1}} }}} + {\frac{1}{{a_{2} \eta^{{b_{2} }} D^{{b_{2} q - 1}} }}} $$
(13)

As shown in Fig. 3b, the relationship between h/D and D in Eq. 13 describes an asymptotic or slightly convex curve, indicating that the seedlings became thinner to obtain more light in the face of overcrowding; however, seedling thickness was not as variable at the stage where the 3/2 power law of self-thinning applied. The degree of similarity in the shapes of different seedlings is therefore maintained under the 3/2 power law because the h/D ratio is largely constant.

Discussion

Because the 3/2 power law of Yoda et al. (1963) has been partially rejected on allometric grounds, several alternative reformulations have been proposed in which the thinning exponent is expressed as a function of species-specific allometric or geometric exponents that describe the relationships between commonly measured components (Mohler et al. 1978; White 1981; Weller 1987b; Newton and Smith 1990).

According to the reformulations proposed by Mohler et al. (1978) and White (1981), the self-thinning exponent α in Eq. 1 is derived (on the assumption of w ∝ D 2 h) as (2 + γ)/2β, where γ and β are species-specific allometric exponents for the relationships between tree height h and stem diameter at breast height D (h ∝ D γ) and between crown basal area C d and D (C d  ∝ D β), respectively. If γ and β are assumed to be equal to 1.0, the value of (2 + γ)/2β becomes 3/2, indicating the 3/2 power law of self-thinning. In the present analysis, because the h/D ratio is asymptotically constant at the latter growth stage of the second year (Fig. 3b), it is considered that the 3/2 power law applied at this stage.

Based on a reformulation of 3/2 power law by Yoda et al. (1963), Weller (1987b) represented the allometric relationships between mean aboveground mass m and mean plant height h, biomass density in occupied space d, or radius of the area occupied by a plant R, as h ∝ m θ, d ∝ m δ, and R ∝ m ϕ, respectively, where θ, δ, and ϕ are parameters; the author formulated the relationship among parameters for self-thinning populations as ϕ = (1–θ–δ)/2. Assuming the 3/2 power law of self-thinning, ϕ = 1/3 because \( m = K\rho^{ - \alpha } = K\rho^{{ - {\frac{1}{2\phi }}}} , \) indicating that δ = 0 when ϕ = 1/3; that is, d = const, meaning in turn that the present model in Case 2 is consistent with Weller’s model.

Newton and Smith (1990) proposed a geometric derivation for excurrent coniferous tree species in which the self-thinning exponent α in Eq. 1 is given as (ε + 1)/ζ based on the assumption that w ∝ ν (White 1981). ε and ζ are the stem form and crown form exponents, respectively, raging in value from 1.0 (paraboloid) to 2.0 (cone). If the values of ε and ζ are equal to 2.0, α becomes 3/2, indicating the 3/2 power law of self-thinning. Since ν ∝ h ε+1, ε = 2.0 leads to h ∝ w 1/3 because ν ∝ h 3.0 ∝ w. In the present analysis, because the value of θ in the equation h ∝ w θ is approximately 1/3 at the latter growth stage of the second year (Eq. 10; Fig. 2), it is considered that the 3/2 power law applied at this stage.

The importance of the self-thinning rule in forest management means that further analyses are required to determine if these reformulated rules provide viable alternatives. Because the above reformulation of the self-thinning exponent in mature forest is applied to the present seedling population, the results obtained in this study provide guidance in forest management practices and the modeling of growth and yield. Ogawa (2008) also demonstrated constant leaf biomass density in mature forest stands after canopy closure. Constant leaf biomass density might therefore be a common feature of both seedling (Fig. 2a) and forest stands irrespective of differences in stand stage. Although the tree slenderness h/D was almost asymptotically constant at the latter growth stage in the second-year seedlings (Fig. 3b), the value of h/D will become smaller in older stands, because tree height is considered to be asymptotic with respect to tree age due to hydraulic and other limits (Ryan and Yoder 1997). Therefore, if the constancy of h/D is not realized, the 3/2 power law of self-thinning cannot be held in the present analysis. Recently, the value of self-thinning exponent (α) is theoretically considered to be 4/3 from a resource-allocation basis in the older trees (West et al. 1997; Enquist et al. 1998). The present modeling implies that one of the reasons why the 3/2 power law from a geometric basis (Yoda et al. 1963; Hutchings 1983) has been rejected depends on whether or not the h/D value is constant in older trees.