Guided Waves in the Multilayered One-Dimensional Hexagonal Quasi-crystal Plates

Abstract

Guided waves in the multilayered one-dimensional quasi-crystal plates are, respectively, investigated in the context of the Bak and elasto-hydrodynamic models. Dispersion curves and phonon and phason displacements are calculated using the Legendre polynomial method. Wave characteristics in the context of these two models are analyzed in detail. Results show that the phonon–phason coupling effects on the first two layers are the same at low frequencies; but, they are more significant on the first layer than those on the second layer at high frequencies. These obtained results lay the theoretical basis of guided-wave nondestructive test on multilayered quasi-crystal plates.

1 Introduction

As a novel kind of solid matter, quasi-crystals (QCs) are of long-range orientational order and symmetries that are prohibitive in crystal matters  [1], such as fivefold, tenfold and twelvefold rotational symmetries. Owing to their unique structures, quasi-crystals own a lot of advantageous performances, such as low adhesion, thermal conductivity and friction coefficient, and high abrasion resistance and resistivity  [2]. Accordingly, quasi-crystals can be utilized as coatings or thin films in engineering  [3, 4].

Multilayered structures are commonly used in engineering to take advantage of the superior performances of each layer. Numerous investigations on mechanical properties of multilayered crystal structures have been conducted  [5,6,7]. Recently, mechanical investigations on multilayered quasi-crystal structures have also received increasing attention  [8,9,10]. However, they were mainly focused on the statics of quasi-crystals because the dynamic deformation of quasi-crystals is extremely complicated owing to the coupled phonon and phason fields. There are two different dynamic models for the dynamic deformation. The Bak model  [11] assumed that the phason field is similar to the phonon field denoted by wave propagation. The elasto-hydrodynamic model presented by Lubensky et al.  [12] considered phason modes to be diffusive with a large diffusive time. These two models are, respectively, used to investigate dynamics of quasi-crystal structures, such as conservation laws  [13], free vibration and harmonic response  [14, 15], bending analyses  [16], wave propagation  [17] and other dynamic problems  [18, 19]. From the above review, rare references of guided waves in the multilayered quasi-crystal structures are available.

Due to the limit of manufacturing techniques and processes, the bonding of the multilayered quasi-crystal plate would cause micro-cracks in joints. Therefore, to ensure the safety of structures, it is necessary to develop an efficient nondestructive testing method. The guided-wave nondestructive test technology has been successfully applied to a lot of crystal structures  [20], which also has promising applications on quasi-crystal structures. However, the prerequisite for using it is to understand guided wave characteristics in detail. Therefore, guided waves in the multilayered one-dimensional (1D) hexagonal quasi-crystal plates in the context of Bak and elasto-hydrodynamic models are, respectively, investigated. The traction-free boundary condition is assumed.

2 Mathematics and Formulation

An infinite horizontally N-layered quasi-crystal plate with a total thickness of $h_{N}$ is illustrated in Fig. 1. The horizontal (x, y)-plane is placed on the top surface, and it occupies the region $0\le z\le h_{N}$ in the positive z-direction.

Fig. 1

Schematic diagram of an infinite multilayered quasi-crystal plate

Combining the Bak’s and elasto-hydrodynamic models, the dynamic governing equations without body forces are as follows  [21]:

$$\begin{aligned} T_{ij,j} =\rho \ddot{{u}}_{i} , {H_{ij,j} =\kappa \dot{{w}}_{i} +\rho _{p} \ddot{{w}}_{i}} \end{aligned}$$

(1)

where $\rho$ is the density; $u_{i}$ and $w_{i}$ represent displacement components; $T_{ij}$ and $H_{ij}$ are phonon and phason stress tensors, respectively; $\kappa =1/\varGamma _{w}$ is the friction coefficient; and $\rho _{p}$ is the effective phason mass density. If $\rho _{p}=0$, the elasto-hydrodynamic model is recovered. If $\kappa =0$ and $\rho _{p}=\rho$, the Bak’s model is recovered.

The generalized relationships of strain–displacement are as follows:

$$\begin{aligned} \varepsilon _{ij} =\frac{1}{2}\left( {\frac{\partial u_{i} }{\partial x_{j} }+\frac{\partial u_{j} }{\partial x_{i} }} \right) , \qquad {w_{ij} =\frac{\partial w_{i} }{\partial x_{j} }} \end{aligned}$$

(2)

where $\varepsilon _{ij}$ and $w_{ij}$ are phonon and phason strain tensors, respectively.

For the multilayered quasi-crystal plate, its initial boundary conditions are required: (a) the normal stresses are 0 at the top and bottom surfaces $(T_{zz} =T_{xz} =T_{yz} =H_{zz} =0)$; (b) the normal stresses and displacements are continuous at the interfaces. To deal with it, a window function is introduced.

$$\begin{aligned} I_{h_{0} ,h_{N} } (z)=\hbox {Heaviside}[h_{0} ]-\hbox {Heaviside}[h_{N} ]=\left\{ {\begin{array}{ll} 1,&{} h_{0} \le z\le h_{N} \\ 0,&{} \hbox {elsewhere} \\ \end{array}} \right. \end{aligned}$$

(3)

where $h_{\mathrm {0}}=0$.

Material parameters of the N-layered quasi-crystal plates are written as:

$$\begin{aligned} C_{ij}^{\left( N \right) }= & {} \sum \limits _{n=1}^N {C_{ij}^{\left( n \right) } I_{h_{n-1} ,h_{n} } },\; K_{i}^{\left( N \right) } =\sum \limits _{n=1}^N {K_{i}^{\left( n \right) } I_{h_{n-1} ,h_{n} } },\; R_{i}^{\left( N \right) } =\sum \limits _{n=1}^N {R_{i}^{\left( n \right) } I_{h_{n-1} ,h_{n} } } \nonumber \\ \rho ^{\left( N \right) }= & {} \sum \limits _{n=1}^N {\rho ^{\left( n \right) }I_{h_{n-1} ,h_{n} } },\; \kappa ^{\left( N \right) }=\sum \limits _{n=1}^N {\kappa ^{\left( n \right) }I_{h_{n-1} ,h_{n} }} \end{aligned}$$

(4)

where $C_{ij}^{\left( n \right) } , K_{i}^{\left( n \right) } , R_{i}^{\left( n \right) } , \rho ^{\left( n \right) }$ and $\kappa ^{\left( n \right) }$ are, respectively, elastic parameters in the phonon and phason fields, phonon–phason coupling coefficients, density and friction coefficient of the nth layer.

For the 1D hexagonal quasi-crystal plate, only one direction is quasi-periodic. If the quasi-periodic axis is consistent with the x-axis, it is named as the x-direction plate. Similarly, there are also the y-direction and z-direction plates. Guided waves in these three cases are investigated in detail, respectively.

(1) The z-direction plate

For the z-direction plate, only the phason displacement in the z-direction is not 0. Therefore, the displacements of guided wave propagating in the x-direction are as follows:

$$\begin{aligned} u_{x} =U(z)\hbox {e}^{\mathrm{i}kx-\mathrm{i}wt},u_{y} =V(z)\hbox {e}^{\mathrm{i}kx-\mathrm{i}wt},u_{z} =W(z)\hbox {e}^{\mathrm{i}kx-\mathrm{i}wt},w_{z} =\gamma (z)\hbox {e}^{\mathrm{i}kx-\mathrm{i}wt} \end{aligned}$$

(5)

where U(z), V(z), W(z) and $\gamma (z)$ represent phonon displacement amplitudes in the x-, y- and z-direction and the phason displacement amplitude, respectively.

The constitutive equations  [22] are as follows:

$$\begin{aligned} T_{xx}= & {} C_{11}^{\left( N \right) } \varepsilon _{xx} +C_{12}^{\left( N \right) } \varepsilon _{yy} +C_{13}^{\left( N \right) } \varepsilon _{zz} +R_{1}^{\left( N \right) } w_{zz}\nonumber \\ T_{yy}= & {} C_{12}^{\left( N \right) } \varepsilon _{xx} +C_{11}^{\left( N \right) } \varepsilon _{yy} +C_{13}^{\left( N \right) } \varepsilon _{zz} +R_{1}^{\left( N \right) } w_{zz} \nonumber \\ T_{zz}= & {} C_{13}^{\left( N \right) } \varepsilon _{xx} +C_{13}^{\left( N \right) } \varepsilon _{yy} +C_{33}^{\left( N \right) } \varepsilon _{zz} +R_{2}^{\left( N \right) } w_{zz} \nonumber \\ T_{yz}= & {} T_{zy} =2C_{44}^{\left( N \right) } \varepsilon _{yz} +R_{3}^{\left( N \right) } w_{zy} \nonumber \\ T_{xz}= & {} T_{zx} =2C_{55}^{\left( N \right) } \varepsilon _{xz} +R_{3}^{\left( N \right) } w_{zx} \nonumber \\ T_{xy}= & {} T_{yx} =2C_{66}^{\left( N \right) } \varepsilon _{xy} \end{aligned}$$

(6a)

$$\begin{aligned} H_{zz}= & {} R_{1}^{\left( N \right) } \varepsilon _{xx} +R_{1}^{\left( N \right) } \varepsilon _{yy} +R_{2}^{\left( N \right) } \varepsilon _{zz} +K_{1}^{\left( N \right) } w_{zz} \nonumber \\ H_{zx}= & {} 2R_{3}^{\left( N \right) } \varepsilon _{xz} +K_{2}^{\left( N \right) } w_{zx} \nonumber \\ H_{zy}= & {} 2R_{3}^{\left( N \right) } \varepsilon _{yz} +K_{2}^{\left( N \right) } w_{zx} \end{aligned}$$

(6b)

Submitting Eqs. (2)–(6) into Eq. (1), the differential equations of wave motion are obtained:

$$\begin{aligned}&-C_{11}^{\left( N \right) } k^{2}U+C_{55}^{\left( N \right) } {U}''+(C_{13}^{\left( N \right) } +C_{55}^{\left( N \right) } )\hbox {i}k{W}'+(R_{1}^{\left( N \right) } +R_{3}^{\left( N \right) } )\hbox {i}k{\gamma }' \nonumber \\&\quad +\left( {C_{55}^{\left( N \right) } } \right) ^{\prime }{U}'+\left( {C_{55}^{\left( N \right) } } \right) ^{\prime }\hbox {i}kW+\left( {R_{3}^{\left( N \right) } } \right) ^{\prime }\hbox {i}k\gamma ]\}=-\rho ^{\left( N \right) }\omega ^{2}U \end{aligned}$$

(7a)

$$\begin{aligned}&-C_{66}^{\left( N \right) } k^{2}V+C_{44}^{\left( N \right) } {V}''+\left( {C_{44}^{\left( N \right) } } \right) ^{\prime }{V}'=-\rho ^{\left( N \right) }\omega ^{2}V \end{aligned}$$

(7b)

$$\begin{aligned}&(C_{13}^{\left( N \right) } +C_{55}^{\left( N \right) } )\hbox {i}k{U}'-C_{55}^{\left( N \right) } k^{2}W+C_{33}^{\left( N \right) } {W}''-R_{3}^{\left( N \right) } k^{2}\gamma +R_{2}^{\left( N \right) } {\gamma }'' \nonumber \\&\quad +\left( {C_{13}^{\left( N \right) } } \right) ^{\prime }\hbox {i}kU+\left( {C_{33}^{\left( N \right) } } \right) ^{\prime }{W}'+\left( {R_{2}^{\left( N \right) } } \right) ^{\prime }{\gamma }'=-\rho ^{\left( N \right) }\omega ^{2}W \end{aligned}$$

(7c)

$$\begin{aligned}&(R_{1}^{\left( N \right) } +R_{3}^{\left( N \right) } )\hbox {i}k{U}'-R_{3}^{\left( N \right) } k^{2}W+R_{2}^{\left( N \right) } {W}''-K_{2}^{\left( N \right) } k^{2}\gamma +K_{1}^{\left( N \right) } {\gamma }'' \nonumber \\&\quad +\left( {R_{1}^{\left( N \right) } } \right) ^{\prime }\hbox {i}kU+\left( {R_{2}^{\left( N \right) } } \right) ^{\prime }{W}'+\left( {K_{1}^{\left( N \right) } } \right) ^{\prime }{\gamma }'=-\rho _{p}^{\left( N \right) } \omega ^{2}\gamma -\kappa ^{\left( N \right) }\hbox {i}\omega \gamma \end{aligned}$$

(7d)

where (${}^{\prime }$) denotes the derivation with respect to z. SH waves are governed by Eq. (9b) that is independent of the phason field. So, SH waves are not investigated in this case.

Subsequently, the phonon and phason displacements of each layer are expanded into the Legendre orthogonal polynomial series.

For the first quasi-crystal layer:

$$\begin{aligned} u_{a}^{1} =\sum \limits _{m=0}^\infty {p_{m}^{a,1} Q_{m}^{1} (z)\exp (\hbox {i}kx-\hbox {i}\omega t)} ,\quad w_{z}^{1} =\sum \limits _{m=0}^\infty {r_{m}^{1} Q_{m}^{1} (z)\exp (\hbox {i}kx-\hbox {i}\omega t)} \end{aligned}$$

(8)

where

$$\begin{aligned} Q_{m}^{1} (z)= & {} \sqrt{\frac{2m+1}{h_{1} -h_{0} }} P_{m} \left( \frac{2z-(h_{1} -h_{0} )}{h_{1} -h_{0} }\right) \\ u_{a}^{1} (z=h_{1} )= & {} u_{a}^{1,h_{1} } =\sum \limits _{m=0}^\infty {p_{m}^{a,1} Q_{m}^{1} (z=h_{1} )\exp (\hbox {i}kx-\hbox {i}\omega t)} \\ w_{z}^{1} (z=h_{1} )= & {} w_{z}^{1,h_{1} } = \sum \limits _{m=0}^\infty {r_{m}^{1} Q_{m}^{1} (z=h_{1} )\exp (\hbox {i}kx-\hbox {i}\omega t)} \end{aligned}$$

where $p_{m}^{a,n} (n=1,2)$, $r_{m}^{1}$ denote expansion coefficients, $P_{m}$ represents the mth Legendre polynomial, and $u_{a}$ are $u_{x}$ and $u_{z}$, respectively.

For the second quasi-crystal layer:

$$\begin{aligned} u_{a}^{2}= & {} u_{a}^{1,h_{1} } +(z-h_{1} )\sum \limits _{m=0}^\infty {p_{m}^{a,2} Q_{m}^{2} (z)\exp (\hbox {i}kx-\hbox {i}\omega t)} \nonumber \\ w_{z}^{2}= & {} w_{z}^{1,h_{1} } +(z-h_{1} )\sum \limits _{m=0}^\infty {r_{m}^{2} Q_{m}^{2} (z)\exp (\hbox {i}kx-\hbox {i}\omega t)} \end{aligned}$$

(9)

where

$$\begin{aligned} Q_{m}^{2} (z)= & {} \sqrt{\frac{2m+1}{h_{2} -h_{1} }} P_{m} \left( \frac{2z-(h_{2} -h_{1} )}{h_{2} -h_{1} }\right) \\ u_{a}^{2} (z=h_{2} )= & {} u_{a}^{2,h_{2} } =u_{a}^{1,h_{1} } +(z-h_{1} )\sum \limits _{m=0}^\infty {p_{m}^{a,2} Q_{m}^{2} (z=h_{2} )\exp (\hbox {i}kx-\hbox {i}\omega t)} \\ w_{z}^{2} (z=h_{2} )= & {} w_{z}^{2,h_{2} } =w_{z}^{1,h_{1} } +(z-h_{1} )\sum \limits _{m=0}^\infty {r_{m}^{2} Q_{m}^{2} (z=h_{2} )\exp (\hbox {i}kx-\hbox {i}\omega t)} \end{aligned}$$

For the Nth quasi-crystal layer:

$$\begin{aligned} u_{a}^{N}= & {} u_{a}^{N-1,h_{N} } +(z-h_{N} )\sum \limits _{m=0}^\infty {p_{m}^{a,N} Q_{m}^{N} (z)\exp (\hbox {i}kx-\hbox {i}\omega t)} \nonumber \\ w_{z}^{N}= & {} w_{z}^{N-1,h_{N} } +(z-h_{N} )\sum \limits _{m=0}^\infty {r_{m}^{N} Q_{m}^{N} (z)\exp (\hbox {i}kx-\hbox {i}\omega t)} \end{aligned}$$

(10)

where

$$\begin{aligned} Q_{m}^{N} (z)= & {} \sqrt{\frac{2m+1}{h_{N} -h_{N-1} }} P_{m} \left( \frac{2z-(h_{N} -h_{N-1} )}{h_{N} -h_{N-1} }\right) \\ u_{a}^{N} (z=h_{N} )= & {} u_{a}^{N,h_{N} } =u_{a}^{N-1,h_{N} } +(z-h_{N} )\sum \limits _{m=0}^\infty {p_{m}^{a,N} Q_{m}^{N} (z=h_{N} )\exp (\hbox {i}kx-\hbox {i}\omega t)} \\ w_{z}^{N} (z=h_{N} )= & {} w_{z}^{N,h_{N} } =w_{z}^{N-1,h_{N} } +(z-h_{N} )\sum \limits _{m=0}^\infty {r_{m}^{N} Q_{m}^{N} (z=h_{N} )\exp (\hbox {i}kx-\hbox {i}\omega t)} \end{aligned}$$

Submitting Eqs. (8)–(10) into Eq. (7), multiplying the obtained equations by $Q_{j}^{1} (z),Q_{j}^{2} (z)\cdots Q_{j}^{N} (z)$ with j running from 0 to M, and integrating over z from $h_{\mathrm {1}}$ to $h_{N}$, the following equation is deduced:

$$\begin{aligned} \left[ {{\begin{array}{*{20}c} {{ }^{n}A_{11}^{m,j} } &{} {{ }^{n}A_{12}^{m,j} } &{} {{ }^{n}A_{13}^{m,j} } \\ {{ }^{n}A_{21}^{m,j} } &{} {{ }^{n}A_{22}^{m,j} } &{} {{ }^{n}A_{23}^{m,j} } \\ {{ }^{n}A_{31}^{m,j} } &{} {{ }^{n}A_{32}^{m,j} } &{} {{ }^{n}A_{33}^{m,j} } \\ \end{array} }} \right] \left\{ {{\begin{array}{*{20}c} {p_{m,j}^{1} } \\ {p_{m,j}^{2} } \\ {r_{m,j} } \\ \end{array} }} \right\} =-\omega ^{2}\left[ {{\begin{array}{*{20}c} {{ }^{n}M_{m,j} } &{} 0 &{} 0 \\ 0 &{} {{ }^{n}M_{m,j} } &{} 0 \\ 0 &{} 0 &{} {{ }^{n}M_{m,j} } \\ \end{array} }} \right] \left\{ {{\begin{array}{*{20}c} {p_{m,j}^{1} } \\ {p_{m,j}^{2} } \\ {r_{m,j} } \\ \end{array} }} \right\} \end{aligned}$$

(11)

where ${ }^{n}A_{q,s}^{m,j} (q=1,2,3{\begin{array}{*{20}c} &{} {\hbox {and}} &{} {s=1,2,3} \\ \end{array} })$ and ${ }^{n}M_{m,j}$ are matrix elements that can be obtained from Eq. (7). Therefore, it is transformed into an eigenvalue problem. Angular frequencies are square roots of eigenvalues. Phonon and phason displacement components can be calculated from eigenvectors.

(2) The y-direction plate

The phonon displacements are the same as those in Eq. (5), and only the phason displacement in the y-direction is not 0, which is as follows:

$$\begin{aligned} w_{y} =\beta (z)\mathrm{e}^{\mathrm{i}kx-\mathrm{i}\omega t} \end{aligned}$$

(12)

where $\beta (z)$ represents the phason displacement amplitude.

The constitutive equations are as follows:

$$\begin{aligned} T_{zz}= & {} C_{11}^{\left( N \right) } \varepsilon _{zz} +C_{12}^{\left( N \right) } \varepsilon _{xx} +C_{13}^{\left( N \right) } \varepsilon _{yy} +R_{1}^{\left( N \right) } w_{yy} \nonumber \\ T_{xx}= & {} C_{12}^{\left( N \right) } \varepsilon _{zz} +C_{22}^{\left( N \right) } \varepsilon _{xx} +C_{13}^{\left( N \right) } \varepsilon _{yy} +R_{1}^{\left( N \right) } w_{yy} \nonumber \\ T_{yy}= & {} C_{13}^{\left( N \right) } \varepsilon _{zz} +C_{13}^{\left( N \right) } \varepsilon _{xx} +C_{33}^{\left( N \right) } \varepsilon _{yy} +R_{2}^{\left( N \right) } w_{yy} \nonumber \\ T_{xz}= & {} T_{zx} =2C_{66}^{\left( N \right) } \varepsilon _{xz} \nonumber \\ T_{yx}= & {} T_{xy} =2C_{44}^{\left( N \right) } \varepsilon _{yx} +R_{3}^{\left( N \right) } w_{yx} \nonumber \\ T_{yz}= & {} T_{zy} =2C_{44}^{\left( N \right) } \varepsilon _{yz} +R_{3}^{\left( N \right) } w_{yz} \end{aligned}$$

(13a)

$$\begin{aligned} H_{yy}= & {} R_{2}^{\left( N \right) } \varepsilon _{yy} +R_{1}^{\left( N \right) } \varepsilon _{zz} +R_{1}^{\left( N \right) } \varepsilon _{xx} +K_{1}^{\left( N \right) } w_{yy} \nonumber \\ H_{yx}= & {} 2R_{3}^{\left( N \right) } \varepsilon _{yx} +K_{2}^{\left( N \right) } w_{yx} \nonumber \\ H_{yz}= & {} 2R_{3}^{\left( N \right) } \varepsilon _{yz} +K_{2}^{\left( N \right) } w_{yz} \end{aligned}$$

(13b)

Submitting Eqs. (12)–(13) and Eq. (2) into Eq. (1), the differential equations of wave motion are obtained:

$$\begin{aligned}&-C_{22}^{\left( N \right) } k^{2}U+C_{66}^{\left( N \right) } {U}''+(C_{12}^{\left( N \right) } +C_{66}^{\left( N \right) } )\hbox {i}k{W}'+\left( {C_{66}^{\left( N \right) } } \right) ^{\prime }{U}'+\left( {C_{66}^{\left( N \right) } } \right) ^{\prime }\hbox {i}kW=-\rho ^{\left( N \right) }\omega ^{2}U\end{aligned}$$

(14a)

$$\begin{aligned}&-C_{44}^{\left( N \right) } k^{2}V+C_{44}^{\left( N \right) } {V}''-R_{3}^{\left( N \right) } k^{2}\beta +R_{3}^{\left( N \right) } {\beta }''+\left( {C_{44}^{\left( N \right) } } \right) ^{\prime }{V}'+\left( {R_{3}^{\left( N \right) } } \right) ^{\prime }{\beta }'=-\rho ^{\left( N \right) }\omega ^{2}V \end{aligned}$$

(14b)

$$\begin{aligned}&(C_{12}^{\left( N \right) } +C_{66}^{\left( N \right) } )\mathrm{i}k{U}'-C_{66}^{\left( N \right) } k^{2}W+C_{11}^{\left( N \right) } {W}''+\left( {C_{12}^{\left( N \right) } } \right) ^{\prime }\hbox {i}kU+\left( {C_{11}^{\left( N \right) } } \right) ^{\prime }{W}'=-\rho ^{\left( N \right) }\omega ^{2}W \end{aligned}$$

(14c)

$$\begin{aligned}&-R_{3}^{\left( N \right) } k^{2}V+R_{3}^{\left( N \right) } {V}''-K_{2}^{\left( N \right) } k^{2}\beta +K_{2}^{\left( N \right) } {\beta }''+\left( {R_{3}^{\left( N \right) } } \right) ^{\prime }{V}'+\left( {K_{2}^{\left( N \right) } } \right) ^{\prime }{\beta }'=-\rho _{p}^{\left( N \right) } \omega ^{2}\beta -\kappa ^{\left( N \right) }\hbox {i}\omega \beta \nonumber \\ \end{aligned}$$

(14d)

The Lamb waves are governed by Eqs. (16a) and (16b) that are independent of the phason field. Therefore, Lamb waves are not investigated in this case.

(3) The x-direction plate

The phonon displacements are also the same as those in Eq. (5), and the phason displacement in the x-direction is not 0, which is:

$$\begin{aligned} w_{x} =\alpha (z)\mathrm{e}^{\mathrm{i}kx-\mathrm{i}\omega t} \end{aligned}$$

(15)

where $\alpha (z)$ represents the phason displacement amplitude.

The constitutive equations are as follows:

$$\begin{aligned} T_{yy}= & {} C_{11}^{\left( N \right) } \varepsilon _{yy} +C_{12}^{\left( N \right) } \varepsilon _{zz} +C_{13}^{\left( N \right) } \varepsilon _{xx} +R_{1}^{\left( N \right) } w_{xx} \nonumber \\ T_{zz}= & {} C_{12}^{\left( N \right) } \varepsilon _{yy} +C_{22}^{\left( N \right) } \varepsilon _{zz} +C_{13}^{\left( N \right) } \varepsilon _{xx} +R_{1}^{\left( N \right) } w_{xx} \nonumber \\ T_{xx}= & {} C_{13}^{\left( N \right) } \varepsilon _{yy} +C_{13}^{\left( N \right) } \varepsilon _{zz} +C_{33}^{\left( N \right) } \varepsilon _{xx} +R_{2}^{\left( N \right) } w_{xx} \nonumber \\ T_{yz}= & {} T_{zy} =2C_{66}^{\left( N \right) } \varepsilon _{yz} \nonumber \\ T_{xz}= & {} T_{zx} =2C_{44}^{\left( N \right) } \varepsilon _{xz} +R_{3}^{\left( N \right) } w_{xz} \nonumber \\ T_{xy}= & {} T_{yx} =2C_{44}^{\left( N \right) } \varepsilon _{xy} +R_{3}^{\left( N \right) } w_{xy} \end{aligned}$$

(16a)

$$\begin{aligned} H_{xx}= & {} R_{2}^{\left( N \right) } \varepsilon _{xx} +R_{1}^{\left( N \right) } \varepsilon _{yy} +R_{1}^{\left( N \right) } \varepsilon _{zz} +K_{1}^{\left( N \right) } w_{xx} \nonumber \\ H_{xz}= & {} 2R_{3}^{\left( N \right) } \varepsilon _{xz} +K_{2}^{\left( N \right) } w_{xz} \nonumber \\ H_{xy}= & {} 2R_{3}^{\left( N \right) } \varepsilon _{xy} +K_{2}^{\left( N \right) } w_{xy} \end{aligned}$$

(16b)

Submitting Eqs. (15)–(16) and Eq. (2) into Eq. (1), the differential equations of wave motion are obtained:

$$\begin{aligned}&-C_{33}^{\left( N \right) } k^{2}U+C_{44}^{\left( N \right) } {U}''+(C_{13}^{\left( N \right) } +C_{44}^{\left( N \right) } )\hbox {i}k{W}'-R_{2}^{\left( N \right) } k^{2}\alpha +R_{3}^{\left( N \right) } {\alpha }'' \nonumber \\&\qquad +\left( {C_{44}^{\left( N \right) } } \right) ^{\prime }{U}'+\left( {C_{44}^{\left( N \right) } } \right) ^{\prime }\hbox {i}kW+\left( {R_{3}^{\left( N \right) } } \right) ^{\prime }{\alpha }'=-\rho ^{\left( N \right) }\omega ^{2}U \end{aligned}$$

(17a)

$$\begin{aligned}&-C_{66}^{\left( N \right) } k^{2}V+C_{44}^{\left( N \right) } {V}''+\left( {C_{44}^{\left( N \right) } } \right) ^{\prime }{V}'=-\rho ^{\left( N \right) }\omega ^{2}V \end{aligned}$$

(17b)

$$\begin{aligned}&(C_{13}^{\left( N \right) } +C_{44}^{\left( N \right) } )\hbox {i}k{U}'-C_{44}^{\left( N \right) } k^{2}W+C_{22}^{\left( N \right) } {W}''+(R_{3}^{\left( N \right) } +R_{1}^{\left( N \right) } )\hbox {i}k{\alpha }' \nonumber \\&\qquad +\left( {C_{13}^{\left( N \right) } } \right) ^{\prime }\hbox {i}kU+\left( {C_{22}^{\left( N \right) } } \right) ^{\prime }{W}'+\left( {R_{1}^{\left( N \right) } } \right) ^{\prime }\hbox {i}k\alpha =-\rho ^{\left( N \right) }\omega ^{2}W \end{aligned}$$

(17c)

$$\begin{aligned}&(R_{1}^{\left( N \right) } +R_{3}^{\left( N \right) } )\hbox {i}k{W}'-R_{2}^{\left( N \right) } k^{2}U+R_{3}^{\left( N \right) } {U}''-K_{1}^{\left( N \right) } k^{2}\alpha +K_{2}^{\left( N \right) } {\alpha }'' \nonumber \\&\qquad +\left( {R_{3}^{\left( N \right) } } \right) ^{\prime }\hbox {i}kW+\left( {R_{3}^{\left( N \right) } } \right) ^{\prime }{U}'+\left( {K_{2}^{\left( N \right) } } \right) ^{\prime }{\alpha }'=-\rho ^{\left( N \right) } \omega ^{2}\alpha \end{aligned}$$

(17d)

The SH waves are governed by Eq. (17b) that is independent of the phason field. Therefore, SH waves are not investigated in this case.

3 Numerical Results

In this section, dispersion curves and phonon and phason displacements are calculated using the software “Mathematica”. For the multilayered 1D quasi-crystal plates, they are composed of two kinds of quasi-crystal materials (simplified as QC1 and QC2), whose material parameters are listed in Table 1. As a special case, the dissipative kinetic coefficients $\varGamma _{\omega }$ of QC1 and QC2 are assumed to be the same.

Table 1 Material parameters of the z-direction QC plate ( [14, 23])

3.1 Validation of the Proposed Method

To our best knowledge, rare references about Lamb wave propagating in the multilayered quasi-crystal plates are available for comparison. However, the accuracy of the proposed method to investigate guided waves in multilayered crystal plates has been detailed in  [7]. Therefore, it is also appropriate for quasi-crystal structures. Subsequently, the convergence of the present method is confirmed. The frequencies with different M of a z-direction sandwich plate (a) with QC1/QC2/QC1-1mm/1mm/1mm are calculated and listed in Table 2. Here, there are two kinds of wave modes in the quasi-crystal plates. A kind of wave modes whose wave characteristics are similar to those of the elastic wave modes in crystal plates are defined as phonon modes. The others are phason modes attributed to the phason field. Comparing these data, we conclude that the present method is convergent. Furthermore, the convergence speed at smaller kh is much faster. For example, when $M=7$, the first three modes are convergent at $kh=3$, but only one mode is convergent at $kh=15$. Hereafter, $M=30$ is assumed in the following calculation.

Table 2 Frequencies $\omega (10^{\mathrm {3}})$ of the three fundamental modes with different M

3.2 Lamb Waves

3.2.1 Comparison Between Two Models

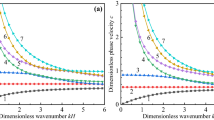
Firstly, the dispersion curves of plate (a) in the context of the Bak and elasto-hydrodynamic models are illustrated in Fig. 2. Meanwhile, the case of the corresponding crystal plate ($R_{i}=K_{i}=0$) is investigated. The phonon modes for Lamb waves are divided into symmetric and anti-symmetric modes, which are similar to the elastic wave modes in crystal plates. Similarly, they are also named as A0, S0, A1, S1....... And the phason modes are named as PL0, PL1....... Moreover, the phonon–phason coupling effect on dispersion curves in the context of Bak model is considerable. The first three modes have no cut-off frequencies, not as to the crystal plates, whose first two modes have no cut-off frequencies. Besides, the phonon–phason coupling effect on phonon modes is weak because $R_{i}$ is far smaller than $C_{ij}$ and $K_{ij}$. For example, the phase velocity of A0 mode in Fig. 2a slightly increases.

Fig. 2

Dispersion curves for plate (a) in the context of two models

For the elasto-hydrodynamic model, it is observed from Fig.  2b($\mathrm{I})$ that there are only phonon modes, no phason modes. Actually, there are phason modes. However, their phase velocities are very low in Fig. 2b($\mathrm{I}\mathrm{I})$. And the roots of phason modes are complex, whose imaginary parts are very large. For example, as $fh=1$ MHz*mm, its imaginary part of the PL0 mode is 522336i. Therefore, they are attenuated instantaneously and not propagative. The reason for this is that their friction coefficients are too large.

Then, the phonon–phason coupling effect on dispersion curves is studied in detail. Figure 3 shows dispersion curves of these two models with different $R_{i}$. All $R_{i}$ are simultaneously varied. It can be seen from Fig. 3a that the phonon–phason coupling effect on the phason modes is more significant than on the phonon modes. Furthermore, the phase velocities of phason modes decrease, and phase velocities of phonon modes increase at high frequencies as $R_{i}$ increase. However, the phonon–phason coupling effect in Fig. 3b only affects the non-propagative phason modes, not the phonon modes. And the phase velocities of phason modes decrease as $R_{i}$ increase. Therefore, only the Bak model is utilized to investigate the phonon–phason coupling effect in the following subsections.

Fig. 3

Dispersion curves of two models with different $R_{i}$

Next, the phonon–phason coupling effects on the first and second layers are, respectively, analyzed. Firstly, the materials of three layers are assumed to be QC1. Then, $R_{i}$ of the first and second layers are multiplied by 5 times, respectively. The dispersion curves are illustrated in Fig. 4. The phonon–phason coupling effects on the first two layers are the same at low frequencies. However, they are more significant on the first layer at high frequencies. The reason lies in the fact that energies at high frequencies mainly propagate in the first layer.

Fig. 4

Dispersion curves of the influence of the first and second layers

3.2.2 Influences of Volume Fractions and Stacking Sequences

Influences of volume fractions and stacking sequences on wave characteristics are illustrated in Fig. 5. Here, we consider other three kinds of z-direction sandwich quasi-crystal plates, which are plate (b): QC1/QC2/QC1-2mm/1mm/1mm; plate (c): QC1/QC2/QC1-1mm/2mm/1mm; and plate (d): QC2/QC1/QC1-1mm/1mm/1mm. Compared with plate (a), the volume fraction of QC1 in plate (b) increases, and that in plate (c) decreases. It is observed from Fig. 5a that phase velocities increase as the volume fraction of QC1 increases, since the wave velocities of QC1 for the phonon and phason modes are larger than those of QC2. Furthermore, it can be observed from Fig. 5b that the stacking sequences have a significant influence on dispersion curves, especially at high frequencies.

Fig. 5

Phase velocity dispersion curves with different volume fractions and stacking sequences

3.2.3 Phonon and Phason Displacements

Displacements of the first three modes at $kh=60$ are illustrated in Fig. 6. It can be seen that the symmetry of the phason displacement component $\gamma$ is always consistent with that of the phonon displacement component W. Furthermore, amplitudes of the phonon displacement components U and W of the phonon modes are far greater than that of the phason displacement component $\gamma$. However, they are opposite to the phason modes. Moreover, the phonon and phason displacements at high frequencies are mainly distributed in the QC2 layer, i.e., energies are mainly distributed in the QC2 layer. This lies in the reason that elastic modulus and stiffness of the QC2 layer are smaller than those of the QC1 layers.

Fig. 6

Displacement distributions of the first three modes at $kh=60$

3.2.4 The Influence of Quasi-Periodic Direction on Wave Characteristics

Figure 7 illustrates the dispersion curves with different quasi-periodic directions. The x-direction sandwich plate with QC1/QC2/QC1-1mm/1mm/1mm is assumed. It is observed that the influence of quasi-periodic direction is weak on the phonon modes, but considerable on the phason modes. The phase velocities of phason modes in the x-direction plate are much higher than those in the z-direction plate.

Fig. 7

Dispersion curves of Lamb waves with different quasi-periodic directions

3.3 SH Waves

Figure 8 shows the dispersion curves of SH waves in a sandwich y-direction plate with QC1/QC2/QC1-1mm/1mm/1mm. It can be seen that the phonon modes of SH waves are similar to the elastic wave modes in the crystal plates. Similarly, they are also named as SH0, SH1....... Phason modes are named as PSH0, PSH1....... Furthermore, the phonon–phason coupling effect on phonon modes is also very weak. Moreover, the trend of the phonon modes is similar to that of the phason modes.

Fig. 8

Dispersion curves of SH waves in the sandwich y-direction QC plate

Subsequently, the phase velocity dispersion curves with different phonon–phason coupling coefficients $R_{i}$ are illustrated in Fig.  9. It can be seen that the influence of phonon–phason coupling coefficients on the phason modes is more significant than on the phonon modes. Furthermore, the influences on the phonon and phason modes are opposite. As $R_{i}$ increase, phase velocities of the phason modes decrease, and those of the phonon modes increase.

Fig. 9

Phase velocity dispersion curves of the sandwich quasi-crystal plate with different $R_{i}$

4 Conclusions

Guided waves in the multilayered 1-D hexagonal quasi-crystal plates in the context of Bak and elasto-hydrodynamic models are, respectively, investigated using the Legendre orthogonal polynomial method. Dispersion curves and phonon and phason displacement distributions are calculated. Based on the numerical results, the following conclusions can be drawn:

• (1) The phonon–phason coupling effects in the context of Bak model on phonon and phason modes are significant. However, the phonon–phason coupling effects in the context of elasto-hydrodynamic model just affect the non-propagative phason modes, not the phonon modes.

• (2) The phonon–phason coupling effects on the first two layers are the same at low frequencies. However, they are more significant on the first layer than those on the second layer at high frequencies.

• (3) Energies of both phonon and phason modes at high frequencies mainly propagate in the layer with smaller elastic modulus and stiffness.