1 Introduction

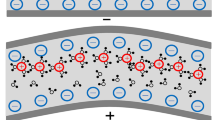
The ionic polymer–metal composite (IPMC), one of the most promising electroactive materials, has a wide range of industrial and medical applications [1,2,3], such as flapping wings [4], grippers [5, 6], fish-like robots [7,8,9], artificial muscles [10], biomedical devices [11], due to the attractive inherent advantages including low excitation voltage, low density, large strain range, flexibility, fast response, and easy design compared to traditional materials [12, 13]. In the absence of electric field, the hydrated cations in the IPMC solution distribute uniformly within the membrane. When an excitation voltage is applied, the hydrated cations are forced to move toward the cathode, resulting in the bending of IPMC toward the anode side [14,15,16,17,18,19]. The above actuation process is schematically shown in Fig. 1.

Fig. 1
figure 1

A schematic diagram of the structure and actuation principle of IPMC

Full size image

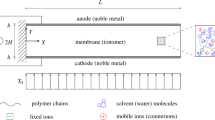
An IPMC generally consists of a layer of ion-exchange membrane (e.g., Nafion, Flemion, and Aciplex) chemically plated with noble metal electrodes (e.g., Pt, Ag) [20,21,22,23,24]. Due to the penetration of metallic particles into the membrane during the electroless deposition process, a layered structure of IPMC forms. There exists a metal–polymer composite layer between the metal electrode layer and the polymer layer, as shown in Fig. 1. A similar structure model has also been used in [25,26,27,28].

Many models have been developed to describe the transduction behaviors and design the complicated applications of IPMC during the last decades [2, 19]. For simplicity, it is assumed in many models that the metal layers of IPMC are bulk material which is perfectly conductive. However, real-world electrodes of IPMC are generally porous metal materials rather than bulk materials. The IPMC materials are fabricated with the method of electroless deposition, where the electrode metal is plated on the surface of a perfluorinated ionic polymer. Shahinpoor and Kim [21] reported that the metal particles coagulated during the electroless deposition process. Based on their research, Kim et al. [25] proposed a geometrical model to estimate the electrical properties of the electrodes, assuming that the electrodes of IPMC are composed of metal particles and voids.

Young’s modulus is one of the basic electromechanical parameters to characterize the performance of IPMC actuators. However, no studies have been found to identify the elastic constants of electrodes taking into account the geometrical properties of IPMC.

In this work, a gradient electrode model is proposed to estimate Young’s modulus and surface resistance of IPMC with a gradient distribution of electrode metal particles in the thickness direction of IPMC. Then, Nafion-based IPMCs with platinum (Pt) electrodes are studied. The gradient electrode model is validated against the experimental results obtained from manufactured IPMC samples.

2 Modeling

The electrode of IPMC is divided into two parts: the metal electrode and the composite electrode, which could be also called the outer electrode and the inner electrode.

2.1 Outer Electrode: Porous Platinum Electrode

It was reported that electroless deposition is one strategy for the fabrication of porous platinum electrodes [29]. Kim’s electrode model for IPMC also indicated that the electrodes of IPMC are porous materials [25].

It is widely acknowledged that the effective properties (e.g., Young’s modulus) of porous material depend on its porosity (volume fraction of voids). And apart from the volume fraction of voids, the shape of void also significantly affects the effective properties of the porous material [29].

In order to simplify the model, several assumptions are made for the outer electrode:

  • The outer electrode is composed of platinum and air voids.

  • All the properties of platinum have been preserved.

  • The voids are spherical and of the same size.

  • The distribution of voids in the outer electrode is uniform. In other words, the porous platinum electrode is isotropic.

2.2 Inner Electrode: Gradient Composite Electrode

The electroless deposition process of IPMC mostly requires two steps: the adsorption and diffusion of platinum salt (e.g., \(\hbox {Pt}[\hbox {NH}_{3}]_{4}\hbox {HCl}\)) within the Nafion membrane, and the successive reduction of the platinum cations absorbed into the polymer to the metallic state using a reducing agent (generally \(\hbox {NaBH}_{4}\) or \(\hbox {Li}\hbox {BH}_{4}\)). The metal grows outward and inward from the surface of Nafion membrane during the successive deposition process, forming the outer platinum electrode and the inner composite electrode, respectively.

It could be inferred that platinum particles penetrate into the Nafion membrane, forming a metal–polymer composite layer between the metal electrode layer and the polymer layer. The content of metallic particles in the composite layer is non-uniform, changing along the thickness direction of IPMC. It is difficult to control the electroless deposition in terms of the thickness and distribution of the composite layer.

For simplicity, several assumptions are made about the inner electrode:

  • The inner electrode is composed of cylindrical platinum and hydrated Nafion.

  • The metal is continuous along the thickness direction of IPMC.

  • The content of platinum particles depends on its location in the composite layer. The volume fraction of the metal varies linearly with the depth of its penetration. Its ultimate value is the volume fraction of water in fully hydrated Nafion.

  • A layer with the same depth in the composite electrode is uniform.

In this work, the electrode of IPMC is modeled as a gradient model, including the outer porous electrode and the inner gradient composite electrode, which is schematically illustrated in Fig. 2. When the IPMC works in a beam configuration, the x, y and z directions are the length, thickness and width of the sample, respectively. The geometric parameters of IPMC are shown in Fig. 2.

Fig. 2
figure 2

Schematic illustration of the gradient model and geometric parameters of IPMC

Full size image

3 Estimation of the Electrode Properties

The electrode properties in terms of Young’s modulus and surface resistance, which are the most important parameters for IPMC modeling, are estimated in this section.

3.1 Young’s Modulus

It is well known that Young’s modulus is primarily important in material science. As mentioned in the previous section, IPMC usually works in a beam configuration. According to the characteristics of IPMC actuator, the Young’s modulus studied in this paper is in the axial direction of IPMC (the x direction shown in Fig. 2).

The equivalent Young’s modulus can be traditionally approximated with the mixture rule as [30]

$$\begin{aligned} E=E_e V_e +E_N V_N \end{aligned}$$
(1)

where \(E_{e}\) and \(V_{e}\) are, respectively, Young’s modulus and volume fraction of the electrode; and \(E_{N }\) and \(V_{N}\) are, respectively, Young’s modulus and volume fraction of the Nafion membrane. However, the effects of the porous properties of IPMC outer electrodes and the existence of internal electrodes on the modulus were not considered in previous research. In this paper, Eq. (1) is changed into

$$\begin{aligned} E=E_o V_o +E_i V_i +E_N V_N \end{aligned}$$
(2)

where \(E_{o}\) and \(E_{i}\) are, respectively, Young’s moduli of the outer and inner electrodes of the IPMC sample; and \(V_{o}\) and \(V_{i}\) are volume fractions of the outer and inner electrodes, respectively.

3.1.1 Young’s Modulus of the Outer Electrode

According to the assumptions in Sect. 2.1, the outer electrode is porous platinum, which could be considered as a single-inclusion problem, wherein the inclusions are spherical pores. The solution of this model goes back to that of Eshelby [31] and Wu [32]. Based on Eshelby’s and Wu’s solution, several well-known effective medium approximations (Maxwell, self-consistent, differential and exponential) could be used to predict the relative Young’s modulus of porous material.

In this work, the exponential approximation is used to predict the relative Young’s modulus of the outer electrode, because it is more adequate for the prediction of Young’s modulus than other relations [33]. The exponential relation is [34],

$$\begin{aligned} E_r^0= & {} \hbox {exp}\left( {\frac{{-2}\varphi }{1-\varphi }} \right) \end{aligned}$$
(3)
$$\begin{aligned} E_{{o}}= & {} E_r^0 \cdot E_{\mathrm {Pt}} \end{aligned}$$
(4)

where \(E_r^{0} \) is the relative Young’s modulus of the outer IPMC electrode, \(E_{\mathrm{Pt}}\) denotes the Young’s modulus of the dense platinum solid, and \(\varphi \) is the volume fraction of voids (the porosity of outer electrode).

Figure 3 shows the relative Young’s modulus of the porous platinum electrode with spheroidal voids versus the porosity. The Young’s modulus of the dense platinum solid is 169 GPa. It is evident that the relative Young’s modulus declines obviously with the increase in porosity, and the exponential relation is adequate as the predictive relation for low and moderate porosities.

Fig. 3
figure 3

Relative Young’s modulus of the outer electrode (\(E_r^0\)) versus porosity (\(\varphi \))

Full size image

3.1.2 Young’s Modulus of the Inner Electrode

The inner electrode of IPMC is a gradient Nafion–platinum composite layer, according to the assumptions in Sect. 2.2. It is also a single-inclusion problem. However, the volume fraction of platinum particles varies linearly with the depth of its penetration. In order for a simple expression about the relationship between the volume fraction and the location of inclusions, a local coordinate system is set up, as shown in Fig. 4.

The volume fraction of the platinum particles \(f(y_{i})\) could be expressed as \(f(y_i )=a\cdot y_i +b\), where a and b are constants. Based on the boundary conditions \(f\left| {_{y_i =0} =0} \right. \) and \(f\left| {_{y_i =t_i } =f_w } \right. \), the following equation is derived

$$\begin{aligned} f(y_i )=\frac{f_w }{t_i }y_i =k\cdot y_i \end{aligned}$$
(5)

where \(t_{i}\) is the thickness of the inner electrode, and \(f_{w}\) is the volume fraction of water in hydrated Nafion, which can be expressed as,

$$\begin{aligned} f_w =\frac{\Delta V}{1+\Delta V}=\frac{\rho _d c_w }{100\rho _w +\rho _d c_w } \end{aligned}$$
(6)

where \(\Delta V={c_w \rho _d }/{(100\rho _w )}\) is the fractional volume change of Nafion membrane due to swelling, \(c_{w}\) is grams of water in hydrated Nafion per 100 g of dry membrane, and \(\rho _{d}\) and \(\rho _{w}\) are the densities of the dry Nafion membrane and water, respectively. \( c_{w}\) can be calculated from the water uptake \(W_\mathrm{up}=(W_{w}-W_{d})/W_{d}\times 100\%\), where \(W_{w}\) and \(W_{d}\) denote the weights of hydrated and dry Nafion membranes, respectively.

A polymer–metal composite layer with thickness \(\hbox {d}y_{i}\) at any \(y_{i}\), is considered to be isotropic. The inclusion volume fraction of such microlayer is constant. In this work, the Mori–Tanaka approach [35] is used to estimate the effective Young’s modulus of the composite layer. For a single-inclusion model, the Mori–Tanaka macroscopic effective stiffness of the layer is:

$$\begin{aligned} {{\varvec{C}}}_{y_i } ={{\varvec{C}}}_{\mathrm{N}} +f(y_i )\left[ {\left( {{{\varvec{C}}}_{\mathrm {Pt}} -{{\varvec{C}}}_{\mathrm{N}} } \right) ^{-1}+\left( {1-f(y_i)} \right) {{\varvec{SC}}}_{\mathrm{N}}^{-1} } \right] ^{-1} \end{aligned}$$
(7)

where \({{\varvec{C}}}_\mathrm{N}\) and \({{\varvec{C}}}_\mathrm{Pt}\) stand for the stiffness tensors of the hydrated Nafion and platinum inclusion, respectively; and S is the Eshelby tensor.

Fig. 4
figure 4

Geometric definitions of the gradient electrode model with a local coordinate system

Full size image

Because the inclusions (platinum particles) of the layer are cylindrical according to the assumption, the Hill constants of the layer \(y_{i }\) are calculated from Eq. (7),

$$\begin{aligned} k_{y_i }= & {} \frac{k_{\mathrm {Pt}} k_{\mathrm{N}} +k_{\mathrm{N}} m_{\mathrm{N}} +m_{\mathrm{N}} (k_{\mathrm {Pt}} -k{ }_{\mathrm{N}})f(y_i )}{m_{\mathrm{N}} +k_{\mathrm {Pt}} +(k{ }_{\mathrm{N}}-k_{\mathrm {Pt}} )f(y_i )} \nonumber \\ m_{y_i }= & {} \frac{m_{\mathrm{N}} m_{\mathrm {Pt}} (k_{\mathrm{N}} +2m_{\mathrm{N}} )+k_{\mathrm{N}} m_{\mathrm{N}}^2 +k_{\mathrm{N}} m_{\mathrm{N}} (m_{\mathrm {Pt}} -m_{\mathrm{N}} )f(y_i )}{k_{\mathrm{N}} m_{\mathrm{N}} +(k_{\mathrm{N}} +2m_{\mathrm{N}} )m_{\mathrm {Pt}} +(k_{\mathrm{N}} +2m_{\mathrm{N}} )(m_{\mathrm{N}} -m_{\mathrm {Pt}} )f(y_i )} \nonumber \\ l_{y_i }= & {} \frac{l_{\mathrm {Pt}} (k_{\mathrm{N}} +m_{\mathrm{N}} )f(y_i )+l_{\mathrm{N}} (k_{\mathrm{N}} +m_{\mathrm{N}} )(1-f(y_i ))}{m_{\mathrm{N}} +k_{\mathrm {Pt}} +(k{ }_{\mathrm{N}}-k_{\mathrm {Pt}} )f(y_i )}\nonumber \\ n_{y_i }= & {} n_{\mathrm{N}} +(n_{\mathrm {Pt}} -n_{\mathrm{N}} )f(y_i )+\frac{l_{y_i }^2 }{k_{y_i } +m_{\mathrm{N}} }-\frac{l_{\mathrm {Pt}}^2 f(y_i )}{k_{\mathrm {Pt}} +m_{y_i } }-\frac{l_m^2 -l_m^2 f(y_i )}{k_{\mathrm{N}} +m_{\mathrm{N}} } \nonumber \\ p_{y_i }= & {} \frac{p_{\mathrm{N}} p_{\mathrm {Pt}} +p_{\mathrm{N}}^2 -p_{\mathrm{N}} (p_{\mathrm{N}} -p_{\mathrm {Pt}} )f(y_i )}{p_{\mathrm{N}} +p_{\mathrm {Pt}} +(p_{\mathrm{N}} -p_{\mathrm {Pt}} )f(y_i )} \end{aligned}$$
(8)

where \(k_{\mathrm{N}}\), \(m_{\mathrm{N}}\), \(l_{\mathrm{N}}\), \(n_{\mathrm{N}}\) and \(p_{\mathrm{N}}\) are the Hill constants of the matrix, and \(k_{\mathrm{Pt}}\), \(m_{\mathrm{Pt}}\), \(l_{\mathrm{Pt}}\), \(n_{\mathrm{Pt}}\) and \(p_{\mathrm{Pt}}\) are the Hill constants of the inclusion, respectively. The effective Young’s modulus can be obtained by using the elasticity standard relation,

$$\begin{aligned} E_{y_i } =\frac{4m_{y_i } (k_{y_i } n_{y_i } -l_{y_i }^2 )}{m_{y_i } n_{y_i } +k_{y_i } n_{y_i } -l_{y_i }^2 } \end{aligned}$$
(9)

And the effective Young’s modulus of the whole inner electrode is obtained by integration,

$$\begin{aligned} E_i =\frac{1}{t_i }\int _0^{t_i } {E_{y_i } } \hbox {d}y_i \end{aligned}$$
(10)

Finally, the effective Young’s modulus of the electrode is,

$$\begin{aligned} E_e =\frac{t_o E_o +t_i E_i }{t_o +t_i } \end{aligned}$$
(11)

where \(t_{o}\) and \(t_{i}\) are the thicknesses of the outer and inner electrodes, respectively.

As shown in Fig. 5, the relative Young’s modulus of the inner electrode increases as the maximum volume fraction of the inclusion (platinum particles) increases. According to the assumptions, the maximum value of \(f_{w}\) is less than the volume fraction of water in the fully hydrated Nafion membrane. The water uptake capacity of Nafion\(\circledR \)-117 membrane is about 30 wt% [22]. Therefore, the ultimate volume fraction of water could be obtained from Eq. (6), which is about 45%. The parameters of the membrane are listed in Table 1.

Fig. 5
figure 5

Relative Young’s modulus of the inner electrode (\(E_{i}/E_{N}\)) versus the maximum volume fraction of inclusion in the inner electrode layer

Full size image
Table 1 Properties of Nafion membrane (from the product information of DuPont\(^\mathrm{TM}\))
Full size table
Fig. 6
figure 6

Effective Young’s modulus of the electrode (\(E_{e}\)) versus a the thickness ratio between the inner and the outer electrodes (\(t=t_{i} /t_{o}\), \(f_{w}=0.4\)) when the outer electrode has different porosities (\(\varphi \)); b the maximum volume fraction (\(f_{w})\) of the inclusion in the inner electrode layer (\(t=1\), \(\varphi =0.6\))

Full size image

Figure 6a shows that the effective Young’s modulus of the whole electrode decreases with the increase in the thickness ratio between the inner and the outer electrodes (\(t=t_{i} / t_{o})\) and/or the increase in the porosity of the outer electrode. As shown in Fig. 6b, the maximum volume fraction (\(f_{w}\)) of the inclusion in inner electrode slightly influences Young’s modulus of the whole electrode.

3.2 Resistance

The surface electrode of IPMC is very thin, typically several microns (\(1{-}20\, \upmu \hbox {m}\)) [21]. In this section, the sheet resistance of the electrode is studied based on the previous model.

It is obvious that an increasing volume fraction of voids leads to an increase in the electrical resistance of the outer electrode. According to the assumptions, voids in the outer electrode are air, which could not conduct electricity. The air voids are considered as non-isolated inclusions in the chemically plated platinum layer. It was reported that the diameters of the coagulated platinum particles could grow to 50–100 nm during the deposition process [21]. The particles are piled up, and the contacts between the particles are not complete. Some researchers studied the influence of the contact area ratio on the electrical properties of IPMC electrodes [25, 36].

Taking into account the above characteristics of the outer electrode, the electrical resistivity of the outer electrode could be calculated by the following equation [37],

$$\begin{aligned} \gamma _o =\gamma _{\mathrm {Pt}} \frac{4}{1-\varphi } \end{aligned}$$
(12)

where \(\gamma _o \) and \(\gamma _{\mathrm {Pt}} \) (\(2.22\times 10^{-7}\,\Omega \,\hbox { m}\)) are the resistivities of the porous and compact platinum metals, respectively. And the sheet resistance of the outer electrode is,

$$\begin{aligned} R_o =\frac{\gamma _o }{t_o }=\frac{4\gamma _{\mathrm {Pt}} }{(1-\varphi )t_o } \end{aligned}$$
(13)

Based on the previous model, the area fraction of voids of the outer electrode equals their volume fraction (\(\varphi \)). As shown in Fig. 7, the sheet resistance of the outer electrode ascends with the increase in porosity (the volume fraction of voids) and declines with the increase in thickness \(t_{o}\).

Fig. 7
figure 7

Sheet resistance of the outer electrode (\(R_o\)) versus porosity (\(\varphi \))

Full size image

The composite layer with thickness \({\text {d}y}_{i}\) in the inner electrode is isotropic, and its conductivity could be derived via the conductivity relation of two-phase system [38],

$$\begin{aligned} \lambda _{y_i } =\lambda _{\mathrm{N}} \left[ {1+\frac{f\left( {y_i } \right) }{\frac{1-f\left( {y_i } \right) }{3}+\frac{\lambda _{\mathrm{N}} }{\lambda _{\mathrm {Pt}} -\lambda _{\mathrm{N}} }}} \right] \end{aligned}$$
(14)

where \(\lambda _{\mathrm {Pt}} \) and \(\lambda _{\mathrm{N}} \) are the electrical conductivities of the compact platinum and Nafion, respectively. The resistivity of the outer electrode is,

$$\begin{aligned} \gamma _{y_i } =\frac{1}{\lambda _{yi} } \end{aligned}$$
(15)

Then the sheet resistance of the single layer is \(R_{y_i } =\frac{\gamma _{y_i } }{\hbox {d}y_i }\), and the resistance of the inner electrode could be obtained from,

$$\begin{aligned} \frac{1}{R_i }=\sum {\frac{1}{R_{y_i } }} =\int _0^{t_i } {\frac{1}{\gamma _{y_i } }\hbox {d}y_i } \end{aligned}$$
(16)

Finally, the resistance of the whole electrode in the x direction is as follows,

$$\begin{aligned} \frac{1}{R}=\frac{1}{R_o }+\frac{1}{R_i } \end{aligned}$$
(17)

The influence of the inner electrode on the resistance of the whole electrode is so little that it could be neglected according to Eq. (17), because the conductivity of Nafion (\(8.3\hbox { S}\, \hbox {m}^{-1})\) is much smaller than that of Pt (\(4.5\times 106 \hbox { S}\, \hbox {m}^{-1})\). For example, if the thickness \( t_{i}\) and the volume fraction \(f(y_{i})\) are assumed to be fixed values of \(10\, \upmu \hbox {m}\) and 0.4, respectively, the sheet resistance of the inner electrode is 11.2 \(\hbox {k}\Omega /\square \), which is far greater than those shown in Fig. 7.

4 Model Verification

4.1 Experiments

Nafion solution was concentrated to form a uniform membrane. Both sides of the membrane strip were firstly roughened with metallographic sandpapers, and then cleaned using ultrasonic irradiation for 10 min. After boiled in 2 mol/L HCl for 1 h, it was rinsed with deionized water consecutively. The pretreated strip was soaked in \(0.1\hbox { mol/L }\hbox {H}_{2}\hbox {SO}_{4}\) solution for 0.5 h and then in \(0.01\hbox { mol/L Pt}[\hbox {NH}_{3}]_{4}\hbox {Cl}_{2}\) solution for 14 h for ion-exchange process. Finally, the Pt-IPMC was produced through two-step reduction. The first reduction step was conducted using \(\hbox {NaBH}_{4}\) as the reducing agent, and the second was performed for electrode development with \(\hbox {N}_{2}\hbox {H}_{4}\) as the reducing agent [2, 39].

Scanning electron microscopy (SEM) and energy-dispersive X-ray spectroscopy (EDX) with a Hitachi S-4800 were used to observe the surfaces, cross sections, and elementary compositions of IPMC samples. The SEM images were obtained to study the porosity of the outer electrode using ImageJ software, which is a quick and effective tool to obtain porosities of porous materials [40, 41].

Three IPMC samples were prepared to test the Young’s modulus by a universal testing machine (QUASAR 2.5), following the ASTM D882 standard. The surface sheet resistance was measured ten times using a ST-2258C multifunction digital four-probe tester.

4.2 Results and Discussion

Fig. 8
figure 8

a SEM images of IPMC samples (\(\times 20,000\)) and b segmentation images obtained using the Otsu’s thresholding method

Full size image

Figure 8a shows the surface SEM images of three IPMC samples. It is clearly seen that a large number of voids distribute in the electrode. This indicates the reasonability of the assumptions in Sect. 2.1. ImageJ software is used to analyze the SEM images to obtain the volume fraction of voids of the IPMC electrode. The simple, intuitive, and widely used Otsu’s thresholding method is applied herein to analyze the SEM image segmentation (as shown in Fig. 8b). The measured volume fractions of voids of the samples are listed in Table 2. It is found that the mean volume fraction of voids reaches up to \(61.1\pm 3.16\)%, suggesting that the bulk material simplification is somehow too strong.

The cross-sectional SEM image of IPMC shown in Fig. 9a also indicates that the outer electrode of IPMC sample is porous. The measured volume fraction of voids of the outer electrode shown in Fig. 9a is 50.0%, which is less than that (\(61.1\pm 3.16\)%) obtained from the surface SEM image of IPMC. The shear and extrusion deformation during the preparation of the viewing cross section of IPMC sample would cause the drop of metal particles and change the structure of the outer electrode and then affect its volume fraction of voids. Therefore, the volume fraction of voids obtained from the IPMC surface SEM images is used to calculate the basic properties of IPMC.

Figure 9b shows the cross-sectional SEM images with EDX line analysis of Pt element. The corresponding EDX line analysis indicates that the electrode consists of metal electrode and composite electrode. The thicknesses of the outer electrode and the inner electrode of IPMC material are obtained from the EDX line analysis of Pt element for different samples prepared at the same time and under the same conditions, which are listed in Table 2.

Fig. 9
figure 9

Cross-sectional SEM images of IPMC: a with segmentation image of outer electrode; and b with EDX line analysis of Pt element

Full size image
Table 2 Parameters of IPMC sample
Full size table
Table 3 Comparisons between calculated and measured values of IPMC sample
Full size table

The Young’s modulus of the whole IPMC is used to verify the validity of the gradient electrode model, because it is difficult to measure the modulus of IPMC electrode directly. According to the parameters listed in Table 2, the Young’s modulus of IPMC sample could be calculated using Eqs. (2) and (11). The comparison between the measured and predicted Young’s moduli of the sample is listed in Table 3. The thicknesses of electrode and membrane of IPMC material were given as \(1\, \upmu \hbox {m}\) and \(340\, \upmu \hbox {m}\), respectively. The Young’s modulus calculated using Eq. (1) is 874.97 MPa, which is much greater than the measured value (115 MPa) and the value (122.8 MPa) obtained by the proposed model.

As studied in Sect. 3.2, the resistance of the inner electrode is negligible compared with that of the whole electrode. Therefore, the resistance of IPMC electrode can be calculated using Eq. (13) and is compared with the measured value (Table 3).

By comparing the predicted values from the gradient electrode model of IPMC actuator with the experimental results, it is found that the electrode model reliably describes the basic properties of the electrode, including Young’s modulus and surface resistance.

5 Conclusion

In this study, a gradient electrode model of the IPMC is proposed to predict the basic electrode properties in terms of Young’s modulus and surface resistance. The influences of factors on the basic properties of the IPMC electrode are quantified, such as the volume fraction of voids in the outer electrode, and the thickness ratio between the inner and the outer electrodes. The model is verified to be in good agreement with the experimental results. From the relationship between the parameters and the properties acquired by the model, it is found that the volume fraction of voids and the thickness of outer electrode have major effects on the modulus and surface electrode resistance of IPMC electrode.