1 Introduction

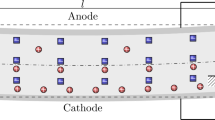
Ionic polymer-metal composites (IPMCs) is one of the electroactive polymers [1]. IPMC consists of an ionomeric layer sandwiched between a couple of electrodes [2, 3]. As shown in Fig. 1, the membrane contains anions linked to the backbone, cations that can move in the membrane, and water molecules [4]. At the applied voltage, the transport of hydrated cations to the cathode leads to the expansion of the membrane on one side of the cathode, which leads to the bending of the IPMC [5] (Fig. 1). IPMC has been widely used in biomedical applications, robotics, flexible sensing, aerospace and automotive industries [6,7,8].

Fig. 1
figure 1

Working principle of an IPMC actuator. Before applying an electrical stimulation (top) and after applying electrical stimulation (bottom)

Full size image

Elastic modulus and surface resistance are the basic mechanical properties of IPMCs, the elastic modulus directly affects the deformation and force output of IPMC, and is key material parameters to assess the behavior and performance of the components. The surface electrode resistance directly determines the distribution characteristics of the excitation electric field and affects the effect of IPMC deformation. Therefore, the elastic modulus and surface resistance dependence of actuation properties are of utmost importance for the IPMCs design and performance prediction. There are many analytical and numerical models available in the literature, such as the rule of hybrid mixture (ROHM) [9], classical laminate theory (CLT) [10], power-law approximations [11], Mori–Tanaka model [12], multiple-inclusion models [13], differential effective medium approximation [14] and finite element simulations [15] to predict the properties of isotropic composite materials with isometric pores. However, only a few authors [16,17,18,19,20] used the functional gradient models to predict the actuation properties of IPMCs. Most of them built models based on sandwich structures and did not predict surface resistance. Moreover, very limited theoretical works have been carried out on intra-ply hybrid gradient layer. Therefore, the main objective of this work is to predict the elastic modulus and surface resistance of copper electrodes IPMCs using an approach based on CLT proposed by Liu [18]. Firstly, according to the functional region distribution characteristics of IPMC structure, the IPMC functional gradient model “outer electrode-inner electrode-ion exchange membrane-inner electrode-outer electrode” is established. Secondly, the elastic modulus of IPMC is calculated, especially the prediction of the elastic modulus of the intra-ply hybrid gradient layer by the Mori–Tanaka method based on the Eshelby’s equivalent inclusion theory, so as to obtain the overall elastic modulus of IPMC. Thirdly, the surface resistance of copper electrode IPMC is predicted rely upon the established optimization functional gradient model. Finally, the predicted elastic modulus and surface resistance are verified by experiments. Through the prediction of elastic modulus and surface electrode resistance, it provides a basis for the subsequent force-electric coupling analysis and model establishment of IPMC.

2 Theoretical formulation

2.1 Functional gradient model

Most of the IPMC electrode layers prepared by chemical deposition method are porous [21]. IPMC is not a simple “electrode-polymer-electrode” sandwich structure. There is a composite layer of electrode metal and matrix polymer between the electrode and the polymer matrix, which is called the inner electrode. The final IPMC structure is “Outer electrode-inner electrode-ion-exchange membrane-inner electrode-outer electrode”, which has also been confirmed by some researchers [19, 22].

According to the distribution characteristics of the functional region of IPMC structure, the functional gradient model of IPMC is established as shown in Fig. 2. The external electrode is a porous metal layer, the inner electrode for metal-polymer gradient layer, the metal content is continuously changed from the outside to the inside, and the IPMC matrix for ion polymer. The external electrode and inner electrode layer structure of IPMC material are complex, it is assumed that the electrode satisfies the following restrictions in the process of model: (a) the metal particles in the inner and outer electrodes are anisotropic, evenly distributed. (b) The performance of the metal particles does not change before and after chemical plating, and they are continuously distributed. (c) The pores in the electrode have the same size and shape, and the metal particles are spherical. (d) The electrode of the IPMC is composed of the metal particles and the voids between the particles; the microstructure of the electrodes can be described in terms of its unit cell. (e) During the deformation of the electrode, the distance between the metal particles and the size of the cube changes accordingly.

Fig. 2
figure 2

Schematic diagram of IPMC gradient function model (ho, hi and hp are the thickness of the outer electrode, inner electrode and ionic polymer, respectively)

Full size image

Here, we perform the calculation of elastic modulus and surface resistance is to understand the IPMC separation and combination, dissociate to analyze the characteristics and properties of each layer, and then the components into the whole IPMC, as shown in Fig. 3.

Fig. 3
figure 3

Schematic of the three species superposition model for IPMCs. In the superposition process, the properties of each species are homogenized

Full size image

2.2 Elastic modulus

This paper presents a method for predicting elastic modulus properties of IPMCs using classical lamination model. The electrode layer is a porous structure by chemical deposition, the porosity plays a significant role in overall properties of composites [23], as for prediction of porous materials properties must be based on the exact solutions of the corresponding single-inclusion problems. Analytical solutions of this type, in the case of elastic properties going back to Eshelby [24], the most prominent and useful of these is the spheroidal pore shape model. For materials with monosized spheroidal pores, the admissible relations for the prediction of the relative elastic modulus are the Maxwell-type approximation

$$ E_{\text{r}} = \frac{1 - \phi }{1 + \phi }. $$
(1)

The generalized self-consistent approximation

$$ E_{\text{r}} = 1 - 2\phi . $$
(2)

The generalized power-law relation

$$ E_{\text{r}} = \left( {1 - \phi } \right)^{2} . $$
(3)

And the generalization of exponential relation

$$ E_{\text{r}} = \exp \left( {\frac{ - 2\phi }{1 - \phi }} \right). $$
(4)

The last exponential relation is more adequate as a predictive relation for elastic modulus than any other of the above relations [25, 26]. Note that all of these relations are admissible in the sense that they obey the Voigt bound and the upper Hashin–Shtrikman bound [27].

$$ E_{\text{r}} \le 1 - \phi , $$
(5)
$$ E_{\text{r}} \le \frac{1 - \phi }{1 + \phi }, $$
(6)

where \( E_{\text{r}} \) stands for relative elastic modulus, and \( \phi \) is the porosity. Therefore, the exponential function is used in this paper to predict the elastic modulus of the outer electrode.

$$ E_{\text{o}} = E_{\text{r}} \times E_{\text{m}} , $$
(7)

where \( E_{\text{o}} \) is elastic modulus of outer electrode, and \( E_{\text{m}} \) for elastic modulus of the metal electrode.

Eshelby equivalent inclusion theory and Mori–Tanaka method [13] were used to obtain the equivalent elastic modulus of the inner electrode of IPMC.

$$ \varvec{L} = \varvec{L}_{0} \left( {\varvec{I} + C\varvec{A}} \right)^{ - 1} , $$
(8)
$$ \varvec{A} = \left\{ {\varvec{L}_{0} + \left( {\varvec{L}_{1} \text{ - }\varvec{L}_{0} } \right)\left[ {C\varvec{I} + \left( {1 - C} \right)\varvec{S}} \right]} \right\}^{ - 1} \left( {\varvec{L}_{0} + \varvec{L}_{1} } \right), $$
(9)

where \( \varvec{A} \) is the strain concentration factor tensor, \( \varvec{L}_{0} \) is the elastic constant tensor of ionic polymer, \( \varvec{L}_{1} \) for the elastic constant tensor of the inclusion phase of metal particles, \( \varvec{L} \) for the elastic constant tensor of the equivalent IPMC inner electrode, \( C \) for the volume ratio of the inclusion phase of metal particles, \( \varvec{I} \) and \( \varvec{S} \) are the fourth-order unit tensor and the Eshelby tensor, respectively.

The fourth-order Eshelby’s tensor S can be written as [28]

$$ \varvec{S} = \left( {\begin{array}{*{20}c} {S_{1111} } & {S_{1122} } & {S_{1133} } & 0 & 0 & 0 \\ {S_{2211} } & {S_{2222} } & {S_{2233} } & 0 & 0 & 0 \\ {S_{3311} } & {S_{3322} } & {S_{3333} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {S_{2323} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {S_{3131} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {S_{1212} } \\ \end{array} } \right). $$
(10)

And the components \( S_{ijkl} \) of Eshelby tensor in the above matrix with Poisson’s ratio \( \nu \) are expressed as follows [29]

$$ S_{ijkl} = S_{jikl} = S_{ijlk} , $$
(11)
$$ S_{1111} = \frac{3}{{8\pi \left( {1 - \nu } \right)}}a_{1}^{2} I_{11} + \frac{1 - 2\nu }{{8\pi \left( {1 - \nu } \right)}}I_{1} , $$
(12)
$$ S_{1122} = \frac{1}{{8\pi \left( {1 - \nu } \right)}}a_{2}^{2} I_{12} + \frac{1 - 2\nu }{{8\pi \left( {1 - \nu } \right)}}I_{1} , $$
(13)
$$ S_{1133} = \frac{1}{{8\pi \left( {1 - \nu } \right)}}a_{3}^{2} I_{13} + \frac{1 - 2\nu }{{8\pi \left( {1 - \nu } \right)}}I_{1} , $$
(14)
$$ S_{1212} = \frac{{a_{1}^{2} + a_{2}^{2} }}{{16\pi \left( {1 - \nu } \right)}}I_{12} - \frac{1 - 2\nu }{{16\pi \left( {1 - \nu } \right)}}\left( {I_{1} + I_{2} } \right), $$
(15)

where all nonzero components can be obtained by the cyclic permutation of indices (1, 2, 3). Other components are zero. In the upper expression, the constant \( I_{i} \) and \( I_{ij} \) can be represented as

$$ I_{i} = 2\pi a_{1} a_{2} a_{3} \int_{0}^{\infty } {\frac{{{\text{d}}u}}{{\left( {a_{i}^{2} + u} \right)\Delta \left( u \right)}}} , $$
(16)
$$ I_{ij} = 2\pi a_{1} a_{2} a_{3} \int_{0}^{\infty } {\frac{{{\text{d}}u}}{{\left( {a_{i}^{2} + u} \right)\left( {a_{j}^{2} + u} \right)\Delta \left( u \right)}}} , $$
(17)

where

$$ \Delta \left( u \right) = \sqrt {\left( {a_{1}^{2} + u} \right)\left( {a_{2}^{2} + u} \right)\left( {a_{3}^{2} + u} \right)} . $$
(18)

The electroless plating metal particles are approximately spherical, with basically the same size and shape, and evenly distributed in the Nafion membrane, the spherical inclusion with a1 = a2 = a3, the components are simplified to [25, 29]

$$ S_{1111} = S_{2222} = S_{3333} = \frac{7 - 5\nu }{{15\left( {1 - \nu } \right)}}, $$
(19)
$$ S_{1122} = S_{2233} = S_{3311} = S_{1133} = S_{2211} = S_{3322} = \frac{5\nu - 1}{{15\left( {1 - \nu } \right)}}, $$
(20)
$$ S_{1212} = S_{2323} = S_{3131} = \frac{4 - 5\nu }{{15\left( {1 - \nu } \right)}}. $$
(21)

And the Eq. (8) can be simplified into [30]

$$ K = K_{\text{p}} \left\{ {1 + \frac{{C\left( {\frac{{K_{\text{m}} }}{{K_{\text{p}} }} - 1} \right)}}{{1 + \left[ {\frac{1 + \nu }{{3\left( {1 - \nu } \right)}} - C} \right]\left( {\frac{{K_{\text{m}} }}{{K_{\text{p}} }} - 1} \right)}}} \right\}, $$
(22)
$$ G = G_{\text{p}} \left\{ {1 + \frac{{C\left( {\frac{{G_{\text{m}} }}{{G_{\text{p}} }} - 1} \right)}}{{1 + \left[ {\frac{{2\left( {4 - 5\nu } \right)}}{{15\left( {1 - \nu } \right)}} - C} \right]\left( {\frac{{G_{\text{m}} }}{{G_{\text{p}} }} - 1} \right)}}} \right\}, $$
(23)

where \( K_{\text{p}} \), \( G_{\text{p}} \) are the bulk modulus and shear modulus of ionic polymer respectively, \( K_{\text{m}} \), \( G_{\text{m}} \) for bulk modulus and shear modulus of the metal particle.

And use the elasticity standard relation [13, 25, 30, 31] to obtain elastic modulus of the inner electrode.

$$ E_{i} = \frac{9KG}{G + 3K}. $$
(24)

IPMC material is a layered structure, and the overall elastic modulus of IPMC can be obtained according to CLT

$$ E = \frac{{h_{\text{o}} E_{\text{o}} + h_{\text{i}} E_{\text{i}} + h_{\text{p}} E_{\text{p}} }}{{h_{\text{o}} + h_{\text{i}} + h_{\text{p}} }}. $$
(25)

2.3 Surface resistance

The surface electrode resistance directly determines the distribution of the excitation voltage of IPMC, and ultimately affects the electric actuation response of IPMC. The prediction and calculation of conductivity are mainly focused on the Maxwell, self-consistent, power-law relation and exponential relation approach. The most popular model relations about conductivity are so-called “effective medium approximations” (EMAs), which can be derived via the following approaches [25]:

Maxwell approach,

$$ \sigma_{\text{r}} = \frac{1 - \phi }{{1 + {\phi \mathord{\left/ {\vphantom {\phi 2}} \right. \kern-0pt} 2}}}. $$
(26)

Self-consistent approach,

$$ \sigma_{\text{r}} = 1 - \frac{3}{2}\phi . $$
(27)

Power-law relation approach,

$$ \sigma_{\text{r}} = \left( {1 - \phi } \right)^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} . $$
(28)

Exponential relation approach,

$$ \sigma_{\text{r}} = \exp \left( {\frac{{ - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}\phi }}{1 - \phi }} \right). $$
(29)

For particles with spherical or isometric shapes, it is well known that the exponential relationship provides a reasonable prediction of the relationship between porosity and conductivity, whereas maxwell predictive model and Power-law relationship usually predict high conductivity, and the self-consistent model needs to be linearly approximated under the assumption of fully insulated pores [25]. Therefore, it is a clear choice to choose an exponential relationship to prediction. The resistivity can be expressed as

$$ \gamma_{\text{o}} = \frac{{\gamma_{\text{m}} }}{{\sigma_{\text{r}} }}, $$
(30)

where \( \gamma_{\text{o}} \) and \( \gamma_{\text{m}} \) are the resistivity of the outer electrode and the coated metal, respectively. The outer electrode resistance can be expressed as:

$$ R_{\text{o}} = \frac{{\gamma_{\text{o}} l}}{S} = \frac{{\gamma_{\text{o}} }}{{h_{\text{o}} }}. $$
(31)

Inner electrode conductivity was calculated based on Ref. [32]

$$ \sigma_{\text{i}} = \sigma_{\text{p}} \left( {1 + \frac{C}{{\frac{1 - C}{3} + \frac{{\sigma_{\text{p}} }}{{\sigma_{\text{m}} - \sigma_{\text{p}} }}}}} \right), $$
(32)

where \( \sigma_{\text{i}} \) is the conductivity of the inner electrode, \( \sigma_{\text{p}} \) and \( \sigma_{\text{m}} \) for ion polymer and metal conductivity.

$$ \gamma_{\text{i}} = \frac{1}{{\sigma_{\text{i}} }}, $$
(33)
$$ R_{\text{i}} = \frac{{\gamma_{\text{i}} l}}{S} = \frac{{\gamma_{\text{i}} }}{{h_{\text{i}} }}. $$
(34)

Ultimately, the resistance of the IPMC integral electrode can be regarded as the parallel formation of the inner electrode resistance and the external electrode resistance:

$$ R = \frac{{R_{\text{o}} R_{\text{i}} }}{{R_{\text{o}} + R_{\text{i}} }}. $$
(35)

3 Materials and methods

We used Nafion-117 as the substrate membrane. The Nafion films with a thickness of 0.183 mm were obtained from DuPont. Others chemical agent were obtained from Tianjin Chemical Reagent Corp. In this paper, copper IPMC is used to verify the theoretical derivation, the specific preparation process is as follows [4].

Pre-treatment: Nafion-117 membrane was cut into 50 mm × 10 mm pieces, which were roughened by hand with 800 Mesh and 1000 Mesh sandpaper, then rinsed in ultrasonic cleaning machine for 30 min; Boiled in 2 mol/L hydrochloric acid solution and deionized water to purify the ionomer membrane.

Ion adsorption: the pre-treated membranes were soaked in silver nitrate for 12 h.

Chemical reduction process: the reaction equation is as follows:

$$ {\text{CuSO}}_{4} \cdot 5{\text{H}}_{2} {\text{O}} + 2{\text{HCHO}} + 4{\text{NaOH}} \to {\text{Cu}} + 2{\text{HCOONa}} + {\text{Na}}_{2} {\text{SO}}_{4} + 7{\text{H}}_{2} {\text{O}} + {\text{H}}_{2} . $$
(36)

Ion exchange: the IPMC samples were immersed in a lithium chloride solution.

The surface morphologies were observed by scanning electron microscopy (SEM, JEM 2010). The elastic modulus was tested by bending test method, and the measurement accuracy is 0.001 with micro-force sensor as the main test element. The surface resistance of IPMC was measured by the digital four-probe tester, and the correction coefficient of sample shape and measuring position is 0.788.

4 Results and discussion

Electroless deposition is a simple, effective, large-area deposition technique [33]. Copper nanoparticles are deposited on Nafion membrane to form an electrode layer, in which the inner electrode is composed of Nafion and copper particles. This special structure makes the physical properties of IPMC special compared with other composite materials. The factors affecting the quality of electrode layer include bath composition, the surface effective charge density of copper particles, size and shape of copper particles, current density, stirring intensity, additive, temperature, etc. [34, 35], which result in different surface morphology and microstructure of IPMC. The scanning electron microscopy of the surface electrode of IPMC is shown in Fig. 4a. IPMC surface was fully covered by copper, it also shows that copper distribution were uniform and compact with smaller copper particles, the Cu2+ are dispersed uniformly in the electroless plating bath, which ensures the uniform dispersion of copper particles on the Nafion membrane. The dispersion methods used in this paper are ultrasonic dispersion and chemical dispersion with surfactant. The ultrasonic dispersion method can make the copper nanoparticles fully dispersed and the content of the composite layer is high so that the electrode layer has better microstructure and properties. In addition, the physical properties of the copper particles themselves affect the ability of the particles to be deposited into Nafion, such as surface wettability, electrical properties and affinity. The surfactant of 2,2-dipyridine (C10H8N2, 99.0%) [4] can improve the wettability and surface charge polarity of the particles, increase the content of copper nanoparticles in Nafion, and improve the surface morphology of the composite coating [36, 37].

Fig. 4
figure 4

Surface electrode of IPMC a surface morphology, b the porosity of the outer electrode, c histogram of Cu particle size

Full size image

It is also evident that there was a large number of pores in the electrode. The porosity rate is a major factor affecting the performance of the outer electrode of the IPMC, and the porosity of the outer electrode is measured by the Image-J image processing software according to the uniformity hypothesis of the IPMC outer electrode. The threshold value of SEM image was set according to binarization algorithm and segmentation was carried out as shown in Fig. 4b, and the porosity rate of the sample was obtained by the Image-J to be about 0.59. To provide a clearer representation of the copper particles deposited on the surface, the histogram is shown in Fig. 4c. On the whole, the particle size of copper is small, the average particle size is \( 1.13 \pm 0.35 \) μm. The size of the copper particle will restrict the behavior of copper particle, which indirectly affects the conductivity of the electrode layer and changes the actuation performance of IPMC.

4.1 Elastic modulus

The electrode layer of Nafion membrane can increase the elastic modulus of IPMC, and the formation and densification further ensure the high elastic modulus. According to the established outer electrode model, the relationship between the elastic module and porosity of the IPMC outer electrode can be obtained through a suitable transformations shown in Fig. 5a, the elastic modulus decreases significantly with the increase of porosity, and the elastic modulus decreasing curve is close to the linear relationship when the porosity is between 0 and 40%. When the porosity is about 50%, the decreasing trend of elastic modulus slows down, and when the porosity is 70%, the elastic modulus is close to 0. It can be seen that the deposition state of copper particles is different under different conditions, resulting in different porosity of copper electrode layer, which affects the change of elastic modulus. It can effectively control various parameters of electroless plating to achieve the need for elastic modulus.

Fig. 5
figure 5

Change of elastic modulus a outer electrode, b inner electrode

Full size image

The elastic modulus of the inner electrode is mainly affected by the volume ratio of metal particles. It can be seen from Fig. 5b that with the increase of copper particle, the elastic modulus is also increasing, and the curve shows an approximately linear relationship. Sufficient particle dispersion and a slow deposition rate contribute to the copper content of the inner electrode.

Combined with the Eqs. (7), (24) and (25), the elastic module of the Cu-IPMC is calculated to be 113 MPa. The average elastic module is 121 MPa by bending method. The margin of error between the predicted and measured of the elastic modulus of Cu-IPMC by the gradient function model is 6.6%. The predicted value is in good agreement with the measured value, which proves the correctness of the IPMC electrode gradient model and can predict the elastic modulus of IPMC.

4.2 Surface resistance

The IPMC outer electrode consists of pores and copper particles. Where the pores are air, non-conductive. Low surface resistance can promote IPMC to drive quickly, improve the response speed of IPMC and shorten its response time.

The relationship between the surface resistance and porosity of the Cu-IPMC outer electrode through a suitable transformation is shown in Fig. 6a. It can be seen that the resistance increases with the increase of porosity, and when the porosity is greater than 60%, the outer resistance begins to grow rapidly. The resistance of the inner electrode shows a decreasing trend with the increase of the volume content of copper metal particles, as shown in Fig. 6b. These behaviors are contrary to the change of elastic modulus. The preparation process must be arranged reasonably during chemical plating to achieve the desired results.

Fig. 6
figure 6

Change of surface resistance a outer electrode, b inner electrode

Full size image

Because the resistance between the inner electrode and outer electrode are parallel, the inner electrode has little effect on the whole electrode resistance of the IPMC. This is also verified by the model calculation, and the surface resistance of IPMC is mainly determined by the outer electrode. Combined with the Eqs. (31), (34) and (35), the model predicted the value of the surface resistance is 0.97 Ω/cm. This is closely related to the shape of the surface electrode, as can be demonstrated in Fig. 4, especially the compact structure reduces the surface resistance. The experimental value is 1.0 Ω/cm. For the surface electrode resistance of the IPMC specimen, the error between the predicted value of the functional gradient model and the experimental value is 3.0%. It can be seen that the functional gradient model of IPMC can be used for the prediction of surface electrode resistance, and the experimental results show that it is effective.

5 Conclusion

A new five-layer structure model (Outer electrode-inner electrode-ion-exchange membrane-inner electrode-outer electrode) is used to predict the elastic modulus and surface resistance of IPMC, which combines a model based on classical lamination theory with the Mori–Tanaka methodology based on the Eshelby’s equivalent inclusion theory. A comparison of the prediction results and experimental results of the IPMC actuator strongly indicates that the model has been successful in predicting elastic modulus and surface resistance of the IPMC. It should be noted that the proposed modeling strategy can be simply extended to other IPMCs actuators with some modifications in the model. The model presented can be used as a preliminary tool to predict other properties such as bulk modulus, shear modulus, poisson ratio and flexural modulus of IPMCs. The overall results have provided useful insight of the elastic modulus and surface resistance effects to the property of the IPMCs, which has guiding significance for the preparation process of IPMC, and also has important reference significance for the establishment of electric force response model of IPMC materials.