Nonlinear Vibration Analyses of Cylindrical Shells Composed of Hyperelastic Materials

Abstract

The nonlinear vibration problem is studied for a thin-walled rubber cylindrical shell composed of the classical incompressible Mooney–Rivlin material and subjected to a radial harmonic excitation. With the Kirchhoff–Love hypothesis, Donnell’s nonlinear shallow shell theory, hyperelastic constitutive relation, Lagrange equations and small strain hypothesis, a system of nonlinear differential equations describing the large-deflection vibration of the shell is derived. First, the natural frequencies of radial, circumferential and axial vibrations are studied. Then, based on the bifurcation diagrams and the Poincaré sections, the nonlinear behaviors describing the radial vibration of the shell are illustrated. Examining the influences of structural and material parameters on radial vibration of the shell shows that the vibration modes are highly sensitive to the thickness–radius ratio when the ratio is less than a certain critical value. Moreover, in terms of the results of multimodal expansion, it is found that the response of the shell to radial motion is more regular than that without considering the coupling between modes, while there are more phenomena for the uncoupled case.

1 Introduction

As typical hyperelastic materials, some important properties of rubber materials (such as high elasticity and large deformation) are an indispensable part of many engineering fields. Correspondingly, these materials have a wide range of products, such as ordinary tires, gaskets and tubing. Cylindrical shells, due to their excellent mechanical properties, are widely used, such as spacecraft housings, conveyor tubes or engine drums. For thin and flexible structures, they produce nonlinear responses to typical disturbances. Under both static and dynamic excitations, nonlinearity becomes an important aspect of structural behavior [1]. In addition, the hyperelastic cylindrical shell can combine the advantages of geometric and physical nonlinearities, so it is worth studying the nonlinear and chaotic vibration characteristics.

As a result, researchers have long been interested in the chaotic dynamic response of cylindrical shells. In the field of mechanics, shell and plate structures are the most economical in practical applications, and the research on chaotic vibration of shell and plate has attracted much attention. Wang et al. [2] investigated the natural frequencies, complex modes and critical speeds of an axially moving rectangular plate. The authors used the classical thin plate theory to formulate the equations of motion of a vibrating plate and discussed the influences of distance ratio, moving speed, immersed depth ratio, boundary conditions, stiffness ratio and aspect ratio of the plate as well as the fluid–plate density ratios on the free vibrations of the moving plate–fluid system. Hao et al. [3] analyzed the nonlinear dynamics of a simply supported functionally graded material rectangular plate in a thermal environment subjected to transversal and in-plane excitations, and gave the periodic, quasi-periodic and chaotic motions. Yang et al. [4] presented a unified solution for the vibration analysis of cylindrical shells with a general stress distribution using the Flügge shell theory and modal orthogonality simplification. Li et al. [5] studied the global bifurcations and multi-pulse chaotic dynamics for a simply supported rectangular thin plate by the extended Melnikov method. Bich et al. [6] analyzed the nonlinear vibration of a functionally graded cylindrical shell subjected to axial and transverse mechanical loads based on the improved Donnell’s shell theory, and they examined the effects of preloaded axial compression, the characteristics of functionally graded materials and dimensional ratios on the behaviors of the shells. Sofiyev et al. [7] employed the first-order shear deformation theory and the homotopy perturbation method to investigate the nonlinear free vibrations of a functionally graded orthotropic cylindrical shell interacting with the two-parameter elastic foundation. Zhu et al. [8] investigated the nonlinear free vibration behaviors of orthotropic piezoelectric cylindrical nano-shells and examined the influences of surface parameters and geometric characteristics. Amabili et al. [9] studied the nonlinear vibration of a water-filled circular cylindrical shell subjected to a radial harmonic excitation experimentally and numerically, and detected the chaotic motion in the frequency region where the traveling wave response was presented. Yamaguchi et al. [10] presented the chaotic vibrations of a shallow cylindrical shell panel under a harmonic lateral excitation and discussed the effect of the in-plane elastic constraint on the chaos of the shell. Han et al. [11] studied the chaotic motion of elastic cylindrical shells by dynamic equations containing quadratic and cubic nonlinear terms, and briefly explained the validity of analyzing chaotic motion with a single-mode model in the conclusions. Kryskoa et al. [12] investigated the chaotic vibrations of a closed cylindrical shell in a temperature field. Zhang et al. [13] studied the resonant responses and chaotic dynamics of a composite laminated circular cylindrical shell and found that there exist the twin phenomena between the Pomeau–Manneville-type intermittent chaos and the period doubling bifurcation. Li et al. [14] analyzed the nonlinear transient dynamic response of a functionally graded material sandwich doubly curved shell with the homogenous isotropic material core and functionally graded face sheet using a new displacement field on the basis of Reddy’s third-order shear theory for the first time. Amabili et al. [15] investigated the geometric nonlinear response of a water-filled, simply supported circular cylindrical shell and manifested the response undergoes some interesting behaviors with the increasing excitation amplitude, such as period doubling bifurcation, sub-harmonic response, quasi-periodic response and chaotic behaviors.

Generally, chaotic motion is a part of nonlinear vibrations, and the study of nonlinear behavior is the basis of analyzing chaotic phenomena. The nonlinear responses of hyperelastic cylindrical shells mainly come from two aspects: One is the large-deflection deformation of the shell and the other is the nonlinear constitutive relations of hyperelastic materials. The large deformation of the structure usually introduces geometric nonlinearity, which is the main difficulty in studying the nonlinear vibrations of cylindrical shells. Amabili [16] presented the original and consistent first-order shear deformation theory that retains all nonlinear terms in the in-plane displacements and rotations, and gave numerical applications of nonlinear forced vibration of a simply supported composite laminated cylindrical shell. In the framework of the classical nonlinear theory, Krysko et al. [17] studied the complex vibrations of a closed infinite cylindrical shell subjected to a transversal local load. Breslavsky et al. [18] studied the nonlinear response of a water-filled, thin circular cylindrical shell that was simply supported at the edges and subjected to multi-harmonic excitations, and explored the nonlinear dynamics. Employing the Lagrangian theory and the multi-scale method, Du et al. [19] studied the nonlinear forced vibrations of an infinite FGM cylindrical shell and revealed the path leading to chaos of the system. In addition to the geometric nonlinearity caused by large deformation, material nonlinearity is another major factor of nonlinear response. Since hyperelastic materials have physical nonlinearity, the corresponding structures are prone to finite deformations, so geometric nonlinearity may occur after deformation. Therefore, the research related to hyperelastic structures usually involves geometric and physical nonlinearities. For this reason, the nonlinear responses of hyperelastic structures have received a lot of attention. Iglesias et al. [20] investigated the large-amplitude axisymmetric free vibrations of an incompressible hyperelastic orthotropic cylinder and proved that the motion of the structure can evolve from periodic to quasi-periodic and chaotic motions. Gonçalve et al. [21] presented detailed analyses of the nonlinear vibration of a pre-stretched hyperelastic circular membrane subjected to finite deformations and a time-varying lateral pressure. Breslavsky et al. [22] investigated the free and forced nonlinear vibrations of a hyperelastic thin square plate, and the results stated that the frequency shift between low- and large-amplitude vibrations of the plate weakens with an increased initial deflection.

There are many studies on cylindrical shells or hyperelastic structures in the field of dynamics, while some involve hyperelastic cylindrical shells. Based on the finite deformation theory, Shahinpoor et al. [23] analyzed the large-amplitude radial vibrations of a thin hyperelastic tube and obtained an exact solution to its simplified problem. Wang et al. [24] examined the radially and axially symmetric nonlinear motions of a hyperelastic cylindrical tube composed of a class of transversely isotropic compressible neo-Hookean materials about the radial direction. Breslavsky et al. [25] studied static and dynamic responses of a circular cylindrical shell made of hyperelastic arterial material and found the complex nonlinear dynamic behaviors in a resonant regime with both driven and companion modes.

At present, there are many studies on the nonlinear vibrations of cylindrical shells; however, most of the studies are based on linear constitutive relationships, while little literature has reported the nonlinear motion of cylindrical shells based on hyperelastic constitutive relations. This paper mainly focuses on the hyperelastic property of rubber materials but not other properties, such as viscoelasticity. The nonlinear behaviors are studied for a rubber cylindrical shell composed of the classical incompressible Mooney–Rivlin material, in which the shell is subjected to a radial harmonic excitation. In Sect. 2, the necessary preliminaries of tensor analysis are given, and a system of nonlinear differential equations describing the motion of the shell is derived based on some necessary hypotheses and reasoning processes. In Sect. 3, for the case of multimodal expansion, the influence of the interaction between modes on the calculation results is first compared. Particularly, the effects of excitation, structural parameters and material parameters on the modes of radially nonlinear vibration of the shell are analyzed in detail by bifurcation diagrams and Poincaré sections, respectively. Finally, the conclusions drawn in this paper are presented in Sect. 4.

2 Formulation

2.1 Preliminaries

Let X be a particle in the initial configuration ${\varvec{\chi }}_0$, and let ${{\varvec{X}}}={\varvec{\chi }}_0 (X)$ be the place of the particle. Correspondingly, in the current configuration ${\varvec{\chi }}_t$, the particle occupies the place ${{\varvec{x}}}$, given by

$$\begin{aligned} {\varvec{x}}={\varvec{\chi }}_t (X)={\varvec{\chi }}_t \left[ {{\varvec{\chi }}_0^{-1} ({\varvec{X}})} \right] ={\varvec{\chi }}({\varvec{X}}) \end{aligned}$$

(1)

In order to analyze the deformation from the initial configuration ${\varvec{\chi }}_0$ to the current configuration ${\varvec{\chi }}_t$, differentiating Eq. (1) with respect to ${{\varvec{X}}}$ yields

$$\begin{aligned} \hbox {d}{{\varvec{x}}}=\frac{\hbox {d}{{\varvec{x}}}}{\hbox {d}{{\varvec{X}}}}\cdot \hbox {d}{{\varvec{X}}}={{\varvec{F}}}\cdot \hbox {d}{{\varvec{X}}} \end{aligned}$$

(2)

where ${{\varvec{F}}}=\hbox {d}{{\varvec{x}}}/\hbox {d}{{\varvec{X}}}$ is the deformation gradient tensor, and for future reference, the standard notation [26] is defined as

$$\begin{aligned} J=\det {{\varvec{F}}} \end{aligned}$$

(3)

and the Green–Lagrange strain tensor is as follows

$$\begin{aligned} {{\varvec{E}}}=\left[ {{\begin{array}{lll} {\varepsilon _{xx} }&{}\quad {\varepsilon _{x\theta } }&{}\quad {\varepsilon _{xz} } \\ {\varepsilon _{\theta x} }&{}\quad {\varepsilon _{\theta \theta } }&{}\quad {\varepsilon _{\theta z} } \\ {\varepsilon _{xz} }&{}\quad {\varepsilon _{\theta z} }&{}\quad {\varepsilon _{zz} } \\ \end{array} }} \right] =\frac{1}{2}\left( {{{\varvec{F}}}^{\mathrm {T}}\cdot {{\varvec{F}}}-{{\varvec{I}}}} \right) \end{aligned}$$

(4)

The polar decomposition theorem is of considerable assistance in the geometrical interpretation of the deformation. With the aid of this theorem, the deformation gradient tensor ${{\varvec{F}}}$ can be decomposed into the product of an orthogonal rotation tensor ${{\varvec{R}}}$ and a symmetric tensor (the right Cauchy stretch tensor ${{\varvec{U}}}$ or the left Cauchy stretch tensor ${{\varvec{V}}}$); then, the general deformation is decomposed into pure stretch and rotation. The polar decomposition theorem states that ${{\varvec{F}}}$ has uniquely right and left decompositions of the following form

$$\begin{aligned} {{\varvec{F}}}={{\varvec{R}}}\cdot {{\varvec{U}}}={{\varvec{V}}}\cdot {{\varvec{R}}} \end{aligned}$$

(5)

Based on the right decomposition of $\mathbf{F}$, the right Cauchy–Green deformation tensor can be expressed as

$$\begin{aligned} {{\varvec{C}}}={{\varvec{F}}}^{\mathrm {T}}\cdot {{\varvec{F}}}={{\varvec{U}}}^{2} \end{aligned}$$

(6)

Substitution of Eq. (6) into Eq. (4) leads to

$$\begin{aligned} {{\varvec{C}}}=2{{\varvec{E}}}+{{\varvec{I}}}=\left[ {{\begin{array}{lll} {2\varepsilon _{xx} +1}&{}\quad {2\varepsilon _{x\theta } }&{}\quad {2\varepsilon _{xz} } \\ {2\varepsilon _{\theta x} }&{}\quad {2\varepsilon _{\theta \theta } +1}&{}\quad {2\varepsilon _{\theta z} } \\ {2\varepsilon _{xz} }&{}\quad {2\varepsilon _{\theta z} }&{}\quad {2\varepsilon _{zz} +1} \\ \end{array} }} \right] \end{aligned}$$

(7)

Then the principal invariants of the right Cauchy–Green deformation tensor ${{\varvec{C}}}$ are given by

$$\begin{aligned} I_1 =\hbox {tr}\left( {{\varvec{C}}} \right) ,I_2 =\frac{1}{2}\left[ {\left( {\hbox {tr}{{\varvec{C}}}} \right) ^{2}+\hbox {tr}\left( {{{\varvec{C}}}^{2}} \right) } \right] ,I_3 =J^{2}=\det \;{{\varvec{C}}} \end{aligned}$$

(8)

2.2 Hyperelastic Materials

As a classical hyperelastic constitutive model, the Mooney–Rivlin model is used to simulate the nonlinear elastic responses of certain rubber and rubber materials, and the associated strain energy function is as follows

$$\begin{aligned} \varPhi =\frac{\mu _1 }{2}\left( {I_1 -3} \right) +\frac{\mu _2 }{2}\left( {I_2 -3} \right) \end{aligned}$$

(9)

where $\mu _1 ,\mu _2$ are material constants; with Eqs. (7) and (8), the detailed expressions of the principal invariants $I_1 ,I_2 ,I_3$ are, respectively, given by

$$\begin{aligned} I_1= & {} 2\left( {\varepsilon _{xx} +\varepsilon _{\theta \theta } +\varepsilon _{zz} } \right) +3 \nonumber \\ I_2= & {} 4\left( {\varepsilon _{xx} \varepsilon _{\theta \theta } +\varepsilon _{xx} \varepsilon _{zz} +\varepsilon _{\theta \theta } \varepsilon _{zz} -\varepsilon _{x\theta }^2 -\varepsilon _{xz}^2 -\varepsilon _{\theta z}^2 } \right) +3 \nonumber \\ I_3= & {} J^{2}=\left( {2\varepsilon _{zz} +1} \right) \left[ {\left( {2\varepsilon _{xx} +1} \right) \left( {2\varepsilon _{\theta \theta } +1} \right) -4\varepsilon _{x\theta }^2 } \right] \nonumber \\&-\,4\varepsilon _{\theta z}^2 \left( {2\varepsilon _{xx} +1} \right) -4\varepsilon _{xz}^2 \left( {2\varepsilon _{\theta \theta } +1} \right) +16\varepsilon _{x\theta } \varepsilon _{\theta z} \varepsilon _{xz} \end{aligned}$$

(10)

The incompressibility constraint requires that $J=1$ [26]. With the third equation in Eq. (10), it gives

$$\begin{aligned} \varepsilon _{zz} =\frac{1+4\varepsilon _{\theta z}^2 \left( {2\varepsilon _{xx} +1} \right) +4\varepsilon _{xz}^2 \left( {2\varepsilon _{\theta \theta } +1} \right) -16\varepsilon _{x\theta } \varepsilon _{\theta z} \varepsilon _{xz} }{2\left[ {\left( {2\varepsilon _{xx} +1} \right) \left( {2\varepsilon _{\theta \theta } +1} \right) -4\varepsilon _{x\theta }^2 } \right] }-\frac{1}{2} \end{aligned}$$

(11)

Under the assumption of small strain, the expression of $\varepsilon _{zz}$ in a polynomial form is derived, namely

$$\begin{aligned} \varepsilon _{zz}= & {} -\left( {\varepsilon _{xx} +\varepsilon _{\theta \theta } } \right) +2\left( {\varepsilon _{xx}^2 +\varepsilon _{\theta \theta }^2 +\varepsilon _{xx} \varepsilon _{\theta \theta } +\varepsilon _{x\theta }^2 +\varepsilon _{\theta z}^2 +\varepsilon _{xz}^2 } \right) -4\varepsilon _{xx} \left( {\varepsilon _{xx}^2 +\varepsilon _{\theta \theta }^2 +2\varepsilon _{x\theta }^2 +\varepsilon _{xz}^2 } \right) \nonumber \\&-\,4\varepsilon _{\theta \theta } \left( {\varepsilon _{\theta \theta }^2 +\varepsilon _{xx}^2 +\varepsilon _{\theta z}^2 +2\varepsilon _{x\theta }^2 } \right) -8\varepsilon _{x\theta } \varepsilon _{xz} \varepsilon _{\theta z} +8\left( {\varepsilon _{xx}^3 \varepsilon _{\theta \theta } +\varepsilon _{xx} \varepsilon _{\theta \theta }^3 +4\varepsilon _{xx} \varepsilon _{\theta \theta } \varepsilon _{x\theta }^2 } \right) \nonumber \\&+\,16\left( {2\varepsilon _{xx} \varepsilon _{x\theta } \varepsilon _{xz} \varepsilon _{\theta z} +2\varepsilon _{\theta \theta } \varepsilon _{x\theta } \varepsilon _{xz} \varepsilon _{\theta z} } \right) +8\left( {\varepsilon _{xx}^4 +\varepsilon _{\theta \theta }^4 +\varepsilon _{x\theta }^4 +\varepsilon _{xx}^2 \varepsilon _{\theta \theta }^2 +3\varepsilon _{xx}^2 \varepsilon _{x\theta }^2 +3\varepsilon _{\theta \theta }^2 \varepsilon _{x\theta }^2 } \right) \nonumber \\&+\,8\left( {3\varepsilon _{\theta \theta }^2 \varepsilon _{x\theta }^2 +\varepsilon _{xx}^2 \varepsilon _{xz}^2 +\varepsilon _{\theta \theta }^2 \varepsilon _{\theta z}^2 +\varepsilon _{x\theta }^2 \varepsilon _{\theta z}^2 +\varepsilon _{x\theta }^2 \varepsilon _{xz}^2 } \right) + \cdots \end{aligned}$$

(12)

Substituting Eqs. (12) and (10) into Eq. (9) yields the specific expression of the strain energy function (9) associated with the incompressible Mooney–Rivlin material. With the consideration of the complexity of computation, expanding the strain energy function for small strains, including $\varepsilon _{xx}$, $\varepsilon _{\theta \theta }$, $\varepsilon _{zz}$, $\varepsilon _{x\theta }$, $\varepsilon _{xz}$ and $\varepsilon _{\theta z}$, up to the fourth order, it gives

$$\begin{aligned} \varPhi\approx & {} 2\mu _1 \left( {\varepsilon _{xx}^2 +\varepsilon _{\theta \theta }^2 +\varepsilon _{xx} \varepsilon _{\theta \theta } +\varepsilon _{x\theta }^2 +\varepsilon _{\theta z}^2 +\varepsilon _{xz}^2 } \right) +8\mu _1 \left( {\varepsilon _{xx}^3 \varepsilon _{\theta \theta } +\varepsilon _{xx} \varepsilon _{\theta \theta }^3 +4\varepsilon _{xx} \varepsilon _{\theta \theta } \varepsilon _{x\theta }^2 } \right) \nonumber \\&-\,4\mu _1 \left[ {\varepsilon _{xx} \left( {\varepsilon _{xx}^2 +\varepsilon _{\theta \theta }^2 +2\varepsilon _{x\theta }^2 +\varepsilon _{xz}^2 } \right) +\varepsilon _{\theta \theta } \left( {\varepsilon _{\theta \theta }^2 +\varepsilon _{xx}^2 +\varepsilon _{\theta z}^2 +2\varepsilon _{x\theta }^2 } \right) +2\varepsilon _{x\theta } \varepsilon _{xz} \varepsilon _{\theta z} } \right] \nonumber \\&+\,8\mu _1 \left[ {4\left( {\varepsilon _{xx} \varepsilon _{x\theta } \varepsilon _{xz} \varepsilon _{\theta z} +\varepsilon _{\theta \theta } \varepsilon _{x\theta } \varepsilon _{xz} \varepsilon _{\theta z} } \right) +\left( {\varepsilon _{xx}^4 +\varepsilon _{\theta \theta }^4 +\varepsilon _{x\theta }^4 +\varepsilon _{xx}^2 \varepsilon _{\theta \theta }^2 +3\varepsilon _{xx}^2 \varepsilon _{x\theta }^2 } \right. } \right. \left. {\left. {+3\varepsilon _{\theta \theta }^2 \varepsilon _{x\theta }^2 } \right) } \right] \nonumber \\&+\,8\mu _1 \left( {3\varepsilon _{\theta \theta }^2 \varepsilon _{x\theta }^2 +\varepsilon _{xx}^2 \varepsilon _{xz}^2 +\varepsilon _{\theta \theta }^2 \varepsilon _{\theta z}^2 +\varepsilon _{x\theta }^2 \varepsilon _{\theta z}^2 +\varepsilon _{x\theta }^2 \varepsilon _{xz}^2 } \right) +2\mu _2 \left[ {\varepsilon _{xx} \varepsilon _{\theta \theta } } \right. \left. {-\left( {\varepsilon _{x\theta }^2 +\varepsilon _{xz}^2 +\varepsilon _{\theta z}^2 } \right) } \right] \nonumber \\&-\,2\mu _2 \left( {\varepsilon _{xx} +\varepsilon _{\theta \theta } } \right) \left[ {\left( {\varepsilon _{xx} +\varepsilon _{\theta \theta } } \right) -2\left( {\varepsilon _{xx}^2 +\varepsilon _{\theta \theta }^2 +\varepsilon _{xx} \varepsilon _{\theta \theta } +\varepsilon _{x\theta }^2 } \right. } \right. \left. {\left. {+\varepsilon _{\theta z}^2 +\varepsilon _{xz}^2 } \right) } \right] \nonumber \\&-\,8\mu _2 \left( {\varepsilon _{xx} +\varepsilon _{\theta \theta } } \right) \left[ {\varepsilon _{xx} \left( {\varepsilon _{xx}^2 +\varepsilon _{\theta \theta }^2 +\varepsilon _{xz}^2 +2\varepsilon _{x\theta }^2 } \right) +\varepsilon _{\theta \theta } \left( {\varepsilon _{\theta \theta }^2 +\varepsilon _{xx}^2 } \right. } \right. \left. {\left. {+\varepsilon _{\theta z}^2 +2\varepsilon _{x\theta }^2 } \right) +2\varepsilon _{x\theta } \varepsilon _{xz} \varepsilon _{\theta z} } \right] \nonumber \\ \end{aligned}$$

(13)

2.3 Shell Theory and Discretization of Displacement

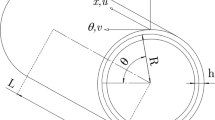
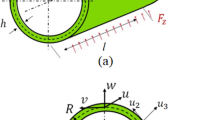
Consider a thin-walled rubber cylindrical shell in the shell cylindrical coordinate system $(x,\theta ,z)$; see Fig. 1. A cylindrical coordinate system is established in the middle surface of the shell, with x, $\theta$ and z the axial, circumferential and radial directions, respectively. Figure 1b shows a cross section with respect to the x direction, and the displacements of a point in the middle surface of the shell are indicated by u, v and w. The displacements of an arbitrary material point in the shell are denoted by $u_1$, $u_2$ and $u_3$. The initial length, initial thickness and radius of the middle surface of the shell are denoted by l, h and R, respectively.

Fig. 1

Sketch map of a cylindrical shell: a symbols used for dimensions and displacements of a generic point; b cross section of the shell about the x direction

In terms of the Kirchhoff–Love hypothesis [27], the relation between the displacement $(u_1 ,u_2 ,u_3 )$ of an arbitrary material point and the displacement (u, v, w) of a point at the middle surface of the shell is that

$$\begin{aligned} u_1 =u\left( {x,\theta } \right) -\frac{\partial w}{\partial x}z,u_2 =v\left( {x,\theta } \right) -\frac{1}{R}\frac{\partial w}{\partial \theta }z,u_3 =w\left( {x,\theta } \right) \end{aligned}$$

(14)

Based on Donnell’s nonlinear shallow shell theory, the relations between strains and displacements are, respectively, given by [28].

$$\begin{aligned} \varepsilon _{xx}= & {} \frac{\partial u}{\partial x}+\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right) ^{2}-\frac{\partial ^{2}w}{\partial x^{2}}z \nonumber \\ \varepsilon _{\theta \theta }= & {} \frac{1}{R}\left( {\frac{\partial v}{\partial \theta }+w} \right) +\frac{1}{2R^{2}}\left( {\frac{\partial w}{\partial \theta }} \right) ^{2}-\frac{1}{R^{2}}\frac{\partial ^{2}w}{\partial \theta ^{2}}z \nonumber \\ \varepsilon _{x\theta }= & {} \frac{1}{R}\frac{\partial u}{\partial \theta }+\frac{\partial v}{\partial x}+\frac{1}{R}\frac{\partial w}{\partial \theta }\frac{\partial w}{\partial x}-2\frac{1}{R}\frac{\partial ^{2}w}{\partial \theta \partial x}z \end{aligned}$$

(15)

Generally, for thin-walled shells, it gives $\varepsilon _{zz} \approx 0,\varepsilon _{xz} \approx 0,\varepsilon _{\theta z} \approx 0$. Then the expressions describing the kinetic energy T and the elastic strain energy P of the shell are given as follows

$$\begin{aligned}&T=\frac{1}{2}\rho \int _0^{2\pi } {\int _0^l {\int _{-\frac{h}{2}}^{\frac{h}{2}} {({\dot{u}}_1^2 +{\dot{u}}_2^2 +{\dot{u}}_3^2 \hbox {)}R\hbox {d}\theta \hbox {d}x} } } \hbox {d}z \end{aligned}$$

(16)

$$\begin{aligned}&P=\int _0^{2\pi } {\int _0^l{\int _{-\frac{h}{2}}^{\frac{h}{2}} {\Phi R\hbox {d}\theta \hbox {d}x} } } \hbox {d}z \end{aligned}$$

(17)

where h, $\rho$ and $\varPhi$ are the thickness, the density of the material and the strain energy function, respectively.

The simply supported boundary conditions at the shell edges, $x=0,l$, require that

$$\begin{aligned} v=w=0 \end{aligned}$$

(18)

In order to simplify the problem, the continuous system with infinite degrees of freedom is discretized into a finite degree of freedom using approximate functions. The base functions describing the intermediate surface displacements, which satisfy identically the geometric boundary conditions, are used to discretize the system, i.e.,

$$\begin{aligned} \left\{ {\begin{array}{l} u(x,\theta ,t)=u_{mn} (t)\cos (n\theta )\cos (\lambda _m x)+u_{10} (t)\cos (\lambda _1 x)+u_{30} (t)\cos (\lambda _3 x) \\ v(x,\theta ,t)=v_{mn} (t)\sin (n\theta )\sin (\lambda _m x)+v_{10} (t)\sin (\lambda _1 x)+v_{30} (t)\sin (\lambda _3 x) \\ w(x,\theta ,t)=w_{mn} (t)\cos (n\theta )\sin (\lambda _m x)+w_{10} (t)\cos (\lambda _1 x)+w_{30} (t)\cos (\lambda _3 x) \\ \end{array}} \right. \end{aligned}$$

(19)

where m and n are the numbers of longitudinal half wave and circumferential wave, $\lambda _m =m\pi /l$, t is time, and $u_{mn} (t)$, $v_{mn} (t)$ and $w_{mn} (t)$ are generalized displacements with respect to t, respectively.

2.4 Lagrange Equations, External Forces and Damping

Let $W_e$ be the virtual work done by the periodic external force and $W_d$ be Rayleigh’s dissipation function [29] describing the virtual work done by the non-conservative damping force. The corresponding expressions are, respectively, given by

$$\begin{aligned}&W_e =\int _0^{2\pi } {\int _0^l {(F_x u+F_\theta v+F_z w)R\hbox {d}\theta \hbox {d}x} } \nonumber \\&W_d =\frac{1}{2}c\int _0^{2\pi } {\int _0^l {({\dot{u}}^{2}+{\dot{v}}^{2}+{\dot{w}}^{2})R\hbox {d}\theta \hbox {d}x} } \end{aligned}$$

(20)

where $F_x$, $F_\theta$ and $F_z$ are distributed forces per unit area acting on the shell in the directions of x, $\theta$ and z, respectively; and c is a coefficient related to the dumping. Simple calculation yields [29]

$$\begin{aligned} W_d =\frac{1}{2}\frac{l}{2}R\sum _{n=1}^N {\sum _{m=1}^M {\psi _n c_{m,n} ({\dot{u}}_{m,n}^2 +{\dot{v}}_{m,n}^2 +{\dot{w}}_{m,n}^2 )} } \end{aligned}$$

(21)

where $\psi _n =\left\{ {{\begin{array}{l} {2\pi ,n=0} \\ {\pi ,\;\;n>0} \\ \end{array} }} \right.$ and $c_{m,n}$ is the damping coefficient related to the modal damping ratio, which can be evaluated from experiments.

Let $\varsigma _{m,n} =c_{m,n} /\left( {2\rho _{m,n} \omega _{m,n} } \right)$, where $\omega _{m,n}$ is the natural frequency of mode $\left( {m,n} \right)$ and $\rho _{m,n}$ is the modal mass of this mode. Let ${{\varvec{q}}}=(u_{m,n} ,v_{m,n} ,w_{m,n} )^{\mathrm {T}}$, where the generic elements of the time-dependent vector ${{\varvec{q}}}$ are referred to as $q_i (i=1,2,\ldots ,9)$. The generalized forces $G_i$ ($i=1,2,\ldots ,9)$ can be obtained by differentiating Rayleigh’s dissipation function and the virtual work done by external forces, i.e.,

$$\begin{aligned} G_i =-\frac{\partial W_d }{\partial {\dot{q}}_i }+\frac{\partial W_e }{\partial q_i }\;\;\;\;\;\;(i=1,2,\ldots ,9) \end{aligned}$$

(22)

Then, the Lagrange equations describing the motion of the shell are given by

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\left( {\frac{\partial L}{\partial {\dot{q}}_i }} \right) -\frac{\partial L}{\partial q_i }=G_i \;\;\;\;\;\;(i=1,2,\ldots ,9) \end{aligned}$$

(23)

where $L=T-P$ is the Lagrangian function associated with the system and i is the number of modes.

Substituting the related expressions into the Lagrange equations (23) yields the nonlinear differential equations

$$\begin{aligned} {{\varvec{M}}}\ddot{{{\varvec{q}}}}+{{\varvec{C}}}{\dot{{{\varvec{q}}}}}+{{\varvec{Kq}}}+{{\varvec{K}}}_2 {{\varvec{q}}}^{2}+{{\varvec{K}}}_3 {{\varvec{q}}}^{3}={{\varvec{F}}}\cos \left( {\varOmega t} \right) \end{aligned}$$

(24)

where ${{\varvec{M}}}$ is the mass matrix, ${{\varvec{K}}}$ is the linear rigid matrix, and ${{\varvec{K}}}_2$ and ${{\varvec{K}}}_3$ are the quadratic and cubic nonlinear rigid matrices, respectively. ${{\varvec{C}}}$ is the Rayleigh damping matrix, and ${{\varvec{C}}}=\beta {{\varvec{K}}}+\gamma {{\varvec{M}}}$, where $\beta$ and $\gamma$ are constants to be determined experimentally. ${{\varvec{q}}}=\left\{ {q_1 ,q_2 ,\ldots ,q_9 } \right\} ^{\mathrm {T}}$, and ${{\varvec{F}}}=\left\{ {F_{x1} ,F_{x2} ,F_{x3} ,F_{\theta 1} ,F_{\theta 2} ,F_{\theta 3} ,F_{z1} ,F_{z2} ,F_{z3} } \right\} ^{\mathrm {T}}$. The elements of the mass and linear stiffness matrices are given in Appendix. This work only considers the radial vibration of the cylindrical shell under a radial periodic excitation, which means that $F_{xj} =F_{\theta j} =0\;\left( {j=1,2,3} \right)$. It is convenient to introduce the following transformations,

$$\begin{aligned} Q_i= & {} \frac{q_i }{h}\hbox { }\left( {i=1,2,\ldots ,9} \right) \end{aligned}$$

(25)

$$\begin{aligned} \bar{{{{\varvec{C}}}}}= & {} {{\varvec{M}}}^{-1}{{\varvec{C}}},{\varvec{\omega }} ={{\varvec{M}}}^{-1}{{\varvec{K}}}, \bar{{{{\varvec{K}}}}}_2 =h{{\varvec{M}}}^{-1}{{\varvec{K}}}_2 ,\bar{{{{\varvec{K}}}}}_3 =h^{2}{{\varvec{M}}}^{-1}{{\varvec{K}}}_3 ,\bar{{{{\varvec{F}}}}}=\frac{{{\varvec{M}}}^{-1}{{\varvec{F}}}}{h} \end{aligned}$$

(26)

Multiplying both sides of Eq. (24) by ${{\varvec{M}}}^{-1}$, with Eqs. (25) and (26), it yields

$$\begin{aligned} {\ddot{{{\varvec{Q}}}}}+\bar{{{{\varvec{C}}}}}{{\varvec{Q}}}+\left( {{\varvec{\omega }} +\bar{{{{\varvec{K}}}}}_2 +\bar{{{{\varvec{K}}}}}_3 } \right) {{\varvec{Q}}}=\bar{{{{\varvec{F}}}}}\cos \left( {\varOmega t} \right) \end{aligned}$$

(27)

where

$$\begin{aligned} \left[ {\bar{{{{\varvec{C}}}}}} \right] =\hbox {diag}\left( {2\zeta _{m,n,1} \omega _{m,n,1} ,2\zeta _{m,n,2} \omega _{m,n,2} ,\ldots ,2\zeta _{m,n,9} \omega _{m,n,9} } \right) \end{aligned}$$

(28)

where $\zeta _i =\omega _{m,n,i} \zeta _{m,n,i} ,\omega _{m,n,i}$ and $\zeta _{m,n,i} \quad \left( {i=1,2, \ldots ,9} \right)$ are natural frequencies and damping ratios, respectively.

In addition, since the in-plane displacement is relatively small compared with the radial displacement, the inertia and damping terms in the corresponding plane are negligible. Currently, most of the literature simplifies the above differential equations into those of radial motion via introducing stress functions and ignoring the inertia and damping terms in the surface. Then the equations are simplified into a differential equation only regarding the radial displacement w. However, after introducing the stress function, the computing process will become more complex. In order to simplify the process, this paper deals with Eq. (27) based on the concept of condensation of degree of freedom. Under the conditions of neglecting the in-plane inertia and damping terms, Eq. (27) may give the following approximate motion and deformation relations

$$\begin{aligned} \left[ {{\begin{array}{lllllll} 1&{}\quad \cdots &{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots \\ 0&{}\quad \cdots &{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0 \\ \end{array} }} \right] _{6\times 9} \left\{ {{\begin{array}{l} 0 \\ \vdots \\ 0 \\ {\ddot{w}_j } \\ \end{array} }} \right\} _{9\times 1} +\left[ {{\begin{array}{lll} {\bar{{K}}_{11} }&{}\quad \cdots &{}\quad {\bar{{K}}_{19} } \\ \vdots &{}\quad \ddots &{}\quad \vdots \\ {\bar{{K}}_{61} }&{}\quad \cdots &{}\quad {\bar{{K}}_{69} } \\ \end{array} }} \right] _{6\times 9} \left\{ {{\begin{array}{l} {u_j } \\ {v_j } \\ {w_j } \\ \end{array} }} \right\} _{9\times 1} =\left\{ 0 \right\} _{6\times 1} \end{aligned}$$

(29)

Moreover,

$$\begin{aligned} \left\{ {{\begin{array}{l} {u_j } \\ {v_j } \\ \end{array} }} \right\} _{6\times 1} =\left[ {S} \right] ^{\mathrm{T}}_{6\times 6} \left\{ {{\begin{array}{l} {w_j } \\ {\ddot{w}_j } \\ \end{array} }} \right\} _{6\times 1} =\left[ {{\begin{array}{lll} {S_{11} }&{}\quad {S_{12} }&{}\quad {S_{13} } \\ \vdots &{}\quad \ddots &{}\quad \vdots \\ {S_{61} }&{}\quad {S_{62} }&{}\quad {S_{63} } \\ \end{array} }} \right] _{6\times 3} \left\{ {w_j } \right\} _{3\times 1} +\left[ {{ \begin{array}{clc} {S_{14} }&{}\quad {S_{15} }&{}\quad {S_{16} } \\ \vdots &{}\quad \ddots &{}\quad \vdots \\ {S_{64} }&{}\quad {S_{65} }&{}\quad {S_{66} } \\ \end{array} }} \right] _{6\times 3} \left\{ {\ddot{w}_j } \right\} _{3\times 1}\nonumber \\ \end{aligned}$$

(30a)

where

$$\begin{aligned} \left[ S \right] ^{\mathrm{T}}=-\left[ {{\begin{array}{lll} {\bar{{K}}_{11} }&{}\quad \cdots &{}\quad {\bar{{K}}_{16} } \\ \vdots &{}\quad \ddots &{}\quad \vdots \\ {\bar{{K}}_{61} }&{}\quad \cdots &{}\quad {\bar{{K}}_{66} } \\ \end{array} }} \right] ^{-1}\left[ {{\begin{array}{llllll} {\bar{{K}}_{17} }&{}\quad {\bar{{K}}_{18} }&{}\quad {\bar{{K}}_{19} }&{}\quad 0&{}\quad 0&{}\quad 0 \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots \\ {\bar{{K}}_{67} }&{}\quad {\bar{{K}}_{68} }&{}\quad {\bar{{K}}_{69} }&{}\quad 0&{}\quad 0&{}\quad 0 \\ \end{array} }} \right] \end{aligned}$$

(30b)

With the aid of Eq. (30), the differential equation of motion is given as follows

$$\begin{aligned} {\ddot{{{\varvec{W}}}}}+{\varvec{\varsigma }} {\dot{{{\varvec{W}}}}}+\left( {{\varvec{\omega }} +\bar{{{{\varvec{K}}}}}_{2c} +\bar{{{{\varvec{K}}}}}_{3c} } \right) {{\varvec{W}}}={{\varvec{F}}}_z \cos \left( {\varOmega t} \right) \end{aligned}$$

(31)

where $W_{j}=w_{j}/h$

3 Numerical Simulations and Results

Next, to simulate numerically the nonlinear oscillation problem considered in this paper, it is necessary to take some material and structure parameters, i.e., $\mu _1 =416185.5\hbox { Pa}$, $\mu _2 =-498.8\hbox { Pa}$, $\rho =1100\hbox { kgm}^{-3}$ (the linearized material parameters of the incompressible Mooney–Rivlin material given in [22]), $R=150\times 10^{-3}\hbox { m}$ (the radius of the cylindrical thin-walled shell) and $\zeta _{m,n,3} =0.0005$ (the damping ratio with $\zeta _{m,n,i} =\zeta _{m,n,1} \omega _{m,n,i} /\omega _{m,n,1}$ given in [30]). To discuss the influences of structural parameters, it is convenient to introduce the following two structural parameters

$$\begin{aligned} \alpha =\frac{h}{R},\hbox { }\beta =\frac{2R}{l} \end{aligned}$$

(32)

where $\alpha$ is the thickness–radius ratio and $\beta$ is the diameter–length ratio.

3.1 Natural Frequencies

To determine the structural damping coefficient, the natural frequencies of the shell are required to be analyzed. The detailed information of natural frequencies can be obtained with the aid of Eq. (24). Additionally, the relations between natural frequencies and different parameters are also obtained, as shown in Fig. 2.

Fig. 2

Natural frequencies of the shell versus the number circumferential waves n for $\alpha =0.02,\beta =0.5$

Comparing among the circumferential, axial and radial directions, Fig. 2 illustrates that the natural frequency of radial motion is usually smallest. To determine the characteristics of fundamental frequency of the shell, further analysis of the radial natural frequency should be conducted.

Some relations between the structural parameters and radial natural frequencies are given via analyzing different combinations of structural parameters, as shown in Fig. 3. Generally, for short cylindrical shells, the diameter–length ratio $\beta >1$; otherwise, they are long shells. In terms of the curves shown in Fig. 3, for moderately long shells, $\beta =0.5$, the comparison among $\alpha =0.005$, $\alpha =0.01$ and $\alpha =0.02$ indicates that the larger is the thickness–radius ratio $\alpha$, the larger are the natural frequencies of modes, and the influence is more significant for the mode with a larger circumferential wave number n. And the comparison among $\beta =0.5$, $\beta =1.0$ and $\beta =1.5$ manifests that the larger is the diameter–length ratio, the larger are the natural frequencies of modes, and the influence is more significant for the mode with a lower circumferential wave number n.

Fig. 3

Relations of radial natural frequencies with different values of $\alpha$ and $\beta$

Additionally, Fig. 3 clearly illustrates that, generally speaking, the fundamental frequency of the shell is not equal to the frequency of the mode with the wave numbers $m=1$ and $n=0$. Comparing the influences of the thickness–radius ratio $\alpha$ and the diameter–length ratio $\beta$, it is obvious that the diameter–length ratio $\beta$ affects the fundamental frequency more significant. With the increasing value of diameter–length ratio $\beta$, the circumferential wave number n of the mode with the lowest frequency increases remarkably. Nevertheless, the higher-order natural vibration mode is difficult to be excited; actually, this paper mainly focuses on the influence of the thickness–radius ratio $\alpha$. Then, further mode analyses with the circumferential wave numbers n = 0–4 are carried out. Next, the influences of structural parameters on the five modal frequencies are considered.

Fig. 4

Relations of radial natural frequencies with $\alpha$ or $\beta$

Fig. 5

Bifurcation diagram describing the radial motion of the shell with the excitation amplitude $F_z$

As shown in Fig. 4a, b, the effects of thickness–radius ratio $\alpha$ on the five modal frequencies of the shell are slightly different. In general, the thickness–radius ratio $\alpha$ has a greater influence on the modes with larger circumferential wave numbers n, which is also consistent with the results in Fig. 3. Furthermore, the intersection of curves in Fig. 4a indicates that, for moderately long shells, if appropriate parameters are selected, the frequencies of modes with different circumferential wave numbers could also be identical, which usually means there is 1:1 internal resonance. Moreover, Fig. 4b manifests that, when the diameter–length ratio is large, the frequencies of the modes with low circumferential wave numbers are close to one another. Figure 4c, d shows that the diameter–length ratio $\beta$ has an extremely complex effect on the natural frequencies of the shell. They also verify the conclusion drawn in Fig. 3 that the frequencies of the modes with low circumferential wave numbers are almost identical when the diameter–length ratio $\beta$ is larger than 1. For certain range of the diameter–length ratio $\beta \in \left( {0.5,2} \right)$, the frequency of the mode ($m=1,n=4$) reaches the lowest value basically; namely, when the thickness–radius ratio $\alpha$ is large, the frequency of the mode ($m=1,n=3$) may be the lowest, but the mode ($m=1,n=4$) is also very close to it. In addition, the crossing of the curves with different circumferential wave numbers versus certain diameter–length ratio $\beta$ manifests that the internal resonance depends on the diameter–length ratio.

Fig. 6

Poincaré sections describing the radial chaotic motions of the shell with different excitation amplitudes

Fig. 7

Bifurcation diagram describing the radial motion of the shell with the excitation frequency

As mentioned above, when the structural parameters satisfy certain conditions, the modal frequencies of the shell may be identical, and the complex internal resonance behavior may occur. The numerical examples show that the amount of computation will increase significantly due to the strong coupling effect caused by the interaction between modes. Therefore, in this paper, only the nonlinear dynamic behaviors of the shell without internal resonance are studied in detail, and some interesting phenomena are obtained, while the phenomena considering the coupling effect are simply analyzed for comparison.

Fig. 8

Poincaré sections describing the radial chaotic motions of the shell with different excitation frequencies

Fig. 9

Bifurcation diagrams describing the radial motions versus the thickness–radius ratio $\alpha$

3.2 Nonlinear Vibrations Without the Coupling Effect

Obviously, Eq. (24), the vibration characteristics of the shell studied in this paper, is strongly nonlinear. Next, the fourth-order Runge–Kutta method is used to solve the equations numerically, and the effects of various parameters on the vibration characteristics of the shell are analyzed. In addition, it can be seen from the above analysis that the fundamental frequency of the shell is usually determined by its radial natural frequency. Therefore, this paper only considers the case when the external excitation equals the fundamental frequency. Based on the analysis of Fig. 3, it is found that when the circumferential wave number $n=4$, the corresponding frequency is the lowest for different combinations of structural parameters and the influences of structural parameters are obvious. Then, the following study should consider the mode $m=1$, $n=4$. Additionally, as is shown in Fig. 3, due to the increase in diameter–length ratio $\beta$, the fundamental mode changes into a higher-order natural vibration mode which has a large circumferential wave number n.

3.2.1 Influences of Excitation Amplitude and Excitation Frequency

Generally, the amplitude of the external excitation has the most direct relation with the response of structures. Therefore, the chaotic dynamic performance of the shell on different excitation amplitudes needs to be analyzed. Setting the structural parameters as $\alpha =0.02, \beta =0.5$, employing the fourth-order Runge–Kutta method to solve the nonlinear equations and selecting the Poincaré sections under different excitation amplitudes, the bifurcation diagram of the radial motion of the shell with respect to the magnitude of the external excitation can be obtained.

Figure 5 illustrates that the radial motion of the shell is periodic for the excitation amplitude satisfying $F_z <5$ N, and when the excitation amplitude $F_z$ is approximately equal to 5.05 N, the chaotic radial motion of the shell appears for the first time. After that, with the increase in the excitation amplitude, the radial vibration presents an alternating change between the periodic and chaotic motions. It is worth noting that the motion of period-3 can be observed in the bifurcation diagram. Remarkably, it is found that the motion of period-3 occurs between the two chaotic regions, and evolves from chaotic to periodic oscillations through the path of period doubling bifurcation. This is consistent with the idea that period-3 implies chaos [31].

Figure 6 illustrates the Poincaré sections with certain excitation amplitudes. Some structures exhibit fractal features, which are referred to as the strange attractors. In general, the attractors can be classified into four different types, namely point attractor, limit cycle attractor, torus attractor and strange attractor. Here we mainly introduce the strange attractor, an attractor in the phase space, where the points never repeat themselves and the orbits never intersect, but stay within the same area of the phase space. Unlike limit cycles or point attractors, strange attractors are non-periodic and can take countless different forms. As the bifurcation parameters change, they will rotate and stretch to different degrees, seemingly with complex structures and various shapes, but in fact, there is a self-similarity between the local instability and the global instability. In addition, the presence of strange attractors also indicates that the moving area of the shell can determine a large-deflection vibration, even if its motion is irregular and unpredictable. In other words, the radial motion of any point of the shell is limited to an area determined by a strange attractor, but it is not possible to confirm the exact location of the point. This is also an important feature of a system with strange attractors: locally instable but globally stable. Two adjacent points in the strange attractor, although will be separated from each other over time, will not escape from the area determined by the strange attractor.

Fig. 10

Poincaré sections describing the radial chaotic motions versus different thickness–radius ratios

The influence of the excitation frequency is also investigated. In addition, the bifurcation diagrams for the fixed force $F_z =5.05$ N are given as follows.

Figure 7 illustrates the radial motion of the shell with a fixed force excitation and different excitation frequencies. Clearly, the periodic motion can be bifurcated from the chaotic region with the variation of frequencies, and vice versa. Additionally, the motion of period-3 can also be observed when the ratio of natural frequency to excitation frequency is at the range of $\left( {1.04,1.05} \right)$.

Figure 8 illustrates the Poincaré sections with certain excitation frequencies. The shape characteristics of those strange attractors, particularly in Fig. 8c, are similar to those in Fig. 6a, while the slender structural features distinguish Fig. 8 from Fig. 6, which means that the strange attractor with a smaller excitation force may be characterized with a slenderer shape.

3.2.2 Influences of Structural Parameters

Furthermore, this subsection analyzes the influences of different values of the thickness–radius ratio $\alpha$ on radial motions of the shell. For a thin-walled shell, set the diameter–length ratio $\beta =0.5$ and the excitation amplitude $F_z =5.05$ N.

As shown in Fig. 9, when the thickness–radius ratio $\alpha$ is about less than 0.02, the radial motions of the shell present a frequently alternate change between periodic and chaotic motions. While the thickness–radius ratio $\alpha$ is larger than 0.02, the radial motion is periodic, which means that the increase in the thickness–radius ratio is beneficial to the motion stability in certain range.

Figure 10 shows the Poincaré sections with certain thickness–radius ratios. Again, it shows the existence of strange attractors. The results show that the strange attractors are similar to the above; and it can be found that for the system with discontinuous chaotic regions, the attractors present some different structures in different parameter ranges. In particular, Fig. 10b presents the motion of period-9. With a small increase in the thickness–radius ratio $\alpha$, the radial motion transforms into the chaotic motion with three isolated attractor domains immediately, as shown in Fig. 10c. Furthermore, Fig. 10d illustrates the motion of period-3, and the periodic motion also evolves into chaos with the increase in thickness–radius ratio $\alpha$. This manifests that a minor variation in the thickness–radius ratio $\alpha$ between the period and chaotic regions may give rise to a great change in vibration behaviors.

3.2.3 Influences of Material Parameters

Since the material parameters of rubber materials are usually obtained by fitting experimental data, the values obtained by different fitting methods may be slightly different. With the assumption that the material parameters fluctuate up and down close to the initial values, i.e., ${\mu }'_1 =k_1 \mu _1 ,{\mu }'_2 =k_2 \mu _2$, where ${\mu }'_1 ,{\mu }'_2$ are the changed material parameters and $k_1 ,k_2 \in \left[ {0.9,1.1} \right]$ are given in the literature, it is necessary to analyze the motion characteristics of the shell with variable parameters.

Fig. 11

Bifurcation diagrams describing the radial motions versus material parameters

Figure 11 shows that the change in the material parameter $\mu _1$ affects the motion characteristics of cylindrical shell, and its chaotic response evolves from the chaotic motion to the periodic motion on the path of periodic doubling bifurcation, while the material parameter $\mu _2$ has little effect on the response of the shell. It manifests that the fitting accuracy of the material parameter $\mu _1$ is more important than that of $\mu _2$.

3.3 Nonlinear Vibrations with the Coupling Effect

Furthermore, in order to analyze the influence of the interaction between modes, three modes ($m=1,n=4$; $m=1,n=0$; and $m=3, n=0$) are selected to discretize the displacement, respectively. Then, the nonlinear dynamic behaviors of the radial motion of the shell are studied, followed by simple comparative analyses with the help of time responses and Poincaré sections.

Fig. 12

Uncoupled case: time responses and Poincaré sections for excitation amplitude $F_z =9.8$ N

Fig. 13

Coupled case: time responses and Poincaré sections for excitation amplitude $F_z =9.8$ N

Figure 12a, b, c shows the solutions obtained by the fourth-order Runge–Kutta method for the uncoupled case. It is found that, under the conditions of multimodal discretization, the chaotic phenomenon may also exist for the uncoupled case, while its fine structural characteristics are no longer obvious compared with the single-mode discretization. This may be caused by the increase in the degree of freedom, which leads to the increase in computational complexity and the decrease in the accuracy consequently. In addition, since the coupling effect is not taken into consideration, the responses between modes are independent. It means that when there is a chaotic response of one mode, the responses of other modes could still be periodic. Moreover, the amplitudes of axisymmetric modes are much smaller than those of non-axisymmetric modes. This manifests that the single-axisymmetric-mode analysis is feasible when the coupling effect is not considered.

Figure 13a, b, c shows the solutions obtained by the fourth-order Runge–Kutta method for the coupled case. It is obvious that the response is more regular, since the quasi-periodic motion replaces the chaos for the axisymmetric mode. To some extent, it means that the coupling effect between modes could improve the stability of motions. At the same time, due to the coupling effect, the modes of each order also have synchronization effect; that is, the properties of the modal responses of each order are similar. As is shown in Fig. 13, the Poincaré sections of all the three modes have five isolated regions.

4 Conclusions

This paper investigated the nonlinear behaviors of a rubber cylindrical shell composed of the incompressible Mooney–Rivlin material under a radial harmonic load. It should be noted that, in general, the description of mechanical behaviors of rubber materials can be approximated by using their associated hyperelastic constitutive relations under certain conditions [32], and this paper only takes the hyperelasticity of rubber materials into consideration, but not other properties, such as viscoelasticity. A system of differential equations describing the nonlinear vibration of the shell is obtained with the aid of Donnell’s shallow shell theory and the small strain hypothesis. The nonlinear dynamic behaviors of the shell are investigated by the corresponding bifurcation diagrams and Poincaré sections. The conclusions from this work are as follows.

• (1) The increases in both the thickness–radius ratio and the diameter–length ratio can raise the natural frequencies of modes, and the thickness–radius ratio has a significant impact on modes with large circumferential wave numbers, while the diameter–length ratio has a significant influence on modes with low circumferential wave numbers.

• (2) When the excitation amplitude is larger than a critical value, the radial motion tends to alternate between the chaotic and the periodic motions in the form of period doubling bifurcation. Moreover, when the excitation amplitude is sufficiently large, the periodic motion can be bifurcated from the chaotic region with the variation of excitation frequency.

• (3) Thickness–radius ratio can significantly affect the chaotic behavior of the cylindrical shell. For a given ratio, when the value is less than the critical value, the vibration of the shell is highly sensitive to the ratio, which means that a small change in the ratio can transform the chaotic motion into the periodic motion, and vice versa.

• (4) For the incompressible Mooney–Rivlin model, the influence of the material parameter $\mu _1$ on the nonlinear vibration behaviors of the rubber cylindrical shell is more significant compared with that of $\mu _2$.

• (5) For the multimodal case, when the coupling effect between different modes is not considered, responses of cylindrical shells are similar to those of the single-mode model. However, if the coupling effect is taken into account, different conclusions can be drawn. Additionally, the coupling effect could improve the stability of structural response.

Appendixes

Elements of the mass matrix:

$$\begin{aligned} {{\varvec{M}}}= & {} \left[ {{\begin{array}{lll} {M_{11} }&{}\quad \cdots &{}\quad 0 \\ \vdots &{}\quad \ddots &{}\quad \vdots \\ 0&{}\quad \cdots &{}\quad {M_{99} } \\ \end{array} }} \right] \nonumber \\ M_{11}= & {} M_{44} =\frac{\pi \rho lRh}{2}, M_{22} =M_{33} =M_{55} =M_{66} =\pi \rho lRh, M_{77} =\frac{\pi \rho h^{3}}{24lR}\left( {n^{2}l^{2}+\pi ^{2}R^{2}} \right) +\frac{\pi \rho lRh}{2},\nonumber \\ M_{88}= & {} \frac{\pi \rho hR}{12l}\left( {12l^{2}+\pi ^{2}h^{2}} \right) , M_{99} =\frac{\pi \rho hR}{4l}\left( {4l^{2}+3\pi ^{2}h^{2}} \right) \end{aligned}$$

(A1)

Elements of the linear stiffness matrix:

$$\begin{aligned} {{\varvec{K}}}= & {} \left[ {{\begin{array}{lll} {K_{11} }&{}\quad \cdots &{}\quad {K_{19} } \\ \vdots &{}\quad \ddots &{}\quad \vdots \\ {K_{91} }&{}\quad \cdots &{}\quad {K_{99} } \\ \end{array} }} \right] \nonumber \\ K_{11}= & {} \frac{\pi n^{2}lh}{2R}\left( {\mu _1 -4\mu _2 } \right) +\frac{2\pi ^{3}Rh}{l}\left( {\mu _1 -\mu _2 } \right) , K_{14} =K_{41} =-\pi ^{2}nh\left( {\mu _1 -\mu _2 } \right) -\frac{\pi ^{2}nh}{2}\left( {\mu _1 -4\mu _2 } \right) ,\nonumber \\ K_{17}= & {} K_{71} =-\pi ^{2}h\left( {\mu _1 -\mu _2 } \right) , K_{12} =K_{13} =K_{15} =K_{16} =K_{18} =K_{19} =0,\nonumber \\ K_{22}= & {} \frac{4\pi ^{3}Rh}{l}\left( {\mu _1 -\mu _2 } \right) , K_{28} =K_{82} =-2\pi ^{2}h\left( {\mu _1 -\mu _2 } \right) ,\nonumber \\ K_{21}= & {} K_{23} =K_{24} =K_{25} =K_{26} =K_{27} =K_{29} =0, K_{33} =\frac{36\pi ^{3}Rh}{l}\left( {\mu _1 -\mu _2 } \right) ,\nonumber \\ K_{39}= & {} K_{93} =-6\pi ^{2}h\left( {\mu _1 -\mu _2 } \right) , K_{31} =K_{32} =K_{34} =K_{35} =K_{36} =K_{37} =K_{38} =0,\nonumber \\ K_{44}= & {} \frac{2\pi n^{2}lh}{R}\left( {\mu _1 -\mu _2 } \right) +\frac{\pi ^{3}Rh}{l}\left( {\mu _1 -4\mu _2 } \right) , K_{47} =K_{74} =\frac{2\pi nlh}{R}\left( {\mu _1 -\mu _2 } \right) ,\nonumber \\ K_{42}= & {} K_{43} =K_{45} =K_{46} =K_{48} =K_{49} =0, K_{55} =\frac{\pi ^{3}Rh}{l}\left( {\mu _1 -4\mu _2 } \right) ,\nonumber \\ K_{51}= & {} K_{52} =K_{53} =K_{54} =K_{56} =K_{57} =K_{58} =K_{59} =0, K_{66} =\frac{9\pi ^{3}Rh}{l}\left( {\mu _1 -4\mu _2 } \right) ,\nonumber \\ K_{61}= & {} K_{62} =K_{63} =K_{64} =K_{65} =K_{67} =K_{68} =K_{69} =0,\nonumber \\ K_{77}= & {} \left( {\frac{2\pi lh}{R}+\frac{\pi n^{4}lh^{3}}{6R^{3}}+\frac{\pi ^{5}Rh^{3}}{6l^{3}}+\frac{\pi ^{3}n^{2}h^{3}}{6lR}} \right) \left( {\mu _1 -\mu _2 } \right) +\frac{\pi ^{3}n^{2}h^{3}}{6lR}\left( {\mu _1 -4\mu _2 } \right) ,\nonumber \\ K_{72}= & {} K_{73} =K_{75} =K_{76} =K_{78} =K_{79} =0, K_{88} =\left( {\frac{4\pi lh}{R}+\frac{\pi ^{5}Rh^{3}}{3l^{3}}} \right) \left( {\mu _1 -\mu _2 } \right) ,\nonumber \\ K_{81}= & {} K_{83} =K_{84} =K_{85} =K_{86} =K_{87} =0, K_{99} =\left( {\frac{4\pi lh}{R}+\frac{27\pi ^{5}Rh^{3}}{l^{3}}} \right) \left( {\mu _1 -\mu _2 } \right) ,\nonumber \\ K_{91}= & {} K_{92} =K_{94} =K_{95} =K_{96} =K_{97} =K_{98} =0. \end{aligned}$$

(A2)