1 Introduction

Functionally graded materials (FGM) are novel and advanced engineering materials designed for specific performance of function, in which a special gradation in structure and/or composition leads to a smooth variation of material properties from point to point [1]. A great variety of potential applications are offered by functionally graded beams, plates and shells with continuous variation of material properties from one surface to another, which can eliminate the stress concentration at the interfaces of layers in the traditional laminated composites. Particularly, an FGM structure made from the constituents of ceramic and metal can minimize the thermal stress concentration produced by the high temperature gradient. Therefore, as the simplest FGM structural elements, the static and dynamic responses of FGM beams have widely attracted the intensive attention of researchers [2, 3]. Numerous studies based on deterministic analysis have been conducted on modeling, analysis and simulation of static and dynamic responses of FGM beam structures based on different beam theories [4,5,6,7,8,9,10,11,12,13, 21,22,23,24,25,26,27,28,29,30,31,32,33, 41,42,45].

The classical beam theory (CBT) or the Euler–Bernoulli beam theory (EBBT) was applied to analyze the static and dynamic response of thin or slender FGM beams [4,5,6,7]. Among them, Simsek and Kocatur [4], and Khalili et al. [5] investigated forced vibration of FGM beams subjected to moving loads. Alshorbagy et al. [6] computed the natural frequencies of FGM slender beams under different boundary conditions by the finite element method (FEM). Yang and Chen [7] performed theoretical analysis on free vibration and elastic buckling of FGM beams containing open edge cracks by using the rotational spring model.

However, for moderately thick FGM beams, the CBT usually underestimates the flexibility and overestimates the natural frequency because of ignoring the transverse shear deformation. In order to overcome the limitation of the CBT, the first-order shear deformation beam theory (FSDBT), or Timoshenko beam theory (TBT) taking into account the transverse shear deformation, was applied to investigate the static and dynamic responses of moderately thick FGM beams [8,9,10,11,12,13]. For example, Li presented a new unified approach to find the analytical solutions for static bending and free vibration of FGM beams by defining a new function to solve the coupled governing equations [8]. Sina et al. [9] derived the Navier equations of motion for FGM beams based on a new beam theory different from the traditional TBT and obtained the free vibration response by analytical method. The effect of shear correction function depending on the spatially continuous variation of material properties was originally studied and evaluated in modal analysis of FGM beams by Murin et al. [10]. Pradhan and Chakraverty [11] used the Rayleigh–Ritz method to analyze the free vibration of both Euler–Bernoulli and Timoshenko FGM beams subjected to different boundary conditions. Esfahani et al. [12] dealt with the nonlinear thermal buckling and post-buckling of FGM beams supported on nonlinear elastic foundation using the generalized differential quadrature method (DQM). Moreover, by incorporating the most general strain gradient elasticity theory into traditional TBT and taking the size-dependent effect into account, Ansari et al. [13] analyzed size-dependent static bending, buckling and free vibration of FGM beams by the DQM.

Obviously, the assumption of constant distribution of transverse shear stress along the depth in TBT violates the shear traction-free conditions at the top and bottom surfaces of the beam. Of course, the through-depth shear stress distribution given by TBT is different from the actual stress state in deep beams. So, in order to compensate the discrepancy between the actual shear stress and the assumed constant shear stress along the depth, a shear correction factor needs to be introduced in TBT.

By giving up the use of a shear correction factor and searching for better prediction of the actual shear stress distribution in the cross section satisfying the zero shear stress conditions at the surfaces, various higher-order shear deformation theories were proposed to deal with the homogenous and laminated composite beams [14,15,16,17,18,19,20]. According to the selections of shape functions in the displacement fields to determine the distribution of transverse shear strain, and hence the shear stress, the higher-order shear deformation beam theories can be divided into different types. The well-known higher-order beam theories are the parabolic shear deformation beam theory (PSDBT) proposed by Levinson [14], Bickford [15] and Reddy [16], the trigonometric shear deformation beam theory (TSDBT) by Touratier [17], the hyperbolic shear deformation beam theory (HSDBT) by Soldatos [18], the exponential shear deformation beam theory (ESDBT) by Karama et al. [19] and a new shear deformation beam theory (ASDBT) by Aydogdu [20]. All the above-mentioned higher-order shear deformation theories consider warping of the cross sections and accurately satisfy the zero transverse shear stress condition at the top and bottom surfaces without a shear correction factor.

In recent years, many researchers extended the higher-order shear deformation beam theories, originally developed for the homogenous and laminated composite beams, to the analysis of the static and dynamic response of thick FGM beams [21,22,23,24,25,26,27,28,29,30,31,32,33]. Based on the PSDBT, Kadoli et al. [21] performed a numerical analysis on the static bending of FGM beams using the finite element method (FEM). Benatta et al. [22] and Sallai et al. [23] derived analytical solutions of static bending of a short hybrid composite beam with continuously variable glass and graphite fiber reinforcement constituents and of a thick sigmoid FGM beam with AI/AI203 constituents subjected to a transverse uniform load and simply supported boundary constraints. Kapuria et al. [24] presented both FEM analysis and experimental validation on the bending and free vibration of FGM beams with layer-wise variation of the material properties through the depth, where the axial displacement was assumed to follow a global third-order variation with a linear variation in each layer across the thickness. Analytical and numerical investigations on static and free vibration responses of FGM beams were also performed by Thai and Vo [25]. Vo et al. [26] used the Navier solution procedure and FEM approach based on different higher-order beam theories. Moreover, considering third-order variation of both the axial and transverse displacements through the depth, Vo et al. [27] developed a finite element model and Navier solutions of functionally graded sandwich beams for various power-law indices, skin-core-skin thickness ratios and boundary conditions. Furthermore, the 1-D Carrera unified formulation (CUF) was used by Filippi et al. [28] to search for numerical solutions of stresses and displacements in static bending FGM beams by FEM. Aydogdu and Taskin [29] investigated free vibration of simply supported FGM beams based on the TBT, PSDBT and ESDBT, in which natural frequencies were obtained by using Navier’s-type solution method. Simsek [30] and Pradhan and Chakraverty [31] examined the effects of different higher-order shear deformation beam theories on the natural frequencies of FGM beams under different boundary conditions by using the Lagrange multiplier formulation and Rayleigh–Ritz methods, respectively. Mahi et al. [32] analyzed the free vibration of FGM beams with temperature-dependent material properties and considered the effect of the initial thermal stress on the natural frequencies. More recently, based on the PSDBT conjunction with von Karman’s nonlinear strain–displacement relation, Shen et al. [33] investigated the nonlinear bending and thermal post-buckling behaviors of functionally graded graphene-reinforced composite laminated beams resting on elastic foundations in thermal environments.

In order to search for higher accuracy in prediction of displacement field and stress state, the 2-D elasticity theory was also used in analyzing thick FGM beams [34,35,36]. For instance, Sankar [34] developed an elasticity solution for simply supported FGM beams subjected to symmetrical sinusoidal transverse loads, with Young’s modulus varying exponentially along the thickness. On the other hand, Zhong and Yu [35] derived a 2-D solution in terms of Airy functions for static bending of a cantilever FGM beam with arbitrary through-the-thickness variation of material properties. Again, Ding et al. [36] considered the plane stress problem of generally anisotropic beams with the elastic compliance parameters being arbitrary functions of the thickness coordinate, derived plane stress functions for the FGM and obtained bending solutions under different boundary conditions.

Different from the above-mentioned investigations on the static and dynamic behaviors of FGM beams based on different shear deformation beam theories by the traditional analytical or numerical approaches, some researchers sought for the correspondence relations between the responses of homogenous and FGM beams based on the shear deformation theories and those of the corresponding homogenous Euler–Bernoulli beams (HEBBs). However, what needs to be specially noted here is the pioneering work contributed by Reddy, Wang and their collaborators, in which they elaborated at length the relationships between the solutions of classical beam theory and those of different shear deformation beam theories for the homogenous material beams [37,38,39,40]. For instance, they presented the bending solutions of Timoshenko beams (TBs) [37], Levinson beams (LBs) [38] and Reddy–Bickford beams (RBBs) [39, 40] analytically in terms of that of the corresponding HEBBs which realized the classical expressions of the static responses of shear deformable homogenous thick beams. More recently, Li et al. extended Reddy and Wang’s work to the analysis of FGM beams with inhomogeneity of the material properties in the depth direction and developed the relationships of static bending/buckling solutions of FGM TBs [41, 42] and FGM LBs [43, 44] to those of the reference homogenous Euler–Bernoulli beams (HEBBs). Consequently, instead of dealing with the complicated differential equations of the FGM beams including tension-bending coupling and shear deformation effects, solutions of the shear deformable FGM beams are simplified as the calculation of some transitional coefficients determined easily by the given gradient profile of the material properties and the geometry of the FGM beams if the solutions of HEBBs are available.

To the best of the authors’ knowledge, there is still a lack of knowledge on how to establish the relationship between the static response of a shear deformable FGM beam and that of the related HEBBs, particularly using the Reddy–Bickford’s higher-order beam theory. Recently, the authors [43, 44] presented classical and homogenized expressions for static bending and buckling responses of the shear deformable FGM beams based on the Levinson beam theory. However, the Levinson beam theory is a quasi-third-order beam theory, or a lower-order beam theory than the Reddy–Bickford beam theory without containing the higher-order stress resultants. Although the assumed displacement fields in the two theories are the same, the derived equations of equilibrium are obviously different. It is well known that the equations of equilibrium of the LBs are derived by using a vector approach [14], but those of the RBBs are obtained by using the principle of virtual displacements which leads to the inclusion of higher-order shear force and bending moment [15, 16]. Therefore, to search for the relationship between the static responses of FGM RBBs and those of the reference HEBBs is still an original theoretical problem.

The objective of this paper is to develop exact correspondence relationships between the static bending solutions of FGM RBBs and those of the reference HEBBs under arbitrary loading and boundary conditions. Governing equations in terms of the displacements for the problem are derived by using the energy-variation principle. By using the equivalence of the applied force, generalized solutions of static bending of FGM RBBs with arbitrary material gradient profile in the depth direction are presented in terms of deflection of the reference HEBBs with the same loading and end constrains. Analytical expressions for the transitional coefficients in the general solutions are given, which depend only on the parameters of the geometry and the material gradient profile of the FGM beams. Finally, particular solutions of the FGM RBBs under specified boundary conditions and loading are given to show the validity of this analytical approach.

2 Mathematical Formulations of the Problem

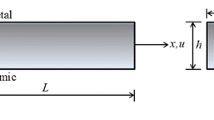
Consider an FGM beam with a uniform rectangular cross section as illustrated in Fig. 1. The length, width and depth are denoted as l, b and h, respectively. The geometry and coordinates of the FGM beam are shown in Fig. 1. It is assumed that the FGM beam is made of two different homogenous constituents, named material 1 (M1) and material 2 (M2), with the parameters of the material properties denoted by \(P_1 \) and \(P_2 \), respectively. Furthermore, it is also assumed that the material properties of the FGM beam vary continuously along the depth from the material properties of full M1 at the top surface to those of full M2 at the bottom one by continuous change of the volume fractions of the constituents.

Fig. 1
figure 1

The geometry and coordinates of an FGM beam

Full size image

According to the pioneering studies by Levinson [14], Bickford [15] and Reddy [16], the displacement field in the FGM beam based on PSDBT can be written as

$$\begin{aligned} u(x,z)=u_0 (x)+z\varphi (x)-\alpha z^{3}\gamma , \quad w(x,z)=w_0 (x), \quad \gamma =\frac{\hbox {d}w_0 }{\hbox {d}x}+\varphi \end{aligned}$$
(1)

where \(u_0 \) and \(w_0 \) represent the displacements of the geometrical middle plane along the x- and z-directions, respectively, \(\varphi (x)\) is the rotation of the cross section about the y-axis, and \(\alpha =4/(3h^{2})\). It is worth noting that the axial displacement \(u_0 \) arises from the stretching-bending coupling due to the asymmetric distribution of the material properties about the geometrical middle surface, and it vanishes in homogenous beams [14,15,16, 37,38,39,40] or in the FGM beams with material gradient distribution profile symmetric with respect to the geometrical middle plane.

Based on the linear deformation assumption, strain components can be readily obtained from displacement field (1),

$$\begin{aligned} \varepsilon _x \left( {x,z} \right)= & {} \frac{\hbox {d}u_0 }{\hbox {d}x}+z\frac{\hbox {d}\varphi }{\hbox {d}x}-\alpha z^{3}\frac{\hbox {d}\gamma }{\hbox {d}x} \end{aligned}$$
(2)
$$\begin{aligned} \gamma _{xz} \left( {x,z} \right)= & {} (1-3\alpha z^{2})\gamma \end{aligned}$$
(3)

Using Hooke’s law, stresses in the FGM beam are

$$\begin{aligned} \sigma _x= & {} E\left( {\frac{\hbox {d}u_0 }{\hbox {d}x}+z\frac{\hbox {d}\varphi }{\hbox {d}x}-\alpha z^{3}\frac{\hbox {d}\gamma }{\hbox {d}x}} \right) \end{aligned}$$
(4)
$$\begin{aligned} \tau _{xz}= & {} \frac{E}{2(1+\nu )}(1-3\alpha z^{2})\gamma \end{aligned}$$
(5)

where the Young’s modulus E is a specified function of coordinate z, but the Poisson’s ratio is assumed to be constant since it is usually very small in the FGM beam. Apparently, the displacement field (1) gives rise to the parabolic variations of shear strain (3), and hence to the shear stress (5) through the depth of the FGM beam in such a way that the shear stress vanishes on the top and bottom surfaces of the beam.

In the Levinson beam theory, the equilibrium equations are derived by using the thickness-integration equivalence of the equations of elasticity [44, 45]. Here, the governing equations together with the boundary conditions for the static bending of FGM RBBs are derived by employing the principle of virtual displacements [15, 16, 21,22,23], i.e.,

$$\begin{aligned} \int _0^l {\int _{-h/2}^{h/2} {(\sigma _x {\delta }\varepsilon _x +\tau _{xz} {\delta }\gamma _{xz} } )b\hbox {d}z\hbox {d}x-\int _0^l {q{\delta }w\hbox {d}x} } =0 \end{aligned}$$
(6)

where \(q=q(x)\) is the transversely distributed external force, and \({\delta }\) is the variational symbol. By substituting Eqs. (2)–(5) into Eq. (6) and performing some mathematical calculations, we have the equilibrium equations of the FGM beams [39]

$$\begin{aligned} \frac{\hbox {d}F_N }{\hbox {d}x}= & {} 0 \end{aligned}$$
(7)
$$\begin{aligned} \frac{\hbox {d}M_{x1} }{\hbox {d}x}= & {} F_{s0} +\alpha \frac{\hbox {d}M_{x3} }{\hbox {d}x}-3\alpha F_{s2} \end{aligned}$$
(8)
$$\begin{aligned} \frac{\hbox {d}F_{s0} }{\hbox {d}x}= & {} -q+3\alpha \frac{\hbox {d}F_{s2} }{\hbox {d}x}-\alpha \frac{\hbox {d}^{2}M_{x3} }{\hbox {d}x^{2}} \end{aligned}$$
(9)

where \(F_N \) is the axial force; \(F_{s0} \) and \(M_{x1} \) are, respectively, the shearing force and bending moment similar to those defined in the Euler–Bernoulli beam theory; \(M_{x3} \) and \(F_{s2} \) are the higher-order bending moment and shearing force, respectively.

The boundary conditions at the two ends of the beam (\(x=0,l)\) are given as the following criteria for the specific problem:

$$\begin{aligned}&\hbox {either } F_N \hbox { or } u_0 \hbox { is specified} \end{aligned}$$
(10)
$$\begin{aligned}&\hbox {either } \bar{{M}}_x =M_{x1} -\alpha M_{x3} \hbox { or } \varphi \hbox { is specified} \end{aligned}$$
(11)
$$\begin{aligned}&\hbox {either } \bar{{F}}_s =F_{s0} -3\alpha F_{s2} +\alpha \frac{\hbox {d}M_{x3} }{ \hbox {d}x} \hbox { or } w_0 \hbox { is specified} \end{aligned}$$
(12)
$$\begin{aligned}&\hbox {either } M_{x3} \hbox { or } \frac{\hbox {d}w_0 }{\hbox {d}x} \hbox { is specified} \end{aligned}$$
(13)

where \(\bar{{F}}_s \) and \(\bar{{M}}_x \) are the total shearing force and bending moment, respectively. The resultant forces and bending moments in the above equations are defined by

$$\begin{aligned} (F_N ,M_{x1} ,M_{x3} )= & {} b\int _{-h/2}^{h/2} {\sigma _x (1,z,z^{3})} \hbox {d}z \end{aligned}$$
(14)
$$\begin{aligned} (F_{s0} ,F_{s2} )= & {} b\int _{-h/2}^{h/2} {(1,z^{2})} \tau _{xz} \hbox {d}z \end{aligned}$$
(15)

It is noted that different from the Levinson beam theory-based equilibrium equations [39, 40], Eqs. (7)–(13) include the higher-order bending moment and shear force, i.e., \(M_{x3}\) and \(F_{s2}\). Also, in the boundary conditions (11) and (13), both the rotational angle and the slope of the deflection are specified independently.

Substituting Eqs. (4) and (5) into Eqs. (14) and (15) gives the resultant forces and bending moments in terms of the displacement components:

$$\begin{aligned} F_N =S_0 \frac{\hbox {d}u_0 }{\hbox {d}x}+S_1 \frac{\hbox {d}\varphi }{\hbox {d}x}-\alpha S_3 \frac{\hbox {d}\gamma }{\hbox {d}x} \end{aligned}$$
(16)
$$\begin{aligned} M_{x1} =S_1 \frac{\hbox {d}u_0 }{\hbox {d}x}+S_2 \frac{\hbox {d}\varphi }{\hbox {d}x}-\alpha S_4 \frac{\hbox {d}\gamma }{\hbox {d}x} \end{aligned}$$
(17a)
$$\begin{aligned} M_{x3} =S_3 \frac{\hbox {d}u_0 }{\hbox {d}x}+S_4 \frac{\hbox {d}\varphi }{\hbox {d}x}-\alpha S_6 \frac{\hbox {d}\gamma }{\hbox {d}x} \end{aligned}$$
(17b)
$$\begin{aligned} F_{s0}= & {} S_{zx0} \gamma \end{aligned}$$
(18a)
$$\begin{aligned} F_{s2}= & {} S_{zx2} \gamma \end{aligned}$$
(18b)

where \(S_i (i=0,1,2,3,4,6)\) and \(S_{zxi} (i=0,2)\) are stiffness coefficients calculated by

$$\begin{aligned} S_i= & {} b\int _{-h/2}^{h/2} {Ez^{i}\hbox {d}z} \; \end{aligned}$$
(19)
$$\begin{aligned} S_{zxi}= & {} b\int _{-h/2}^{h/2} {\frac{E}{2(1+\nu )}z^{i}(1-3\alpha z^{2})\hbox {d}z} \end{aligned}$$
(20)

By choosing a reference homogenous material beam with Young’s modulus \(E_1 \), the stiffness coefficients can be expressed as

$$\begin{aligned} S_i =E_1 Ah^{i}\phi _i (i=0,1,3,4,6), S_2 =E_1 I\phi _2 , S_{zxi} =E_1 Ah^{i}\phi _{zxi} (i=0,2) \end{aligned}$$
(21)

Herein, \(\phi _i \) and \(\phi _{zxi} \) are the dimensionless stiffness coefficients that can be analytically determined from Eqs. (19)–(21) for the designed material gradient distribution profile along the beam depth; \(E_1 \) is also the Young’s modulus at the bottom surface of the FGM beam; \(A=bh\) and \(I=bh^{3}/12\).

For the convenience of the following analysis, some dimensionless quantities are further introduced as:

$$\begin{aligned} (\delta ,\xi ,U,W)= & {} (h,x,u_0 ,w_0 )/l \end{aligned}$$
(22a)
$$\begin{aligned} (f_N ,m_{x1} ,m_{x3} ,f_{s0} ,f_{s2} ,Q)= & {} (F_N l^{2},M_{x1} l,M_{x3} /l,F_{s0} l^{2},F_{s2} ,ql^{3})/(E_1 I) \end{aligned}$$
(22b)

Then, by substituting Eqs. (16)–(18) into Eqs. (7)–(9) and using Eqs. (21) and (22), we arrive at the dimensionless equilibrium equations in terms of the displacements, i.e.,

$$\begin{aligned}&\phi _0 \frac{\hbox {d}^{2}U}{\hbox {d}\xi ^{2}}+\delta \phi _1 \frac{\hbox {d}^{2}\varphi }{\hbox {d}\xi ^{2}}-\frac{4\delta \phi _3 }{3}\frac{\hbox {d}^{2}\gamma }{\hbox {d}\xi ^{2}}=0 \end{aligned}$$
(23)
$$\begin{aligned}&\delta \left( {\phi _1 -\frac{4}{3}\phi _3 } \right) \frac{\hbox {d}^{2}U}{\hbox {d}\xi ^{2}}+\frac{\delta ^{2}}{12}\left( {\phi _2 -\hbox {16}\phi _4 } \right) \frac{\hbox {d}^{2}\varphi }{\hbox {d}\xi ^{2}}-\frac{4\delta ^{2}}{3}\left( {\phi _4 -\frac{4}{3}\phi _6 } \right) \frac{\hbox {d}^{2}\gamma }{\hbox {d}\xi ^{2}}=\left( {\phi _{xz0} -4\phi _{xz2} } \right) \gamma \end{aligned}$$
(24)
$$\begin{aligned}&\frac{16\phi _3 }{\delta }\frac{\hbox {d}^{3}U}{\hbox {d}\xi ^{3}}+16\phi _4 \frac{\hbox {d}^{3}\varphi }{\hbox {d}\xi ^{3}}-\frac{64}{3}\phi _6 \frac{\hbox {d}^{3}\gamma }{\hbox {d}\xi ^{3}}+\frac{12}{\delta ^{2}}\left( {\phi _{xz0} -4\phi _{xz2} } \right) \frac{\hbox {d}\gamma }{\hbox {d}\xi }=-Q \end{aligned}$$
(25)

Different from the governing equations of the homogenous RBBs [39], the axial displacement as an independent unknown function is included in Eqs. (23)–(25). This leads to the stretching-bending and stretching-warping couplings between the three differential equations. The full coupling between the independent variables, U, W and \(\varphi \), makes it difficult to find the analytical solutions of Eqs. (23)–(25) by using direct approach.

3 General Solutions

First, by eliminating the axial displacement U in Eqs. (23)–(25), it yields

$$\begin{aligned}&\left( {\frac{1}{c}+c_{\alpha 1} } \right) \frac{\hbox {d}^{2}\varphi }{\hbox {d}\xi ^{2}}+(c_{\alpha 1} -c_{\alpha 2} )\frac{\hbox {d}^{2}\gamma }{\hbox {d}\xi ^{2}}=\left( {\frac{1}{c_{s0} }-\frac{1}{c_{s2} }} \right) \gamma \end{aligned}$$
(26)
$$\begin{aligned}&-c_{\alpha 1} \frac{\hbox {d}^{3}\varphi }{\hbox {d}\xi ^{3}}+c_{\alpha 2} \frac{\hbox {d}^{3}\gamma }{\hbox {d}\xi ^{3}}+\left( {\frac{1}{c_{s0} }-\frac{1}{c_{s2} }} \right) \frac{\hbox {d}\gamma }{\hbox {d}\xi }=-Q \end{aligned}$$
(27)

The dimensionless parameters in Eqs. (26) and (27) are defined by

$$\begin{aligned} c= & {} \frac{1}{\phi _2 -12\phi _1 ^{2}/\phi _0 }, \quad c_{\alpha 1} =16\left( {\frac{\phi _1 \phi _3 }{\phi _0 }-\phi _4 } \right) , \quad c_{\alpha 2} =\frac{64}{3}\left( {\frac{\phi _3 ^{2}}{\phi _0 }-\phi _6 } \right) \end{aligned}$$
(28a)
$$\begin{aligned} c_{s0}= & {} \frac{\delta ^{2}}{12\phi _{xz0} }, \quad c_{s2} =\frac{\delta ^{2}}{48\phi _{xz2} } \end{aligned}$$
(28b)

The above five dimensionless coefficients integrate the information of material properties, beam geometry and beam theories. Meanwhile, they also depend on the material gradient profile in the depth and the aspect ratio of the FGM beam. A special case is that an FGM RBB reduces to a homogenous material RBB by letting \(E\equiv E_1 \). Thus, by using Eqs. (19)–(21), we can obtain the dimensionless coefficients as

$$\begin{aligned} \phi _1= & {} \phi _3 =0, \quad \phi _0 =\phi _2 =1, \quad \phi _4 =\frac{1}{80}, \quad \phi _6 =\frac{1}{448}, \quad \phi _{xz0} =\frac{1}{3(1+\nu )}, \quad \phi _{xz2} =\frac{1}{60(1+\nu )} \\ c= & {} 1, \quad c_{\alpha 1} =-\frac{1}{5}, \quad c_{\alpha 2} =-\frac{1}{21}, \quad c_{s0} =\frac{1}{4}(1+\nu )\delta ^{2}, \quad c_{s2} =\frac{5}{4}(1+\nu )\delta ^{2} \end{aligned}$$

Consequently, the tension-bending coupling and tension-warping coupling terms in Eqs. (23)–(25) vanish [39] in this special case.

Herein, it is assumed that the bending solution of the reference HEBB is already known. For the reference HEBB subjected to the same applied load \(Q(\xi )\), we have the following equations

$$\begin{aligned} \frac{\hbox {d}m_E^*}{\hbox {d}\xi }=f_{sE}^*, \quad \frac{\hbox {d}f_{sE}^*}{\hbox {d}\xi }=-\frac{\hbox {d}^{4}W_E^*}{\hbox {d}\xi ^{4}}=-Q \end{aligned}$$
(29)

where \(W_E^*\), \(m_E^*\) and \(f_{sE}^*\) are the dimensionless deflection, bending moment and shearing force of the reference HEBB, respectively.

Furthermore, elimination of function \(\varphi (\xi )\) from Eqs. (26) and (27) gives

$$\begin{aligned} c_{s0} (cc_{\alpha 1} c_{\alpha 1} +c_{\alpha 2} )\frac{\hbox {d}^{3}f_{s0} }{\hbox {d}\xi ^{3}}+\left( {1-\frac{c_{s0} }{c_{s2} }} \right) \frac{\hbox {d}f_{s0} }{\hbox {d}\xi }=-(1+cc_{\alpha 1} )Q \end{aligned}$$
(30)

where \(f_{s0} =\gamma /c_{s0} \). Then, integration of Eq. (30) and use of Eq. (29) yield

$$\begin{aligned} c_{s0} (cc_{\alpha 1} c_{\alpha 1} +c_{\alpha 2} )\frac{\hbox {d}^{2}f_{s0} }{\hbox {d}\xi ^{2}}+\left( {1-\frac{c_{s0} }{c_{s2} }} \right) f_{s0} =(1+cc_{\alpha 1} )(f_{sE}^*+\beta _1 ) \end{aligned}$$
(31)

in which \(\beta _1 \) is an integration constant.

Equation (31) can be written as

$$\begin{aligned} \frac{\hbox {d}^{2}f_{s0} }{\hbox {d}\xi ^{2}}-\lambda ^{2}f_{s0} =-\mu (f_{sE}^*+\beta _1 ) \end{aligned}$$
(32)

where

$$\begin{aligned} \lambda =\left( {\frac{c_{s0} -c_{s2} }{c_{s0} c_{s2} (c_{\alpha \hbox {2}} +cc_{\alpha \hbox {1}} ^{2})}} \right) ^{1/2}\hbox { , }\mu =-\frac{1+cc_{\alpha 1} }{c_{s0} (c_{\alpha \hbox {2}} +cc_{\alpha \hbox {1}} ^{2})} \end{aligned}$$
(33)

It is easy to get the general solution of differential equation (32) as

$$\begin{aligned} f_{s0} (\xi )=\beta _7 \sinh \lambda \xi +\beta _8 \cosh \lambda \xi +g(\xi ) \end{aligned}$$
(34)

where \(\beta _7 \) and \(\beta _8 \) are integration constants; \(g(\xi )\) is a particular solution of Eq.(32), which depends on the dimensionless shearing force, \(f_{sE}^*\), of the reference HEBB. From the definition of parameters \(\lambda \) and \(\mu \), one can see that solution (34) contains the integrated information of material properties and geometry of FGM beams in the sense of the Reddy–Bickford beam theory. It also contains the information of the reference HEBB in terms of \(f_{sE}^*\). The integral constants in the general solution (34) will be determined by the boundary conditions for specific end constrains.

The terms of \(f_{s0} \) in Eq. (26) can be eliminated by using Eq. (32), then

$$\begin{aligned} \frac{\hbox {d}^{2}\varphi }{\hbox {d}\xi ^{2}}=-cc_{s0} c_{\alpha 1} \frac{\hbox {d}^{2}f_{s0} }{\hbox {d}\xi ^{2}}+c(f_{sE}^*+\beta _1 ) \end{aligned}$$
(35)

Twice integration of Eq. (35) and use of Eq. (29) arrive at the general solution of the rotational angle as

$$\begin{aligned} \varphi =-c\frac{\hbox {d}W_E^*}{\hbox {d}\xi }-cc_{s0} c_{\alpha 1} f_{s0} +\frac{c\beta _1 }{2}\xi ^{2}+\beta _2 \xi +\beta _3 \end{aligned}$$
(36)

where \(\beta _2 \) and \(\beta _3 \) are dimensionless constants.

Furthermore, from the dimensionless form of Eq. (18a,18b), we have

$$\begin{aligned} \frac{\hbox {d}W}{\hbox {d}\xi }=-\varphi +c_{s0} f_{s0} \end{aligned}$$
(37)

Substitution of Eq. (36) into Eq. (37) gives the general solution of the dimensionless deflection as

$$\begin{aligned} W=cW_E^*+K\int _0^\xi {f_{s0} \hbox {(}\zeta \hbox {)d}\zeta } -\frac{c\beta _1 }{6}\xi ^{3}-\frac{\beta _2 }{2}\xi ^{2}-\beta _3 \xi +\beta _4 \end{aligned}$$
(38)

where \(\beta _4 \) is a dimensionless constant, and \(K=c_{s0} (1+cc_{\alpha 1} )\).

Integration of Eq. (23) yields the general solution of the dimensionless axial displacement as

$$\begin{aligned} U=-\frac{\delta \phi _1 }{\phi _0 }\varphi +\frac{4\delta }{3}\frac{\phi _3 }{\phi _0 }c_{s0} f_{s0} +\beta _5 \xi +\beta _6 \end{aligned}$$
(39)

where \(\beta _5 \) and \(\beta _6 \) are dimensionless constants. So far, we have obtained general solutions for the displacement components of FGM RBBs expressed in terms of the dimensionless deflection of the reference HEBB.

By substituting Eqs. (36)–(39) into the dimensionless forms of Eqs. (16)–(18) (see “Appendix”), general solutions of the dimensionless resultant forces and bending moments can be expressed in terms of the solution of the reference HEBB as

$$\begin{aligned} f_N= & {} \frac{12}{\delta ^{2}}\phi _0 \beta _5 \end{aligned}$$
(40)
$$\begin{aligned} m_{x1}= & {} m_E^*+\beta _1 \xi +\frac{\beta _2 }{c}+\frac{12}{\delta }\phi _1 \beta _5 \end{aligned}$$
(41)
$$\begin{aligned} m_{x3}= & {} \frac{3}{4}\delta ^{2}\left( {-cc_{\alpha 1} m_E^*+c_{s0} (c_{\alpha 2} +cc_{\alpha 1} c_{\alpha 1} )\frac{\hbox {d}f_{s0} }{\hbox {d}\xi }-c_{\alpha 1} (c\beta _1 \xi +\beta _2 )} \right) +12\delta \phi _3 \beta _5 \end{aligned}$$
(42)
$$\begin{aligned} f_{s2}= & {} \frac{\delta ^{2}c_{s0} }{4c_{s2} }f_{s0} \end{aligned}$$
(43)

Equations (36)–(43) constitute the general solutions of FGM RBBs in terms of the deflection of the reference HEBB, which are valid for arbitrary gradient profile of the material properties in the depth direction. Herein, it is assumed that deflection \(W_E^*\) is produced by the same loading and has satisfied the boundary conditions of the reference HEBB. Then, the load information has been included in the solution of \(W_E^*(\xi )\). Accordingly, constants \(\beta _i \) (\(i=1,2,\ldots ,8)\) will actually be determined only by the difference between the boundary conditions of the FGM RBB and the reference HEBB. Eventually, we realize a homogenized and classical expression for the bending solution of FGM beams based on the Reddy–Bickford beam theory. In the case of homogenous material beam, the axial displacement vanishes and general solutions (34), (36), (38) and (41)–(43) reduce to the bending solutions of homogenous RBBs as given by Reddy et al. [37, 38]

In order to express the natural boundary conditions in Eqs. (10)–(13), the total bending moment and the total shearing force are further written in dimensionless forms as

$$\begin{aligned} m_R= & {} \frac{l\bar{{M}}_x }{E_\mathrm{1} I}=m_{x1} -\frac{4}{3\delta ^{2}}m_{x3} \nonumber \\= & {} (1+cc_{\alpha 1} )\left( {m_E^*+\beta _1 \xi +\frac{\beta _2 }{c}} \right) +\frac{12}{\delta }(\phi _1 -4\phi _3 /3)\beta _5 +c_{s0} (c_{\alpha 2} +cc_{\alpha 1} ^{2})\frac{\hbox {d}f_{s0} }{\hbox {d}\xi } \end{aligned}$$
(44a)
$$\begin{aligned} f_R= & {} \frac{l^{2}\bar{{F}}_s }{E_\mathrm{1} I}=\frac{l^{2}}{E_b I}\left( {\frac{\hbox {d}M_{x1} }{\hbox {d}x}} \right) =\frac{\hbox {d}m_{x1} }{\hbox {d}\xi }=f_{sE}^*+\beta _1 \end{aligned}$$
(44b)

4 Particular Solutions

In this section, particular solutions for the FGM RBBs under specified end constraints and load conditions are given to validate the application of the theory and methodology. Three kinds of the end constraints of beams are considered: clamped (C), simply supported (S) and free (F). The eight integral constants in the general solutions can be determined by the boundary conditions of a given problem. In the analysis of static bending of the FGM RBBs with small deformation, we assume that there are no axially external forces acting on the beam, and the beam is axially static determined so that \(f_N \equiv 0\), which leads to \(\beta _5 \equiv 0\) by using Eq. (40). Constant \(\beta _6 \) represents the rigid body movement in the axial direction which vanishes for the axially static determined FGM RBBs. Consequently, it can be seen from Eq. (39) that for the homogenous beam or FGM beam with the material properties symmetrical about the geometrical middle surface, we have \(U\equiv 0\) due to \(\phi _1 =\phi _3 =0\).

As examples to derive the particular solutions of the FGM RBBs based on the general solutions (36)–(43), we consider the beams with four kinds of boundary conditions (S-S, C-C, C-F and C-S) and subjected to uniformly distributed transverse load \(Q=1\).

4.1 Simply Supported Beam (S-S)

Firstly, we consider a beam with both ends simply supported. The particular solution of the reference HEBB is given by

$$\begin{aligned} W_E^*(\xi )=\frac{\xi }{24}(1-2\xi ^{2}+\xi ^{3}), \quad f_{sE}^*\hbox {(}\xi \hbox {)=}\frac{1}{2}(1-2\xi ) \end{aligned}$$
(45)

The corresponding non-homogeneous solution of Eq. (32) is

$$\begin{aligned} g(\xi )=\;\frac{\mu }{\lambda ^{2}}\left[ {\frac{1}{2}(1-2\xi )+\beta _1 } \right] \end{aligned}$$
(46)

Dimensionless boundary conditions are written by

$$\begin{aligned} W(0)= & {} 0, \quad m_{x1} (0)=0, \quad m_{x3} (0)=0 \end{aligned}$$
(47a)
$$\begin{aligned} W(1)= & {} 0, \quad m_{x1} (1)=0, \quad m_{x3} (1)=0 \end{aligned}$$
(47b)

By substituting the related general solutions (36)–(43) into Eq. (47) and remembering that deflection \(W_E^*\) has satisfied its boundary conditions beforehand, we determine the integral constants as follows:

$$\begin{aligned} \beta _1 =\beta _2 =\beta _3 =\beta _{4}=0 , \quad \beta _\mathrm{7} =\frac{\mu }{\lambda ^{3}}, \quad \beta _8 =-\frac{\mu }{\lambda ^{3}}\tanh \left( {\frac{\lambda }{2}} \right) \end{aligned}$$
(48)

Then, the particular solution of the S-S FGM RBB becomes:

$$\begin{aligned} f_{s0} (\xi )= & {} \frac{\mu }{\lambda ^{3}}\left[ {\frac{\sinh \lambda (\xi -1/2)}{\cosh (\lambda /2)}+\frac{\lambda }{2}(1-2\xi )} \right] \end{aligned}$$
(49a)
$$\begin{aligned} U(\xi )= & {} \frac{\delta c\phi _1 }{\phi _0 }\frac{\hbox {d}W_E^*}{\hbox {d}\xi }+\frac{\delta c_{s0} }{\phi _0 }\left( {cc_{\alpha 1} \phi _1 +\frac{4}{3}\phi _3 } \right) f_{s0} \end{aligned}$$
(49b)
$$\begin{aligned} W(\xi )= & {} cW_E^*+\frac{K\mu }{\lambda ^{4}}\left[ {\frac{\cosh \lambda (\xi -1/2)}{\cosh (\lambda /2)}-1+\frac{\lambda ^{2}}{2}\xi (1-\xi )} \right] \end{aligned}$$
(49c)
$$\begin{aligned} \varphi (\xi )= & {} -c\frac{\hbox {d}W_E^*}{\hbox {d}\xi }-cc_{s0} c_{\alpha 1} f_{s0} \end{aligned}$$
(49d)
$$\begin{aligned} m_{x1}= & {} m_E^*, \quad m_R =(1+cc_{\alpha 1} )m_E^*+c_{s0} (c_{\alpha 2} +cc_{\alpha 1}^2 )\frac{\hbox {d}f_{s0} }{\hbox {d}\xi }, \quad f_R (\xi )=f_{SE}^*(\xi ) \end{aligned}$$
(49e)

4.2 Clamped Beam (C-C)

The particular solutions of the reference HEBB with C-C ends are

$$\begin{aligned} W_E^*(\xi )= & {} \frac{\xi ^{2}}{24}(1-\xi )^{2} \end{aligned}$$
(50a)
$$\begin{aligned} f_E^*(\xi )= & {} \frac{1}{2}(1-2\xi ) \end{aligned}$$
(50b)

The non-homogeneous solution of Eq. (32) for FGM RBB with C-C ends is the same as Eq. (46). According to Eqs. (11)–(13), the boundary conditions for this problem are written by

$$\begin{aligned} W(0)=0, \quad {W}'(0)=0, \quad \varphi (0)=0 \end{aligned}$$
(51a)
$$\begin{aligned} W(1)=0, \quad {W}'(1)=0, \quad \varphi (1)=0 \end{aligned}$$
(51b)

Similarly, the integral constants can be determined as follows:

$$\begin{aligned} \beta _1= & {} \beta _2 =\beta _3 =\beta _4 =0 \end{aligned}$$
(52a)
$$\begin{aligned} \beta _7= & {} \frac{\mu }{2\lambda ^{2}}\coth (\lambda /2), \quad \beta _8 =-\frac{\mu }{2\lambda ^{2}} \end{aligned}$$
(52b)

Particular solutions of the C-C FGM RBB are given by

$$\begin{aligned} f_{s0} (\xi )= & {} \frac{\mu }{2\lambda ^{2}}\left[ {\frac{\sinh \lambda (\xi -1/2)}{\sinh (\lambda /2)}+(1-2\xi )} \right] \end{aligned}$$
(53a)
$$\begin{aligned} U(\xi )= & {} \frac{c\delta \phi _1 }{\phi _0 }\frac{\hbox {d}W_E^*}{\hbox {d}\xi }+\frac{\delta c_{s0} }{\phi _0 }\left( {\phi _1 cc_{\alpha 1} +\frac{4\phi _3 }{3}} \right) f_{s0} \end{aligned}$$
(53b)
$$\begin{aligned} W= & {} cW_E^*+\frac{K\mu }{2\lambda ^{3}}\left[ {\frac{\cosh \lambda (\xi -1/2)-\cosh (\lambda /2)}{\sinh (\lambda /2)}+\lambda \xi (1-\xi )} \right] \end{aligned}$$
(53c)
$$\begin{aligned} \varphi (\xi )= & {} -c\frac{\hbox {d}W_E^*}{\hbox {d}\xi }-cc_{s0} c_{\alpha 1} f_{s0} \end{aligned}$$
(53d)
$$\begin{aligned} m_{x1} (\xi )= & {} m_E^*, m_R (\xi )=(1+cc_{\alpha 1} )m_E^*+c_{s0} (c_{\alpha 2} +cc_{\alpha 1}^2 )\frac{\hbox {d}f_{s0} }{\hbox {d}\xi }, \quad f_R (\xi )=f_{SE}^*\end{aligned}$$
(53e)

It needs to be noted here that solution (53a) gives \(f_{s0} (0)=f_{s0} (1)=0\), which is obviously inconsistent with the clamped-end supports. This is because, in the derivation of equilibrium equations (7) and the boundary conditions (8) from Eq. (6), both the rotational angle and the derivative of the deflection are treated as independent variables at the same time. This will lead to a physically inconsistent result, i.e., \(\gamma (0)=\gamma (1)=0\), or \(f_{s0} (0)=f_{s0} (1)=0\) at the clamped ends. However, the resultant shearing force \(f_R (\xi )\) does not vanish but equals the shearing force of the reference HEBB at the clamped ends. Detailed discussions on this physical inconsistency can be found in [45].

4.3 Cantilever Beam (C-F)

Consider a cantilever beam with the left end clamped and the right end free (C-F). The particular solution of the reference HEBB with C-F ends is

$$\begin{aligned} W_E^*(\xi )= & {} \frac{1}{24}\xi ^{2}(6-4\xi +\xi ^{2}) \end{aligned}$$
(54a)
$$\begin{aligned} f_E^*(\xi )= & {} (1-\xi ) \end{aligned}$$
(54b)

The corresponding non-homogeneous particular solution of Eq. (32) is

$$\begin{aligned} g(\xi )= \frac{\mu }{\lambda ^{2}}[ (1-\xi )+\beta _{1}] \end{aligned}$$
(55)

Boundary conditions of the C-F FGM RBB are

$$\begin{aligned} U(0)= & {} 0, \quad W(0)=0, \quad {W}'(0)=0, \quad \varphi (0)=0 \end{aligned}$$
(56a)
$$\begin{aligned} f_N (1)= & {} 0,\quad m_{x1} (1)=0, \quad m_{x3} (1)=0, \quad f_R (1)=0 \end{aligned}$$
(56b)

The integration constants are determined as follows:

$$\begin{aligned} \beta _1= & {} \beta _2 =\beta _3 =\beta _4 =0 \end{aligned}$$
(57a)
$$\begin{aligned} \beta _7= & {} \frac{\mu }{\lambda ^{3}}\frac{1+\lambda \sinh \lambda }{\cosh \lambda }, \quad \beta _8 =-\frac{\mu }{\lambda ^{2}} \end{aligned}$$
(57b)

The particular solutions of this problem are

$$\begin{aligned} f_{s0} (\xi )= & {} \frac{\mu }{\lambda ^{2}}\left( {\frac{\sinh \lambda \xi -\lambda \cosh \lambda (1-\xi )}{\lambda \hbox {cosh}\lambda }+(1-\xi )} \right) \end{aligned}$$
(58a)
$$\begin{aligned} U(\xi )= & {} \frac{c\delta \phi _1 }{\phi _0 }\frac{\hbox {d}W_E^*}{\hbox {d}\xi }+\frac{c_{s0} \delta }{\phi _0 }\left( {\phi _1 cc_{\alpha 1} +\frac{4\phi _3 }{3}} \right) f_{s0} \end{aligned}$$
(58b)
$$\begin{aligned} W(\xi )= & {} cW_E^*+\frac{K\mu }{\lambda ^{4}}\left[ {\frac{\cosh \lambda \xi -1+\lambda [\sinh \lambda (1-\xi )-\sinh \lambda ]}{\hbox {cosh}\lambda }+\lambda ^{2}\xi \left( {1-\frac{\xi }{2}} \right) } \right] \end{aligned}$$
(58c)
$$\begin{aligned} \varphi (\xi )= & {} -c\frac{\hbox {d}W_E^*}{\hbox {d}\xi }-cc_{s0} c_{\alpha 1} f_{s0} \end{aligned}$$
(58d)
$$\begin{aligned} m_{x1} (\xi )= & {} m_E^*, \quad m_R (\xi )=(1+cc_{\alpha 1} )m_E^*+c_{s0} (c_{\alpha 2} +cc_{\alpha 1}^2 )\frac{\hbox {d}f_{s0} }{\hbox {d}\xi }, \quad f_R (\xi )=f_{SE}^*\end{aligned}$$
(58e)

4.4 Beams with C-S Ends

Finally, we consider the bending solution of the FGM RBB with clamped simply supported (C-S) ends. The particular solution of the reference HEBB with C-S ends is

$$\begin{aligned} W_E^*(\xi )= & {} \frac{1}{\hbox {48}}\xi ^{2}(\hbox {3}-\hbox {5}\xi +\hbox {2}\xi ^{2}) \end{aligned}$$
(59a)
$$\begin{aligned} f_E^*(\xi )= & {} \frac{\hbox {1}}{\hbox {8}}(\hbox {5}-\hbox {8}\xi ) \end{aligned}$$
(59b)

The corresponding non-homogeneous particular solution of Eq. (32) is

$$\begin{aligned} g(\xi )=\;\frac{\mu }{\lambda ^{2}}\left[ {\frac{\hbox {1}}{\hbox {8}}(5-8\xi )+\beta _1 } \right] \end{aligned}$$
(60)

Boundary conditions of the C-S FGM RBB are

$$\begin{aligned} U(0)= & {} 0, \quad W(0)=0, \quad {W}'(0)=0, \quad \varphi (0)=0 \end{aligned}$$
(61a)
$$\begin{aligned} f_N (1)= & {} 0, \quad W(1)=0,\quad m_{x1}(1)=0, \quad m_{x3} (1)=0 \end{aligned}$$
(61b)

By using the boundary conditions, the integration constants in the general solutions are determined as follows:

$$\begin{aligned} \beta _3= & {} \beta _4 =0, \quad \beta _2 =-c\beta _1 \end{aligned}$$
(62a)
$$\begin{aligned} \beta _8= & {} -\frac{\mu }{\lambda ^{2}}\left( {\frac{5}{8}+\beta _1 } \right) , \quad \beta _7 =\frac{\mu }{\lambda ^{2}}\left( {\frac{5}{8}+\beta _1 } \right) \tanh \lambda +\frac{\mu }{\lambda ^{3}}\hbox {sech}\lambda \end{aligned}$$
(62b)
$$\begin{aligned} \beta _1= & {} \frac{\frac{\mu }{8\lambda ^{2}}(5\tanh \lambda -\lambda )-\frac{\mu }{\lambda ^{3}}(1-\hbox {sech}\lambda )}{\frac{\mu }{\lambda ^{2}}(\lambda -\tanh \lambda )+\frac{c\lambda }{3K}} \end{aligned}$$
(62c)

Then, the particular solutions of this problem are given by

$$\begin{aligned} f_{s0} (\xi )= & {} \beta _7 \sinh \lambda \xi +\beta _8 \cosh \lambda \xi +\frac{\mu }{\lambda ^{2}}\left[ {\frac{1}{8}(5-8\xi )+\beta _1 } \right] \end{aligned}$$
(63a)
$$\begin{aligned} W(\xi )= & {} cW_E^*+\frac{K}{\lambda }\left[ \beta _7 (\cosh \lambda \xi -1)+\beta _8 \sinh \lambda \xi \right. \nonumber \\&\left. +\frac{\mu }{\lambda ^{2}}\left( {\frac{1}{8}(5-\xi )\xi +\beta _1 \xi } \right) \right] +\frac{c\beta _1 }{6}(3-\xi )\xi ^{2} \end{aligned}$$
(63b)
$$\begin{aligned} \varphi (\xi )= & {} -c\frac{\hbox {d}W_E^*}{\hbox {d}\xi }-cc_{s0} c_{\alpha 1} f_{s0} \end{aligned}$$
(63c)
$$\begin{aligned} U= & {} -\frac{\delta \phi _1 }{\phi _0 }\varphi +\frac{4\delta }{3}\frac{\phi _3 }{\phi _0 }c_{s0} f_{s0} +\beta _5 \xi +\beta _6 \end{aligned}$$
(63d)
$$\begin{aligned} m_{x1}= & {} m_E^*+\beta _1 (\xi -1), \quad m_R =(1+cc_{\alpha 1} )m_{x1} +c_{s0} (c_{\alpha 2} +cc_{\alpha 1} ^{2})\frac{\hbox {d}f_{s0} }{\hbox {d}\xi }, \nonumber \\&\qquad \qquad \qquad f_R (\xi )=f_{SE}^*+\beta _1 \end{aligned}$$
(63e)

From the above four examples, we can find that the particular solutions of the FGM RBBs consist of two parts. The first one is the solution of the classical beam theory which is proportional to that of the HEBB. The second part is a correction to the classical solution based on the RBB theory which is related to the parameters defined in Eq. (28).

In the special case of homogenous material, we have checked that the reduced forms of solutions (49) and (58) for S-S and C-F RBBs are in good agreement with those given by Reddy et al. [39], which validates the present results to some extent.

Table 1 Dimensionless deflection (\(W(0.5)\times 10^{3})\) of an S-S FGM beam for different values of p and \(\delta \) (\(Q=1)\)
Full size table
Fig. 2
figure 2

Dimensionless deflection, W(0.5), versus the power index, p, of a C-C FGM beam by different beam theories: a\(l=5h\); b\(l=10h\); c\(l=20h\); d\(l=40h\)

Full size image
Fig. 3
figure 3

Variation of the dimensionless shear force \(f_{s0} (\xi )\) with the beam length for the FGM RBBs with C-C and S-S ends

Full size image
Fig. 4
figure 4

Zoom-in of the variation of the dimensionless shear force \(f_{s0} (\xi )\) near the simply supported ends for specific values \(p=0.5\), \(l=5h,10h\) and 20h

Full size image

5 Numerical Results

In this section, some numerical results of the particular solutions will be given to show the accuracy and validity of the analytical solutions in this paper. The FGM beam is assumed to be made of metal (aluminum) and ceramic (alumina) with the Young’s moduli of \(E_1 =E_m =70\,\hbox {GPa}\) and \(E_2 =E_c =380\,\hbox {GPa}\), respectively. The Poisson’s ratios of the two constituents are \(\nu _c =\nu _m =0.23\). The effective material properties of the FGM beam vary along the depth as power-law functions [41,42,43,44]. Then, the Young’s moduli of the FGM beam that vary in the depth are given by

$$\begin{aligned} E=E_1 +\left( {E_2 -E_1 } \right) \left( {\frac{1}{2}+\frac{z}{h}} \right) ^{p} \end{aligned}$$
(64)

where \(p\in [0,\infty )\) is the power index and stands for the material gradient level. By substituting Eq. (64) into Eqs. (19)–(21), the analytical expressions of dimensionless coefficients, \(\phi _i \) and \(\phi _{zxi} \), are obtained and given in “Appendix.”

In Table 1, we listed the values of dimensionless deflections at the center of an S-S FGM beam subjected to uniformly distributed load, \(Q(\xi )=1\), for some specific values of the thickness to length ratio, \(\delta \), and the material gradient parameter, p, based on the Timoshenko beam theory [41], the Levinson beam theory [43] and the Reddy–Bickford beam theory, respectively. Furthermore, Fig. 2 plots the continuous variation of the center deflection versus the material gradient parameter of a C-C FGM beam subjected to a uniformly distributed load for some specific values of the length to thickness ratio. From Table 1 and Fig. 2, we can find that the differences between the deflections of the FGM beam predicted by different shear deformable beam theories are not obvious. However, the differences get significant when the beam becomes thicker.

Figure 3 shows the continuous variation of the first-order dimensionless shearing force \(f_{s0} (\xi )\) along the beam axis for the FGM RBB subjected to the uniformly distributed unit load, \(Q(\xi )=1\), with S-S and C-C end constraints, respectively. It is apparent that the first-order shear force vanishes at the clamped ends and converges to the linearly varying distribution of the resultant shear force \(f_R (\xi )\) equaling the shearing force of HEBB, \(f_{sE}^*(\xi )\). The zero values of the first-order shearing force at the two clamped ends arise from the use of essential boundary conditions, \({W}'(0)={W}'(1)=0\). This is physically inaccurate as the beam can actually rotate at the clamped edge due to the presence of transverse shear rotation [45]. However, the values of the first-order shearing force of the FGM RBB with simply supported ends are roughly equal to those of \(f_{sE}^*(\xi )\) even at the end points. Zoom-in of the variation of the dimensionless shear force \(f_{s0} (\xi )\) near the simply supported ends for specific values, \(p=0.5\), \(l=5h,10h\) and 20h, is illustrated in Fig. 4. The differences between the values of \(f_{s0} (\xi )\) and \(f_{sE}^*(\xi )\) at the end points become more significant with the increase in the thickness to length ratio.

6 Conclusions

This paper presents the exact relationships between the static bending solutions of the reference HEBB and those of the FGM RBB with material properties varying continuously along the depth. Firstly, based on the Reddy–Bickford higher-order shear deformation beam theory, equilibrium equations of static bending for the FGM beam were derived in terms of the axial displacement, the deflection and the rotation of the cross section by using the energy-variation principle. Meanwhile, the stretching-bending and stretching-shearing coupling effects are included due to the inhomogeneity of the material properties in the depth direction. By using the load equivalence between the two kinds of beams, general solutions of the displacements, rotation and bending moments for the FGM RBB are derived in terms of the deflection of the corresponding HEBB with the same geometry, end constraints and applied forces. Consequently, the bending solution of an FGM RBB is simplified to that of an HEBB, together with the calculation of those dimensionless transition coefficients, such as c, \(c_{s0} \), \(c_{s2} \), \(c_{\alpha 1} \), and \(c_{\alpha 2} \), which are only dependent on the material gradient profile and the beam geometry. Particular solutions for the FGM RBBs under four specified end constraints and load conditions are given to show the validity of application of the theory and methodology. Finally, we arrived at the homogenized and classical expressions for the static bending solutions of the non-homogeneous FGM RBBs. This relationship enables us to easily obtain the third-order beam theory solutions of FGM beams without dealing with the complicated boundary value problems of the resulting coupling differential equations.