1 Introduction

Nanocrystalline ceramics display excellent physical properties such as high electrical resistivity, good biocompatibility, superior strength and low density [1] and are widely employed in biomedical fields such as dental implants and total joint prostheses, where highly reliable biomaterials are required [2]. Nevertheless, apart from these advantageous properties, some drawbacks such as low tensile ductility and low fracture toughness at room temperature severely limit their practical applications. Therefore, in order to solve this problem, a large number of methods have been proposed to improve the fracture toughness of nanocrystalline ceramics [1, 3,4,5]. In recent years, rapidly growing attention has been concentrated on the dispersion toughness of nano-particles (\(<100\) nm) (Mo, Co, Ti, Ni, Cu) in a ceramic matrix (\(\hbox {Al}_{2}\hbox {O}_{3}\), \(\hbox {ZrO}_{2})\), which can notably enhance the mechanical properties of ceramic materials [6]. The method of particle dispersion toughening originates from the concept of mixing brittle ceramics with ductile metals, and the toughening can be increased through bridging ligaments or crack deflection by the ductile phase [7].

During the past two decades, the incorporation of \(\hbox {ZrO}_{2}\) into \(\hbox {Al}_{2}\hbox {O}_{3}\) to form \(\hbox {ZrO}_{2}/\hbox {Al}_{2}\hbox {O}_{3}\) composite has been prevailing, and evoked great interest from many scholars and practitioners [8,9,10,11,12]. The toughness of alumina-based ceramics containing zirconia \((\hbox {ZrO}_{2})\) as a second phase is substantially enhanced. This is mainly attributed to the martensitic transformation of zirconia from the tetragonal to the monoclinic phase when subjected to the applied stress [13, 14]. Phase transformation toughening is one of the effective methods in enhancing the fracture toughness of brittle materials and has been demonstrated by extensive experimental observations and theoretical results [5, 15,16,17]. The transformation that generally occurs in the vicinity of the crack tip can give rise to the generation of residual strain which, in part, can release the high local stress and absorb fracture energy [7]. Earlier models of transformation toughening were on the basic of energy changes combined with phase transformation [18]. Due to the difficulties of these earlier models in predicting the experimental results, McMeeking and Evans [19] proposed an alternative approach to characterize the transformation toughening of ceramic materials by considering the reduction in stress intensity factors (SIFs) in crack tip. Later, Cai and Faber [20] extended the model to investigate the effect of elastic mismatch between the particle and matrix phases on transformation toughening. Recently, Li et al. [21] established a methodology associated with J-integral over the transformation areas to examine the influence of the dilatant transformation of particles/fibers on fracture toughness in composite materials.

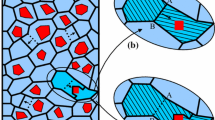
In general, the researchers mentioned above have been discussing the effect of phase transformation on fracture toughness in ceramic materials without considering the effect of lattice dislocations emitted from the crack tip. In fact, lattice dislocations play an important role in mediating the plastic deformation, especially when the grain size is beyond 15 nm. The emission of lattice dislocations along a slip plane can result in blunting of the crack tip, which may further hamper the crack growth and enhance the fracture toughness of ceramic materials [2, 22, 23]. Recently, the phenomenon of several dislocations adjacent to the micro-crack piling up near a \(\hbox {ZrO}_{2}\) particle [13] was observed by the transmission electron microscope (TEM), as shown in Fig. 1. Besides, researchers found that the mechanical properties of \(\hbox {ZrO}_{2}/\hbox {Al}_{2}\hbox {O}_{3}\) composite can be considerably increased by reducing the corresponding grain size [24]. At the same time, the \(\hbox {ZrO}_{2}/\hbox {Al}_{2}\hbox {O}_{3}\) nanocomposite was prepared by using the method of versatile \(\hbox {CO}_{2}\) laser co-vaporization [25], and the average grain sizes of \(\hbox {ZrO}_{2}\) and \(\hbox {Al}_{2}\hbox {O}_{3}\) were \(216\pm 2\) nm and \(270\pm 3\) nm, respectively [26], which met the conditions that the spontaneous transformation of ZrO2 grains occurs more readily if the grain size is below a critical value (500 nm) [27]. Based on these experimental evidences, the goal of the paper is to study the effect of martensitic transformation particle on the dislocation emission from a crack tip by developing a theoretical model of the \(\hbox {ZrO}_{2}/\hbox {Al}_{2}\hbox {O}_{3}\) nanocomposite.

Fig. 1
figure 1

TEM image of the micro-nano \(\hbox {ZrO}_{2}/\hbox {Al}_{2}\hbox {O}_{3}\) composite showing that the dislocations adjacent to the micro-crack piled up near a \(\hbox {ZrO}_{2}\) particle [13]

Full size image

2 Problem Description and Modeling

The physical problem to be considered is schematically depicted in Fig. 2a. The nanocomposite specimen of alumina-based ceramics subjected to mode-I loadings from the infinite contains a semi-infinite crack and nanoscale \(\hbox {ZrO}_{2}\) particles embedded in the intragrain or grain boundaries of \(\hbox {Al}_{2}\hbox {O}_{3}\) grains. The sample is supposed to be elastic and isotropic with shear modulus \(\mu \) and Poisson’s ratio v. The emission of lattice dislocations from the crack tip is stimulated under the high stress intensity near the crack tip. In this case, it is not very easy to explore the fundamentals of mechanical behavior in \(\hbox {ZrO}_{2}/\hbox {Al}_{2}\hbox {O}_{3}\) nanocomposite with complicated microstructures. For simplicity, we consider a typical structure in a two-dimensional section composed of a semi-infinite crack and a cylindrical \(\hbox {ZrO}_{2}\) particle, as shown in Fig. 2b. Furthermore, we assume that the \(\hbox {ZrO}_{2}\) particle located at the triple junction has experienced a complete martensitic transformation from the tetragonal to the monoclinic phase, and is no longer influenced by the applied stress. In addition, the \(\hbox {ZrO}_{2}\) particles are isolated from one another, and the effect produced by the interaction between the same neighboring structures is negligible. Subjected to an applied uniaxial tension \(\sigma _0\), the dislocations are induced to emit from the crack tip along the same slip plane with the dislocation lines parallel to the z-axis.

On the basis of the above descriptions, the current problem is simplified and illustrated in Fig. 2b. For convenience of analysis, the Cartesian coordinate system is established with its origin located at the tip of the crack. The radius of the \(\hbox {ZrO}_{2}\) particle is denoted by R, and the distance between the \(\hbox {ZrO}_{2}\) particle and the crack tip is taken as d. Finally, since the amount of the \(\hbox {ZrO}_{2}\) particle is relatively less than that of the alumina-based ceramics, the ceramic matrix can be regarded as an infinite plane for the plane strain problem.

Fig. 2
figure 2

The \(\hbox {ZrO}_{2}/\hbox {Al}_{2}\hbox {O}_{3}\) nanocomposite specimen consisting of a semi-infinite crack and dislocations (a) general view (b) the magnified inset highlighting the generation of edge dislocations emitted from a crack tip near a \(\hbox {ZrO}_{2}\) particle

Full size image

For the plane strain problem, all components of the stress fields and displacement fields can be described in terms of two Muskhelishvili’s complex potentials \({\varPhi }(z)\) and \({\varOmega }(z)\) as [28]

$$\begin{aligned} \sigma _{xx} +\sigma _{yy}= & {} 2\left[ {{\varPhi }(z)+\overline{{\varPhi }(z)} } \right] \end{aligned}$$
(2.1)
$$\begin{aligned} \sigma _{yy} +\mathrm{i}\sigma _{xy}= & {} \left[ {\overline{{\varPhi }(z)} +{\varOmega }(z)+(\bar{{z}}-z){{\varPhi }}'(z)} \right] \end{aligned}$$
(2.2)
$$\begin{aligned} 2\mu \left( {u_{x,x} +\mathrm{i}u_{y,x} } \right)= & {} k{\varPhi }(z)-\overline{{\varOmega }(z)} -(z-\bar{{z}})\overline{{{\varPhi }}'(z)} \end{aligned}$$
(2.3)

where \({{\varPhi }}'(z)=\hbox {d}\left[ {{\varPhi }(z)} \right] /\hbox {d}z\), \(k=3-4v\) for plane strain, the over-bar indicates a complex conjugate and the prime represents the derivation with respect to argument z.

To be more specific, the stress components in the Cartesian coordinate system can be rewritten as

$$\begin{aligned} \sigma _{xx}= & {} \hbox {Re}[3\overline{{\varPhi }(z)} -{\varOmega }(z)+(z-\bar{{z}}){{\varPhi }}'(z)] \end{aligned}$$
(2.4)
$$\begin{aligned} \sigma _{xy}= & {} \hbox {Im}\left[ {\overline{{\varPhi }(z)} +{\varOmega }(z)+(\bar{{z}}-z){{\varPhi }}'(z)} \right] \end{aligned}$$
(2.5)
$$\begin{aligned} \sigma _{yy}= & {} \hbox {Re}\left[ {\overline{{\varPhi }(z)} +{\varOmega }(z)+(\bar{{z}}-z){{\varPhi }}'(z)} \right] \end{aligned}$$
(2.6)

Besides, for the current problem, the stress components at the crack surfaces should satisfy the following boundary condition

$$\begin{aligned} \sigma _{yy} (t)+\mathrm{i}\sigma _{xy} (t)=0 \quad (t\in \hbox { crack}) \end{aligned}$$
(2.7)

3 Solutions of the Stress Functions

3.1 Dislocation-Based Strain Nucleus Located in an Infinite Matrix

According to the work of Suo [29], it is known that the elastic stress fields produced by an edge dislocation with Burgers vector b and located at point s in an infinite homogeneous medium can be expressed as

$$\begin{aligned}&\displaystyle {\varPhi }(z)=\frac{M\eta }{z-s} \end{aligned}$$
(3.1)
$$\begin{aligned}&\displaystyle {\varOmega }(z)=\frac{M\eta (\bar{{s}}-s)}{(z-s)^{2}}-\frac{M\bar{{\eta }}}{z-s} \end{aligned}$$
(3.2)

where \(M=\mu /\left[ {\mathrm{i}{\pi }(1+k)} \right] \), \(\eta =b\mathrm{e}^{\mathrm{i}\psi }\), and \(\psi \) denotes the orientation angle of the \(x_{0}\)-axis (associated with the principal strain \({\upvarepsilon }_{x0}\)) with respect to the global x-coordinate axis.

A differential element shown in Fig. 3 with an area \(\mathrm{d}A=\mathrm{d}x_0 \mathrm{d}y_0\) is taken into account, which undergoes an unconstrained irreversible transformation with two principal strains \(\varepsilon _{x0} \) and \(\varepsilon _{y0}\) expressed in local principal coordinates \(x_0\) and \(y_0\). At the same time, the infinitesimal element with transformation strain can be modeled by an assembly of four dislocations; the potentials for which in the global coordinate system can be written as [30]

$$\begin{aligned} \begin{array}{l} {\varPhi }_j (z)=\frac{M\eta _j }{z-s_j }\\ {\varOmega }_j (z)=\frac{M\eta _j (\bar{{s}}_j -s_j )}{(z-s_j )^{2}}-\frac{M\bar{{\eta }}_j }{z-s_j }\\ \end{array} \quad (j=1,2,3,4) \end{aligned}$$
(3.3)

where

$$\begin{aligned} \eta _1= & {} \mathrm{e}^{\mathrm{i}\psi }(\varepsilon _{x_0 } \hbox {d}x_0 ),\,s_1 =s-\mathrm{e}^{\mathrm{i}\psi }\mathrm{e}^{\mathrm{i}\frac{{\pi }}{2}}\left( \frac{\hbox {d}y_0 }{2}\right) \nonumber \\ \eta _2= & {} \mathrm{e}^{-\mathrm{i}\frac{{\pi }}{2}}\mathrm{e}^{\mathrm{i}\psi }(\varepsilon _{y_0 } \hbox {d}y_0 ),\,s_2 =s-\mathrm{e}^{\mathrm{i}\psi }\left( \frac{\hbox {d}x_0 }{2}\right) \nonumber \\ \eta _3= & {} \mathrm{e}^{\mathrm{i}{\pi }}\mathrm{e}^{\mathrm{i}\psi }(\varepsilon _{x_0 } \hbox {d}x_0 ),\,s_3 =s+\mathrm{e}^{\mathrm{i}\psi }\mathrm{e}^{\mathrm{i}\frac{{\pi }}{2}}\left( \frac{\hbox {d}y_0 }{2}\right) \nonumber \\ \eta _4= & {} \mathrm{e}^{\mathrm{i}\frac{{\pi }}{2}}\mathrm{e}^{\mathrm{i}\psi }(\varepsilon _{y_0 } \mathrm{d}y_0 ),\,s_4 =s+\mathrm{e}^{\mathrm{i}\psi }\left( \frac{\hbox {d}x_0 }{2}\right) \end{aligned}$$
(3.4)

The subscripts refer to the numbered dislocations depicted in Fig. 3, and the Burgers vector \(\eta _j \,(j=1,2,3,4)\) represents the residual deformation of the differential element resulting from the martensitic transformation.

Fig. 3
figure 3

A concentrated transformed strain located in an infinite matrix

Full size image

The potentials with principal values \(\varepsilon _{x0}\) and \(\varepsilon _{y0} \) can be reached by superposing the four potentials as

$$\begin{aligned} {\varPhi }(z)= & {} \sum _{j=1}^4 {{\varPhi }_j (z)} \nonumber \\ {\varOmega }(z)= & {} \sum _{j=1}^4 {{\varOmega }_j (z)} \end{aligned}$$
(3.5)

After a straightforward manipulation, we can obtain

$$\begin{aligned} {\varPhi }(z)= & {} \hbox {i}M\hbox {e}^{2\mathrm{i}\psi }\frac{\varepsilon _{y_0 } -\varepsilon _{x_0 } }{(z-s)^{2}}\hbox {d}x_0 \hbox {d}y_0 \nonumber \\= & {} \hbox {i}M\hbox {e}^{2{\mathrm{i}}\psi }\frac{\varepsilon _{y_0 } -\varepsilon _{x_0 } }{(z-s)^{2}} \hbox {d}A \end{aligned}$$
(3.6)
$$\begin{aligned} {\varOmega }(z)= & {} \hbox {i}M\left[ {\frac{2(\varepsilon _{x_0 } +\varepsilon _{y_0 } )- \hbox {e}^{2{\mathrm{i}}\psi }(\varepsilon _{y_0 } -\varepsilon _{x_0 } )}{(z-s)^{2}}+\frac{2 \hbox {e}^{2{\mathrm{i}}\psi }(\varepsilon _{y_0 } -\varepsilon _{x_0 } )(\bar{{s}}-s)}{(z-s)^{3}}} \right] \hbox {d}x_0 \hbox {d}y_0 \nonumber \\= & {} \hbox {i}M\left[ {\frac{2(\varepsilon _{x_0 } +\varepsilon _{y_0 } )-\hbox {e}^{2{\mathrm{i}}\psi }(\varepsilon _{y_0 } -\varepsilon _{x_0 } )}{(z-s)^{2}}+\frac{2\hbox {e}^{2{\mathrm{i}}\psi }(\varepsilon _{y_0 } -\varepsilon _{x_0 } )(\bar{{s}}-s)}{(z-s)^{3}}} \right] \hbox {d}A \end{aligned}$$
(3.7)

For convenience, Eqs. (3.6) and (3.7) can be expressed in a compact form as

$$\begin{aligned} {\varPhi }(z)= & {} {\varPhi }_0 (z)\hbox {d}A \nonumber \\ {\varOmega }(z)= & {} {\varOmega }_0 (z)\hbox {d}A \end{aligned}$$
(3.8)

where \({\varPhi }_{0} (z)=\frac{C_1 }{(z-s)^{2}}\), \({\varOmega }_0 (z)=\frac{C_2 }{(z-s)^{2}}+\frac{C_3 (\bar{{s}}-s)}{(z-s)^{3}}\), \(\hbox {d}A=\hbox {d}x_0 \hbox {d}y_0 \), \(C_1 =\hbox {i}M\hbox {e}^{2{\mathrm{i}}\psi }(\varepsilon _{y_0 } -\varepsilon _{x_0 } ), C_2 =\mathrm{i}M[2(\varepsilon _{x_0 } +\varepsilon _{y_0 } )-\hbox {e}^{2{\mathrm{i}}\psi }(\varepsilon _{y_0 } -\varepsilon _{x_0 } )]\) and \(C_3 =\mathrm{i}M[2\hbox {e}^{2{\mathrm{i}}\psi }(\varepsilon _{y_0 } -\varepsilon _{x_0})].\) It is worth mentioning that when \(\varepsilon _{x0} =\varepsilon _{y0} \), the current solutions will reduce to the case of a purely dilatational transformation. Conversely, if \(\varepsilon _{x0} =-\varepsilon _{y0} \), the solution for a pure shear transformation will be achieved.

3.2 Stress Field Arising from Martensitic Transformation Particle

In the previous section, the solutions of complex potentials \({\varPhi }_0 (z)\) and \({\varOmega }_0 (z)\) for a transformation strain nucleus located in an infinite matrix have been obtained without a crack. Next, we consider the current problem with a semi-infinite crack near a \(\hbox {ZrO}_{2}\) transformation particle in the \(\hbox {ZrO}_{2}/\hbox {Al}_{2}\hbox {O}_{3}\) nanocomposites. Referring to the work of Muskhelishvili [28], the complex potentials for a transformation strain nucleus with a crack can be written as

$$\begin{aligned} {\varPhi }_{p0} (z)= & {} \frac{C_1 }{(z-s)^{2}}+{\varPhi }_{p0}^*(z) \end{aligned}$$
(3.9)
$$\begin{aligned} {\varOmega }_{p0} (z)= & {} \frac{C_2 }{(z-s)^{2}}+\frac{C_3 (\bar{{s}}-s)}{(z-s)^{3}}+{\varOmega }_{p0}^*(z) \end{aligned}$$
(3.10)

where \({\varPhi }_{p0}^*(z)\) and \({\varOmega }_{p0}^*(z)\) are holomorphic and determined by the stress boundary condition in Eq. (2.7).

Together with Eq. (2.2), the boundary condition in Eq. (2.7) can be rewritten as

$$\begin{aligned}&\left[ {{\varOmega }(t)-\bar{{{\varPhi }}}(t)} \right] ^{+}-\left[ {{\varOmega }(t)-\bar{{{\varPhi }}}(t)} \right] ^{-}=0 \qquad (t\in \hbox {crack}) \end{aligned}$$
(3.11)
$$\begin{aligned}&\left[ {{\varOmega }(t)+\bar{{{\varPhi }}}(t)} \right] ^{+}+\left[ {{\varOmega }(t)+\bar{{{\varPhi }}}(t)} \right] ^{-}=0 \qquad (t\in \hbox {crack}) \end{aligned}$$
(3.12)

where the superscripts “\(+\)” and “−” represent the boundary values of the physical quantities as approached from the upper half-plane and the lower half-plane of the semi-infinite crack, respectively.

The substitution of Eqs. (3.9) and (3.10) into Eq. (3.11) yields

$$\begin{aligned} {\varOmega }_{p0}^*(z)=\bar{{{\varPhi }}}_{p0}^*(z) \end{aligned}$$
(3.13)

Then, inserting Eqs. (3.9) and (3.10) into Eq. (3.12), the following Riemann–Hilbert boundary problem is reached as

$$\begin{aligned} \left[ {{\varOmega }_{p0}^*(t)} \right] ^{+}+\left[ {{\varOmega }_{p0}^*(t)} \right] ^{-}=h(t)\quad (t\in (-\infty ,0)) \end{aligned}$$
(3.14)

where

$$\begin{aligned} h(t)=-\frac{\bar{{C}}_1 }{(t-\bar{{s}})^{2}}-\frac{C_2}{(t-s)^{2}}-\frac{C_3 (\bar{{s}}-s)}{(t-s)^{3}} \end{aligned}$$

With reference to the work of Muskhelishvili [28], the above boundary value problem can be solved by utilizing the Cauchy-type integral as

$$\begin{aligned} {\varOmega }_{p0}^*(z)=\frac{X_0 (z)}{2\pi \hbox {i}}\int _{-\infty }^0 {\frac{h(t)}{X_0^+ (t)}} \frac{\hbox {d}t}{t-z}+X_0 (z)P_n (z) \end{aligned}$$
(3.15)

where \(X_0 (z)=1/\sqrt{z}\) and \(P_n (z)=D_n z^{n}+D_{n-1} z^{n-1}+\cdot \cdot \cdot +D_0 \). Here, \(P_n (z)=0\) due to \({\varOmega }_{p0}^*(z)=o(1/z^{2})\).

The solution of Eq. (3.15) is given as

$$\begin{aligned} {\varOmega }_{p0}^*(z)=\frac{1}{2\sqrt{z}}\left[ {\frac{\bar{{C}}_1 }{2\sqrt{\bar{{s}}}(\sqrt{z}+\sqrt{\bar{{s}}})^{2}}+\frac{C_2 }{2\sqrt{s}(\sqrt{s}+\sqrt{z})^{2}}-\frac{C_3 (\bar{{s}}-s)(3\sqrt{s}+\sqrt{z})}{8s^{3/2}(\sqrt{s}+\sqrt{z})^{3}}} \right] \end{aligned}$$
(3.16)

Inserting Eq. (3.16) into Eq. (3.13), we have

$$\begin{aligned} {\varPhi }_{p0}^*(z)=\frac{1}{2\sqrt{z}}\left[ {\frac{C_1 }{2\sqrt{s}(\sqrt{z}+\sqrt{s})^{2}}+\frac{\bar{{C}}_2 }{2\sqrt{\bar{{s}}}(\sqrt{\bar{{s}}}+\sqrt{z})^{2}}-\frac{\bar{{C}}_3 (s-\bar{{s}})(3\sqrt{\bar{{s}}}+\sqrt{z})}{8\bar{{s}}^{3/2}(\sqrt{\bar{{s}}}+\sqrt{z})^{3}}} \right] \end{aligned}$$
(3.17)

Substituting Eqs. (3.16) and (3.17) into Eqs. (3.10) and (3.9), respectively, leads to the solutions of a transformation strain nucleus with a crack. Finally, the complex potentials created by the transformation strain of \(\hbox {ZrO}_{2}\) particle can be achieved by an integral of transformation area as

$$\begin{aligned} {\varPhi }_p (z)= & {} \int _0^R {\int _0^{2{\pi }} {{\varPhi }_{p0} (z)} } \rho \hbox {d}\varphi \hbox {d}\rho \end{aligned}$$
(3.18)
$$\begin{aligned} {\varOmega }_p (z)= & {} \int _0^R {\int _0^{2{\pi }} {{\varOmega }_{p0} (z)} } \rho \hbox {d}\varphi \hbox {d}\rho \end{aligned}$$
(3.19)

4 Force on the First Dislocation Emission

For the first dislocation emission from a semi-infinite crack tip with the martensitic transformation particle, we consider a typical situation where the dislocations are of edge character and their Burgers vectors lie along the same slip plane making an angle \(\theta \) with the x-axis shown in Fig. 2b. The force acting on the edge dislocation is composed of three parts: (1) the force due to the martensitic transformation of \(\hbox {ZrO}_{2}\) particle; (2) the image force caused by the crack-free surface; (3) the external load.

Firstly, we calculate the force exerted on the edge dislocation arising from the transformation strain of \(\hbox {ZrO}_{2}\) particle, which can be expressed by using the Peach–Koehler formula as [31]

$$\begin{aligned} f_p= & {} f_{px} -\hbox {i}f_{py} =\left[ {\sigma _{xy}^p (z_0 )b_x +\sigma _{yy}^p (z_0 )b_y } \right] +\mathrm{i}\left[ {\sigma _{xx}^p (z_0)b_x +\sigma _{xy}^p (z_0 )b_y } \right] \nonumber \\= & {} \frac{\mu b^{2}}{4{\pi }M(1-v)}\left\{ {\frac{\overline{{\varPhi }_p (z_0 )} +{\varPhi }_p (z_0 )}{\eta }-\frac{\left[ {(\bar{{z}}_0 -z_0 ){{\varPhi }}'_p (z_0 )+{\varOmega }_p (z_0 )-{\varPhi }_p (z_0 )} \right] }{\bar{{\eta }}}} \right\} \end{aligned}$$
(4.1)

in which \(\sigma _{xx}^p\), \(\sigma _{xy}^p\) and \(\sigma _{yy}^p\) are the stress components of the elastic fields due to the martensitic transformation strain of \(\hbox {ZrO}_{2}\) particle.

Secondly, we assess the image force produced by the crack-free surface. Supposing that the first edge dislocation emitted from the crack tip is located at point \(z_0 =r_0 \hbox {e}^{\mathrm{i}\theta }\) in the xoy coordinate system depicted in Fig. 2b, and then using the same approach as the above-mentioned, the elastic fields of an edge dislocation in an infinite matrix can be obtained as

$$\begin{aligned}&{\varPhi }_d (z)=\frac{M\eta }{2}\left[ {\frac{1}{z-z_0 }\left( {\sqrt{\frac{z_0 }{z}}+1} \right) +\frac{1}{z-\bar{{z}}_0 }\left( {\sqrt{\frac{\bar{{z}}_0 }{z}}-1} \right) } \right] -\frac{M\bar{{\eta }}(z_0 -\bar{{z}}_0 )}{4(z-\bar{{z}}_0 )^{2}}\left( {\sqrt{\frac{\bar{{z}}_0 }{z}}+\sqrt{\frac{z}{\bar{{z}}_0}}-2} \right) \nonumber \\ \end{aligned}$$
(4.2)
$$\begin{aligned}&{\varOmega }_d (z)=\frac{M\eta (\bar{{z}}_0 -z_0 )}{4(z-z_0 )^{2}}\left( {\sqrt{\frac{z_0 }{z}}+\sqrt{\frac{z}{z_0 }}+2} \right) -\frac{M\bar{{\eta }}}{2}\left[ {\frac{1}{z-\bar{{z}}_0 }\left( {\sqrt{\frac{\bar{{z}}_0 }{z}}-1} \right) +\frac{1}{z-z_0 }\left( {\sqrt{\frac{z_0 }{z}}+1} \right) } \right] \nonumber \\ \end{aligned}$$
(4.3)

The above results are completely in line with those obtained by Zhang and Li [32], and the image force can be examined by means of the Peach–Koehler formula as [31]

$$\begin{aligned} f_d= & {} f_{\mathrm{d}x} -\hbox {i}f_{\mathrm{d}y} =\left[ {\sigma _{xy}^d (z_0 )b_x +\sigma _{yy}^d (z_0 )b_y } \right] +\mathrm{i}\left[ {\sigma _{xx}^d (z_0 )b_x +\sigma _{xy}^d (z_0 )b_y } \right] \nonumber \\= & {} \frac{\mu b^{2}}{4{\pi }M(1-v)}\left[ {\frac{\overline{{\varPhi }_d (z_0 )} +{\varPhi }_d (z_0 )}{\eta }-\frac{\left( {\bar{{z}}_0 -z_0 } \right) {{\varPhi }}'_d (z_0 )+{\varOmega }_d (z_0 )-{\varPhi }_d (z_0 )}{\bar{{\eta }}}} \right] \end{aligned}$$
(4.4)

where \(\sigma _{xx}^d\), \(\sigma _{xy}^d\) and \(\sigma _{yy}^d\) are the components of the perturbation stress resulting from the interaction between the edge dislocation and the crack surface.

Thirdly, the external load imposed on the edge dislocation can be written as [23]

$$\begin{aligned} f_\infty =b\sigma _{r\theta } =\frac{b({\varTheta }_1 K_\mathrm{I}^{\mathrm{app}} +{\varTheta }_2 K_{{\mathrm{I}\mathrm{I}}}^{\mathrm{app}} )}{\sqrt{2{\pi }r}} \end{aligned}$$
(4.5)

where \({\varTheta }_1 =\frac{1}{2}\sin \theta \cos \frac{\theta }{2}\), \({\varTheta }_2 =\sin ^{2}\frac{\theta }{2}\cos \frac{\theta }{2}+\cos \frac{3\theta }{2}\), \(K_{\mathrm{I}}^{\mathrm{app}}\) and \(K_{{\mathrm{II}}}^{\mathrm{app}}\) denote the generalized SIFs for mode I and mode II due to the applied load, respectively, and \(b(=b_x +\hbox {i}b_y )\) is the Burgers vector of the first edge dislocation.

Lastly, the force exerted on the first dislocation emitted from the crack tip is derived by using the superposition principle as

$$\begin{aligned} f_{\mathrm{emit}} =\hbox {Re}[f_d +f_p ]\cos \theta -\hbox {Im}[f_d +f_p ]\sin \theta +f_\infty \end{aligned}$$
(4.6)

It is a general criterion that if a new dislocation can be spontaneously emitted from a crack tip, the force acting on it must be greater than zero, and the distance between the dislocation and the crack surface is no smaller than the dislocation core radius \(r_0\) [33]. In view of Eqs. (3.18)–(4.6) and the critical condition \(f_{\mathrm{emit}} =0\), the critical SIFs for the first dislocation emission from the crack tip are obtained as

$$\begin{aligned} K_{\mathrm{I}}^{\mathrm{app}} =0,\,K_{{\mathrm{I}\mathrm{I}}}^{\mathrm{app}} =\frac{\sqrt{2\pi r}}{b{\varTheta }_2 }(\hbox {Im}[f_d +f_p ]\sin \theta -\hbox {Re}[f_d +f_p ]\cos \theta ) \end{aligned}$$
(4.7)

for mode-II crack, and

$$\begin{aligned} K_{\mathrm{I}\mathrm{I}}^{\mathrm{app}} =0,\,K_{\mathrm{I}}^{\mathrm{app}} =\frac{\sqrt{2\pi r}}{b{\varTheta }_1 }(\hbox {Im}[f_d +f_p ]\sin \theta -\hbox {Re}[f_d +f_p ]\cos \theta ) \end{aligned}$$
(4.8)

for mode-I crack.

5 Number of Dislocations Emitted from the Semi-infinite Crack Tip

In this section, we will estimate the maximum number \(N_{\max }\) of emitted dislocations from the crack tip along a slip plane. It assumes that the first emitted dislocation stops in the vicinity of the transformation particle with a distance of d from the crack tip, and then the equilibrium positions of other dislocations are calculated according to the force balance equation of effective stress as

$$\begin{aligned} \sigma _{r\theta }^e (r_i ,\theta )=\sigma _{r\theta }^{K_{\mathrm{I}}} (r_i ,\theta )+\sigma _{r\theta }^{im} (r_i ,\theta )+\sigma _{r\theta }^p (r_i ,\theta )+\sum _{\begin{array}{c} j=0, \\ j\ne 1 \end{array}}^N {\sigma _{r\theta }^d (r_i ,r_j ,\theta )} \end{aligned}$$
(5.1)

where the stresses \(\sigma _{r\theta }^{K_\mathrm{I}} (r_i ,\theta )\), \(\sigma _{r\theta }^{im} (r_i ,\theta )\) and \(\sigma _{r\theta }^p (r_i ,\theta )\) are created by the applied tension \(\sigma _0 \), the crack-free surface and the transformation strain particle, respectively. Besides, \(\sigma _{r\theta }^d (r_i ,r_j ,\theta )\) represents the stress exerted by the jth dislocation (that is already emitted and stays along the slip direction) at the position of (\(r_j ,\theta )\) on the newly emitted dislocation at the position of (\(r_i ,\theta )\).

Following the Rice–Thompson criterion [33], we assume that the emission of the first dislocation can occur if this dislocation is repelled from the crack tip when the distance from the dislocation to the crack tip exceeds the dislocation core radius \(r_0 \). Therefore, the first dislocation emission should satisfy the following critical condition

$$\begin{aligned} \left. {\sigma _{r\theta }^{K_{\mathrm{I}}} (r,\theta )+\sigma _{r\theta }^{im} (r,\theta )+\sigma _{r\theta }^p (r,\theta )} \right| _{r=r_0 } >0 \end{aligned}$$
(5.2)

To be specific, we will only take the necessary, but not the sufficient condition into account due to the fact that the real conditions for the dislocation emission are stricter than those presented in the following formula. At the same time, it is assumed that dislocation emission can be possible even if the width of attraction zone for the crack tip exceeds the dislocation core radius. In this case, it is supposed that the (\(N+1)^{th}\) dislocation (\(N=1,2,{\ldots }\)) can emit within the interval \(0<r<d\) where this dislocation is repelled from the crack tip. In this region, the following inequality should be valid

$$\begin{aligned} \sigma _{r\theta }^{K_{\mathrm{I}}} (r_{N+1} ,\theta )+\sigma _{r\theta }^{im} (r_{N+1} ,\theta )+\sigma _{r\theta }^p (r_{N+1} ,\theta )+\sum _{j=0}^N {\sigma _{r\theta }^d (r_{N+1} ,r_j ,\theta )} >0\quad (N=1,2,\ldots ) \end{aligned}$$
(5.3)

The stress \(\sigma _{r\theta }^{K_{\mathrm{I}}} (r,\theta )\) and \(\sigma _{r\theta }^{im} (r,\theta )\) are given by Lin and Thomson [33] as

$$\begin{aligned}&\sigma _{r\theta }^{K_{\mathrm{I}}} (r,\theta )=\frac{K_{\mathrm{I}} \sin \theta \cos (\theta /2)}{2\sqrt{2{\pi }r}}\end{aligned}$$
(5.4)
$$\begin{aligned}&\sigma _{r\theta }^{im} (r,\theta )=-\frac{\mu b}{4{\pi }(1-v)r} \end{aligned}$$
(5.5)

In addition, the stresses \(\sigma _{r\theta }^p (r,\theta )\) created by the transformation strain particle and \(\sigma _{r\theta }^d (r,\theta )\) due to the emitted dislocations can be reached by inserting Eqs. (3.18), (3.19) and Eqs. (4.2), (4.3) into Eq. (2.2), respectively, before using the following equation

$$\begin{aligned} \sigma _{r\theta } =(\sigma _{yy} -\sigma _{xx} )\sin \theta \cos \theta +\sigma _{xy} \cos (2\theta ) \end{aligned}$$
(5.6)

6 Results and Discussion

In this section, we mainly discuss the influences of vital parameters such as the size of \(\hbox {ZrO}_{2}\) particle, dislocation emission angle and the distance from the crack tip to the transformation particle on the emission of the first dislocation. Furthermore, the critical SIFs for the first dislocation emission and the maximum number of emitted dislocations along a slip plane are also examined in detail. For simplicity, it is assumed that the Burgers vector of the edge dislocation is b=0.25 nm, and the core radius of dislocation is \(r_0 =b/2\). Here, we mainly focus on the effect of purely dilatational transformation (i.e., \(\varepsilon _{x0} =\varepsilon _{y0} )\) on dislocation emission with neglecting the shear component of the transformation. For the system of \(\hbox {ZrO}_{2}\)/\(\hbox {Al}_{2}\hbox {O}_{3}\) nanocomposite, the appropriate values of elastic constants are given as \(\mu =150\) GPa, \(v=0.27\) for \(\hbox {Al}_{2}\hbox {O}_{3}\) and \(\mu _1=80\) GPa, \(v_1=0.3\) for \(\hbox {ZrO}_{2}\) [34], and the equivalent eigenstrains \(\varepsilon _{x0} \), \(\varepsilon _{y0} \) from the transformation strains of \(\hbox {ZrO}_{2}\) particle can be calculated by [35]

$$\begin{aligned} \varepsilon _{x_0 } =\varepsilon _{y_0 } =\varepsilon _0 =\left( {\frac{1-2v}{1-2v_1 }} \right) \left( {\frac{\mu _1 }{\mu }} \right) \left[ {1-\left( {\frac{S_{11} +S_{12} }{h}} \right) } \right] \varepsilon ^{T} \end{aligned}$$
(6.1)

where \(S_{11} +S_{12} =\frac{1}{2(1-v)}\) and \(h=\frac{(1-2v_1 )\mu }{(1-2v_1)\mu -(1-2v)\mu _1 }\) with the experimental value of the transformation strain \(\varepsilon ^{T}\approx \)0.024.

6.1 Influences of Particle Size and Location on the Critical SIFs for the First Dislocation Emission

For the current semi-infinite crack, Eq. (4.8) is considered with the normalized mode-I critical SIF defined as \(K_{\mathrm{I}C}^{\mathrm{app}} =K_{\mathrm{I}}^{\mathrm{app}}/(\mu \sqrt{b})\). The variations of the normalized mode-I critical SIF \(K_{\mathrm{I}C}^{\mathrm{app}}\) with respect to the distance from the tip of the crack to the transformation particle are shown in Fig. 4. It is observed that with the increase in the distance, the normalized critical SIF decreases and gradually tends toward a constant. At the same time, at a certain distance, the larger is the transformation particle, the relatively larger is the value of the normalized critical SIF. The results imply that the transformation of \(\hbox {ZrO}_{2}\) particle shows a shielding effect on the dislocation emission from the crack tip, and the shielding effect enhances with an increase in the size of transformation particle. Figure 5 plots the normalized mode-I critical SIF versus the size of transformation particle at different distances d. From the graph, it can be seen that as the radius of \(\hbox {ZrO}_{2}\) particle rises, the normalized mode-I critical SIF increases. On the other hand, for a certain size of transformation particle, a decrease in the distance will raise the normalized modes I critical SIF. The normalized mode-I critical SIF as a function of the dislocation emission angle \(\theta \) is illustrated in Fig. 6. It is obvious that the absolute values of normalized mode-I critical SIF first decrease, and then increase with the increase in the dislocation emission angle. According to Huang and Li [36], the sign of the SIFs depends on the direction of the Burgers vector of the emerging dislocations, indicating that the normalized mode-I critical SIFs may be positive or negative. In this case, there exists a probable angle \({\vert }\theta {\vert }\approx 74^{\circ }\) making the dislocation emission easiest.

Fig. 4
figure 4

Dependence of the dimensionless critical mode-I SIFs on dislocation emission with different sizes of \(\hbox {ZrO}_{2}\) particle for \(\theta ={\pi }/3\)

Full size image
Fig. 5
figure 5

Dependence of the dimensionless critical mode-I SIFs on dislocation emission with different distances d for \(\theta ={\pi }/3\)

Full size image
Fig. 6
figure 6

Dependence of the dimensionless critical mode-I SIFs on dislocation emission with \(d=100\) nm, \(R=50\) nm

Full size image

6.2 Influence of Distance from the Crack Tip to the Transformation Particle on the Maximum Number of Dislocation Emissions from the Semi-infinite Crack Tip

With the calculation procedure described in Sect. 5, the maximum number of edge dislocations emitted along the same slip plane as a function of the distance d is illustrated in Fig. 7. Specifically, we choose the material parameters as: crack length \(l=200\) nm, the size of transformation particle \(R=50\) nm, dislocation emission angle \(\theta =\pi /3\), the Burgers vector magnitude \(b=0.25\) nm and \(K_{\mathrm{I}} =\sqrt{4\mu \gamma /(1-v)}\) (\(\gamma =1.69\,\hbox {J}/\hbox {m}^{2}\) for \(\hbox {Al}_{2}\hbox {O}_{3}\) representing the specific surface energy). We can see from Fig. 7 that the number \(N_{\max }\) of emitted dislocations increases with an increase in distance d. At the same time, it should be noted that the value of \(N_{\max }\) is relatively small, which suggests that the significant crack blunting induced by dislocation emission is not easy for small grain size (the distance d is approximate to the size of \(\hbox {Al}_{2}\hbox {O}_{3}\) grain) but prone to the growth of crack.

Fig. 7
figure 7

The maximum number \(N_{\max }\) of edge dislocations emitted from the semi-infinite crack tip as a function of the distance d with \(l=200\) nm, \(R=50\) nm, \(\theta =\pi /3\)

Full size image

7 Conclusions

The problem of martensitic transformation particle interacting with a semi-infinite crack is addressed by building up a theoretical model in ceramic-matrix nanocomposites. On the basis of the model of dislocation strain nucleus and the Green’s function method, the solutions of complex potentials arising from the martensitic transformation are obtained analytically. The critical SIFs for the first-lattice dislocation emission and the maximum number of emitted dislocations are evaluated. The influences of typical parameters such as the size and location of transformation particle as well as the distance from the crack tip to the transformation particle on dislocation emission are examined in detail. Some main conclusions are summarized below:

  1. (1)

    The transformation of \(\hbox {ZrO}_{2}\) particle shows a shielding effect on the dislocation emission from the crack tip, and the shielding effect enhances with an increase in the size of transformation particle.

  2. (2)

    As the radius of \(\hbox {ZrO}_{2}\) particle rises, the normalized mode-I critical SIF increases. On the other hand, for a certain size of transformation particle, the decrease in distance will raise the normalized mode-I critical SIF.

  3. (3)

    The normalized mode-I SIF is closely related with the dislocation emission angle, and there exists a probable angle \({\vert }\theta {\vert }\approx 74^{\circ }\) making the dislocation emission easiest.

  4. (4)

    The significant crack blunting induced by the dislocation emission is not easy for small grain size, but prone to the growth of crack.