1 Introduction

Boron Nitride Nanotubes (BNNTs) are similar to carbon nanotubes (CNTs) in structure and excellent mechanical properties, but own higher temperature resistance to oxidation and stronger piezoelectric characteristics. In addition, BNNTs also possess stable semiconductive properties. Therefore, BNNTs are considered as one of the most promising reinforcement materials. With the development of science and technology, a new sort of smart nanocomposite, consisting of BNNTs as the reinforcement and piezoelectric material as the matrix, has attracted increasing interest from the scientific community. It is noted that the investigations on piezoelectric structure reinforced with BNNTs are limited in number and mostly discuss the static problem only. Therefore, it is necessary to conduct more extensive research on the dynamic behavior of this structure.

For the moment, most studies are restricted to discussing the dynamic behavior of piezoelectric structure without the reinforcement of BNNTs. An et al. [1] provided a Melnikov method to study the subharmonic bifurcations and chaotic motions of the nonlinear viscoelastic plates subjected to external loads and subsonic flow. Employing the physical neutral surface concept and Euler–Bernoulli beam theory, Fu et al. [2] studied the thermo-piezoelectric buckling, nonlinear free vibration and dynamic stability of the functionally graded piezoelectric beams. In view of elastic piezoelectric theory and higher-order shear plate theory, Mao et al. [3] studied the active vibration control and nonlinear dynamic response of the functionally graded piezoelectric plate. By using a novel element-free IMLS-Ritz model based on Reddy’s higher-order shear deformation theory, Selim et al. [4] studied the active vibration control of composite plates with piezoelectric layers reinforced with carbon nanotube. Applying the higher-order shear deformation plate theory, Fakhari et al. [5] developed the finite element (FE) formulation to discuss nonlinear natural frequencies, time and frequency responses of functionally graded plate with surface-bonded piezoelectric layers under electrical, thermal and mechanical loadings. Detroux et al. [6] exploited the harmonic balance for detecting and tracking bifurcations of nonlinear systems. Based on the finite element method under different sets of electrical and mechanical loadings, Behjat and Khoshravan [7] analyzed the nonlinear static behavior and free vibration of functionally graded piezoelectric plates. Using the thin plate theory with nonlocal viscoelasticity, Li et al. [8] dealt with the transverse vibrations and steady-state responses of axially moving viscoelastic piezoelectric two-dimensional nanostructures. Larbi et al. [9] presented the theoretical formulation and the finite element implementation of vibroacoustic problems with piezoelectric composite structures connected to electric shunt circuits. By means of the random Melnikov method, Liu et al. [10] investigated the chaos of the piezoelectric system with fractional order physical properties subjected to periodic excitations. Dash et al. [11] addressed the nonlinear free vibration characteristic of laminated composite plate with embedded and surface-bonded piezoelectric layer. Based on Reddy’s higher-order shear deformation theory, Song et al. [12] discussed the active vibration control of CNT-reinforced composite cylindrical shells via piezoelectric patches. Using Reddy’s higher-order shear deformation theory, Selim et al. [13] studied the active vibration control of the FGM plates with piezoelectric layers. Zhang and Shen [14] presented an analytical formulation for the structural vibration control of laminated plates consisting of composite layers reinforced with 1–3 piezoelectric fiber. Zhang et al. [15] addressed the impact response of functionally graded composite cylindrical shell reinforced with carbon nanotube. Using the Euler Bernoulli kinematic model as well as von Kármán geometric nonlinearity, Krysko et al. [16] discussed the chaos of flexible beams considering temperature and piezoelectric effects. Based on the first-order shear deformation theory (FSDT), von Kármán geometric nonlinearity along with the Hamilton’s principle, Mohammadzadeh-Keleshteri et al. [17] studied the nonlinear free vibration of composite annular plates bonded with piezoelectric layers. Saviz and Mohammadpourfard [18] addressed the dynamic analysis for simply-supported piezoelectric cylindrical shell under local ring/pinch loads. Using the Euler–Bernoulli beam theory, von Kármán geometric nonlinearity and the physical neutral surface concept, Rafiee et al. [19] illustrated the large amplitude vibration of carbon nanotube reinforced functionally graded composite beams with piezoelectric layers. Under boundary random excitations, Ying and Zhu [20] analyzed the random response of a piezoelectric thick shell in the plane strain state. Rezaee et al. [21] addressed the nonlinear chaotic vibrations and stability of a simply-supported functionally graded Piezoelectric (FGP) rectangular plate bonded with piezoelectric layer.

Recently, some studies of piezoelectric structure reinforced with BNNTs have emerged. Barzoki et al. [22] studied the torsional linear buckling of a PVDF cylindrical shell reinforced with BNNTs, and found that the buckling strength increased substantially as harder foam cores were employed. Based on the harmonic differential quadrature method (HDQM), Barzoki et al. [23] also illustrated the nonlinear buckling of BNNT-reinforced piezoelectric shell. Using the virtual displacement method based on nonlocal cylindrical shell theory, Arani et al. [24] discussed the axial buckling of double-walled BNNTs embedded in an elastic medium under combined electro-thermo-mechanical loadings. Applying the technique of differential scanning calorimetry (DSC), Kadir et al. [25] presented a simple mechanical model for the buckling behavior of BNNT surrounded by an elastic matrix. Under electro-thermal loadings, Arani et al. [26] investigated the nonlinear vibration and stability of a smart composite micro-tube made of PVDF reinforced with BNNTs embedded in an elastic medium. Based on the Euler–Bernoulli beam model with von-Kármán geometric nonlinearity and nonlocal elasticity theory, Arani et al. [27] discussed the stability and the nonlinear dynamic behavior of an embedded smart composite micro-tube subjected to thermal loadings and imposed electric potential. Arani et al. [28] developed an analytical method of the small-scale parameter on the vibration of single-walled Boron Nitride nanotube (SWBNNT) under a moving nanoparticle. Considering the effects of transverse shear deformation and rotary inertia, Ansari et al. [29] presented the instability and nonlinear free vibration of fluid-conveying SWBNNTs in the thermal environment. Yang et al. [30] discussed the nonlinear dynamic response of electro-thermo- mechanically loaded piezoelectric cylindrical shell reinforced with BNNTs. So far as we know, the research on bifurcation and chaos of piezoelectric structure reinforced with BNNTs has not been reported in the open literature.

Motivated by this consideration, we aim to study the bifurcation and chaos of piezoelectric shell reinforced with BNNTs under combined electro-thermo-mechanical loadings. By employing the Reissner variational principle, the nonlinear governing equations of the shell are obtained. By introducing the Galerkin method and additional state variables, the nonlinear equations are turned into first-order nonlinear ordinary differential equations and then solved by the fourth-order Runge–Kutta method. Numerical results are presented in graphical forms, showing the influences of voltage, temperature and volume fraction on the bifurcation and chaos of BNNT-reinforced piezoelectric shell.

2 Basic Equations

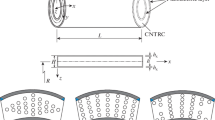
Figure 1 shows a BNNT-reinforced piezoelectric shell with the coordinate system (x, y, z). The origin of the coordinates is at the end of the shell. The radius of the middle surface of the shell is R, the thickness is h, the length is L and mass density is\(\rho _0 \). In addition, the shell is subjected to transverse dynamic load q(x, y, t), applied voltage V and a uniform temperature rise \(\Delta T\).

Fig. 1
figure 1

a Geometry of the piezoelectric cylindrical shell reinforced with BNNTs, and b section of the cylindrical shell

Full size image

2.1 The Strain Displacement Relationships

The displacements along the coordinates of x, y, z are denoted as \(\bar{{u}},\bar{{v}},\bar{{w}}\) respectively, and the corresponding displacements of mid-plane are denoted as u, v, w. Then, the displacement field for the piezoelectric shell can be expressed as

$$\begin{aligned} \begin{array}{l} \bar{{u}}(x,y,z,t)=u(x,y,t)-zw_{,x} (x,y,t) \\ \bar{{v}}(x,y,z,t)=v(x,y,t)-zw_{,y} (x,y,t) \\ \bar{{w}}(x,y,z,t)=w(x,y,t) \\ \end{array} \end{aligned}$$
(1)

where the symbol “,”represents the partial derivative of the coordinate variable.

Based on the von Kármán-Donnell-type kinematic relations of classical shell theory, the nonlinear strain–displacement relations can be written as:

$$\begin{aligned} \bar{{\varepsilon }}_x =\varepsilon _x +z\kappa _x ,\bar{{\varepsilon }}_y =\varepsilon _y +z\kappa _y ,\bar{{\varepsilon }}_{xy} =\varepsilon _{xy} +z\kappa _{xy} \end{aligned}$$
(2)

where \(\varepsilon _x,\varepsilon _y,\varepsilon _{xy}\) are the strain components of mid-plane and \(\kappa _x ,\kappa _y ,\kappa _{xy} \) are the curvatures of mid-plane [33], and

$$\begin{aligned} \begin{array}{l} \varepsilon _{x} =u_{,x}+\frac{1}{2}w_{,x}^2 ,\varepsilon _y =v_{,y} -\frac{w}{R}+\frac{1}{2}w_{,y}^2 ,\varepsilon _{xy} =u_{,y}+v_{,x}+w_{,x} w_{,y} \\ \kappa _x =-w_{,xx} ,\kappa _y =-w_{,yy} ,\kappa _{xy} =-2w_{,xy} \\ \end{array} \end{aligned}$$
(3)

2.2 Constitutive Equations

The constitutive equations for a piezoelectric shell under combined thermal, mechanical and electrical loadings can be written as [24]

$$\begin{aligned} \begin{array}{l} \upsigma _i =C_{ik} (\bar{{\varepsilon }}_k -\alpha _k \Delta T)-e_{ij}^T E_j \quad \quad (i,k=1,2,\ldots 6) \\ D_l =e_{lk} (\bar{{\varepsilon }}_k -\alpha _k \Delta T)-\varepsilon _{lj}^{*} E_j \quad \quad (l,j=1,2,3) \\ \end{array} \end{aligned}$$
(4)

where \(\Delta T\), \(\alpha _\kappa \) and \(E_\kappa (\kappa =x,y,z)\) represent temperature rise, thermal expansion coefficient and electric field, respectively. \(\varepsilon _{ii}^{*} ,C_{ij} ,e_{ij} (i,j=1,\ldots ,6)\) are dielectric constants, elastic constants and piezoelectric constants, respectively.

The smart composite shell is composed of PVDF and BNNTs, which are used as the matrix and reinforced materials, respectively. The material constants of the structure can be calculated recurring to the ’XY (orYX) rectangle model\('^{ }\) [31, 32], as those in [30].

2.3 Governing Equations

For the BNNT-reinforced piezoelectric shell, the total potential energy \(\varPi \) can be expressed as:

$$\begin{aligned} \varPi =K-U+\varGamma \end{aligned}$$
(5)

where U indicates the strain energy, K indicates the kinetic energy and \(\varGamma \) indicates the work done by the transverse dynamic load.

The expression of the strain energy is

$$\begin{aligned} U=\frac{1}{2}\int \int \int _V {\sigma _i \bar{{\varepsilon }}_i } \hbox {d}V-\frac{1}{2}\int \int \int _V {E_i D_i } \hbox {d}V \end{aligned}$$
(6)

Because of the zigzag structure for BNNTs employed here, and the longitudinal arrangement of strips in the matrix, \(E_y =E_z =0\). Denoting V as the voltage applied on both ends of the shell, the electric field component is

$$\begin{aligned} E_x =V/L \end{aligned}$$
(7)

The kinetic energy is given in the following form

$$\begin{aligned} K=\frac{1}{2}\int _{-h/2}^{h/2} {\int \int _A {\rho _0 [(\dot{\bar{{u}}})^{2}+(\dot{\bar{{v}}})^{2}+(\dot{\bar{{w}}})^{2}]\hbox {d}x\hbox {d}y} } \end{aligned}$$
(8)

The work done by the transverse dynamic load q(x, y, t) is

$$\begin{aligned} \varGamma =\int \int _A {q(x,y,t)w} \hbox {d}x\hbox {d}y \end{aligned}$$
(9)

Using the variational principle (\(\delta \varPi =0)\), the dynamic governing equations of the BNNTs-reinforced piezoelectric shell can be reduced as:

$$\begin{aligned} \begin{array}{l} N_{x,x} +N_{xy,y} =\rho _0 hu_{,tt} \\ N_{xy,x} +N_{y,y} =\rho _0 hv_{,tt} \\ M_{x,xx} +2M_{xy,xy} +M_{y,yy} +N_y /R+N_x w_{,xx} +2N_{xy} w_{,xy} +N_y w_{,yy} +q=\rho _0 hw_{,tt} \\ \end{array} \end{aligned}$$
(10)

where

$$\begin{aligned} \left\{ {{\varvec{N}}} \right\} =\left[ {{\varvec{A}}} \right] \left\{ \varvec{\varepsilon } \right\} -\left\{ {{{\varvec{N}}}^{\mathrm{T}} } \right\} -\left\{ {{{\varvec{N}}}^{\mathrm{p}} } \right\} , \quad \left\{ {{\varvec{M}}} \right\} =\left[ {{\varvec{D}}} \right] \left\{ \varvec{\kappa } \right\} -\left\{ {{{\varvec{M}}}^{\mathrm{T}} } \right\} -\left\{ {{{\varvec{M}}}^{\mathrm{p}} } \right\} \end{aligned}$$
(11)

in which

$$\begin{aligned} \left\{ {{{\varvec{N}}}^{\mathrm{T}} ,{{\varvec{M}}}^{\mathrm{T}} } \right\} =\int _{-h/2}^{h/2} {\left[ {C_{ij} } \right] \left\{ {\alpha _k } \right\} (1,z)\Delta T} \hbox {d}z, \quad \left\{ {{ {{\varvec{N}}}}^\mathbf{p} ,{{{\varvec{M}}}}^\mathbf{p} } \right\} =\int _{-h/2}^{h/2} {\left[ {e_{ij} } \right] \left\{ {E_k } \right\} (1,z)} \hbox {d}z \end{aligned}$$
(12)

In the above equations, the \(A_{ij} ,D_{ij} \) are the tensile and bending rigidity and that can be defined as

$$\begin{aligned} (A_{ij},D_{ij})=\int _{-h/2}^{h/2} {C_{ij} (1,z^{2})\hbox {d}z} \quad (i,j=1,2,6) \end{aligned}$$
(13)

In axisymmetric circumstances, the circumferential displacement \(v=0\) and u, w is only the function of coordinate x. Hence, the second equation of Eq. (10) is automatically balanced and can be omitted. In accordance with Eqs. (3), (11) and (12), and introducing the following dimensionless parameters,

$$\begin{aligned} \xi =\frac{x}{L},W=\frac{w}{h},U=\frac{u}{L},Q=\frac{qL^{4}}{A_{22}h^{3}},M_\xi =\frac{L^{2}M_x }{A_{22} h^{3}},H=\frac{L}{h},K=\frac{L^{2}}{Rh},\tau =\frac{t}{L^{2}}\sqrt{A_{22}^ h/\rho _0 } \end{aligned}$$
(14)

the nonlinear dynamic governing equations of axisymmetric piezoelectric shell reinforced with BNNTs under electro-thermo-mechanical loadings can be reduced as

$$\begin{aligned}&S_{11A}U_{,\xi \xi } -S_{12A}\frac{K}{H^{2}}W_{,\xi } +S_{11A} \frac{1}{H^{2}}W_{,\xi } W_{,\xi \xi } =\frac{S_{22A}}{H^{2}}U_{,\tau \tau } \nonumber \\&\quad -\,\frac{1}{12}S_{11D}W_{,\xi \xi \xi \xi } +(S_{11A}H^{2}U_{,\xi }\nonumber \\&\quad +\frac{S_{11A}}{2}W_{,\xi }^2 -S_{12A}KW-H^{2}(S_{11A}\alpha _x +\,S_{12A} \alpha _y )\Delta T-H^{2}e_{11} E_x )W_{,\xi \xi } \nonumber \\&\quad +\,S_{12A}KH^{2}U_{,\xi } +\frac{S_{12A}K}{2}W_{,\xi }^2\nonumber \\&\quad -\,S_{22A} K^2 W_ -H^{2}K(S_{12A} \alpha _x +S_{22A} \alpha _y )\Delta T-H^{2}Ke_{12} E_x +S_{22A}Q=S_{22A}W_{,\tau \tau } \end{aligned}$$
(15)

where \(S_{ijA}=A_{ij}/h_ ,S_{ijD}=D_{ij} /(h^3 /12)\).

Both ends of the shell are supposed to be simply-supported, then the dimensionless boundary conditions are as follows:

$$\begin{aligned} \begin{array}{l} N_\xi (0)=0,W(0)=0,\hbox { }W,_{\xi \xi } (0)=0 \\ N_\xi (1)=0,W(1)=0,\hbox { }W,_{\xi \xi } (1)=0 \\ \end{array} \end{aligned}$$
(16)

where

$$\begin{aligned} N_\xi =\left[ S_{11A} \left( U_{,\xi } +\frac{1}{2H^{2}}W_{,\xi }^2 \right) -S_{12A} \frac{K}{H^{2}}W-\left( S_{11A}\alpha _x +S_{12A}\alpha _y \right) \Delta T\right] -e_{11} E_x \end{aligned}$$
Fig. 2
figure 2

Nonlinear dynamic response of BNNT-reinforced piezoelectric cylindrical shells

Full size image
Table 1 The mechanical, electrical and thermal properties of PVDF and BNNT
Full size table
Fig. 3
figure 3

Effect of volume ratio on the bifurcation diagram of piezoelectric shell reinforced with BNNTs (\(V=0\), \(\Delta T= 0 )\). a Bifurcation diagram \(V_f =0.2\), and b bifurcation diagram \(V_f =0.6\)

Full size image
Fig. 4
figure 4

Comparison of the nonlinear dynamic characteristics of piezoelectric shell reinforced with BNNTs under different volume ratios (\(F_0 =530.22)\). a Phase-plane trajectory \(V_f =0.2\), b phase-plane trajectory\(V_f =0.6\), c Poincaré map \(V_f =0.2\), d Poincaré map \(V_f =0.6\), e time course curve \(V_f =0.2\), and f time course curve \(V_f =0.6\)

Full size image
Fig. 5
figure 5

The nonlinear dynamic characteristics of piezoelectric shell reinforced with BNNTs \((V=-80)\). a Bifurcation diagram, b time course curve, c phase-plane trajectory, and d Poincaré map

Full size image
Fig. 6
figure 6

The nonlinear dynamic characteristics of piezoelectric shell reinforced with BNNTs \((V=0)\). a Bifurcation diagram, b time course curve, c phase-plane trajectory, and d Poincaré map

Full size image
Fig. 7
figure 7

The nonlinear dynamic characteristics of piezoelectric shell reinforced with BNNTs \((V=+80)\). a Bifurcation diagram, b time course curve, c phase-plane trajectory, and d Poincaré map

Full size image

3 Solution Methodology

In order to satisfy the boundary conditions of Eq. (16), the formal solutions of Eq. (15) are assumed as [34]

$$\begin{aligned} \begin{array}{l} W=\mathop \sum \limits _{m=1,3,}^\infty {{\tilde{w}}_m (\tau )} \sin (m\pi \xi ) \\ U=-\frac{1}{2\pi }g(\eta )\sin (2\pi \xi )+\mathop \sum \limits _{m=1,3,}^\infty {{\tilde{u}}_m (\tau )} \cos (m\pi \xi ) \\ \end{array} \end{aligned}$$
(17)

where \(g(\eta )\) are defined as

$$\begin{aligned} g(\eta )=\frac{1}{2H^{2}}W_{,\xi } ^{2}-\varphi _1 ,\,\,\, \mathrm{on}\,\,\, \xi =0\, \,\,\,\mathrm{and}\,\,\,\, \xi =1 \end{aligned}$$

and

$$\begin{aligned} \varphi _1 =\left[ \frac{e_{11} E_x }{S_{11D} }+\left( \frac{S_{11A} }{S_{11D} }\alpha _x +\frac{S_{12A} }{S_{11D} }\alpha _y \right) \Delta T\right] +\frac{S_{12A} K}{S_{11D} H^{2}}W \end{aligned}$$

The transverse dynamic load is taken as follows:

$$\begin{aligned} Q=F\sin (\pi \xi ), F=F_0 \sin (\omega \tau ) \end{aligned}$$

In the formula, \(F_0 \) and \(\omega \) are, respectively, the dimensionless amplitude and frequency of the transverse dynamic load.

Substituting Eq. (17) into Eq. (15), multiplying the first resulting equation by \(\cos i\pi \xi \) and the second by \(\sin i\pi \xi \), integrating the functions from 0 to 1 and taking the first-order Galerkin truncation at the same time, the nonlinear constant differential equations expressed in terms of time functions \({\tilde{u}}\) and \({\tilde{w}}\) are derived as follows:

$$\begin{aligned} \begin{array}{l} L_{11} {\tilde{u}}+L_{12} {\tilde{w}}+L_{13} {\tilde{w}}^{2}+L_{14} =0 \\ L_{31} {\tilde{w}}+L_{32} {\tilde{w}}^{3}+L_{33} {\tilde{u}}{\tilde{w}}+L_{34} {\tilde{w}}^{2}+L_{35} {\tilde{u}}+L_{36} +pF=p\ddot{{\tilde{w}}} \\ \end{array} \end{aligned}$$
(18)

where

$$\begin{aligned} L_{11}= & {} \int _0^1 {S_{11A} \varLambda _{1,\xi \xi } } \varLambda _1 \hbox {d}\xi \\ L_{12}= & {} \int _0^1 {(-S_{12A} \frac{K}{H^2 })\varLambda _{3,\xi } } \varLambda _1 \hbox {d}\xi \\ L_{13}= & {} \int _0^1 {\frac{S_{11A} }{H^2 }(\varLambda _{4,\xi \xi } +\varLambda _{3,\xi } \varLambda _{3,\xi \xi } )\varLambda _1 } \hbox {d}\xi \\ L_{14}= & {} \int _0^1 {S_{11A} \varLambda _{6,\xi \xi } \varLambda _1 } \hbox {d}\xi \\ L_{31}= & {} \int _0^1 \left[ -\frac{S_{11D} }{12}\varLambda _{3,\xi \xi \xi \xi } +\left( -S_{11A} H^2 \frac{2}{\pi ^{2}}\varphi _2 \varLambda _{4,\xi } +\varphi _2 \right) \varLambda _{3,\xi \xi } -S_{22A} K^{2}\varLambda _3 \right] \varLambda _3 \hbox {d}\xi \\ L_{32}= & {} \int _0^1 {S_{11A} \left( \varLambda _{4,\xi } +\frac{1}{2}\varLambda _{3,\xi } ^{2}\right) \varLambda _{3,\xi \xi } } ]\varLambda _3 \hbox {d}\xi \\ L_{33}= & {} \int _0^1 {S_{11A} H^2 \varLambda _{1,\xi } \varLambda _{3,\xi \xi } } \varLambda _3 \hbox {d}\xi \\ L_{34}= & {} \int _0^1 {S_{12A} K(-\varLambda _3 \varLambda _{3,\xi \xi } +\varLambda _{4,\xi } +\frac{1}{2}\varLambda _{3,\xi } ^{2})} \varLambda _3 \hbox {d}\xi \\ L_{35}= & {} \int _0^1 {S_{12A} KH^2 \varLambda _{1,\xi } } \varLambda _3 \hbox {d}\xi \\ L_{36}= & {} \int _0^1 {\varphi _3 } \varLambda _3 \hbox {d}\xi \\ p= & {} \int _0^1 {S_{22A} } \varLambda _3 ^{2}\hbox {d}\xi \\ \varLambda _1= & {} \cos (\pi \xi ),\varLambda _3 =\sin (\pi \xi ),\varLambda _4 =-\frac{\pi }{4}\sin (2\pi \xi ),\varLambda _6 =\frac{\varphi _2 }{2\pi }\sin (2\pi \xi ) \\ \varphi _2= & {} -H^{2}(S_{11A} \alpha _x +S_{12A} \alpha _y )\Delta T-H^{2}e_{11} E_x \\ \varphi _3= & {} -H^{2}K(S_{12A} \alpha _x +S_{22A} \alpha _y )\Delta T-H^{2}Ke_{12} E_x \end{aligned}$$

The \({\tilde{u}}\) in the first formula of Eqs. (18) can be solved as

$$\begin{aligned} {\tilde{u}}=-\frac{1}{L_{11} }(L_{12} {\tilde{w}}+L_{13} {\tilde{w}}^{2}+L_{14} ) \end{aligned}$$
(19)

which is denoted as

$$\begin{aligned} {\tilde{u}}=\varGamma _0 +\varGamma _1 {\tilde{w}}+\varGamma _2 {\tilde{w}}^{2} \end{aligned}$$
(20)

When substituting Eq. (20) into the second formula of Eq. (18) and introducing the linear damping term \(\mu \dot{{\tilde{w}}}\) at the same time, the nonlinear governing equation expressed by \({\tilde{w}}\) for the piezoelectric plate reinforced with BNNTs can be written as:

$$\begin{aligned} \phi _1 {\tilde{w}}+\phi _2 {\tilde{w}}^{2}+\phi _3 {\tilde{w}}^{3}+\phi _4 +pF-\mu \dot{{\tilde{w}}}=p\ddot{{\tilde{w}}} \end{aligned}$$
(21)

where

$$\begin{aligned} \begin{array}{l} \phi _1 =L_{31} +L_{33} \varGamma _0 +L_{35} \varGamma _1 \\ \phi _2 =L_{34} +L_{33} \varGamma _1 +L_{35} \varGamma _2 \\ \phi _3 =L_{32} +L_{33} \varGamma _2 \\ \phi _4 =L_{36} +L_{35} \varGamma _0 \\ \end{array} \end{aligned}$$

By introducing the state variables \(y_1 (\tau )={\tilde{w}}(\tau ),y_2 (\tau )=\dot{{\tilde{w}}}(\tau )\), Eq. (21) can be changed into the following first-order nonlinear ordinary differential equations

$$\begin{aligned} \begin{array}{l} {\dot{y}}_1 =y_2 \\ {\dot{y}}_2 =p^{-1}(\phi _1 y_1 +\phi _2 y_1 ^{2}+\phi _3 y_1 ^{3}+\phi _4 -\mu y_2 +pF) \\ \end{array} \end{aligned}$$
(22)

The fourth-order Runge–Kutta method is adopted to obtain a numerical solution of Eq. (22). The initial value is set as \(\{y_1 ,y_2 \}=\{0,1\}\) and the first 800 cycles are removed to eliminate transient response. Then, the bifurcation diagram, the Poincaré map, the phase-plane trajectory and the time course curve can be obtained by combining with the numerical analysis method for nonlinear dynamics.

4 Numerical Results and Discussion

To validate the present analysis, the nonlinear dynamic response of the piezoelectric shell reinforced with BNNTs under electro-thermo-mechanical loadings is considered first. The geometric and material parameters of the shell are the same as those used in [30]. The present results for the time history of the dimensionless central deflection W0 are compared in Fig. 2 with those given by Yang et al. [30]. It can be seen that good agreement is achieved with a relative error of 9.1%.

The bifurcation and chaos of the piezoelectric shell reinforced with BNNTs under electro-thermo- mechanical loadings are then studied in the following calculation. Both ends of the shell are simply-supported. The geometric parameters of the piezoelectric shell are L/R = 5/3, and R/h = 10. The external excitation frequency \(\omega \) is equal to 5. The reinforced material is BNNT, and the matrix material is PVDF. The material constants are listed in Table 1.

Figure 3 shows the effect of volume ratio (\(V_f )\) on the bifurcation diagram of deflection versus load for the piezoelectric shell reinforced with BNNTs. In this case, the voltage \(V=0\) and the temperature \(\Delta T= 0 \). It can be seen from the figure that with the increase in load, the system undergoes the one period motion, the multiple period bifurcation motion, the one period motion, the multiple period bifurcation motion, and finally enters a complex state consisting of multiple periodic motions, quasi-periodic motions or chaotic motions. However, due to the difference between the volume ratios of BNNT, the critical loads of the system entering the chaotic motion are different for the two kinds of situations. And the critical load increases with the increase in volume ratio\(V_f \).

Figure 4 shows the nonlinear dynamic characteristics of piezoelectric shell reinforced with BNNTs under different volume ratios when the load \(F_0 =530.22\). It can be seen that the piezoelectric shell with \(V_f =0.2\) exhibits the chaotic motion, but the piezoelectric shell with \(V_f =0.6\) is in double period motion. Therefore, the piezoelectric shell will delay the multiply periodic motion or chaotic motion as the volume ratio of BNNT increases. That is to say, increasing the volume ratio of BNNT can make the dynamic characteristics of the piezoelectric structure more stable, which will be beneficial to the dynamic stability of the structure.

The effect of voltage on the nonlinear dynamic characteristics of piezoelectric shell reinforced with BNNTs is discussed in Figs. 5, 6 and 7. The volume ratio of BNNTs \(V_f \) is equal to 0.6, the temperature rise \(\Delta T\) is zero, and the given load is \(F=580\). Figures. 5, 6 and 7 give the bifurcation diagram, time course curve, phase-plane trajectory and poincaré map with respect to different voltages. When applying negative voltage to the piezoelectric shell, the system exhibits one periodic motion and the poincaré map has one isolated fixed point (See Fig. 5). When the voltage applied to the piezoelectric shell is zero, the system exhibits double periodic bifurcation motion and the poincaré map has two isolated fixed points (See Fig. 6). When applying positive voltage to the piezoelectric shell, the system exhibits chaotic motion and the poincaré map has the fractal features similar to clouds (See Fig. 7). Therefore, the positive voltage weakens the dynamic stability of the piezoelectric shell reinforced with BNNTs, and the negative voltage plays a role in enhancing the stability of the system.

The effect of temperature on the bifurcation diagram of the piezoelectric shell reinforced with BNNTs is presented in Fig. 8. The applied voltage V is zero, and the volume ratio of BNNTs \(V_f \) is equal to 0.6. From the figure, it can be seen that with the increase in the load, the system undergoes the one periodic motion, the multiple periodic bifurcation motion, the one periodic motion, the multiple periodic bifurcation motion, and finally enters a complex state of the chaotic motion. However, because of the different temperatures, the critical loads of the system entering the chaotic motion are different. Figures 9 and  10 are, respectively, the phase-plane trajectories and the Poincaré map when the system first enters the chaotic state under two different temperatures. From the two figures, it can be seen that the critical load of the system first entering the chaotic motion is \(F_0 =603\) when the temperature T=0, and the critical load is \(F_0 =547\) when the temperature T=200. Therefore, the increase in temperature will make the multiple periodic motion or chaotic motion of the piezoelectric shell appear in advance. This indicates that the increase in temperature is not favorable for the dynamic stability of the structure.

Fig. 8
figure 8

The effect of temperature on the bifurcation diagram of the piezoelectric shell reinforced with BNNTs. a\(T=0\), b\(T=200\)

Full size image
Fig. 9
figure 9

The phase-plane trajectories of the piezoelectric shell reinforced with BNNTs at different temperatures. a\(T=0\), b\(T=200\)

Full size image
Fig. 10
figure 10

The poincaré map of the piezoelectric shell reinforced with BNNTs at different temperatures. a\( T=0\), and b\(T=200\)

Full size image

5 Conclusions

The bifurcation and chaos of piezoelectric shell reinforced with BNNTs under combined electro- thermo-mechanical loadings are studied. The variational principle is adopted to derive the governing equations, and the Runge–Kutta method is adopted to study the bifurcation and chaos of the BNNT- reinforced piezoelectric shell. The numerical results indicate that the decrease in temperature or voltage and the increase in volume ratio can delay the multiple periodic motion or chaotic motion of the piezoelectric shell, which is useful for the dynamic stability of the structure.