1 Introduction

Anisotropy is an inherent characteristic of cold-rolled sheet metals. For accurate simulations of sheet metal forming processes, it is critical to sufficiently describe the anisotropy of sheet metals. Enormous efforts have been contributed to develop yield functions to accurately describe the anisotropy of various sheet metals. Hill [1] made a pioneering effort and proposed the first anisotropic yield function based on the quadratic isotropic von Mises yield function. The Hill48 yield function has been extensively applied in both analytical and numerical analyses of metal forming processes owing to its simplicity, capability for full stress states and involvement of the shear stress. The Hill48 yield function was proved to reasonably describe the anisotropic plastic behavior of carbon steel sheets with \(R>1\). However, Pearce and Woodthorpe [2, 3] found that the Hill48 yield function predicted a lower yield stress in the balanced biaxial tension than that in the uniaxial tension for metals with \(R<1\), such as the dual phase, TRIP and TWIP steel sheets and aluminum alloys, which was named as the anomalous behavior. Hosford and Logan [4, 5] extended the non-quadratic Hershey yield function for orthotropic metals. The Hosford79 yield function, however, did not couple the effect of shear stress on yielding. Thus, it cannot be employed to describe the anisotropy between orthotropic axes, which blocks its application in finite element analysis. To involve the shear stress in the non-quadratic yield function, Barlat and Lian [6] modified the Hosford79 yield function for sheet metals, which is referred as the Yld89 yield function. The Yld89 yield function is only applicable to plane stress problems and cannot encompass the anomalous behavior for aluminum alloys. Barlat et al. [7] applied a fourth-order linear transformation tensor to introduce anisotropic parameters into the Hershey yield function for the description of anisotropic plasticity in full stress spaces. Barlat et al. [8] developed another yield function based on the Hosford79 anisotropic yield function and the fourth-order linear transformation tensor used in the Yld91 yield function [7]. The Yld96 yield function [8], however, is too complicated for full stress states. Barlat et al. [9] developed a simple yield function for plane stress conditions to describe the anisotropic behavior of both the yield stresses and the R-values. In addition, the Yld89 yield function was extended to enhance its flexibility for sheet metals [10,11,12,13]. Barlat et al. [14] applied two specific convex functions for full stress problems of anisotropic metals. These anisotropic yield functions reviewed above provide different flexibilities for the description of anisotropy, not only for simple plane stress, but also for full stress states. The quantitative evaluation of yield functions, however, has not been carried out based on the anisotropy of sheet metals, although the selection of a yield function is essential for accurate simulations of sheet metal forming processes. Huh et al. [15] compared the most popular yield functions mathematically, but there were no simulated results with various yield functions.

This paper compares the performances of anisotropic yield functions based on the root-mean-square error (RMSE). The anisotropic yield functions were briefly reviewed first. The anisotropic parameters for the yield functions were calculated using the downhill simplex method with experimental data. The anisotropic parameters calculated were used to construct the yield surfaces of two steel sheets and two aluminum alloys. The yield surfaces constructed were compared with experimental data to evaluate their accuracy. In addition, directionalities of the yield stress and the R-value were also described by the anisotropic yield functions. Accuracy of the anisotropic yield functions was evaluated from the yield surfaces, the yield stresses and the R-values based on the experimental data of sheet metals. The RMSE was finally calculated for the yield stresses and the R-values in order to evaluate the accuracy of the anisotropic yield functions quantitatively. Finally, the effects of anisotropic parameter evaluation methods on predictability were investigated for the Hill48, Yld89 and Yld91 yield functions.

2 Phenomenological Yield Functions

A yield function describes the yielding stress state and is generally expressed in an implicit form:

$$\begin{aligned} f\left( {\sigma _{{\textit{ij}}} } \right) -{\bar{\sigma }}=0 \end{aligned}$$
(1)

where f is the yield function and \({\bar{\sigma }}\) is the equivalent stress obtained from experiments, preferably the uniaxial tension in the rolling direction. Most yield functions have been developed under the assumption of plane stress condition, which is the critical feature of sheet metal forming problems. The most commonly used yield functions such as Hill48, Yld89, Yld91, Yld96, Yld2000-2d, BBC2000 and Yld2004-18p have been briefly reviewed in [15].

3 Predicted Yield Stresses and R-values

3.1 Predicted Uniaxial Tensile Yield Stresses

The yield stress in uniaxial tension at an angle of \(\theta \) away from the rolling direction (RD) is denoted as \(\sigma _\theta \). Then, the stress components in the orthotropic coordinates of x (the rolling direction) and y (the transverse direction or TD) are computed as follows:

$$\begin{aligned} \sigma _{xx} =\sigma _\theta \cos ^{2}\theta ,\quad \sigma _{yy} =\sigma _\theta \sin ^{2}\theta ,\quad \sigma _{xy} =\sigma _\theta \sin \theta \cos \theta \end{aligned}$$
(2)

Then, the substitution of these stress components in Eq. (2) into Eq. (1) provides the expression for uniaxial yield stress of \(\sigma _\theta \) as below:

$$\begin{aligned} {\bar{\sigma }}=f\left( {\sigma _{xx} , \sigma _{yy} ,\sigma _{xy} } \right) =f\left( {\sigma _\theta \cos ^{2}\theta ,\sigma _\theta \sin ^{2}\theta ,\sigma _\theta \sin \theta \cos \theta } \right) \end{aligned}$$
(3)

For the Hill48 yield function, the predicted uniaxial tensile yield stress \(\sigma _\theta \) is calculated in a form of

$$\begin{aligned} \sigma _\theta =\left[ {\frac{2}{\left( {F+H} \right) \sin ^{4}\theta +\left( {G+H} \right) \cos ^{4}\theta -2H\sin ^{2}\theta \cos ^{2}\theta +2N\sin ^{2}\theta \cos ^{2}\theta }} \right] ^{\frac{1}{2}}{\bar{\sigma }} \end{aligned}$$
(4)

3.2 Predicted Yield Stress in Balanced Biaxial Tension

In balanced biaxial tension, the stress state is characterized by two equal stresses in orthotropic directions. Assuming that the yield stress in balanced biaxial tension is \(\sigma _b \), the stress components at this state are obtained as:

$$\begin{aligned} \sigma _{xx} =\sigma _{yy} =\sigma _b ,\quad \sigma _{xy} =0 \end{aligned}$$
(5)

The predicted balanced biaxial yield stress of \(\sigma _b \) is obtained by substituting the stress components in Eq. (5) into Eq. (1) as below:

$$\begin{aligned} {\bar{\sigma }}=f\left( {\sigma _{xx} ,\sigma _{yy} ,\sigma _{xy} } \right) =f\left( {\sigma _b ,\sigma _b ,0} \right) \end{aligned}$$
(6)

The uniaxial tensile yield stress \(\sigma _\theta \) predicted by the Hill48 yield function has a form as below:

$$\begin{aligned} \sigma _b =\left( {\frac{2}{F+G}} \right) ^{\frac{1}{2}}{\bar{\sigma }} \end{aligned}$$
(7)

3.3 Associated Flow Rules

According to the associated flow rules, the plastic potential function is identical to the equivalent stress function of Eq. (1). The associated flow rules also assume that the direction of plastic strain increment is perpendicular to the yield surface. Based on the associated flow rules, the plastic strain increments are computed as below:

$$\begin{aligned} \mathrm{d}\varepsilon _{{\textit{ij}}}^p =\frac{\partial f\left( {\sigma _{{\textit{ij}}} } \right) }{\partial \sigma _{{\textit{ij}}} }\mathrm{d}\lambda \end{aligned}$$
(8)

where \(\mathrm{d}\varepsilon _{{\textit{ij}}}^p \) denotes the plastic strain increments and \(\mathrm{d}\lambda \) is the plastic strain multiplier. For the Hill48 yield function, the plastic strain increments are computed according to the associated flow rules as follows:

$$\begin{aligned} \mathrm{d}\varepsilon _{xx}^p= & {} \frac{\mathrm{d}\lambda }{2{\bar{\sigma }}}\left[ {H\left( {\sigma _{xx} -\sigma _{yy} } \right) -G\sigma _{xx} } \right] \end{aligned}$$
(9)
$$\begin{aligned} \mathrm{d}\varepsilon _{yy}^p= & {} \frac{\mathrm{d}\lambda }{2{\bar{\sigma }}}\left[ {F\sigma _{yy} -H\left( {\sigma _{xx} -\sigma _{yy} } \right) } \right] \end{aligned}$$
(10)
$$\begin{aligned} \mathrm{d}\varepsilon _{xy}^p= & {} \mathrm{d}\varepsilon _{yx}^p =2\frac{d\lambda }{2{\bar{\sigma }}_p }N_p \sigma _{xy} \end{aligned}$$
(11)

The plastic strain increments for other yield functions are calculated straightforward based on the associated flow rules by applying Eq. (8) to other yield functions, the plastic strain increments of which, however, are not provided in this paper due to their complicated and extremely lengthy expressions.

3.4 Predicted R-values in Uniaxial Tension

The R-value in uniaxial tension at an angle of \(\theta \) away from the RD is calculated as below:

$$\begin{aligned} R_\theta =-\frac{\mathrm{d}\varepsilon _{xx}^p \sin ^{2}\theta +\mathrm{d}\varepsilon _{yy}^p \cos ^{2}\theta -\mathrm{d}\varepsilon _{xy}^p \sin \theta \cos \theta }{\mathrm{d}\varepsilon _{xx}^p +\mathrm{d}\varepsilon _{yy}^p } \end{aligned}$$
(12)

The R-values in uniaxial tension in any directions are obtained by substituting the plastic strain increments of Eq. (8) into Eq. (12). For example, the R-values in uniaxial tension predicted by the Hill48 yield function are computed by substituting Eqs. (9), (10) and (11) into Eq. (12) as below:

$$\begin{aligned} R_\theta =\frac{H+H\tan ^{2}\theta \sin ^{2}\theta +2N\sin ^{2}\theta -\left( {F+G+3H} \right) \sin ^{2}\theta }{G+F\tan ^{2}\theta } \end{aligned}$$
(13)

3.5 Predicted R-values in Balanced Biaxial Tension

The R-value in the balanced biaxial tension is formulated as the ratio of the plastic strain increment in the TD expressed as \(\mathrm{d}\varepsilon _{yy}^p \) to that in the RD \(\mathrm{d}\varepsilon _{xx}^p \) as below:

$$\begin{aligned} R_b =\frac{\mathrm{d}\varepsilon _{yy}^p }{\mathrm{d}\varepsilon _{xx}^p } \end{aligned}$$
(14)

\(R_b \) can be easily computed with the associated flow rules in Eq. (8) by setting the stress state \(\left( {\sigma _{xx} ,\sigma _{yy},\sigma _{xy} } \right) \) as \(\left( {\sigma _b ,\sigma _b ,0} \right) \).

4 Calibration of Anisotropic Parameters

4.1 Calculation for the Hill48 Yield Function

For simplicity, the anisotropic parameters in the Hill48 yield function can be explicitly expressed by experimental data. Generally, four anisotropic parameters of F, G, H and N are calculated by the uniaxial yield stress in the RD, \(\sigma _0 \), and three uniaxial tensile R-values, \(R_0 ,R_{45} \) and \(R_{90} \). Setting the tensile direction angle \(\theta \) in Eq. (13) as \(0{^{\circ }}\), \(45{^{\circ }}\) and \(90{^{\circ }}\) gives the expressions for \(R_0 ,R_{45} \) and \(R_{90} \) as follows:

$$\begin{aligned} R_0= & {} \frac{H}{G} \end{aligned}$$
(15)
$$\begin{aligned} R_{45}= & {} \frac{2N-\left( {F+G} \right) }{2\left( {F+G} \right) }\end{aligned}$$
(16)
$$\begin{aligned} R_{90}= & {} \frac{H}{F} \end{aligned}$$
(17)

The uniaxial tensile yield stresses of \(\sigma _0 ,\sigma _{45} \) and \(\sigma _{90} \) are obtained by setting \(\theta \) in Eq. (4) as \(0{^{\circ }}\), \(45{^{\circ }}\) and \(90{^{\circ }}\) as follows:

$$\begin{aligned} \sigma _0= & {} \left( {\frac{2}{G+H}} \right) ^{\frac{1}{2}}{\bar{\sigma }} \end{aligned}$$
(18)
$$\begin{aligned} \sigma _{45}= & {} \left( {\frac{4}{F+G+2N}} \right) ^{\frac{1}{2}}{\bar{\sigma }} \end{aligned}$$
(19)
$$\begin{aligned} \sigma _{90}= & {} \left( {\frac{2}{F+H}} \right) ^{\frac{1}{2}}{\bar{\sigma }} \end{aligned}$$
(20)

Normally, the strain hardening behavior is characterized by uniaxial tensile tests in the RD, which indicates that \(\sigma _0 ={\bar{\sigma }}\). Thus, Eq. (18) reduces to a form as below:

$$\begin{aligned} G+H=2 \end{aligned}$$
(21)

By solving Eqs. (15–17) and (21), the anisotropic parameters of F, G, H and N are obtained as

$$\begin{aligned} F= & {} \frac{2R_0 }{R_{90} \left( {1+R_0 } \right) } \end{aligned}$$
(22)
$$\begin{aligned} G= & {} \frac{2}{1+R_0 } \end{aligned}$$
(23)
$$\begin{aligned} H= & {} \frac{2R_0 }{1+R_0 } \end{aligned}$$
(24)
$$\begin{aligned} N= & {} \frac{\left( {R_0 +R_{90} } \right) \left( {1+2R_{45} } \right) }{2R_{90} \left( {1+R_0 } \right) } \end{aligned}$$
(25)

In addition, the anisotropic parameters of F, G, H and N can also be evaluated using four yield stresses, i.e., \(\sigma _0 ,\sigma _{45} ,\sigma _{90} \) and \(\sigma _b \), by solving Eqs. (7) and (19–21) as below:

$$\begin{aligned} F= & {} \frac{{\bar{\sigma }}_0^2 }{\sigma _{90}^2 }+\frac{{\bar{\sigma }}_0^2 }{\sigma _b^2 }-1 \end{aligned}$$
(26)
$$\begin{aligned} G= & {} 1+\frac{{\bar{\sigma }}_0^2 }{\sigma _b^2 }-\frac{{\bar{\sigma }}_0^2 }{\sigma _{90}^2 } \end{aligned}$$
(27)
$$\begin{aligned} H= & {} 1+\frac{{\bar{\sigma }}_0^2 }{\sigma _{90}^2 }-\frac{{\bar{\sigma }}_0^2 }{\sigma _b^2 } \end{aligned}$$
(28)
$$\begin{aligned} N= & {} \frac{4{\bar{\sigma }}_0^2 }{\sigma _{45}^2 }-\frac{{\bar{\sigma }}_0^2 }{\sigma _b^2 } \end{aligned}$$
(29)

The anisotropic parameters of F, G, H and N obtained from Eqs. (22–25) are for the purpose of comparison with other yield functions. The difference between these two approaches for the calculation of anisotropic parameters is discussed later in Sect. 7.

4.2 Calculation for the Yld89 Yield Function

The anisotropic parameters of a, c, h and p are calculated either by \(\sigma _0 ,R_0 ,R_{45} \) and \(R_{90} \) or by \(\sigma _0 ,\sigma _{45} ,\sigma _{90} \) and \(\sigma _b \). For simplicity purpose, only one method is introduced in this study, i.e., calculation of these four anisotropic parameters by \(\sigma _0 ,R_0 ,R_{45} \) and \(R_{90} \). The uniaxial tensile yield stress in the RD denoted by \(\sigma _0 \) is expressed as below:

$$\begin{aligned} \left( {a+c} \right) \sigma _0^m =2{\bar{\sigma }}^{m} \end{aligned}$$
(30)

Since the strain hardening behavior is generally obtained from uniaxial tensile tests in the RD, it can be concluded that \(\sigma _0 ={\bar{\sigma }}\). Thus, Eq. (30) reduces to

$$\begin{aligned} a+c=2 \end{aligned}$$
(31)

Moreover, based on the associated flow rule and R-value calculation in Eq. (12), \(R_0 ,R_{45} \) and \(R_{90} \) are expressed by a function of a, c, h and p. Hence, the anisotropic parameters are shown to be functions of \(R_0 ,R_{45} \) and \(R_{90} \) as follows:

$$\begin{aligned} c= & {} 2-a=\sqrt{\frac{R_0 }{1+R_0 }\frac{R_{90} }{1+R_{90} }} \end{aligned}$$
(32)
$$\begin{aligned} h= & {} \sqrt{\frac{R_0 }{1+R_0 }\frac{1+R_{90} }{R_{90} }} \end{aligned}$$
(33)

The anisotropic parameter p cannot be computed explicitly, but can be evaluated by a function of \(R_{45} \) as below:

$$\begin{aligned}&R_{45} \left[ {a\left( {{K}'_1 +{K}'_2 } \right) ^{m-1}\left( {2{K}'_2 \left( {1+h} \right) +\frac{\left( {1-h} \right) ^{2}}{2}} \right) +a\left( {{K}'_1 -{K}'_2 } \right) ^{m-1}\left( {2{K}'_2 \left( {1+h} \right) -\frac{\left( {1-h} \right) ^{2}}{2}} \right) } \right. \nonumber \\&\qquad \left. +\, {c\left| {2{K}'_2 } \right| ^{m-1}\left( {1-h} \right) ^{2}}\phantom {R_{45} \left[ {a\left( {{K}'_1 +{K}'_2 } \right) ^{m-1}\left( {2{K}'_2 \left( {1+h} \right) +\frac{\left( {1-h} \right) ^{2}}{2}} \right) +a\left( {{K}'_1 -{K}'_2 } \right) ^{m-1}\left( {2{K}'_2 \left( {1+h} \right) -\frac{\left( {1-h} \right) ^{2}}{2}} \right) } \right. } \right] +a\left( {{K}'_1 +{K}'_2 } \right) ^{m-1}\left( {{K}'_2 \left( {1+h} \right) +\frac{\left( {1-h} \right) ^{2}}{4}-p^{2}} \right) \nonumber \\&\qquad +\,a\left( {{K}'_1 -{K}'_2 } \right) ^{m-1}\left( {{K}'_2 \left( {1+h} \right) -\frac{\left( {1-h} \right) ^{2}}{4}+p^{2}} \right) +2c\left( {2{K}'_2 } \right) ^{m-1}\left[ {\frac{\left( {1-h} \right) ^{2}}{4}-p^{2}} \right] =0 \end{aligned}$$
(34)

with

$$\begin{aligned} {K}'_1 =\frac{1+h}{4},\quad {K}'_2 =\frac{\sqrt{\left( {1-h} \right) ^{2}+4p^{2}}}{4} \end{aligned}$$
(35)

4.3 Calculation for the Yld91 Yield Function

The anisotropic parameters of \(c_1 ,c_2 ,c_3 \) and \(c_6 \) in the Yld91 yield function are calibrated by \(\sigma _0 ,\sigma _{45} ,\sigma _{90} \) and \(\sigma _b \), which are predicted by substituting the Yld91 equivalent stress into Eqs. (3) and (6). The predicted yield stresses are compared with the experimental results to construct an error function as below:

$$\begin{aligned} \hbox {err}\left( {c_1 ,c_2 ,c_3 ,c_6 } \right) =\left( {\frac{\sigma _0^{\mathrm{pred.}} }{\sigma _0^{\exp .} }-1} \right) ^{2}+\left( {\frac{\sigma _{45}^{\mathrm{pred.}} }{\sigma _{45}^{\exp .} }-1} \right) ^{2}+\left( {\frac{\sigma _{90}^{\mathrm{pred.}} }{\sigma _{90}^{\exp .} }-1} \right) ^{2}+\left( {\frac{\sigma _b^{\mathrm{pred.}} }{\sigma _b^{\exp .} }-1} \right) ^{2} \end{aligned}$$
(36)

Solving this error function provides the values of four anisotropic parameters.

4.4 Calculation for the Yld96 Yield Function

There are seven anisotropic parameters related to the in-plane properties in the Yld96 yield function: \(c_1 ,c_2 ,c_3 ,c_6 ,\alpha _x ,\alpha _y \) and \(\alpha _{z1} \). These anisotropic parameters are evaluated by four yield stresses, \(\sigma _0 ,\sigma _{45} ,\sigma _{90} \) and \(\sigma _b \), as well as three R-values, \(R_0 ,R_{45} \) and \(R_{90} \). These yield stresses and R-values are predicted by Eqs. (3), (6) and (12). Comparison of these predicted yield stresses and R-values with experimental data generates an error function in a form of

$$\begin{aligned} \hbox {err}\left( {c_1 ,c_2 ,c_3 ,c_6 ,\alpha _x ,\alpha _y ,\alpha _{z1} } \right)= & {} \left( {\frac{\sigma _0^{\mathrm{pred.}} }{\sigma _0^{\exp .} }-1} \right) ^{2}+\left( {\frac{\sigma _{45}^{\mathrm{pred.}} }{\sigma _{45}^{\exp .} }-1} \right) ^{2}+\left( {\frac{\sigma _{90}^{\mathrm{pred.}} }{\sigma _{90}^{\exp .} }-1} \right) ^{2}+\left( {\frac{\sigma _b^{\mathrm{pred.}} }{\sigma _b^{\exp .} }-1} \right) ^{2}\nonumber \\&+\left( {\frac{R_0^{\mathrm{pred.}} }{R_0^{\exp .} }-1} \right) ^{2}+\left( {\frac{R_{45}^{\mathrm{pred.}} }{R_{45}^{\exp .} }-1} \right) ^{2}+\left( {\frac{R_{90}^{\mathrm{pred.}} }{R_{90}^{\exp .} }-1} \right) ^{2} \end{aligned}$$
(37)

This error function is solved to calculate the seven anisotropic parameters in the Yld96 yield function.

4.5 Calculation for the Yld2000-2d and BBC2000 Yield Functions

Eight anisotropic parameters are incorporated into the Yld2000-2d and BBC2000 yield functions to characterize the anisotropic behavior of sheet metals. These anisotropic parameters are calibrated by four yield stresses, \(\sigma _0 ,\sigma _{45} ,\sigma _{90} \) and \(\sigma _b\), as well as four R-values, \(R_0 ,R_{45} ,R_{90} \) and \(R_b \). These eight values of yield stresses and R-values are calculated by substituting the Yld2000-2d and BBC2000 equivalent stresses into Eqs. (3), (6), (12) and (14). Error functions are set up by computing the difference between the predicted yield stresses and R-values and the experimental results as below:

$$\begin{aligned} \hbox {err}= & {} \left( {\frac{\sigma _0^{\mathrm{pred.}} }{\sigma _0^{\exp .} }-1} \right) ^{2}+\left( {\frac{\sigma _{45}^{\mathrm{pred.}} }{\sigma _{45}^{\exp .} }-1} \right) ^{2}+\left( {\frac{\sigma _{90}^{\mathrm{pred.}} }{\sigma _{90}^{\exp .} }-1} \right) ^{2}+\left( {\frac{\sigma _b^{\mathrm{pred.}} }{\sigma _b^{\exp .} }-1} \right) ^{2} \nonumber \\&+\left( {\frac{R_0^{\mathrm{pred.}} }{R_0^{\exp .} }-1} \right) ^{2}+\left( {\frac{R_{45}^{\mathrm{pred.}} }{R_{45}^{\exp .} }-1} \right) ^{2}+\left( {\frac{R_{90}^{\mathrm{pred.}} }{R_{90}^{\exp .} }-1} \right) ^{2}+\left( {\frac{R_b^{\mathrm{pred.}} }{R_b^{\exp .} }-1} \right) ^{2} \end{aligned}$$
(38)

Eight anisotropic parameters are computed after the optimization of this error function.

4.6 Calculation for the Yld2004-18p Yield Function

The Yld2004-18p yield function has 18 anisotropic parameters which substantially enhance its flexibility. Among these 18 anisotropic parameters, 14 are related to the in-plane anisotropic properties. These anisotropic parameters are recommended to be calibrated using the 16 experimental results in Tables 1 and 2: eight yield stresses and eight R-values. An error function is formulated by comparing the predicted yield stresses and R-values with the experimental results as below:

$$\begin{aligned} \hbox {err}= & {} w_s \left[ {{\begin{array}{l} {\left( {\frac{\sigma _0^{\mathrm{pred.}} }{\sigma _0^{\exp .\phantom {^2}}}-1} \right) ^{2}+\left( {\frac{\sigma _{15}^{\mathrm{pred.}} }{\sigma _{15}^{\exp .\phantom {^2}} }-1} \right) ^{2}+\left( {\frac{\sigma _{30}^{\mathrm{pred.}} }{\sigma _{30}^{\exp .\phantom {^2}} }-1} \right) ^{2}+\left( {\frac{\sigma _{45}^{\mathrm{pred.}} }{\sigma _{45}^{\exp .\phantom {^2}} }-1} \right) ^{2}} \\ {+\left( {\frac{\sigma _{60}^{\mathrm{pred.}} }{\sigma _{60}^{\exp .\phantom {^2}} }-1} \right) ^{2}+\left( {\frac{\sigma _{75}^{\mathrm{pred.}} }{\sigma _{75}^{\exp .\phantom {^2}} }-1} \right) ^{2}+\left( {\frac{\sigma _{90}^{\mathrm{pred.}} }{\sigma _{90}^{\exp .\phantom {^2}} }-1} \right) ^{2}+\left( {\frac{\sigma _b^{\mathrm{pred.}} }{\sigma _b^{\exp .\phantom {^2}} }-1} \right) ^{2}} \\ \end{array} }} \right] \nonumber \\&+w_R \left[ {{\begin{array}{l} {\left( {\frac{R_0^{\mathrm{pred.}} }{R_0^{\exp .\phantom {^2}} }-1} \right) ^{2}+\left( {\frac{R_{15}^{\mathrm{pred.}} }{R_{15}^{\exp .\phantom {^2}} }-1} \right) ^{2}+\left( {\frac{R_{30}^{\mathrm{pred.}} }{R_{30}^{\exp .\phantom {^2}} }-1} \right) ^{2}+\left( {\frac{R_{45}^{\mathrm{pred.}} }{R_{45}^{\exp .\phantom {^2}} }-1} \right) ^{2}} \\ {+\left( {\frac{R_{60}^{\mathrm{pred.}} }{R_{60}^{\exp .\phantom {^2}} }-1} \right) ^{2}+\left( {\frac{R_{75}^{\mathrm{pred.}} }{R_{75}^{\exp .\phantom {^2}} }-1} \right) ^{2}+\left( {\frac{R_{90}^{\mathrm{pred.}} }{R_{90}^{\exp .\phantom {^2}} }-1} \right) ^{2}+\left( {\frac{R_b^{\mathrm{pred.}} }{R_b^{\exp .\phantom {^2}} }-1} \right) ^{2}} \\ \end{array} }} \right] \end{aligned}$$
(39)

Since the number of experimental data points is larger than that of the calibrated anisotropic parameters, the error function of Eq. (39) cannot be optimized to be zero. Therefore, different weight values of \(w_s \) and \(w_R \) are added to the yield stress terms and the R-value terms, respectively. In addition, the error in yield stresses is more significant than that in R values. Thus, the weight of \(w_s \) for yield stress terms is set to be 10 times of the weight of \(w_R \) for R-value terms.

Table 1 Yield stresses of steel sheets and aluminum alloys according to the loading conditions [MPa]
Full size table
Table 2 R-values of steel sheets and aluminum alloys according to the loading conditions
Full size table

4.7 Downhill Simplex Method

The error functions in Eqs. (36–39) are solved to calibrate the anisotropic parameters in the yield functions. Normally, these error functions are minimized by the Newton–Raphson algorithm. The Newton–Raphson algorithm, however, requires the derivatives of error functions with respect to the anisotropic parameters, which are extremely complicated for non-quadratic anisotropic yield functions. This requirement increases the complexity during minimization of the error functions.

A simple and computationally compact approach, i.e., the downhill simplex method [16], is introduced herein to minimize the error functions for calibrating the anisotropic parameters of yield functions. The downhill simplex method was also used to calibrate the anisotropic-asymmetric parameters in a modified Yld2000-2d yield function for correct modeling of the anisotropic and asymmetric yielding of sheet metals [17]. The simplicity and compactness of the downhill simplex method is due to the fact that this method does not require derivatives of error functions but only needs function evaluations. The downhill simplex method constructs a simplex consisting of \(n+1\) points, where n is the number of variables. The worst point is iteratively updated by four operations: reflection, expansion, one-dimensional contraction and multiple contractions. The flowchart of the downhill simplex method is shown in Fig. 1. Details of the downhill simplex method are described by Nelder and Mead [16].

Fig. 1
figure 1

Flowchart of the downhill simplex method

Full size image

4.8 Anisotropic Parameters

Two steel sheets, 718AT and 719B, and two aluminum alloy sheets, AA5182-O and AA6022-T4E32, were selected to evaluate the accuracy of the anisotropic yield functions summarized in Sect. 2. The material data are referred from Stoughton and Yoon [18]. The experimental data of yield stresses and R-values of these metals are listed in Tables 1 and 2 according to various loading conditions. These experimental results are utilized to calculate the anisotropic parameters of the anisotropic yield functions using the methods introduced in Sects. 3 and 4. The anisotropic parameters are summarized in Table 3 for the Hill48 yield function, Table 4 for the Yld89 yield function, Table 5 for the Yld91 yield function, Table 6 for Yld96 yield function, Table 7 for Yld2000-2d yield function, Table 8 for the BBC2000 yield function and Table 9 for the Yld2004-18p yield function, respectively.

Table 3 Anisotropic parameters in the Hill48 yield function computed by \(\sigma _0 ,R_0 ,R_{45} \) and \(R_{90} \)
Full size table
Table 4 Anisotropic parameters in the Yld89 yield function evaluated by \(\sigma _0 ,R_0 ,R_{45} \) and \(R_{90} \)
Full size table
Table 5 Anisotropic parameters in the Yld91 yield function calibrated by \(\sigma _0 ,\sigma _{45} ,\sigma _{90} \) and \(\sigma _b \)
Full size table
Table 6 Anisotropic parameters in the YLD96 yield function
Full size table
Table 7 Anisotropic parameters in the YLD2000-2d yield function
Full size table
Table 8 Anisotropic parameters in the BBC2000 yield function
Full size table
Table 9 Anisotropic parameters in the YLD2004-18p yield function
Full size table

5 Results

5.1 Comparison of Yield Surfaces

The yield surfaces were constructed by using the anisotropic parameters calculated by the downhill simplex method in Sect. 3 and compared with the experimental data points in Fig. 2. The difference between different anisotropic yield functions can be clearly observed in the equibiaxial tension region, as illustrated in Fig. 2. In the equibiaxial tension region, the Hill48 yield function overestimates the yield stress for two steel sheets and underestimates the yield stress for two aluminum alloy sheets. The underestimation of equibiaxial yield stress with the Hill48 yield function takes place for the metals with \(R < 1\), such as the aluminum alloys, due to the anomalous behavior [2]. The Yld89 yield function tends to underestimate the yield stress in the equibiaxial tension region. Other advanced anisotropic yield functions provide accurate yield stresses in the uniaxial and equibiaxial tension regions because the yield stresses at three loading conditions are utilized to calculate the anisotropic parameters. Based on the comparison between the yield surfaces constructed and the experimental yield stresses, the Yld91, Yld96, Yld2000-2d, BBC2000 and Yld2004-18p yield functions are acceptable for simulating sheet metal forming processes when the dominant loading condition is equibiaxial tension.

Fig. 2
figure 2

Comparison of yield surfaces: a 718AT; b 719B; c AA5182-O; d AA6022-T4E32

Full size image

5.2 Comparison of Yield Stress Directionality

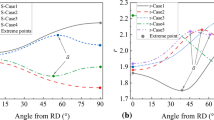
The predicted yield stress directionality is compared with the experimental results with respect to the loading direction for various anisotropic yield functions, as illustrated in Fig. 3. The comparison indicates that the Hill48 and Yld89 yield functions cannot predict the yield stress directionality for all materials. The Yld91, Yld96, Yld2000-2d and BBC2000 yield functions utilize the yield stresses at 45 degree and 90 degree to improve their flexibility. These yield functions can sufficiently describe the yield stress directionality for metals with intermediate anisotropy, such as the two aluminum alloys, i.e., AA5182-O and AA6022-T4E32. For steel sheets, the yield functions with more flexibility such as Yld2004-18p are required to accurately describe the yield stress directionality.

Fig. 3
figure 3

Comparison of yield stress directionality: a 718AT; b 719B; c AA5182-O; d AA6022-T4E32

Full size image

5.3 Comparison of R-value Directionality

The anisotropy in R-values was predicted with various anisotropic yield functions, as compared with the experimental data points in Fig. 4. The Hill48, Yld89, Yld96, Yld2000-2d and BBC2000 yield functions are observed to be of great capability in correctly modeling the anisotropy in R-values for all sheet metals. The comparison also suggests that the Yld000-18p yield function is superior in approximating the R-values with respect to the loading direction for severe textured metals with strong directionality in R-values. However, the Yld91 yield function should be avoided when describing the R-value directionality, due to its poorest performance among the anisotropic yield functions being studied, as proved in Fig. 4 for 718AT and 719B. The Yld2004-18p yield function is still the best choice for sheet metal forming simulations to guarantee the highest accuracy owing to its good approximation for anisotropic R-values. If fewer experimental data are available, the Hill48, Yld89, Yld96, Yld2000-2d and BBC2000 yield functions can also be used with acceptable accuracy to describe the anisotropy in R-values of sheet metals.

Fig. 4
figure 4

Comparison of R-value directionality: a 718AT; b 719B; c AA5182-O; d AA6022-T4E32

Full size image

5.4 RMSEs of Yield Stresses and R-values

To evaluate accuracy of the anisotropic yield functions quantitatively, the RMSEs of the yield stresses and R-values are calculated as follows:

$$\begin{aligned} \hbox {RMSE}^{\sigma }=\sqrt{\frac{\sum \nolimits _{i=1}^n {(\sigma _i^{\exp .} -\sigma _i^{\mathrm{pred.}})}}{n}},\quad \hbox {RMSE}^{R}=\sqrt{\frac{\sum \nolimits _{i=1}^n {(R_i^{\exp .} -R_i^{\mathrm{pred.}} )} }{n}} \end{aligned}$$
(40)

where \(\sigma _i^{\exp .} \) and \(R_i^{\exp .} \) are the yield stresses and R-values from experiments, respectively; \(\sigma _i^{\mathrm{pred}.} \) and \(R_i^{\mathrm{pred}.} \) are the yield stresses and R-values predicted by the anisotropic yield functions, respectively; and the subscript i represents the loading conditions set in Tables 1 and 2.

The RMSEs of the yield stresses and R-values were calculated for various yield functions to compare their performances in describing the anisotropy of sheet metals. The calculated RMSEs are presented in Table 10 for yield stresses and Table 11 for R-values. For the Hill48 and Yld89 yield functions, the RMSEs of yield stresses are high, but the RMSEs of R-values are moderate. The RMSE of R-values for the Yld91 yield function reaches the highest, which indicates its poor accuracy in modeling anisotropic R-values. The poor accuracy of these three yield functions is due to the smaller numbers of anisotropic parameters used in describing the anisotropy of metals explained in Sect. 2. The performance of anisotropic yield functions is remarkably improved by the Yld96, Yld2000-2d and BBC2000 yield functions for sheet metals, since the anisotropic parameters are almost doubled in these anisotropic yield functions. It is also noticed in Tables 10 and 11 that the RMSEs of uniaxial tensile yield stresses and R-values for the Yld2000-2d yield function are identical to those for the BBC2000 yield function. Moreover, the yield surfaces and anisotropies in the uniaxial tensile yield stresses and R-values predicted for the Yld2000-2d and BBC2000 yield functions are observed to be overlapped. These observations validate the conclusion of Barlat et al. [19] from the quantity point of view. The lowest RMSE is obtained by the Yld2004-18p yield function because 14 anisotropic parameters in the Yld2004-18p yield function are calibrated based on the experimental data of yield stresses and R-values at every 15\(^\circ \) from the rolling direction. Although the Yld2004-18p yield function provides the best predictability for all sheet metals, the calibration of 14 anisotropic parameters requires tremendous experimental work and limits its application to metals with intermediate anisotropy. Alternatively, the Yld96, Yld2000-2d and BBC2000 yield functions provide a great balance between the accuracy and the experimental efforts required for the calculation of anisotropic parameters for materials with intermediate anisotropy, such as AA5182-O and AA6022-T4E32. The RMSEs calculated can offer useful information in evaluating the performance of yield functions quantitatively. It serves as a guide to the selection of an anisotropic yield function for reliable simulations of sheet metal forming processes.

Table 10 Comparison of the RMSEs with respect to yield stresses [%]
Full size table
Table 11 Comparison of the RMSEs with respect to R-values [%]
Full size table

6 Application

In order to investigate the computational efficiency and accuracy of the proposed anisotropic functions, user subroutines are written in ABAQUS/Explicit for Yld96, Yld2000-2d and Yld2004-18p anisotropic functions under AFR. The Euler’s backward integration and return mapping technique are utilized to compute the plastic strain increment.

The numerical simulation of the drawing of a circular cup is performed in order to analyze the influence of anisotropic yield functions on the final cup’s geometry. The test is based on the work of Yoon et al. [20], which involves both the tensile and compressive stress states. In fact, as long as the stress component in the thickness direction is small, the outer flange is under a compressive stress state, and the earing profile is mainly dependent on the in-plane distributions of the yield stress and R-value (Yoon et al. [21]).

6.1 Problem Description

The schematic of the cup drawing process, together with the main dimensions, is shown in Fig. 5. Considering geometric and material symmetries, only a quarter of the global structure is modeled. The contact under frictional condition is described by Coulomb’s law, with a constant coefficient of friction, \(\upmu \), of 0.1. The blank sheet is circular in shape with a radius of 158.76 mm and thickness of 1.6 mm. The blank-holder force is 22.2 kN, corresponding to the minimum predicted value to avoid wrinkling. Although not shown here, for this blank-holder force, it is observed that the stress state component in the thickness direction is small, up to a punch displacement of approximately 25 mm, thus not altering the compressive stress state in the circumferential direction for the material points located at the outer flange (Barros et al. [22]).

Fig. 5
figure 5

Schematic of the cup drawing and main dimensions

Full size image

6.2 Mechanical Behavior of Material

The yield criterion parameters are identified in accordance with the experimental data for the 2090-T3 aluminum alloy presented in Table 1, which consider the experimental uniaxial tensile and compressive yield stresses, as well as the anisotropy coefficients for different orientations with the rolling direction. The experimental data of yield stress and R-value obtained from the balance biaxial test and disk compression test are also presented [23].

6.3 Modeling and Simulation

The sheet is discretized with 8-node hexahedral finite elements, combined with a selective reduced integration technique [24]. 5890 8-node linear brick elements C3D8R were employed in the earing simulations to show the generality of Yld2004-18p yield function which accommodates the full 3D stress components, with two elements used in the thickness direction. The axisymmetric boundary condition is imposed. In addition, the compatible simulation is conducted with the plane stress components in YL96 and Yld2000-2d yield functions, where 10,437 S4R shell elements are used.

The experimental results in Table 12 are utilized to calculate the anisotropic parameters of Yld96, Yld2000-2d and Yld2004-18p anisotropic yield functions using the methods introduced in Sects. 3 and 4. The anisotropic parameters are summarized in Table 13 for the Yld96 yield function, Table 14 for the Yld2000-2d yield function and Table 15 for the Yld2004-18p yield function, respectively.

Table 12 Experimental uniaxial tensile and compressive yield stresses and R-values for the 2090-T3 aluminum alloy [23]
Full size table
Table 13 Anisotropic parameters in the YLD96 yield function
Full size table
Table 14 Anisotropic parameters in the YLD2000-2d yield function
Full size table
Table 15 Anisotropic parameters in the YLD2004-18p yield function
Full size table
Fig. 6
figure 6

Deformed configurations of completely drawn cups using a Yld96; b Yld2000-2d; c Yld2004-18p

Full size image

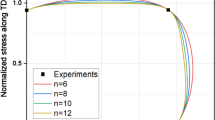
Figure 6 shows the deformed configurations of the completely drawn cups by using the Yld96, Yld2000-2d and Yld2004-18p yield functions, respectively. In Fig. 7, the predicted cup height profiles are compared with the experimental results of AA2090-T3. For an orthotropic material, the cup height profile between 0 and 90 should be a mirror image of the cup height profile between 90 and 180 with respect to the 90 axis [25]. However, the measured earing profile slightly deviates from this condition. This deviation might have occurred because the center of the blank was not aligned properly with the centers of the die and the punch during the drawing experiment. Generally, this plot shows that the earing profiles obtained from the three yield functions are in very good agreement with the measured profile. Using the Yld2000-2d and Yld2004-18p yield functions, the small ears around 0 (or 360) and 180 are well predicted. The earing profile obtained from Yld96, however, exhibits only four ears, which is included in the plot. Unlike many usual phenomenological yield functions, the Yld2004-18p and Yld2000-2d yield functions combined with FE simulations have the capability of predicting more than four ears in cup drawing.

Fig. 7
figure 7

Cup height profiles: experimental data and simulation results using Yld96, Yld2000-2d and Yld2004-18p

Full size image

Figure 8 shows the thickness strain distributions along the rolling and transverse directions by using the Yld96, Yld2000-2d and Yld2004-18p yield function, respectively. Compared with the cases of Yld96 and Yld2000-2d, some improvement in the thickness strain distribution can be observed for the case of Yld2004-18p because of the enhanced predicted R-value and yield stress directionality. For thickness strain distribution, the simulation discrepancy between Yld96 and Yld2000-2d is negligible.

Fig. 8
figure 8

Comparison between predicted and measured thickness strains: a along the rolling direction; b along the transverse direction

Full size image
Fig. 9
figure 9

Performance evaluation of the Hill48 yield function calibrated with two methods for 718AT: a yield surfaces; b uniaxial yield stresses; and cR-values

Full size image

7 Discussions

In Sect. 4.1, two approaches were introduced for the calibration of anisotropic parameters in the Hill48 yield function: one using one yield stress of \(\sigma _0 \) and three R-values of \(R_0 ,R_{45} \) and \(R_{90} \); and the other based on four yield stresses of \(\sigma _0\), \(\sigma _{45}\), \(\sigma _{90}\) and \(\sigma _b \). For simplicity purpose, only the former approach is adopted to calculate anisotropic parameters of the Hill48 yield function in Sect. 4.8 and construct the yield surfaces in Sect. 5. Here these two approaches are compared based on their performance on describing the anisotropic behavior of sheet metals. The anisotropic parameters calculated by \(\sigma _0\), \(R_0\), \(R_{45}\) and \(R_{90} \) are summarized in Table 3, while the anisotropic parameters are calibrated for 718AT by \(\sigma _0\), \(\sigma _{45}\), \(\sigma _{90}\) and \(\sigma _b \) as represented in Table 16. The yield surfaces predicted by the Hill48 yield function are compared in Fig. 9a, while Fig. 9b, c compares the predicted anisotropy in uniaxial yield stresses and R-values, respectively. It is obvious that the balanced biaxial yield stress and directionality of uniaxial yield stresses are reasonably modeled when the anisotropic parameters are calibrated by \(\sigma _0\), \(\sigma _{45}\), \(\sigma _{90} \) and \(\sigma _b \), but the anisotropy in R-values cannot be correctly described. When the anisotropic parameters are computed by \(\sigma _0\), \(R_0\), \(R_{45} \) and \(R_{90} \), the anisotropy in R-values is properly predicted by the Hill48 yield function, but the balanced biaxial yield stress and directionality in uniaxial yield stresses cannot be described correctly. That is the main reason why Stoughton [18] combined the Hill48 yield function with the non-associated flow rule to enhance the accuracy for both yield stresses and R-values. Similarly, the Yld89 and Yld91 yield functions also incorporate four anisotropic parameters related to the in-plane anisotropic behavior of sheet metals. These anisotropic parameters can be calibrated by either \(\sigma _0\), \(\sigma _{45}\), \(\sigma _{90} \) and \(\sigma _b \), or \(\sigma _0\), \(R_0\), \(R_{45} \) and \(R_{90} \). However, none of the Hill48, Yld89 and Yld91 yield functions can provide acceptable predictability for both yield stress and R-values under associated flow rules.

It is shown from the application example that, associated with the phenomenological Yld2004-18p yield function, FE simulations of the cup drawing process can predict cups with six or eight ears. However, in order to obtain this result, the anisotropy of the tensile properties must be described very accurately. In the present case, the R-value and flow stress anisotropies are very well captured with Yld2004-18p (Table 15).

Table 16 Anisotropic parameters in the Hill48 yield function calculated by \(\sigma _0 ,\sigma _{45} ,\sigma _{90} \) and \(\sigma _b \)
Full size table

8 Conclusions

This paper evaluated the accuracy of anisotropic yield functions for two steel sheets and two aluminum alloys. The evaluation demonstrates that the Hill48, Yld89 and Yld91 yield functions cannot properly describe the anisotropic behavior in both yield stresses and R-values due to the limit numbers of anisotropic parameters of these yield functions. Thus, these three yield functions are not suggested to model the anisotropic plastic deformation of sheet metals. The Yld96, Yld2000-2d and BBC2000 yield functions reasonably predict both the yield stresses and the R-values. In addition, the Yld2000-2d and BBC2000 yield functions have the same accuracy in modeling the anisotropy in both yield stresses and R-values. The Yld2004-18p yield function is recommended to be utilized in modeling anisotropic sheet metals. If the experimental data are limited, the Yld96, Yld2000-2d and BBC2000 yield functions are suggested to describe the anisotropy of yield stresses and R-values with acceptable accuracy.

In order to investigate the earing phenomenon, the circular cup drawing test of a circular blank was performed for the 2090-T3 sheet sample. The use of Yld96 and Yld2000-2d with the coefficients determined by the tensile test results led to acceptable predictions compared to the experimental results. However, the best agreement with experimental results in both earing and thickness strain was obtained when Yld2004-18p was used because more tensile test results were implemented. In consideration of the balance between accuracy and efficiency, the Yld2000-2d and BBC2000 yield functions are recommended.