Introduction

Recently the literature on animal behavior has witnessed a boost of publications employing network analysis for the description of complex social interaction patterns (for overviews see May 2006; Krause et al. 2007; Croft et al. 2008; Wey et al. 2008; Whitehead 2008). Introduced by Moreno (1946) in the social sciences in the 1940s, social network analysis is not an entirely new concept, and also its application to the study of animal sociality has already been suggested decades ago (Wilson 1975). The reason for its renaissance is twofold. First, the need to analyze dynamics in large technical, economic, and social networks such as the Internet, the World Wide Web, and global trade networks led to the development of new concepts and algorithms; and second, the development of faster and much more powerful computers allows algorithms that would have required months or years of processing time a few years ago to be run on a normal desktop computer within a reasonable timeframe.

According to Hinde the social structure of a group can be described “in terms of the properties of the constituent relationships and how those relationships are patterned” (Hinde 1983, p. 6). While this definition found broad consent in the scientific community, its implementation in the research programme was hampered by the complexity of those patterns and the unresolved question of how to analyze them. As a consequence, students of animal behavior focused predominantly on single individuals and dyads, or restricted themselves to statements about averaged behavioral activities at the group level. Even dyadic social interactions within groups bring along considerable difficulties, as individuals will interact with several other group members, and likewise their interaction partners will interact with several others, leading to statistical dependencies that are difficult to deal with. While network analysis is not a magic bullet that does away with all statistical problems, it can help to shed light on complex interactions by considering interindividual dependencies not as obstacles but as the very subject of investigation.

The social organization of primate groups has received considerable attention for two reasons. First, as primate species differ markedly in their organizational structure it is of interest which environmental factors shaped those systems, which evolutionary pressures are at work, and which constraints they burden upon the individual (Crook and Gartlan 1966; Gray 1985; Wrangham 1987). Insights won in this area might not least be telling for the evolution of human social organizations and certain aspects of social behavior (Runciman et al. 1996). Second, the structure of a group is likely to influence all kinds of social behaviors, from mating behavior and foraging to cooperation and social learning. Thus, including the social structure as an explanatory variable might be crucial for the understanding of any social behavior (Dunbar 1994; Hemelrijk 1996).

The most basic approach to define the social organization of a primate group might be just to determine the number and sex of regularly associated conspecifics (Struhsaker 1969). As a next step, information on the hierarchy can be included by describing groups as “egalitarian” or “despotic” according to how pronounced the hierarchy in the group is (Sade 1972; de Waal and Lutttrell 1989; Matsumura 1999). Other possible determinants of the social systems of primates are ecological factors and life-history traits such as body size, activity, and pattern of infant care as well as the mating system and spatiotemporal cohesiveness (Kappeler 1999). However, primatologists soon felt uneasy with most classification schemes for social systems when they did not capture the specific features needed, or when it became evident that certain species did not fit properly into one of the categories. As a consequence some tried to refine the models by including more and more distinctions (e.g., Kappeler 1999; Janson 2000; Koenig 2002), while others argue to abandon this categorization approach at all (Thierry 2008). Here, network analysis might be more than a straw to clutch at. As it introduces measures, usually on a continuous scale, that describe certain structural characteristics, it allows us to get rid of the categorization schemes: instead of squeezing species into one of two categories (e.g., “centralized” or “egalitarian”) one can give a centralization index for each species, drawing a much finer and less controversial picture.

While the potential of these new analytical tools is definitely very tempting, the prodigious amount of measures, ratios, and indices leaves the novice puzzling over which ones to choose. An extensive collection of such measures is presented by Wasserman and Faust (1994), although unfortunately more recently developed tools cannot be found there. Croft et al. (2008) give an excellent introduction on exploring animal social networks, and Whitehead (2008) is a must-read for all those seriously interested in this topic, though he primarily focuses on analyses based on association data. Here, we focus on those metrics that might help to characterize the overall structure of a network of sociopositive interactions such as grooming, contact sitting or social play, which are frequently recorded in observational studies on primates. In the following we try to explain our choice of measure and why we believe that these measures are most likely to capture the specifics of primate networks. Thus, the aim of this paper is to (1) suggest a set of network measures that we believe to be useful to characterize interaction patterns within primate groups and (2) present a global analysis of interaction networks of 70 primate groups. The latter will be of use to demonstrate the variability of the social systems within primates and to reveal which network measures show interesting disparities. We explore whether measures vary systematically between taxonomic units and we emphasize that such a comparative approach can be used to search for relations between network characteristics and ecological parameters or life-history patterns.

Methods

The analyzed dataset consists of the sociopositive interaction matrices of 70 primate groups. They were partly taken from the literature and partly from unpublished material either collected by the authors or shared by colleagues. The dataset comprises 30 species of 5 families and 17 genera, including prosiminans, New World and Old World monkeys. Thirty-six groups were kept in captivity, 6 in parks or larger outdoor enclosures (semi-free-ranging), and 28 were observed in the wild. The behaviors that we considered as sociopositive were grooming (45 groups), social play (1 group), body contact (6 groups), a combination of grooming and body contact (7 groups), and in 11 cases the authors gave summarized data of “socio-positive behavior” by pooling two or more of these behavioral categories. These behaviors have in common that they require close proximity of the involved individuals, usually over a prolonged time period.

Since more than a third of the interaction matrices (all except grooming) included nondirected behaviors, we treated all matrices as undirected. The sociomatrices were symmetrized by combining them with their transposed form M sym = M + M′. Decimal values were transformed to integers by rounding or scaling multiplication. For our purpose we defined a group as the set of those individuals who are directly or indirectly connected with each other through sociopositive interactions. That means that single individuals or small subgroups of individuals that never showed sociopositive interaction with other group members were excluded from the sample. In two cases this procedure led to the removal of a single individual, in two cases of two individuals, and in one case of an isolated subgroup of four individuals. This was done for two reasons: first it can be argued that a group is a collection of animals that interact with each other, and consequently individuals that do not interact with the others might not be considered as belonging to the group. Second, and more importantly, a network is per definition a set of connected individuals and several network measures do not deliver meaningful results when applied to disconnected graphs.

Social network analysis is rooted in the mathematical framework of graph theory. A group of primates can be represented as a graph (G), consisting of vertices (or nodes) resembling individuals and edges (or connections) resembling social interactions between them. We can write G = (V, E), where V is the set of vertices (v) and E the set of edges (e). A graph can be defined by its adjacency matrix A whose elements a ij take the value 1 if an edge connects the vertex i to the vertex j and 0 otherwise (with i, j = 1,…, N, where N is the number of individuals in the network).

Primate social groups are expected not to differ so much in the presence or absence of connections between individuals but rather in the number of interactions between different dyads. Theoretically we can consider primate networks as more or less complete graphs, which means that most of the group members interact with each other, though some perhaps only very rarely. Missing social ties might often be due to lack of observation rather that an indication that certain individuals never interact with each other (see also Lusseau et al. 2008). Representing the groups as weighted graphs allows us to acknowledge the importance of quantitative differences in the relationships between different individuals. That means that each edge is assigned a specific weight that derives from the entry in the interaction matrix representing the strength of a relationship (the frequency of interaction within a dyad). The matrix W with entries w ij specifies the weights on the edges connecting the vertices (with w ij  = w ji in case of a symmetric matrix).

All analyses were carried out using Mathematica 6.0 (Wolfram Research Inc.). Mean values are reported together with their standard deviation, and whenever we gave the median of a measure, we indicated the first and third quartile in brackets. For the calculation of independent contrasts phylogenetic distances of the primate species were taken from Purvis (1995) and completed with data from Schneider et al. (2001), Cortés-Ortiz et al. (2003), and Steiper and Ruvolo (2003).

Results

The group sizes of our sample range from 4 to 35, with a median of 9 (6–16) individuals. These figures are quite close to those of a rough literature survey of 184 primate species (Rowe 1996) that suggests a median size of primate groups of 9 (4–20). However, the median group size is only a very rough summary measure that does not do justice to the specifics of any single species.

Density and diameter

The density of a graph gives the proportion of existing edges (dyadic relationships) relative to the total number (Wasserman and Faust 1994). For the primate interaction networks the median density was 0.75 (0.49–0.93) and the median diameter, as the geodesic distance between the two vertices which are furthest away from each other (Wasserman and Faust 1994), was 2 (2–3), suggesting that the groups are overall very densely connected. This questions the usefulness of these metrics to characterize primate social networks, as they do not yield interesting disparities. Consequently, also those measures that are based on topological distances such as average paths length, closeness, and betweenness might be of only limited use. Hence, this corroborates our previously expressed view that a thoughtful network analysis of primate groups has to incorporate quantitative differences in interaction frequencies and consequently has to rely on weighted graph measures.

Degree and vertex strength distribution

The degree k of a vertex is the number of edges that connect to it. The distribution of vertex degrees can give a first impression of the homogeneity or heterogeneity of a group. If we also consider the weights of those edges connecting to a specific vertex, we do not speak of degree but of vertex strength. The vertex strength s of vertex i is given by:

$$ s_{i} = \sum\limits_{j = 1}^{N} {a_{ij} w_{ij} } , $$
(1)

where a is the entry in the adjacency matrix and w the corresponding weight. As a measure that summarizes the shape of the vertex strength distribution we can calculate the skewness h as a ratio of the third to the second central moment:

$$ h = {{{\tfrac{1}{N}}\sum\limits_{i} {(s_{i} - \bar{s})^{3} } } \mathord{\left/ {\vphantom {{{\tfrac{1}{N}}\sum\limits_{i} {(s_{i} - \bar{s})^{3} } } {\left( {{\tfrac{1}{N}}\sum\limits_{i} {(s_{i} - \bar{s})^{2} } } \right)^{3/2} }}} \right. \kern-\nulldelimiterspace} {\left( {{\tfrac{1}{N}}\sum\limits_{i} {(s_{i} - \bar{s})^{2} } } \right)^{3/2} }}. $$
(2)

In 50 out of 70 cases the vertex strength distribution was positively skewed, with a median skewness of 0.3 (−0.1 to 0.6). This means that a higher number of individuals have a relatively low number of sociopositive interactions and a small number of individuals have many sociopositive interactions. However, while the strength distributions were generally skewed to the right, we found no convincing fit with a power-law distribution. We emphasize the lack of this fit, because it has repeatedly been stated in a more general context that biological networks often show degree distributions that follow a power law (Jeong et al. 2000; Barabasi and Albert 2007). While this might be true for protein interaction or metabolic networks, we found no indication for such a similarity in the primate interaction networks. Practically, the strength distribution shows how much individuals differ in their participation in sociopositive interactions. In this respect the skewness of the strength distribution is related to degree and strength centrality, which we will discuss later. The application of these measures is not restricted to sociopositive interactions but they are equally useful for analyzing involvement in agonistic interactions.

Edge weight distribution and disparity

While the degree and vertex strength distribution give a rough picture of the different “importance” of the individuals within a group, the edge weight distribution reveals the variation in the quality of social relations: whether all relations are equally strong in terms of interaction frequencies or whether there are pronounced differences. At the individual level, social interactions can be distributed evenly between all interaction partners or unevenly, with some interaction partners receiving much more attention than others. This can be visualized easily by the sociograph or by a histogram of an individual’s edge weights. To quantify the edge weight disparity Barthelemy et al. (2003, 2005) introduced the quantity Y 2(v i ) for each individual i given by:

$$ Y_{2} (v_{i} ) = \sum\limits_{j = 1}^{N} {\left( {{\frac{{w_{ij} }}{{s_{i} }}}} \right)^{2} } . $$
(3)

Calculating the arithmetic mean over all Y 2(v i ) gives the group-level disparity Y 2. If all weights are of the same order then Y 2 should be close to 1/(N − 1). Figure 1 shows the disparity measure for the primate groups, confirming the skewed distribution of the edge weights. According to Barthelemy et al. (2003) the inverse of Y 2 can be interpreted as an estimate of the number of important edges with high weights. While this interpretation makes the quantity more tangible, it cannot always be taken literally as, e.g., a network with one strong connection and four equally strong intermediate connection could deliver a disparity measure 1/Y 2 = 2.4. Nevertheless, edge weight disparity seems to be a very useful descriptor for the level of heterogeneity in social relationships. Again, these relationships can be of agonistic or affiliative nature.

Fig. 1
figure 1

Edge weight disparity, a measure for the homogeneity of the interactions with all interaction partners, plotted against group size for all groups (N = 70)

Full size image

Centrality

Centrality measures indicate the “importance” (the location) of an individual within a social network and on a global level it serves to better understand group structure. The definition of this “importance” can be reached technically by degree, closeness, betweenness, and eigenvector centrality, among many others. Centrality is a measure that shows the involvement of an individual in social relationships regardless of their direction (they might be directed towards it as well as pointing from it to another individual) (Wasserman and Faust 1994). If the direction of the edges is taken into consideration, further statements can be made concerning the prestige (how many edges are pointing towards this individual) or the sociability (how many behaviors this individual directs to others) of a given individual. Which centrality measure will be most useful depends on the specifics of the measured variable and the question in mind. Several centrality measures such as betweenness centrality and closeness centrality are based on topological distances and might be useful for the analysis of large and sparse networks such as those observed in dolphins (Lusseau 2007) but are of limited value for complete or near-to-complete graphs as we find in primates. Thus, for the purpose of our study we used degree and eigenvector centrality, although in the following paragraph we will also give a short overview of some of the most commonly used metrics. Software packages for network analysis sometimes allow the inclusion of edge weights for the computation of centrality measures. However, these edge weights are usually interpreted as distance, which leads to different results than if they were interpreted as interaction frequencies.

Degree and strength centrality

Individuals with high degree have many relationships with others and thereby occupy a central location in the network. In our analysis a “central location” for an individual means that it is involved in most or many affiliative interactions. If we want to include the effect of edge weights on the centrality measures we can easily modify the definition of actor degree centrality (Wasserman and Faust 1994) by replacing degree with vertex strength (Barrat et al. 2004). The vertex strength centrality C s for vertex v i is given by:

$$ C_{s} (v_{i} ) = {\tfrac{{s_{i} }}{N - 1}}. $$
(4)

This standardized index is independent of group size N, which enables us to compare this measure across groups of different sizes. C s ranges from 0 to 1, with 1 being the highest possible strength centrality, reached only by the central individual in a star-like network, and 0 being the strength centrality of a completely isolated individual (though the latter were removed from our sample). There are different methods to derive a group centralization measure. While Freeman (Freeman 1979) recommends the use of his general centralization index, Snijders (1981) suggests the variance of degree centrality as an indicator for dispersion or heterogeneity. The variance attains its minimum value of 0 when the vertex strengths of all vertices are equal, while the maximum value will depend on the group size N.

In the primate database the highest individual centralization index C s (v i ) was 0.92, reached by an individual in a nearly star-like group of five individuals, while the lowest of 0.001 was reached by an individual in a group of 33 baboons. In a group-level comparison the variances of the strength centrality varied between 0.007 and 0.32 (Fig. 2).

Fig. 2
figure 2

Group vertex strength centralization index as a measure of centrality for each group, plotted against group size

Full size image

Eigenvector centrality

The eigenvector centrality of an individual is based on the sum of the centralities of its neighbors, which enables an individual to gain high centrality in two different ways: it can itself have strong relationships with many other individuals or be in contact with those individuals that are most central. While the interpretation of eigenvector centrality is not as intuitive as for degree or strength centrality, it can be a valuable tool when it comes to processes that involve the spreading of information within a group (Ramos-Fernandez et al. 2009) or collective movement decisions (Sueur and Petit 2008). Technically we can consider the importance of interaction partners by making the centrality c i of vertex v i proportional to the average of the centralities of v i ’s neighbors:

$$ c_{i} = {\tfrac{1}{\lambda }}\sum\limits_{j = 1}^{N} {w_{ij} c_{j} } , $$
(5)

where λ is a constant. If we define the vector of centralities as c = (c 1, c 2,…,c N ), we can rewrite Eq. 5 as \( \lambda c = Wc, \) where it follows that c is an eigenvector of the edge weight matrix W with eigenvalue λ. The eigenvector centrality is then given by the eigenvector corresponding to the largest eigenvalue (Bonacich 1972; Ruhnau 2000). The eigenvector can then be normalized using the Euclidean norm

$$ c_{i}^{n} = \sqrt 2 {\tfrac{{c_{i} }}{{\left( {\sum\nolimits_{i = 1}^{N} {c_{i}^{2} } } \right)^{1/2} }}}. $$
(6)

As a group measure for the whole graph we can calculate a centralization index C e as

$$ C_{e} = {\tfrac{{\sum\nolimits_{i = 1}^{N} {(c_{i}^{n,\max } - c_{i}^{n} )} }}{{\max G \in G_{n} \left( {\sum\nolimits_{i = 1}^{N} {(c_{i}^{n,\max } - c_{i}^{n} )} } \right)}}}, $$
(7)

where the nominator is the difference in the normalized centralities to the maximal value occurring in the graph \( c_{i}^{n,\max }, \) and the denominator gives the maximal difference maxG with respect to all possible graphs G n . As follows from Eq. 7 the centralization index C e lies in the interval [0,1]. While for topological graphs the star with \( E = \{ (v_{1} ,v_{i} )|i = 2, \ldots ,N\} \) produces the maximal difference, there is no simple solution to find maxG for weighted graphs. If we take the topological star as the denominator, we allow for centralization indices >1, however, the index is still easy to interpret: graphs with a centralization index >1 are more centralized as a topological star. We could refer to such graphs as “supercentral.” Figure 3 gives the eigenvector centralization indices for the 70 primate groups. In general, the primate groups showed relative high centralization, with a mean eigenvector centralization index of 0.68 ± 0.28. Nine groups qualified as supercentral, with an eigenvector centralization index of larger than 1. The highest centralization of 1.5 was reached by a group of 35 baboons (Fig. 4f).

Fig. 3
figure 3

Eigenvector centrality for all groups (N = 70) plotted against group size. The solid line at y = 1 indicates the eigenvector centrality for the star as the most centralized topological structure

Full size image
Fig. 4
figure 4

Graph representation of six example groups: vertices represent individuals and edges represent relationships between individuals. The thickness of the edges is proportional to the edge weight. Different symbols for the vertices indicate assignment to different subgroups based on an algorithm developed by Newman and Girvan (2004). Graphs represent groups of a captive squirrel monkeys, Samiri sciureus (Vaitl 1977), b wild adult male chimpanzees, Pan troglodytes (Nishida and Hosaka 1996), c wild wedge-capped capuchin monkeys, Cebus olivaceus (O’Brien 1993), d captive long-tailed macaques, Macaca fascicularis (Butovskaya et al. 1996), e wild bonnet macaques, Macaca radiata (Koyama 1973), and f wild baboons, Papio papio (Sugawara 1979). Examples were chosen to demonstrate groups with high (+) or low (−) values of the following network metrics: edge weight disparity (Y 2), network flow (NF), eigenvector centrality (Ce), community modularity (Q), strength assortativity (bw), and vertex strength centralization (Cs)

Full size image

Other centrality measures

Closeness centrality measures how close an individual is to others in the network in terms of its ability to quickly interact with others. It is assessed on the basis of geodesic distances and does not only depend on direct but also indirect edges. The shorter the geodesics of an individual, the closer it is to its group members (Wasserman and Faust 1994).

Betweenness is a measure of the extent to which a vertex lies on the paths between others and therefore has control over the information flowing between others (Newman 2005). This closeness measure considers the fact that interactions between two individuals do not need to depend on direct connections but are also possible via other individuals that lie on paths between these two individuals. Betweenness and closeness centrality are frequently employed in network analysis; however, as they are strictly topological measures calculated on the basis of geodesics, they are of only limited use to analyze dense networks of small groups.

Community modularity

Community modularity is a structural graph measure introduced by Newman and Girvan (2004). It measures the degree of fragmentization of a group into subgroups by comparing interaction frequencies within and between subgroups. The distinction into subgroups can be based on specific characteristics of the animals such as sex, age class or matriline, or one can try to find the partitioning into subgroups that maximizes the community modularity (e.g., Lusseau and Newman 2004; Wolf et al. 2007). For the latter we use an agglomerative algorithm suggested by Clauset (2005), though several alternatives exist (Newman 2006). After the vertex set V of graph G is divided into j exclusive subsets S we can calculate the community modularity Q as:

$$ Q = \sum\limits_{i}^{j} {p_{ii} - o_{i}^{2} } , $$
(8)

where p ii is the proportion of edges within community S i , and o i is the proportion of edges that start from community S i . For a random partition of V, Q should be close to 0, while Q close to 1 indicates strong structuring. The measure was originally developed for binary graphs; however, by representing edge weights as multi-edges it can also be used to quantify community structure in weighted graphs (Fig. 4). Applying this algorithm to the primate data, groups were partitioned into 1–6 subgroups (median 2, 2–3) with a median subgroup size of 4 (3–5) individuals. The groups showed considerable variation in their overall community modularity (mean 0.21 ± 0.16, Fig. 5), demonstrating that primate groups can be either strongly structured with clearly identifiable subgroups or much more homogeneous with respect to their social interactions. While this finding will not strike the experienced primatologist as a new insight, as it is well known that primate social structures are highly variable, we want to emphasize the usefulness of this measure to quantify the degree of heterogeneity of a social system. With a quantitative measure at hand it will be much easier to compare different groups or to relate group heterogeneity with other social or ecological variables.

Fig. 5
figure 5

Community modularity for all groups (N = 70) plotted against group size

Full size image

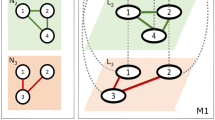
However, at this point we also have to caution against too much confidence in network analysis. If the subgroup assignment is not based on individual characteristics (such as sex, age or kin) but on a modularity-maximizing algorithm, then one should ask for the biological interpretation of this partitioning. In most cases the algorithms will confirm the perception of the observer, but under certain conditions the suggested partitioning will split matrilines or group individuals together that do not seem to have much in common. To illustrate this potential pitfall we give two artificial examples in Fig. 6. This problem is especially severe if the network analysis is based on a poor data set. Then, even small changes in the raw data might lead to completely different partitions. How robust the subgroup assignment is against sampling errors or natural random variation can be estimated using a bootstrap procedure (Lusseau et al. 2008) where bootstrapped data are resampled with replacement from the original raw data. For each of the 70 groups we ran 100 bootstraps, each time evaluating the subgroup assignment. For 41 groups this resulted in the same partitioning in over 50% of the runs, for 23 groups in over 90%, and for 16 groups in 100%. Thus, in the majority of the cases this procedure is relatively robust to random noise, but we recommend verifying in every single case.

Fig. 6
figure 6

A hypothetical example of a macaque group with two matrilines (F1–F4 and F5–F7) and two males (M1 and M2). In a, the Q-maximizing algorithm would group F1–F4 into subgroup 1 (circles), F5–F7 into subgroup 2 (squares), and M1 and M2 into subgroup 3 (hexagons). In b, we assume that M1 intensifies grooming with the two alpha-females of the matrilines, as might happen when these females are in estrus, while the other grooming relations remain unchanged. In this case the algorithm would group F2-F4 into subgroup 1, M2, F6, and F7 into subgroup 2, and M1, F1, and F5 into subgroup 3

Full size image

The group-level measure for community modularity seems to be quite robust against random sampling noise, with an average bootstrapped standard deviation of 0.02. For our dataset the standard deviation for community modularity seems to be independent of the mean [analysis of variance (ANOVA), N = 70, P = 0.13, R 2 = 0.02] and the number of different assignments (ANOVA, N = 70, P = 0.64, R 2 = 0.003), which means that, even when bootstrapping resulted in several different subgroup assignments, this does not influence the estimate for the community modularity measure in a significant way.

Clustering coefficient

The clustering coefficient characterizes the local group cohesiveness by evaluating the extent to which vertices adjacent to any vertex i are also adjacent to each other (Watts and Strogatz 1998; Watts 1999). It is given by:

$$ cc_{i} = {{\left| {E\left( {\Upgamma v_{i} } \right)} \right|} \mathord{\left/ {\vphantom {{\left| {E\left( {\Upgamma v_{i} } \right)} \right|} {\left( {{\frac{{k_{i} }}{2}}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {{\frac{{k_{i} }}{2}}} \right)}}, $$
(9)

where the neighborhood Γv of a vertex v is the subgraph that consists of the vertices directly connected to v. It can be interpreted as a measure of individual sociality (Croft et al. 2004). The average clustering coefficient over all vertices, CC, measures the global density of connected vertex triplets in the network and can be interpreted as an indicator for the cohesiveness of the group. For weighted networks Barrat et al. (2004) formulated the weighted clustering coefficient as:

$$ cc_{i}^{w} = {\tfrac{1}{{s_{i} (k_{i} - 1)}}}\sum\limits_{j,l} {{\tfrac{{(w_{ij} + w_{il} )}}{2}}a_{ij} a_{il} a_{jl} } , $$
(10)

where k i is the degree of vertex i, given by \( k_{i} = \sum\nolimits_{j = 1}^{N} {a_{ij} } . \) CC w is then defined as the weighted clustering coefficient averaged over all vertices of the graph. In a recent study Lehmann and Boesch (2009) used the weighted clustering coefficient to detect structural changes in a community of female chimpanzees over a period of 10 years. We find high variation in both the coefficients within groups with an average range of 0.31 (0–0.66) and the average coefficients between groups (median 0.84, 0.57–1). Comparing the weighted clustering coefficient with its topological analog, CC, we gain global information on the correlation between weights and topology (Fig. 7). In the case of a fully connected graph it is easy to see that CC w = CC = 1. In more heterogeneous weighted networks, however, we can face two opposite cases. If the interconnected triads are more likely to have high edge weights, then this is reflected by CC w/CC > 1. On the other hand, CC w/CC < 1 indicates a group in which the topological clustering is generated by edges with low weight.

Fig. 7
figure 7

Ratio of the weighted clustering coefficient (CC w) to the topological clustering coefficient (CC) for all groups (N = 70) sorted by group size. A ratio larger than 1 indicates groups where interconnected triads are more likely to be strongly connected (with high edge weights), while a ratio smaller than 1 indicates groups where triads are more likely to be only weakly connected

Full size image

By calculating clustering coefficient and community modularity we are asking for the existence of cohesive subgroups within a group. Such a concept is useful when the network is based on affiliative interactions or proximity data. However, it seems to make little sense when the data stem from agonistic interactions. Grouping together all those individuals that regularly fight with each other will usually not comply with the general conception of a subgroup.

Both the clustering coefficient and the community modularity are local measures. This means that they can be calculated without knowledge of the whole network; the vertices in question and their direct surroundings are sufficient. This is a very useful property when it comes to very large networks containing several thousands to millions of participants, where the researcher can only observe a small sample of the whole population. While all the groups that we used for the present analyses were regarded as small closed social units that would not require such a measure, local measures would also allow to analyze data sets where researchers focused just on a part of the whole network, e.g., a single matriline in a large band of baboons or macaques.

Network flow and resilience

A metric that is related to the above-mentioned betweenness measures is network flow. It is useful to describe information or disease transmission between individuals in affiliative or proximity networks. The advantages of network flow are that it takes into account edge weights and that it is conceptually easier to grasp. We think of a network as a system of pipes where edges are pipes and the edge weight gives the diameter of the pipes. Along these pipes a certain amount of liquid can pass according to their diameter. The maximum flow between any two vertices is the amount of liquid that can flow from one to the other. The liquid is not constrained to take the shortest path between the two vertices but can be sent through all pipes. As one might guess, this measure was originally developed for technical problems to calculate the capacity of power grids or data networks such as the Internet. However, it was suggested that it is useful to model information flow in many kind of networks, including social networks (Ahuja et al. 1993). The network flow can be evaluated for two specific vertices or averaged over all possible pairs of vertices, giving measure for the connectivity of the group (Newman 2004).

The max-flow/min-cut theorem (Ford and Fulkerson 1956) allows an additional interpretation of network flow. This theorem states that for weighted networks the maximum flow between any two vertices equals the weight of the minimum edge cut set that separates the same two vertices (Newman 2004). Thus, a larger network flow means that more or stronger connections have to be cut to disconnect these vertices. Network flow is therefore also a measure for the resilience of a network against being disconnected by the removal of connections between individuals. Figure 8 shows the network flow for the primate groups. As we standardized the edge weights (so that \( \sum {W = 1} \)), it is not surprising that the overall network flow (and hence resilience) of a group decreases with group size. This also makes sense intuitively, as in large groups information is less likely to reach all members easily, and larger groups seem more vulnerable to be split apart. Besides that, we find reasonable variation in the network flow between groups of the same size. These disparities might be even more interesting, as they allow to compare different groups and to ask whether this resilience metric accords with differences in the social behavior of these groups.

Fig. 8
figure 8

Network flow for all groups (N = 70) plotted against group size

Full size image

Another way to look at the resilience of a network is not to ask how easily the removal of connections will disconnect the network, but how the system reacts to the removal of specific individuals (Albert et al. 2000). There are two main procedures to remove vertices that are commonly applied in social network analysis. Vertices can either be removed randomly or high-degree vertices can be attacked selectively (Newman 2003a). The same network can show different values of resilience towards these two forms of vertex removal; for example, Lusseau (2003) found high resilience to random vertex removal, but elevated vulnerability when it comes to targeted sabotage by removal of high-degree vertices, in a dolphin network with a strongly positive skewed degree distribution. In an inspiring study Flack et al. (2006) inspected the resilience of macaque networks against changes in mean degree, assortative mixing, and clustering after the hypothetical knockout of several vertices that represented individuals with high status. They compared these changes with the results when they experimentally removed animals from a captive group, and thereby provided a wonderful example of how predictions from social network analyses can be tested empirically.

To demonstrate the effect of vertex removal we selected an example group of intermediate size (N = 10, Fig. 4d) and systematically removed each vertex separately, then each combination of two vertices, three vertices, and so forth up to N−2 vertices, calculating the remaining network flow after each removal. The results of this procedure are given in Fig. 9. Even for a group of only ten individuals there are already 1,012 different combinations of vertices to be removed from the network. For a group of 25 we would already require over 33 million removal operations and recalculations of the network flow. As this approach would result in extremely long computation times it seems only suitable for very small groups. For larger groups repeated random vertex removal as described by Newman (2003a) will be a more efficient way to determine the robustness of the network.

Fig. 9
figure 9

To demonstrate resilience against vertex removal, the network flow of an example group of ten individuals was recalculated after vertex removal. Each possible combination of vertices from one up to eight (N−2) vertices was removed. For each number of removed vertices (x axis) the corresponding values of the network flow are given. The horizontal lines show the means of network flow for all combinations with the same number of removed vertices. Depending on which vertex was removed, elimination of a single vertex leads to a reduced network flow between 90 and 55%. Removal of two vertices already reduces flow on average to 50%

Full size image

Assortativity

Do individuals of certain classes interact preferentially with individuals of the same class than with others? Or, more general, do individuals with a certain characteristic preferentially interact with others who are similar to them with respect to this characteristic? If they do, then this is referred to as assortative mixing (Newman 2003b). Frequently considered classes include sex, age, social rank and kin (e.g., Lusseau and Newman 2004) and interactions can be of any kind, spatial relationships, affinity or aggression; for example, one can ask whether males direct more interactions towards other males or females or whether juveniles preferentially groom others of their own age class. Such questions are usually approached using matrix correlations (Hemelrijk 1990a, b; de Vries 1993). The concept of assortativity is, however, not restricted to the above-mentioned characteristics, but can be applied equally well to network characteristics of the individuals. That is, one might ask if animals which have a high number of interaction partners preferentially interact with others that also have many interaction partners. Pastor-Satorras et al. (2001) introduced the average degree of nearest neighbors k nn(k), which indicates whether vertices with high degree have a larger probability to be connected with other high-degree vertices. Barrat et al. (2004) suggested the weighted average nearest-neighbors degree as a measure of the effective affinity to connect with high- or low-degree neighbors according to the magnitude of the actual interactions. For this purpose they calculated a local weighted average of the nearest-neighbor degree and normalize by the weight of the connecting edges. For each individual the weighted average nearest-neighbors degree is given by

$$ k_{{\rm nn},i}^{w} = {\frac{1}{{s_{i} }}}\sum\limits_{j = 1}^{N} {a_{ij} w_{ij} k_{j} } . $$
(11)

If the nearest-neighbors degree k nn,i is smaller than the weighted version \( k_{{\rm nn},i}^{w} \) this indicates that edges with larger weights are pointing to the neighbors with larger degree. However, we think that for our purpose this measure considers edge weights only half-heartedly. While it accounts for the strength with which a vertex connects to the other vertices it considers only the degree of these vertices but not their strengths. As we emphasized the importance of using weighted measures, we think that we should consequently also reformulate our question: instead of asking for the affinity to a vertex due to its degree we should ask for its affinity due to its strength. Thus, we want to introduce the relative strength assortativity as

$$ b_{s,i}^{w} = {\frac{1}{{s_{i} }}}\sum\limits_{j = 1}^{N} {a_{ij} w_{ij} s_{j} } . $$
(12)

For better comparability between groups we standardize the edge weights by multiplying them by \( N/\sum W \). With this scaling \( \ln b_{s,i}^{w} > 0 \) indicates strength assortativity of a vertex (i.e., edges leading to strong vertices have high weights), while \( \ln b_{s,i}^{w} < 0 \) indicates strength disassortativity (i.e., edges leading to strong vertices have low weights). Only 16% of all vertices had negative logarithms of their relative strength assortativity, and group medians were positive in 68 out of 70 groups (Fig. 10), indicating overall positive assortativity of vertices according to their strength.

Fig. 10
figure 10

Natural logarithms of relative strength assortativity plotted for all groups (N = 70), ordered by size. Points indicate group medians, vertical lines the range

Full size image

Phylogenetic independent contrasts

Our data set stems from 30 different primate species that are phylogenetically related to each other to different extents, hence the data cannot be considered as statistically independent. Felsenstein (1985) proposed to deal with these dependencies by replacing the actual species means by contrasts that are corrected for phylogenetic distance. For a sample of 30 different species we can estimate 29 phylogenetically independent contrasts. We calculated independent contrasts for network flow, community modularity, vertex strength centrality, and assortativity. We can see that independent contrasts decrease with phylogenetic distance in all cases (Fig. 11). Furthermore it becomes apparent that the variance in the contrasts decreases with phylogenetic distance as well. That means that contrasts between closely related species or taxonomic groups can be both high and low, while contrasts between more distant taxonomic groups are generally low, indicating that all the investigated network measures do not differ systematically between higher taxonomic groups.

Fig. 11
figure 11

Phylogenetic independent contrasts (N = 29) are plotted against the estimated phylogenetic distance in million years: Phylogenetic independent contrasts were calculated for a community modularity, b network flow, c assortativity, and d vertex strength centrality

Full size image

Discussion

In this paper we presented results of a general network analysis from 70 primate interaction networks. We found considerable variability in the network measures, reflecting the high degree of diversity of primate social organization. The advantage of a network approach to social groups is that it enables us to draw a much finer picture of structural differences between groups. Instead of being restricted to verbal descriptions such as “egalitarian” or “hierarchically structured” we can actually offer quantitative measures for centrality, modularity or resilience. This can be useful both for species comparison (Sundaresan et al. 2007, this study) or comparison between groups of the same species. In long-term studies it can even be used to detect structural changes within a group over time (Henzi et al. 2009; Lehmann and Boesch 2009; Ramos-Fernandez et al. 2009). Finally, McCowan et al. (2008) demonstrated that, besides its heuristic value for the study of primate behavior, social network analysis might also have practical applications for management of captive primate groups.

Primate social systems are difficult to characterize, and attempts to do so have been criticized as being overly simplifying, formulated only on a verbal level or simply inconsistent (Thierry 2008). Classification schemes where social organization forms are separated into distinct categories might run into trouble if real differences are not as clear-cut as believed. And this problem cannot be resolved by including more and more parameters in the model because, if the parameters that shape the overall social structure change on a continuous gradient rather than being dichotic, any splitting into categories might be mistaken or arbitrary at best. An alternative to categorizing is to define group structure by one or more network metrics that more adequately reflect its internal structure.

In our analysis we focused on structural measures, mostly on the group level. The list of measures that we presented is by no means complete. Network analysis allows for much more than we could demonstrate here, and which measures are most useful will depend on the specifics of the research question. However, not all measures are adequate for the analysis of primate groups, as many were developed for much larger nets with specific underlying assumptions that might not be met in our case. As we have already mentioned, purely topological measures that do not consider quantitative differences in relationships might be inadequate to capture important details; e.g., vertex strength distribution and edge weight distribution are much more informative than the mere degree distribution, and eigenvector centrality might be more telling than betweenness or closeness centrality (e.g., Ryder et al. 2008; Sueur and Petit 2008; Ramos-Fernandez et al. 2009).

The network measures described herein are static: if a vertex is removed, the system does not react to this operation in the sense that vertices would then connect to other vertices instead. This does of course not correspond with reality, where we would expect flexible behavior. Network measures reflect the properties of a given fixed structure. They are descriptors of the structure, not predictors of how a group of reactive individuals will actually change over time. Dynamic network models that allow for reactive behavior of individuals do exist (e.g., Santos et al. 2006; Li et al. 2007; Voelkl and Noë 2008; Voelkl and Kasper 2009), although their discussion would go beyond the intent of this paper.

There are several excellent software packages available, both stand-alone programs and routine libraries for R or MATLAB, that might serve those interested in social network analysis well. A few of these programs capable of analyzing weighted social network data can be found in Appendix 1. For a more detailed overview of the currently available programs we recommend Whitehead (2008) and Huisman and van Duijn (2005). However, along with Whitehead (2009) we would like to advise caution for the use of “ready-to-go” software as it does not release the user of considering thoroughly how the measures fit with their dataset and questions. For example, in some programs weights are attributed to edges to denote the distance of two vertices rather than the attraction between them. The validity of a network measure will very much depend on the quality of the data. It is therefore important to estimate the robustness of a measure against sampling errors or natural variation in the raw data using bootstrap or jack-knife resampling procedures (Lusseau et al. 2008). Because this is, unfortunately, not possible with most stand-alone programs we generally recommend programs or routine libraries embedded in a programming environment such as R, MATLAB or Mathematica, which allows the user to tailor a routine for its particular use.