Introduction

Integer ambiguity resolution-enabled precise point positioning (PPP-RTK) is the global navigation satellite system (GNSS) positioning mode that delivers single-receiver ambiguity-resolved parameter solutions. Its realization relies, next to satellite orbit and clock corrections, on the provision of satellite bias corrections which are often determined by a network of reference receivers (Wubbena et al. 2005; Ge et al. 2005; Collins 2008; Teunissen et al. 2010; Geng et al. 2012; Odijk et al. 2016). Such corrections can also be computed and provided to positioning users via only one single reference receiver, the so-called provider. With such single-receiver PPP-RTK corrections (Khodabandeh and Teunissen 2015), nearby positioning users are able to correct their code and phase data, recovering the integerness of their phase ambiguities, thereby achieving high-precision positioning solutions.

Despite their random nature, the PPP-RTK corrections are often treated as nonrandom (deterministic) quantities either for implementation simplicity or because of the vast amount of information that needs to be transmitted to the user (Odijk et al. 2014). The justification behind this randomness is that the provider data used to generate these corrections are accompanied by an amount of uncertainty. Would the user, therefore, want to obtain minimum-variance positioning solutions, he needs to involve the true stochastic model of his corrected data so as to correctly incorporate their quality description into his estimation process. When the latter is characterized solely by the user data uncertainty, the weight matrices underlying the user model do not represent the inverse of the actual variance matrices. In such cases, the user’s parameter solutions may lose their ‘minimum-variance’ property and become sub-optimal.

This becomes even more pronounced when one considers that, in real-time GNSS applications, the PPP corrections are not usually provided at an instant to the user but with a certain time delay or latency. Therefore, the users have to predict the corrections in time, based on the information and methodology given by the provider, see (IGS 2020), in order to bridge the gap between the correction generation time and the user positioning time, with a penalty on the achieved positioning accuracy as shown for PPP (Yang et al. 2017) and PPP-RTK (Wang et al. 2017). Similar correction prediction approaches have been earlier developed for standard differential positioning applications (Teunissen 1991). A far more serious problem than the accuracy degradation is that the provided quality description of the user’s parameters fails to represent the actual one since the amount of uncertainty that lies in the corrections may get amplified as the time delay increases.

Based on a single-station framework for the generation and time-prediction of multi-epoch PPP-RTK corrections, Khodabandeh (2021) showed the effect of high latency on the PPP-RTK user ambiguity resolution performance. The uncertainty involved in the time-predicted corrections is also expected to impact the user’s ambiguity-resolved positioning performance and its accompanied precision description, for which an analysis is missing. This becomes especially relevant for peer-to-peer positioning applications that are enabled in such a single-station setup, without the need for instantaneous exchange of information, and are of great interest in light of the rapid development and utilization of low-cost GNSS devices (Banville et al. 2019; Psychas et al. 2019; Wang et al. 2021).

In this contribution, we aim to demonstrate and analyze the user ambiguity resolution and positioning performance in case one neglects the uncertainty of the time-predicted single-station PPP-RTK corrections, and to show to what extent his performance gets different from its true counterpart. Next to the user positioning estimation results, particular emphasis is given to the quality description that accompanies them. We develop and present two alternatives to the fully populated variance matrix of the PPP-RTK corrections that the user optimally requires. While such alternative variance matrices can be fully structured at the user side via a limited amount of information from the provider, they are proven to be sufficient enough for the user to weigh his corrected data and achieve close-to-optimal results for high latencies.

This contribution is organized as follows. We first present our underlying observation model and estimable parameters for both the single-station provider and the user setups. Further, we describe our processing strategy and show the importance of conducting a quality judgment on the combined rather than the individual corrections. By considering various latencies and different strategies regarding the uncertainty of single-station PPP-RTK corrections, the single-epoch ambiguity resolution performance is then investigated based on GPS and Galileo dual-frequency observations through a formal and empirical success rate analysis. Afterward, the corresponding positioning performance is analyzed for the ambiguity-float and -fixed cases, in terms of both the positioning accuracies and the precision description that goes along with them. The results are discussed, and concluding remarks are presented.

Observation model

In this section, we first present the estimable parameters of the PPP-RTK provider and user models based on uncombined GNSS observation equations. Then, we introduce how the user obtains the time-predicted combined corrections along with their variance matrix.

Single-station provider

Let us commence with the linearized observation equations of the observed-minus-computed, single-epoch, uncombined phase (\(\Delta \phi_{r,j}^{s}\)) and code (\(\Delta p_{r,j}^{s}\)) observables of a satellite \(s\,\,(s = 1, \ldots ,m)\) on frequency \(j\,\,(j = 1, \ldots ,f)\) that are collected by the provider \(r\):

$$\begin{aligned} {\rm E}(\Delta \phi_{r,j}^{s} ) & = g_{r}^{{s^{T} }} \Delta x_{r} + {\text{d}}t_{r} - {\text{d}}t^{s} + m_{r}^{s} \tau_{r} - \mu_{j} \iota_{r}^{s} + \lambda_{j} (\delta_{r,j} - \delta_{,j}^{s} + a_{r,j}^{s} ) \\ {\rm E}(\Delta p_{r,j}^{s} ) & = g_{r}^{{s^{T} }} \Delta x_{r} + {\text{d}}t_{r} - {\text{d}}t^{s} + m_{r}^{s} \tau_{r} + \mu_{j} \iota_{r}^{s} + (d_{r,j} - d_{,j}^{s} ) \\ \end{aligned}$$
(1)

where \(m\) and \(f\) denote the number of satellites and frequencies, respectively. Here and in the following, the observed-minus-computed observations are assumed to include the precise orbital corrections. The position increment \(\Delta x_{r}\) is linked to the observations through the receiver-satellite direction vector \(g_{r}^{s}\). The common receiver and satellite clock parameters are denoted with \({\text{d}}t_{r}\) and \({\text{d}}t^{s}\), respectively. The zenith tropospheric delay (ZTD) for receiver \(r\), after removing the a priori (dry) value, and its mapping function for receiver \(r\) and satellite \(s\) are represented by \(\tau_{r}\) and \(m_{r}^{s}\), respectively. The first-order slant ionospheric delay experienced between the receiver \(r\) and satellite \(s\) on the first frequency is denoted by \(\iota_{r}^{s}\), and its linkage to the observations is done through the coefficient \(\mu_{j} = \lambda_{j}^{2} /\lambda_{1}^{2}\) that depends on the wavelength \(\lambda_{j}\). \(\delta_{r,j}\) and \(\delta_{,j}^{s}\) stand for the receiver and satellite phase biases, respectively, while \(d_{r,j}\) and \(d_{,j}^{s}\) denote those for the code observations, respectively. The integer phase ambiguity is represented by \(a_{r,j}^{s}\). All parameters are expressed in units of range, apart from \(\delta_{r,j}\), \(\delta_{,j}^{s}\) and \(a_{r,j}^{s}\) that are expressed in units of cycles. \(E( \cdot )\) denotes the expectation operator. Note that, the receiver position is precisely known for the provider and therefore absent from (1), but unknown for the user receiver.

However, the lack of information content in the above system of GNSS observation equations does not allow us to unbiasedly determine all the individual parameters. By applying the \({\mathcal{S}}{\text{ - system}}\) theory (Baarda 1973; Teunissen 1985) and by constraining a minimum set of parameters, namely the \({\mathcal{S}}{\text{ - basis}}\), we can remove the underlying model rank deficiencies and determine, instead of the original, estimable functions of the original parameters.

As the \({\mathcal{S}}{\text{ - basis}}\) is dependent not only on the measurement model but also on the assumptions regarding the dynamic model of the involved parameters, we need to make such models explicit. Some of the above parameters are known to behave constant in time, e.g., the phase ambiguities, while others may rapidly change in time, such as the satellite clocks. Therefore, to provide the user with the capability to time-predict the delayed corrections, one may take recourse to a minimum-mean-squared-error filtering technique such as the Kalman filter (Kalman 1960).

In this study, we choose a constant-state process for modeling the temporal behavior of the ionospheric delays, ambiguities and code/phase biases:

$$\alpha (i) = \alpha (i - 1) + n_{\alpha } (i),\,\,\,\,i = 2, \ldots ,k$$
(2)

and a constant-velocity process to describe the temporal behavior of the satellite clocks:

$$\begin{aligned} \beta (i) & = \beta (i - 1) + \Delta t\partial \beta (i - 1) + n_{\beta } (i), \\ \partial \beta (i) & = \partial \beta (i - 1) + n_{\partial \beta } (i),i = 2, \ldots ,k \\ \end{aligned}$$
(3)

where \(\alpha\) and \(\beta\) denote parameters the temporal behavior of which is modeled with a constant-state (random-walk) and a constant-velocity process, respectively. \(\partial \beta\) denotes the first-order time derivative of \(\beta\). \(i\), \(k\) and \(\Delta t\) denote the epoch index, the total number of epochs and the sampling period, respectively. The system noises \(n_{\alpha }\), \(n_{\beta }\) and \(n_{\partial \beta }\) are assumed to be zero mean (Teunissen 2001).

The reason behind the selection of the above processes for the time variations of the parameters is justified as follows. The phase ambiguities are assumed to be time constant unless cycle slips occur, while the receiver and satellite biases are reported to behave rather stable over time (Komjathy et al. 2005; Zhang et al. 2018). Thus, their system noises are set to be identically zero. As for the ionospheric delays, it is known that they do not show significant time variations in short time spans, indicating that a constant-state process can sufficiently describe their temporal behavior. Such a process, though, seems not adequate to capture the temporal variation of the satellite clocks due to their rapid changes in time (Wang et al. 2017). Finally, the receiver clocks are assumed to be completely unlinked in time.

Based on the above assumptions, the full-rank version of the provider’s model can be expressed as (Khodabandeh 2021):

$$\begin{aligned} & {\text{I}}:\left\{ \begin{gathered} {\rm E}(\Delta \phi_{r,j}^{s} (i)) = {\text{d}}\tilde{t}_{r} (i) - {\text{d}}\tilde{t}^{s} (i) - \mu_{j} \tilde{\iota }_{r}^{s} (i) + \lambda_{j} (\tilde{\delta }_{r,j} (i) - \tilde{\delta }_{,j}^{s} (i)) \\ {\rm E}(\Delta p_{r,j}^{s} (i)) = {\text{d}}\tilde{t}_{r} (i) - {\text{d}}\tilde{t}^{s} (i) + \mu_{j} \tilde{\iota }_{r}^{s} (i) + (\tilde{d}_{r,j} (i) - \tilde{d}_{,j}^{s} (i)) \\ \end{gathered} \right. \\ & {\text{II}}:\left\{ \begin{gathered} {\text{d}}\tilde{t}^{s} (i) = {\text{d}}\tilde{t}^{s} (i - 1) + \Delta t\partial {\text{d}}\tilde{t}^{s} (i - 1) + n_{{{\text{d}}t^{s} }} (i) \\ \partial {\text{d}}\tilde{t}^{s} (i) = \partial {\text{d}}\tilde{t}^{s} (i - 1) + n_{{\partial dt^{s} }} (i) \\ \tilde{\iota }_{r}^{s} (i) = \tilde{\iota }_{r}^{s} (i - 1) + n_{{\iota_{r}^{s} }} (i) \\ \tilde{\delta }_{r,j} (i) = \tilde{\delta }_{r,j} (i - 1) + n_{{\delta_{r,j} }} (i) \\ \tilde{d}_{r,j} (i) = \tilde{d}_{r,j} (i - 1) + n_{{d_{r,j} }} (i) \\ \tilde{\delta }_{,j}^{s} (i) = \tilde{\delta }_{,j}^{s} (i - 1) + n_{{\delta_{,j}^{s} }} (i) \\ \tilde{d}_{,j}^{s} (i) = \tilde{d}_{,j}^{s} (i - 1) + n_{{d_{,j}^{s} }} (i) \\ \end{gathered} \right. \\ \end{aligned}$$
(4)

where the estimability and interpretation of the parameters, along with the \({\mathcal{S}}{\text{ - basis}}\), are listed in Table 1. Set I and II consist of the measurement and dynamic models, respectively.

Table 1 Estimable parameters and \({\mathcal{S}}{\text{ - basis}}\) parameters of the single-system, multi-frequency, single-station provider model, in case of the constant-velocity setup for the satellite clocks
Full size table

The inclusion of the satellite clock velocity parameter \(\partial {\text{d}}\tilde{t}^{s} (i)\) as unknown in the dynamic model brought an extra rank-deficiency, which was removed by considering the receiver clock at the second epoch as part of the \({\mathcal{S}}{\text{ - basis}}\). This is the reason why the receiver clock, the satellite clocks and their velocities are biased by the receiver clock velocity \(\partial {\text{d}}t_{r} (2)\). As a consequence, two epochs of data are required to initialize the filter.

The stochastic model, as encapsulated in the variance–covariance (vc-) matrix of the phase and code measurements, is given as

$$Q_{{y_{r} y_{r} }} = {\text{D}}\left( {\left[ {\begin{array}{*{20}c} {\Delta \phi_{r} (i)} \\ {\Delta p_{r} (i)} \\ \end{array} } \right]} \right) = {\text{blkdiag}}(C_{\phi \phi } ,C_{pp} ) \otimes W_{r}^{ - 1} (i)$$
(5)

where \(y_{r} = \left[ {\Delta \phi_{r}^{{\text{T}}} (i),\,\,\Delta p_{r}^{{\text{T}}} (i)} \right]^{{\text{T}}}\) and \(\Delta \phi_{r} (i) = \left[ {\Delta \phi_{r,1}^{1} (i), \ldots ,\Delta \phi_{r,1}^{m} (i), \ldots \Delta \phi_{r,f}^{1} (i), \ldots \Delta \phi_{r,f}^{m} (i)} \right]^{{\text{T}}}\) is the \(fm - {\text{vector}}\) containing the provider’s phase measurements at epoch \(i\). Similarly, \(\Delta p_{r} (i)\) stands for the code measurements vector. The \(f \times f\) matrices \(C_{\phi \phi }\) and \(C_{pp}\) are, respectively, the covariance matrices of the phase and code observables at zenith. The \(m \times m\) matrix \(W_{r} (i) = {\text{diag}}(w_{r}^{1} (i), \ldots ,w_{r}^{m} (i))\) contains the weights for every receiver-satellite link at epoch \(i\). \(D( \cdot )\) denotes the dispersion operator and \(\otimes\) the Kronecker product. The notations \({\text{diag}}\) and \({\text{blkdiag}}\) represent a ‘diagonal’ and a ‘block-diagonal’ matrix, respectively.

In case of the dynamic model, the receiver and satellite biases are assumed constant in time, and thus their system noises are set to be identically zero. As stated previously, the temporal behavior of the satellite clocks and slant ionospheric delays is modeled by a constant-velocity and a constant-state process, respectively. Therefore, the resulting covariance matrix \(S\) of their associated system noises, linking the parameters at two successive epochs, read as (Wang et al. 2017):

$$S = {\text{D}}\left( {\left[ {\begin{array}{*{20}c} {n_{{dt^{s} }} } \\ {n_{{\partial dt^{s} }} } \\ {n_{{\iota_{r}^{s} }} } \\ \end{array} } \right]} \right) = {\text{blkdiag}}\left( {q_{{dt^{s} }}^{2} \left[ {\begin{array}{*{20}c} {\frac{\Delta t}{2}} & 0 \\ 0 & {\frac{1}{2\Delta t}} \\ \end{array} } \right],\,\,q_{{\iota_{r}^{s} }}^{2} \,\Delta t} \right) \otimes I_{m}$$
(6)

where \(q_{{dt^{s} }}^{2}\) and \(q_{{\iota_{r}^{s} }}^{2}\) denote the spectral density (in units of \({\text{m}}^{{2}} {\text{/s}}\)) of the clock and ionosphere velocity parameters, respectively. \(I_{m}\) denotes an \(m \times m\) unit matrix.

PPP-RTK user

Given that the correction generation time, say \(k\), differs from the user positioning time, say \(l\,(l > k)\), the user needs to time-predict the PPP-RTK corrections using the individual corrections \(d\hat{\tilde{t}}^{s} (k),\,\,\partial d\hat{\tilde{t}}^{s} (k),\,\,\hat{\tilde{\iota }}_{r}^{s} (k),\,\,\hat{\tilde{\delta }}_{,j}^{s} (k),\,\,\hat{\tilde{d}}_{,j}^{s} (k)\). Although the provided satellite code and phase biases are characterized by higher time stability than the other parameters and could be provided with a lower transmission rate, we assume here that all the PPP-RTK corrections are provided at the same epoch \(k\) for notational convenience. The time-prediction of the corrections at the user positioning time follows as:

$$\begin{aligned} {\text{d}}\hat{\tilde{t}}^{s} (l) & = {\text{d}}\hat{\tilde{t}}^{s} (k) + [l - k]\Delta t\partial d\hat{\tilde{t}}^{s} (k) \\ \hat{\tilde{\iota }}_{r}^{s} (l) & = \hat{\tilde{\iota }}_{r}^{s} (k) \\ \hat{\tilde{\delta }}_{,j}^{s} (l) & = \hat{\tilde{\delta }}_{,j}^{s} (k) \\ \hat{\tilde{d}}_{,j}^{s} (l) & = \hat{\tilde{d}}_{,j}^{s} (k) \\ \end{aligned}$$
(7)

where \([l - k]\,\,\Delta t\) is referred to hereafter as latency. Collecting the corrections at epoch \(k\) in a vector, \(\hat{c}_{k} = \left[ {d\hat{\tilde{t}}^{1} (k), \ldots d\hat{\tilde{t}}^{m} (k),\,\partial d\hat{\tilde{t}}^{1} (k), \ldots ,\partial d\hat{\tilde{t}}^{m} (k),\,\hat{\tilde{\iota }}_{r}^{1} (k), \ldots ,\hat{\tilde{\iota }}_{r}^{m} (k),\,\hat{\tilde{\delta }}_{,j}^{1} (k), \ldots ,\hat{\tilde{\delta }}_{,j}^{m} (k),\,\hat{\tilde{d}}_{,j}^{1} (k), \ldots ,\hat{\tilde{d}}_{,j}^{m} (k)} \right]^{{\text{T}}}\), and their corresponding variance matrix \(Q_{{c_{k} c_{k} }}\), the time-prediction of the corrections in matrix–vector notation reads as follows:

$$\hat{c}_{l} = \Phi_{l|k} \,\hat{c}_{k} ,\,\,\,\,Q_{{c_{l} c_{l} }} = \Phi_{l|k} \,Q_{{c_{k} c_{k} }} \,\Phi_{l|k}^{{\text{T}}} + S_{l}$$
(8)

where \(S_{l}\) is the system noise variance matrix after replacing \(\Delta t\) with \([l - k]\,\Delta t\) in (6), and \(\Phi_{l|k}\) is the state transition matrix:

$$\Phi_{l|k} = {\text{blkdiag}}\left( {\left[ {\begin{array}{*{20}c} 1 & {[l - k]\,\Delta t} \\ 0 & 1 \\ \end{array} } \right],\,1,\,I_{f} ,\,I_{f - 2} } \right) \otimes I_{m}$$
(9)

It is reasonably implied here that the provider’s dynamic model settings are given to the user either in real time or through an offline accessible database. The user is then able to obtain the applicable PPP-RTK corrections in their combined form \(\hat{c}_{u,l} = \left[ {\hat{c}_{\phi ,l}^{{\text{T}}} ,\,\hat{c}_{p,l}^{{\text{T}}} } \right]^{{\text{T}}} = \left[ {\hat{c}_{\phi ,1,l}^{{\text{T}}} , \ldots \hat{c}_{\phi ,f,l}^{{\text{T}}} ,\,\hat{c}_{p,1,l}^{{\text{T}}} , \ldots ,\hat{c}_{p,f,l}^{{\text{T}}} } \right]^{{\text{T}}}\) as follows:

$$\hat{c}_{u,l} = H\,\hat{c}_{l} ,\,\,\,\,Q_{{c_{l} c_{l} }}^{u} = H\,Q_{{c_{l} c_{l} }} \,H^{{\text{T}}}$$
(10)

with

$$H = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {e_{f} } & 0 & { + \mu } \\ \end{array} } & \Lambda & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {e_{f} } & 0 & { - \mu } \\ \end{array} } & 0 & {E_{f} } \\ \end{array} } \\ \end{array} } \right] \otimes I_{m}$$
(11)

where \(\Lambda\) is an \(f \times f\) diagonal matrix holding the frequency-specific wavelengths as its entries, \(\mu\) is an \(f - {\text{vector}}\) with the ionospheric coefficients as its entries, and \(E_{f}\) is an \(f \times f\) identity matrix with its first two columns removed. Note that, \(E_{f}\) is structured in this way because the satellite code biases are estimable only from the third frequency onward in the \({\mathcal{S}}{\text{ - basis}}\) choice given here (see Table 1).

Given the correction component (10), the user’s single-epoch, corrected phase and code observation equations are expressed as follows:

$$\begin{aligned} {\text{E}}(\Delta \phi_{u,j}^{s} (l) + \hat{c}_{\phi ,j,l}^{s} ) & = g_{u}^{{s^{{\text{T}}} }} \Delta x_{u} (l) + {\text{d}}\tilde{t}_{u} (l) - \mu_{j} \,\tilde{\iota }_{u}^{s} (l) + \lambda_{j} \,(\tilde{\delta }_{u,j} (l) + \tilde{a}_{u,j}^{s} (l)) \\ {\text{E}}(\Delta p_{u,j}^{s} (l) + \hat{c}_{p,j,l}^{s} ) & = g_{u}^{{s^{{\text{T}}} }} \Delta x_{u} (l) + {\text{d}}\tilde{t}_{u} (l) + \mu_{j} \,\tilde{\iota }_{u}^{s} (l) + \tilde{d}_{u,j} (l) \\ \end{aligned}$$
(12)

with the interpretation of the user’s estimable parameters shown in Table 2. In this study, we focus on the impact of time-predicted corrections on the user positioning performance. We confine our study to a single-epoch user setup as it is the ultimate goal of real-time applications and, at the same time, provides a lower bound for the precision of the corresponding user’s multi-epoch solutions. It is worth mentioning that the user ambiguities are of double-differenced form, and therefore integer-valued.

Table 2 Estimable parameters and \({\mathcal{S}}{\text{ - basis}}\) parameters of the single-system, multi-frequency user model, in case of single-station provider corrections
Full size table

Similar to the provider’s stochastic model, the vc-matrix of the user’s phase and code measurements is given as follows:

$$Q_{{y_{u} y_{u} }} = {\text{D}}\left( {\left[ {\begin{array}{*{20}c} {\Delta \phi_{u} (l)} \\ {\Delta p_{u} (l)} \\ \end{array} } \right]} \right) = \underbrace {{{\text{blkdiag}}(C_{\phi \phi } ,\,C_{pp} ) \otimes W_{u}^{ - 1} (l)}}_{{Q_{{y_{u} y_{u} }}^{0} }} + Q_{{c_{l} c_{l} }}^{u}$$
(13)

where \(\Delta \phi_{u} (l)\) and \(\Delta p_{u} (l)\) are the \(fm - {\text{vectors}}\) containing the user’s phase and code measurements at epoch \(l\), respectively. We remark here that the phase \(C_{\phi \phi }\) and code \(C_{pp}\) covariance matrices are not necessarily the same for the provider and the user but depend on the employed receivers. Note that, the user’s measurement vc-matrix (13) takes into account the uncertainty of the time-predicted PPP-RTK corrections. This is usually ignored in most PPP-RTK studies since the corrections are assumed to be sufficiently precise so that they can be treated as if they are deterministic. An additional reason is that the provider needs to transmit, apart from the correction estimates, their associated vc-matrix, the vast information of which makes it impossible to transmit due to the large bandwidth required and neglects the whole purpose of the state-space-representation (SSR).

Experimental results and analysis

In this section, we first introduce the experimental setup and processing strategy followed at both the provider and user components. We then analyze why one should conduct a quality judgment of the combined PPP-RTK corrections rather than the individual ones. In the following, we numerically demonstrate and analyze the user instantaneous ambiguity resolution and positioning performance.

Data selection and processing strategy

In this study, 1 Hz GPS L1/L2 and Galileo E1/E5a code and phase data were collected at the stations CUBS and UWA0 (Perth, Australia) on DOY 218 of 2018. The 8 km distance between the stations allows to reasonably assume that the ionospheric delays experienced at both receivers are almost identical. Both stations are equipped with Septentrio PolaRx5 receivers. The cutoff elevation mask for the data analysis in this work is set to be 10°, with 8 GPS and 6 Galileo satellites being tracked on average.

In our numerical analysis, the Multi-GNSS Experiment (MGEX; Montenbruck et al. 2017) GPS and Galileo satellite orbits calculated by the Centre for Orbit Determination in Europe (CODE) were utilized as known parameters for both the provider and the user. The ground-truth coordinates of the stations were a priori precisely known and were used as known parameters in the single-station correction generation, while in the user processing, they served only for the evaluation of the positioning errors. Moreover, the Saastamoinen model (Saastamoinen 1972) with the Ifadis tropospheric mapping function (Ifadis 1986) was used to obtain a priori tropospheric corrections. It has also been assumed that the residual troposphere has been lumped to the generated satellite clock offset and, due to the short distance between the employed stations, the differential tropospheric delays have been neglected, i.e., \(\tau_{u} \approx \tau_{r}\). The receiver and satellite phase center offsets and variations, tidal and ocean loading effects, phase windup, relativistic effects have been corrected with standard models (Kouba 2015).

To estimate the zenith referenced code and phase standard deviations (STDs), we applied the least-squares variance component estimation (LS-VCE) method (Teunissen and Amiri-Simkooei 2008) to the code and phase residuals computed for the baseline CUBS-UWA0 with fixed coordinates. Table 3 lists the estimated zenith-referenced STDs for both GPS and Galileo frequencies. The observation weights were computed based on the elevation-dependent exponential function (Euler and Goad 1991).

Table 3 Estimated zenith referenced standard deviations of the code (cm) and phase (mm) observables for GPS L1/L2 and Galileo E1/E5a for the baseline CUBS-UWA0
Full size table

In carrying out our analysis, we considered the station CUBS as the provider and computed the single-station PPP-RTK corrections under the multi-epoch full-rank model (4) based on a Kalman filter. To initialize the filter, we performed a standard least-squares estimation based on two epochs of data. For the clock and ionospheric system noise standard deviations, we used the following values (Wang et al. 2017; Khodabandeh et al. 2019): \(q_{{dt^{s} }}^{G} = 1\,{\text{mm /}}\sqrt {\text{s}}\), \(q_{{dt^{s} }}^{E} = 0.3\,{\text{mm /}}\sqrt {\text{s}}\) and \(q_{{\iota_{r}^{s} }} = 0.5\,{\text{mm /}}\sqrt {\text{s}}\). We empirically selected a system-specific clock system noise as it is known that Galileo, due to the use of very precise passive hydrogen maser clocks in the majority of the constellation, has a larger percentage of satellites with smaller clock noise compared to GPS (Carlin et al. 2021), which has also been shown through signal-in-space clock error analysis (Hauschild and Montenbruck 2021).

The recursively estimated corrections were then provided to the user station UWA0 with a latency of 10 and 15 s. Then, the user time-predicted the corrections based on (8) and (10) and performed single-epoch positioning on the basis of (12) using about 10,000 epochs of data. The user’s double-differenced float-estimated ambiguities were decorrelated and fixed to their integers with the integer least-squares (ILS) estimator, which is efficiently mechanized in the LAMBDA (Least-squares AMBiguity Decorrelation Adjustment) method (Teunissen 1995). In this case, we did not make use of any ambiguity validation method to evaluate the empirical success rate and also the impact of both the latency and the correction uncertainty on it.

Quality of individual and combined corrections

In the attempt to evaluate the quality of the estimated corrections, one is usually inclined to inspect the formal standard deviations of the individual PPP-RTK corrections, see Zhang et al. (2013). However, it has to be reminded that the high correlation existing between them dictates that such a quality judgment should only be based on the combined version of these corrections (Khodabandeh and Teunissen 2015).

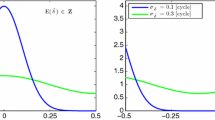
To highlight the role of the stated correlation, we show the time series of the formal standard deviation (STD) of both the individual and the combined PPP-RTK corrections during the first 3600 epochs for latencies up to 15 s in Fig. 1. Since the PPP-RTK corrections are effective at the between-satellite level for user positioning (Khodabandeh and Teunissen 2015), the aforementioned values are expressed for a representative satellite pair. One can observe from the figure that, even though the individual corrections are characterized by a code-precision level, especially at the beginning, the precision of the combined phase corrections is at the phase-noise level.

Fig. 1
figure 1

Formal standard deviations of the estimated between-satellite clocks (top-left), slant ionospheric delays (top-right), phase biases (bottom-left), and combined code/phase PPP-RTK corrections (bottom-right) with a latency of 0 (green), 10 (blue) and 15 (red) seconds. The results correspond to the E1 data of a Galileo satellite pair (PRNs 5 and 30)

Full size image

PPP-RTK user performance

This section presents and analyzes the user single-epoch ambiguity resolution and positioning performance for various cases regarding the error vc-matrix of the time-predicted corrections.

Let us first distinguish the assumptions that these cases are based on, for which a summarizing flowchart is given at Fig. 2. As a starting point, we take the ‘correct variance matrix’ case (case I) where the user takes the uncertainty of the single-station PPP-RTK corrections into account and performs a best linear unbiased estimation (BLUE). Although this is a stringent assumption because it means that the error vc-matrix of the corrections (\(Q_{{c_{k} c_{k} }}\)) is made available to the user, this result will serve later on in analyzing the performance loss due to the inconsideration of the correctional uncertainty.

Fig. 2
figure 2

Flowchart of the steps for obtaining the weighted least-squares user parameter solutions \(\hat{x}\) based on the strategy employed for the corrections’ error vc-matrix \(Q_{{c_{k} c_{k} }}\). \(y_{u}\) is the vector of corrected observations, \(Q_{{y_{u} y_{u} }}^{0}\) is the user’s data vc-matrix, \(Q_{{y_{u} y_{u} }}\) is the user’s corrected data vc-matrix, \(A\) is the user design matrix, \(A^{ + }\) is the least-squares inverse, \(Q_{{c_{l} c_{l} }}^{u}\) is the error vc-matrix of the time-predicted combined corrections, \(S_{k}\) and \(S_{l}\) are the system noise vc-matrices at epochs \(k\) and \(l\). The steps inside the green box are optionally performed by an analyzer (e.g., the provider)

Full size image

Then, we have the ‘incorrect variance matrix’ case (case II) which is the one used in practice, since the error vc-matrix of the corrections is often not provided to the users (Odijk et al. 2014). In this case, the user assumes that the corrections may be precise enough to be considered deterministic and, thus, weighs his corrected data based only on the uncertainty of his un-corrected data (\(Q_{{y_{u} y_{u} }}^{0}\)). As a consequence, his weighted least squares parameter solutions may lose their minimum-variance property, although he assumes that he performs BLUE-estimation. This will have an effect not only on the parameter solutions but also on their quality description. In fact, the variance matrices reported by the incorrectly assumed BLUE become incorrect and fail to provide the actual quality of the estimates. In such a case, we assume that an analyzer (e.g., the provider) exists who, given that the user’s data uncertainty and the provider’s correction uncertainty are known, can perform a variance propagation law to obtain the actual quality of the user’s positioning solutions.

As a first solution to mimic the information content within the fully populated error vc-matrix of the corrections, we consider the ‘sub-optimal variance matrix’ case (case III). In this case, the user attempts to approximate the stated error vc-matrix based only on the system-noise-variance part (\(H\,S_{l} \,H^{{\text{T}}}\)) of the error vc-matrix of the corrections. The realization of this approximation is based on the fact that the provider’s dynamic model settings have been made available to the user either in real time or through an external database the user has access to. Even though the user is still not in a position to obtain BLUE solutions, we investigate whether this approximation is sufficient enough so that the PPP-RTK user achieves close-to-optimal results. Also in this case, we consider an analyzer who, given the user’s data uncertainty is known, is able to apply the variance propagation law and obtain the actual precision description.

Finally, we have the ‘reconstructed variance matrix’ case (case IV), in which we propose a second solution to the aforementioned issue. Although the error vc-matrix of the time-predicted PPP-RTK corrections is not made available to the user, he attempts to fully reconstruct it based on a model-driven recursive engine he is equipped with. Given that the provider shares with the user information about the dynamic model settings, measurement precision, filter starting time and the approximate receiver location, the user is able to mimic the correctional error vc-matrix by recursively estimating it as if he would be the provider. Having such a tool available, which runs in parallel to the user’s single-epoch processing, we investigate whether he is able to achieve (almost) identical results as if the error vc-matrix of the corrections would be made available directly by the provider.

Ambiguity resolution results

As a measure to analyze the instantaneous user ambiguity resolution performance for the selected cases, we utilize the easy-to-compute integer-bootstrapped (IB) success rate, which lower bounds that of the optimal ILS estimator (Teunissen 1999). The formal IB success rate is computed as (Teunissen 1998) follows:

$$P(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{ILS} = a) = P(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z}_{ILS} = z) \ge P(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z}_{IB} = z) = \prod\limits_{i = 1}^{f(m - 1)} {\left( {2\Phi \left( {\frac{1}{{2\,\sigma_{{\hat{z}_{i|I} }} }}} \right) - 1} \right)}$$
(14)

with \(\Phi (x) = \int_{ - \,\infty }^{x} {\frac{1}{{\sqrt {2{\uppi }} }}\exp \left\{ { - \frac{1}{2}x^{2} } \right\}dx}\); \(P(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z}_{ILS} )\) and \(P(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z}_{IB} )\) are the ILS and IB success rates of the decorrelated ambiguities \(z\), respectively. \(\sigma_{{\hat{z}_{i|I} }}\) denotes the conditional standard deviations of the \(i\)th decorrelated ambiguities, with \(i = 1, \ldots ,f(m - 1)\) and \(I = 1, \ldots ,i - 1\), which are given as the square roots of the entries of the diagonal matrix \(D\) after and \(L^{{\text{T}}} DL\)-decomposition of the user’s decorrelated ambiguity vc-matrix.

Table 4 presents the user empirical and formal ambiguity success rates for all cases and for latencies of 0, 5 and 15 s. The formal values are computed by taking an average of the formal success rates of all the processing epochs, while the empirical success rate is given as the ratio of the number of processing epochs with correctly fixed ambiguities to the total number of the processing epochs. To validate whether the double-difference ambiguities are correctly fixed, we compared their ILS solution with the reference integer ambiguities computed from a geometry-fixed multi-epoch model.

Table 4 Instantaneous empirical and formal success rate (%) at station UWA0 for the four precision description cases (I, II, III, IV) as a function of the latency. The results refer to the GPS-only L1/L2, Galileo-only E1/E5a and GPS-plus-Galileo L1/L2 + E1/E5a solutions obtained with 1 Hz data collected on DOY 218 of 2018
Full size table

The results in Table 4 show that, when the corrections are provided at an instant, the user achieves a 100% success rate in all cases for both single- and multi-system solutions. However, when the user ignores the correction uncertainty for nonzero latencies, there is a drop in the empirical success rates that becomes more pronounced the longer the latency becomes. Reducing the number of used GPS satellites to obtain a coverage similar to that of Galileo showed that the ambiguity success rate further reduces from 77.5 to 70.9%, indicating the impact the number of satellites has on the ambiguity resolution performance. The dual-system integration pushes the success rate to 96.8% due to the increased number of used satellites, as observed by Khodabandeh (2021).

In addition, the results in the same table state that, upon employing the two proposed strategies for obtaining (part of) the error vc-matrix of the time-predicted corrections, the success rate increases dramatically, with the second method (case IV) bringing identical results to the case that the user is provided with the full error vc-matrix. This is an indicator that a user equipped with such a model-driven recursive engine is able to achieve optimal performance.

Positioning results

Table 5 lists the single-epoch empirical and formal standard deviations of user’s position components for both the ambiguity-float and -fixed cases, considering cases I-IV and delays up to 15 s. The formal values are obtained from taking the average of the single-epoch position vc-matrices for all processing epochs, while the empirical values are determined by comparing the estimated positions to the ground-truth coordinates. The ambiguity-fixed outcomes are computed based on the correctly fixed solutions.

Table 5 Instantaneous empirical and formal position standard deviations (mm) of station UWA0 for the four precision description cases (I, II, III, IV) as a function of the latency \(\Delta\), for both the ambiguity-float and -fixed cases. The results refer to the GPS-only L1/L2, Galileo-only E1/E5a and GPS-plus-Galileo L1/L2 + E1/E5a solutions obtained with 1 Hz data collected on DOY 218 of 2018. For each case, two values per coordinate components are given, which are the empirical (left) and formal (right) position standard deviations
Full size table

3

Starting from the GPS-only results in case I, it can be observed that the ambiguity-float empirical and formal values remain almost invariant for increasing latency. This is due to the lower noise level of the time-predicted corrections compared to the one of the code data for the investigated time delays (see Fig. 1). Also, the empirical and formal solutions are in overall in good agreement, validating the stochastic model used for the processing.

Compared to the ambiguity-float results with dm-level precision for zero latency, one can observe two orders of magnitude improvement after successful ambiguity resolution. However, the same improvement is not present for increased latency due to an increase in the ambiguity-fixed empirical and formal STDs. This is due to the fact that the phase data are affected by the uncertainty of the time-predicted PPP-RTK corrections, thereby restricting the range of improvement.

Despite the closeness between the fixed formal and empirical values for case I, in which the error vc-matrix of corrections is made available to the user, this agreement tends not to hold when the user assumes the corrections to be of nonrandom nature (case II) for nonzero latencies. In these cases, the larger the latency becomes, the difference between the two values increases. Therefore, although precise positioning can still be achieved with an incorrect measurement noise, it becomes clear that the estimation results are not accompanied by a realistic precision description. With an incorrectly specified stochastic model, the BLUE reported position standard deviations are incorrect and overoptimistic.

In case the user approximates the error vc-matrix of corrections with only their system-noise-variance part (case III), we observe only a slight improvement in terms of the difference between the formal and empirical values for the fixed results. This result suggests that, upon using the system-noise-variance part of the error vc-matrix of the corrections, one can achieve close-to-optimal ambiguity resolution performance (see Table 4), but the precision description of position components is still not realistic enough. However, when the user is equipped with the proposed model-driven recursive engine (case IV) in an attempt to reconstruct the full error vc-matrix of the corrections, it can be observed that he obtains identical positioning performance as the one observed in case I. Therefore, one can expect to obtain optimal positioning performance even when the provider does not provide the correction uncertainty, given that the user has all the necessary information to reconstruct it.

Similar conclusions can be drawn for the Galileo-only solutions. The GPS-plus-Galileo integrations deliver, in general, better positioning results compared to the single-system solutions, which is expected as the satellite geometry is strengthened with a larger number of used satellites.

To gain a better understanding of the impact that the inconsideration of the correction uncertainty has on the user positioning precision description for nonzero latencies, the horizontal positioning errors of user station UWA0 are visualized and analyzed. Shown in Fig. 3 are the scatter plots of 10,000 single-epoch horizontal component estimation errors based on GPS L1/L2 data for increased latency (looking from left to right) and the aforementioned cases (looking from top to bottom). Since the use of the model-driven recursive engine (case IV) delivered identical results to the optimal case, we do not present the scatter plots of the former for brevity.

Fig. 3
figure 3

GPS L1/L2 single-epoch user east-north position error scatterplots of station UWA0 using multi-epoch single-station PPP-RTK corrections with latencies \(\Delta\) of 0 (left column), 10 (middle column) and 15 (right column) seconds. From top to bottom, the first three figures refer to the ‘correct variance matrix’ case (case I) where the user considers the correctional uncertainty, thus producing the optimal minimum-variance results. The middle row figures refer to the ‘incorrect variance matrix’ case (case II) where the user ignores the correctional uncertainty but the analyzer is able to obtain the actual formal measures based on correct variance propagation. The last row figures refer to the ‘sub-optimal variance matrix’ case (case III) where the user considers only the system-noise-part of the correctional uncertainty but the analyzer is able to obtain the actual formal measures based on correct variance propagation. The gray, green and red dots represent the solutions with float, correctly fixed, and wrongly fixed ambiguities, respectively. The 95% empirical confidence ellipses (ECE) are shown in black, while the 95% formal confidence ellipses (FCE) are shown in blue (assumed FCE) and orange (actual FCE)

Full size image

The solutions shown in each panel are categorized into three types; ambiguity-float solutions as gray dots, correctly fixed solutions as green dots, and wrongly fixed solutions as red dots. The provided 95% confidence ellipses are derived from the empirical and formal vc-matrices of the position solutions. The empirical vc-matrix is determined by the positioning errors derived from comparing the estimated and the ground-truth positions. The formal vc-matrix is given from the mean of the single-epoch position vc-matrices of all considered epochs. Note that, in the panels of the second and third row, we provide the assumed confidence ellipse (blue), which is the one reported by the incorrectly assumed BLUE-estimation, and the actual confidence ellipse (orange), which is the one computed with correct variance propagation law from an analyzer.

In the unrealistic case that the user has access to the error vc-matrix of the corrections (top row), one can observe only a small number of incorrectly fixed solutions, with the achieved empirical success rate being above 99% even for the 15 s latency case (see Table 4). Despite this fact, it is shown that as the latency increases, the success rate slightly decreases while the ambiguity-fixed position error scatter gets amplified. This is actually expected since the user’s phase data are affected by the uncertainty of the time-predicted corrections, which increases as the latency gets higher. Most importantly, it can be observed that the formal confidence ellipse is in good agreement with the empirical one, indicating that one can expect a proper quality description when one considers the true uncertainty of one’s corrected data.

When the user ignores the correctional uncertainty (middle row), a 100% success rate is achieved in the zero-latency case. However, the success rate experiences a significant reduction for increasing latencies. In the case of a 15 s latency, there are many incorrectly fixed solutions (red dots), leading to a 77.5% success rate. Worse than that, the fixed precision description reported by the incorrectly assumed BLUE is misleading as it provides a quite overoptimistic confidence ellipse with respect to the empirical one. After applying a correct variance propagation, the analyzer is able to obtain the actual precision description of the correctly fixed solutions that nicely fits the empirical one.

As a solution to the above issue, we now investigate whether the error vc-matrix of the corrections can be sufficiently approximated by the system-noise-variance part of the former (bottom row), given that the provider’s dynamic model settings are known to the user. One notices the considerable improvement in terms of the ambiguity resolution performance, which is also shown in Table 4. However, the position precision description that comes along with these results, although more representative than the one in case of ignoring the correctional uncertainty, is still not good enough to describe the empirical positioning errors.

Although not shown in the figure for brevity, this is where the role of the model-driven recursive engine becomes prominent. Despite the various settings that need to be provided by the single-station provider and the engine the user needs to utilize in parallel, he is able to obtain optimal performance in terms of both ambiguity resolution and positioning, as if he would be provided with the error vc-matrix the provider computed.

The user’s corresponding solutions based on Galileo E1/E5a and dual-system data are shown in Figures 4 and 5, respectively. Similar conclusions can be drawn as in the GPS-only case. The Galileo-only solutions show a smaller fixed position error scatter compared to GPS, despite the increased latency. We consider these to be results of the highly time-stable clocks of the Galileo satellites, which allows the user to more accurately time-predict the clocks. It is interesting to note that incorporating only the system-noise-variance part of the error vc-matrix of the corrections, rather than the full part, leads to almost-optimal results even for 15 s latency.

Fig. 4
figure 4

Galileo E1/E5a single-epoch user east-north position error scatterplots of station UWA0 using multi-epoch single-station PPP-RTK corrections (see Fig. 3)

Full size image
Fig. 5
figure 5

GPS L1/L2 + Galileo E1/E5a single-epoch user east-north position error scatterplots of station UWA0 using multi-epoch single-station PPP-RTK corrections (see Fig. 3)

Full size image

Finally, it is obvious that, compared to the single-system solutions, the dual-system integration delivers better positioning results and shows smaller sensitivity to the inconsideration of the correctional uncertainty. However, the lack of the actual stochastic model of user’s measurements still leads to an over-optimistic quality description.

3.6 Relevance to multi-station PPP-RTK

Despite the fact that our numerical analysis is focused on the single-station PPP-RTK corrections, this does not affect the generality of our analysis as it can also be applied for when corrections from a multi-station (or network) setup are utilized. The advantage of the network approach over the single-station setup is that the area of coverage of the corrections is enlarged, which is especially important for the ionospheric component. The users may take recourse to the aforementioned strategies for the error variance matrix of the corrections.

One could, instead, make use of the fact that the network PPP-RTK corrections are formed as a weighted average of the multiple single-station corrections (Khodabandeh and Teunissen 2015), thereby requiring less information from the provider to reconstruct the error vc-matrix of the corrections. This, however, implies that the employed receivers collect measurements of the same precision level, which might not hold true in case of receivers of different types.

Conclusions

In this contribution, we studied and presented the impact that the single-station time-predicted corrections have on the PPP-RTK user ambiguity resolution and positioning performance when the error variance matrix of the corrections is neglected. In a single-epoch user setup, we numerically demonstrated whether and to what extent the user’s parameter solutions differ from their minimum-variance counterpart. Next to the user positioning estimation results, our focus was also placed on their precision description.

It was first shown how a subset of the single-receiver estimable parameters, provided as PPP-RTK corrections to the user with a certain time delay, is translated into the combined code- and phase- corrections that enable single-receiver user ambiguity resolution. The pitfall of analyzing the quality of individual corrections was addressed, for which we demonstrated that such an analysis is far from sufficient as it is the high correlation between the corrections that needs to be taken into account so that a proper quality judgment is done.

Further, the instantaneous PPP-RTK user performance was assessed with real GPS and Galileo dual-frequency 1 s data collected at two stations in Australia. It was shown that the user ambiguity success rate exceeds 99% even for a latency of 15 s when the uncertainty of the corrections is properly taken into account. When the corrections were assumed to be nonrandom, the success rate experienced a reduction for nonzero latencies, that was more pronounced the longer the latency became.

In both the ambiguity-float and -fixed cases, the empirical and formal positioning results showed a good agreement, thus validating the stochastic model used for the processing. Single-receiver ambiguity resolution resulted in two orders of magnitude precision improvement compared to the dm-level float solutions. This was shown not to hold for increased latency due to the fact that the phase data were affected by the uncertainty of the time-predicted corrections. It was then demonstrated that the inconsideration of the correctional uncertainty led to a discrepancy between the formal and empirical results that was enlarged the longer the time delay. As a result, one cannot expect to obtain a realistic precision description in the positioning domain when the uncertainty of the corrections is not considered. Next to the user-estimated quality information, our illustrations included the actual precision description in the user positioning domain, as estimated with a correct variance propagation from an external analyzer (e.g., the provider), who is aware of the uncertainties of the corrections and of the user’s data. Our findings revealed that the actual formal precision matched well with the empirical one, indicating the extent to which the user-assumed quality information differs from the user-actual one.

Finally, to circumvent these limitations, we developed and presented two alternatives to the fully populated error variance matrix of the PPP-RTK corrections that can be structured from the user via a limited amount of information from the provider. With the first strategy considering the system noise variance matrix as an approximation to the error variance matrix of the time-predicted corrections, it was numerically shown that the user can achieve close-to-optimal ambiguity resolution performance, with the success rate exceeding 95%, in both single- and dual-system models for latencies up to 15 s. However, the positioning precision description proved to be not sufficient enough to realistically describe the empirical position errors.

Our second alternative encompasses using a model-driven recursive engine that can recursively estimate, at the user side, the error variance matrix of the provider’s corrections using information shared by the provider. In this case, we showed that the user is able to obtain optimal performance for both ambiguity resolution and positioning, even for high latencies, as if the user would be provided with the original error variance matrix estimated by the provider. With the above real data results, we believe that the proposed strategies enable a wide variety of applications that can make use of corrections with high latency and, at the same time, meet high accuracy and reliability requirements.