Introduction

The development of BDS-3, Galileo, QZSS, and modernization of GPS and GLONASS, more satellites and frequencies are becoming available that benefit global navigation satellite system (GNSS) applications, such as precise point positioning (PPP) and real-time kinematic (RTK) positioning (Yang et al. 2018; Su and Jin 2019). Whereas satellite-based positioning, navigation and timing (PNT) solutions can be provided by a single GNSS constellation, better accuracy, integrity, and availability can be achieved by multi-constellation and multi-frequency combinations (Odolinski et al. 2014a; Nadarajah et al. 2018).

Intra- and inter-system biases (ISBs) are included in the single-differenced (SD)-based multi-GNSS RTK model and are generally considered to be constants, which restricts the performance of RTK positioning (Odolinski and Teunissen 2017). Intra-system biases include differential code biases (DCBs) and differential phase biases (DPBs), which are the offsets between the hardware delays experienced by multi-frequencies in a single GNSS constellation (Coster et al. 2013; Choi et al. 2019; Elghazouly et al. 2019). DCBs and DPBs cannot be ignored in RTK positioning, and their lumped effects are also considered as a major source of error in the determination of vertical total electron content (VTEC) (Håkansson et al. 2017; Li et al. 2018, 2019). ISBs are the offsets between the receiver-dependent hardware delays but are only experienced between different constellations (Odijk and Teunissen 2012; Paziewski and Wielgosz 2014). To maximize the benefit of combined processing of data from different GNSS, the ISBs must be considered (Jiang et al. 2017; Gao et al. 2018).

The short-term temporal variability of DCBs, DPBs and ISBs is ignored in practice (Gao et al. 2017; Håkansson et al. 2017), which can make the performance of RTK positioning worse. Previous studies have been involved in analyzing the short-term temporal variations of receiver-dependent DCBs and DPBs, but they only focus on the impact of short-term variations on ionospheric TEC estimates (Zhang and Teunissen 2015; Zhang et al. 2017; Zha et al. 2019). Initial investigations of the characteristics of ISBs have been carried out while adopting the double-differenced (DD) model and focusing on overlapping frequencies (Dalla Torre and Caporali 2015; Gioia and Borio 2016; Gao et al. 2017). Mi et al. (2019a) proposed a method of ISBs estimation based on SD observations, which is applicable for the estimation of ISBs for non-overlapping frequencies. In addition, previous studies have generally assumed that ISBs are stable over a period of time, and on that basis, the influence of ISBs on ambiguity resolution has been studied (Paziewski et al. 2015; Odijk et al. 2017).

The primary goal of our research is to bring to light another possible cause that affects SD-based RTK positioning performance, that is, the variations of receiver DCBs, DPBs and ISBs over relatively short time intervals like a few hours to one entire day. In this contribution, we first formulate a model that allows DCBs, DPBs and ISBs to be estimated simultaneously. We then use the proposed method to characterize the short-term temporal variations of GNSS receiver DCBs, DPBs and ISBs based on different types of receivers separated by zero/short baselines and analyze the relationship between the variations and ambient temperature fluctuation. Finally, the RTK positioning performance based on BDS-3, Galileo, GPS and QZSS observations with modeling DCBs, DPBs and ISBs as a function of temperature is discussed.

Estimation and application of intra-system biases and ISBs

We assume that we have a baseline length of at most a few kilometers, for which the relative ionospheric and tropospheric delays can be considered to be absent (Odolinski et al. 2015; Mi et al. 2019b). However, even in this case, the SD code and phase observables are not full rank, with the rank defects between the columns of the receiver clock and the code/phase delays and those of the phase delays and the ambiguities (Odolinski et al. 2014b). In this case, the rank-deficient dual-GNSS RTK model can be formulated as

$$\begin{aligned} p_{12,j}^{{s_{A} }} (i) & = g_{2}^{{s_{A}^{T} }} (i) \cdot x_{12} (i) + dt_{12} (i) + d_{12,j}^{A} (i){ + }\varepsilon_{12,j}^{{s_{A} }} \\ \phi_{12,j}^{{s_{A} }} (i) & = g_{2}^{{s_{A}^{T} }} (i) \cdot x_{12} (i) + dt_{12} (i) + \delta_{12,j}^{A} (i) + \lambda_{j} z_{12,j}^{{s_{A} }} { + }e_{12,j}^{{s_{A} }} \\ p_{12,j}^{{s_{B} }} (i) & = g_{2}^{{s_{B}^{T} }} (i) \cdot x_{12} (i) + dt_{12} (i) + d_{12,j}^{B} (i){ + }\varepsilon_{12,j}^{{s_{B} }} \\ \phi_{12,j}^{{s_{B} }} (i) & = g_{2}^{{s_{B}^{T} }} (i) \cdot x_{12} (i) + dt_{12} (i) + \delta_{12,j}^{B} (i) + \lambda_{j} z_{12,j}^{{s_{B} }} { + }e_{12,j}^{{s_{B} }} \\ \end{aligned}$$
(1)

where 1 and 2 represent two receivers and \(( \cdot )_{12} = ( \cdot )_{2} - ( \cdot )_{1}\) is the notation for between-receiver SDs, \(p_{12,j}^{{s_{A} }} (i)\) and \(\phi_{12,j}^{{s_{A} }} (i)\) denote the vectors of the SD code and phase observables of the satellite \(s_{A}\) at frequency \(j\) for the constellation \(A\), respectively, and \(p_{12,j}^{{s_{B} }} (i)\) and \(\phi_{12,j}^{{s_{B} }} (i)\) are their counterparts for constellation \(B\) with the epoch i. The symbol \(x_{ 1 2} (i)\) denotes a column vector of geometric unknowns, and the corresponding coefficient \(g_{ 2}^{{s_{A}^{T} }} (i)\) or \(g_{ 2}^{{s_{B}^{T} }} (i)\) is the receiver-to-satellite unit vector. \(dt_{12} (i)\) is the receiver clock, \(\lambda_{j}\) is the wavelength corresponding to frequency \(j\), and \(z_{ 1 2,j}^{{s_{A} }}\) (\(z_{12,j}^{{s_{B} }}\)) is SD integer ambiguities. \(d_{12,j}^{A} (i)\)(\(d_{12,j}^{B} (i)\)) and \(\delta_{12,j}^{A} (i)\)(\(\delta_{12,j}^{B} (i)\)) are the receiver code and phase biases, respectively. Finally, \(\varepsilon\) and \(e\) are the SD random observation noise and unmodeled effects such as multipath for the code and phase observations, respectively.

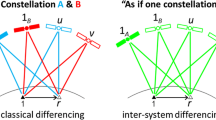
Due to the different ways to overcome the rank defects between the columns of the receiver clock and the code/phase delays in the case of multi-constellations, two different models can be evolved, namely ‘classical differencing’ and ‘inter-system differencing.’ In classical differencing, the rank defects between the columns of the receiver clock and the code/phase delays are solved by fixing the hardware delays on the first frequency of each system (Deng et al. 2014; Mi et al. 2019c). Once all rank deficiencies have been solved, the full-rank dual-GNSS RTK positioning model of classical differencing can be described as:

$$\begin{aligned} p_{12,j}^{{s_{*} }} (i) & = g_{2}^{{s_{*}^{T} }} (i) \cdot x_{12} (i) + d\tilde{t}_{12}^{*} (i) + \tilde{d}_{12,j}^{*} (i){ + }\varepsilon_{12,j}^{{s_{*} }} \\ \phi_{12,j}^{{s_{*} }} (i) & = g_{2}^{{s_{*}^{T} }} (i) \cdot x_{12} (i) + d\tilde{t}_{12}^{*} (i) + \tilde{\delta }_{12,1}^{*} (i) + \tilde{\delta }_{12,j}^{*} (i) + \lambda_{j} \tilde{z}_{12,j}^{{1_{*} s_{*} }} { + }e_{12,j}^{{s_{*} }} \\ \end{aligned}$$
(2)

The symbol \(*\) equals different constellations A or B, \(d\tilde{t}_{12}^{ *} (i) = dt_{12}^{ *} (i) + d_{12,1}^{ *} (i)\) is the receiver clock with code delays on \(j = 1\), and \(\tilde{z}_{12,j}^{{1_{*} s_{*} }} = z_{12,j}^{{s_{*} }} - z_{12,j}^{{1_{*} }}\) is double-differenced (DD) integer ambiguities obtained by eliminating the rank defect between the columns of the phase delays and the ambiguities. \(\tilde{d}_{ 1 2,j}^{*} (i)\) is the receiver DCBs, and it only exists for \(j \ge 2\). Note that, after the rank defects are eliminated, the receiver DPBs is traditional expressed as \(\bar{\delta }_{ 1 2 ,j}^{ *} (i) = \delta_{ 1 2 ,j}^{*} (i) - d_{12,1}^{*} (i) + \lambda_{j} z_{ 1 2 ,j}^{{1_{*} }}\) (Odolinski et al. 2015). However, in that case, \(d_{12,1}^{*} (i)\) exists in the DPBs of each frequency, while the correlation between the receiver clock and the DPBs brought by \(d_{12,1}^{*} (i)\) will introduce code observation noise into the DPBs and ultimately affect the accurate determination of the DPBs. With this in mind, the receiver DPB of the first frequency (\(\tilde{\delta }_{ 1 2 , 1}^{ *} (i)\)) is introduced into the phase observation equation of each frequency to construct the receiver DPBs (\(\tilde{\delta }_{ 1 2,j}^{ *} (i)\)) without \(d_{12,1}^{*} (i)\). Theoretically, the form of the receiver DPBs is the same as that of Odolinski et al. (2015), which can be seen through the re-parameterization \(\bar{\delta }_{ 1 2 ,j}^{ *} (i) = \tilde{\delta }_{ 1 2 , 1}^{*} (i) + \tilde{\delta }_{ 1 2 ,j}^{*} (i)\) when \(j \ge 2\). The interpretation of these bias parameters is given in Table 1.

Table 1 Various biases involved in multi-frequency and multi-constellation RTK positioning in equation (2)
Full size table

Alternatively, we can fix the hardware delays on the first frequency of only one system to eliminate the rank defects between the columns of the receiver clock and the code/phase delays, and this approach can be characterized as inter-system differencing. Once the rank deficiencies above have been solved, ISBs are introduced, and in this case, the full-rank, dual-GNSS and RTK model of inter-system differencing can be expressed as

$$\begin{aligned} p_{12,j}^{{s_{A} }} (i) & = g_{2}^{{s_{A}^{T} }} (i) \cdot x_{12} (i) + d\tilde{t}_{12}^{A} (i) + \tilde{d}_{12,j}^{A} (i){ + }\varepsilon_{12,j}^{{s_{A} }} \\ \phi_{12,j}^{{s_{A} }} (i) & = g_{2}^{{s_{A}^{T} }} (i) \cdot x_{12} (i) + d\tilde{t}_{12}^{A} (i) + \tilde{\delta }_{12, 1}^{A} (i) + \tilde{\delta }_{12,j}^{A} (i) + \lambda_{j} \tilde{z}_{12,j}^{{1_{A} s_{A} }} { + }e_{12,j}^{{s_{A} }} \\ p_{12,j}^{{s_{B} }} (i) & = g_{2}^{{s_{B}^{T} }} (i) \cdot x_{12} (i) + d\tilde{t}_{12}^{A} (i) + \tilde{d}_{12,j}^{AB} (i){ + }\varepsilon_{12,j}^{{s_{B} }} \\ \phi_{12,j}^{{s_{B} }} (i) & = g_{2}^{{s_{B}^{T} }} (i) \cdot x_{12} (i) + d\tilde{t}_{12}^{A} (i) + \tilde{\delta }_{12, 1}^{A} (i) + \tilde{\delta }_{12,j}^{AB} (i) + \lambda_{j} \tilde{z}_{12,j}^{{1_{B} s_{B} }} { + }e_{12,j}^{{s_{B} }} \\ \end{aligned}$$
(3)

where \(\tilde{d}_{12,j}^{AB} (i){ = }d_{ 1 2 ,j}^{B} (i) - d_{ 1 2 ,1}^{A} (i)\) and \(\tilde{\delta }_{12,j}^{AB} (i) = \delta_{ 1 2,j}^{B} (i) - \delta_{ 1 2,1}^{A} (i) + \lambda_{j}^{{}} z_{ 1 2,j}^{{1_{B} }} - \lambda_{1}^{{}} z_{ 1 2,1}^{{1_{A} }}\) are the estimable code and phase ISBs, and the interpretation of the other parameters is the same as in (2).

To more accurately calibrate these biases, the baseline and DD ambiguities are precisely determined using the entire observation time series and subtracted from \(p_{12,j}^{{s_{A} }} (i)\) and (\(p_{ 1 2,j}^{{s_{B} }} (i)\)) and \(\phi_{ 1 2,j}^{{s_{A} }} (i)\) and (\(\phi_{ 1 2,j}^{{s_{B} }} (i)\)), which is also referred to as the geometry-fixed model. After that, the joint estimation RTK model of the intra-system biases and ISBs can be expressed as

$$\begin{aligned} \tilde{p}_{12,j}^{{s_{A} }} (i) & = d\tilde{t}_{12}^{A} (i) + \tilde{d}_{12,j}^{A} (i){ + }\varepsilon_{12,j}^{{s_{A} }} \\ \tilde{\phi }_{12,j}^{{s_{A} }} (i) & = d\tilde{t}_{12}^{A} (i) + \tilde{\delta }_{12, 1}^{A} (i) + \tilde{\delta }_{12,j}^{A} (i){ + }e_{12,j}^{{s_{A} }} \\ \tilde{p}_{12,j}^{{s_{B} }} (i) & = d\tilde{t}_{12}^{A} (i) + \tilde{d}_{12,j}^{A} (i) + \tilde{d}_{12,j}^{AB} (i){ + }\varepsilon_{12,j}^{{s_{B} }} \\ \tilde{\phi }_{12,j}^{{s_{B} }} (i) & = d\tilde{t}_{12}^{A} (i) + \tilde{\delta }_{12, 1}^{A} (i){ + }\tilde{\delta }_{12,j}^{AB} (i){ + }e_{12,j}^{{s_{B} }} \\ \end{aligned}$$
(4)

where \(\tilde{p}_{12,j}^{{s_{A} }} (i) = p_{12,j}^{{s_{A} }} (i) - g_{2}^{{s_{A}^{T} }} (i) \cdot x_{12}\) and \(\tilde{\phi }_{12,j}^{{s_{A} }} (i) = \phi_{12,j}^{{s_{A} }} (i) - g_{2}^{{s_{A}^{T} }} (i) \cdot x_{12} - \lambda_{j} \tilde{z}_{12,j}^{{1_{A} s_{A} }}\) for the constellation \(A\), and their counterparts \(\tilde{p}_{12,j}^{{s_{B} }} (i) = p_{12,j}^{{s_{B} }} (i) - g_{2}^{{s_{B}^{T} }} (i) \cdot x_{12}\) and \(\tilde{\phi }_{12,j}^{{s_{B} }} (i) = \phi_{12,j}^{{s_{B} }} (i) - g_{2}^{{s_{B}^{T} }} (i) \cdot x_{12} - \lambda_{j} \tilde{z}_{12,j}^{{1_{B} s_{B} }}\) for the constellation \(B\). Note that satellite orbits and clocks have already been corrected for through the broadcast ephemerides. We conclude this step by solving for these biases using least-square estimation.

Experiment setup

We deployed four multi-GNSS receivers, including two Trimble Alloy and two Septentrio PolaRx5S, at the roof of an office building of the Institute of Geodesy and Geophysics in Wuhan (114.4° E, 33.6° N in WGS84). The data were collected over ten consecutive days (September 24 to October 8, 2019) from GPS, BDS-3, Galileo and QZSS at a 30-s interval. The information of the dual-frequency carrier phase and code observations used in this study is listed in Table 2. These receivers are classified according to whether or not they have been connected to a common antenna. The two receivers IGG01/03, sharing one antenna (South GR3-G3), were installed in the rooftop plant room of building 707 with an air-conditioning. About two meters away from this antenna, another antenna of the same type was connected via a splitter to receivers IGG02/04 on the same building. It is worth mentioning that the air-conditioning system operates in 4 days (DOYs 269–270 and 276–277) between 12:00 and 22:00 UTC. Moreover, we recorded the ambient environmental temperatures to which these four receivers were exposed with a time resolution of 1 min.

Table 2 Overview of dual-frequency GNSS observation codes in this study
Full size table

In the DCBs, DPBs and ISBs short-term temporal variations analysis, we will refer to three independent receiver pairs that form two short baselines and a zero baseline, which are briefly summarized in Table 3. For data analysis, we make use of the detection, identification and adaptation (DIA) procedure to eliminate outliers (Teunissen 2018), and the LAMBDA method is used for integer ambiguity resolution (Teunissen 1995).

Table 3 A general overview of the characteristics of three experimental receiver pairs. Observation period is DOY 267–280, 2019
Full size table

Consider that the datum system should always have a certain number of visible satellites to assure sufficient internal redundancy for the estimable ISBs, and thus, BDS-3 is chosen as the reference because it had the largest number of visible satellites during the observation period. Therefore, the next task will be to analyze intra-system biases within BDS-3, and ISBs between BDS-3 and other GNSSs (see equation 4).

In the estimation of DCBs, DPBs and ISBs, the baseline is precisely determined using the entire observation time series. On this basis, Kalman filtering without switching the reference satellites is used to estimate DD ambiguities to solve the possible jump of DPBs and phase ISBs caused by switching the reference satellites (Zhang et al. 2016). After the baseline and DD ambiguities are removed from the observations, least squares is used to estimate DCBs, DPBs and ISBs on an epoch-by-epoch basis. The estimation and modeling of biases are based on the data from DOYs 276–277, 2019.

Characterization of DCBs and DPBs estimates

Figures 1, 2 and 3 depict the variation of the epoch-by-epoch estimated BDS-3 DCBs and DPBs with the intraday temperature values for the baselines IGG01–IGG02, IGG01–IGG03 and IGG03–IGG04 on DOY 276 and 277 in 2019. The figures represent a baseline combination of two Trimble receivers, one Trimble and one Septentrio receiver, and two Septentrio receivers, respectively. At least two conclusions can be drawn from these figures. First, the variability of DCBs/DPBs (blue lines) does not fall within their noise level (generally below 3 ns for DCBs and 0.03 ns for DPBs). This time variability can thus be considered to be significant. In other words, these DCBs and DPBs variations should be considered in both RTK positioning and determination of VTEC. Second, the correlation between the time series of DCBs and DPBs estimates and that of temperatures (red lines) is evident, thereby suggesting that the variability in DCBs and DPBs estimates is correlated with the changes of ambient temperature. Also, the DCBs and DPBs on different frequencies respond differently to temperature (Zhang et al. 2020).

Fig. 1
figure 1

Two-day time series for short baseline IGG01–IGG02 with two Trimble receivers. The red lines denote intraday temperature values. BDS-3 DCBs (top) and DPBs (bottom) estimates are depicted by blue lines. The relationship shown in the top refers to the negative value of DCBs (-DCB)

Full size image
Fig. 2
figure 2

Two-day time series for zero baseline IGG01–IGG03 with Trimble and Septentrio. The red lines denote intraday temperature values. BDS-3 DCBs (top) and DPBs (bottom) estimates are depicted by blue lines. The relationship shown in the top refers to the negative value of DCBs (− DCB)

Full size image
Fig. 3
figure 3

Two-day time series for short baseline IGG03–IGG04 with two Septentrio receivers. The red lines denote intraday temperature values. BDS-3 DCBs (top) and DPBs (bottom) estimates are depicted by blue lines. The relationship shown in the top refers to the negative value of DCBs (− DCB)

Full size image

To illustrate this relationship between biases and temperature, Fig. 4 shows the close-to-linear dependence of the BDS-3 DCBs and DPBs estimates of the three baselines taken from Figs. 1, 2 and 3 on the corresponding temperatures. These estimates and temperatures correspond to the period when the receivers are operating in a controlled temperature environment, and we measure the linear dependence between DCBs/DPBs and temperature in terms of the Pearson correlation coefficients (PCCs). Table 4 shows the PCCs and the STDs of the mean PCCs, from which we can see that most of the PCCs between those estimates and temperatures are higher than 0.5, with very small STDs, which shows that this relationship is significant. Considering this significant sensitivity of the receiver DCBs and DPBs to the temperature effect, it makes sense to establish a functional relationship between DCBs, DPBs and ambient temperatures rather than assuming them to be time invariant.

Fig. 4
figure 4

Scatter plots display DCBs (left) and DPBs (right) estimates versus ambient temperatures depicted in Fig. 1 (top), Fig. 2 (middle) and Fig. 3 (bottom); superimposed on each scatter plot is the least-squares regression line in red

Full size image
Table 4 PCCs between DCBs and temperature, and those between DPBs and temperature, as well as the STDs of the mean PCCs
Full size table

Characterization of ISBs estimates

Figures 5, 6 and 7 depict the code and phase ISBs of BDS-3-GPS B1C-L1, BDS-3-Galileo B1C-E1 and BDS-3-QZSS B1C-L1 for the baselines IGG01–IGG02, IGG01–IGG03 and IGG03–IGG04 for DOY 276 and 277 of 2019. The figures represent again a baseline combination of two Trimble receivers, one Trimble and one Septentrio receiver, and two Septentrio receivers, respectively. Note that the ISBs here are all based on overlapping frequencies (Table 2). Different from the time-variant DCBs and DPBs, although the variability seems to be significant, the code and phase ISBs appear to be stable (see the corresponding small STDs of the mean PCC) and can thus be assumed not to change over time in the short term. In addition, the temperature has no significant effect on such ISBs, where the PCCs between the two variables are significantly small (generally below 0.1). Taken together, we find that, for overlapping frequencies considered, both code and phase ISBs are stable and independent of temperature. Based on the previous analysis of the relationship between the intra-system biases and temperature (Zhang et al. 2020), we conjecture that the stability of the overlapping frequencies ISBs is due to the fact that the hardware delays of the same frequencies in different systems have the same responses to temperature. Moreover, the ISBs are a linear combination of these delays (see equation 3). Therefore, ISBs for baselines consisting of identical receiver types can be considered as absent, while ISBs formed by different receiver types can be corrected through pre-calibration.

Fig. 5
figure 5

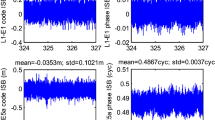
Two-day time series of ISBs estimates from the short baseline IGG01–IGG02 (with two Trimble receivers), including ISBs estimates of BDS-3-Galileo B1C-E1 (top), of BDS-3-QZSS B1C-L1 (middle) and of BDS-3-GPS L1 (bottom). The bottom left panel is denoted with red color because it indicates that ISBs exist in baselines composed of the same type of receiver, which we think is due to the inconsistent firmware versions (Version 5.42 for IGG01 and Version 5.37 for IGG02) of the two Trimble Alloy receivers

Full size image
Fig. 6
figure 6

Two-day time series of ISBs estimates from the zero baseline IGG01–IGG03 (with Trimble and Septentrio receivers), including ISBs estimates of BDS-3-Galileo B1C-E1 (top), of BDS-3-QZSS B1C-L1 (middle) and of BDS-3-GPS L1 (bottom)

Full size image
Fig. 7
figure 7

Two-day time series of ISBs estimates from the short baseline IGG03–IGG04 (with two Septentrio receivers), including ISBs estimates of BDS-3-Galileo B1C-E1 (top), of BDS-3-QZSS B1C-L1 (middle) and of BDS-3-GPS L1 (bottom)

Full size image

The rank defects between the columns in the design matrix corresponding to receiver clock and code/phase delays are solved by fixing the code delay on \(j = 1\) of the reference constellation. In this way, code and phase ISBs on non-overlapping frequencies become estimable, which is detailed in equation 3 of Mi et al. (2019b). We base our analysis of the non-overlapping frequencies ISBs on BDS-3-Galileo, BDS-3-GPS and BDS-3-QZSS. In the following, for the sake of brevity, we report only the results related to BDS-3-Galileo ISBs and DOY 276 and 277 of 2019, which are representative of all the results that we have obtained.

Figures 8, 9 and 10 depict the epoch-by-epoch estimated BDS-3-Galileo B1C-E5a ISBs and the intraday temperature values for three baselines on DOY 276 and 277 in 2019. Different from ISBs with overlapping frequencies, the figures show that the variability of the non-overlapping frequencies ISBs is significantly large. We believe that this situation is because the hardware delays of the non-overlapping frequencies of different systems are inconsistent in response to environmental changes, as are the cases with DCBs and DPBs, which is detailed in Zhang et al. (2020). In addition, the change in ISBs is consistent with that in temperature, which forces us to consider the possible relationship between ISBs and temperature just as that between DCBs, DPBs and temperature.

Fig. 8
figure 8

Two-day time series of BDS-3-Galileo B1C-E5a code (upper) and phase (bottom) ISBs estimates (blue lines) from the short baseline IGG01–IGG02 with two Trimble receivers. The red lines denote intraday temperature values, and the relationship shown in the top is between the negative value of code ISBs (-Code ISBs) and the temperature

Full size image
Fig. 9
figure 9

Two-day time series of BDS-3-Galileo B1C-E5a code (upper) and phase (bottom) ISBs estimates (blue lines) from the zero baseline IGG01–IGG03 with Trimble and Septentrio receivers. The red lines denote intraday temperature values, and the relationship shown in the top is between the negative value of code ISBs (− Code ISBs) and the temperature

Full size image
Fig. 10
figure 10

Two-day time series of BDS-3-Galileo B1C-E5a code (upper) and phase (bottom) ISBs estimates (blue lines) from the short baseline IGG03–IGG04 with two Septentrio receivers. The red lines denote intraday temperature values, and the relationship shown in the top is between the negative value of code ISBs (− Code ISBs) and the temperature

Full size image

In order to verify our conjecture about the relation between non-overlapping frequencies ISBs and temperature, the PCCs between them have been analyzed. Figure 11 shows the close-to-linear dependence of the BDS-3-Galileo B1C-E5a estimates of three baselines taken from Figs. 8, 9 and 10 on the corresponding temperature. Table 5 depicts the corresponding PCC information, from which we can see that the ISBs on non-overlapping frequencies are responsive to the change of temperature. Therefore, in order to avoid the possible influence of significant sensitivity to temperature effect on the ISB, it appears reasonable to model the non-overlapping frequencies as a linear function of temperature.

Fig. 11
figure 11

Scatter plots code (left column) and phase ISBs (right column) estimates versus ambient temperatures depicted in Fig. 8 (top), Fig. 9 (middle) and Fig. 10 (bottom)

Full size image
Table 5 PCCs between code ISBs and temperature, and those between phase ISBs and temperature, as well as the STDs of the mean PCCs
Full size table

Impact of the variations of DCBs, DPBs and ISBs on RTK positioning

After pre-calibrating and modeling of the biases for the baselines at hand, and applying them to independent data, the RTK model of inter-system differencing can be expressed as:

$$\begin{aligned} \tilde{\tilde{p}}_{12,j}^{{s_{A} }} (i) = & g_{2}^{{s_{A}^{T} }} (i) \cdot x_{12} (i) + d\tilde{t}_{12}^{A} (i){ + }\varepsilon_{12,j}^{{s_{A} }} \\ \tilde{\tilde{\phi }}_{12,j}^{{s_{A} }} (i) = & g_{2}^{{s_{A}^{T} }} (i) \cdot x_{12} (i) + d\tilde{t}_{12}^{A} (i) + \tilde{\delta }_{12, 1}^{A} (i) + \tilde{\tilde{\delta }}_{12,j}^{A} + \lambda_{j} \tilde{z}_{12,j}^{{1_{A} s_{A} }} { + }e_{12,j}^{{s_{A} }} \\ \tilde{\tilde{p}}_{12,j}^{{s_{B} }} (i) = & g_{2}^{{s_{B}^{T} }} (i) \cdot x_{12} (i) + d\tilde{t}_{12}^{A} (i){ + }\varepsilon_{12,j}^{{s_{B} }} \\ \tilde{\tilde{\phi }}_{12,j}^{{s_{B} }} (i) = & g_{2}^{{s_{B}^{T} }} (i) \cdot x_{12} (i) + d\tilde{t}_{12}^{A} (i) + \tilde{\delta }_{12, 1}^{A} (i) + \tilde{\tilde{\delta }}_{12,j}^{AB} + \lambda_{j} \tilde{z}_{12,j}^{{1_{B} s_{B} }} { + }e_{12,j}^{{s_{B} }} \\ \end{aligned}$$
(5)

Note that \(\lambda_{j} z_{ 1 2,j}^{{1_{A} }} - \lambda_{ 1} z_{ 1 2, 1}^{{1_{A} }}\) is included in the DPBs (\(\tilde{\delta }_{ 1 2,j}^{A} (i)\)) and \(\lambda_{j}^{{}} z_{ 1 2,j}^{{1_{B} }} - \lambda_{1}^{{}} z_{ 1 2,1}^{{1_{A} }}\) is included in the phase ISBs (\(\tilde{\delta }_{12,j}^{AB} (i)\)), which makes it difficult to calibrate DPBs and phase ISBs. Considering the time-varying characteristics of DPBs and non-overlapping frequencies phase ISBs, both of them are divided into time-varying and time-invariant parts and are expressed as \(\tilde{\delta }_{12,j}^{A} (i) = \tilde{\tilde{\delta }}_{12,j}^{A} (i) + \tilde{\tilde{\delta }}_{12,j}^{A}\) and \(\tilde{\delta }_{12,j}^{AB} (i) = \tilde{\tilde{\delta }}_{12,j}^{AB} (i) + \tilde{\tilde{\delta }}_{12,j}^{AB}\), respectively. The time-varying parts of DPBs (\(\tilde{\tilde{\delta }}_{12,j}^{A} (i)\)) and phase ISBs (\(\tilde{\tilde{\delta }}_{12,j}^{AB} (i)\)) refer to fractional parts, which is also the basis for modeling the relationship of DPBs and phase ISBs with the temperature above. The meaning of the corrected observations is given in Table 6.

Table 6 Meaning of the corrected observations and the corrected biases for equation (5)
Full size table

As mentioned earlier, the whole purpose of calibrating the short-term variations of DCBs, DPBs and ISBs is to improve the performance of multi-GNSS ambiguity resolution, which is essential to high-precision RTK positioning performance. We base our analysis of the performance of RTK positioning on three different strategies, which are detailed in Table 7. In addition, no matter which strategy (Table 7), the Kalman filter with ambiguities kept as time constant is used and the baseline is solved epoch by epoch, and the final output is the baseline of the fixed solution.

Table 7 Three different RTK positioning strategies used the experimental analysis
Full size table

Five days in the observation period (DOY 273–275 and 278–279, 2019) from three baselines (IGG01–IGG02, IGG010–IGG03, and IGG03–IGG04, see detail in Table 2) were selected to analyze the effects of different DCBs, DPBs and ISBs processing strategies on RTK positioning, which are independent of biases estimation and modeling (DOY 276 and 277).

The results of ambiguity resolution in terms of empirical success rates for different cutoff elevation angles between 10° and 40° for BDS-3 + Galileo and BDS-3 + Galileo + GPS + QZSS are given in Figs. 12 and 13, respectively. The depicted success rates are based on the mean of all the results for the selected days. Note that the empirical ambiguity success rate is defined as the number of epochs with correctly resolved integer ambiguities divided by the total number of epochs. The reference ambiguities were estimated by a batch solution using a combined system with multiple frequencies and assuming the ambiguities time constant over the whole time span.

Fig. 12
figure 12

Empirical integer ambiguity success rates of BDS-3 + Galileo for baselines IGG01–IGG02 (top), IGG01–IGG03 (middle) and IGG03–IGG04 (bottom) with cutoff elevation angles of 10–40° (DOYs 273–275 and 278–279, 2019). The yellow line (S3) represents the case where temperature changes are taken into account

Full size image
Fig. 13
figure 13

Empirical integer ambiguity success rates of BDS-3 + Galileo + GPS + QZSS for baselines IGG01–IGG02 (top), IGG01–IGG03 (middle) and IGG03–IGG04 (bottom) with cutoff elevation angles of 10–40° (DOYs 273–275 and 278–279, 2019). The yellow line (S3) represents the case where temperature changes are taken into account

Full size image

We pay attention, first of all, to the three cases depicted in Fig. 12a–c, from which two conclusions can be drawn. First, by comparing three curves in each case, we further find that the empirical integer ambiguity success rate of inter-system differencing (both S2 and S3) is higher than classical differencing (S1) no matter whether or not the time-varying parts of DCBs, DPBs and ISBs are corrected. Second and most importantly, the RTK performance of inter-system differencing that excludes the time-varying parts of DCBs, DPBs and ISBs by taking into account temperature changes is significantly improved compared to the commonly used inter-system differencing. Take Fig. 12 as an example, from which we can see that the success rates remain at stable values close to 100% for cutoff angles up to 30° for each case. The same conclusions are verified in Fig. 13 and will not be repeated here.

In order to intuitively compare the RTK positioning performance of three different strategies, the result of baseline IGG01–IGG02 with the cutoff angle of 30° on DOY 278 of 2019 is to be reported.

Figures 14 and 15 show the positioning results based on correctly fixed solutions for BDS-3+ Galileo and BDS-3 + Galileo + GPS + QZSS of IGG01–IGG02 and for three different biases processing strategies on DOY 278 of 2019, where the horizontal position scatter and the vertical position time series are depicted. These results were obtained by comparing the estimated positions to precise benchmark coordinates obtained through long-term observations. Note that there is a ‘spike’ in the vertical at bottom row of Fig. 14 after 08:00. The reason is that there were fewer visible satellites during that period; therefore, the positioning results were poorer. This spike becomes less apparent in case of more satellites as in Fig. 15.

Fig. 14
figure 14

Horizontal (E = East and N = North) position scatter and vertical (U = Up) time series of BDS-3+ Galileo for short baseline IGG01–IGG02 based on S1, S2 and S3 (see detail in Table 7)

Full size image
Fig. 15
figure 15

Horizontal (E = East and N = North) position scatter and vertical (U = Up) time series of BDS-3+ Galileo + GPS + QZSS for short baseline IGG01–IGG02 based on S1, S2 and S3 (see detail in Table 7)

Full size image

From the comparison of three different models in the positioning results for both BDS-3 + Galileo (Fig. 14) and BDS-3 + Galileo + GPS + QZSS (Fig. 15), we can see that the success rate of the commonly used inter-system differencing (S2) is improved compared with the classical differencing (S1), which is due to the increase in the number of redundant observations. Notably, after correcting DCBs, DPBs and ISBs through modeling, the positioning performance of the inter-system differencing further improved significantly, which is due to the higher success rate for S3.

Table 8 provides STDs and improvements of the empirical correctly fixed positioning while using BDS-3 + Galileo and BDS-3 + Galileo + GPS + QZSS for short baseline IGG01–IGG02 for an elevation cutoff angle of 30°. From the results of both BDS-3 + Galileo and BDS-3 + Galileo + GPS + QZSS, we can see that the 3D positioning precision (STDs) of the commonly used inter-system differencing (S2) is improved by 10–20% compared with the classical differencing (S1). In addition, after correcting DCBs, DPBs and ISBs through modeling, the positioning performance of the inter-system differencing improved significantly, by more than 15% in three directions, and more than 25% compared with the classical differencing.

Table 8 Statistics of the positioning results of correctly fixed solutions for IGG01–IGG02 of  BDS-3+ Galileo and BDS-3 + Galileo + GPS + QZSS (bold) using three different strategies, demonstrating the improvement achieved with S3 and S2 compared with S1 (Table 7), and S3 compared with S2 (parenthesis). The corresponding success rates are depicted in Figs. 14 and 15
Full size table

Conclusions

We developed a method for the simultaneous estimation of DCBs, DPBs and ISBs using the S-system theory to construct the full-rank functional model to analyze parameter estimability. We addressed both the short-term variation characteristics of DCBs, DPBs and ISBs, and the impact of modeling these biases based on temperature on multi-constellation RTK positioning.

We applied the method detailed above to a number of sets of multi-GNSS and multi-frequency data to analyze the short-term variation characteristics of DCBs, DPBs and ISBs. According to the experimental results, we found that the estimation of DCBs, DPBs and ISBs could indeed have significant short-term variations, and we further identified the changes in ambient temperature in the environment of the receivers as the leading cause for this variability. Considering that these biases can vary far above the noise level, we suggest taking this important issue into account when using multi-constellation and multi-frequency GNSS data for positioning. To demonstrate the usefulness of our proposal, we modeled the temperature-sensitive DCBs, DPBs and ISBs using a few days of data. Subsequently, the modeled DCBs, DPBs and ISBs were applied to multi-GNSS RTK positioning on an epoch-by-epoch basis on consecutive days and based on independent data. As expected, applying the modeled DCBs, DPBs and ISBs to multi-system RTK resulted in a 10–20% improvement in the success rates and a 15–35% improvement in the 3D positioning accuracy, in comparison with the time-invariant estimation of those biases only. In addition, it is worth mentioning that the DCBs, DPBs and ISBs are dependent on the type and version of the receiver, which means that these biases should be modeled on a case-by-case basis in practice.

We have only analyzed the short-term variations of the DCBs, DPBs and ISBs at artificially controlled temperatures and their effects based on static data. In practice, the temperature fluctuations may be more complex, particularly for highly dynamic receivers. This means that studying the short-term variations of those biases and their impact on RTK will be an important consideration for future work, which is crucial for high-precision positioning in a range of environments.