Introduction

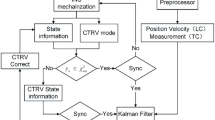
Traditional loosely coupled (LC) GNSS/INS integration uses GNSS position and velocity to correct the INS state and calibrate the inertial sensors, in which a Kalman filter (KF) is usually adopted to realize the data fusion between GNSS and INS. The standard KF requires both system and measurement noises to be white. For most integration algorithms, this assumption contributes to simplified implementation (Shin 2001). However, this will lead to a severe mismatch between the computed covariance matrix in the KF and the actual estimation error level. As a consequence, the integrated navigation accuracy is greatly restricted. Some researchers suggest that this discrepancy can be somehow relieved by tuning the process and measurement error covariance, i.e., Q and R matrix (Groves 2008). But this is just a compromise. In fact, the inertial error is colored noise (Nassar and El-Sheimy 2006), and the GNSS position error is time- and space-correlated (Niu et al. 2014). This means white noise is not always optimal to model the inertial error and GNSS position error. However, vehicular navigation requires optimal GNSS/INS integration to meet real-time and high-accuracy demands, which entails accurate modeling of both inertial and GNSS errors.

From the perspective of the KF time update, the navigation state and its covariance will undergo time-dependent error growth until GNSS update is available. The predicted navigation estimates can be improved if an accurate inertial error model is implemented, especially when GNSS outage happens for a relatively long time. Generally, the inertial error can be divided into systematic error and stochastic error. The former error can be depicted by discretizing the INS mechanization (Groves 2008) or by directly nonlinear approaches (Shin and El-Sheimy 2007), while the latter mainly refer to the residual biases after laboratory calibration, depicted by a series of stochastic models. Both errors are included in total error state to describe the INS error dynamics. Closely related to inertial sensors itself, the stochastic error modeling has raised much attention in current research. The first-order Gauss–Markov (GM) stochastic process is widely used using auto-correlation sequence (ACS) analysis (Brown and Hwang 1997; Shin 2001). However, it is unrealistic to acquire accurate ACS from finite experimental data. Moreover, the required stationarity assumption may not hold true for inertial sensor residual biases (El-Sheimy et al. 2004). To overcome the limitations of traditional GM model, it has been suggested to model the stochastic errors using auto-regression (AR) processes of high orders (Nassar and El-Sheimy 2006; Noureldin et al. 2009). Although recommended in post-processing for direct georeferencing, this method may encounter difficulties in real-time navigation due to the higher order. Moreover, the estimation accuracy will be easily deteriorated with some model parameters identified improperly by the overly data-dependent AR method (IEEE 2008). Another popular technique for inertial sensor error is the Allan variance (AV) analysis approach (El-Sheimy et al. 2008; Han and Wang 2011). Its validity is tested with both relative inertial measurement (Chen et al. 2015) and absolute INS-based navigation (Quinchia et al. 2013; Zhang et al. 2013, 2017). The newly developing generalized method of wavelet moments (GMWM) is also attempting to analyze and model the inertial stochastic noise better (Stebler et al. 2014; Radi et al. 2017). However, the above-mentioned AV-based methods are mainly focused on post-processing position errors, ignoring real-time navigation accuracy evaluation, especially for velocity and attitude. In addition, computation burden and numerical stability may also suffer from the AV-based method if five main identified stochastic errors, i.e., quantization noise (QN), white noise (WN), bias instability (BI), random walk (RW), and rate ramp (RR), are all included in the KF. It is still necessary to provide a practical guideline for colored inertial noise modeling in real-time navigation.

From the perspective of KF measurement update, the enhanced estimated state can be obtained with proper measurement error modeling, which favors INS in turn. Recently, the time/temporal correlation of GNSS positioning has been widely recognized. The colored noise should be appropriately addressed to remedy the standard KF for potential accuracy enhancement. Either the state-augmentation (Wang et al. 2012) or measurement time-differencing approach (Petovello et al. 2009) cannot tackle the problem effectively. In practice, it is impossible to accurately model the colored GNSS position errors (Chang 2014b). However, the AV analysis for 1 Hz GNSS position errors justifies the simplified white model in either stand-alone GNSS or differential GNSS mode (Niu et al. 2014). Therefore, accurate covariance parameters are essential for proper integration between GNSS and MEMS-INS. Adaptive Kalman filter (AKF) technique is usually used for systems with the unknown process and measurement noises, which estimates the noise covariances based on innovation sequences to adaptively adjust the Kalman gain (Mohamed and Schwarz 1999; Ding et al. 2007). However, implicit estimation coupling between state and noise parameters may result in negative-definite covariance matrix or even divergence. To guarantee the stability and reliability, an adaptively robust Kalman filter (ARKF) scheme is proposed by combining robust M estimation with the technique of adaptive factor (Yang et al. 2001; Yang and Gao 2006). The key to ARKF is to obtain the robust estimation solution of the total state, which is used to form adaptive factor based on the discrepancies between the robust solution and predicted state. Unfortunately, the robust solution of attitude and inertial biases cannot be obtained solely by GNSS, leading to the failure of the adaptive factor formation in GNSS/INS navigation. In addition, robust KF can be established based on innovation sequence to resist the adverse effects of outliers (Chang 2014a), but it is short of experimental validations. Although these works provide instructive references, it is still a challenge for accurate GNSS/MEMS-INS navigation with unknown noise parameters.

From the perspective of frequency domain, the high-frequency components in INS state are eliminated by the sum or integral operation of white system noise (Yan et al. 2012; Ban et al. 2013), resulting in low-frequency system noise component in KF measurement output, while the wideband white noise is directly superimposed upon the external measurement. Therefore, the measurement noise can be separated by the frequency division of measurement outputs. In fact, AV calculation is equivalent to a band-pass filter, suitable for such frequency division. It should also be noted that the traditional variance of white noise equals to its AV value. This paves the way for estimating measurement noise parameters. Motivated by the above studies, we propose an AV-based adaptive GNSS/MEMS-INS integrated navigation approach to improve stochastic model and noise parameter estimation for overall accuracy enhancements.

This study differs from previous research in the following aspects. First, we focus on analyzing the real-time overall navigation performance (i.e., position, velocity, and attitude) in a field test rather than only on post-processing position accuracy, aiming to provide a complete evaluation for different methods. Second, the Allan variance is not only used to identify and model the inertial sensor errors but also adaptively estimate the measurement noise parameters online. Precise model structures and parameters of both process and measurement noises are definitely instructive for fulfilling the potential accuracy of GNSS/INS navigation.

Methodology

The objective is to improve GNSS/MEMS-INS navigation accuracy. To accomplish this, the following aspects should be improved:

  1. 1.

    The error state covariance prediction accuracy,

  2. 2.

    The measurement noise parameter optimization,

since both subjects depend on the used models of both INS sensor error and GNSS error. Better inertial sensor error models are used with an AV-based method instead of the commonly recommended AR process. In addition, the quality of measurement update is controlled by eliminating GNSS outliers using the proposed innovation-based robust approach, especially for SPP results. Meanwhile, enhanced accuracy is further achieved by adaptively estimating the unknown measurement covariance based on AV calculation. The combined algorithm is also evaluated with a field test. In the following, each method will be discussed and analyzed.

AV analysis method

First proposed for the frequency stability of atomic clock, the time-domain AV analysis technique is increasingly used for potential stochastic process identification and modeling in various devices such as inertial sensors (El-Sheimy et al. 2008; Han and Wang 2011) and GNSS (Niu et al. 2014; Zhang et al. 2013).

The Allan variance definition can be found in IEEE (2008):

$$\sigma^{2} (\tau ) = \frac{1}{{2(N_{\text{C}} - 1)}} \cdot \sum\limits_{i = 1}^{{N_{\text{C}} - 1}} {\left(\bar{y}_{i + 1} - \bar{y}_{i} \right)^{2} }$$
(1)

where \(N_{\text{C}}\) is the number of clusters corresponding to cluster time τ; \(\bar{y}_{i}\) is the mean of ith cluster; \(\sigma^{2} (\tau )\) is the Allan variance. The typical log–log plot is shown in Fig. 1 with different noise types. As indicated in IEEE (2008), five types of typical stochastic processes can be identified by the slope in the specified time regions for inertial sensors. The related parameters are listed in Table 1.

Fig. 1
figure 1

Sample plot of Allan variance analysis results

Full size image
Table 1 Five types of stochastic errors with related parameters
Full size table

The AV calculation accuracy is dependent on the data length N and the cluster length k. The relative accuracy \(\varepsilon (k)\) of \(\sigma (\tau )\) corresponding to \(\tau = k\tau_{0}\) is given by

$$\varepsilon \left( k \right) = \frac{1}{{\sqrt {2\left( {\frac{N}{k} - 1} \right)} }}$$
(2)

where \(\varepsilon (k)\) means the percentage error in estimating \(\sigma (\tau )\) using clusters with \(\tau = k\tau_{0}\) from an N-point dataset. Equation (2) indicates that for fixed data length N, the estimation error is small when cluster number is large (i.e., short cluster time). In other words, the improvement in estimation accuracy for \(\sigma (\tau )\) requires increased data length N. Assuming the estimation error is required to be less than \(\varepsilon_{ \hbox{min} }\) at the maximum cluster time \(\tau_{\hbox{max} } = k_{\hbox{max} } \tau_{0}\), the corresponding data amount \(N_{\hbox{min} }\) is given by,

$$N_{\hbox{min} } \ge k_{\hbox{max} } \cdot \left( {1 + \frac{1}{{2\varepsilon_{\hbox{min} }^{2} }}} \right)$$
(3)

where \(N_{\hbox{min} }\) means the least points needed for required accuracy in calculating Allan variance.

Improving stochastic modeling for inertial sensor errors with AV analysis

For GNSS/INS integration, the error state equation is obtained by discretizing the INS mechanization (Groves 2008):

$$\left\{ {\begin{array}{*{20}l} {\delta \dot{r}^{n} = - \omega_{en}^{n} \times \delta r^{n} + \delta v^{n} } \hfill \\ {\delta \dot{v}^{n} = f^{n} \times \psi - \left( {2\omega_{ie}^{n} + \omega_{en}^{n} } \right) \times \delta v^{n} + \delta g^{n} + C_{b}^{n} \delta f^{b} } \hfill \\ {\dot{\psi } = - \,\left( {\omega_{ie}^{n} + \omega_{en}^{n} } \right) \times \psi - C_{b}^{n} \delta \omega_{ib}^{b} } \hfill \\ \end{array} } \right.$$
(4)

where \(\delta r\), \(\delta v\), and \(\psi\) represent errors in position, velocity, and attitude, \(C_{\text{A}}^{\text{B}}\) represents transformation matrix from A-frame to B-frame, \(\omega_{\text{AB}}^{\text{C}}\) is the angular rate of B-frame relative to A-frame resolved in C-frame, and \(\delta \omega_{ib}^{b} ,\delta f^{b}\) are the stochastic errors of gyros and accelerometers, which can be expressed as:

$$\left\{ {\begin{array}{*{20}l} {\delta \omega_{ib}^{b} = \delta \omega_{Q}^{b} + \delta \omega_{N}^{b} + \delta \omega_{\text{colored}}^{b} = \delta \omega_{Q}^{b} + \delta \omega_{N}^{b} + \delta \omega_{B}^{b} + \delta \omega_{K}^{b} + \delta \omega_{R}^{b} } \hfill \\ {\delta f^{b} = \delta f_{Q}^{b} + \delta f_{N}^{b} + \delta f_{\text{colored}}^{b} = \delta f_{Q}^{b} + \delta f_{N}^{b} + \delta f_{B}^{b} + \delta f_{K}^{b} + \delta f_{R}^{b} } \hfill \\ \end{array} } \right.$$
(5)

where \(\delta \omega_{Q/N/B/K/R}^{b}\) and \(\delta f_{Q/N/B/K/R}^{b}\) are the equivalent noise components in angular rate and specific acceleration according to AV analysis.

Among these noises, white noise can be directly regarded as system noise in KF, and quantization noise can be transformed into the form of white noise by state transformation. The other three noises should be augmented into the KF error state with the derived differential stochastic equations.

Transformation of quantization noise

The state transformation is defined as

$$\left\{ {\begin{array}{*{20}l} {\delta \hat{v}^{n} = \delta v^{n} - C_{b}^{n} \delta v_{Q}^{b} } \hfill \\ {\hat{\psi } = \psi - C_{b}^{n} \delta \alpha_{Q}^{b} } \hfill \\ \end{array} } \right.$$
(6)

where \(\delta v_{Q}^{b}\) and \(\delta \alpha_{Q}^{b}\) are the velocity quantization noise and angle quantization noise, i.e., \(\delta \omega_{Q}^{b} { = }\delta \dot{\alpha }_{Q}^{b} ,\delta f_{Q}^{b} { = }\delta \dot{v}_{Q}^{b}\). Substitute (6) into (4), then

$$\left\{ {\begin{array}{*{20}l} {\delta \dot{r}^{n} = - \,\omega_{en}^{n} \times \delta r^{n} + \delta \hat{v}^{n} + \underline{{C_{b}^{n} \delta v_{Q}^{b} }} } \hfill \\ \begin{aligned} \delta \dot{\hat{v}}^{n} & = f^{n} \times \hat{\psi } - \left( {2\omega_{ie}^{n} + \omega_{en}^{n} } \right) \times \delta \hat{v}^{n} + \delta g^{n} + C_{b}^{n} \delta f_{\text{colored}}^{b} \\ \quad & \quad + \,\,\left\{ {\underline{{C_{b}^{n} \delta f_{N}^{b} + \left( {f^{n} \times C_{b}^{n} } \right)\delta \alpha_{Q}^{b} - \left( {C_{b}^{n} \left( {\omega_{ib}^{b} \times } \right) + \left( {\omega_{ie}^{n} \times } \right)C_{b}^{n} } \right)\delta v_{Q}^{b} }} } \right\} \\ \end{aligned} \hfill \\ {\dot{\hat{\psi }} = - \,\left( {\omega_{ie}^{n} + \omega_{en}^{n} } \right) \times \hat{\psi } - C_{b}^{n} \delta \omega_{\text{colored}}^{b} - \left\{ {\underline{{C_{b}^{n} \left( {\omega_{ib}^{b} \times } \right)\delta \alpha_{Q}^{b} + C_{b}^{n} \delta \omega_{N}^{b} }} } \right\}} \hfill \\ \end{array} } \right.$$
(7)

The above-modified error state equation is driven by equivalent white noises.

Comparing (7) with (4), the equivalent white noises are enhanced as the underlined terms. It can be observed that the state transformation only affects the covariance propagation in KF. This manipulation for quantization noise actually magnifies the process noise covariance.

Stochastic modeling of colored noises

The stochastic differential equation for colored noise can be derived by Fourier inversion transform of the shaping filter’s transfer function, which can be obtained from the spectral factorization of PSD function. The AV-based stochastic model for colored noise is presented briefly here; see Han and Wang (2011) for detailed derivations.

  1. (a)

    Bias instabilityIts differential equation can be approximated as

    $$\dot{d}_{B} (t) + \beta d_{B} (t) = \beta Bu(t)$$
    (8)

    where \(u(t)\) is unit white noise, and β is the reciprocal of the correlation time. Coincidently, this is standard first-order Gaussian–Markov (GM) process with correlation time and variance as \({1 \mathord{\left/ {\vphantom {1 \beta }} \right. \kern-0pt} \beta }\) and \({{\beta B^{2} } \mathord{\left/ {\vphantom {{\beta B^{2} } 2}} \right. \kern-0pt} 2}\), in which β and B are determined using AV analysis.

  2. (b)

    Random walkIts stochastic differential equation is:

    $$\dot{d}_{K} (t) = Ku(t)$$
    (9)

    where K can be obtained from AV analysis.

  3. (c)

    Rate rampThe approximate differential equation is:

    $$\ddot{d}_{R} (t) + \sqrt 2 \omega_{0} \dot{d}_{R} (t) + \omega_{0}^{2} d_{R} (t) = Ru(t)$$
    (10)

    where \(\omega_{0}\) is the natural frequency parameter; both \(\omega_{0}\) and \(R\) can be determined using AV analysis. In fact, Eq. (10) is exactly a second-order GM process.

Discussions on augmentation of the KF with AV-based models

Instead of the fourth-order differential equation of all identified noise terms for each sensor as employed in Han and Wang (2011), it is suggested to model the primary stochastic errors here, considering the balance between real-time implementation and accuracy. On the one hand, higher state order brought by modeling minor error terms exacerbates computation burden and undermines real-time implementation. Moreover, the solution of high-order equation is prone to numerical instability by small disturbances in some model parameter, deteriorating the estimation accuracy, which is also encountered by higher-order AR models (Quinchia et al. 2013). On the other hand, the subsequent results show that only a little accuracy enhancement could be accomplished with all identified errors modeled, in contrast to the method with only major errors modeled.

Among the above-mentioned five error types, the rate ramp is more like a systematic error instead of stochastic noise, caused by gradual temperature changes. Quantization noise can be transformed to the form of white noise. As a result, the stochastic error modeling is focused on three noises, i.e., white noise, bias instability, and random walk. The AV analysis results of actual accelerometers or gyros can give us the possible combination of these noises, resulting in corresponding stochastic error model and augmented Kalman filter.

Improving GNSS stochastic modeling with AV calculation

GNSS positioning provides the position of antenna phase center \(\hat{r}_{\text{GNSS}}^{n}\). But INS outputs the position of IMU center \(\hat{r}_{\text{INS}}^{n}\). Both positions are different and form a lever-arm vector which needs compensation:

$$Z_{\varvec{r}} = \hat{r}_{\text{INS}}^{n} + C_{b}^{n} {\ell }^{b} - \hat{r}_{\text{GNSS}}^{n} \approx \delta r^{n} + \left( {C_{b}^{n} {\ell }^{b} \times } \right)\psi + e_{r}$$
(11)

where \({\ell }^{b}\) is the lever-arm vector referenced in body-frame from IMU center to GNSS center, and \(e_{r}\) is GNSS position error.

The velocity \(\hat{v}_{\text{GNSS}}^{n}\) can be obtained by GNSS Doppler observations. The KF velocity measurement is constructed:

$$\begin{aligned} Z_{r} & = \hat{v}_{\text{INS}}^{n} - \left( {\omega_{in}^{n} \times } \right)C_{b}^{n} \ell^{b} - C_{b}^{n} (\ell^{b} \times )\omega_{ib}^{b} - \hat{v}_{\text{GNSS}}^{n} \\ & \approx \delta v^{n} - \left( {\omega_{in}^{n} \times } \right)\left( {C_{b}^{n} \ell^{b} \times } \right)\psi - C_{b}^{n} \left( {\ell^{b} \times \omega_{ib}^{b} } \right) \times \psi - C_{b}^{n} \left( {\ell^{b} \times } \right)\delta \omega_{ib}^{b} + e_{v} \\ \end{aligned}$$
(12)

where the gyro bias \(\delta \omega_{ib}^{b}\) relates to inertial sensor error model, and \(e_{v}\) is GNSS velocity error. Generally, GNSS position and velocity errors in less than 1 Hz are modeled as white noise with covariance \(E\left[ {[e_{ri}^{T} ,e_{vi}^{T} ]^{T} \cdot [e_{rk}^{T} ,e_{vk}^{T} ]} \right] = R_{k} \delta_{ik}\) (Niu et al. 2014).

The standard KF algorithm uses constant measurement covariance matrix \(R_{k}\) by experiences. For example, in open areas, the accuracy of SPP position ranges from a few meters to several decameters, while it is within several centimeters for the carrier phase-based DGNSS position, i.e., real-time kinematic (RTK). However, this simplification cannot guarantee proper integration between GNSS and MEMS-INS. Moreover, accuracy degradation or outliers could occur due to signal blockage, attenuation, or interference in urban areas. To overcome these adverse effects, the following two-tier approach is proposed.

Robust Kalman filtering based on normalized measurement innovation

The KF innovation sequence \(\{ v_{k} = Z_{k} - H_{k} x_{k}^{ - } \}\) satisfies the following property:

$$\begin{aligned} E\left[ {v_{k} } \right] & = 0,\quad \forall k \\ E\left\{ {v_{k} v_{j}^{T} } \right\} & = C_{k} \delta_{kj} ,\quad C_{k} = {\rm H}_{k} P_{k}^{ - } {\rm H}_{k}^{T} + R_{k} \\ \end{aligned}$$
(13)

However, if there is some violation to assumed models, e.g., measurement outliers or contaminated noise, Eq. (13) will no longer hold. The hypothesis test can be conducted to detect such modeling errors. Assuming the null hypothesis as \(v_{k} \sim N(0,C_{k} )\), the test statistics \(\gamma_{k}\) is devised as the square of the Mahalanobis distance between measurement \(Z_{k}\) and its predicted mean \(H_{k} x_{k}^{ - }\),

$$\gamma_{k} = M_{k}^{2} = v_{k} C_{k}^{ - 1} v_{k}^{T}$$
(14)

where \(M_{k} = \sqrt {\left( {Z_{k} - {\rm H}_{k} x_{k}^{ - } } \right)^{T} C_{k}^{ - 1} \left( {Z_{k} - {\rm H}_{k} x_{k}^{ - } } \right)}\) is the Mahalanobis distance. If the innovation sequence \(v_{k}\) satisfies the null hypothesis, the test statistics should be of the \(\chi^{2}\) distribution with the degree of freedom as m, i.e., \(\gamma_{k} \sim \chi^{2} (m)\), in which m represents the measurement dimension. For a given small significance level, say 0.01%, the null hypothesis is rejected under the condition that the computed statistics \(\tilde{\gamma }_{k}\) with actual measurement \(\tilde{Z}_{k}\) is larger than the α-quantile \(\chi_{\alpha }^{2} (m)\). Considering the reliability and short-term accuracy of INS, the test rejection means some violations of the assumed model or outliers are detected with the misjudgment risk of α, which is written mathematically as:

$$\Pr \left\{ {\tilde{\gamma }_{k} > \chi_{\alpha }^{2} \left( m \right)} \right\} = \alpha$$
(15)

where \({ \Pr }( \cdot )\) represents the probability of a random event. Equation (15) indicates that the occurrence of \(\tilde{\gamma }_{k} > \chi_{\alpha }^{2} (m)\) is a small probability event. If this event happens, it is reasonable to conclude that the measurement is inconsistent with the assumption, i.e., an outlier is detected. In order to resist the adverse effects of outliers, a robust KF (RKF) with scaling factor \(\lambda_{k}\) is devised based on \(\tilde{\gamma }_{k}\) and \(\chi_{\alpha }^{2} (m)\). It runs the same way as the standard KF when no outlier is detected, i.e., \(\tilde{\gamma }_{k} < \chi_{\alpha }^{2} (m)\). Otherwise, the scaling factor \(\lambda_{k}\) is used to inflate the covariance matrix \(C_{k}\):

$$\bar{C}_{k} { = }\lambda_{k} C_{k}$$
(16)

So the following should be satisfied,

$$\tilde{\gamma }_{k} = v_{k} \bar{C}_{k}^{ - 1} v_{k}^{T} = \chi_{\alpha }^{2} (m)$$
(17)

where

$$\lambda_{k} \varvec{ = }\left\{ {\begin{array}{*{20}l} 1 \hfill & {\tilde{\gamma }_{k} \le \chi_{\alpha }^{2} (m)} \hfill \\ {\frac{{\tilde{\gamma }_{k} }}{{\chi_{\alpha }^{2} (m)}}} \hfill & {\tilde{\gamma }_{k} > \chi_{\alpha }^{2} (m)} \hfill \\ \end{array} } \right.$$
(18)

This analytical solution to \(\lambda_{k}\) avoids the iterations in Chang (2014a). This factor is used in measurement update to adjust the KF gain adaptively.

It should be noted that the centimeter-level accuracy of RTK position mainly relies on the quality of cycle slip detection and ambiguity resolution. By contrast, the pseudo-range measurements are very coarse in the level of several meters. Moreover, the multi-path effect will affect pseudo-range observations more than carrier phase observations. Consequently, observation outliers may cause a greater influence on SPP positions (Xie 2009). Therefore, the above robust KF is indispensable for SPP/MEMS-INS integration.

AV-based adaptive estimation for measurement covariance

For MEMS-INS, the inertial sensor noises are generated by an internal mechanism, meaning the parameters are relatively stable and should be determined in advance by inertial stochastic error modeling as accurately as possible. As for GNSS, position and velocity noises are dependent on external environments, such as satellite geometry, landscapes, buildings, tunnels, and trees, meaning the parameters are unpredictable to some extent. Consequently, the standard KF fails to perform best with inaccurate measurement noise covariance. To solve this mismatch, an AV-based adaptive estimation for measurement noise covariance is introduced to modify the standard KF, termed as AV-based adaptive KF (AV-based AKF).

From the perspective of frequency domain, the high-frequency components in INS state error \(w_{k}\) are eliminated by the integral operation of white system noise (Ban et al. 2013), resulting in low-frequency system noise in KF measurement \(Z_{k}\); while the white noise \(e_{k}\) is directly reflected in \(Z_{k}\). So the overall noise of \(Z_{k}\) can be denoted as \(\varepsilon_{{Z_{k} }} = w_{k} + e_{k}\). The parameter \(\hat{R}_{k} = E[e_{k} \cdot e_{k}^{T} ]\) can be separated by frequency division for KF measurements using AV calculation, considering its band-pass property and the equivalence between traditional variance and Allan variance (IEEE 2008).

For simplicity, it is assumed that no correlation exists between the measurement noise vector components. The Allan variance is calculated for each component with the shortest cluster time τ, corresponding to AV analysis of high frequency. The procedure can be written by transforming (1) into the recursive form:

$$\begin{aligned} \hat{R}_{k} & = \frac{1}{2(k - 1)} \cdot \sum\limits_{i = 2}^{k} {(y_{i} - y_{i - 1} )^{2} } \\ & = \frac{k - 2}{k - 1}\left[ {\frac{1}{2(k - 2)}\sum\limits_{i = 2}^{k - 1} {(y_{i} - y_{i - 1} )^{2} } } \right] + \frac{1}{2(k - 1)}(y_{k} - y_{k - 1} )^{2} \\ & = \left( {1 - \frac{1}{k - 1}} \right)\hat{R}_{k - 1} + \frac{1}{2(k - 1)}(y_{k} - y_{k - 1} )^{2} \\ \end{aligned}$$
(19)

where \(k = 2,3,4, \ldots\). The initialization of \(\hat{R}_{1}\) is set as typical accuracy value in specific GNSS positioning mode. Compared with the traditional AKF (Mohamed and Schwarz 1999), this algorithm avoids the difficulty in adjusting window length and reduces the risk of divergence due to the complete independence between noise parameter estimation and Kalman filtering.

Experimental work

To assess the performance of the proposed algorithm compared to the conventional counterparts, a field test was conducted in March 2015 in Wuhan urban areas. This section is divided into three parts to introduce the experimental work, i.e., equipment, test setup, and data processing details.

Equipment

Two types of IMUs are used in the experiment. The first is the Sensonor STIM300 MEMS-grade IMU, which is integrated with a prototype GNSS receiver based on NovAtel OEMV-3 and HX-BS581A (Harxon) multi-frequency GNSS antenna that utilizes the suggested approach. The second is the MP-POS830 position and orientation system developed by Wuhan MP Space–Time Technology Company. The data collected by POS830 are integrated using the GINS software developed by MP. The GINS provides a smoothed GNSS/INS tightly coupled navigation solutions, which is accurate enough to act as the reference to compare the performance and effectiveness of the proposed algorithm when applied to MEMS-based INS. The performance parameters of two systems are listed in Tables 2 and 3. The equipment is shown in Fig. 2, in which the test vehicle is used as the rover station with both systems mounted on the roof, and a base station is established nearby.

Table 2 STIM300 MEMS IMU specifications
Full size table
Table 3 MP-POS830 performance (1σ statistics in post-processing mode)
Full size table
Fig. 2
figure 2

Data acquisition equipment of rover (up) and base (bottom) in field test

Full size image

Test setup

Several field tests were carried out with the above configuration. The longest test trajectory around Wuhan City is chosen for analysis lasting about 1 h, as shown in Fig. 3. The number of observable GNSS satellites and the corresponding position dilution of precision (PDOP) are shown in Fig. 4. The statistics indicate that the average number of available satellites is 8 (GPS), 10 (BDS), and 18 (GPS + BDS), with the corresponding PDOP mean as 2.2 (GPS), 2.7 (BDS) and 1.4 (GPS + BDS). Obviously, the number of available BDS satellites is greater than that of GPS satellites, but the PDOP of GPS is slightly better than that of BDS. This may be caused by the special BDS constellation design of five GEOs and five IGSOs as shown in Fig. 5 (middle). For comparison, the sky plot of GPS and GPS + BDS is illustrated in Fig. 5. It is obvious that the combined constellation of GPS + BDS is superior to that of the individual system. So GNSS data are processed in the combined constellation (GPS + BDS) mode.

Fig. 3
figure 3

Trajectory in Wuhan City, China

Full size image
Fig. 4
figure 4

Number of observable GPS, BDS, GPS + BDS satellites (top) and the corresponding PDOP (bottom) during the whole test

Full size image
Fig. 5
figure 5

Sky plot of the observable GPS (top), BDS (middle), and GPS + BDS (bottom) in the test

Full size image

Data acquisition and processing

During the whole test, POS830 collects raw inertial measurements and GNSS observations to provide reference after post-processing, while the prototype system outputs the real-time navigation results. For both SPP and RTK, the cutoff elevation angle is set to 10° to delete low-quality observations. The initial position is (30.407°N, 114.282°E, 20.985 m); the maximum speed is 62 km/h. The initial uncertainty in position, velocity, and attitude is set as \(5\sqrt 5\) m, 0.2 m/s, and 5.72°, respectively. The standard variance of SPP position and velocity is set as 9.0 m and 0.2 m/s, respectively. The RTK position standard variance is set as 0.05 m.

In order to evaluate the proposed method, nineteen 60-sec outages are simulated and intentionally introduced every 2 min after KF reaches convergence with 500-sec initial alignment. The continuous GNSS and simulated outages are used to demonstrate the effectiveness of the proposed algorithm in both RTK and SPP modes.

Results and analysis

In this section, we will discuss the field test results in great detail to illustrate the proposed algorithm for improving the navigation accuracy. The Allan analysis of MEMS-based inertial sensors is conducted first to acquire AV-based stochastic error models. Then, the performance advantages of the AV model, AV-based adaptive estimation, and the combined algorithm are demonstrated by the field test for both RTK and SPP.

AV analysis of MEMS-based inertial sensors

The AV analysis of 12-h STIM300 static dataset is shown in Fig. 6, which shows the accelerometers and gyros have N, B and K with slopes close to − 1/2, 0 and 1/2, meaning white noise (N) is the dominant term for the short cluster time below 10 s and bias instability (B) is the dominant term in the large cluster time region around 100 s, while random walk (K) is the dominant term for the long cluster time above 2000 s. According to (2), the estimation accuracy for N, B and K is about 0.34, 4.82 and 15.56%, respectively. This explains the reason that AV-identified parameters need to be manually tuned in KF (Niu et al. 2007). In Table 4, the parameters of the identified random terms are estimated by nonnegative constrained identification algorithm (Lv et al. 2014) and used for modeling inertial sensor errors. Accordingly, two possible models should be considered:

$$\left\{ {\begin{array}{*{20}l} {\delta \omega_{ib}^{b} = \delta \omega_{N}^{b} + \delta \omega_{B}^{b} } \hfill \\ {\delta f^{b} = \delta f_{N}^{b} + \delta f_{B}^{b} } \hfill \\ \end{array} } \right.$$
(20)
$$\left\{ {\begin{array}{*{20}l} {\delta \omega_{ib}^{b} = \delta \omega_{N}^{b} + \delta \omega_{B}^{b} + \delta \omega_{K}^{b} } \hfill \\ {\delta f^{b} = \delta f_{N}^{b} + \delta f_{B}^{b} + \delta f_{K}^{b} } \hfill \\ \end{array} } \right.$$
(21)

where N is modeled as white noise, B is modeled as first-order GM process, and K is modeled as random walk process, as illustrated previously.

Fig. 6
figure 6

Allan plots of MEMS-based inertial sensors (STIM300, 125 Hz)

Full size image
Table 4 Parameter estimates of random terms in STIM300 IMU
Full size table

Since the introduction of (20) and (21) increases the order of KF to 15 and 21, respectively, the corresponding error models are termed as “AV15” and “AV21” here. The comparison between the two models in overall performance is instructive for providing a guideline for better inertial sensor modeling.

Impact of the AV model over the AR model

The impact of the proposed AV-based stochastic modeling for each inertial sensor on the overall navigation accuracy is examined by the field test with RTK as external aid. Two AV-based models (i.e., AV15 and AV21) are established to compare the accuracy with conventional AR method (Nassar and El-Sheimy 2006; Noureldin et al. 2009). Figures 7 and 8 compare the navigation errors among these methods during continuous GNSS and simulated outages.

Fig. 7
figure 7

Error comparison between AV and AR models with GNSS aiding. Plots from top to bottom show the errors of position, velocity and attitude. For each plot, the vertical axis represents the norms of corresponding error vectors

Full size image
Fig. 8
figure 8

Error comparison between AV and AR models during 60-sec outages. Plots from top to bottom show the errors of position, velocity, and attitude. For each plot, the vertical axis represents the norms of corresponding error vectors

Full size image

It is observed in Fig. 7 and Table 5 that the AV-based methods outperform the AR model in attitude accuracy during short outages (e.g., 1 s), with almost identical position and velocity accuracy. Similar to the findings in Quinchia et al. (2013), higher-order AR models, such as AR(2) and AR(3), undergo serious numerical instability or divergence problem. This is the reason that only AR(1) is used here.

Table 5 Maximum error comparison between AV and AR models with actual GNSS aiding
Full size table

It is obvious in Fig. 8 that the AV-based methods have significant advantages over the AR model in overall navigation accuracy during relatively long outages (e.g., 60 s). Compared with AR model, Table 6 indicates that AV15 model provides 67.22, 71.12, and 42.81% higher accuracy in position, velocity, and attitude, while AV21 method improves by 72.95, 74.90, and 48.60%. Therefore, it is safe to conclude AV-based methods are superior to AR model.

Table 6 Maximum error comparison between AV and AR models during 60-sec outages
Full size table

Moreover, Table 5 shows that the accuracy of the AV15 model is very close to that of AV21. Even during 60-sec outages, the improvement brought by AV21 is only about 10% for position and less for velocity and attitude as listed in Table 6. Although soaring computation load is caused by state augmentation, little accuracy enhancement is accomplished with all identified errors modeled (AV21) in contrast to that with only major errors modeled (AV15). This phenomenon could be explained by inaccurate model parameters caused by inevitable approximations and AV calculation errors for random terms of large cluster time.

Based on the above results, it is recommended to model major inertial sensor errors and ignore the minor sources for balance between accuracy and real time. Here the proposed AV15 model is suggested for real-time navigation. It happens to be a modified GM model but overcomes the difficulty in model parameters estimation of traditional method (Nassar and El-Sheimy 2006; Quinchia et al. 2013).

Impact of the AV-based adaptive estimation for measurement covariance

Using the AV15 error model, the impact of AV-based adaptive estimation for GNSS measurement covariance on the overall navigation accuracy is compared to the standard KF using either 1 Hz RTK or 1 Hz SPP during the field test.

RTK Aiding

Guaranteed by cycle slip detection and ambiguity resolution, the high quality of RTK solution is suitable for the proposed AV-based AKF. Figure 9 compares the integrated navigation errors between the standard KF and AV-based AKF, in which solid red lines are below the blue dotted line. Their root-mean-square errors (RMSEs) are compared in Table 7, which shows 47.25 and 15.47% overall improvements in position and attitude. Brought by adaptive estimation for RTK covariance, the accuracy enhancement demonstrates the effectiveness of the proposed AV-based AKF method.

Fig. 9
figure 9

Error comparison between KF and AV-based AKF in RTK/MEMS-INS using AV15 error model. Plots from top to bottom show the errors of position, velocity, and attitude. For each plot, the vertical axis represents the norms of corresponding error vectors

Full size image
Table 7 RMSE comparison between KF and AV-based AKF in RTK/MEMS-INS
Full size table

SPP Aiding

For SPP/MEMS-INS integration, it is necessary to detect and control the possible outliers before applying the AV-based AKF method. Figure 10 shows the navigation errors among standard KF, robust KF, and AV-based AKF. Their RMSEs are compared in Table 8.

Fig. 10
figure 10

Error comparison among KF, RKF and AV-based AKF in SPP/MEMS-INS using AV15 error model. Plots from top to bottom show the errors of position, velocity and attitude. For each plot, the vertical axis represents the norms of corresponding error vectors

Full size image
Table 8 RMSE comparison among KF, RKF, and AV-based AKF in SPP/MEMS-INS
Full size table

Figure 10 shows the standard KF (black dashed) is very sensitive to measurement outliers; while the proposed robust KF (blue dotted) is immune from outlying GNSS results, ensuring stability and reliability. Table 8 indicates the proposed robust KF also slightly improves overall accuracy by 11.93% for position and 5.32% for velocity. Thanks to POS830 post-processing reference, Fig. 11 shows the existence of SPP outliers in position and velocity, with the detected outlier epochs marked by red stars.

Fig. 11
figure 11

Actual errors in position and velocity obtained by SPP. The blue dashed line represents the PDOP value, the green dotted line represents the SPP position error, and the black dotted line represents the SPP velocity error

Full size image

Figure 10 shows that almost all the red lines are below the blue dotted lines, indicating further improvement caused by adaptive measurement covariance estimation. Table 8 shows there are significant accuracy improvements of 18.04, 55.97, and 18.58% in position, velocity and attitude, compared with the standard KF scheme.

The accuracy enhancements in both RTK and SPP cases demonstrate the effectiveness of the proposed AV-based AKF method.

Impact of the combined algorithm

For the combined algorithm of both stochastic modeling and adaptive estimation, its evaluation is achieved by the comparison with traditional AR method, AV-based error modeling only, AV-based AKF only cases.

RTK Aiding

Table 9 summarizes the results of traditional AR method, AV-based error modeling only, AV-based AKF only, and the combined case for navigation errors with RTK aiding.

Table 9 RTK/MEMS-INS RMSE comparison before and after AV-based error modeling and AV-based AKF
Full size table

It is obvious that the combined case of sensor error AV-based modeling and adaptive covariance estimation provides better results than the individual approaches. Compared with the AV-based AKF only case, it only improves attitude accuracy by 34.62% with slightly degraded position and velocity accuracy. However, it is unsafe to conclude that AR model is superior to AV model only from the above position accuracy comparison just as is done in most classical literature (Nassar and El-Sheimy 2006; Noureldin et al. 2009; Quinchia et al. 2013). It should be stressed that the IMU error modeling should be evaluated by overall navigation performance instead of only position accuracy.

Compared with the AV15 only case, the combined solution improves accuracy in position, velocity and attitude by 47.25, 7.11 and 15.47%. It should be observed that most of the improvements come after AV-based AKF. This indicates that both approaches should be applied together as a combined algorithm to improve overall navigation accuracy. As expected, the combined algorithm definitely accomplishes overall accuracy improvements in position, velocity, and attitude by about 18, 8, and 38%, compared with standard KF using AR(1) error model method.

SPP Aiding

Table 10 summarizes the results of the same four cases for navigation errors but with SPP aiding.

Table 10 SPP/MEMS-INS RMSE comparison before and after AV-based error modeling and AV-based AKF
Full size table

It is obvious that the combined case provides better results than any individual approach. Compared with the AV-based AKF only case, it improves velocity and attitude accuracy by 38.57 and 46.55% with almost identical position accuracy. Compared with the AV15 only case, the combined solution improves accuracy by 18.04% (position), 55.97% (velocity) and 18.58% (attitude). It shows that most improvements come after AV-based AKF, which also indicates the potential of the combined algorithm in overall integrated accuracy enhancements. As expected, the combined algorithm accomplishes overall accuracy improvements by about 15.10% (position), 75.30% (velocity), and 76.67% (attitude), compared with standard KF using AR(1) error model method.

Conclusions

Based on Allan variance technique, we have suggested an accuracy enhancement method for accurate MEMS-based GNSS/INS data fusion from two levels. The first is at the level of inertial sensor by proper stochastic modeling for the residual bias errors based on AV analysis. The second lies at the level of GNSS by adaptively estimating the error covariance based on AV calculation. It has been demonstrated that AV-based error models show superior performance to AR model for relatively long GNSS outages which may frequently occur in urban areas. Moreover, it has been shown that considerable accuracy enhancements can be obtained by augmenting the AV-based adaptive estimation for GNSS error covariance within innovation-based robust Kalman filter. Finally, it is suggested to apply the combined algorithm of both AV-based stochastic modeling and adaptive covariance estimation into GNSS/MEMS-INS loose integration. Using field tests, overall navigation errors are examined and compared using AV-based error modeling only, AV-based adaptive covariance estimation only, and the combined algorithm. The results show that navigation errors are reduced by about 18% (position), 8% (velocity), and 38% (attitude) for RTK/MEMS-INS, and by about 15% (position), 75% (velocity) and 77% (attitude) for SPP/MEMS-INS integration by the combined algorithm, compared with corresponding traditional counterparts.