Introduction

In addition to systematic atmospheric errors, three typical kinds of biases are involved in precise point positioning (PPP) of global navigation satellite systems (GNSS): initial phase bias, inter-frequency bias and differential code bias. They have been extensively studied in the recent years. In traditional PPP processing (Zumberge et al. 1997), the real-valued undifferenced ambiguities (absorbing the initial phase biases) for the ionosphere-free carrier phase are estimated together with station coordinates, receiver clock and zenith troposphere delay (ZTD). In order to recover the integer characteristics of undifferenced ambiguity and then improve the positioning accuracy, these initial phase biases must be firstly extracted and then provided to PPP users (Ge et al. 2008; Geng et al. 2010; Zhang et al. 2013). A significant inconsistency between triple-frequency carrier phases, named here inter-frequency clock bias, was observed for the GPS and Beidou systems by the GNSS community (Montenbruck et al. 2012, 2013; Li et al. 2013a, b). For estimation of ionospheric delay or total electron content (TEC) using code observation, the between-frequency differential code biases (DCBs; P1–P2 or C1–P2) are computed (Sardon et al. 1994; Goodwin and Breed 2001; Otsuka et al. 2002). These DCBs are also important in the single-frequency positioning to compensate the hardware delays (Bree and Tiberius 2012). In addition, another kind of DCB from C1 and P1 observation on one frequency is also noticed (Gao et al. 2001) to obtain the consistent parameters estimated with C1 and P1.

In satellite clock estimation, the ionosphere-free phase and code observations from different types of receivers are used. While some receivers merely track the C1 and P2 observables, other receivers track P1 and P2. The estimated satellite clocks with the two types of observables are different, since there is a DCB bias between the C1 and P1 observables. To maintain the consistency of the estimated clocks, the DCB of C1–P1 must be applied to the receiver observing C1 and P2. Currently, the satellite clock products are computed by using the ionosphere-free phase (L1/L2) and code (P1/P2) observations. For a receiver just tracking C1 and P2 observations, the DCB (C1–P1) should be considered carefully to realize precise undifferenced positioning. Since the high-quality float ambiguity solution depends on the quality of the observation and the rigorous modeling of error sources, it is rather important to study the biases in the ionosphere-free code combination. A 30-day (DOY 205–234, 2012) dual-frequency GPS data set collected with two types of receivers on eight stations from European Reference Frame (EUREF) Permanent Network (EPN) is processed to show the effect of the DCB (C1–P1) on the estimated undifferenced ambiguity value. The performances of the DCB (C1–P1) in the code-based single-point positioning (SPP), PPP convergence and wide-lane (WL) ambiguity are analyzed using the estimated DCB (C1–P1). First, we outline the mathematical models for computing the C1–P1 DCBs, and then processing and analysis are presented. Finally, some conclusions are given.

Mathematical models

Considering the contribution of code observation to GNSS ambiguity, many methods can be used to compute the undifferenced ambiguity. The ionosphere-free phase ambiguity can be estimated using PPP and by differencing the ionosphere-free phase and code observations. There is a difference between the satellite clocks estimated with the ionosphere-free phase (L1/L2) and code (P1/P2) versus the ionosphere-free phase (L1/L2) and code (C1/P2), and the difference is a scaled satellite DCB (C1–P1). The scaled DCB (C1–P1) will affect the estimated ambiguity values, when these satellite clocks estimated with different combinations are used to realize PPP. Based on this consideration, a new method for estimating the DCB (C1–P1) is presented.

DCB (C1–P1) estimation

For a receiver tracking C1 and P2 observations, for example, the receivers of LEICA GRX1200 + GNSS and NOV OEMV3, one can also form the ionosphere-free phase and code combinations:

$${\text{IF}}(L_{1} ,L_{2} ) = \rho + T + \delta_{r} - \delta^{s} + N \cdot \lambda + {\text{upd}}_{r}^{s} + \varepsilon_{p}$$
(1)
$${\text{IF}}(C_{1} ,P_{2} ) = \rho + T + \delta_{r} - \delta^{s} + \varepsilon_{c}$$
(2)

where ρ and T are the geometric range and tropospheric delay between receiver and satellite, δ r and δ s are the receiver and satellite clocks of the ionosphere-free combinations L1/L2 and C1/P2, respectively, N is the ionosphere-free carrier phase integer ambiguity and its corresponding wavelength is λ, upd s r is the uncalibrated phase delays (UPDs) of receiver and satellite, ε p and ε c are the noises of the ionosphere-free phase and code observations. Differencing the ionosphere-free code and phase combinations (1) and (2), the geometric range, tropospheric delay and clocks of receiver and satellite are canceled, giving:

$$n = {\text{IF}}(L_{1} ,L_{2} ) - {\text{IF}}(C_{1} ,P_{2} ) + \varepsilon_{p} - \varepsilon_{c}$$
(3)

where n = N · λ + upd s r . Assuming the same satellites are tracked and no cycle slip exists over m epochs, the ambiguity is computed as:

$$n = {{\sum\limits_{k = 1}^{m} {[w_{k} \times ({\text{IF}}_{k} (L_{1} ,L_{2} ) - {\text{IF}}_{k} (C_{1} ,P_{2} ))]} } \mathord{\left/ {\vphantom {{\sum\limits_{k = 1}^{m} {[w_{k} \times ({\text{IF}}_{k} (L_{1} ,L_{2} ) - {\text{IF}}_{k} (C_{1} ,P_{2} ))]} } {\sum\limits_{k = 1}^{m} {w_{k} } }}} \right. \kern-0pt} {\sum\limits_{k = 1}^{m} {w_{k} } }}$$
(4)

where w k is the weight of the difference between the ionosphere-free phase and code observations. The subscript k denotes the epoch number. We take the elevation-dependent function as follows:

$$w(\theta_{k} ) = \left\{ {\begin{array}{ll} {1/\sigma_{C}^{2} + \sigma_{P}^{2} } & {30^{^\circ } \le \theta_{k} \le 90^{^\circ } } \\ {2\sin (\theta_{k} )/\sigma_{C}^{2} + \sigma_{P}^{2} } & {10^{^\circ } \le \theta_{k} < 30^{^\circ } } \\ \end{array} } \right.$$
(5)

where θ k is the satellite elevation, σ c and σ p are the standard deviations in zenith of ionosphere-free code and phase, respectively.

In clock estimating, the ionosphere-free combinations L1/L2 and P1/P2 are used and the satellite clock products can be written as:

$$\overline{{\delta^{s} }} = \delta^{s} + b^{s}$$
(6)

where \(b^{s} = \frac{{f_{1}^{2} }}{{f_{1}^{2} - f_{2}^{2} }}{\text{DCB}}^{s}\) is the bias introduced by the satellite DCB(C1–P1), the DCBs is the satellite DCB, and \(\overline{{\delta^{s} }}\) is the satellite clock of L1/L2 and P1/P2. When the clock product is directly applied, the used observations formed with C1 and P2 can be rewritten as:

$$\overline{\text{IF}} (L_{1} ,L_{2} ) = \rho + T + \delta_{r} - \overline{{\delta^{s} }} + (N \cdot \lambda + {\text{upd}}_{r}^{s} + b^{s} ) + \varepsilon_{p}$$
(7)
$$\overline{\text{IF}} (C_{1} ,P_{2} ) = \rho + T + \delta_{r} - \overline{{\delta^{s} }} + \varepsilon_{c}$$
(8)

Based on (7) and (8), the PPP computations or differencing is implemented and the b s is not corrected; the real-valued undifferenced ambiguity is:

$$\overline{n} = N \cdot \lambda + {\text{upd}}_{r}^{s} + b^{s} = n + b^{s}$$
(9)

Inserting the estimated \(\overline{n}\) into (4), the term of ambiguity is removed and the satellite bias is computed:

$$b^{s} = \overline{n} - \left({{\sum\limits_{k = 1}^{m} {[w_{k} \times ({\text{IF}}_{k} (L_{1} ,L_{2} ) - {\text{IF}}_{k} (C_{1} ,P_{2} ))]} } \mathord{\left/ {\vphantom {{\sum\limits_{k = 1}^{m} {[w_{k} \times ({\text{IF}}_{k} (L_{1} ,L_{2} ) - {\text{IF}}_{k} (C_{1} ,P_{2} ))]} } {\sum\limits_{k = 1}^{m} {w_{k} } }}} \right. \kern-0pt} {\sum\limits_{k = 1}^{m} {w_{k} } }}\right)$$
(10)

Equation (10) shows the difference between the two sets of ionosphere-free phase ambiguity resolved with (1), (2) and (7), (8). It can be explained that there is a difference between (2) and (8), due to considerations of the different satellite clocks estimated with the observations of L1/L2 and C1/P2 and the observation of L1/L2 and P1/P2. Because of the contribution of the code observation to the ambiguity, the two sets of ionosphere-free phase ambiguities have a bias. Based on (7) and (8), the PPP computation is implemented and the DCB (C1–P1) is retrieved using (8); PPP results of receiver clock, tropospheric delay and geometric range are given in Tang et al. (2011). The ambiguity n in (3) also can be obtained by PPP based on (1) and (2) and the satellite clock of L1/L2 and C1/P2. However, the current satellite clock products come from the observations of L1/L2 and P1/P2. When the IGS satellite clock is used to obtain the ambiguity n, the DCB (C1–P1) must be corrected. So, the difference between (1) and (2) is used in DCB (C1–P1) estimation.

It is assumed that there are l stations in the network. For each station, the satellite bias b s can be computed. The mean bias can be calculated by averaging b s over the network:

$$\overline{{b^{s} }} = {{\sum\limits_{i = 1}^{l} {b^{s} (i)} } \mathord{\left/ {\vphantom {{\sum\limits_{i = 1}^{l} {b^{s} (i)} } l}} \right. \kern-0pt} l}$$
(11)

where i is station number, \(\overline{{b^{s} }}\) is the average of the bias. Equation (6) indicates b s is a scaled DCB (C1–P1):

$$\overline{{b^{s} }} = \frac{{f_{1}^{2} }}{{f_{1}^{2} - f_{2}^{2} }}{\text{DCB}}(C1 - P1)^{s}$$
(12)

Equation (12) shows that once the bias b s is obtained, one can compute the satellite DCB (C1–P1) as:

$${\text{DCB}}(C1 - P1)^{s} = \frac{{f_{1}^{2} - f_{2}^{2} }}{{f_{1}^{2} }}\overline{{b^{s} }}$$
(13)

When the observations are collected from a network, the DCB can be calculated by the mean bias.

Effect of DCB (C1–P1) on WL ambiguity

The Hatch–Melbourne–Wübbena observation (Hatch 1982; Moulborne 1985; Wübbena 1985) is used to estimate the wide-lane (WL) uncalibrated phase delay (UPD) and the WL ambiguity in PPP ambiguity fixing. To realize PPP ambiguity fixing, the WL ambiguity must be consistent with the ionosphere-free phase ambiguity. As discussed above, the bias in the code observation also dominates the WL ambiguity and UPD estimation values. Thus, different strategies for considering DCB (C1–P1) should be implemented according to the used code observation and satellite clock products in undifferenced processing. If PPP computation is implemented using (1) and (2), it is not necessary to consider the DCB (C1–P1) in WL ambiguity and WL UPD estimation and the observation C1/P2 dominates the undifferenced ambiguity. In this case, the satellite clock estimated with L1/L2 and C1/P2 should be used. When (7) and (8) are used to realize PPP, the undifferenced Hatch–Melbourne–Wübbena observation can be written as:

$$\begin{aligned} N_{w} \lambda_{w} + {\text{upd}}_{w,r}^{s} & = \left(\frac{{f_{1} }}{{f_{1} - f_{2} }}L_{1} - \frac{{f_{2} }}{{f_{1} - f_{2} }}L_{2} \right) - \left(\frac{{f_{1} }}{{f_{1} + f_{2} }}C_{1} - \frac{{f_{1} }}{{f_{1} + f_{2} }}{\text{DCB}}(C1 - P1) - \frac{{f_{2} }}{{f_{1} + f_{2} }}P_{2}\right) \\ & = L_{w} - P_{w} + \frac{{f_{1} }}{{f_{1} + f_{2} }}{\text{DCB}}(C1 - P1) \\ \end{aligned}$$
(14)

where L w and P w are WL phase and code observations, N w and λ w are WL integer ambiguity and wavelength, upd s w,r is WL UPD from receiver and satellite. The effect of DCB (C1–P1) on the WL UPD can be expressed as:

$$\Delta {\text{upd}} = \frac{{f_{1} }}{{f_{1} + f_{2} }}{\text{DCB}}(C1 - P1)/\lambda_{w} - \text{int} \left(\frac{{f_{1} }}{{f_{1} + f_{2} }}{\text{DCB}}(C1 - P1)/\lambda_{w}\right)$$
(15)

where Δupd is the influence of DCB (C1–P1) on the WL UPD, int is a function returned an integer.

Data processing

To evaluate the presented strategy, the 30-day (DOY 205–234, 2012) GPS dual-frequency data collected with sampling interval of 30 s and cutoff elevation of 10° from eight stations of EPN are processed. The information of these eight stations is shown in Table 1, for which, two types of receivers are involved. In processing, the IGS (Dow et al. 2009) orbit and clock products are used. Preprocessing of phase data for detecting cycle slip is based on the Hatch–Melbourne–Wübbena and geometry-free (L1–L2) combinations.

Table 1 Information of the eight stations
Full size table

DCB (C1–P1)

According to the theory provided above, the bias b s is computed, where we must compute the precise undifferenced ambiguity \(\overline{n}\) first. An observation span of greater than 3 h is taken to compute the converged ambiguity. The means and standard deviations (STD) of the biases for all satellites are computed based on the 30-day daily bias results. The results for two types of receivers of LARM, ROVE and SMLA are illustrated in Fig. 1.

Fig. 1
figure 1

Means and STDs of the bias b s for LARM, ROVE and SMLA

Full size image

Figure 1 shows that the DCB (C1–P1) indeed exists for all satellites though with different magnitudes. Most of biases are stable with generally smaller than 10-cm STDs, especially for the ROVE. In traditional PPP computation, the satellite clocks come from L1/L2 and P1/P2. If the observation from a receiver that merely tracks the C1 and P2 is processed, the DCB (C1–P1) correction should be considered carefully so that it does not affect the PPP ambiguity and also the positioning solution. It is observed from Fig. 1 that the biases of each satellite are different and the values of the same satellite estimated with different stations are nearly equal. These results further indicate that the biases are satellite dependent. The small difference between the values estimated for different stations can be explained by the influence of the code observations on the accuracy of the estimated bias. The means of these biases are computed with (11) for all satellites using eight network stations, and then the DCBs are calculated with (13). The calculated DCB and IGS products are compared and the differences are shown in Fig. 2. The differences indicate that the estimated DCBs are better than 0.13 m.

Fig. 2
figure 2

Difference between the estimated DCB and IGS product

Full size image

Performance of DCB (C1–P1) in SPP

Biases in the code observation not only affect code observation-based positioning but also affect the ambiguity solution. This requires rigorous modeling of all error sources affecting carrier phase and code observations in undifferenced processing (Banville et al. 2013). Thus, the performance of DCB (C1–P1) in SPP is investigated to study its effect on code observation. The ionosphere-free model (8) of C1 and P2 code observations is used. A 5-day (DOY 245–249, 2012) data set from the station DUTH of EPN is processed epoch by epoch. The elevation-dependent weights for the ionosphere-free code observations are determined. The corrections, earth tides, relativistic effects and antenna phase center offsets are implemented. The tropospheric delay is corrected using the Saastamoinen model. A least square technique is used to solve the epoch-wise coordinates in the two strategies. In strategy #1, no DCB correction is applied, while in strategy #2, the estimated DCBs from eight stations in Table 1 are used. In all strategies, the IGS final clocks and orbits are used.

The RMS values of SPP solution errors with respect to the ground truth coordinates are computed for the coordinate components north, east and up. As shown in Table 2, comparing with strategy #1 without DCB corrections, significant improvements are achieved in all three coordinate components for strategy #2 with DCB corrections. The improvements are similar for both strategies, and the relative improvements are about 58, 43 and 57 % for north, east and up components. The performance results also show that the influence of the DCB (C1–P1) on the up direction is more obvious than on the north and east directions.

Table 2 RMS (m) and RMS improvement (m) between the two approaches
Full size table

Performance of DCB (C1–P1) in PPP convergence

We study the performance of the DCB (C1–P1) in the PPP convergence. The same data sets, 5-day (DOY 245–249, 2012) from DUTH, are processed following the observation Eqs. (7) and (8). Two strategies, #3 and #4, are designed, for which the bias of combined DCB (C1–P1) is ignored and corrected, respectively. The elevation-dependent weighting function is applied with different standard deviations (Table 3) for ionosphere-free code and phase in zenith, although the 1:100 variance ratio for the phase to code observations is generally taken into account (Hauschild and Montenbruck, 2009; Zhang et al., 2011). We test the different variance ratios considering the fact that the code precision could be remarkably different for different receiver types and may significantly improve with the receiver technology development (Li et al. 2008).

Table 3 Comparison of convergence time (min)
Full size table

The data are processed in the static mode, where the earth tides, the relativistic effects and the antenna phase center offset are corrected with classic models. The Saastamoinen model is used to get the a priori correction, and the remaining wet part is estimated by setting up a piecewise constant (PWC) at an interval of 1 h. The convergence time is defined as the elapsed time when the estimated coordinate errors in the north, east and up directions are smaller than 10 cm. The convergence times of two strategies are shown in Table 3.

Table 3 shows that the convergence time becomes longer with increasing code weights when the bias of the scaled DCB is not corrected. This makes sense since the bias of the scaled DCB in the code observation will bias the solutions more significantly when the code weights become larger. However, if the bias is corrected, the convergence time shortens when the code precision decreases to 0.15 m. The result reveals that the reliable and high-quality PPP solution depends on all error sources affecting code observations. The result also advices that the setting of code weights is very important and reasonable weights should be taken to obtain optimal solutions (Seepersad and Bisnath 2014). Therefore, in the real application, one should apply the stochastic model evaluation method to re-assess the stochastic modeling of the used GNSS receivers (Wang et al.1998, 2002; Li et al. 2008). This is, however, beyond our scope in this study.

Performance of DCB (C1–P1) in WL UPD estimation

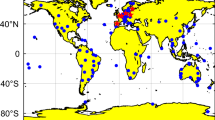
Much research focuses on dealing with the UPD and recovering the integer characteristics of PPP ambiguity (Ge et al. 2008; Collins 2008; Laurichesse et al. 2009; Teunissen et al. 2010; Zhang et al. 2013). The PPP ambiguity is fixed by fixing the WL and narrow-lane (NL) ambiguities, which needs to estimate the UPDs of WL and NL ambiguities. We design two strategies #5 and #6 to study the performance of the scaled DCB (C1–P1) in WL UPD estimation. In strategy #5, the bias is corrected, but in strategy #6, it is not corrected. The data of DOY 245, 2012 from all IGS stations in Fig. 3 are used to compute WL UPDs. The result is illustrated in Fig. 4. It shows that the estimated WL UPDs with and without bias corrections are different, which further demonstrates that the DCB affects the accuracy of the UPDs and the DCB should be considered in estimation of UPD. The difference can be explained with the effect of DCB (C1–P1) on the undifferenced ambiguity. To maintain consistency between the ionosphere-free and WL ambiguities, the DCB (C1–P1) correction does not need to be considered in UPD and WL ambiguity estimations when (1) and (2) and the satellite clock from L1/L2 and C1/P2 are used in PPP. The DCB (C1–P1) correction should be considered when (7) and (8) and the satellite clock from L1/L2 and P1/P2 are used in PPP. The influence of DCB (C1–P1) on the WL UPD is computed according to (15) and shown in Table 4. The values in the table indicate that the influence of DCB (C1–P1) on each satellite is different, and some values are larger than 0.3 cycles. This tells us that the DCB (C1–P1) should be considered carefully in PPP ambiguity resolution.

Fig. 3
figure 3

Distribution of the IGS stations used in estimation of WL UPDs. Red dots denote the stations tracking the signals of P1 and P2, and green dots the stations tracking the signals of C1 and P2

Full size image
Fig. 4
figure 4

Estimated WL UPDs with two strategies #5 and #6

Full size image
Table 4 Influence (Δupd) of the DCB (C1–P1) on the WL UPD for DOY 245, 2012 (cycle)
Full size table

Conclusions and discussion

A strategy for estimating DCB (C1–P1) and the performance evaluation in terms of SPP accuracy, PPP convergence and the effect on WL UPD is presented. Using 30-day (DOY 205–234, 2012) data from two types of receivers of the eight stations from EPN, the influence of the DCB (C1–P1) on ambiguity value is investigated. In investigating, two sets of the ionosphere-free phase ambiguities are resolved: One is computed by differencing the raw ionosphere-free phase and code combination formed with C1 and P1, and the other is resolved by PPP using the ionosphere-free combination formed with C1 and P1 and the satellite clock estimated with P1/P2 and L1/L2. In both cases, the DCB (C1–P1) from the satellite is not corrected. Investigation indicates that there is a bias between the two sets of ambiguities. This bias is a scaled DCB (C1–P1), and it merely contains the satellite part. The computed 30-day biases show that they are stable in the short term. The satellite DCB (C1–P1) is computed with the scaled bias. Comparison between the estimated DCB and that of IGS product shows that the estimated DCB (C1–P1) is better than 0.13 m. The difference between the two sets of ambiguities shows that the bias in the code observations affects the undifferenced ambiguity value. Similar to the difference between the two sets of ambiguities, the DCB (C1–P1) should be considered carefully in WL ambiguity and WL UPD estimation with the Hatch–Melbourne–Wübbena combination. The performance of the DCB (C1–P1) in the WL UPD estimation is analyzed. The results show that the influence on UPD of each satellite is different and some values are larger than 0.3 cycles. Also the performance of the DCB (C1–P1) in SPP is studied and it shows that the accuracy can be improved by 50 % when the DCB (C1–P1) is corrected. Aiming to learn about the contribution of code observation for accelerating PPP positioning, the performance of DCB (C1–P1) in PPP convergence is studied. The results demonstrate that the DCB (C1–P1) correction benefits PPP initialization.