Introduction

GLONASS traditionally provides signals with frequency division multiple access (FDMA) technique for users, causing inter-frequency biases (IFB) in the G1 and G2 observations (Sleewaegen et al. 2012; Leick et al. 2015). With the development and modernization of the GLONASS system, Russia has been planning to send new signals with code division multiple access (CDMA) technique since 2011 (Montenbruck et al. 2017). As of January 2021, there are 24 GLONASS operational satellites (IAC 2021), including 18 GLONASS-M, 4 GLONASS-M +, and 2 GLONASS-K1 satellites (listed in Table 1), wherein GLONASS-M + and -K1 satellites provide CDMA signals on the G3 frequency. That is, there are six satellites (PRN: R04, R05, R09, R12, R21, and R26) that transmit both CDMA observations on G3 frequency and FDMA observations on G1, G2 frequency currently, making it possible for joint use of GLONASS FDMA and CDMA signals for precise point positioning (PPP).

Table 1 List of frequency channels and satellite types
Full size table

Currently, much research on GPS, BDS and Galileo triple-frequency observations has been reported (Wang et al. 2015; Fan et al. 2021; Li et al. 2019, 2020); nevertheless, research on GLONASS CDMA signals is rare. Zaminpardaz et al. (2017) investigated the integer ambiguity resolution and positioning using the data of the satellite pair R21–R26. Following, they evaluated GLONASS short-baseline RTK performance with FDMA + CDMA observations (Zaminpardaz et al. 2021). Some studies also paid attention to investigating GLONASS FDMA ambiguity resolution. Teunissen and Khodabandeh (2019) proposed a new integer-estimable GLONASS FDMA model. The model is generally applicable and performs well in several different ambiguity-resolution critical applications. Hou et al. (2020) further developed the integer-estimable model and proposed a Kalman-filter-based data processing strategy to analyze the model of ionosphere-fixed, ionosphere-weighted, and ionospheric-free formulations. Besides, Brack et al. (2020) investigated GLONASS FDMA data for RTK positioning and Zhang et al. (2021a) further studied the GLONASS PPP-RTK model and performance based on the integer-estimable FDMA model proposed in Teunissen and Khodabandeh (2019). Under the background of developing multi-frequency signals, the assessment of GLONASS triple-frequency PPP performance is of great importance.

However, there are two main obstacles to GLONASS triple-frequency PPP. First, a triple-frequency PPP model that simultaneously uses CDMA and FDMA signals is currently absent. Second, significant inter-frequency clock bias (IFCB) errors, defined as the difference between satellite clocks computed with different ionospheric-free carrier phase combinations (Montenbruck et al. 2012; Li et al. 2015), must be carefully understood and corrected. For the former, based on the traditional dual-frequency FDMA PPP model (Zhou et al. 2017), we present a new GLONASS triple-frequency undifferenced uncombined PPP model, where IFB is processed carefully. For the latter, IFCB characteristics are investigated and corrected in the presented model.

A summary of research about GNSS satellite IFCBs is listed in Table 2. The table shows that the satellite IFCB series presents different magnitudes for different types of satellites. For Galileo, BDS3, and QZSS satellites, they are insignificant. However, they cannot be neglected definitely for GPS BLOCK-IIF, BDS2 satellites. Pan et al. (2017a) studied the impact of IFCB errors on GPS triple-frequency PPP and results indicate that 3 h positioning accuracy of triple-frequency PPP can be improved by 19%, 13% and 21% after IFCB corrections. For the IFCB errors of six GLONASS satellites, they have not been comprehensively studied and understood yet. Their long-term variation characteristics, predictability, and the effect on the GLONASS FDMA + CDMA triple-frequency PPP have not been reported, which will be comprehensively investigated in this work.

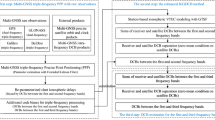
Table 2 Statistics about magnitudes of triple-frequency GNSS satellite IFCB series
Full size table

In this contribution, we aim to provide insight into the GLONASS triple-frequency uncombined PPP capabilities of standalone using both FDMA and CDMA signals. Especially, IFCB errors are carefully investigated and calibrated. A GLONASS FDMA + CDMA PPP model considering IFCB errors is presented first. The data and processing strategies are introduced. Next, GLONASS IFCB characteristics are investigated in detail. Then GLONASS FDMA + CDMA PPP performance is evaluated and studied. Finally, summaries and conclusions are provided.

GLONASS triple-frequency undifferenced and uncombined PPP model

We start from GLONASS traditional dual-frequency FDMA signals, then integrate CDMA signals to develop a new FDMA + CDMA undifferenced and uncombined PPP model, especially, inter-frequency clock bias (IFCB) errors are carefully investigated and calibrated.

FDMA model

Raw FDMA observations of GLONASS pseudorange \(P_{r,i}^{s}\) and carrier phase \(G_{r,i}^{s}\) can be expressed in a unit of meter

$$\left\{ \begin{aligned} P_{{r,i}}^{s} = & \rho _{r}^{s} + c\left( {t_{r} - t^{s} } \right) + \mu _{i}^{{}} \cdot \gamma _{{r,1}}^{s} \\ & + m_{r}^{s} \cdot T_{r} + d_{{r,i}}^{s} - d_{i}^{s} \\ G_{{r,i}}^{s} = & \rho _{r}^{s} + c\left( {t_{r} - t^{s} } \right) - \mu _{i}^{{}} \cdot \gamma _{{r,1}}^{s} \\ & + m_{r}^{s} \cdot T_{r} + \lambda _{i}^{s} \cdot N_{{r,i}}^{s} + \lambda _{i}^{s} \cdot \left( {b_{{r,i}}^{s} - b_{i}^{s} } \right) \\ \end{aligned} \right.$$
(1)

where s, r, i, and f are the satellite pseudorandom noise code (PRN) number, receiver, frequency number (i = 1, 2), and frequency. \(\rho_{r}^{s}\) symbolizes the satellite to receiver distance, c is the speed of light in vacuum, \(t_{r}\) and \(t^{s}\) are the receiver and satellite clock errors, respectively. \(\gamma_{r,1}^{s}\) and \(\mu_{i}^{{}} { = }\frac{{f_{1}^{2} }}{{f_{i}^{2} }}\) denote the ionospheric delays on G1 frequency and its coefficient. Note that the subscript s of frequency f has been dropped for brevity. \(T_{r}\) and \(m_{r}^{s}\) indicate the zenith tropospheric delay with its mapping function, \(d_{r,i}^{s}\) and \(d_{i}^{s}\) denotes pseudorange hardware bias at station r and at satellite s in the unit of meters, respectively. Similarly, \(b_{r,i}^{s}\) and \(b_{i}^{s}\) symbolize phase hardware bias at station r and at the satellite in the unit of cycles. \(N_{r,i}^{s}\) is the integer ambiguity, \(\lambda_{i}^{s} = \frac{c}{{f_{i}^{{}} }}\) represents the wavelength. For brevity, multipath effects, measurement noises, etc. are ignored in this study.

As we know, the code (phase) receiver hardware bias \(d_{r,i}^{s}\) (\(b_{r,i}^{s}\)) of GLONASS FDMA signals depends on both receiver and satellite, which causes the existence of inter-frequency biases. Generally, GLONASS phase IFBs will be absorbed by ambiguity parameters. Therefore, code IFBs will be focused on here, that is

$$d_{r,i}^{s} = d_{r,i}^{{s_{0} }} + \Gamma_{r,i}^{s}$$
(2)

where \(d_{r,i}^{{s_{0} }}\) represents the code receiver hardware bias for the satellite with a frequency number of zero, \(\Gamma_{r,i}^{s}\) denotes the code IFB, s0 represents the satellite whose frequency number is zero (R11). Next, we resubmit (2) into (1), clock errors, ionosphere delays, and ambiguity parameters can be reparametrized and hence the undifferenced and uncombined GLONASS FDMA PPP model can be obtained as

$$\left\{ \begin{gathered} p_{r,1}^{s} = - \tau_{r}^{s} \cdot {\mathbf{y}}_{r} + c \cdot \widetilde{t}_{r}^{{s_{0} }} + \overline{\gamma }_{r,1}^{s} + m_{r}^{s} \cdot T_{r} \hfill \\ p_{r,2}^{s} = - \tau_{r}^{s} \cdot {\mathbf{y}}_{r} + c \cdot \widetilde{t}_{r}^{{s_{0} }} + \mu_{2}^{{}} \cdot \overline{\gamma }_{r,1}^{s} + m_{r}^{s} \cdot T_{r} + \Gamma_{r,12}^{s} \hfill \\ g_{r,1}^{s} = - \tau_{r}^{s} \cdot {\mathbf{y}}_{r} + c \cdot \widetilde{t}_{r}^{{s_{0} }} - \overline{\gamma }_{r,1}^{s} + m_{r}^{s} \cdot T_{r} + \lambda_{1}^{s} \cdot B_{r,1}^{s} \hfill \\ g_{r,2}^{s} = - \tau_{r}^{s} \cdot {\mathbf{y}}_{r} + c \cdot \widetilde{t}_{r}^{{s_{0} }} - \mu_{2}^{{}} \cdot \overline{\gamma }_{r,1}^{s} + m_{r}^{s} \cdot T_{r} + \lambda_{2}^{s} \cdot B_{r,2}^{s} \hfill \\ \end{gathered} \right.$$
(3)

where \(p_{r,i}^{s}\) and \(g_{r,i}^{s}\) represent the observed-minus-calculated code and phase observable, \(\tau_{r}^{s}\) and \({\mathbf{y}}_{r}\) denote the vector of the line-of-sight direction and receiver coordinates. The detailed estimable parameters are listed in Table 3.

Table 3 Estimable parameters in Eq. (3)
Full size table

where \(d_{{IF_{12} }}^{s} = \alpha_{12}^{{}} \cdot d_{1}^{s} + \beta_{12}^{{}} \cdot d_{2}^{s}\), \(d_{{r,IF_{12} }}^{{s_{0} }} = \alpha_{12}^{{}} \cdot d_{r,1}^{{s_{0} }} + \beta_{12}^{{}} \cdot d_{r,2}^{{s_{0} }}\), coefficients are \(\alpha_{12}^{{}} = \frac{{f_{1}^{2} }}{{f_{1}^{2} - f_{2}^{2} }}{\kern 1pt} {\kern 1pt}\),\(\beta_{12}^{{}} = \frac{{ - f_{2}^{2} }}{{f_{1}^{2} - f_{2}^{2} }}\). We have noted that \(\Gamma_{r,12}^{s}\) and \(\widetilde{\gamma }_{r,1}^{s}\) are linearly dependent. To overcome this problem, the constraint \(\sum\nolimits_{t = 1}^{n} {\Gamma_{r,12}^{t} } = 0\) (where n denotes the number of satellites) is performed to remove the datum deficiency (Zhou et al. 2017).

FDMA + CDMA model

In addition to the traditional dual-frequency FDMA signals, GLONASS transmits CDMA observations on the third-frequency band for users. Raw CDMA pseudorange \(P_{r,3}^{s}\) and carrier phase \(G_{r,3}^{s}\) observations in the unit of meter can be depicted as

$$\left\{ \begin{aligned} P_{{r,3}}^{s} = & \rho _{r}^{s} + c\left( {t_{r} - t^{s} } \right) + \mu _{3}^{{s_{{}} }} \cdot \gamma _{{r,1}}^{s} \\ & + m_{r}^{s} \cdot T_{r} + d_{{r,3}}^{{}} - d_{3}^{s} \\ G_{{r,3}}^{s} = & \rho _{r}^{s} + c\left( {t_{r} - t^{s} } \right) - \mu _{3}^{{s_{{}} }} \cdot \gamma _{{r,1}}^{s} \\ & + m_{r}^{s} \cdot T_{r} + \lambda _{3} \cdot N_{{r,3}}^{s} + \lambda _{3} \cdot \left( {b_{{r,3}}^{{}} - b_{3}^{s} } \right) \\ \end{aligned} \right.$$
(4)

where \(N_{r,3}^{s}\) and \(\lambda_{3} = \frac{c}{{f_{3} }}\) are the integer carrier phase ambiguity and wavelength, respectively. \(b_{r,3}^{{}}\) and \(d_{r,3}^{{}}\) are phase and pseudorange hardware biases at station r, \(b_{3}^{s}\) and \(d_{3}^{s}\) denote phase and pseudorange hardware biases at satellite s. Other parameters can be found in (1). Fortunately, similar to other CDMA systems, e.g., GPS and BDS, the code (phase) receiver hardware biases \(d_{r,3}^{{}}\) (\(b_{r,3}^{{}}\)) of new GLONASS CDMA observations are independent of satellites; hence, they are free from the effect of inter-frequency biases. For brevity, multipath effects, measurement noises, etc. are also ignored.

To perform precise point positioning, precise clock products are necessary. Current precise clock products provided by International GNSS Service (IGS) take the form of

$$\widetilde{t}^{s} = t^{s} { + }\frac{1}{c} \cdot \left( {\alpha_{12}^{{}} {\kern 1pt} \cdot d_{1}^{s} + \beta_{12}^{{}} d_{2}^{s} } \right)$$
(5)

where \(\widetilde{t}^{s}\) denotes the precise satellite clock products. Generally, IGS precise satellite clock product is calculated with G1/G2 ionosphere-free combinations. However, if the clock products are used to correct satellite clock error on G3 frequency, inter-frequency clock bias, an unfavorable error, shall be introduced into the model. Based on Eq. (1) and (4), after employing precise clock product corrections, the linearized FDMA + CDMA PPP model can be represented as

$$\left\{ \begin{gathered} p_{r,1}^{s} = - \tau_{r}^{s} \cdot {\mathbf{y}}_{r} + c \cdot \widetilde{t}_{r}^{{s_{0} }} + \overline{\gamma }_{r,1}^{s} + m_{r}^{s} \cdot T_{r} \hfill \\ p_{r,2}^{s} = - \tau_{r}^{s} \cdot {\mathbf{y}}_{r} + c \cdot \widetilde{t}_{r}^{{s_{0} }} + \mu_{2}^{{}} \cdot \overline{\gamma }_{r,1}^{s} + m_{r}^{s} \cdot T_{r} + \Gamma_{r,12}^{s} \hfill \\ p_{r,3}^{s} = - \tau_{r}^{s} \cdot {\mathbf{y}}_{r} + c \cdot \widetilde{t}_{r}^{{s_{0} }} + \mu_{3}^{s} \cdot \overline{\gamma }_{r,1}^{s} + m_{r}^{s} \cdot T_{r} + \Pi_{r}^{s} \hfill \\ g_{r,1}^{s} = - \tau_{r}^{s} \cdot {\mathbf{y}}_{r} + c \cdot \widetilde{t}_{r}^{{s_{0} }} - \overline{\gamma }_{r,1}^{s} + m_{r}^{s} \cdot T_{r} + \lambda_{1}^{s} \cdot B_{r,1}^{s} \hfill \\ g_{r,2}^{s} = - \tau_{r}^{s} \cdot {\mathbf{y}}_{r} + c \cdot \widetilde{t}_{r}^{{s_{0} }} - \mu_{2}^{{}} \cdot \overline{\gamma }_{r,1}^{s} + m_{r}^{s} \cdot T_{r} + \lambda_{2}^{s} \cdot B_{r,2}^{s} \hfill \\ g_{r,3}^{s} = - \tau_{r}^{s} \cdot {\mathbf{y}}_{r} + c \cdot \widetilde{t}_{r}^{{s_{0} }} - \mu_{3}^{s} \cdot \overline{\gamma }_{r,1}^{s} + m_{r}^{s} \cdot T_{r} + \lambda_{3}^{{}} \cdot B_{r,3}^{s} + \Theta_{UC}^{s} \hfill \\ \end{gathered} \right.$$
(6)

with

$$\left\{ \begin{gathered} \Pi_{r}^{s} = - \mu_{3}^{s} \cdot \beta_{12}^{{}} \cdot \left( {d_{r,1}^{{s_{0} }} - d_{r,2}^{{s_{0} }} + d_{1}^{s} - d_{2}^{s} } \right) + d_{{IF_{12} }}^{s} - d_{{r,IF_{12} }}^{{s_{0} }} - \mu_{3}^{s} \cdot \Gamma_{r,1}^{s} + d_{r,3} - d_{3}^{s} \hfill \\ B_{r,3}^{s} = \left( {N_{r,3}^{s} + b_{r,3}^{{}} - b_{3}^{s} } \right) + {{\left( {d_{{IF_{12} }}^{s} - d_{{r,IF_{12} }}^{{s_{0} }} + \mu_{3}^{s} \cdot \Gamma_{r,1}^{s} + \mu_{3}^{s} \cdot \beta_{12}^{{}} \cdot \left( {d_{r,1}^{{s_{0} }} - d_{r,2}^{{s_{0} }} + d_{1}^{s} - d_{2}^{s} } \right)} \right)} \mathord{\left/ {\vphantom {{\left( {d_{{IF_{12} }}^{s} - d_{{r,IF_{12} }}^{{s_{0} }} + \mu_{3}^{s} \cdot \Gamma_{r,1}^{s} + \mu_{3}^{s} \cdot \beta_{12}^{{}} \cdot \left( {d_{r,1}^{{s_{0} }} - d_{r,2}^{{s_{0} }} + d_{1}^{s} - d_{2}^{s} } \right)} \right)} {\lambda_{3}^{{}} }}} \right. \kern-\nulldelimiterspace} {\lambda_{3}^{{}} }} \hfill \\ \end{gathered} \right.$$
(7)

whereas a common reparametrized receiver clock parameter \(\widetilde{t}_{r}^{{s_{0} }}\), which absorbed the ionospheric-free receiver hardware delays, is used for both CDMA and FDMA observations, a third-frequency IFB parameter \(\Pi_{r}^{s}\) needs to be introduced into G3 code observations (Pan et al. 2018). \(p_{r,3}^{s}\) and \(g_{r,3}^{s}\) represent the observed-minus-calculated code and phase observable, \(B_{r,3}^{s}\) denotes the reparametrized ambiguity parameter. Also, \(\Theta_{UC}^{s}\) denotes the inter-frequency clock bias. Other estimable parameters are shown in Table 3.

For CDMA systems, i.e., GPS, BDS2/3, and Galileo, IFCB errors have been well studied. Studies show that GPS IFCB errors are time-variant and can reach tens of centimeters (Zhang et al. 2021b). In the case of GLONASS, the peak-to-peak GLONASS IFCB amplitude of satellite R21 reaches 0.3 m (Zhang et al. 2022), which is even larger than GPS and will be investigated in detail in this study. Therefore, GLONASS phase IFCB errors must be carefully calibrated beforehand. The observation equation of IFCB can be depicted as (Pan et al. 2020; Zhang et al. 2022):

$$DIF\left( {G_{r,1}^{s} ,G_{r,2}^{s} ,G_{r,3}^{s} } \right) = IF_{{r,G_{r,1}^{s} G_{r,2}^{s} }}^{s} - IF_{{r,G_{r,1}^{s} G_{r,3}^{s} }}^{s} = B_{DIF}^{s} + \Theta_{IF,r}^{s}$$
(8)

where \(IF_{{r,G_{i} G_{j} }}^{s} = \frac{{f_{i}^{2} }}{{f_{i}^{2} - f_{j}^{2} }}G_{r,i}^{s} {\kern 1pt} - {\kern 1pt} \frac{{f_{j}^{2} }}{{f_{i}^{2} - f_{j}^{2} }}G_{r,j}^{s}\) denotes the ionospheric-free combination of \(G_{i}\) and \(G_{j}\) carrier phases, DIF represents the difference between G1/G2- and G1/G3-based ionospheric-free combination, \(\Theta_{IF,r}^{s}\) is the ionospheric-free IFCB, \(B_{DIF}^{s}\) denotes a constant which absorbs the time-invariant phase hardware biases. In this contribution, we choose to perform IFCB estimation based on the epoch-differenced method. Starting from (8), the ionospheric-free IFCB can be obtained by

$$\Theta_{IF,r}^{s} = DIF\left( {G_{r,1}^{s} ,G_{r,2}^{s} ,G_{r,3}^{s} } \right) - B_{DIF}^{s}$$
(9)

Then, the epoch-differenced IFCB can be formed to remove \(B_{DIF}^{s}\). Next, to ensure the quality of IFCB estimation, multi-station weighted adjustment (Zhang et al. 2021b) is performed to get satellite-dependent IFCB \(\Delta \Theta_{IF}^{s}\), that is

$$\Delta \Theta_{IF}^{s} \left( t \right) = {{\sum\limits_{r = 1}^{nsta} {\left( {\Delta \Theta_{IF,r}^{s} \left( t \right) \cdot \chi_{r}^{s} } \right)} } \mathord{\left/ {\vphantom {{\sum\limits_{r = 1}^{nsta} {\left( {\Delta \Theta_{IF,r}^{s} \left( t \right) \cdot \chi_{r}^{s} } \right)} } {\sum\limits_{r = 1}^{nsta} {\chi_{r}^{s} } }}} \right. \kern-\nulldelimiterspace} {\sum\limits_{r = 1}^{nsta} {\chi_{r}^{s} } }}$$
(10)
$$\chi_{r}^{s} = \left\{ {\begin{array}{*{20}c} \begin{gathered} 2\sin e_{r}^{s} \hfill \\ 1 \hfill \\ \end{gathered} & \begin{gathered} 10^{ \circ } \le e_{r}^{s} < 30^{ \circ } \hfill \\ e_{r}^{s} \ge 30^{ \circ } \hfill \\ \end{gathered} \\ \end{array} } \right.$$
(11)

where \(\Delta \Theta_{IF}^{s}\) denotes the satellite-dependent IFCB obtained from the multi-station weighted adjustment, \(\chi_{r}^{s}\) is the elevation-dependent weight, \(e_{r}^{s}\) represents elevation angle, and nsta denotes the number of stations. Finally, the ionospheric-free IFCB for satellite s at epoch k takes the form of

$$\Theta_{IF}^{s} \left( t \right) = \Theta_{IF}^{s} \left( {t_{0} } \right){ + }\sum\limits_{{m = t_{0} + 1}}^{t} {\Delta \Theta_{IF}^{s} \left( m \right)}$$
(12)

where \(\Theta_{IF}^{s} \left( {t_{0} } \right)\) is the IFCB at the reference epoch \(t_{0}\). Similar to Zhang et al. (2021b), we constrain the IFCB at the first epoch to zero, which would certainly introduce a common bias to all epochs. However, this common bias does not affect PPP float solutions since it will be integrated with the ambiguities in parameter estimation (Pan et al. 2017b). To ensure the quality of the estimates, ten to hundreds of stations are necessary for reliable estimation. As Li et al. (2012) and Fan et al. (2019) pointed out, the time-variant part of the receiver IFCB is assumed to be small enough to be ignored, and hence only satellite phase IFCB is studied.

To calibrate undifferenced and uncombined IFCB \(\Theta_{UC}^{s}\) in (6) with our estimated ionospheric-free IFCB \(\Theta_{IF}^{s}\), we use the conversion between them,

$$\Theta_{UC}^{s} = \frac{{f_{1}^{2} - f_{3}^{2} }}{{f_{3}^{2} }}\Theta_{IF}^{s}$$
(13)

Once the IFCB error \(\Theta_{UC}^{s}\) is calibrated, a rank-full GLONASS triple-frequency undifferenced and uncombined PPP model can be achieved. The parameters to be estimated include

$${\mathbf{X}} = \left[ {\begin{array}{*{20}c} {{\mathbf{y}}_{r} } & {\widetilde{t}_{r}^{{s_{0} }} } & {\widetilde{\gamma }_{r,1}^{s} } & {T_{r} } & {\Gamma_{r,12}^{s} } & {\Pi_{r}^{s} } & {B_{r,1}^{s} } & {B_{r,2}^{s} } & {B_{r,3}^{s} } \\ \end{array} } \right]^{{\text{T}}}$$
(14)

In our presented model, the code inter-frequency bias of traditional FDMA signals and inter-frequency clock bias after integrating new CDMA signals are rigorously considered. With precise IFCB products, GLONASS triple-frequency PPP can be performed.

Data and processing strategy

As mentioned above, four GLONASS-M + satellites, including R04, R05, R12, R21, and the two GLONASS-K1 satellites, including R09, R26 (R26 is under testing mode), are designed to transmit CDMA signals on the G3 frequency currently (as shown in Table 1). To investigate variation characteristics of GLONASS IFCBs and calibrate them beforehand, 135 globally distributed MGEX (Montenbruck et al. 2017) stations (represented by blue points in Fig. 1) recorded from DOY 1–150, 2020 are selected for IFCB estimation.

Fig. 1
figure 1

Distribution of 135 MGEX stations with GLONASS triple-frequency observations used in the experiment. Blue points represent stations that were used to estimate IFCB, and another six stations marked by red pentagrams were used for PPP validation

Full size image

To perform triple-frequency PPP, observations from six Europe stations of DOY 120–150, 2020 are utilized (marked by red pentagrams in Fig. 1). These stations can all provide enough GLONASS G3 observations and their detailed information, as shown in Table 4. Noted that satellite R26 is under the testing mode, and corresponding precise products, e.g., ephemeris and clock products, have not been released currently; therefore, satellite R26 is not involved in our PPP process. Three groups of GLONASS PPP solutions were performed and compared: dual-frequency PPP (solution A), triple-frequency PPP without IFCB corrections (solution B), and triple-frequency PPP with IFCB corrections (solution C).

Table 4 Detailed information about six stations for PPP validation
Full size table

Our processing strategies for GLONASS triple-frequency PPP are summarized in Table 5. All GLONASS satellites are utilized in our PPP experiments no matter whether they have G3 measurements or not. We perform PPP experiments based on a modified open-source software RTKLIB (version, 2.4.3, can be accessed from http://www.rtklib.com).

Table 5 Processing strategies of GLONASS triple-frequency PPP
Full size table

Results and discussion

The variation characteristics and predictability of GLONASS IFCBs are investigated first. Then, GLONASS FDMA + CDMA PPP is performed and evaluated. Some discussions are given finally.

Investigation of GLONASS IFCBs

Currently, GLONASS IFCB errors have not been studied and understood yet. Their long-term variation characteristics, predictability, and effect on the GLONASS FDMA + CDMA triple-frequency PPP have not been reported. To fully understand the IFCB characteristics of six GLONASS satellites and perform triple-frequency PPP, this section will investigate the IFCB series in detail.

First, we estimate the three-day IFCB series of six GLONASS satellites with the epoch-differenced method as shown in Fig. 2. From the figure, we know that the IFCB series of satellites R04, R05, R12, R21, and R26 vary significantly with an RMS of 0.06, 0.07, 0.15, 0.26, and 0.21 m, respectively, while that of satellite R09 vary insignificantly with an RMS of less than 0.01 m. Three-day IFCB peak-to-peak amplitudes are − 0.204–0.149 (R04), − 0.079–0.194 (R05), -0.020–0.023 (R09), − 0.152–0.332 (R12), − 0.540–0.214 (R21) and − 0.386–0.454 (R26) m, respectively.

Fig. 2
figure 2

Three-day IFCB series of the satellites R04, R05, R09, R12, and R21 on DOY 120–122, 2020

Full size image

Furthermore, some satellite IFCB series, e.g., R05, R12, R21, R26, show clearly sine-wave characteristics, which are expected to be modeled future. Limited by the number of G3 observations and data quality, the estimated quality of satellite R04 is relatively poor. There are no G3 observations of satellite R04 at some epochs and hence no IFCB estimates are obtained in Fig. 2. Therefore, G3 observations of satellite R04 are not involved in our PPP process.

In addition to the analysis of IFCB intra-day characteristics, inter-day characteristics are also a focus. Figure 3 shows the 150-day IFCB series of six GLONASS satellites. From the figure, we found that IFCB variation characteristics vary from satellite to satellite. IFCB series of GLONASS-K1 satellite R09 vary insignificantly with an RMS of less than 0.01 m. while that of satellite R04, R05, R12, R21, and R26 vary significantly with an RMS of 0.11, 0.14, 0.13, 0.16 and 0.67 m. Peak-to-peak amplitudes are (− 0.53–0.36 (R04), (− 0.42, –0.52, R05), (− 0.04, − 0.04, R09), (− 0.68, − 0.52, R12), (− 0.62, − 0.50, R21) and (− 1.68, − 1.16, R26) in meters, respectively. No obvious IFCB errors of satellite R09 can be observed. The possible cause is that R09 belongs to the newly launched GLONASS-K1 satellites, while other satellites (R04, R05, R12, and R21. R26 is excluded since it is under the testing mode) belong to old GLONASS-M + satellites. Therefore, this difference of IFCBs may originate from GLONASS satellite types.

Fig. 3
figure 3

IFCB series of the satellite R04, R05, R09, R12, and R21 from DOY 1–150, 2020. Note that the ordinate of the R26 y-axis is different from that of R21

Full size image

Following Montenbruck et al. (2012) and Pan et al. (2017a), we know that internal temperature variations of satellites due to varying sun illumination (depending on the relative geometry of the sun-spacecraft-earth) cause the IFCB variations. During the eclipse phase, the IFCB amplitude increases by a factor of up to ten times.

Furthermore, it can be seen from the figure that the IFCB series of satellites R05, R12, R21, and R26 show periodic repetition characteristics, which can be expected to be modeled even predicted future. The similarity degree between single-day IFCB time series of two different days can be assessed by the cross-correlation (Bona 2000). It is found that the repetition cycle of the IFCB series is about eight days. Cross-correlation analysis is performed on the single-day IFCB time series for two days with an interval of eight days. The normalized cross-correlation results for each satellite are shown in Fig. 4. For R05, R21, and R26, results show that the cross-correlation values are larger than 0.6 for most cases, and average values are about 0.88, 0.96, and 0.93, respectively, indicating pretty high correlations. For R04 and R12, the average cross-correlation values are 0.66 and 0.76, which also show high similarity between waveforms of the IFCB series for two days. Besides, R09 shows low similarity for the two days, which may be attributed to the insignificant IFCB variations.

Fig. 4
figure 4

Cross-correlations between IFCB time series of two days with an interval of eight days

Full size image

It has been presented by Zhang et al. (2021b) that GPS triple-frequency PPP performance can be significantly degraded without IFCB corrections, whose IFCB peak-to-peak amplitudes are about 0.2 m. In this contribution, GLONASS satellites show larger IFCB peak-to-peak amplitudes. Therefore, the impact of IFCB errors on the GLONASS triple-frequency PPP model must be carefully investigated.

Validation of triple-frequency uncombined PPP considering IFCB errors.

As discussed above, there are currently no precise products for satellite R26; hence, R26 is not involved in our PPP process. Besides, due to the lack of enough observations, G3 observations of satellite R04 are neglected. Therefore, G3 observations of GLONASS satellites R05, R09, R12, and R21 are utilized in the following experiments of this contribution. The positioning accuracy is evaluated using the float PPP solutions at the last epoch.

PPP performance at station BRUX is analyzed first. GLONASS CDMA-transmitting satellites at BRUX station on DOY 120 of 2020 are tracked. Their receiver-satellite geometry is shown in the skyplot of Fig. 5. Figure 6 shows the three groups of GLONASS PPP solutions at station BRUX on DOY 120, 2020. The figure shows that triple-frequency PPP with IFCB corrections achieves the best convergence performance among all three schemes. After calibrating IFCB errors correctly, the positioning accuracy of triple-frequency PPP can be significantly improved from (3.7, 10.7, 10.3, 15.2) mm to (2.0, 1.5, 9.8, 10.1) mm, with an improvement of (44.1%, 86.0%, 4.9%, 33.8%) in the north, east, up, 3D directions, respectively. Compared with dual-frequency PPP solutions, triple-frequency PPP with IFCB corrections improves positioning accuracy on the 3D direction component by about 11.7%. The improvement is relatively marginal, which may be partly because of the limited number of G3 observations available currently. Besides, it is found that without calibrating IFCB errors, triple-frequency PPP performance can be even worse than dual-frequency. That’s to say, calibrating IFCB errors is of great necessity for GLONASS triple-frequency PPP.

Fig. 5
figure 5

Skyplot of the GLONASS CDMA-transmitting satellites at BRUX station on DOY 120 in 2020, with the cutoff elevation angle of 10°

Full size image
Fig. 6
figure 6

Three groups of GLONASS PPP solutions at station BRUX on DOY 120 in 2020

Full size image

Measurement noises and other unmodeled errors are usually part of the observation a posteriori residual. To further evaluate the PPP model and validate IFCB, the phase a posteriori residual analysis is carried out. Figure 7 shows the distribution of phase a posteriori residuals of GLONASS triple-frequency PPP at station BRUX on DOY 120, 2020. From the figure, we know that the RMS value of a posteriori phase residuals with IFCB corrections on G1, G2, and G3 frequency is significantly reduced from (4.2, 11.1, 11.9) mm to (2.6, 2.2, 2.3) mm, with an improvement of (38.1%, 80.2%, 80.7%). The periodic term on each frequency is effectively eliminated.

Fig. 7
figure 7

Posteriori phase residuals of GLONASS triple-frequency uncombined PPP at BRUX station on DOY 120 in 2020

Full size image

Then a posteriori phase residual of each satellite on G1, G2 and G3 frequency is calculated and plotted in Fig. 8. From the figure, it can be seen that the RMS values of a posteriori phase residuals of satellites R05, R09, R12, and R21 on each frequency are significantly reduced after IFCB corrections, especially on the G2 and G3 frequency.

Fig. 8
figure 8

RMS of a posteriori phase residuals of satellites R05, R09, R12, and R21 on G1, G2, and G3 frequency with and without IFCB corrections on DOY 120 in 2020

Full size image

Table 6 shows the average 30-day triple-frequency PPP positioning errors at above six stations recorded from DOY 120 to 150, 2020. After calibrating IFCBs, GLONASS triple-frequency PPP achieves an average positioning accuracy from (5.8, 11.4, 11.3, 16.9) mm to (3.6, 5.4, 7.7, 10.1) mm, with an improvement of (37.9%, 52.6%, 31.9%, 40.2%) in north, east, up, 3D components, respectively. The statistical results further indicate the necessity of correcting IFCB errors for GLONASS triple-frequency PPP.

Table 6 Average 30-day triple-frequency PPP positioning errors at six stations in the north, east, up, 3D components of each scheme
Full size table

Compared with dual-frequency PPP solutions, after integrating CDMA signals and employing IFCB corrections, triple-frequency PPP improves the 3D positioning accuracy from 11.2 to 10.1 mm, and the marginal improvement is only about 1 mm. The additional third CDMA frequency has only a marginal contribution to positioning accuracy. This result is not surprising because the additional third frequency almost does not contribute to the improvement of satellites’ spatial geometries (Zhou and Xu 2021, Elsobeiey 2015). Also, our triple-frequency PPP performance is currently limited by the number of third CDMA observations. With more new GLONASS CDMA signals available in the future, PPP performance integrating FDMA and CDMA signals can be expected to be further improved.

Summarily, triple-frequency solutions with IFCB corrections achieve the best PPP performance. Besides, we have noted that if IFCB corrections are not employed, GLONASS triple-frequency PPP performance is even worse than dual-frequency. Therefore, IFCB errors must be calibrated beforehand to perform GLONASS triple-frequency PPP.

There are three main benefits of our contribution. First, long-term GLONASS IFCB variation characteristics and predictability of 4 GLONASS-K1 and 2 GLONASS-M + satellites are comprehensively investigated and understood. Some important conclusions have been drawn. Second, a new triple-frequency FDMA + CDMA PPP model considering IFCB corrections is presented and FDMA + CDMA PPP performance is evaluated. Experimental results indicate the necessity of correcting GLONASS IFCB errors. Besides, the additional third CDMA frequency significantly improves positioning accuracy compared with dual-frequency solutions. Finally, given that high-accuracy float solutions can be achieved by the GLONASS triple-frequency PPP presented here, the GLONASS triple-frequency PPP with ambiguity resolution can be developed further based on this.

Conclusions

With the modernization of the GLONASS system, six satellites are transmitting both CDMA observations on G3 frequency and FDMA observations on G1, G2 frequency currently, making it possible for joint use of GLONASS FDMA and CDMA signals simultaneously for PPP. In this contribution, GLONASS IFCBs are comprehensively investigated, and FDMA + CDMA PPP is validated. Some conclusions can be summarized as follows.

  1. 1.

    Intra-day IFCB series of satellite R04, R05, R12, R21, and R26 vary significantly with an RMS of 0.06, 0.07, 0.15, 0.26, and 0.21 m, respectively, while that of satellite R09 vary insignificantly with an RMS of less than 0.01 m; The variation characteristics of long-term 150-day IFCB series are also investigated, results indicate that GLONASS IFCB variation characteristics vary from satellite to satellite. Peak-to-peak amplitudes of the IFCB series are (− 0.53–0.36 (R04), (− 0.42, − 0.52, R05), (− 0.04, − 0.04, R09), (− 0.68, − 0.52, R12), (− 0.62, − 0.50, R21) and (− 1.68, − 1.16, R26) in meters, respectively. No obvious IFCB errors of satellite R09 can be observed. The possible cause is that R09 belongs to the newly launched GLONASS-K1 satellites, while other satellites (R04, R05, R12, and R21. R26 is excluded since it is under the testing mode) belong to old GLONASS-M + satellites. Therefore, the difference in IFCBs may originate from GLONASS satellite types. Besides, it is found that the repetition cycle of the IFCB series is about eight days. The average normalized cross-correlation values of satellite R05, R21, and R26 between IFCB series of two days with an interval of eight days are about 0.88, 0.96, and 0.93, respectively, which can be expected to be modeled even predicted future.

  2. 2.

    After employing IFCB corrections, GLONASS triple-frequency PPP achieves an average positioning accuracy from (5.8, 11.4, 11.3, 16.9) mm to (3.6, 5.4, 7.7, 10.1) mm, with an improvement of (37.9%, 52.6%, 31.9%, 40.2%) in north, east, up, 3D components, respectively, suggesting the necessity of correcting IFCB errors. The RMS value of a posteriori phase residuals with IFCB corrections on G1, G2, and G3 frequency is significantly reduced from (4.2, 11.1, 11.9) mm to (2.6, 2.2, 2.3) mm, with an improvement of (38.1%, 80.2%, 80.7%). The periodic term on each frequency is effectively eliminated. Besides, compared with dual-frequency PPP solutions, after integrating CDMA signals and employing IFCB corrections, triple-frequency PPP improves the 3D positioning accuracy from 11.2 to 10.1 mm, the marginal improvement is only about 1 mm. Limited by the number of observations, the additional third CDMA frequency has only a marginal contribution to positioning accuracy currently. Summarily, triple-frequency solutions with IFCB corrections achieve the best PPP performance.

  3. 3.

    Given that high-accuracy float solutions can be obtained by the GLONASS triple-frequency PPP presented here, the GLONASS triple-frequency PPP with ambiguity resolution can be further developed based on this.