Introduction

In order to obtain precise positioning results over long baselines, one typically uses dual-frequency GPS phase and code measurements to eliminate ionosphere delays and to estimate the phase ambiguities. The existing dual-frequency GPS long-range approach can achieve centimeter-level positioning results with an observation period of several hours provided that the systematic errors are carefully handled (Blewitt 1989). There are many applications for this technique, e.g., estimation of surface displacements caused by major earthquakes (Yang et al. 2000), the establishment of reference coordinate systems (Schwarz and Wade 1990; Overgaauw et al. 1994; Yang et al. 2001), and the determination of velocity field of tectonic plates (Ching et al. 2011).

In the new Global Navigation Satellite Systems (GNSS), the mutually interoperable modernized GPS and Galileo constellations are available for civil use. Compared with the current dual-frequency GPS (BLOCK IIA, IIR, and IIM), the new modernized GPS (BLOCK IIF and BLOCK III) provides three civil frequencies. In addition to the former frequencies L1 and L2, a third frequency L5 has been added (Braschak et al. 2010). Also, the Galileo constellation developed by the European Union will provide three civilian frequencies (E1, E5b, and E5a). Galileo is highly compatible and interoperable to GPS with respect to the time reference system, the geodetic coordinate reference frame, and the signal structure (Hofmann-Wellenhof et al. 2008). Regarding the time reference systems, GPS and Galileo operate on separate time systems, which results in an offset called GGTO (GPS-Galileo Time Offset); fortunately, GGTO can be easily removed in baseline computation or by introducing an additional parameter (Moudrak et al. 2004). As to the geodetic coordinate reference frames, WGS84 and GTRF are associated with GPS and Galileo, respectively. The discrepancy between WGS84 and GTRF will be limited to within 3 cm (2 sigma) (Gendt et al. 2011), which is negligible for most precise applications. For the signal structures, parts of the frequency spectra of Galileo overlap the frequency spectra of GPS (Rebeyrol et al. 2007). Combining GPS and Galileo provides a better positioning accuracy because of more available satellites (O’Keefe 2001). Over baselines up to tens of kilometers, combining GPS and Galileo can effectively improve the ambiguity resolution performance as well as the internal and external reliability (Verhagen 2002); also, it is possible to achieve the level of 95 % success rate in instantaneous ambiguity resolution performance over 20–30 km baselines (Tiberius et al. 2002).

Baseline computation utilizes the phase measurements to obtain centimeter-level positions, but the associated integer ambiguities must be determined. Considering the determination of triple-frequency ambiguities in the future, many methods have been proposed for GPS and Galileo, such as TCAR (Three-Carrier Ambiguity Resolution) (Vollath et al. 1998) and LAMBDA (Least-squares AMBiguity Decorrelation Adjustment) (Teunissen 1995; Teunissen et al. 2002). The basic theory of TCAR uses a geometry-free bootstrapping and rounding method to obtain integer ambiguities. The early TCAR is restricted by baseline lengths (Hatch et al. 2000). Hence, a long-range TCAR unifying the geometry-free method and elimination of ionosphere delays has been developed (Feng and Li 2008; Feng and Rizos 2009; Li et al. 2010). Different from the concept of bootstrapping, LAMBDA reduces the correlations in the covariance matrix of ambiguities.

With the expected benefits of combining modernized GPS and Galileo, it is of interest to investigate the performance improvements of long baselines up to hundreds or thousands of kilometers for geodetic and geophysical studies. Therefore, in this study, we develop a GPS/Galileo long-range approach, which is based on the current dual-frequency GPS long-range approach, to process the mutually compatible GPS and Galileo triple-frequency measurements. In order to evaluate the performance improvements, actual GPS measurements and the associated GPS/Galileo simulated data are used.

Double-differenced ionosphere-free phase and phase-code linear combinations

Linear combinations of double-differenced (DD) dual-frequency GPS measurements have been regularly used to eliminate satellite and receiver clock errors, hardware delays, and to reduce atmosphere delays (Bossler et al. 1980). For long baseline computation, the L1/L2 ionosphere-free (IF) combination has been used to eliminate first-order ionosphere delays, and the L1/L2/P1/P2 phase-code (PC) combination has been used to resolve wide-lane ambiguities (Melbourne 1985; Blewitt 1989). With the advent of the triple-frequency modernized GPS and Galileo, besides the L1/L2 IF and PC combinations, more IF and PC linear combinations are available.

DD measurements of modernized GPS and Galileo

The DD triple-frequency phase and code measurements of modernized GPS and Galileo can be, respectively, given as (Hofmann-Wellenhof et al. 2008),

$$ \varDelta \nabla \varPhi_{i} = \varDelta \nabla \rho - \frac{{f_{1}^{2} }}{{f_{i}^{2} }} \cdot \varDelta \nabla I + \varDelta \nabla T + \lambda_{i} \cdot \varDelta \nabla N_{i} + \varepsilon_{{\varDelta \nabla \varPhi_{i} }} $$
(1)
$$ \varDelta \nabla P_{i} = \varDelta \nabla \rho + \frac{{f_{1}^{2} }}{{f_{i}^{2} }} \cdot \varDelta \nabla I + \varDelta \nabla T + \varepsilon_{{\varDelta \nabla P_{i} }} $$
(2)

where the subscript i equals 1, 2, or 3 and refers to the three frequencies associated with modernized GPS and Galileo, respectively (Table 1). The symbol Δ∇ refers to the DD operator, Φ is the phase measurement in range, P is the pseudorange or code, f is the frequency, ρ refers to the geometric distance between the satellite and the receiver, I is the ionosphere delay on frequency L1 or E1; T is the troposphere delay, N is the ambiguity, λ is the wavelength, and ɛ is the noise plus multipath effect.

Table 1 Triple-frequency signals of the modernized GPS and Galileo
Full size table

The general form of triple-frequency linear combinations

A linear function transforms simultaneous triple-frequency measurements into one specific measurement. Following Feng (2008), the linear combination equation for the phase and code measurements is expressed as

$$ \varDelta \nabla \varPhi_{(i,j,k)} = \frac{{i \cdot f_{1} \varDelta \nabla \varPhi_{1} + j \cdot f_{2} \varDelta \nabla \varPhi_{2} + k \cdot f_{3} \varDelta \nabla \varPhi_{3} }}{{i \cdot f_{1} + j \cdot f_{2} + k \cdot f_{3} }} $$
(3)
$$ \varDelta \nabla P_{(l,m,n)} = \frac{{l \cdot f_{1} \varDelta \nabla P_{1} + m \cdot f_{2} \varDelta \nabla P_{2} + n \cdot f_{3} \varDelta \nabla P_{3} }}{{l \cdot f_{1} + m \cdot f_{2} + n \cdot f_{3} }} $$
(4)

The combined phase and code measurements are, respectively, defined as

$$ \varDelta \nabla \varPhi_{(i,j,k)} = \varDelta \nabla \rho - \beta_{(i,j,k)} \cdot \varDelta \nabla I + \varDelta \nabla T + \lambda_{(i,j,k)} \cdot \varDelta \nabla N_{(i,j,k)} + \varepsilon_{{\varDelta \nabla \varPhi_{(i,j,k)} }} $$
(5)
$$ \varDelta \nabla P_{(l,m,n)} = \varDelta \nabla \rho + \beta_{(l,m,n)} \cdot \varDelta \nabla I + \varDelta \nabla T + \varepsilon_{{\varDelta \nabla P_{(l,m,n)} }} $$
(6)

where i, j, k, l, m and n are predefined integer coefficients. The wavelength of the combined phase measurement is

$$ \lambda_{(i,j,k)} = \frac{c}{{i \cdot f_{1} + j \cdot f_{2} + k \cdot f_{3} }} $$
(7)

where c is the speed of light. The ambiguity of the combined phase measurement is

$$ \varDelta \nabla N_{(i,j,k)} = i \cdot \varDelta \nabla N_{1} + j \cdot \varDelta \nabla N_{2} + k \cdot \varDelta \nabla N_{3} $$
(8)

The amplifying factors of first-order ionosphere delays for the combined phase and code measurements are expressed as

$$ \beta_{(i,j,k)} = \frac{f_{1}^{2} \cdot (i/f_1 + j/f_{2} + k/f_{3})}{i \cdot f_1+j\cdot f_2+k\cdot f_3}$$
(9)
$$ \beta_{(l,m,n)} = \frac{f_{1}^{2} \cdot (l/f_{1} + m /f_{2} + n/f_{3})}{l\cdot f_1+m\cdot f_2+n\cdot f_3} $$
(10)

The variance of the combined phase measurements can be obtained by the error propagation theorem (Leick 2004), given as

$$ \begin{aligned} \sigma_{{\varDelta \nabla \varPhi_{(i,j,k)} }}^{2} &= \frac{{(i \cdot f_{1} )^{2} + (j \cdot f_{2} )^{2} + (k \cdot f_{3} )^{2} }}{{(i \cdot f_{1} + j \cdot f_{2} + k \cdot f_{3} )^{2} }} \cdot \sigma_{\varDelta \nabla \varPhi }^{2} \hfill \\ &= A_{{_{(i,j,k)} }}^{2} \cdot \sigma_{\varDelta \nabla \varPhi }^{2} \hfill \\ \end{aligned} $$
(11)

where it is assumed that the variances of DD triple-frequency phase measurements are the same, i.e., \( \sigma_{{\varDelta \nabla \varPhi_{1} }}^{2} = \sigma_{{\varDelta \nabla \varPhi_{2} }}^{2} = \sigma_{{\varDelta \nabla \varPhi_{3} }}^{2} = \sigma_{\varDelta \nabla \varPhi }^{2} \). The amplifying factor of the combined phase measurements is A (i,j,k). Similarly, the variance of the combined code measurements is

$$ \begin{aligned} \sigma_{{\varDelta \nabla P_{(l,m,n)} }}^{2} &= \frac{{(l \cdot f_{1} )^{2} + (m \cdot f_{2} )^{2} + (n \cdot f_{3} )^{2} }}{{(l \cdot f_{1} + m \cdot f_{2} + n \cdot f_{3} )^{2} }} \cdot \sigma_{\varDelta \nabla P}^{2} \hfill \\ \, &= A_{(l,m,n)}^{2} \cdot \sigma_{\varDelta \nabla P}^{2} \hfill \\ \end{aligned} $$
(12)

where it is assumed that the variances of DD triple-frequency code measurements are the same, i.e., \( \sigma_{{\varDelta \nabla P_{1} }}^{2} = \sigma_{{\varDelta \nabla P_{2} }}^{2} = \sigma_{{\varDelta \nabla P_{3} }}^{2} = \sigma_{\varDelta \nabla P}^{2} \). The amplifying factor of the combined code measurements is A (l,m,n).

The IF phase combinations

The ionosphere delay is one of the main errors on phase and code measurements. In order to eliminate the most significant first-order delays, specific predefined integer coefficients for phase combinations can be derived as a function of the frequencies (Leick 2004). Table 2 shows the predefined integer coefficients and the related information for the IF combinations; the definition of the integer coefficients can be found in Odijk (2003). The IF combinations are given in (5), and the specific coefficients are listed in Table 2. With the amplifying factors of ionosphere delays β (i,j,k) equal to zero, the IF combinations are not affected by the first-order ionosphere delays.

Table 2 IF combinations and the related information for the modernized GPS and Galileo
Full size table

However, it is impossible to resolve the ambiguity on each frequency due to rank deficiency in the least-squares adjustment if we only use the phase IF combinations (Teunissen and Odijk 2003); in order to overcome the problem, additional information obtained from wide-lane ambiguity solutions is generally applied (Blewitt 1989).

The PC combinations

For resolving the additional information of wide-lane ambiguity solutions, the PC combination is used. The PC combination is a function of the phase and code measurements and is also called the Melbourne-Wübbena (MW) linear combination (Melbourne 1985), which is a very popular combination to obtain wide-lane ambiguity solutions. Combining (5) and (6), the PC combination is given as (Feng and Rizos 2009):

$$ \begin{aligned} \varDelta \nabla N_{PC, (i,j,k,l,m,n )} &= \varDelta \nabla \varPhi_{ (i,j,k )} - \varDelta \nabla P_{ (l,m,n )} \hfill \\ &= \lambda_{ (i,j,k )} \cdot \varDelta \nabla N_{(i,j,k)} - (\beta_{ (i,j,k )} + \beta_{ (l,,m,n )} ) \cdot \varDelta \nabla I + \varepsilon_{{\varDelta \nabla N_{{{\text{PC}}, (i,j,k,l,m,n )}} }} \hfill \\ &= \lambda_{ (i,j,k )} \cdot \varDelta \nabla N_{(i,j,k)} - \beta_{ (i,j,k ,l,m,n )} \cdot \varDelta \nabla I + \varepsilon_{{\varDelta \nabla N_{{{\text{PC}}, (i,j,k,l,,m,n )}} }} \hfill \\ &= \lambda_{ (i,j,k )} \cdot \varDelta \nabla N_{(i,j,k)} + \varepsilon_{{\varDelta \nabla N_{{{\text{PC}}, (i,j,k,l,m,n )}} }} \, \hfill \\ \end{aligned} $$
(13)

where the predefined coefficients are given in Table 3. The PC combination is independent of the geometry and troposphere delays; moreover, the first-order ionosphere delays can be eliminated as well because the amplifying factor of the ionosphere delay β (i,j,k,l,m,n) in (13) is zero. Hence, only the wide-lane ambiguity and the noise terms remain in the PC combination.

Table 3 PC combinations and the related information for the modernized GPS and Galileo
Full size table

Again, by the error propagation theory, the variance of the PC combination is given as

$$ \begin{aligned} \sigma_{{\varDelta \nabla N_{{{\text{PC}},(i,j,k,l,m,n)}} }}^{2} &= \left( {0.01^{2} \cdot A_{(i,j,k)}^{2} + A_{(l,m,n)}^{2} } \right) \cdot \sigma_{\varDelta \nabla P}^{2} \hfill \\ \, &= A_{(i,j,k,l,m,n)}^{2} \cdot \sigma_{\varDelta \nabla P}^{2} \hfill \\ \end{aligned} $$
(14)

where it is assumed that \( \sigma_{\varDelta \nabla \varPhi }^{2} = 0.01^{2} \cdot \sigma_{\varDelta \nabla P}^{2} \) and A (i,j,k,l,m,n) refer to the amplifying factor of the PC combination.

The generalized GPS/Galileo long-range approach

The existing dual-frequency long-range GPS approach combines the L1/L2 IF and PC combinations to resolve the integer phase ambiguities and obtains the positioning solutions. However, the triple-frequency GPS/Galileo additionally provides the L1/L5, L2/L5, E1/E5b, E1/E5a, and E5b/E5a IF and PC combinations, as defined in Tables 2 and 3. Thus, a computer program created to make use of the L1/L2 and additional IF and PC combinations is called the generalized GPS/Galileo long-range approach (GLA) in this study. GLA is capable of processing dual or triple-frequency and single or dual-constellation measurements.

Systematic errors handling

In general, when a baseline exceeds 20 km, some systematic errors in GNSS have to be considered. The handling of the systematic errors and the detailed strategies used in GLA are shown in Table 4.

Table 4 Strategies of systematic error handling
Full size table

The observation sets

Since multiple IF and PC combinations are available for triple-frequency GPS/Galileo, we can define different observation sets to process these combinations. An observation set consists of an IF combination and its associated PC combination. For example, the L1/L2 observation set comprises the L1/L2 IF and PC combinations. Hence, from Tables 2 to 3, we can generate observation sets L1/L2, L1/L5, L2/L5 for triple-frequency GPS, and E1/E5b, E1/E5a, E5b/E5a for Galileo.

However, the above six observation sets are not mutually independent; for instance, the L2/L5 IF combination is a linear combination of the L1/L2 and L1/L5 IF combinations, and also the E5b/E5a IF combination is a linear combination of the E1/E5b and E1/E5a IF combinations. As a result, only four observation sets can be considered. The four observation sets are chosen as L1/L2, L1/L5, E1/E5b, and E1/E5a since the amplifying factors of the four IF combinations are smaller than those of the L2/L5 and E5b/E5a IF combinations (Table 2).

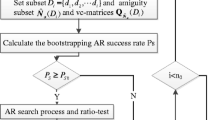
Because each observation set only uses dual-frequency measurements, it only represents a dual-frequency single-constellation case. In order to represent triple-frequency and/or dual-constellation situations, multiple observation sets should be used. Fig. 1 illustrates six main cases and their associated observation sets. The six main cases are dual-frequency GPS, dual-frequency Galileo, dual-frequency GPS/Galileo, triple-frequency GPS, triple-frequency Galileo, and triple-frequency GPS/Galileo, respectively.

Fig. 1
figure 1

Six main cases and their observation sets

Full size image

Parameter estimation

The least-squares adjustment is used to estimate the unknown parameters. The estimated parameters are given as follows (Leick 2004):

$$ \varvec{L} = \varvec{Ax} + \varvec{v}\quad \varvec{v}\sim N(0,\varvec{W}^{ - 1} ) $$
(15)
$$ \hat{\varvec{x}} = (\varvec{A}^{T} \varvec{WA})^{ - 1} \varvec{A}^{T} \varvec{WL} $$
(16)

where L is the vector of measurements involving the chosen observation sets, and A is the linearization design matrix. The estimated parameter vector \( \hat{\varvec{x}} \) includes three baseline vector (dx, dy, dz), DD ambiguities on each involved frequency (e.g., \( \varDelta \nabla N_{1} \), \( \varDelta \nabla N_{2} \), and \( \varDelta \nabla N_{3} \) in the triple-frequency case), and ZTD parameters. The covariance matrix of measurements is \( \varvec{W}^{ - 1} \), which is derived according to the error propagation theorem.

The initial adjustment yields the float solution. GLA uses the LAMBDA method to find integer ambiguity, and the result is called the fix solution. For obtaining the fix solution, integer ambiguity validation is necessary. The well-known ratio test value is adopted for the validation in GLA. Generally, the larger the ratio test value, the more reliable the integer resolution is obtained (Euler and Schaffrin 1990).

Validating positioning accuracy of GLA

Two test baselines are used for the validation. The first baseline is about 134 km in length, connecting the two tracking stations CKSV and LSB0 located in Taiwan. The second baseline is about 2,243 km, connecting the IGS station TSKB of Japan to the tracking station FLNM of Taiwan. Such long baselines are often used for computing daily solutions, which are required in many geodetic and geophysical activities, such as tectonic motion monitoring.

The continuous 7 daily measurements collected at these sites are used to compute the daily solutions. In order to validate the positioning accuracy of GLA, a comparison with Bernese GPS Software v5.0 is made. Bernese GPS Software v5.0, developed at the University of Bern, is widely used for scientific studies (Beutler et al. 2007). It is generally acknowledged that the Bernese results are very reliable.

The 7-day baseline vectors (dx, dy, dz) are computed for the case L1/L2, where the elevation cutoff angle was 15°, and the number of ZTD parameters is one per station per hour. Also, we obtained the computational results by the Bernese software. The comparison is shown in Table 5. The mean differences are quite small in comparison, and the STD values are also very compatible (the 3D STD is ±0.010 m for Bernese and ±0.012 m for GLA over CKSV-LSB0; ±0.017 m for Bernese and ±0.015 m for GLA over TSKB-FLNM). The comparison shows that the long-range relative positioning accuracy of Bernese and GLA is in good agreement.

Table 5 Mean and STD values of the continuous 7-day baseline vectors over the test baselines
Full size table

Analysis of performance improvements

Here, we discuss the performance improvements with respect to positioning accuracy and ambiguity resolution, respectively. In order to analyze the improvements, a data simulator based on the commercial package Satellite Navigation Toolbox 3.0 (GPSoft 2003) has been developed at National Cheng Kung University. The simulator is used to generate GPS and Galileo triple-frequency measurements of the baselines for the six main cases, represented as L1/L2, E1/E5b, L1/L2/L5, E1/E5b/E5a, L1/L2/E1/E5b, and L1/L2/L5/E1/E5b/E5a, respectively.

Even when the IGS precise orbit is used, there is still orbital error remaining on the measurements (Dow et al. 2005). Besides the orbital error, measurement noises and multipath effects are magnified in the IF and PC combinations. The orbital error and magnified noises and multipath effects are thus the limiting factors of the performance of long baseline computation (Kleusberg and Teunissen 1996). So, in the analysis, it is assumed that the orbital error is simulated at the level of the precise orbit, and we aim at analyzing the influence of measurement noises and the multipath effects for the six cases.

Data simulation

Table 6 shows the information of the GPS and Galileo constellations used by the simulator. The constellations are set to circular orbits to approximate the actual elliptic orbits for simplification as the eccentricities of the actual elliptic orbits are very small (Liu et al. 2007). The simulator calculates geometric distances between the satellite and receiver using the information in Table 6 and adds simulated errors to the geometric distance. The simulator takes into considerations the major errors existed in the observations, including measurement noises, atmosphere delays, orbital errors, and multipath effects. The noises are generated by Gaussian distribution with a zero mean and presented as white noise. The multipath effect is to pass a chosen white noise through a first-order low-pass Butterworth filter (Rafael and Woods 2002), as illustrated in Fig. 2. The atmosphere errors are created using known models. The ionosphere delays are produced by the Klobuchar model (Klobuchar 1987) and the troposphere delays by the modified Hopfield model (Hopfield 1969). Finally, the orbital error is treated as white noise and generated by Gaussian distribution with a zero mean.

Table 6 Constellation characteristics used by the simulator
Full size table
Fig. 2
figure 2

Illustration of the simulated multipath effect (colored noises) on the L1 phase of PRN1

Full size image

The triple-frequency GPS/Galileo measurements of the two baselines are then generated by the simulator. The detailed description of the simulated errors is given in Table 7. In order to analyze the influence of different levels of measurement noise, equal precision for all frequencies can be assumed for the phase and code measurements (Ji et al. 2007).

Table 7 Simulated errors of the test baselines
Full size table

Improvement on positioning

We first assess the positioning accuracy of the two baselines for the six cases. Based on the mean baseline vector derived from Bernese in Table 5, continuous 7-day measurements with chosen levels of phase and code noises and multipath effects were simulated. After successfully obtaining the fix solutions with GLA, the 3D RMS (root mean square) values associated with the 7-day baseline errors for the six cases are displayed in Table 8. The 3D RMS values of the four single-constellation cases (L1/L2, L1/L2/L5, E1/E5b, and E1/E5b/E5a) are very similar to one another (1 mm maximum difference) and consistent with the 3D STD obtained from Bernese (see Table 5). Compared with the 3D RMS value of the L1/L2 single-constellation case, those of the two GPS/Galileo cases (L1/L2/E1/E5b and L1/L2/L5/E1/E5b/E5a) are improved by 4 mm (40 %) and 7 mm (41 %), for the two baselines, respectively. The results indicate that the use of the GPS/Galileo measurements is the main factor to improve long-range positioning accuracy thanks to the combined geometry of the two constellations.

Table 8 Comparison of 3D RMS values of the 7-day test baselines for the six cases
Full size table

Improvement on ambiguity resolution

Here, we discuss the influences of noise and multipath on the ambiguity resolution. The ambiguity resolution effectiveness of the six cases with respect to rapid static positioning is assessed since the influences of noise and multipath cannot be effectively lessened with a short observation period (Kleusberg and Teunissen 1996). We start with the first epoch and compute the accumulated epoch-by-epoch ratio test values for a short period of 30 min. A 30-min data span of TSLB-FLNM is used, during which there are 7 GPS and 7 Galileo satellites in view.

The performances with different levels of phase and code noise are evaluated first. In Fig. 3a, the selected phase noise of ±3 mm corresponds to the typical phase measurement resolution of about 0.01 cycles, and the selected code noise of ±0.3 m corresponds to the typical P-code noise (Hofmann-Wellenhof et al. 2008). The result shows that the GPS/Galileo cases (L1/L2/E1/E5b and L1/L2/L5/E1/E5b/E5a) produce higher ratio test values than the single-constellation cases (L1/L2, L1/L2/L5, E1/E5b, and E1/E5b/E5a), indicating that combined geometry can improve ambiguity resolution. The triple-frequency single-constellation cases (L1/L2/L5 and E1/E5b/E5a) produce higher ratio test values than the dual-frequency single-constellation cases (L1/L2 and E1/E5b), and also, the triple-frequency GPS/Galileo case (L1/L2/L5/E1/E5b/E5a) produces higher values than the dual-frequency GPS/Galileo case (L1/L2/E1/E5b), which means that the use of triple-frequency measurements can improve ambiguity resolution as well.

Fig. 3
figure 3

Ratio test values for the levels of noise (no multipath effects); (top) \( \sigma_{\varPhi ,n} \) = ±3 mm, \( \sigma_{P,n} \) = ±0.3 m; (middle) \( \sigma_{\varPhi ,n} \) = ±6 mm, \( \sigma_{P,n} \) = ±0.3 m; (bottom) \( \sigma_{\varPhi ,n} \) = ±3 mm, \( \sigma_{P,n} \) = ±3 m

Full size image

In Fig. 3b, the influence of phase noise is examined. The ratio test values of all cases at ±6 mm are significantly lower than those at ±3 mm. It indicates that the phase noise is a very important factor affecting ambiguity resolution in all cases.

In Fig. 3c, the influence of code noise is assessed. Compared with the ratio test values of the dual-frequency cases (L1/L2, E1/E5b, and L1/L2/E1/E5b) with code noise at ±0.3 m, the ratio test values of these cases with code noise at ±3 m (corresponding to the C/A-code noise) have decreased substantially, indicating that code noise produces severe effects on dual-frequency ambiguity resolution. On the other hand, triple-frequency ambiguity resolution (i.e., cases L1/L2/L5, E1/E5b/E5a, and L1/L2/L5/E1/E5b/E5a) is apparently less affected by the increased code noise.

The multipath effect is then analyzed, and the result is shown in Fig. 4. The magnitude of the simulated multipath is given at ±3 mm for the phase and ±3 m for the code. The ratio test values of the six cases in Fig. 4 have all become lower than those in Fig. 3c, as a result of the added multipath. However, the ratio test values of the triple-frequency cases (L1/L2/L5, E1/E5b/E5a, and L1/L2/L5/E1/E5b/E5a in particular) are notably higher than those of the dual-frequency cases (L1/L2, E1/E5b, and L1/L2/E1/E5b). This indicates that the multipath is also an important factor affecting ambiguity resolution, yet the use of triple-frequency GPS/Galileo measurements can considerably improve ambiguity resolution performance under the influence of multipath.

Fig. 4
figure 4

Ratio test values for the noise plus the multipath effect (\( \sigma_{\varPhi ,n} \) = ±3 mm, \( \sigma_{P,n} \) = ±3 m, \( \sigma_{\varPhi ,m} \) = ±3 mm, \( \sigma_{P,m} \) = ±3 m)

Full size image

Conclusions

In order to implement integrated GPS/Galileo data processing for long baseline computation up to thousands of kilometers, we have adopted a generalized long-range approach (GLA) for the handling of triple-frequency GPS/Galileo double-differenced measurements. The approach is capable of processing dual- or triple-frequency and single- or dual-constellation observations. It is demonstrated by using continuous 7-day GPS tracking data of two test baselines that GLA produces highly compatible long baseline results with the Bernese software.

The performances of positioning accuracy and ambiguity resolution of long baseline computation were examined using GLA and simulated GPS/Galileo measurements. The satellite geometry plays a critical role on the level of accuracy of daily baseline solutions. Dual-constellation GPS/Galileo can improve the accuracy as compared with the single-constellation cases. Additional frequencies and constellation can improve ambiguity resolution performance over the first 30 min of static data processing. However, the use of triple-frequency signals is the main factor for improving ambiguity resolution performance when code noise or multipath is large. In environments where large code noise or multipath is present, the single-constellation (GPS-only or Galileo-only) triple-frequency ambiguity resolution can outperform the GPS/Galileo dual-constellation dual-frequency case.