Asset allocation strategies based on penalized quantile regression

Abstract

It is well known that the quantile regression model used as an asset allocation tool minimizes the portfolio extreme risk whenever the attention is placed on the lower quantiles of the response variable. By considering the entire conditional distribution of the dependent variable, we show that it is possible to obtain further benefits by optimizing different risk and performance indicators. In particular, we introduce a risk-adjusted profitability measure, useful in evaluating financial portfolios from a ‘cautiously optimistic’ perspective, as the reward contribution is net of the most favorable outcomes. Moreover, as we consider large portfolios, we also cope with the dimensionality issue by introducing an $\ell _1$-norm penalty on the assets’ weights.

1 Introduction

Starting from the seminal contribution by Markowitz (1952) with the mean–variance portfolio theory, portfolio estimation and asset selection have received increasing attention from both a practitioner and an academic viewpoint. In the financial industry, asset allocation and security selection play central roles in designing portfolio strategies for both private and institutional investors. In contrast, academia focuses on developing the Markowitz approach over different research lines—linking it to market equilibrium, as done by Sharpe (1964), Lintner (1965a, b) and Mossin (1966); modifying the objective function both when it is set as a utility function and when it takes the form of a performance measure (Alexander and Baptista 2002; Farinelli et al. 2008) and developing tools to estimate and forecast the Markowitz model inputs, with great emphasis on return and risk.

Among the various methodological advancements, we focus on those associated with variations of the objective function or, more generally, those based on alternative representations of the asset allocation problem. Some of the various asset allocation approaches proposed in the last decades share a common feature: they have a companion representation in the form of regression models where the coefficients correspond or are linked to the assets’ weights in a portfolio. Two examples are given by estimating efficient portfolio weights by means of linear regression of a constant on asset excess returns (Britten-Jones 1999) and estimating the global minimum variance portfolio weights using the solution of a specific regression model; see e.g. Fan et al. (2012).

In the previously cited cases, portfolio variance plays a fundamental role in risk quantification. However, even if we agree regarding the relevance of variance (or volatility) for risk measurement and management, the financial literature now includes a large number of other indicators that might be more appropriate. For example, for an investor whose preferences or attitudes regarding risk are summarized by utility functions where extreme risk is present, volatility might be replaced by tail expectation. Moving away from the least squares estimation, although remaining confined within the regression models, it is possible to optimize non-standard objective functions. The leading example is given by Bassett et al. (2004), who proposed a pessimistic asset allocation strategy relying on the quantile regression method introduced by Koenker and Bassett (1978).

Bassett et al. (2004) start from the linear regression model, the solution to which provides the global minimum variance portfolio weights. The authors next show that estimating a low quantile, denoted as the $\alpha$-quantile (typically $\alpha =\{0.01,0.05,0.1\}$), of the response variable using the quantile regression method minimizes a measure of the portfolio extreme risk—the so-called $\alpha$-risk (Bassett et al. 2004). Therefore, a change in the estimation approach allows moving from the global minimum variance portfolio to the minimum $\alpha$-risk portfolio. Variants of the $\alpha$-risk are known under a variety of names, such as ‘expected shortfall’ (Acerbi and Tasche 2002), ‘conditional value-at-risk’ (Rockafellar and Uryasev 2000), and ‘tail conditional expectation’ (Artzner et al. 1999). Consequently, the pessimistic asset allocation strategy of Bassett et al. (2004) corresponds to an extreme risk minimization approach. The work by Bassett et al. (2004) also represents the starting point of our contributions. Building on quantile regression methods, we introduce innovative asset allocation strategies coherent with the maximization of a risk-adjusted performance measure. Moreover, we combine quantile regression with regularization methods, such as the least absolute shrinkage and selection operator (LASSO) (Tibshirani 1996), to cope with the problematic issues arising from the large portfolios’ dimensionality and the increasing estimation errors.

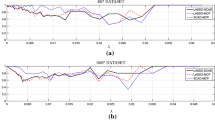
Our contributions provide an answer to specific research questions, with a potential application in the financial industry. The first research question originates from a limitation of the pessimistic asset allocation approach of Bassett et al. (2004), which is a risk minimization-driven strategy. Is it possible to maintain the focus on the $\alpha$-risk and at the same time maximize a performance measure, thus also taking into account rewards? Our first contribution consists of showing that quantile regression models can be used not only to build financial portfolios with minimum extreme risk, as already detailed in the literature, but also to optimize other risk and performance measures by exploiting the information contained in all the support of the response variable conditional distribution. We first note that under reasonable assumptions, at the median level, the quantile regression solution corresponds to the minimization of the mean absolute deviation of portfolio returns. We then show that at high quantile levels the quantile regression solution provides portfolio weights with an outstanding performance in terms of profitability and risk-adjusted returns. Such a solution corresponds to the maximization of a specific reward measure—the conditional expected return net of the most favorable outcomes. As a by-product, we introduce a risk-adjusted ratio that, to our knowledge, has not yet been investigated in the literature. Notably, it quantifies the magnitude of all the negative returns balanced by a subset of positive results, net of the most favorable ones. This method translates into a so-called ‘cautiously optimistic’ asset allocation that explicitly accounts for markets’ rebounds. In fact, in 55% of the cases in our dataset, the extreme positive outcomes (i.e. the assets’ returns exceeding their respective 90% in-sample percentiles) are preceded by the negative ones on average (see Fig. 1a).¹ Furthermore, the markets’ rebounds are frequent in periods of high volatility and crises; indeed, on average, the percentage of the extreme positive returns preceded by extreme negative returns (the ones lower than their 10% in-sample percentiles) is equal to 20% (Fig. 1b).² This evidence suggests that the extreme positive returns are not completely imputable to economic overperformance but rather to the bouncing back of the market. In other words, abnormal positive returns could be assumed to be reactions to high volatilities in crisis periods, rather than the outperformance of effective stocks. However, the evidence of negative rebounds, where we take into account the extreme negative outcomes (the returns lower than their 10% percentiles) preceded by positive or extreme positive returns, is slightly weaker.³ In addition, it is important to highlight that including the potential extreme negative outcomes in the optimization problem and simultaneously excluding the extreme positive ones emphasizes the prudential spirit of the asset allocation strategy we propose.

Fig. 1

Results for the constituents of the Standard & Poor’s 500 index continuously available from November 4, 2004 to November 21, 2014; see Sect. 3 for further details. Panels (a) and (b) display the proportion (%) of the extreme positive outcomes (that is the assets’ returns greater than their 90% percentiles) preceded by negative returns (a), or extreme negative returns, that is the assets’ returns lower than their 10% percentiles (b). We report in panels (a)–(b) the median and the first and the third quartiles over the rolled subsamples. The stocks are ordered according to the magnitude of their respective medians

Much of the work in the financial literature also highlights the unsatisfactory out-of-sample performance of the mean–variance approach introduced by Markowitz (1952). One of the most important reasons underlying this phenomenon refers to the estimation of the expected returns, which implies serious problems in terms of estimation errors; see, e.g. Brodie (1993) and Chopra and Ziemba (1993). Given that the markets’ rebounds contribute to the instability of the expected returns’ estimates, the idea of isolating their effect, as pointed out in our work, could be very useful in obtaining portfolios more robust to estimation errors. In general, given the impact of the estimation errors in the expected returns, the minimum variance portfolio has attracted significant attention, because it relies just on the estimation of the variance–covariance matrix (Brodie 1993; Chopra and Ziemba 1993). Similarly, our approach does not require the estimation of the stocks’ expected returns. Therefore, the strategy we propose could be useful for risk-seeking investors who compose financial portfolios in a context characterized by uncertainty and whose preferences do not depend just on risk but also on profitability, although in a robust and cautiously optimistic way.

The second research question stems from empirical evidence and practitioners’ needs. Financial portfolios are frequently built after picking the desired assets from a large universe. In maintaining a cautiously optimistic asset allocation strategy, we face a clear trade-off; on one hand, a large portfolio offers diversification benefits, but on the other hand the number of parameters to estimate with the quantile regression approach quickly increases as the portfolio dimension grows. As a result, the accumulation of estimation errors becomes a problem that must be addressed. Therefore, the question is whether we can control the estimation errors by maintaining the focus on the cautiously optimistic asset allocation approach. Our solution consists of imposing a penalty on the $\ell _1$-norm of the quantile regression coefficients along the line of the LASSO introduced by Tibshirani (1996) in a standard least squares regression framework. Recent studies show that applications of the LASSO to the mean–variance portfolio framework provide benefits in terms of the sparsity of the portfolio (indirectly associated with diversification/concentration and turnover) and good out-of-sample properties; see e.g. Brodie et al. (2009), DeMiguel et al. (2009), Fan et al. (2012), Yen and Yen (2014) and Fastrich et al. (2015). Gotoh and Takeda (2011) point out the better performance of both the norm-constrained value-at-risk minimization and the robust portfolio optimization in index tracking, reporting empirical results with the $\ell _2$-norm. In the statistical literature, the $\ell _1$-norm became a widely used tool not only in linear regression but also for quantile regression models (see, e.g. Koenker 2005; Belloni and Chernozhukov 2011; Li and Zhu 2008) while applications in asset allocation are still scarce. Härdle et al. (2014) used the penalized quantile regression as an asset selection tool in the index tracking framework to determine the assets to include in the portfolio; the assets’ weights are then estimated by optimizing as an objective function the Cornish–Fisher value-at-risk (CF–VaR). In contrast, in the approach we introduce, the penalized quantile regression model automatically selects and estimates the relevant assets’ weights in a single step. To the best of our knowledge, such an approach has never been investigated in the literature.

We evaluate the proposed ‘cautiously optimistic’ approach using extensive empirical analysis in which we compare the performance of the asset allocation strategies built from the quantile regression models at different quantile levels. In contrast to Bassett et al. (2004), we use both simulated and real-world data. Moreover, we analyse both the in-sample and the out-of-sample performances by implementing a rolling window procedure. Finally, we focus on portfolios with a large cross-sectional dimension, including almost 500 assets, which is not common in the literature being limited to just a few recent contributions (e.g. Aït-Sahalia and Xiu 2015; Fan et al. 2016). The in-sample results for both real-world and simulated data show that each strategy performs consistently according to expectations, optimizing their respective objective functions—the $\alpha$-risk, the mean absolute deviation and the upper tail-based reward measures. Indeed, the quantile regression applied at low probability levels outperforms the other strategies in terms of extreme risk. Least squares and median regression models turn out to be the best strategies in terms of volatility, as the former minimizes the portfolio variance and the latter minimizes the mean absolute deviation of portfolios’ returns. It transpires that the quantile regression at the high probability levels provides the best results in terms of profitability and risk-adjusted return. The out-of-sample results show that the quantile regression models maintain their in-sample properties but only at high probability levels.⁴ Finally, we highlight the critical importance of regularizing the quantile regression problem to improve the out-of-sample performance of portfolios characterized by a large cross-sectional dimension.

The work is structured as follows. In Sect. 2, we introduce the quantile regression model behind our ‘cautiously optimistic’ approach. In Sect. 3, we describe the empirical set-up. In Sect. 4, we discuss the main empirical findings and in Sect. 5 we provide the conclusion.

2 Asset allocation based on quantile regression

2.1 Portfolio performance as a function of quantile levels

Several asset allocation strategies estimate portfolio weights by optimizing a function typically taking the form of a utility, a risk or a performance measure or a combination of these. A subset of these asset allocation approaches has a companion representation in the form of a regression model where the estimated coefficients correspond to the portfolio weights. The leading example is the global minimum variance portfolio (GMVP), the composition of which is the solution to the ordinary least squares regression model.

In the case of a financial portfolio consisting of n stocks, let $\mathbf{R}=[R_1,\ldots ,R_n]$ be the row vector of the assets’ returns⁵ with covariance matrix , and let the row vector of weights be denoted by $\mathbf{w}=[w_1,\ldots ,w_n]$; given the $(1 \times n)$ unit vector $\mathbf{1}$, we impose the so-called budget constraint, that is $\mathbf{1} \mathbf{w}'=1$. The portfolio return is then $R_p=\mathbf{R} \mathbf{w}'$, but, as suggested by Fan et al. (2012), for example, we can also use a companion representation to directly include the budget constraint in the linear model. First, we set $R^*_i=R_n-R_i$ for $i=1,\ldots ,n-1$ and then use these deviations to compute the portfolio return, which becomes $R_p=R_n-w_1 R^*_1-\cdots -w_{n-1}R^*_{n-1}$, where the nth asset weight ensures the weights sum to 1. It is then possible to show that the minimization of the portfolio variance can be expressed as follows:

(1)

where $\xi$ is the intercept of the linear regression model, $\mathbf{w}_{-n}$ denotes the weights’ vector excluding $w_n$, with $w_n=1-\sum _{i=1}^{n-1}w_i$ to satisfy the budget constraint.

In Eq. (1), the portfolio variance, $\mathbf{w}\pmb {\varSigma }{} \mathbf{w}'$, is rewritten as . The latter corresponds to the variance of the errors for the linear regression of asset n returns, $R_n$, with respect to $R_i^*$. Therefore, it is possible to minimize $\mathbf{w}\pmb {\varSigma }{} \mathbf{w}'$ by minimizing the sum of squared errors of a linear regression model, with response variable $R_n$ and covariates $R^*_1,\ldots ,R^*_{n-1}$. Thus, estimating the coefficients $w_1,\ldots ,w_{n-1}$, along with the intercept $\xi$, is equivalent to finding the GMVP weights (Fan et al. 2012).⁶

Moving away from the least squares regression framework, the portfolio composition could be determined by optimizing alternative performance measures. For instance, Bassett et al. (2004) proposed a pessimistic asset allocation strategy that relies on quantile regression to minimize a risk measure, the so-called $\alpha$-risk. The latter equals:

$$\begin{aligned} \varrho _{\nu _\alpha }(R_p)=-\int _{0}^{1}F_{R_p}^{-1}(\vartheta )d\nu (\vartheta )=-\alpha ^{-1}\int _{0}^{\alpha }F_{R_p}^{-1}(\vartheta )d\vartheta , \end{aligned}$$

(2)

where $F_{R_p}(r_p)$ denotes the distribution function of $R_p$ evaluated at $r_p$, whereas $\vartheta$ is the quantile index such that $\vartheta \in \mathcal {U}$, with $\mathcal {U} \subset (0,1)$.

The $\alpha$-risk is a coherent measure of risk according to the definition of Artzner et al. (1999). Many variants of $\varrho _{\nu _\alpha }(R_p)$ have been discussed in the financial literature using a variety of names—expected shortfall (Acerbi and Tasche 2002), conditional value-at-risk (Rockafellar and Uryasev 2000) and tail conditional expectation (Artzner et al. 1999).⁷ Notably, (2) might be taken as the target risk measure for portfolio allocation; see e.g. Basak and Shapiro (2001), Krokhmal et al. (2002), Ciliberti et al. (2007) and Mansini et al. (2007). In such a case, $\varrho _{\nu _\alpha }(R_p)$ can be minimized by resorting to the quantile regression method, as suggested by Bassett et al. (2004), in a framework similar to the estimation of the GMVP weights in (1), where $R_n$ is the response variable and $R^*_1,\ldots ,R^*_{n-1}$ are the covariates. Within a quantile regression framework, the conditional $\vartheta$th quantile of $R_n$ is estimated by minimizing the expected value of the asymmetric loss function:

$$\begin{aligned} \rho _\vartheta (\epsilon )=\epsilon \left[ \vartheta -I(\epsilon <0)\right] , \end{aligned}$$

(3)

where $\epsilon =R_n-\xi (\vartheta )-w_1(\vartheta )R^*_1-\cdots -w_{n-1}(\vartheta )R^*_{n-1}, \xi (\vartheta )$ is the model intercept, and $I(\cdot )$ denotes the indicator function taking the value of 1 if the condition in $(\cdot )$ is satisfied and 0 otherwise.

The estimated $\vartheta$th conditional quantile of $R_n$ is equal to $\widehat{\xi }(\vartheta )+\widehat{w}_1(\vartheta )R^*_1+\cdots +\widehat{w}_{n-1}(\vartheta )R^*_{n-1}$, where $\left[ \widehat{\xi }(\vartheta ),\widehat{w}_1(\vartheta ),\ldots ,\widehat{w}_{n-1}(\vartheta )\right]$ is the coefficients’ vector minimizing (3) at a specific quantile level $\vartheta$. In the case in which $\vartheta =\alpha$, it can be shown that:

(4)

where and $\varrho _{\nu _\alpha }(R_p)$, as in (2).

Let $r_{n,t}$ and $r^*_{i,t}$ be, respectively, the observed values of $R_n$ and $R^*_i$ for $i=1,\ldots ,n-1$ at time t. Then, from (4), the quantile regression model

(5)

$$\begin{aligned} s.t.\; \mu _p=c \end{aligned}$$

allows minimizing the empirical $\alpha$-risk of a financial portfolio, with the constraints that the expected portfolio return is equal to a target c and that the sum of the assets’ weights is equal to 1.⁸

Similar to Model (1), $\left[ \widehat{w}_1(\alpha ),\ldots ,\widehat{w}_{n-1}(\alpha )\right]$, the estimated coefficients’ vector of the covariates $R_1^*,\ldots , R_{n-1}^*$ in the quantile regression model, is then the weights’ vector of $R_1,\ldots ,R_{n-1}$ for the portfolio with minimum $\alpha$-risk; the weight of the nth asset is equal to $w_n(\alpha )=1-\sum _{i=1}^{n-1}w_i(\alpha )$, given the budget constraint. In this formulation, the portfolio weights do not change if we choose another asset as the numeraire. As the constraint $\mu _p=c$ in (5) requires the estimation of expected returns, which is known to be a challenging task due to large estimation errors (see e.g. Brodie 1993; Chopra and Ziemba 1993), we hereby choose to focus on:

(6)

which is the minimization of the portfolio $\alpha$-risk, subject only to the budget constraint.⁹

As the portfolio performance does not depend just on extreme risk but also on the occurrence of returns over their entire density support, we introduce an approach that emphasizes a novel risk-adjusted indicator. The main idea stems from observing that (2) can be associated with profitability and no longer only with extreme risk if we replace $\alpha$ with a high quantile level $\psi$, which is associated with the right tail of the $r_{n,t}$ distribution in the minimization problem (6), for example $\psi =\{0.9,0.95,0.99\}$. In this way, the $\alpha$-risk in (2) translates into the following quantity:

$$\begin{aligned} \varPsi _1(R_p,\psi )=-\psi ^{-1}\int _{0}^{\psi } F_{R_p}^{-1}(\vartheta )d\vartheta . \end{aligned}$$

(7)

Given that , the quantile regression model applied at $\psi$ allows one to minimize $\varPsi _1(R_p,\psi )$ and, consequently, to maximize the conditional portfolio expected return. The agent would then employ a cautiously optimistic allocation strategy by minimizing $\varPsi _1(R_p,\psi )$, in the sense that such a choice leads to the maximization of the portfolio expected return net of the most favorable outcomes, as the interval $(\psi ,1]$ is not included in the objective function. In this way, for instance, it is possible to attenuate the effects of the markets’ rebounds. Moreover, as $\lim _{\psi \rightarrow 1}-\varPsi _1(R_p,\psi )=\int _{0}^{\psi } F_{R_p}^{-1}(\vartheta )d\vartheta$, it is possible to obtain benefits in terms of the unconditional portfolio expected return, given that we maximize a quantity that approximates . Note that the minimization of $\varPsi _1(R_p,\psi )$ (or the maximization of the conditional portfolio expected return) does not require providing explicit estimates of the expected returns of the stocks included in the portfolio, which implies serious problems in terms of estimation errors.

Given $\varPsi _1(R_p,\psi )$, we go further and introduce a new performance indicator by decomposing the integral in Eq. (7). In particular, let $\bar{\vartheta }$ be the value of $\vartheta$ such that $F_{R_p}^{-1}(\bar{\vartheta })=0$, where the integral $\int _{0}^{\bar{\vartheta }} F_{R_p}^{-1}(\vartheta )d\vartheta$ reaches its lowest value; for instance, $\bar{\vartheta }=0.5$ when the distribution is symmetric at 0. Given $\bar{\vartheta }<\psi <1$, (7) is then equal to:

$$\begin{aligned} \varPsi _1(R_p,\psi )= & {} -\psi ^{-1}\int _{0}^{\psi } F_{R_p}^{-1}(\vartheta )d\vartheta \nonumber \\= & {} -\psi ^{-1} \left[ \int _{0}^{\bar{\vartheta }} F_{R_p}^{-1}(\vartheta )d \vartheta +\int _{\bar{\vartheta }}^{\psi } F_{R_p}^{-1}(\vartheta )d \vartheta \right] , \end{aligned}$$

(8)

where $\int _{0}^{\bar{\vartheta }} F_{R_p}^{-1}(\vartheta )d \vartheta$ is computed from negative realizations and quantifies their magnitude. In contrast, $\int _{\bar{\vartheta }}^{\psi } F_{R_p}^{-1}(\vartheta )d \vartheta$ quantifies the magnitude of a part of the positive outcomes, excluding the most favorable ones, given that the area beyond $\psi$ is not considered. The quantile regression model, applied at the $\psi$th level, minimizes $\varPsi _1(R_p,\psi )$ and thus $-\varsigma =-\left( \int _{0}^{\bar{\vartheta }} F_{R_p}^{-1}(\vartheta )d \vartheta +\int _{\bar{\vartheta }}^{\psi } F_{R_p}^{-1}(\vartheta )d \vartheta \right)$. When $f_{R_p}(r_p)$ is characterized by a null or a negative skewness, $\varsigma$ is negative, whereas $\varsigma$ could be positive in the case of positive skewness. In the first case, $\varsigma$ could be seen as a net loss. In contrast, in the latter case, $\varsigma$ is a net profit. Therefore, the quantile regression model leads to the minimization of a loss ($\varsigma <0$) or to the maximization of a profit ($\varsigma >0$), as in (8) $\varsigma$ is multiplied by the constant $-\psi ^{-1}<0$. In other words, the quantile regression model minimizes $|\varsigma |$ if $\varsigma <0$ or maximizes $|\varsigma |$, if $\varsigma >0$, with benefits in terms of the ratio:

$$\begin{aligned} \varPsi _2(R_p,\psi )=\frac{\int _{\bar{\vartheta }}^{\psi } F_{R_p}^{-1}(\vartheta )d\vartheta }{\left| \int _{0}^{\bar{\vartheta }} F_{R_p}^{-1}(\vartheta )d\vartheta \right| }. \end{aligned}$$

(9)

Therefore, the ratio $\varPsi _2(R_p,\psi )$ is a risk-adjusted measure because it quantifies the magnitude of all the negative outcomes balanced by a part of the positive results, net of the most favorable ones. Although high $\varPsi _2(R_p,\psi )$ values correspond to low $\varPsi _1(R_p,\psi )$ levels, when different strategies are compared, there are no guarantees that the strategy that minimizes $\varPsi _1(R_p,\psi )$ is the one that maximizes $\varPsi _2(R_p,\psi )$. In other words, the ranking of different strategies built on the sum between $\int _{\bar{\vartheta }}^{\psi } F_{R_p}^{-1}(\vartheta )d \vartheta$ and $\int _{0}^{\bar{\vartheta }} F_{R_p}^{-1}(\vartheta )d \vartheta$ may not coincide with the ranking built on the basis of their ratio. For example, suppose that for a certain strategy $A, \int _{0}^{\bar{\vartheta }} F_{R_p}^{-1}(\vartheta )d \vartheta =-34.04$ and $\int _{\bar{\vartheta }}^{\psi } F_{R_p}^{-1}(\vartheta )d \vartheta =8.13$. In contrast, strategy B returns $\int _{0}^{\bar{\vartheta }} F_{R_p}^{-1}(\vartheta )d \vartheta =-33.74$ and $\int _{\bar{\vartheta }}^{\psi } F_{R_p}^{-1}(\vartheta )d \vartheta =7.95$. B is better in terms of $\varPsi _1(R_p,\psi )$, but A outperforms B in terms of $\varPsi _2(R_p,\psi )$.

We stress that while (7) relates to tail-based risk measures and is not a proper absolute performance measure (see Caporin et al. 2014), indicator (9) is novel. It is interesting to note that $\varPsi _2(R_p,\psi )$ is related both to the Omega measure proposed by Keating and Shadwick (2002) and to the modified Rachev ratio (Ortobelli et al. 2005). Nevertheless, there are some important differences between these quantities. First, $\varPsi _2(R_p,\psi )$ differs from Omega because the latter compares the entire regions associated with negative and positive outcomes. In contrast, (9) is more restrictive because its numerator takes into account just part of the positive outcomes, as long as $\psi <1$. In the case of the Rachev ratio, the difference arises from the fact that it compares the extreme outcomes associated with the distribution tails, thus fully neglecting the impact of the central part of the portfolio returns distribution.

In the empirical application, we use the non-parametric estimator proposed by Chen (2008) to estimate both the $\alpha$-risk and $\varPsi _1(R_p,\psi )$. In fact, both quantities have the same expression, as we note by comparing Eqs. (2) and (7). They differ just in the quantile level at which they are computed, given that $\psi > \alpha$. In the case of $\varPsi _1(R_p,\psi )$, the non-parametric estimator introduced by Chen (2008) reads as follows:

$$\begin{aligned} \widehat{\varPsi }_1(r_p,\psi )=-\frac{\sum _{t=1}^{T}r_{p,t} I \left( r_{p,t} \le \widehat{Q}_{\psi }(r_p) \right) }{\sum _{t=1}^{T}I \left( r_{p,t} \le \widehat{Q}_{\psi }(r_p) \right) }. \end{aligned}$$

(10)

where $r_{p,t}$ denotes the portfolio return observed at $t, \widehat{Q}_{\psi }(r_p)$ denotes the estimated $\psi$th quantile of the portfolio returns (by means of quantile regression), $I(\cdot )$ is the indicator function taking the value of 1 if the condition in $(\cdot )$ is true and 0 otherwise. Replacing $\psi$ with $\alpha$ gives the estimator of the $\alpha$-risk. Notably, the asymptotic variance of the estimator proposed by Chen (2008) is a negative function of $\vartheta$; therefore the estimate of the $\alpha$-risk is subject to a higher volatility with respect to $\widehat{\varPsi }_1(r_p,\psi )$. Similarly, we compute the sample counterpart of $\varPsi _2(R_p,\psi )$ as follows:

$$\begin{aligned} \widehat{\varPsi }_2(r_p,\psi )=\frac{\sum _{t=1}^{T}r_{p,t} I \left( 0 \le r_{p,t} \le \widehat{Q}_{\psi }(r_p) \right) }{\left| \sum _{t=1}^{T}r_{p,t} I \left( r_{p,t} < 0 \right) \right| }. \end{aligned}$$

(11)

The $\alpha$-risk focuses on lower quantiles, while $\varPsi _1(R_p,\psi )$ and $\varPsi _2(R_p,\psi )$ point at upper quantiles. However, resorting to quantile regression also allows dealing with the central $\vartheta$ values. If we focus on the median regression and assume that the portfolio expected return and the median regression intercept $\xi (\vartheta =0.5)$ are both equal to zero, it is possible to verify that the median regression allows minimizing a specific risk volatility measure, the mean absolute deviation (MAD) of Konno and Yamazaki (1991). To summarize, the quantile regression model allows reaching different purposes. First, we should choose a low probability level, $\alpha$, when we want to minimize the extreme risk, quantified by the $\alpha$-risk. Second, when the attention is focused on volatility minimization, quantified by MAD, we should use median regression. Finally, with a high probability level $\psi$ we minimize $\varPsi _1(R_p,\psi )$, with positive effects in terms of $\varPsi _2(R_p,\psi )$.

As a preliminary exercise, we verify these properties using simulated data, comparing quantile-based portfolio allocation approaches based on the minimization of Eq. (5) with an OLS regression model (i.e. the global minimum variance allocation). Our simulation exercise considers several simulated datasets reproducing important features of the financial returns series, such as the existence of mutual dependence and the presence of asymmetry and leptokurtosis in the underlying distributions (Cont 2001). We simulate data from a multifactor model as suggested by Fan et al. (2012) and also from the multivariate skew-t (Azzalini 2014) and the multivariate normal distributions, the parameters of which are calibrated on real data. Moreover, we also generate data from a block resampling technique using the xy-pair method (Kocherginsky 2003; Davino et al. 2014) on the Standard & Poor’s 100 (S&P100) index constituents returns described in Sect. 3. Our expectations are validated by the simulated exercise, given that the OLS (or GMVP) approach minimizes the portfolio variance, while optimizing with respect to the 10% quantile minimizes the $\alpha$-risk. The median optimization minimizes the mean absolute deviation. The minimization at the 90% quantile optimizes both $\widehat{\varPsi }_1(r_p,0.9)$ and $\widehat{\varPsi }_2(r_p,0.9)$. “Appendix A” reports the simulation results.

2.2 $\ell _1$-Norm penalized quantile regression

Selecting assets from a large pool and building large portfolios should allow taking advantage of the diversification benefits. Nevertheless, Statman (1987) and recently Fan et al. (2012), among others, show that the inclusion of additional assets in the portfolio involves relevant benefits but only up to a certain number of assets. Moreover, the number of parameters to estimate increases as the portfolio dimensionality grows. As a result, the consequent accumulation of estimation errors becomes a problem that must be addressed. For, instance, Kourtis et al. (2012) defined the estimation error as the price to pay for diversification. Furthermore, when large portfolios are built using regression models, as shown in Sect. 2.1, the assets’ returns are typically highly correlated. The estimated portfolios’ weights are then poorly determined and exhibit high variance.

We propose here a further extension to the quantile regression model described in Sect. 2.1 that allows to optimally select the desired assets from a large pool and to better deal with the estimation errors.¹⁰ Our solution builds on regularization techniques widely applied in the recent financial literature; see, for example, Hastie et al. (2009), DeMiguel et al. (2009), Gotoh and Takeda (2011), Fan et al. (2012), Fastrich et al. (2015), Yen and Yen (2014), Ando and Bai (2015), Xing et al. (2014) and Tian et al. (2015). Among all the possible methods, we make use of the $\ell _1$-norm penalty, useful in the context of variable selection, with which we penalize the absolute size of the regression coefficients. In the last 10 years, it has become a widely used tool not only in linear regression, but also in quantile regression models; see, for example, Koenker (2005), Belloni and Chernozhukov (2011) and Li and Zhu (2008).

As for financial portfolio selection, Härdle et al. (2014) used the $\ell _1$-norm penalty in a quantile regression model where the response variable is a core asset, represented by the Standard & Poor’s 500 (S&P500) index, whereas the covariates are hedging satellites, that is, a set of hedge funds. After setting the quantile levels according to a precise scheme, the aim is to buy the hedge funds the coefficients of which, estimated using the penalized quantile regression model, are different from zero. Therefore, in the work by Härdle et al. (2014) the penalized quantile regression is used as a security selection tool in an index tracking framework. In a second step, by placing the focus on the downside risk, Härdle et al. (2014) determine the optimal weights of the funds previously selected by optimizing the objective function given by the CF–VaR.

In contrast, we use a penalized quantile regression model that allows solving in just one step both the asset selection and the weight estimation problems. The response and the covariates are determined from the assets included in the portfolio, without considering external variables (such as market indexes) with the aim of optimizing different performance measures according to different $\vartheta$ levels.

In particular, given $1 \le k \le n$, we introduce the following model:

(12)

where the parameters $(\xi (\vartheta ),\mathbf{w}_{-k}(\vartheta ))$ depend on the probability level $\vartheta , \mathbf{w}_{-k}(\vartheta )$ is the weights’ vector that does not include $w_k$, that is, the weight of the kth asset selected in (12) as numeraire and $\lambda$ is the tuning parameter.

The larger the $\lambda$, the smaller the number of portfolio constituents. Therefore, by penalizing the sum of the absolute coefficients’ values, that is, $\ell _1$-norm, some of the weights are set to zero, depending on the value of $\lambda$, with benefits in terms of smaller monitoring and transaction costs due to the smaller portfolio size.

Clearly, an important issue is the choice of the optimal $\lambda$ value, which determines the portfolio size. Here, we follow the approach proposed by Belloni and Chernozhukov (2011), which is state-of-art in the statistical literature. They considered the problem of dealing with a large number of explanatory variables with respect to the sample size T, where only at most $s \le n$ regressors have a non-null impact on each conditional quantile of the response variable. In this context, where the ordinary quantile regression estimates are not consistent, they showed that by penalizing the $\ell _1$-norm of the regressors coefficients the estimates are uniformly consistent over the compact set $\mathcal {U} \subset (0,1)$. To determine the optimal $\lambda$ value, they proposed a data-driven method with optimal asymptotic properties. This method takes into account the correlation among the variables involved in the model and leads to different optimal $\lambda$ values according to the $\vartheta$ level. The penalization parameter is built using the following random variable:

(13)

where $e_1,\ldots ,e_T$ are i.i.d. uniform (0, 1) random variables independently distributed from the covariates $\mathbf{r}^*$ and $\hat{\sigma }_j^2=T^{-1}\sum _{t=1}^{T}(r_{j,t}^*)^2$. As recommended in Belloni and Chernozhukov (2011), we simulate the $\varLambda$ values by running 100,000 iterations. The optimal tuning parameter is then computed as:

$$\begin{aligned} \lambda ^*=\frac{\tau \sqrt{\vartheta (1-\vartheta )}}{T}, \end{aligned}$$

(14)

where $\tau =2\widehat{Q}_{0.9}(\varLambda |\mathbf{r}^*)$, with $\widehat{Q}_{0.9}(\varLambda |\mathbf{r}^*)$ being the 90th percentile of $\varLambda$ conditional on the explanatory variables’ values. Section 4 reports the empirical results derived from selecting the optimal $\lambda$ in Eq. (14). In particular, $\lambda ^*$ is computed for different $\vartheta$ levels from the full sample data and is kept fixed across the subsamples determined by the rolling window procedure.¹¹ Next, for each rolled window, $\lambda ^*$ is used in the minimization problem given in (12) to estimate the optimal assets’ weights $w_j$ for $j \ne k$.

3 Empirical set-up

The empirical analysis is performed on the daily returns of the constituents of the S&P100 and the S&P500 indexes, respectively. In particular, we focus on the constituents belonging continuously to the baskets of the two indexes from November 4, 2004 to November 21, 2014; in the first dataset (S&P100) we deal with 94 assets, whereas in the second one (S&P500) we have 452 stocks.¹² The set of stocks we considered excludes 6 assets from S&P100 and 48 assets from S&P500, due to poor performances of the companies, mergers and acquisitions (M&A) or institutions that more recently entered the market. As a result, we have a form of survivorship bias. Nevertheless, our analyses never compare the performances of the indexes to those of the allocation strategies. Therefore, our results do not suffer from any bias associated with the absence of adherence to the index basket, as the competitive asset allocation strategies are consistently applied over the same investment universe. A descriptive analysis of the data is given in “Appendix C”.

The empirical analysis relies on a rolling window scheme to analyse the out-of-sample performance. Iteratively, the original assets’ returns time series with dimension ($T \times n$) are divided in subsamples with window size ${ ws}$. The first subsample includes the daily returns from the first to the ${ ws}$th day. The second subsample is obtained by removing the oldest observations and including those of the $(ws+1)$th day. The procedure goes on until the $(T-1)$th day is reached. In the empirical analysis, we make use of two different window sizes, that is, ${ ws}=\{500,1000\}$, to check how the portfolio performance changes according to the portfolio dimensionality and the sample size.

For each window, we estimate the portfolio weights, denoted by $\widehat{\mathbf{w}}_t$ for $t=ws,\ldots ,T-1$, by means of a given asset allocation strategy. Let $\mathbf{r}_{t-ws+1,t}$ be the $(ws \times n)$ matrix the rows of which contain the assets’ returns vectors recorded in the period between $t-ws+1$ and t. The portfolio returns are then computed both in-sample and out-of-sample. In the first case, for each rolled subsample, we multiply each row of $\mathbf{r}_{t-ws+1,t}$ by $\widehat{\mathbf{w}}_t$, obtaining ${ ws}$ in-sample portfolio returns, from which we can compute the performance indicators described below. Overall, from all the $T-ws$ submatrices $\mathbf{r}_{t-ws+1,t}$, we obtain $T-ws$ values of each performance indicator.

Unlike the in-sample analysis, where we assess the estimated performance indicators, the aim of the out-of-sample analysis is to check whether the expectations find confirmation in the actual outcomes, leading to profitable investment strategies. Therefore, the out-of-sample performance plays a critical role, given that it quantifies the actual impacts on the wealth when assuming that investors daily revise their portfolios. In particular, for $t=ws,\ldots ,T-1, \widehat{\mathbf{w}}_t$ is multiplied by $\mathbf{r}_{t+1}$, that is, the assets’ returns vector observed at $t+1$, to obtain the out-of-sample portfolio returns. In this way, for each asset allocation strategy, we obtain one series of out-of-sample portfolio returns, that is, a vector with length $T-ws$, from which we compute the performance indicators described below.

We assess and compare the performance of the competitive strategies using several indicators to provide information about profitability, risk and turnover. Some of the performance measures, namely $\alpha$-risk, $\varPsi _1(R_p,\psi ), \varPsi _2(R_p,\psi )$ and MAD have already been introduced in Sect. 2.1. In addition, those statistics are accompanied by other portfolio indicators typically used in financial studies that although not optimized by the proposed quantile regression method are considered for completeness. The first one is the Sharpe ratio, defined as the ratio between the sample mean ($\bar{r}_p$) and standard deviation $(\hat{\sigma }_p$) of the portfolio returns, assuming that the risk-free rate is equal to zero. As stated above, in the in-sample case, $\bar{r}_p$ and $\hat{\sigma }_p$ are computed for each of the rolled subsamples $\mathbf{r}_{t-ws+1,t}$ for $t=ws,\ldots ,T-1$. Consequently, we obtain $T-ws$ Sharpe ratios. In contrast, in the out-of-sample case, we have one portfolio return for each window, obtaining overall a single vector of portfolio returns with length equal to $T-ws$, from which we compute the Sharpe ratio just once. In the empirical analysis, we also test whether the Sharpe ratios generated using the competitive strategies are statistically different by means of the test proposed by Ledoit and Wolf (2008). In addition to the $\alpha$-risk, we also consider the value-at-risk, computed as the 0.1th quantile and taken with the negative sign, of the portfolio returns. Finally, we assess the impact of the trading fees on the portfolio rebalancing activity through the turnover, computed as ${ Turn} = \frac{1}{T-ws} \sum _{t=ws+1}^{T}\sum _{j=1}^{n} \left| \widehat{w}_{j,t} - \widehat{w}_{j,t-1} \right|$, where $\widehat{w}_{j,t}$ is the weight of the jth asset determined by an asset allocation strategy at day t. The higher the turnover, the larger the impact of the costs arising from the rebalancing activity.

4 Out-of-sample results

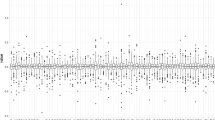
The first aspect we analyse refers to the impact of the $\ell _1$-norm penalty on the portfolio weights. For the quantile regression model, we estimate the optimal tuning parameter $\lambda$ according to the method proposed by Belloni and Chernozhukov (2011). For each quantile level, we compute $\lambda ^*$, as defined in (14), using the full sample data, for both S&P100 and S&P500.¹³ After implementing the rolling window procedure, we compute the number of active and short positions for each rolled sample, the average values of which are denoted by $\bar{n}_a$ and $\bar{n}_s$, respectively. The asset allocation strategy built using Model (12), which explicitly incorporates the $\ell _1$-norm penalty, is denoted as ${ PQR}(\vartheta )$, whereas the strategy built using the non-penalized quantile regression is denoted as ${ QR}(\vartheta )$ for $\vartheta \in (0,1)$. We also consider the standard least squares regression in (1) with the $\ell _1$ constraint and denote it as ${ LASSO}$. For ${ LASSO}, \lambda ^*$ is calibrated to obtain comparable results in terms of $\bar{n}_a$ to those generated using the quantile regression model at $\vartheta =0.5$. For simplicity, we show in Table 1 the $\lambda ^*$ values and the average number of active and short positions over the rolled windows just for ${ PQR}(0.1), { PQR}(0.5), { PQR}(0.9)$ and ${ LASSO}$.¹⁴

We note that $\lambda ^*$ changes according to the $\vartheta$ levels, reaching relatively higher values at the center of the $\vartheta$ domain. This leads to the attenuation of the quantile regression approach tendency for an increase of active positions around the median, as shown in Table 1. Moreover, we analyse the evolution over time of the portfolio weights estimated using both the ordinary least squares and the quantile regression approaches. We check that the weights become more stable with the $\ell _1$-norm penalty and that the effect is clearer with ${ ws}=1000$. This result is due to the fact that the $\ell _1$-norm penalty shrinks the portfolio dimensionality that, accompanied by a larger window size, reduces the impact of the estimation errors.

Table 1 The impact of the $\ell _1$-norm penalty on active and short positions

Fig. 2

Out-of-sample results generated by the strategies built using the ordinary least squares (with (LASSO) and without (OLS) $\ell _1$-norm penalty) and the quantile regression (with (${ PQR}(\vartheta )$) and without (${ QR}(\vartheta )$) $\ell _1$-norm penalty) models and the portfolio with minimum variance subject to the no short-selling constraint (MVNSS). The quantile regression model is estimated for 9 quantile levels, that is, $\vartheta =\{0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9\}$. The strategies are applied on the returns series of the Standard & Poor’s 100 index constituents, and the rolling analysis is carried out with a window size of 1000 observations. In the subfigures, from (a)–(d), we respectively consider the following measures: standard deviation of portfolio returns (%), mean absolute deviation (%), value-at-risk (%) and $\alpha$-risk (%) at the level of 10%

Fig. 3

Out-of-sample results generated by the strategies built using the ordinary least squares (with (LASSO) and without (OLS) $\ell _1$-norm penalty) and the quantile regression (with (${ PQR}(\vartheta )$) and without (${ QR}(\vartheta )$) $\ell _1$-norm penalty) models and the portfolio with minimum variance subject to the no short-selling constraint (MVNSS). The quantile regression model is estimated for 9 quantile levels, that is, $\vartheta =\{0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9\}$. The strategies are applied on the returns series of the Standard & Poor’s 500 index constituents, and the rolling analysis is carried out with a window size of 1000 observations. In the subfigures, from (a)–(d), we respectively consider the following measures: standard deviation of portfolio returns (%), mean absolute deviation (%), value-at-risk (%) and $\alpha$-risk (%) at the level of 10%

Fig. 4

Out-of-sample results generated by the strategies built using the ordinary least squares (with (LASSO) and without (OLS) $\ell _1$-norm penalty) and from the quantile regression (with (${ PQR}(\vartheta )$) and without (${ QR}(\vartheta )$) $\ell _1$-norm penalty) models and the portfolio with minimum variance subject to the no short-selling constraint (MVNSS). The quantile regression model is estimated for 9 quantile levels, that is, $\vartheta =\{0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9\}$. The strategies are applied on the returns series of the Standard & Poor’s 100 index constituents, and the rolling analysis is carried out with a window size of 1000 observations. In the subfigures, from (a)–(d), we respectively consider the following measures: $\widehat{\varPsi }_1(r_p,\psi )$ (%) and $\widehat{\varPsi }_2(r_p,\psi )$ at $\psi =0.9$, mean return (%) and Sharpe ratio (%). Figure 4d is accompanied by Table 2, where we report the p values of the test proposed by Ledoit and Wolf (2008) to assess the statistical significance of the differences among the Sharpe ratios generated by the competitive strategies

Fig. 5

Out-of-sample results generated by the strategies built using the ordinary least squares (with (LASSO) and without (OLS) $\ell _1$-norm penalty) and from the quantile regression (with (${ PQR}(\vartheta )$) and without (${ QR}(\vartheta )$) $\ell _1$-norm penalty) models and the portfolio with minimum variance subject to the no short-selling constraint (MVNSS). The quantile regression model is estimated for 9 quantile levels, that is, $\vartheta =\{0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9\}$. The strategies are applied on the returns series of the Standard & Poor’s 500 index constituents, and the rolling analysis is carried out with a window size of 1000 observations. In the subfigures, from (a)–(d), we respectively consider the following measures: $\widehat{\varPsi }_1(r_p,\psi )$ (%) and $\widehat{\varPsi }_2(r_p,\psi )$ at $\psi =0.9$, mean return (%) and Sharpe ratio (%). Figure 4d is accompanied by Table 2, where we report the p values of the test proposed by Ledoit and Wolf (2008) to assess the statistical significance of the differences among the Sharpe ratios generated by the competitive strategies

Finally, we analyse and compare the performance of the strategies mentioned above, including as a competitor the portfolio with minimum variance subject to the no short-selling constraint (MVNSS). Indeed, MVNSS could be considered as a special case of LASSO, as, in such a case, the $\ell _1$-norm is just the sum of the constrained weights that is equal to 1 given the budget constraint. The properties of MVNSS and its remarkable performance were first analysed by Jagannathan and Ma (2003) and then linked to LASSO by Fan et al. (2012). Moreover, we accompany the measures of central importance in the present work, being directly linked to quantile regression (i.e. $\alpha$-risk, MAD, $\widehat{\varPsi }_1(R_p,\psi )$ and $\widehat{\varPsi }_2(R_p,\psi )$, described in Sect. 2.1), with other portfolio indicators.¹⁵ We refer to the mean portfolio return, the portfolio standard deviation, the Sharpe ratio, the value-at-risk and the turnover (see Sect. 3).

The in-sample results are consistent with the expectations.¹⁶ In fact, at low quantile levels, ${ QR}(\vartheta )$ minimizes the extreme risk, quantified by the $\alpha$-risk and the value-at-risk. At $\vartheta =0.5$, the median regression minimizes the mean absolute deviation. Finally, at high quantile levels, ${ QR}(\vartheta )$ is the best strategy in terms of $\widehat{\varPsi }_1(r_p,0.9)$ and $\widehat{\varPsi }_2(r_p,0.9)$. As for the complementary performance indicators, the ordinary least squares method minimizes the portfolio standard deviation, as expected, as its objective function is given by the portfolio variance. Interestingly, the inclusion of the $\ell _1$-norm penalty implies significant benefits in terms of the average portfolio return and the Sharpe ratio for both the least squares and the quantile regression models.

In the out-of-sample analysis, we compare the strategies arising from the quantile regression model, with and without $\ell _1$-norm penalty, built on 9 quantile levels, namely $\vartheta =\{0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8, 0.9\}$. The results obtained from the rolling window procedure with ${ ws}=1000$ are displayed in Figs. 2, 3, 4 and 5; similar results apply for ${ ws}=500$.¹⁷

Figures 2d and 3d show that the quantile regression model applied at low quantile levels is no longer the best strategy in terms of extreme risk, being dominated by the ordinary least squares subject to the $\ell _1$-norm penalty (LASSO). Nevertheless, it is important to highlight that the $\ell _1$-norm penalty turns out to be very effective, given that it reduces the exposure of the quantile regression model to the $\alpha$-risk and the gap with the ordinary least squares method. Similar considerations apply for the value-at-risk (Figs. 2c, 3c); in contrast to the expectations and the in-sample performance, the quantile regression model works better at central $\vartheta$ levels. The quantile regression model works better in terms of mean absolute deviation at central $\vartheta$ values, as expected; nevertheless, it is outperformed by the ordinary least squares model, which records the lowest MAD.

It is important to note that the $\ell _1$-norm penalty reduces the MAD of all the strategies (Figs. 2b, 3b). The quantile regression model applied at high $\vartheta$ values dominates all the other strategies in terms of both $\widehat{\varPsi }_1(r_p,0.9)$ and $\widehat{\varPsi }_2(r_p,0.9)$; see Figs. 4a, b and 5a, b. The impact of the $\ell _1$-norm penalty is evident when the ratio between the sample size and the portfolio dimensionality is not sufficiently large (Fig. 5a, b); in this case, the inclusion of the $\ell _1$-norm penalty regularizes and makes clear the decreasing (increasing) trend of $\widehat{\varPsi }_1(r_p,0.9)$ ($\widehat{\varPsi }_2(r_p,0.9)$) over the entire set of $\vartheta$.

When considering the complementary performance measures, the ordinary least squares model including the $\ell _1$-norm penalty dominates in terms of standard deviation, consistent with the expectations. The quantile regression method applied at high $\vartheta$ levels provides the highest mean return and Sharpe ratio, and the effect of the $\ell _1$-norm penalty is evident in the case of the S&P500 index constituents (Figs. 4c, d, 5c, d). Interestingly, the Sharpe ratio and $\widehat{\varPsi }_2(r_p,0.9)$ follow a similar trend over $\vartheta$ for both ${ QR}(\vartheta )$ and ${ PQR}(\vartheta )$.

We also checked whether the differences between the Sharpe ratios are statistically significant, and for this purpose we implemented the test introduced by Ledoit and Wolf (2008). Notably, the null hypothesis of the test is that the difference between the Sharpe ratios of two competitive strategies is not statistically significant. We report the p values of the test in Table 2. It is possible to see that the quantile regression model including the $\ell _1$-norm penalty and applied at $\vartheta =0.9$ (${ PQR}(0.9)$) records the highest number of rejections of the null hypothesis, further supporting its capability of outperforming the other strategies.

Without regularizations, large portfolios are affected by relevant variability in the portfolios’ weights, with negative effects in terms of trading fees. In this context, the inclusion of the $\ell _1$-norm penalty could be useful because it allows obtaining sparse portfolios, stabilizing the portfolios’ weights over time. This phenomenon is confirmed in our results. In fact, we observe in Fig. 6 that the inclusion of the $\ell _1$-norm penalty causes a sharp drop in the turnover for all the considered strategies. The quantile regression model sensibly benefits from regularization, as the excessive turnover recorded for ${ QR}(\vartheta )$ vanishes.

To summarize the out-of-sample results, the $\ell _1$-norm penalty regularizes the portfolio weights, with noticeable positive effects on turnover. Moreover, it leads to clear improvements in both the portfolio risk and profitability when dealing with large portfolios. In general, the ordinary least squares model turns out to be the best strategy in terms of risk, given that it implies the lowest levels of volatility and extreme risk.

The quantile regression applied at low $\vartheta$ values does not minimize the out-of-sample $\alpha$-risk, contrary to the expectations and the good in-sample performance. The same conclusions hold for the median regression, which does not minimize the out-of-sample mean absolute deviation. In contrast, at high quantile levels, the quantile regression model is consistent with the expectations, providing the best performance in terms of $\widehat{\varPsi }_1(r_p,0.9), \widehat{\varPsi }_2(r_p,0.9)$ and Sharpe ratio. We also analyse the trend over time of the wealth generated by the competitive strategies when investing an initial amount equal to $100. We check that the quantile regression model applied at high $\vartheta$ levels dominates the other strategies for the highest levels of wealth and that the benefits of the $\ell _1$-norm penalty are clear in the case of the S&P500 dataset.

The different behaviour between the in-sample and the out-of-sample framework of the quantile regression model at different quantile levels represents an interesting research issue. In “Appendix D” we give a possible explanation of this phenomenon, considering the role of the models’ intercepts and residuals.

The empirical analysis discussed so far applies to data recorded from November 4, 2004 to November 21, 2014. Those years are characterized by special events, namely the subprime crisis, which originated in the United States and was marked by the Lehman Brothers default in September 2008, and the sovereign debt crisis, which hit the Eurozone some years later. Those events had a deep impact on financial markets, and it is therefore important to check whether they affect the performance of the considered asset allocation strategies. Moreover, in this way, we can analyse on one hand whether and how the performance of the strategies depends on the state of the market—the state characterized by financial turmoil and the state of relative calm. On the other hand, we can take into account the effects of the markets’ rebounds, which typically occur during crisis periods. For this purpose, we divided the series of the out-of-sample portfolios returns into two subperiods. When the window size is equal to 1000, the first subperiod goes from July 31, 2008 to October 31, 2011, whereas it covers the days between October 31, 2006 and October 31, 2010 at ${ ws}=500$. We can associate this subperiod with the state of financial turmoil, given the proximity to the above-mentioned crises. The second subperiod includes the remaining days until November 21, 2014. As expected, the strategies record a better out-of-sample performance in the second subperiod compared to the first one, as we can see, for instance, from Table 3, where we report the results obtained from the S&P500 dataset, applying the rolling procedure with a window size of 1000 observations.¹⁸ Similar to the analysis of the entire sample, in the first subperiod LASSO records the best performance in terms of risk, evaluated by means of standard deviation, mean absolute deviation, value-at-risk and $\alpha$-risk. In contrast, in the second subperiod, ${ PQR}(0.5)$ dominates the other strategies in terms of risk. ${ PQR}(0.9)$ is the best strategy in terms of $\widehat{\varPsi }_1(r_p,0.9), \widehat{\varPsi }_2(r_p,0.9)$, mean return, Sharpe ratio and final wealth.

Table 2 Testing the differences in the Sharpe ratios

Fig. 6

Turnover of the strategies built from the ordinary least squares (with (LASSO) and without (OLS) $\ell _1$-norm penalty) and from the quantile regression (with (${ PQR}(\vartheta )$) and without (${ QR}(\vartheta )$) $\ell _1$-norm penalty) models and the portfolio with minimum variance subject to the no short-selling constraint. The strategies are applied on the returns series of the Standard & Poor’s 100 (Subplot (a)) and 500 (Subplot (b)) indices constituents. The rolling analysis is carried out with window size of 1000 observations

5 Concluding remarks

By considering a quantile regression-based asset allocation model, we introduce a ‘cautiously optimistic’ approach that aims to optimize a novel performance measure clearly related to specific portfolio return distribution quantiles. Moreover, to cope with the potentially large cross-sectional dimension of the portfolios and at the same time control for estimation error, we combine quantile regression and regularization based on the $\ell _1$-norm penalty to estimate portfolio weights. Our empirical evidence, based both on simulations and real data examples, highlights the features and the benefits of our methodological contributions. The new provided tools are of potential interest in several areas, including performance evaluation and the quantitative development of asset allocation strategies.

Table 3 Out-of-sample analysis partitioned on two subperiods

A critical point concerns the high turnover some strategies exhibit. Even if the inclusion of the $\ell _1$-norm penalty significantly reduces the number of active weights, the turnover from the portfolio rebalancing could be further controlled by incorporating new penalty functions into the optimization problem; we point out this possible solution for future research. Our agenda also includes other penalty functions in addition to the $\ell _1$-norm, such as the non-convex ones, that also have a direct interpretation as measures of portfolio diversification (e.g. $\ell _q$-norm with $0 \le q \le 1$). They have already proven useful in the standard least squares regression to identify investment strategies with better out-of-sample portfolio performance, while promoting more sparsity than the $\ell _1$-norm penalty; see, for example, Fastrich et al. (2015). Testing them in a quantile regression framework would then allow a more robust optimal allocation. In our future research we will consider alternative linear (and even non-linear) constraints on portfolio weights within our allocation strategy, to be consistent with the specific regulatory rules. Finally, we aim at developing a method to simultaneously choose the optimal quantile level and the optimal intensity of the penalty.

Appendices

Appendix

A Simulation analysis

Bassett et al. (2004) applied the model in (5) using the simulated returns of 4 assets, showing its better performance in terms of extreme risk with respect to the classic Markowitz (1952) portfolio. Nevertheless, in the real world, investors trade financial portfolios consisting of many more assets, primarily to achieve a satisfactory diversification level and to better deal with the risk-return trade-off (Markowitz 1952). To further prove the relevance of quantile regression approaches for portfolio allocation, we consider a simulation exercise for portfolios containing 94 assets.¹⁹

We repeat the simulation exercise according to the different simulated datasets. First, we simulate the data from the three-factor model, using the method proposed by Fan et al. (2012). For this purpose, we make use of the Fama–French 3 factors built by Kenneth R. French,²⁰ whereas the parameters are calibrated to the S&P100 index constituents described in Sect. 3. Second, we simulate the data from the multivariate skew-t distribution (Azzalini 2014), the parameters of which are calibrated to the S&P100 index constituents to reproduce the peculiar features of the financial time series, especially in terms of kurtosis and skewness. Third, from the constituents of the S&P100 index, we build random samples using the block resampling technique (the block size is set equal to 5). In addition, we make use of the xy-pair method (Kocherginsky 2003; Davino et al. 2014) to keep the dependence structure among the considered stocks in each of the resampled blocks. Finally, we simulate the data from the multivariate normal distribution, the parameters of which are calibrated from the S&P100 index constituents.

For each of the approaches described above, we simulated 10,000 samples with size equal to ($500 \times 94$), comparing 4 strategies—the standard as in (1), denoted as OLS, and the ones arising from the quantile regression models applied at three probability levels, that is, $\vartheta =\{0.1,0.5,0.9\}$, denoted respectively as ${ QR}(0.1), QR(0.5)$ and ${ QR}(0.9)$. The portfolios weights determined using the 4 strategies are estimated from each of the 10,000 simulated samples, and the portfolios’ returns are computed in-sample.²¹ Thus, for each strategy and for each sample, we obtain 500 portfolio returns from which we compute the following statistics: variance, mean absolute deviation, $\alpha$-risk (with $\alpha =0.1$), $\widehat{\varPsi }_1(R_p,\psi )$ and $\widehat{\varPsi }_2(R_p,\psi )$, at $\psi =0.9$. In Fig. 7, we display the results obtained using the method proposed by Fan et al. (2012).²²

As expected, OLS and ${ QR}(0.5)$ provide the best results in terms of portfolio volatility, as the former minimizes the portfolio variance (Fig. 7a) and the latter minimizes the portfolio MAD (Fig. 7b). ${ QR}(0.1)$ minimizes the $\alpha$-risk at $\alpha =0.1$ (Fig. 7c); in contrast, ${ QR}(0.9)$ is the best strategy in terms of profitability. Indeed, as it is possible to see from Fig. 7d, e, it outperforms the other three strategies in terms of both $\widehat{\varPsi }_1(r_p,0.9)$ and $\widehat{\varPsi }_2(r_p,0.9)$.

Fig. 7

In-sample results using simulated data. We use the Fama-French 3 factors (http://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html) built by Kenneth R. French to simulate the three-factor model, as in Fan et al. (2012), whereas the parameters are calibrated to the Standard & Poor’s 100 index constituents described in Sect. 3. The analysis is based on 10,000 simulated samples with size equal to $(500 \times 94)$. The subfigures, from (a)–(e), respectively report the boxplots of the following statistics: variance (%), mean absolute deviation (%), $\alpha$-risk at $\alpha =0.1$ (%), $\widehat{\varPsi }_1(r_p,\psi )$ at $\psi =0.9$ (%) and $\widehat{\varPsi }_2(r_p,\psi )$ at $\psi =0.9$. A, B and C denote the strategies built from quantile regression models applied at probabilities levels of 0.1, 0.5 and 0.9, respectively, whereas D refers to the ordinary least squares regression model

B In-sample analysis

See Table 4.

Table 4 Descriptive statistics relating to the in-sample performance indicators

C Data description

The average returns of the S&P500 index constituents are close to zero, being symmetrically distributed around the median (0.055%); their maximum and minimum values are equal to 0.242 and −0.044%, respectively. The distribution of the standard deviations is centered at the median value of 2.137% and ranges from 1.013 to 5.329%, with the presence of a few particularly volatile companies associated with the extreme right-tailed values. The kurtosis index distribution is right-skewed, with extremely large values at the right tail. The median is equal to 12.379, whereas the minimum and the maximum are equal, respectively, to 5.948 and 72.867, indicating that the returns’ distributions are affected by heavy tails, as expected (see Cont 2001 for stylized facts of financial returns).

The skewness index is symmetrically distributed around the median value of 0.209. It ranges from −3.088 to 2.640, with the presence of some extreme values in both tails; therefore, the returns have leptokurtic and asymmetric distributions. The distribution of the 10th percentile of the returns’ series is affected by a slight negative asymmetry, centered at the median of −2.044%, with the minimum and the maximum equal to −3.703 and −1.004%, respectively. Finally, we focus on the distribution of the wealth we obtain on November 21, 2014 from the single assets, after investing $100 in each of them on November 4, 2004. The final wealth distribution, right-skewed, is affected by relevant extreme values in its right tail. It ranges from $2.42 to $7757.07, with a median value of $221.65; therefore, on average, we record an increase in stocks’ values.

D The role of the intercept and the residuals

We observed that, in the out-of-sample performance, some strategies built using quantile regression models at different quantiles levels kept their in-sample properties, whereas other ones failed in that regard. It is important to study the reason underlying this phenomenon, and in the following we provide one explanation associated with the model intercept. Given the numeraire $R_k, 1 \le k \le n$ and the covariates $R^*_j, j \ne k$, for simplicity we denote the residual term associated with the quantile regression model at the level $\vartheta$ as $\epsilon (\vartheta )$. In the rolling window procedure, the estimated parameters change over time, having their own variability. To take into account their dependence on time, we denote the coefficients estimated in t as $(\widehat{\xi }_t(\vartheta ),\widehat{\mathbf{w}}_{-k,t}(\vartheta ))$, using the data recorded in the interval $[t-ws+1;t]$ for $t=ws,\ldots ,T-1$. The out-of-sample $\vartheta$th quantile of $R_k$, computed in $t+1$, depends on both the estimates obtained in t and the realizations of $\mathbf{R}$ in $t+1$, being equal to $\widehat{\xi }_t(\vartheta )+\sum _{j \ne k}^{}\widehat{w}_{j,t}(\vartheta )r_{j,t+1}^*$. Therefore, the corresponding out-of-sample residual is computed as:

$$\begin{aligned} \epsilon _{t+1}(\vartheta )=r_{k,t+1}-\left[ \widehat{\xi }_t(\vartheta )+\sum _{j \ne k}^{}\widehat{w}_{j,t}(\vartheta )r_{j,t+1}^*\right] . \end{aligned}$$

(15)

Given that the portfolio return under the budget constraint can be written as $R_p(\vartheta )=R_k-\sum _{j \ne k}^{}w_{j}(\vartheta )R_{j}^*$, from the (15) we obtain:

$$\begin{aligned} r_{p,t+1}(\vartheta )=\epsilon _{t+1}(\vartheta )+\widehat{\xi }_t(\vartheta ). \end{aligned}$$

(16)

From (16) we can see that the out-of-sample portfolio return depends on two components—the intercept and the residual. When all the regressors are equal to zero, the estimated intercept corresponds to the estimated quantile of the response variable, and, in general, we should expect that $\widehat{\xi }_t(\vartheta )$ is a positive function of $\vartheta$. This phenomenon is particularly accentuated when the so-called location-shift hypothesis holds, that is, when the slopes of the quantile regression models are constant across $\vartheta$ so that the estimated quantiles change according to the intercept levels. Consequently, at high/low $\vartheta$ values, we should expect that the intercept term is a positive/negative component of the portfolio return in (16). In contrast, at high/low $\vartheta$ values, the magnitude of the positive residuals is lower/greater than the magnitude of the negative ones; therefore, we should expect that $\epsilon _t(\vartheta )$ is a negative/positive component of the portfolio return in (16).

Table 5 Analysis of the intercepts of the quantile regression models

Table 6 Analysis of the out-of-sample residuals distributions

Given the opposite behaviour of $\epsilon _{t+1}(\vartheta )$ and $\widehat{\xi }_t(\vartheta )$ over $\vartheta$, it is useful to study their distributions to understand the different out-of-sample performances of the strategies built from the quantile regression models. For simplicity, we compare the results obtained using three quantile levels, that is, $\vartheta =\{0.1,0.5,0.9\}$.

We start by analysing the intercepts’ distributions, reporting in Table 5 the mean and the standard deviation of $\widehat{\xi }_t(\vartheta )$ when $t=ws,\ldots ,T-1$.

We checked that, as expected, the support of the $\widehat{\xi }(\vartheta )$ distribution moves to the right as $\vartheta$ increases. As a result, from the second and the fourth columns of Table 5 it is possible to see that, on average, $\widehat{\xi }_t(\vartheta )$ is a positive component of the out-of-sample portfolio return generated from the quantile regression model at $\vartheta =0.9$. We have the opposite result at $\vartheta =0.1$, whereas at the median level the intercept takes, on average, values close to zero. We can see from the third and the fifth columns of Table 5 that, at the median level, the intercept distribution is characterized by the lowest dispersion, consistent with the fact that the median regression implies, among all the quantile regression models, the lowest out-of-sample portfolio volatility. In all the cases, the largest window size of 1000 observations reduces the intercepts’ dispersions, mainly at $\vartheta =\{0.1,0.9\}$.

Having analysed the impact of the intercept, we now study the behaviour of the out-of-sample residuals.

In contrast to the intercept case, the residuals’ supports move to the right as $\vartheta$ decreases, as expected. Consequently, as it is possible to see from the second and the fourth columns of Table 6, the residuals are, on average, negative/positive components of the portfolios’ returns in (16) at high/low $\vartheta$ levels. In comparing Tables 5 and 6, it is important to notice that the residuals’ distributions have larger volatilities compared to those of the intercepts.

To summarize, if we build an asset allocation strategy using a quantile regression model with high/low $\vartheta$ levels, we can obtain benefits/losses in terms of positive/negative intercept values. In contrast, with low/high $\vartheta$ levels, we derive benefits/losses from the residuals. The opposite effects are, on average, balanced. Nevertheless, the intercepts’ distributions have a lower dispersion with respect to the residuals’ distributions. Therefore, at high $\vartheta$ values, we obtain benefits from a component (the intercept) characterized by greater stability; however, we are penalized by a second component (the residuals) that are more volatile. In contrast, when we use quantile regressions models at low quantile levels, the benefits of positive residuals are more volatile than the losses of negative intercepts. The more stable benefits characterizing the strategies built using the quantile regression models at high $\vartheta$ levels support their better out-of-sample performance.