On the efficiency of Gini’s mean difference

Abstract

The asymptotic relative efficiency of the mean deviation with respect to the standard deviation is 88 % at the normal distribution. In his seminal 1960 paper A survey of sampling from contaminated distributions, J. W. Tukey points out that, if the normal distribution is contaminated by a small $\epsilon$-fraction of a normal distribution with three times the standard deviation, the mean deviation is more efficient than the standard deviation—already for $\epsilon < 1\,\%$. In the present article, we examine the efficiency of Gini’s mean difference (the mean of all pairwise distances). Our results may be summarized by saying Gini’s mean difference combines the advantages of the mean deviation and the standard deviation. In particular, an analytic expression for the finite-sample variance of Gini’s mean difference at the normal mixture model is derived by means of the residue theorem, which is then used to determine the contamination fraction in Tukey’s 1:3 normal mixture distribution that renders Gini’s mean difference and the standard deviation equally efficient. We further compute the influence function of Gini’s mean difference, and carry out extensive finite-sample simulations.

1 Introduction

Let $X$ be a random variable with distribution $F$, and define $F^\star _{a,b}$ as the distribution of $a X + b$. We call any function $s$ that assigns a non-negative number to any univariate distribution $F$ (potentially restricted to a subset of distributions, e.g. with finite second moments) a measure of variability, (or a measure of dispersion or simply a scale measure) if it satisfies

$$\begin{aligned} s\left( F^\star _{a,b}\right) = |a|\,s(F) \quad \hbox { for all } a, b \in \mathbb {R}. \end{aligned}$$

(1)

In this article, our focus is on three very common descriptive measures of variability,

• (i) the standard deviation $\sigma (F) = \{ E(X-EX)^2 \}^{1/2}$,

• (ii) the mean absolute deviation (or mean deviation for short) $d(F) = E|X-md(F)|$, where $md(F)$ denotes the median of $F$, and

• (iii) Gini’s mean difference $g(F) = E|X-Y|$.

Here, $X$ and $Y$ are independent and identically distributed random variables with distribution function $F$. Recall that the variance can also be written as $\sigma ^2(F) = E(X-Y)^2/2$. We define the median $md(F)$ as the center point of the set $\{ x \in \mathbb {R}\, |\, F(x-) \le 1/2 \le F(x)\}$, where $F(x-)$ denotes the left-hand side limit. Suppose now we observe data $\mathbb {X}_n = (X_1,\ldots ,X_n)$, where the $X_i$, $i = 1, \ldots , n$, are independent and identically distributed with cdf $F$. Let $\hat{F}_n$ be the corresponding empirical distribution function. The natural estimates for the above scale measures are the functionals applied to $\hat{F}_n$. However, we define the sample versions of the standard deviation and the mean deviation slightly different. Let

• (i) $\displaystyle \sigma _n = \sigma _n(\mathbb {X}_n) = \Big \{ \frac{1}{n-1} \sum _{i=1}^n \left( X_i - \bar{X}_n \right) ^2 \Big \}^{1/2}$ denote the sample standard deviation,

• (ii) $\displaystyle d_n = d_n(\mathbb {X}_n) = \frac{1}{n-1} \sum _{i=1}^n |X_i - md(\hat{F}_n)|$ the sample mean deviation and

• (iii) $\displaystyle g_n = g_n(\mathbb {X}_n) = \frac{2}{n(n-1)} \sum _{1 \le i < j \le n} |X_i - X_j|$ the sample mean difference.

While it is common practice to use $1/(n-1)$ instead of $1/n$ in the definition of the sample variance, due to the thus obtained unbiasedness, it is not so clear which finite-sample version of the mean deviation to use. The factor $1/(n-1)$ does generally not yield unbiasedness, but it leads to a significantly smaller bias in all our finite-sample simulations, see Sect. 4. Little appears to be known for which distributions $d_n$ as defined above is indeed unbiased. The computation of $E(d_n)$ requires the knowledge of the expectations of the order statistics, which are known in principle, but generally rather cumbersome to evaluate analytically. An exception is the uniform distribution, where the order statistics are known to follow a beta distribution, and it turns out that $d_n$ is unbiased for odd $n$, but not for even $n$. For details, see Lemma 1 in “Appendix”. This is also in line with the simulation results reported in Table 7.

Furthermore, there is the question of the location estimator, which applies, in principle, to the mean deviation as well as to the standard deviation, and also to their population versions. While it is again established to use the mean along with the standard deviation, the picture is less clear for the mean deviation. We propose to use the median, mainly due to conceptual reasons: the median minimizes the mean deviation as the mean minimizes the standard deviation. This also suggests to apply the $1/(n-1)$ bias correction in both cases. However, our main results concern asymptotic efficiencies at symmetric distributions, for which the choice of the location measure as well as $n$ versus $n-1$ question is largely irrelevant.

The standard deviation is, with good cause, the by far most popular measure of variability. One main reason for considering alternatives is its lack of robustness, i.e. its susceptibility to outliers and its low efficiency at heavy-tailed distributions. The two alternatives considered here are—in the modern understanding of the term—not robust, but they are more robust than the standard deviation. The extreme non-robustness of the standard deviation, which also emerges when comparing it with the mean deviation, played a vital role in recognizing the need for robustness and thus helped to spark the development of robust statistics, cf. e.g. Tukey (1960). The purpose of this article is to introduce Gini’s mean difference into the old debate of mean deviation versus standard deviation (e.g. Gorard 2005)—not as a compromise, but as a consensus. We will argue that Gini’s mean difference combines the advantages of the standard deviation and the mean deviation.

When proposing robust alternatives to any normality-based standard estimator, the gain in robustness is usually paid by a loss in efficiency at the normal model. The two aspects, robustness and efficiency, have to be analyzed and be put into relation with each other.

As far as the robustness properties are concerned, it is fairly easy to see that all three estimators have an asymptotic breakdown point of zero and an unbounded influence function. There are some slight advantages for the mean deviation and Gini’s mean difference: their influence functions increase linearly as compared to the quadratic increase for the standard deviation, and they require only second moments to be asymptotically normal, as compared to the 4th moments for the standard deviation. The influence functions of the three estimators are given explicitly in Sect. 3. For the standard normal distribution, they are plotted (Fig. 2) and compared to the respective empirical sensitivity curves (Fig. 3). The influence function of Gini’s mean difference appears to not have been published elsewhere.

However, the main concern in this paper is the efficiency of the estimators. We compute and compare their asymptotic variances at several distributions. We restrict our attention to symmetric distributions, since we are interested primarily in the effect of the tails of the distribution, which arguably have the most decisive influence on the behavior of the estimators. We consider in particular the $t_\nu$ distribution and the normal mixture distribution, which are both prominent examples of heavy-tailed distributions, and are often employed in robust statistics to investigate the behavior of estimators in heavy-tailed scenarios. To summarize our findings, in all relevant situations where Gini’s mean difference does not rank first among the three estimators in terms of efficiency, it does rank second with very little difference to the respective winner. A more detailed discussion is deferred to Sect. 5.

We complement our findings by also giving the respective values for the median absolute deviation¹ (MAD, Hampel 1974) and the $Q_n$ by Rousseeuw and Croux (1993). The sample version of the median absolute deviation, which we denote by $m_n = m_n(\mathbb {X}_n)$ is the median of the values $|X_i-md(\hat{F}_n)|$, $1 \le i \le n$, and the corresponding population value $m(F)$ is the median of the distribution of $|X-md(F)|$, where $X \sim F$. The $Q_n$ scale estimator is the $k$th order statistic of the $\left( {\begin{array}{c}n\\ 2\end{array}}\right)$ values $|X_i-X_j|$, $1 \le i < j \le n$, with $k = \left( {\begin{array}{c}\lfloor n/2\rfloor + 1\\ 2\end{array}}\right)$ and will be denoted by $Q_n(\mathbb {X}_n)$. Its population version $Q(F)$ is the lower quartile of the distribution of $|X-Y|$, where $X$ and $Y$ are independent with distribution $F$.² So for the MAD as well as the $Q_n$, we omit any consistency factors, which are often included to render them consistent for $\sigma$ at the normal distribution. These can be deduced from Table 4. However, these estimators are included in the comparison, but not studied here in detail. For the derivation of the respective results, we will refer to the literature. We neither attempt a complete review of scale measures. For background information on robust scale estimation see, e.g., Huber and Ronchetti (2009, Chapter 5). A numerical study comparing many robust scale estimators is given, e.g., by Lax (1985).

The paper is organized as follows: In Sect. 2, asymptotic efficiencies of the scale estimators are compared. We study in particular their asymptotic variances at the normal mixture model. In Sect. 3, the influence functions are computed, and finite-sample simulations results are reported in Sect. 4. Section 5 contains a summary. Proofs are given in “Appendix”.

2 Asymptotic efficiencies

We gather the general expressions for the population values and asymptotic variances of the three scale measures (Sect. 2.1) and then evaluate them at several distributions (Sect. 2.2). We study the two-parameter family of the normal mixture model in some detail in Sect. 2.3.

2.1 General results

If $E X^2 < \infty$, Gini’s mean difference and the mean deviation are asymptotically normal. For the asymptotic normality of $\sigma _n$, fourth moments are required. Strong consistency and asymptotic normality of $g_n$ and $\sigma _n^2$ follow from general $U$-statistic theory (Hoeffding 1948), and thus for $\sigma _n$ by a subsequent application of the continuous mapping theorem and the delta method, respectively.

Letting

$$\begin{aligned} d_n(\mathbb {X}_n,t) = \frac{1}{n-1}\sum _{i=1}^n |X_i - t|, \end{aligned}$$

the asymptotic normality of $d_n(\mathbb {X}_n,t)$ for any fixed location $t$ holds also under the existence of second moments and is a simple corollary of the central limit theorem. Consistency and asymptotic normality of $d_n(\mathbb {X}_n,t_n)$, where $t_n$ is a location estimator, is not equally straightforward (cf. e.g. Bickel and Lehmann 1976, Theorem 5 and the examples below). A set of sufficient conditions is that $\sqrt{n}(t_n-t)$ is asymptotically normal and $F$ is symmetric around $t$. See also Babu and Rao (1992, Theorem 2.5).

Letting $s_n$ be any of the estimators above and $s$ the corresponding population value, we define the asymptotic variance $ASV(s_n) = ASV(s_n;F)$ of $s_n$ at the distribution $F$ as the variance of the limiting normal distribution of $\sqrt{n}(s_n- s)$, when $s_n$ is evaluated at an independent sample $X_1,\ldots ,X_n$ drawn from $F$. We note that, in general, convergence in distribution does not imply convergence of the second moments without further assumptions (uniform integrability), but it is usually the case in situations encountered in statistical applications. Specifically it is true for the estimators considered here, and we may write

$$\begin{aligned} {\textit{ASV}}(s_n) = \lim _{n\rightarrow \infty } n\, \mathrm {var}(s_n). \end{aligned}$$

We are going to compute asymptotic relative efficiencies of $g_n$ and $d_n$ with respect to $\sigma _n$. Generally, for two estimators $a_n$ and $b_n$ with $a_n \mathop {\longrightarrow }\limits ^{p}\theta$ and $b_n \mathop {\longrightarrow }\limits ^{p}\theta$ for some $\theta \in \mathbb {R}$, the asymptotic relative efficiency of $a_n$ with respect to $b_n$ at distribution $F$ is defined as

$$\begin{aligned} {\textit{ARE}}(a_n,b_n; F) = \textit{ASV}(b_n;F)/\textit{ASV}(a_n;F). \end{aligned}$$

In order to make two scale estimators $s_n^{(1)}$ and $s_n^{(2)}$ comparable efficiency-wise, we have to standardize them appropriately, and define their asymptotic relative efficiency at the population distribution $F$ as

$$\begin{aligned} \textit{ARE}(s_n^{(1)},s_n^{(2)};F) \ = \ \frac{\textit{ASV}(s_n^{(2)};F)}{\textit{ASV}(s_n^{(1)};F)} \left\{ \frac{s^{(1)}(F)}{s^{(2)}(F)}\right\} ^2, \end{aligned}$$

(2)

where $s^{(1)}(F)$ and $s^{(2)}(F)$ denote the corresponding population values of the scale estimators $s_n^{(1)}$ and $s_n^{(2)}$, respectively.

The exact finite-sample variance of the empirical variance $\sigma ^2_n$ is

$$\begin{aligned} \mathrm {var}(\sigma _n^2) \ = \ \frac{1}{n}\left\{ \mu _4 - 4\mu _3 \mu _1 + 3\mu _2^2 - 2\sigma ^4 \frac{2n-3}{n-1} \right\} , \end{aligned}$$

(3)

where $\mu _k = EX^k$, $k \in \mathbb {N}$, is the $k$th non-central moment of $X$, in particular $\sigma ^2 = \sigma ^2(F) = \mu _2 - \mu _1^2$. Thus $ASV(\sigma ^2_n) = \mu _4 + 3\mu _2^2 - 4\left\{ \mu _3 \mu _1 + \sigma ^4\right\}$, and hence we have by the delta method

$$\begin{aligned} \textit{ASV}(\sigma _n) = \frac{\mu _4 - 4\mu _3 \mu _1 + 3\mu _2^2}{4\sigma ^2} - \sigma ^2. \end{aligned}$$

(4)

Formula (3) appears to be a classical textbook example, but we did not find a reference for this general form. The special case $\mu _1 = 0$ is stated, e.g., in Kenney and Keeping (1952, p. 164).

If the distribution $F$ is symmetric around $E(X)=\mu _1$ and has a Lebesgue density $f$, the mean deviation $d = d(F)$ can be written as

$$\begin{aligned} d \ = \int _{-\infty }^{\infty } |x-\mu _1| f(x)\, dx \ = \ 2 \int _{\mu _1}^{\infty } (x-\mu _1) f(x)\, dx \end{aligned}$$

(5)

The asymptotic variance of $d_n$ is $\textit{ASV}(d_n) = \sigma ^2 - d^2$. See, e.g., Pham-Gia and Hung (2001) for a review on the properties of the mean deviation.

For any $F$ possessing a Lebesgue density $f$, Gini’s mean difference $g = g(F)$ is

$$\begin{aligned} g \ = \ \int _{-\infty }^{\infty } \int _{-\infty }^{\infty } |x - y|\, f(x)\, f(y)\, dy\, dx \ = \ 2 \int _{-\infty }^{\infty } \int _{x}^{\infty } (y - x)\, f(x)\, f(y)\, dy\, dx, \end{aligned}$$

(6)

which can be further reduced to

$$\begin{aligned} g \ = \ 4 \int _{-\infty }^{\infty } \int _{x}^{\infty } y \, f(y) \, dy\, f(x)\, dx \ = \ 8 \int _{0}^{\infty } \int _{x}^{\infty } y \, f(y) \, dy\, f(x)\, dx \end{aligned}$$

(7)

if $F$ is symmetric around 0. Lomnicki (1952) gives the variance of the sample mean difference $g_n$ as

$$\begin{aligned} \mathrm {var}(g_n) = \frac{1}{ n(n-1) } \left\{ 4(n-1) \sigma ^2 + 16 (n-2) J - 2 (2n-3) g^2 \right\} , \end{aligned}$$

(8)

where

$$\begin{aligned} J = J(F) = \int _{x = -\infty }^{\infty } \int _{y = -\infty }^{x} \int _{z = x}^{\infty } (x-y)(z-x) f(z) f(y) f(x)\, dz\, dy\, dx. \end{aligned}$$

(9)

Thus, the asymptotic variance of $g_n$ is $ASV(g_n) = 4 \{ \sigma ^2 + 4 J - g^2 \}$.

2.2 Specific distributions

Table 1 lists the densities and first four moments of the following distribution families: normal, Laplace, uniform, $t_\nu$ and normal mixture.

Table 1 Densities and non-central moments of several parametric families

The normal mixture distribution $N\!M(\lambda ,\epsilon )$, sometimes also referred to as contaminated normal distribution, is defined as

$$\begin{aligned} N\!M(\lambda ,\epsilon ) \ = \ (1-\epsilon ) N(0,1) + \epsilon N(0,\lambda ^2), \quad 0 \le \epsilon \le 1, \lambda \ge 1. \end{aligned}$$

For these distribution families, expressions for $\sigma (F)$, $d(F)$ and the asymptotic variances of their sample versions are given in Table 2, and for Gini’s mean difference, including the integral $J$, in Table 3. The contents of Table 2 are well known and straightforward to derive. The results for Gini’s mean difference require the evaluation of the integrals (7) and (9), which is non-trivial for many distributions. The expressions for the normal case are due to Nair (1936). Results for the normal mixture distribution and the $t_\nu$ are subject of the following two theorems.

Table 2 Specific values of $\sigma$, $d$ and the respective asymptotic variances for the distribution families given in Table 1

Table 3 Population values, cf. (6), expressions for $J$, cf. (9), and resulting asymptotic variances for Gini’s mean difference at the parametric families of Table 1

Theorem 1

At the normal mixture distribution $NM(\lambda ,\epsilon )$, $0 \le \epsilon \le 1$, $\lambda \ge 1$, the value of Gini’s mean difference is

$$\begin{aligned} g(N\!M(\lambda ,\epsilon )) = \frac{2}{\sqrt{\pi }} \Big \{ \lambda \epsilon ^2 + (1-\epsilon )^2 \, + \epsilon (1-\epsilon )\sqrt{2\left( 1+\lambda ^2\right) } \Big \} \end{aligned}$$

and the value of the integral $J$, cf. (9), is

$$\begin{aligned}&J(N\!M(\lambda ,\epsilon )) \ = \ \Big (\frac{1}{3}+\frac{\sqrt{3}}{2\pi }\Big ) \{ \epsilon ^3 \lambda ^2 + (1-\epsilon )^3 \} \ - \ \frac{\epsilon \lambda ^2 + 1 - \epsilon }{2} \\&\quad + \ \epsilon ^2(1-\epsilon ) \bigg [ \frac{\lambda ^2}{2} + \frac{1}{4} + \frac{3 \lambda \zeta (\lambda )}{2 \pi } + \frac{\lambda ^2}{\pi } {{\mathrm{atan}}}\Big \{ \frac{\lambda }{\zeta (\lambda )}\Big \} + \frac{1}{2\pi } {{\mathrm{atan}}}\Big \{ \frac{1}{\lambda \zeta (\lambda )} \Big \} \bigg ] \\&\quad + \ \epsilon (1-\epsilon )^2 \bigg [ \frac{\lambda ^2}{4} + \frac{1}{2} + \frac{3 \sqrt{1+2\lambda ^2}}{2\pi } + \frac{\lambda ^2}{2\pi } {{\mathrm{atan}}}\Big \{\frac{\lambda }{\zeta (1/\lambda )}\Big \} + \frac{1}{\pi } {{\mathrm{atan}}}\Big \{ \frac{1}{\lambda \zeta (1/\lambda )} \Big \} \bigg ], \end{aligned}$$

where $\zeta (\lambda ) = \sqrt{2+\lambda ^2}$.

Theorem 2

The value of Gini’s mean difference at the $t_\nu$ distribution, $\nu > 1$, is

$$\begin{aligned} g(t_\nu ) = \frac{4\sqrt{\nu }}{\nu -1} \frac{B\big (\frac{\nu }{2}+\frac{1}{2},\, \nu - \frac{1}{2}\big )}{ B\big (\frac{\nu }{2}, \frac{1}{2}\big ) B\big (\frac{\nu }{2}, \,\nu \big ) }, \end{aligned}$$

where $B(\,\cdot \, ,\, \cdot \,)$ denotes the beta function. The value of the integral $J$, cf. (9), at the $t_\nu$ distribution, $\nu > 2$, is

$$\begin{aligned} J(t_\nu ) = \frac{2\, \nu }{(\nu -1)^2} \frac{ B\big (\frac{3 \nu }{2}-1,\, \frac{1}{2}\big ) }{ B\big (\frac{\nu }{2}, \frac{1}{2}\big )^3} -\frac{\nu }{2(\nu -2)} + \int _{-\infty }^{\infty } x^2 f_\nu (x) F_\nu ^2(x) \, dx. \end{aligned}$$

where $F_\nu$ and $f_\nu$ are the cdf and the density, respectively, of the $t_\nu$ distribution.

Resulting numerical values of the three scale measures and their asymptotic variances are listed in Tables 4 and 5. Table 6 contains the corresponding asymptotic relative efficiencies, cf. (2), with respect to the standard deviation.

Table 4 Values of the standard deviation $\sigma$, Gini’s mean difference $g$, the mean absolute deviation $d$, the median absolute deviation $m$ and the $Q_n$ scale measure at the standard normal distribution $N(0,1)$, the standard Laplace distribution $L(0,1)$, the uniform distribution $U(0,1)$ and several members of the $t_\nu$ family and the normal mixture family $N\!M(\lambda ,\epsilon )$

Table 5 Asymptotic variances of the standard deviation $\sigma _n$, Gini’s mean difference $g_n$, the mean absolute deviation $d_n$, the median absolute deviation $m_n$ and the $Q_n$ scale estimator at the standard normal distribution $N(0,1)$, the standard Laplace distribution $L(0,1)$, the uniform distribution $U(0,1)$ and several members of the $t_\nu$ family and the normal mixture family $N\!M(\lambda ,\epsilon )$

Table 6 Asymptotic relative efficiencies of Gini’s mean difference $g_n$, the mean absolute deviation $d_n$, the median absolute deviation $m_n$ and the $Q_n$ scale estimator at the standard normal distribution $N(0,1)$, the standard Laplace distribution $L(0,1)$, the uniform distribution $U(0,1)$ and several members of the $t_\nu$ family and the normal mixture family $N\!M(\lambda ,\epsilon )$

In particular, we have at the normal model

$$\begin{aligned}&\textit{ARE}(g_n, \sigma _n) = \left\{ \frac{2}{3} \pi + 4 (\sqrt{3}-2) \right\} ^{-1} = 0.9779, \\&\textit{ARE}(d_n, \sigma _n) = \frac{1}{\pi - 2} = 0.876, \end{aligned}$$

and at the Laplace (or double exponential) model

$$\begin{aligned} \textit{ARE}(g_n, \sigma _n) = 135/112 = 1.2054, \quad ARE(d_n, \sigma _n) = 5/4. \end{aligned}$$

The mean deviation (with scaling $1/n$) is the maximum likelihood estimator of the scale parameter $\alpha$ of the Laplace distribution, cf. Table 1. Thus, at the normal as well as the Laplace distribution, Gini’s mean difference has an efficiency of more than 96 % with respect to the respective maximum likelihood estimator.

Furthermore, we observe that Gini’s mean difference $g_n$ is asymptotically more efficient than the standard deviation $\sigma _n$ at the $t_\nu$ distribution for $\nu \le 40$. The mean deviation $d_n$ is asymptotically more efficient than $\sigma _n$ for $\nu \le 15$ and more efficient than $g_n$ for $\nu \le 8$. Thus in the range $9 \le \nu \le 40$, Gini’s mean difference is the most efficient of the three.

One can view the uniform distribution as a limiting case of very light tails. While our focus is on heavy-tailed scenarios, we include the uniform distribution in our study as a simple approach to compare the estimators under light tails. We find a similar picture as under normality: Gini’s mean difference and the standard deviation perform equally well, while the mean deviation has a substantially lower efficiency. However, it must be noted that the uniform distribution itself is rarely encountered in practice. The limited range is a very strong information, which allows a super-efficient inference.

The numerical results of Tables 1, 2 and 3 are rounded off by the respective values for the MAD and $Q_n$. Analytical expressions are generally not available for these estimators, and their population values and asymptotic variances are obtained from the general expressions given in Hall and Welsh (1985) and Rousseeuw and Croux (1993), respectively.

Finally, we take a closer look at the normal mixture distribution and explain our choices for $\lambda$ and $\epsilon$ in Table 6.

2.3 The normal mixture distribution

The normal mixture distribution captures the notion that the majority of the data stems from the normal distribution, except for some small fraction $\epsilon$ which stems from another, usually heavier-tailed, contamination distribution. In case of the normal mixture model, this contamination distribution is the Gaussian distribution with standard deviation $\lambda$. This type of contamination model has been popularized by Tukey (1960), who also argues that $\lambda = 3$ is a sensible choice in practice.

It is sufficient to consider the case $\lambda \ge 1$, since the parameter pair $(\lambda ,\epsilon )$ yields (up to scale) the same distribution as $(1/\lambda ,1-\epsilon )$. Now, letting $\lambda > 1$, the case where $\epsilon$ is small is the interesting one. In this case the mixture distribution is heavy-tailed (measured, say, by the kurtosis) which strongly affects the behavior of our scale measures. The case $\epsilon$ close to 1 is of lesser interest: it corresponds to a normal distribution with a contamination concentrated at the origin, which affects the scale measures to a much lesser extent.

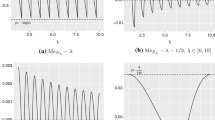
From the expressions for $\sigma$, $d$ and the corresponding asymptotic variances, as given in Table 2, we obtain the asymptotic relative efficiency $\textit{ARE}(d_n,\sigma _n)$ as a function of $\lambda$ and $\epsilon$. This function is plotted in Fig. 1 (top left). The parameter $\epsilon$ is on a log-scale since we are primarily interested in small contamination fractions. Fixing $\lambda = 3$, we find that for $\epsilon = 0.00175$, the mean deviation is as efficient as the standard deviation. It is interesting to note that Tukey (1960) gives a value of $\epsilon = 0.008$, which is frequently reported. In Huber and Ronchetti (2009, p. 3), correct values are given. The more precise value of $0.00175$ is also in line with the simulation results of Sect. 4, and it supports even more so Tukey’s main message: the percentage of contamination in the 1:3 normal mixture model for which the mean deviation becomes more efficient than the standard deviation is surprisingly low.

Fig. 1

Top row asymptotic relative efficiencies of the mean deviation (left) and Gini’s mean difference (right) wrt the standard deviation in the normal mixture model as a function of $\lambda$ and $\log (\epsilon )$. Bottom the curves for which values of $\lambda$ and $\epsilon$ the scale measures have the same asymptotic efficiency

The asymptotic relative efficiency $\textit{ARE}(g_n,\sigma _n)$ of Gini’s mean difference with respect to the standard deviation is depicted in the upper right plot of Fig. 1. For $\lambda = 3$, Gini’s mean difference is as efficient as the standard deviation for $\epsilon$ as small as $0.000309$. In the lower plot of Fig. 1, equal-efficiency curves are drawn. They represent those parameter values $(\lambda ,\epsilon )$ for which each two of the scale measures have equal asymptotic efficiency. So for instance, the solid black line corresponds to the contour line at height 1 of the 3D surface depicted in the top right plot.

3 Influence functions

The influence function $I\!F(\cdot ,s,F)$ of a statistical functional $s$ at distribution $F$ is defined as

$$\begin{aligned} I\!F(x,s,F) = \lim _{\epsilon \searrow 0} \frac{1}{\epsilon } \{ s(F_{\epsilon ,x}) - s(F) \}, \end{aligned}$$

where $F_{\epsilon ,x} = (1-\epsilon )F + \epsilon \Delta _x$, $0 \le \epsilon \le 1$, $x \in \mathbb {R}$, and $\Delta _x$ denotes Dirac’s delta, i.e., the probability measure that puts unit mass in $x$. The influence function describes the impact of an infinitesimal contamination at point $x$ on the functional $s$ if the latter is evaluated at distribution $F$. For further reading see, e.g., Huber and Ronchetti (2009) or Hampel et al. (1986). The influence functions of the standard deviation and the mean deviation are well known:

$$\begin{aligned}&I\!F(x,\sigma (\cdot );F) \ = \ (2\sigma (F))^{-1}\{ (E(X) - x)^2 - \sigma ^2(F) \}, \\&I\!F(x,d(\cdot ); F) \ = \ |x-md(F)| - d(F). \end{aligned}$$

For the formula for $d(\cdot )$ to hold in the last display, $F$ has to fulfill certain regularity conditions in the vicinity of its median $md(F)$. Specifically, $(md(F_{\epsilon ,x})-md(F)) = O(\epsilon )$ as $\epsilon \rightarrow 0$ for all $x \in \mathbb {R}$ and $F(md(F_{\epsilon ,x})) \rightarrow 1/2$ are a set of sufficient conditions. They are fulfilled, e.g., if $F$ possesses a positive Lebesgue density in a neighborhood of $md(F)$. The influence function of Gini’s mean difference appears to not have been published before.

Proposition 1

The influence function of Gini’s mean difference $g$ at the distribution is

$$\begin{aligned} I\!F(x,g(\cdot ); F) = 2 \left\{ x [ F(x) + F(x-) - 1 ] + E[X 1\!\!1_{ \{ X\ge x \} } ] - E[X 1\!\!1_{ \{ X \le x \} } ] - g(F) \right\} . \end{aligned}$$

For the standard normal distribution, these expressions for the influence functions of the three scale measures reduce to

$$\begin{aligned}&I\!F(x,\sigma (\cdot );N(0,1)) \ = \ (x^2-1)/2, \\&I\!F(x,d(\cdot ); N(0,1)) \ = \ |x| - \sqrt{2/\pi }, \\&I\!F(x,g(\cdot ); N(0,1)) \ = \ 4\phi (x) + 2 x \{ 2\varPhi (x) - 1 \} - 4/\sqrt{\pi }, \end{aligned}$$

where $\phi$ and $\varPhi$ denote the density and the cdf of the standard normal distribution, respectively. These curves are depicted in Fig. 2. Figure 3 shows empirical versions of the influence functions. Let $\mathbb {X}_n$ be a sample of size $n$ drawn from $N(0,1)$, and let $\mathbb {X}_n'(x)$ be the sample obtained from $\mathbb {X}_n$ by replacing the first observation by the value $x \in \mathbb {R}$. Then $n \{ s_n(\mathbb {X}_n'(x)) - s_n(\mathbb {X}_n) \}$ is called a sensitivity curve for the estimator $s_n$ (e.g. Huber and Ronchetti 2009, p. 15). Sensitivity curves usually strikingly resemble the corresponding influence function also for very moderate $n$. In Fig. 3, average sensitivity curves for $\sigma _n$, $d_n$ and $g_n$ are drawn (averaged over 10,000 samples of size $n =100$). Figures 2 and 3 confirm the general impression mediated by Table 6 that Gini’s mean difference is in-between the standard and the mean deviation, and support our claim that it combines the advantages of the other two: its influence function grows linearly for large $|x|$, but it is smooth at the origin.

Fig. 2

Influence functions of the standard deviation, the mean deviation and Gini’s mean difference at the standard normal distribution

Fig. 3

Empirical influence functions (averaged sensitivity curves for $n=100$, averaged over 10,000 samples) of the standard deviation, the mean deviation and Gini’s mean difference at the standard normal distribution

The influence functions of the MAD and the $Q_n$ can be found in Huber and Ronchetti (2009, p. 136) and Rousseeuw and Croux (1993), respectively.

4 Finite sample efficiencies

In a simulation study we want to check if the asymptotic efficiencies computed in Sect. 2 are useful approximations for the actual efficiencies in finite samples. For this purpose we consider the following nine distributions: the standard normal $N(0,1)$, the standard Laplace $L(0,1)$ (with parameters $\mu =0$ and $\alpha = 1$, cf. Table 1), the uniform distribution $U(0,1)$ on the unit interval, the $t_\nu$ distribution with $\nu = 5, 16, 41$ and the normal mixture with the parameter choices as in Tables 4, 5 and 6. The choice $\nu = 5$ serves as a heavy-tailed example, whereas for $\nu = 16$ and $\nu = 41$ we have witnessed at Table 6 that the mean deviation and the Gini mean difference, respectively, are asymptotically as efficient as the standard deviation.

For each distribution and each of the sample sizes $n = 5, 8, 10, 50, 500$, we generate 100,000 samples and compute from each sample five scale measures: the three moment-based estimators $\sigma _n$, $d_n$, $g_n$, and the two quantile-based estimators $m_n$ and $Q_n$. The results for $N(0,1)$, $L(0,1)$ and $U(0,1)$ are summarized in Table 7, for the $t_\nu$ distributions in Table 8, and for the normal mixture distributions in Table 9.

Table 7 Simulated variances, biases and relative efficiencies of $\sigma _n$, $g_n$, $d_n$, $m_n$ and $Q_n$ at $N(0,1)$, $L(0,1)$ and $U(0,1)$ for several sample sizes, $d_n^*$: mean deviation with $1/n$ scaling

Table 8 Simulated variances, biases and relative efficiencies of $\sigma _n$, $g_n$, $d_n$, $m_n$ and $Q_n$ at $t_\nu$ distributions for several sample sizes and values of $\nu$; $d_n^*$: mean deviation with $1/n$ scaling

Table 9 Simulated variances, biases and relative efficiencies of $\sigma _n$, $g_n$, $d_n$, $m_n$ and $Q_n$ at normal mixture distributions for $\lambda =3$ and $\epsilon = 0.008, 0.00175, 0.000309$; $d_n^*$: mean deviation with $1/n$ scaling

For each estimate, population distribution and sample size, the following numbers are reported: the sample variance of the 100,000 estimates multiplied by the respective value of $n$ (the “$n$-standardized variance” which approaches the asymptotic variance given in Table 5 as $n$ increases), the squared bias relative to the variance, and the relative efficiencies with respect to the standard deviation. With this information (variance and the squared-bias-to-variance ratio) the mean squared error is also implicitly given. For the relative efficiency computation, it is important to note that the standardization, cf. (2), is done not by the asymptotic value, but by the empirical finite-sample value, i.e. the sample mean of the 100,000 estimates. For Gini’s mean difference, the simulated variances are also compared to the true finite-sample variances, cf. (8).

We observe the following: For large and moderate sample sizes ($n = 50, 500$), the simulated values are near the asymptotic ones from Tables 4, 5 and 6, and we may conclude that the asymptotic efficiency generally provides a useful indication for the actual efficiency in large samples, although to a much lesser extent for the quantile-based estimators.

In small samples, however, the simulated relative efficiencies may substantially differ from the asymptotic values. The ranking of the three moment-based estimators stays the same, but for the quantile-based estimators the picture is different: they exhibit quite a heavy bias for small samples, potentially of the same magnitude as the standard deviation of the estimator, complicating the comparison of the estimators. It is known that the finite-sample behavior, in terms of bias as well as variance, of robust quantile-based estimators in general may largely differ from the asymptotic approximation, particularly so in the case of the $Q_n$. Most striking certainly is the bias increase from $n=5$ to $n=8$ for the mean deviation $d_n$ and, much more tremendously, for the $Q_n$. In case of the mean deviation, the reason lies in the different behavior of the sample median for odd and even numbers of observations, cf. also Lemma 1 in “Appendix”. As for the $Q_n$, the definition of its sample version (see end of Sect. 1) also implies a qualitatively different behavior depending on whether $n$ is odd or even. Specifically, for $n=5$, the 3rd order statistic of 10 values is taken, whereas for $n=8$, the 10th order statistic out of 28 observations is taken, both being compared to the 1/4 quantile of the respective population distribution. To reduce the bias as well as finite-sample variance, a smoothed version of the $Q_n$ (i.e. a suitable linear combination of several order statistics) is certainly worth considering, for which the price to pay would be a small loss in the breakdown point.

We also include the mean deviation with factor $1/n$ instead of $1/(n-1)$ in the study, denoted by $d_n^*$ in the tables. Since $d_n$ and $d_n^*$ differ only by multiplicative factor, the efficiencies are the same, and we only report the (squared) bias (relative to the variance). We find that $d_n^*$ is quite heavily biased for small samples for all distributions considered, whereas $d_n$ has in all situations a smaller bias than $\sigma _n$. Particularly, note that the bias of $d_n$ at the uniform distribution is indeed zero for $n=5$, but not for even $n$, cf. Lemma 1 in “Appendix”.

Finally, the simulations confirm the unbiasedness of Gini’s mean difference and the formula (8), due to Lomnicki (1952), for its finite-sample variance.

The simulations were done in R (R Development Core Team 2010), using the function Qn() from the package robustbase (Rousseeuw et al. 2014), the function mad() from the standard package stats, and an implementation for Gini’s mean difference by A. Azzalini.³ The default setting for both functions Qn() and mad() is to multiply the result by the asymptotic consistency factor for the standard deviation at normality, which is, for both functions, controlled by the parameter constant. This parameter was set to 1 in our simulations.

5 Summary and discussion

Several authors have argued that, when comparing the standard deviation with the mean deviation, the better robustness of the latter is a crucial advantage, which outweighs its disadvantages, and that the mean deviation is hence to be preferred out of the two. We share this view. However, we recommend to use Gini’s mean difference instead of the mean deviation. While it has qualitatively the same robustness and the same efficiency under long-tailed distributions as the mean deviation, it lacks its main disadvantage as compared the standard deviation: the lower efficiency at strict normality. For near-normal distributions—and also for very light-tailed distribution, as the results for the uniform distribution suggest—Gini’s mean difference and the standard deviation are for all practical purposes equally efficient. For instance, at the normal and all $t_\nu$ distributions with $\nu \ge 23$, the (properly standardized) asymptotic variances of $g_n$ and $\sigma _n$ are within a 3 % margin of each other. At heavy-tailed distributions, Gini’s mean difference is, along with the mean deviation, substantially more efficient than the standard deviation.

To summarize our efficiency comparison, Gini’s mean difference performs well over a wide range of distributions, including much heavier than normal tails. Here we basically consider the range up to the $t_5$ distribution, where no higher than fourth moments exist, and within this range, Gini’s mean difference is clearly non-inferior to all competitors considered here.

However, the main advantage of Gini’s mean difference is its finite-sample performance. First of all, being a $U$-statistic, it is unbiased—at all distributions with finite first moments. We do not know any other scale measure satisfying (1) of practical relevance for which this is true. Second, its finite-sample variance is known, which allows for instance better approximative confidence intervals. Neither of that is true for the standard deviation, and one can consequently argue that Gini’s mean difference is a superior scale estimator even under strict normality. The latter statement is also a remark on the discussion by Yitzhaki (2003), who compares Gini’s mean difference primarily to the variance.

When comparing Gini’s mean difference to the mean deviation, both being similar $L_1$-type measures, the question arises, if an intuitive explanation can be given to why the former is more efficient at the normal distribution but less efficient at heavy tails. We leave this as an open question here. However, since Gini’s mean difference can be viewed as a symmetrized version of the mean deviation, we remark that a similar effect can be observed in many instances of symmetrization. Other examples include the Hodges–Lehmann location estimator as a symmetrized version of the median, or Kendall’s tau as a symmetrized verion of the quadrant correlation. In both cases, the original estimator has a rather low efficiency under normality, which is considerably increased by symmetrization, but the symmetrized estimator performs slightly worse at very heavy-tailed models. The median, for instance, is more efficient than the Hodges–Lehmann estimator at a $t_3$ distribution. But in general, symmetrization is a successful technique to increase the efficiency of highly robust estimators while retaining a large degree of robustness. The most prominent example may be the $Q_n$, the symmetrized version of the MAD.

Appendices

Appendix 1: Proofs

Towards the proof of Theorem 1, we spare a few words about the derivation of the corresponding result for the normal distribution. When evaluating the integral $J$, cf. (9), for the standard normal distribution, one encounters the integral

$$\begin{aligned} I_1 = \int _{-\infty }^{\infty } x^2 \phi (x) \varPhi (x)^2 dx, \end{aligned}$$

where $\phi$ and $\varPhi$ denote the density and the cdf of the standard normal distribution, respectively. Nair (1936) gives the value $I_1 = 1/3 + 1/(2\pi \sqrt{3})$, resulting in $J = \sqrt{3}/(2 \pi ) - 1/6$, but does not provide a proof. The author refers to the derivation of a similar integral (integral 8 in Table I, Nair 1936, p. 433), where we find the result as well as the derivation doubtful, and to an article by Hojo (1931), which gives numerical values for several integrals, but does not contain an explanation for the value of $I_1$ either. We therefore include a proof here. Writing $\varPhi (x)$ as the integral of its density and changing the order of the integrals in thus obtained three-dimensional integral yields

$$\begin{aligned} I_1 = (2\pi )^{-3/2} \int _{y=-\infty }^0 \int _{z=\infty }^0 \int _{x=-\infty }^\infty x^2 e^{x^2/2} e^{(y+x)^2/2} e^{(z+x)^2/2} \, d x\, d z\, d y. \end{aligned}$$

Solving the inner integral, we obtain

$$\begin{aligned} I_1 = (18\pi \sqrt{3})^{-1} \int _{y=0}^\infty \int _{z=0}^\infty [ (y+z)^2 + 3 ] \exp \left\{ - \frac{1}{3} \left[ y^2 + z^2 - y z \right] \right\} \, d z\, d y. \end{aligned}$$

Introducing polar coordinates $\alpha , r$ such that $y = r \cos \alpha$, $z = r \sin \alpha$, and solving the integral with respect to $r$, we arrive at

$$\begin{aligned} I_1 = \frac{1}{4\pi \sqrt{3}} \int _{\alpha =0}^\pi \frac{4+\sin \alpha }{(2-\sin \alpha )^2} \, d \alpha . \end{aligned}$$

This remaining integral may be solved by means of the residue theorem (e.g. Ahlfors 1966, p. 149). Substituting $\gamma = e^{i \alpha }$ and using $\sin \alpha = (e^{i \alpha } - e^{- i \alpha })/(2i)$, we transform $I_1$ into the following line integral in the complex plane,

$$\begin{aligned} I_1 = \frac{1}{4\pi \sqrt{3}} \int _{\varGamma _0} \frac{\gamma ^2 + 8 i \gamma -1 }{(\gamma ^2- 4 i \gamma -1 )^2} \, d \gamma , \end{aligned}$$

(10)

where $\varGamma _0$ is the upper unit half circle in the complex plane, cp. Fig. 4. Let us call $h$ the integrand in (10), its poles (both of order two) are $\gamma _{1/2} = (2\pm \sqrt{3})i$, so that $\gamma _2$ lies within the closed upper half unit circle $\varGamma$. The residue of $h$ in $\gamma _2$ is $-\sqrt{3} i /2$. Integrating $h$ along $\varGamma _1$, i.e. the real line from $-$1 to 1, cf. Fig. 4, and applying the residue theorem to the closed line integral along $\varGamma$ completes the derivation.

Fig. 4

Residue theorem: the line integral over $h$ along the closed curve $\varGamma =\varGamma _0\, \cup \, \varGamma _1$ is determined by the residue of $h$ in $\gamma _2$

Proof

(Proof of Theorem 1)

Evaluating the integral $J$ for the normal mixture distribution, we arrive after lengthy calculations at

$$\begin{aligned} J= & {} \Big [ \epsilon ^3 \lambda ^2 + (1-\epsilon )^3 \Big ] \Big [ 2 A(1) + C(1) + E(1) \Big ] \ - \ (\epsilon \lambda ^2 + 1 - \epsilon )B \\&\quad + \ \epsilon ^2(1-\epsilon ) \Big [ 2 (2+ \lambda ^2) A(1/\lambda ) + C(\lambda ) + 2\lambda ^2 D(1/\lambda )+ \lambda (2+ \lambda ^2)E(1/\lambda ) \Big ] \\&\quad + \ \epsilon (1-\epsilon )^2 \Big [ 2 (2\lambda ^2+ 1 ) A(\lambda ) + \lambda ^2C(1/\lambda ) + 2 D(\lambda )+ (\lambda ^{-1} + 2 \lambda )E(\lambda ) \Big ], \end{aligned}$$

where

$$\begin{aligned} A(\lambda )= & {} \int _{-\infty }^\infty x \phi ^2(x) \varPhi (x/\lambda ) dx \ = \ \frac{1}{4 \pi \sqrt{ 1 + 2 \lambda ^2 }}, \quad \\ B= & {} \int _{-\infty }^\infty x^2 \phi (x) \varPhi (x) dx \ = \ \frac{1}{2}, \\ C(\lambda )= & {} \int _{-\infty }^\infty x^2 \phi (x) \varPhi ^2(x/\lambda ) dx \ = \ \frac{1}{4} + \frac{\lambda }{\pi (1 + \lambda ^2)\sqrt{ 2 + \lambda ^2 }}\\&+ \frac{1}{2 \pi } \arctan \left( \frac{1}{\lambda \sqrt{2+\lambda ^2}}\right) , \\ D(\lambda )= & {} \int _{-\infty }^\infty x^2 \phi (x) \varPhi (x) \varPhi (x/\lambda ) dx \ = \ \frac{1}{4} + \frac{3\lambda ^2 + 1}{4 \pi (1 + \lambda ^2)\sqrt{ 2 \lambda ^2 + 1 }}\\&+ \frac{1}{2 \pi } \arctan \left( \frac{1}{\sqrt{2\lambda ^2+ 1}}\right) , \\ E(\lambda )= & {} \int _{-\infty }^\infty \phi ^2(x) \phi (x/\lambda ) dx \ = \ \frac{1}{2 \pi \sqrt{ 1 + 2 \lambda ^2 }}, \end{aligned}$$

for all $\lambda > 0$. As before, $\phi$ and $\varPhi$ denote the density and the cdf of standard normal distribution. The tricky integrals are $C(\lambda )$ and $D(\lambda )$, which, for $\lambda = 1$, both reduce to the integral $I_1$ above. Proceeding as before for the integral $I_1$, solving the respective two inner integrals yields

$$\begin{aligned}&C(\lambda ) = \frac{\lambda ^3}{2 \pi \sqrt{2+\lambda ^2}} \int _0^{\pi /2} \frac{ 3 + \lambda ^2 + \sin (2\alpha )}{ \{1 + \lambda ^2 - \sin (2 \alpha )\}^2} d\alpha , \\&D(\lambda ) = \frac{1}{2 \pi \sqrt{1+2\lambda ^2}} \int _0^{\pi /2} \frac{ 2 + \lambda ^2 (2+ \sin (2\alpha )) + (3\lambda ^4 - \lambda ^2 - 2) \sin ^2(\alpha )}{ \{ 2 - \sin (2\alpha ) + (\lambda ^2-1) \sin ^2(\alpha ) \}^2 } d \alpha . \end{aligned}$$

These integrals are again solved by the residue theorem, which completes the proof. $\square$

For the proof of Theorem 2, the following identities are helpful:

$$\begin{aligned}&\textstyle \int x \left( 1 + \frac{x^2}{\beta } \right) ^\alpha dx \ = \ \frac{\beta }{2(\alpha +1)} \left( 1 + \frac{x^2}{\beta }\right) ^{\alpha +1}, \quad \alpha \ne -1, \ \beta \ne 0. \end{aligned}$$

(11)

$$\begin{aligned}&\textstyle \int _{-\infty }^\infty \left( 1 + \frac{x^2}{\nu }\right) ^{-\nu } dx \ = \ \frac{1}{c_{2\nu -1}} \sqrt{\frac{\nu }{2\nu -1}}, \quad \nu > 0, \end{aligned}$$

(12)

$$\begin{aligned}&\textstyle \int _{-\infty }^\infty \left( 1 + \frac{x^2}{\nu }\right) ^{-\frac{3\nu -1}{2}} dx \ = \ \frac{1}{c_{3\nu -2}} \sqrt{\frac{\nu }{3\nu -2}}, \quad \nu > 0, \end{aligned}$$

(13)

where $c_{\nu }$ is the scaling factor of the $t_\nu$ density, cf. Table 1. The identities (12) and (13) can be obtained by transforming the respective left-hand sides into a $t_\nu$-densities by substituting $y = ((2\nu -1)/\nu )^{1/2} \, x$ and $y = ((3\nu -2)/\nu )^{1/2}\, x$, respectively.

Proof

(Proof of Theorem 2) For computing $g$, we evaluate (7), successively making use of (11) and (12), and obtain

$$\begin{aligned} g \ = \ 4 \frac{ \nu \, c_\nu ^2}{\nu -1} \int _{-\infty }^{\infty } \Big ( 1 + \frac{x^2}{\nu } \Big )^{-\nu } \, dx \ = \ \frac{4 \, \nu ^{3/2} \, c_{\nu }^2}{(\nu -1)\, \sqrt{2\nu -1}\, c_{2\nu -1}}, \end{aligned}$$

which can be written as in Theorem 2 by using $B(x,y) = \varGamma (x)\varGamma (y)/\varGamma (x+y)$. For evaluating $J$, we write $J$ as $J = \int _\mathbb {R}A(x) f_{\nu }(x)\, dx$ with $f_\nu$ being the $t_\nu$ density and

$$\begin{aligned} A(x)= & {} \int _{-\infty }^x \int _x^{\infty } x z f_\nu (z) f_\nu (y) \,dz\, dy \ - \ \int _{-\infty }^x \int _x^{\infty } y z f_\nu (z) f_\nu (y) \,dz\, dy \\&- \int _{-\infty }^x \int _x^{\infty } x^2 f_\nu (z) f_\nu (y) \,dz\, dy \ + \ \int _{-\infty }^x \int _x^{\infty } x y f_\nu (z) f_\nu (y) \,dz\, dy \\= & {} A_1(x) - A_2(x) - A_3(x) + A_4(x). \end{aligned}$$

Using (11), we obtain

$$\begin{aligned} A_1(x) + A_4(x) \ = \ \frac{c_\nu \, \nu \, x}{\nu -1}\left( 1 + \frac{x^2}{\nu } \right) ^{-\frac{\nu -1}{2}} \, \int _{-x}^x f_\nu (y) \, dy, \end{aligned}$$

and

$$\begin{aligned} - A_2(x) \ = \ \left( \frac{c_\nu \,\nu }{\nu -1} \right) ^2 \, \left( 1+ \frac{x^2}{\nu }\right) ^{-\nu +1}. \end{aligned}$$

Hence, $J = B_1 + B_2 - B_3$ with

$$\begin{aligned} \textstyle&B_1 \ = \ \int _{-\infty }^{\infty } \frac{c_\nu \, \nu \, x}{\nu -1} \left( 1 + \frac{x^2}{\nu } \right) ^{-\frac{\nu -1}{2}} f_\nu (x) \, \int _{-x}^x f_\nu (y) \, dy \, dx, \\&\textstyle B_2 \ = \ \int _{-\infty }^{\infty } \left( \frac{c_\nu \,\nu }{\nu -1} \right) ^2 \, \left( 1+ \frac{x^2}{\nu }\right) ^{-\nu +1} \! f_\nu (x) \, dx, \\&B_3 \ = \ \int _{-\infty }^{\infty } x^2 F_\nu (x) \left( 1 - F_\nu (x) \right) f_\nu (x) \, dx \ = \ \frac{\nu }{2(\nu -2)} - \int _{-\infty }^{\infty } x^2 f_\nu (x) F_\nu ^2(x) \, dx, \end{aligned}$$

where $F_\nu$ is the cdf of the $t_\nu$ distribution. By employing (11) and (13), we find

$$\begin{aligned} B_1 \ = \ B_2 \ = \ \frac{2}{c_{3\nu -2}}\, \left( \frac{c_\nu \,\nu }{\nu -1} \right) ^2 \, \sqrt{\frac{\nu }{3\nu -2}} \end{aligned}$$

and arrive, again by employing $B(x,y) = \varGamma (x)\varGamma (y)/\varGamma (x+y)$, at the expression for $J$ given in Theorem 2. $\square$

The remaining integral

$$\begin{aligned} K_\nu \ = \int _{-\infty }^{\infty } x^2 f_\nu (x) F_\nu ^2(x) \, dx \end{aligned}$$

cannot be solved by the same means as the analogous integral $I_1$ for the normal distribution, and we state this as an open problem. However, this one-dimensional integral can easily be approximated numerically, and the expression is quickly entered into a mathematical software like R (R Development Core Team 2010).

Proof

(Proof of Proposition 1) We have

$$\begin{aligned}&g(F_{\epsilon ,x}) = 2 \int _{-\infty }^{\infty } \int _{y}^{\infty } (z - y)\, d F_{\epsilon ,x} (z)\, d F_{\epsilon ,x}(y), \\&\quad = (1-\epsilon )^2 g(F) + 2 \epsilon (1-\epsilon ) \int _{-\infty }^{\infty } (x-z) \left\{ 1\!\!1_{ (-\infty ,x] } (y) - 1\!\!1_{ [x,\infty ) } (y) \right\} \, d F(y) \end{aligned}$$

and hence

$$\begin{aligned}&I\!F(x,g(\cdot ); F) = \lim _{\epsilon \searrow 0} \frac{1}{\epsilon } \{ g(F_{\epsilon ,x}) - g(F) \} \\&\quad = \ - 2 g(F) + 2 \left\{ x [ F(x) + F(x-) - 1 ] + E[X 1\!\!1_{ \{ X\ge x \} } ] - E[X 1\!\!1_{ \{ X \le x \} } ] \right\} , \end{aligned}$$

which completes the proof. $\square$

With the influence function known, it is also possible use the relationship

$$\begin{aligned} ASV(s_n;F) = \int _\mathbb {R}I\!F(x,s,F)^2 F(dx) \end{aligned}$$

instead of referring to the terms given in Sect. 2 to compute the asymptotic variance of the estimators. This leads to the same integrals.

Appendix 2: Miscellaneous

Lemma 1

For $X_1,\ldots , X_n$ being independent and $U(a,b)$ distributed for $a,b \in \mathbb {R}$, $a < b$, we have for the sample mean deviation (about the median)

$$\begin{aligned} E(d_n) = {\left\{ \begin{array}{ll} (b-a)/4 &{} \quad \hbox {for odd } n \, (n \ge 3), \\ \displaystyle \frac{b-a}{4}\frac{n^2}{n^2-1} &{} \quad \hbox { for even } n. \end{array}\right. } \end{aligned}$$

Proof

For notational convenience we restrict our attention to the case $a=0$, $b=1$. Let $X_{(i)}$ denote the $i$th order statistic, $1 \le i \le n$. The random variable $X_{(i)}$ has a Beta$(\alpha ,\beta )$ distribution with parameters $\alpha = i$ and $\beta = n+1-i$, and hence $E(X_{(i)}) = i/(n+1)$. If $n$ is odd, we write $d_n$ as $d_n = (n-1)^{-1} \sum _{i=1}^{\lfloor n/2 \rfloor } (X_{(n+1-i)} - X_{(i)})$ and obtain

$$\begin{aligned} E(d_n) = \frac{1}{n-1} \sum _{i=1}^{\lfloor n/2 \rfloor } \left( \frac{n+1-i}{n+1} - \frac{i}{n+1} \right) = \frac{1}{4}. \end{aligned}$$

If $n$ is even, we have $d_n = (n-1)^{-1} \sum _{i=1}^{n/2} (X_{(n+1-i)} - X_{(i)})$, and hence

$$\begin{aligned} E(d_n) = \frac{1}{n-1} \sum _{i=1}^{n/2} \left( \frac{n+1-i}{n+1} - \frac{i}{n+1} \right) = \frac{n^2}{4(n^2-1)}, \end{aligned}$$

which completes the proof. $\square$