Introduction

In past few decades, the first law of thermo-dynamics has been used to investigate efficiency of heat transfer. However, in recent years, scientists have observed the entropy generation to analyze the irreversible behavior of matter during heat transfer. It is evident from the literature that many thermal mechanisms show irreversible behavior as irreversibility in a thermal process develops a continuous entropy generation, which demolish the energy of a system. This energy loss is mainly due to heat transfer, viscosity, buoyancy and magnetic field, which occurs in different modes. A detailed discussion on entropy generation for different flow systems was first presented by Bejan [1] who gave the concept of entropy generation; according to him, entropy generation is due to irreversible nature of heat transfer and viscosity effects with the fluid at solid boundaries. Benedetti et al. [2] obtained the numerical results for rate of entropy generation in a tube. Entropy generation in a pipe due to non-Newtonian fluid flow was presented by Pakdemirli et al. [3]. They observed that heat transfer rate and fluid friction increase with the increase in Brinkman number, and entropy number increases. Qasim et al. [4] analyzed the entropy generation in fluid flowing through wavy channel by using Maxwell's thermal conductivity model. Rashidi et al. [5] studied the entropy generation of a nanofluid flow with slip conditions by using effective Prandtl model. Beside these models, different researchers [6,7,8,9] presented the convective heat transfer problems with entropy generation in different geometries and observed that entropy generation plays an important role in the flow field.

Heat transfer enhancement in biological fluids is an important area of modern biomechanics and biomedical engineering. Heat regulation is essential for all mammals, human beings and living organism, therefore in modern biomedical engineering [10,11,12,13,14] due to its multifarious applications, has gained lots of importance.

The study of thermodynamics deals with the properties of substances associated with pressure, density, velocity, viscosity, nanofluids and their relationship with energy. Nanofluids are colloidal suspensions of nanosized solid particles in a liquid, which was first studied by Choi [15]. More recently conducted experiments have shown that nanofluids have substantially higher thermal conductivity than base fluids. Among the many advantages of nanofluids over conventional solid–liquid suspensions, the following are worth mentioning: (i) higher specific surface area, (ii) higher stability of the colloidal suspension, (iii) lower pumping power required to achieve the equivalent heat transfer, (iv) reduced particle clogging compared to conventional colloids, (v) higher level of control of the thermodynamics and transport properties by varying the particle material, (vi) concentration, size, (vii) and shape to name a few Neild et.al [16] extended the corresponding problems of porous medium. There are lot of nanoparticles in blood that are one thousand times smaller than a human hair and the presence of these nanoparticles contribute to severe diseases such as neutropenia, blood cancer, eosinophilia, leukocytosis, etc. In many cases, common methods cannot be used to eliminate these particles. Presently, nanotechnology is being used to separate these nanoparticles from plasma [17].

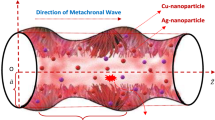
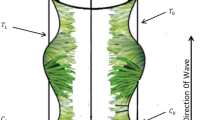
Ciliary movement has been a special subject in the field of experimental and theoretical biology. The first comprehensive study about cilia was presented by Shack in 1835. It look 20 years to explain the complex structure of cilia motion, and Cilia causes fluid motion due to its cyclic and symmetric movement. To study the fluid motion due to ciliary movement, different approaches have been used in the literature [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34] such as Lagrange method [21] and particle approach [30] of Lattice Boltzmann method. Cilia are present in respiratory tract, sensory organs, male reproductive system and in fallopian tube. The fallopian tube is lined with the ciliated epithelium where the embryo develops. Blockage of fallopian tube may resist the embryo development which may lead to infertility. The development of embryo takes place in an oviduct which is extended laterally from the uterus and is approximately 10 cm long. The oviducts have two parts: one is wider and longer near the ovaries, and other is narrow and smaller near the uterus which facilitates the transportation of sperm from uterus to egg in the ovaries. The oviducts use the ciliary and peristaltic movement for the development of embryo in ovaries. If oviduct shrinks due to blockage in wider and narrow part, then the embryo development will be badly effected and that may cause abnormalities in fetus.

The drug delivery of nanoparticles to the affected part, like the blocked portion in the oviduct is a safe way. The nanoparticles help to transfer medicine with high efficiency with no side effects. The drug may damage the fetus growing in the ovary, but the drug delivery by nanoparticles helps to protect the fetus growing in oviduct. There are different routes that can be used to deliver the drugs in human body like through the mouth, skin, nose rectum and uterus. The drug delivery by nanoparticles can be enhanced by the thermal conductivity of convective flow which require energy balance. Also, in bio-heat transfer, we are interested in maximizing the energy which requires the reduction in the entropy generation.

Keeping all above views in mind, this study is designed to see the advantages of nanoparticles for drug delivery in the flow of tangent hyperbolic fluid during the embryo development by reducing the entropy generation. The flow of tangent hyperbolic fluid is observed by the law of conservation of mass and momentum and reduction in entropy generation is measured by the law of conservation of energy. The momentum equation for tangent hyperbolic fluid is modeled by the envelop model approach of ciliary movement. The two-dimensional coupled equations are simplified using the assumption of large oviduct moving peristaltically (long wavelength) and high viscosity of the blood in oviduct (small Reynolds' number). The resulting equations are solved by analytical method HPM and software MATHEMATICA™.

Mathematical modeling

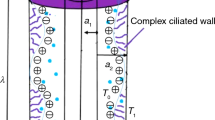
Consider a two-dimensional flow of Tangent hyperbolic copper nanofluid model in a tube of width \(2h\). Blood is considered as base fluid, and copper nanoparticles are immersed in blood. Assume that an infinite number of continuously beating cilia are present at the inner walls of tube generating a symplectic metachronal wave which moves towards positive \(z\)-axis with wave speed c as mentioned in Fig. 1.

Fig. 1
figure 1

Geometry of ciliated tube

Full size image

Governing equations for an incompressible Tangent hyperbolic nanofluid are defined as follows

$$\nabla .{\varvec{V}} = 0,$$
(1)

where

$$V = \left[ {u, 0, w} \right],$$
(2)

and

$$\rho_{{\text{f}}} \frac{{{\text{d}}{\varvec{V}}}}{{\text{d}}t} = div{\varvec{\tau}},$$
(3)
$$\left( {\rho c} \right)_{{\text{f}}} \frac{{\text{d}}T}{{{\text{d}}t}} = k_{{{\text{nf}}}} \nabla^{2} T + trace\left( {{\varvec{S}}.{\varvec{L}}} \right).$$
(4)

where V is the velocity components, \(w\) is the axial component of velocity, u is the radial component of velocity, \(\user2{ S}\) is the extra stress tensor, \(\frac{{\text{d}}}{{\text{d}}t} = \frac{\partial }{\partial t} + {\varvec{V}}.\nabla\) is the total derivative, \(\rho_{\text{f}}\) is the density of nanofluid, \(T\) is the temperature profile and \(L\) is gradient of velocity.

Here, the appropriate stress tensors for the tangent hyperbolic fluid model [35] are as follows

$${\varvec{\tau}} = - p{\varvec{I}} + {\varvec{S}},$$
(5)
$${\varvec{S}} = \left[ {\left( {\eta_{\infty } + \left( {\eta_{0} + \eta_{\infty } } \right)\tanh \left( {{{\Gamma \dot{\gamma }}}} \right)^{\text{m}} } \right)\dot{\gamma }_{{\text{i}}} } \right],$$
(6)

in which \({\varvec{\tau}}\) is the Cauchy stress tensor, \(\eta_{0}\) represents zero shear rate viscosity, \(\eta_{\infty }\) is the infinite shear rate viscosity, \(\Gamma\) is time constant and \(m\) shows the power law index.

$$\begin{aligned} & \dot{\gamma } = \sqrt {\frac{1}{2}{\varvec{\pi}}} , \\ & {\text{where}}\;{\varvec{\pi}} = trace\left( {grad{\varvec{V}} + grad{\varvec{V}}^{\text{T}} } \right)^{2} , \\ \end{aligned}$$
(7)

where \({\varvec{\pi}}\) is second-order tensor. We study the above equation for the case where \(\eta_{\infty } = 0\) and \({{\Gamma \dot{\gamma }}} < 1\). The elements of extra stress tensor can be written as

$$\dot{\gamma }_{{\text{i}}} = {\varvec{L}} + {\varvec{L}}^{\text{T}} ,$$
(8)
$$\overline{\tau } = \eta_{0} \left( {\left( {{{\Gamma \dot{\gamma }}}} \right)^{m} } \right)\dot{\gamma }_{{\text{i}}} = \eta_{0} \left( {1 + {{\Gamma \dot{\gamma }}} - 1} \right)^{\text{m}} \dot{\gamma }_{{\text{i}}} = \eta_{0} \left( {1 + m\left( {{{\Gamma \dot{\gamma }}} - 1} \right)} \right)\dot{\gamma }_{{\text{i}}}$$
(9)

where thermal conductivity of nanofluid is defined as

$$\rho_{{{\text{nf}}}} = \left( {1 - \varphi } \right)\rho_{{\text{f}}} + \varphi \rho_{{\text{s}}} ,$$
(10a)
$$\eta_{{{\text{nf}}}} = \frac{{\eta_{{\text{f}}} }}{{\left( {1 - \varphi } \right)^{2.5} }},$$
(10b)
$$\left( {\rho c_{{\text{p}}} } \right)_{{{\text{nf}}}} = \left( {1 - \varphi } \right)\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} + \varphi \left( {\rho c_{{\text{p}}} } \right)_{{\text{s}}} ,$$
(10c)
$$\alpha_{{{\text{nf}}}} = \frac{{k_{{{\text{nf}}}} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{{\text{nf}}}} }},$$
(10d)
$$k_{{{\text{nf}}}} = k_{{\text{f}}} \left( {\frac{{k_{{\text{s}}} + 2k_{{\text{f}}} - 2\varphi \left( {k_{{\text{f}}} - k_{{\text{s}}} } \right)}}{{k_{{\text{s}}} + 2k_{{\text{f}}} + 2\varphi \left( {k_{{\text{f}}} - k_{{\text{s}}} } \right)}}} \right)$$
(10d)

where \(k_{{{\text{nf}}}}\) is the thermal conductivity of nanofluid, \(k_{{\text{f}}}\) is the thermal conductivity of base fluid, \(k_{{\text{s}}}\) is the thermal conductivity of solid nanoparticles and \(\varphi\) is the solid volume fraction. The Mathematical model for geometry of cilia tips in the wave frame is

$$h = 1 + \epsilon \cos 2\pi z,$$
(11a)
$$w\left( h \right) = - 1 - 2\pi \epsilon \alpha \beta \cos 2\pi z.$$
(11b)

where \(\epsilon\) is the cilia length parameter, \(\alpha\) is the eccentricity of elliptic wave and \(\beta\) is the wave number.

The governing equations of motion of tangent hyperbolic fluid model in a tube are specified as follows.

$$\frac{\partial u}{{\partial r}} + \frac{u}{r} + \frac{\partial w}{{\partial z}} = 0,$$
(12)
$$\rho_{{\text{f}}} \left[ {u\frac{\partial w}{{\partial r}} + w\frac{\partial w}{{\partial z}}} \right] = - \frac{\partial p}{{\partial z}} + \frac{1}{r}\frac{\partial }{\partial z}\left( {rS_{{{\text{rz}}}} } \right) + \frac{{\partial S_{{{\text{zz}}}} }}{\partial z}$$
(13)
$$\rho_{{\text{f}}} \left[ {u\frac{\partial u}{{\partial r}} + w\frac{\partial u}{{\partial z}}} \right] = - \frac{\partial p}{{\partial r}} + \frac{1}{r}\frac{\partial }{\partial r}\left( {rS_{{{\text{rr}}}} } \right) + \frac{{\partial S_{{{\text{zr}}}} }}{\partial z},$$
(14)
$$\left( {\rho c} \right)_{{\text{f}}} \left[ {u\frac{\partial T}{{\partial r}} + w\frac{\partial T}{{\partial z}}} \right] = k_{{{\text{nf}}}} \left( {\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial T}{{\partial r}}} \right) + \frac{{\partial^{2} T}}{{\partial z^{2} }}} \right) + S_{{{\text{zr}}}} \frac{\partial w}{{\partial r}}.$$
(15)

where \(\rho_{{\text{f}}}\) is the fluid density, \(u\) and \(w\) are the radial and axial components of velocity, \(c\) is the wave speed and \(\eta_{{\text{f}}}\) is the apparent viscosity of fluid.

The following non-dimensional parameters can be introduced for further analysis.

$${z}^{*}=\frac{z}{\lambda }, {r}^{*}=\frac{r}{a}, {u}^{*}=\frac{u}{\beta c}, {w}^{*}=\frac{w}{c}, {h}^{*}=\frac{h}{a}, {p}^{*}=\frac{a\beta }{c{\eta }_{\mathrm{f}}}p,\beta =\frac{a}{\lambda }, {{S}_{\mathrm{ij}}}^{*}=\frac{a}{{\eta }_{\mathrm{f}}c}{S}_{\mathrm{ij}}, {\lambda }_{1}=\frac{c{\lambda }_{1}}{a}, \mathrm{Re}=\frac{\rho ac}{{\eta }_{\mathrm{f}}}, \mathrm{We}=\frac{\Gamma c}{a}, {\alpha }_{\mathrm{f}}=\frac{k}{{\left(\rho c\right)}_{\mathrm{f}}} , \theta =\frac{T-{T}_{0}}{{T}_{0}} , \mathrm{Br}=\frac{{a}^{2}{\eta }_{\mathrm{f}}}{{k}_{\mathrm{f}}{T}_{0}}, \mathrm{Pr}=\frac{{\eta }_{\mathrm{f}}{c}_{\mathrm{p}}}{{k}_{\mathrm{f}}} , \mathrm{Ec}=\frac{{c}^{2}}{{c}_{\mathrm{p}}{T}_{0}} .$$
(16)

where \(\lambda\), \(a\), \(c\) symbolize the wavelength, width of velocity and wave speed, respectively, \(\mathrm{Re}\) is the Reynolds' numbers, \(\beta\) is the wave number and \({D}_{\mathrm{a}}\) is the Darcy's number. In terms of dimensionless parameters, the momentum equations and shear stresses are

$$\frac{\partial u}{\partial r}+\frac{u}{r}+\frac{\partial w}{\partial z}=0,$$
(17)
$$\mathrm{Re}\beta \left[u\frac{\partial w}{\partial r}+w\frac{\partial w}{\partial z}\right]=-\frac{\partial p}{\partial z}+\frac{1}{r}\frac{\partial }{\partial z}\left(r{S}_{\mathrm{rz}}\right)+\beta \frac{\partial {S}_{\mathrm{zz}}}{\partial z}$$
(18)
$$\mathrm{Re}{\beta }^{2}\left[u\frac{\partial u}{\partial r}+w\frac{\partial u}{\partial z}\right]=-\frac{\partial p}{\partial r}+\frac{\beta }{r}\frac{\partial }{\partial r}\left(r{S}_{\mathrm{rr}}\right)+{\beta }^{2}\frac{\partial {S}_{\mathrm{zr}}}{\partial z}-\beta \frac{\partial {S}_{\theta \theta }}{\partial z},$$
(19)
$$\beta {\left(\rho c\right)}_{\mathrm{f}}\left[u\frac{\partial \theta }{\partial r}+w\frac{\partial \theta }{\partial z}\right]={k}_{\mathrm{nf}}\left(\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial \theta }{\partial r}\right)+{\beta }^{2}\frac{{\partial }^{2}\theta }{\partial {z}^{2}}\right)+{S}_{\mathrm{zr}}\frac{\partial w}{\partial r},$$
(20)
$${S}_{\mathrm{rz}}=\left(1+m\left(\mathrm{We}\frac{\partial w}{\partial r}-1\right)\right)\frac{\partial w}{\partial r}.$$
(21)

Using long wavelength approximation (β → 0) given in [36], the governing equations and boundary conditions are as follows

$$\frac{\partial p}{\partial z}=\left(1-m\right)\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial w}{\partial r}\right)+m\mathrm{We}\frac{1}{r}\frac{\partial }{\partial r}\left(r{\left(\frac{\partial w}{\partial r}\right)}^{2}\right)$$
(22)
$$-\frac{\partial p}{\partial r}=0,$$
(23)
$$\frac{{k}_{\mathrm{nf}}}{{k}_{\mathrm{f}}}\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial \theta }{\partial r}\right)=-\mathrm{Br}\frac{{\eta }_{\mathrm{nf}}}{{\eta }_{\mathrm{f}}}\left(1+m\left(\mathrm{We}\frac{\partial w}{\partial r}-1\right)\right){\left(\frac{\partial w}{\partial r}\right)}^{2}.$$
(24)
$$\frac{\partial w}{\partial r}=0, \frac{\partial \theta }{\partial r}=0 \mathrm{at} r=0,$$
(25a)
$$w=w\left(h\right), \theta =0 \mathrm{at} r=h.$$
(25b)

Integration of Eq. (17) over the tube width is given as:

$${\int }_{0}^{h}\left[\frac{1}{r}\frac{\partial \left(ru\right)}{\partial r}+\frac{\partial w}{\partial z}\right]r{\text{d}}r=0,$$
(26)
$$hu\left(h\right)+\frac{1}{2}\frac{\partial q}{\partial z}-h\frac{\partial h}{\partial z}w\left(h\right)=0,$$
(27)

where \(q=2{\int }_{0}^{h}rwdr\).

Equation (27) can be written as

$$\frac{\partial q}{\partial z}=2h\left(\frac{\partial h}{\partial z}w\left(h\right)-u\left(h\right)\right),$$
(28)

The relation between \(q\) and dimensionless volume flow rate \(Q\) is given by

$$Q=2{\int }_{0}^{h}RWdR=2{\int }_{0}^{h}\left(w+1\right)rdr=q+{h}^{2},$$
(29)

The mean volume flow rate for the time period \(T=\frac{\lambda }{c}\) is

$$\stackrel{-}{Q}=\frac{1}{T}{\int }_{0}^{T}Qd{t}^{*}=q+1+\frac{{\epsilon }^{2}}{2},$$
(30)

where \(\lambda\) is the wavelength of metachronal wave, \(c\) is the wave speed and \({t}^{*}\) is the mean average time.

Solution of the problem

To obtain the solution of governing equations, we use homotopy perturbation method [37] which is described as follows

$$H\left(j,w\right)=\left(1-j\right)\left(\mathcal{L}\left(w\right)-\mathcal{L}\left({w}_{0}\right)\right)+j\left(\mathcal{L}\left(w\right)-\frac{1}{{\left(1-\varphi \right)}^{2.5}}\frac{\partial p}{\partial z}+\frac{1}{r}\frac{\partial }{\partial r}\left(rm\mathrm{We}{\left(\frac{\partial w}{\partial r}\right)}^{2}\right)\right),$$
(31)
$$H\left(j,\theta \right)=\left(1-j\right)\left(\mathcal{L}\left(\theta \right)-\mathcal{L}\left({\theta }_{0}\right)\right)+j\left(\mathcal{L}\left(\theta \right)-\frac{Br}{{\left(1-\varphi \right)}^{2.5}}\frac{{k}_{\mathrm{f}}}{{k}_{\mathrm{nf}}}\left(1+m\left(\mathrm{We}\frac{\partial w}{\partial r}-1\right)\right){\left(\frac{\partial w}{\partial r}\right)}^{2}\right),$$
(32)

The linear operator and initial guesses are chosen as

$$\mathcal{L}\left(w\right)=\frac{1}{r}\frac{\partial }{\partial r}\left(r\left(1-m\right)\frac{\partial }{\partial r}\right),$$
(33)
$$\mathcal{L}\left(\theta \right)=\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial }{\partial r}\right).$$
(34)
$${w}_{0}=\frac{{\left(1-\varphi \right)}^{2.5}}{4\left(1-m\right)}\frac{d{p}_{0}}{dz}\left({r}^{2}-{h}^{2}\right)+w\left(h\right),$$
(35)
$${\theta }_{0}=\frac{{r}^{2}-{h}^{2}}{4}.$$
(36)

According to homotopy perturbation method,

$$w={w}_{0}+j{w}_{1}+{j}^{2}{w}_{2}\dots ,$$
(37a)
$$\theta ={\theta }_{0}+j{\theta }_{1}+{j}^{2}{\theta }_{2}\dots ,$$
(37b)
$$p={\theta }_{0}+j{p}_{1}+{j}^{2}{p}_{2}\dots ,$$
(37c)

where \(j\in \left[\mathrm{0,1}\right]\) is the homotopy perturbation parameter and \(j=0\) gives initial guess and \(j=1\) gives the final solution. With the help of Eqs. (31)–(37), the second-order solution for the velocity and temperature profile are given as follows

$$w=w\left(h\right)+{A}_{1}\left({r}^{2}-{h}^{2}\right)+{A}_{2}\left({r}^{3}-{h}^{3}\right),$$
(38)

And temperature profile can be found in following manner

$$\theta =\frac{1}{{\left(1-\varphi \right)}^{2.5}}\frac{{k}_{\mathrm{f}}}{{k}_{\mathrm{nf}}}\left(\frac{{A}_{3}}{16}\left({r}^{4}-{h}^{4}\right)+\frac{{A}_{4}}{25}\left({r}^{5}-{h}^{5}\right)+\frac{{A}_{5}}{36}\left({r}^{6}-{h}^{6}\right)\right)+\frac{1}{{\left(1-\varphi \right)}^{2.5}}\frac{{k}_{\mathrm{f}}}{{k}_{\mathrm{nf}}}\left(\frac{{A}_{6}}{49}\left({r}^{7}-{h}^{7}\right)+\frac{{A}_{7}}{64}\left({r}^{8}-{h}^{8}\right)\right).$$
(39)

Integrating Eq. (27) using software MATHEMATICA™ calculating pressure gradient as

$$\frac{dp}{dz}=\frac{-{A}_{9}\pm \sqrt{{A}_{9}^{2}-4{A}_{8}{A}_{10}}}{2{A}_{8}}.$$
(40)

Entropy generation

Entropy generation can be written as

$${{S}^{\prime\prime\prime}}_{\mathrm{gen}}=\frac{{k}_{f}}{{T}_{\infty }^{2}}\left({\left(\frac{\partial T}{\partial r}\right)}^{2}+{\left(\frac{\partial T}{\partial r}\right)}^{2}\right)+\frac{1}{{T}_{0}}{\tau }_{\mathrm{zr}}\frac{\partial w}{\partial r}.$$
(41)

Dimensionless form of Entropy generation can be written as

$${N}_{\mathrm{S}}=\frac{{S}_{\mathrm{gen}}^{\prime\prime\prime}}{{S}_{\mathrm{G}}^{\prime\prime\prime}}={\left(\frac{\partial \theta }{\partial r}\right)}^{2}+\mathrm{Br}{\Lambda }\left(1+m\left(\mathrm{We}\frac{\partial w}{\partial r}-1\right)\right){\left(\frac{\partial w}{\partial r}\right)}^{2}$$
(42)
$${S}_{\mathrm{G}}^{\prime\prime\prime}=\frac{{k}_{\mathrm{f}}{T}_{0}^{2}}{{\stackrel{-}{\theta }}_{0}^{2}{a}^{2}},\Lambda =\frac{{\stackrel{-}{\theta }}_{0}}{{T}_{0}}.$$
(43)

Results and discussion

In this section, the graphical results show the effects of different parameters of interest. The cilia-induced flow of a Tangent hyperbolic nanofluid in circular tube is investigated. The effect of emerging parameters for the entropy generation, and stream functions are observed by keeping all other parameters fixed as suggested in Ref. [38]

Axial velocity for different values of, cilia length \(\epsilon ,\) power law index \(m\) and nanoparticle volume fraction of the fluid \(\varphi\) are observed in Fig. 2a–c. In Fig. 2a, the velocity of fluid decreases by increasing cilia length parameter as increase in cilia length resist the fluid flow at the centre of tube. Figure 2b shows that velocity of fluid decreases by increasing power law index \(m\) because for increasing \(m\) fluid behaves like a shear thickening fluid which causes the decrease in velocity of fluid. Figure 2c shows that velocity increases by increasing nanoparticle volume fraction of the fluid because when nanoparticles are more in fluid, due to their smaller size they will move with high speed.

Fig. 2
figure 2

a–c The effect of cilia length parameter \(\epsilon ,\) power law index \(m\) and nanoparticles volume fraction \(\varphi\) fraction on axial velocity.

Full size image

Temperature profile for different values of nanoparticle volume fraction of the fluid \(\varphi\), power law index \(m\) and Brickman number \(Br\) is observed in Fig. 3a–c. It can be seen that temperature is maximum at the centre of tube and minimum at the ciliated walls where it is effected by ciliated walls. Figure 3a illustrates that by increasing nanoparticle volume fraction of the fluid \(\varphi\), temperature profile decreases. Graphical results show that nanofluids can increase heat transfer rate by decreasing the wall temperature. Also, Fig. 3b shows that by increasing power law index \(m\) temperature profile decreases. Brinkman number is the ratio of viscous heat generation to external heating. So by increasing Brinkman number viscous heat generation will increase as compared to external heating; therefore, temperature will increase.

Fig. 3
figure 3

a–c The effect of nanoparticles volume fraction \(\varphi ,\) power law index \(m\) and Brinkman number \(Br\) on temperature profile

Full size image

In Fig. 4a–c, entropy generation for different values of nanoparticle volume fraction of the fluid \(\varphi ,\) power law index \(m\) and Brinkman number \(Br\) are observed. It can be depicted from the graphs that entropy generation is maximum at the ciliated walls and minimum at the centre of tube.

Fig. 4
figure 4

a–c The effect of nanoparticles volume fraction \(\varphi ,\) Brinkman number \(Br\) and power law index \(m\) on entropy generation

Full size image

Bejan number for different values of nanofluid volume fraction \(\varphi ,\) power law index \(m\) and Brinckman number \(Br\) is observed in Fig. 5a–c. Since due to less temperature gradient at the centre of tube, heat transfer is small and very less resistance occurs at center due to which Bejan number decreases at center of tube and has maximum values at boundaries. Furthermore, by increasing \(\varphi\), Bejan number decreases while by increasing Brickman number \(Br\) Bejan number increases.

Fig. 5
figure 5

a–c The effect of nanoparticles volume fraction \(\varphi ,\) power law index \(m\) and Brinkman number \(Br\) on Bejan number

Full size image

Figure 6a, b shows the comparison of symplectic and antiplectic wave patterns for different values of nanoparticles volume fraction \(\varphi\) and power law index \(m.\) It can be seen that symplectic wave pattern is more efficient than antiplectic wave pattern for increasing values of nanoparticles volume fraction \(\varphi\) and power law index \(m\).

Fig. 6
figure 6

a, b Comparison of symplectic and antiplectic wave for different values of nanoparticles volume fraction \(\varphi\) and power law index \(m\)

Full size image

Conclusions

In this study, we have developed a mathematical model of velocity and temperature profile in the presence of nanoparticles in base fluids. Fluid motion is produced by the periodic beating of ciliated surface. The surface of cilia is considered as a continuous envelop whose motion is found by the metachronal wave formed by the coordinated cilia. The boundary conditions are defined at mean radius of cylinder; therefore, horizontal and vertical velocities are defined at the mean radius \(\left(r=a\right)\). The governing differential equations involve the parameter depend upon, volume fractions of nanoparticles. The differential equations are solved by homotopy perturbation method (HPM).

  • This study helps the treatment of heart patient, when clots on blockages have been observed in blood, nanoparticles will help to remove the clot and blockages from blood.

  • Axial velocity of the fluid increases by inserting nanoparticles.

  • Thermal conductivity of fluid increases by adding nanoparticles.

  • The entropy generation due to nanoparticles will decrease the viscosity on the wall so of tube and blood will flow with less/normal pressure.