1 Introduction

Biomechanical interactions between blood flow and the vessel wall are central to the initiation and progression of most cardiovascular diseases. Indeed, the majority of computational and experimental investigations into blood flow seek to understand how local flow mechanics relates to disease progression in or on the vessel wall. Blood flow conditions in diseased vessels are usually spatially and temporally complex and are challenging to characterize (Shadden and Taylor 2008; Shadden and Arzani 2015), even without reference to the coupled biochemical or biophysical processes driving disease progression. Nonetheless, the role of blood flow mechanics in the “near-wall” region is of utmost importance since this is where such couplings are most profound. In the near-wall region, blood flow serves to impart mechanical stresses on the vessel wall, as well as regulate the local transport of reactive material between the tissue and fluid domains. It is this latter mechanism that motivates the work presented herein.

A compelling scenario involving the interaction between blood flow and the vessel wall is atherosclerosis, which is a leading cause of death worldwide. Atherosclerosis occurs mainly in locations of disturbed blood flow patterns (Caro et al. 1969; Schwartz et al. 1991). The local transport of several substances near and at the vessel wall is known to influence atherosclerosis progression (Vincent and Weinberg 2014). For example, previous studies have looked into transport of low density lipoproteins (LDL) (Dabagh et al. 2009; Fazli et al. 2011; Lantz and Karlsson 2012; Cilla et al. 2013), high-density lipoproteins (HDL) (Meng et al. 2009; Hao and Friedman 2014), oxygen (Coppola and Caro 2008; Iori et al. 2015), nitric oxide (NO) (Plata et al. 2010; Liu et al. 2012), monocytes (Chiu et al. 2003; Cilla et al. 2013), and adenine triphosphate ATP and adenine diphosphate ADP (Choi et al. 2007; Comerford et al. 2008; Boileau et al. 2013) as important mass transport processes involved in atherosclerosis.

Intravascular thrombosis is another compelling pathology associated with most cardiovascular diseases where near-wall transport becomes important (Basmadjian 1990; Hathcock 2006). The trajectories of individual platelets and the accumulation and residence time of chemical solutes including ADP, thrombin, and various blood factors control clot formation. These solutes, and especially in activated form, are generated at the vessel wall or from bound platelets. Complex hemodynamics and flow stagnation are often associated with prothrombotic conditions. For example, intraluminal thrombus in abdominal aortic aneurysm (AAA) (Wilson et al. 2013; Tong and Holzapfel 2015) complicates disease progression and is thought to be strongly coupled to flow stagnation and recirculation. The chaotic flow field in AAAs (Arzani and Shadden 2012) leads to complex WSS distributions (Arzani and Shadden 2016) and interesting near-wall flow structures (Arzani et al. 2016). Thrombosis in the left ventricle (Seo et al. 2016), aortic dissection (Menichini and Xu 2016), stented arteries (Jiménez et al. 2014), and flow diverter-treated cerebral aneurysms (Peach et al. 2014) represent other applications of complex transport potentially affecting local thrombosis.

Near-wall transport can either be (i) explicitly modeled for a specific transport problem or (ii) inferred from appropriate hemodynamics measures. For explicit modeling, most computational investigations of intravascular transport have relied on continuum models that solve the advection–diffusion equations in the blood flow domain. However, due to the high Schmidt numbers (Sc) in most arterial flows, thin concentration boundary layers are typically formed next to the wall where most interesting biological processes occur (Ethier 2002). The thin concentration boundary layer thickness causes numerical difficulties in resolving the near-wall dynamics (Hansen and Shadden 2016), which is precisely the region of greatest interest. Hansen and Shadden (2016) recently proposed a continuum surface transport model to study mass transport in the thin concentration boundary layer next to the wall. This model is based on the idea that the core flow minimally influences the mass transport in the concentration boundary layer in high Sc flows, and thus surface transport PDEs can be derived in terms of the WSS vector field.

On the other hand, to report, compare and more generally evaluate hemodynamic processes, it is important to develop simple measures that effectively quantify physiologically relevant aspects of near-wall transport. Flow stagnation is one important aspect of transport, which has been widely regarded as an event promoting atherogenic and thrombogenic processes. In order to quantify near-wall stagnation, particle-tracking techniques have been used to define near-wall residence time (Longest and Kleinstreuer 2003). While the Lagrangian nature of this measure is desirable for capturing emergent behavior of the flow, a very high resolution of particles is often needed to accurately sample the near-wall region. A more readily obtained measure is relative residence time (RRT), which is defined as the inverse of time average WSS (TAWSS) vector magnitude (Himburg et al. 2004; Lee et al. 2009). The relevance of this measure could be explained as follows. As discussed in Hansen and Shadden (2016), Arzani et al. (2016), the WSS vector can be scaled to obtain the near-wall fluid velocity, and because displacements of fluid in the concentration boundary layer are small over each cardiac cycle, the time-averaged WSS vector field dominates transport. Therefore, in regions of low TAWSS vector magnitude (high RRT) the near-wall species are displaced to smaller extent, implying higher near-wall stagnation. However, because RRT is an instantaneous Eulerian measure, it cannot as effectively provide information about the concentration or origin of near-wall species when compared to a Lagrangian measure. This can be valuable information, since high near-wall stagnation and concentration are both essential for effective atherogenic or thrombogenic processes to occur.

Fig. 1
figure 1

The full computational models where image-based CFD was performed. The highlighted region shows the region of interest where post-processing was performed. P1–P6 are the abdominal aortic aneurysm (AAA) models, P7–P8 are carotid artery models, P9 is a cerebral aneurysm model, and P10 is a coronary aneurysm model

Full size image

In this paper, we present a WSS exposure time (WSSET) measure that is computed from Lagrangian tracking of surface-born tracers, which can account for stagnation (low flow) and species redistribution. It has the advantage of being a Lagrangian-based measure that accounts for the emergent role of transport, but has significantly less computational cost compared to explicitly solving a full transport problem. We compare WSSET with RRT in different vascular pathologies. To this end, image-based models of aortic aneurysm, carotid bifurcation, cerebral aneurysm, and coronary aneurysm are used. WSS divergence is also computed, and its relevance to near-wall transport is discussed. Because a key importance of altered hemodynamics is the effect on chemical species distribution near the lumen, these measures were compared with surface concentration fields obtained from the solution of a complete 3D advection–diffusion transport problem. We demonstrate that WSSET is able to better approximate the locations of near-wall stagnation and concentration build-up of chemical species. This improvement comes at an increased computational cost when compared to RRT; however, this cost is far below that needed to explicitly solve the full 3D transport problem. To further demonstrate the relevance of the WSSET measure and to characterize the near-wall flow topology, stable and unstable manifolds of fixed points in the TAWSS vector field are computed and related to WSSET fields. These manifolds help explain observed WSSET and surface concentration patterns. Namely, unstable manifolds determine the regions where concentration build-up occurs, and stable manifolds can mark the basins of attraction, e.g., the regions where near-wall species become attracted to particular TAWSS fixed points or TAWSS unstable manifolds. Because these manifolds can be computed directly from the topology of the TAWSS vector field, they can help predict surface transport patterns without having to actually perform the Lagrangian surface transport calculations required to compute WSSET.

2 Methods

2.1 Computational fluid dynamics (CFD)

Six patient-specific AAA models were used in this study, and WSS data were obtained from computational fluid dynamics (CFD) simulations using the software package SimVascular (Updegrove et al. 2016). Modeling details were described in Arzani et al. (2014). The models were constructed from magnetic resonance imaging and started from the supra celiac aorta and continued to the iliac arteries, including the major branch arteries. Inflow and outflow boundary conditions were tuned to match measured, patient-specific flow rates and blood pressures. A stabilized finite element method was used to solve the Navier–Stokes equations, using linear tetrahedral elements. The mesh edge size next to the wall was 200 \(\upmu \)m, and the time step divided the cardiac cycle into 1000 time steps. Using SimVascular, two carotid artery models were constructed from computed tomography angiography. Linear tetrahedral elements were used with a global edge size of 400 \(\upmu \)m and a boundary layer meshing with next to wall edge size of 50 \(\upmu \)m. The mean common carotid volumetric flow rate used in a previous study (Lee et al. 2008) was assigned as inlet boundary condition for both patients. Resistance boundary conditions were used at the outlets to divide 70% of the flow rate to the internal carotid artery and 30% to the external carotid artery. The time step was chosen to divide the cardiac cycle (T = 0.88 s) into 5000 time steps. A cerebral aneurysm model used in a previous study (Gambaruto and João 2012) was remeshed with a higher mesh resolution (next to wall edge size of 100 \(\upmu \)m). The same boundary conditions and parameters used in Gambaruto and João (2012) were specified. A typical volumetric waveform was used at the inlet with the flow rate scaled according to the inlet cross section area. Zero pressure gradient was applied at the outlet. The time step divided the cardiac (T = 0.85 s) cycle to 100 time steps. Similarly, a coronary aneurysm model (Kawasaki disease) used in a previous study (Sengupta et al. 2012) was remeshed with a higher resolution (next to wall edge size of 60 \(\upmu \)m in the aneurysm branch). The same boundary conditions and parameters were used for the flow solution (this model and simulation parameters were obtained from vascularmodel.com). A typical aortic waveform was prescribed at the inlet, and a circuit analogy lumped parameter network was coupled to the outlets to model coronary pressure and flow. The simulation time step was 1 ms. Rigid wall and Newtonian blood rheology were assumed in all simulations. The cerebral aneurysm simulation was done in OpenFOAM (finite volume method), and all the other simulations were carried out in SimVascular (finite element method). Figure 1 shows the full computational models, and the highlighted region shows the region of interest where flow conditions were analyzed using the WSSET, RRT and WSS divergence measures.

2.2 Near-wall stagnation

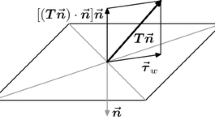
In this section, the WSS measures used to quantify near-wall stagnation are defined. The WSS vector field (\(\varvec{\tau }\)) is computed as the tangential component of traction on the wall. Relative residence time (RRT), a traditional measure used in characterization of near-wall stagnation, is defined as

$$\begin{aligned} \hbox {RRT} = \frac{ 1}{ \Vert \frac{1}{T} \int _0^T \varvec{\tau } {\hbox {d}}t \Vert } = \frac{1}{ \Vert \overline{\varvec{\tau } } \Vert } \;, \end{aligned}$$
(1)

where T is the cardiac cycle duration, and \( \overline{\varvec{\tau } } = \frac{1}{T} \int _0^T \varvec{\tau } {\hbox {d}}t \) is the TAWSS vector. Note that this definition is the same as the more common form written in terms of oscillatory shear index (OSI)

$$\begin{aligned} \hbox {RRT}= & {} \frac{1}{ \left( 1-2 \cdot {\hbox {OSI}}\right) \int _0^T\Vert \varvec{\tau }\Vert {\hbox {d}}t } \;, \nonumber \\ \hbox {OSI}= & {} \frac{1}{2}\left( 1 - \frac{\Vert \overline{\varvec{\tau } } \Vert }{\int _0^T\Vert \varvec{\tau }\Vert {\hbox {d}}t } \right) \;. \end{aligned}$$
(2)

The form in Eq. (1) provides a clearer correspondence to TAWSS vectors and near-wall transport. We also compute time-averaged WSS divergence (WSSdiv)

$$\begin{aligned} \hbox {WSSdiv} = \frac{1}{T} \int _0^T \nabla \cdot \varvec{\tau } {\hbox {d}}t \; . \end{aligned}$$
(3)

Positive WSSdiv represents expansion of WSS vectors, and negative WSSdiv shows contraction, which could exemplify flow impingement and separation, respectively. The relevance of this measure to near-wall flow will be demonstrated.

In this study, a recent method for characterization of near-wall stagnation based on WSS trajectories is used. The near-wall fluid velocity can be represented based on the WSS vector field to first order (Gambaruto et al. 2010; Lévêque 1928) as

$$\begin{aligned} \varvec{u}_{\pi } = \frac{\varvec{\tau } \delta n}{\mu } + \textit{O}(\delta n ^2) \;, \end{aligned}$$
(4)

where \( \varvec{u}_{\pi } \) is the near-wall tangential velocity evaluated in a small normal to the wall distance \(\delta n\), and \(\mu \) is the dynamic viscosity. A mass diffusion coefficient of \(D = 1\times 10^{-5} \frac{{\hbox {cm}}^2}{\hbox {s}} \) (Coppola and Caro 2008) is assumed to estimate the species concentration boundary layer thickness \(\delta _c = \delta Sc ^{\frac{-1}{3}}\), where \(\delta \) is the momentum boundary layer thickness, and \(Sc = \frac{\nu }{D}\) where \(\nu \) is blood’s kinematic viscosity. A normal to wall distances of \(\delta n = 15\), 0.7, 1, and \(1\, \upmu \)m are chosen in this study, which are within \(\delta _c\) in the AAA, carotid artery, cerebral aneurysm, and coronary aneurysm models, respectively. The significance of this choice is discussed in our previous study (Arzani et al. 2016).

The methods used in Zhang et al. (2006), Chen et al. (2007) for surface streamline tracing were extended to unsteady surface vector fields to generate WSS pathlines. Trajectories are seeded on the entire surface of the region of interest uniformly and integrated based on the near-wall fluid velocity (Eq. 4). Thus, we consider here the evolution of surface-born species. In order to obtain a uniform initial distribution of surface trajectories, OpenFlipper (www.openflipper.org) was used to remesh the triangular surface mesh to the desired number of vertices while enforcing a uniform distribution of vertices. These vertices were used as the initial location of the surface trajectories. Trajectories were computed using a forward Euler integration with sufficiently small time step. These WSS trajectories were computationally confined to stay on the surface, while they represent the trajectories in a small near-wall distance \(\delta n\). To confine these trajectories on the curved surface, the computation is conducted within the individual triangular (i.e., linear) elements of the surface, which are locally planar. The coordinate conversion between two neighboring triangles during the numerical integration is achieved via the transformation of the two corresponding local coordinate systems.

Fig. 2
figure 2

The procedure used in computation of WSS exposure time (WSSET) and TAWSS stable (red lines) and unstable (blue lines) manifolds. Trajectories are seeded on the aneurysm surface and advected in forward time to compute WSSET. Stable and unstable manifolds of the TAWSS vector field corresponding to saddle-type fixed points are computed with backward and forward time integration, respectively. These manifolds usually terminate in fixed points of other types (e.g., source or sink)

Full size image

In order to quantify near-wall stagnation, WSSET (Arzani et al. 2016) is computed for each triangular surface element as the accumulated amount of time that all the WSS trajectories spend inside that element, with proper normalizations

$$\begin{aligned} \hbox {WSSET}(e)= & {} \frac{1}{ \mathcal {T} } \sqrt{\frac{A_m}{A_e}} \sum \limits _{p=1}^{N_t} {\int }_0^{\mathcal {T}} H_e(p,t) \; {\hbox {d}}t \nonumber \\ H_e= & {} {\left\{ \begin{array}{ll} 1 \; \hbox {if} \; \varvec{x} _p(t) \in e \\ 0 \; \hbox {if} \; \varvec{x}_p(t) \notin e \end{array}\right. }, \end{aligned}$$
(5)

where \( A_e \) is the area of the surface element, \( A_m \) is the average area of all the surface elements, \(\mathbf {x}_p(t) \) is the position of the WSS trajectory, \( H_e \) is the indicator function for element e, \( N_t \) is the total number of trajectories released, and \(\mathcal {T}\) is the integration time. An integration time of 100 cardiac cycles (\(\mathcal {T} = 100T \)) was used for each patient, and the WSS data were assumed periodic to enable trajectory integration for such time scale.

2.3 Advection–diffusion transport

Simulations of chemical concentration fields on surface of each model were computed by solving the 3D advection–diffusion equation to provide a comparison of the wall-bounded WSS measures with the full 3D transport. The advection–diffusion equation can be written as

$$\begin{aligned} \frac{\partial c}{\partial t} + \varvec{u} \cdot \nabla c = D \nabla ^2 c \;, \end{aligned}$$
(6)

where c is a non-dimensional concentration, \(\varvec{u}\) is the velocity, and D is the same mass diffusivity as above. A Neumann boundary condition of \(\frac{\partial c}{\partial n} = 5~{\hbox {cm}}^{-1}\) was prescribed at the no-slip wall representing a uniform flux of concentration into the lumen. Zero Dirichlet boundary conditions were used at the inlet and outlets. Homogenous Dirichlet outlet boundary conditions were preferred to homogenous Neumann, due to backflow at the outlets. The outlet boundary was extended based on the available CFD data (between 1 and 3 times the diameter) to ensure minimal influence of the outlet boundary condition and improve convergence. The advection–diffusion equation was solved using the finite element method implemented in the FEniCS package (Logg et al. 2012). Second-order tetrahedral elements were used with an edge size of 0.1 cm , 400, 400, and 200 \(\upmu \)m in the interior for the AAA, carotid artery, cerebral aneurysm, and coronary aneurysm models, respectively. A boundary layer mesh was generated with next to wall edge size of 6.6, 1.5, 1.6, and 1.6 \(\upmu \)m for the AAA, carotid artery, cerebral aneurysm, and coronary aneurysm models, respectively. The velocity field obtained from the CFD simulation was linearly interpolated to the (more highly resolved in the near-wall region) advection–diffusion mesh. The simulations were run for at least 25 cardiac cycles until the surface concentration reached steady state, with very small intracycle fluctuations.

Fig. 3
figure 3

Contour plots of WSS exposure time (WSSET), relative residence time (RRT), WSS divergence (WSSdiv), and surface concentration for the six abdominal aortic aneurysm patients. RRT and WSSdiv units are \(\frac{{\hbox {cm}}^2}{\hbox {dynes}}\) and \(\frac{\hbox {dynes}}{\hbox {cm}^3}\), respectively. WSSET and concentration are defined dimensionless. Th \(C_{\hbox {max}}\) value in the colorbar is equal to 0.08 for Patients 1, 2, 4, and 5. It is equal to 0.03 and 0.04 for Patients 3 and 6, respectively. Same view as Fig. 1 is shown

Full size image

2.4 WSS stable/unstable manifolds

We have previously demonstrated emergence of Lagrangian coherent structures (LCS) computed from WSS (WSS LCS) and how they relate to the near-wall transport in AAAs (Arzani et al. 2016). The WSS LCS were computed by integrating a high resolution of surface tracers and identifying the distinct material lines formed. These structures match the stable and unstable manifolds of the TAWSS vector in high Schmidt numbers, where \(\delta n \sim \delta _c\) is small (Arzani et al. 2016). Therefore, the TAWSS vector field alone could be used in characterization of near-wall flow topology in such flows, as opposed to the time-dependent WSS vector field (assuming periodicity of the flow field for TAWSS to be sensible). Employing this observation, we use a different method than our previous study (Arzani et al. 2016) to directly compute WSS LCS by computing stable and unstable manifolds of the (steady) TAWSS vector field. A stable and unstable manifolds corresponding to a saddle-type fixed point of a vector field are the set of all the trajectories that asymptote to the fixed point in forward and backward time integrations, respectively. The unstable manifold tends to attract nearby trajectories, and the stable manifold tends to repel nearby trajectories in time, and therefore these structures are often identified as attracting and repelling LCS, particularly in the context of unsteady vector fields. This direct approach captures all WSS stable and unstable manifolds, whereas our previous method only identified the more prominent ones. Moreover, this approach significantly reduces computational time since it does not require Lagrangian surface transport computation, but is rather based on topological analysis of the TAWSS vector field.

Fig. 4
figure 4

Contour plots of WSS exposure time (WSSET), relative residence time (RRT), WSS divergence (WSSdiv), and surface concentration for the carotid (P7–P8), cerebral aneurysm (P9), and coronary aneurysm (P10) patients. RRT and WSSdiv units are \(\frac{{\hbox {cm}}^2}{\hbox {dynes}}\) and \(\frac{\hbox {dynes}}{{\hbox {cm}}^3}\), respectively. WSSET and concentration are defined dimensionless. Th \(w_{\hbox {max}}\) value in the colorbar is equal to 2 for Patients 10 and 1 for the rest of the patients. \(R_{\hbox {max}} \) is equal to 1.5 for P7–P8, 0.3 for P9, and 0.5 for P10. \(d_{\hbox {max}} \) is equal to 10 for P7–P8 and 20 for P9–P10. \(c_{\hbox {max}} \) is equal to 0.04 for P10 and 0.05 for the other patients

Full size image
Fig. 5
figure 5

Scatter plots of WSS divergence (WSSdiv) vs. relative residence time (RRT), colored with the WSS exposure time (WSSET) value for all the patients. High WSSET occurs mostly in regions of high RRT and negative WSSdiv. RRT and WSSdiv units are \(\frac{\hbox {cm}^2}{\hbox {dynes}}\) and \(\frac{\hbox {dynes}}{\hbox {cm}^3}\), respectively. WSSET is defined dimensionless

Full size image
Fig. 6
figure 6

Scatter plots of relative residence time (RRT) rank vs. surface concentration rank for all the patients. Table 1 provides quantitative correlations based on these plots

Full size image
Fig. 7
figure 7

Scatter plots of WSS exposure time (WSSET) rank vs. surface concentration rank for all the patients. Table 1 provides quantitative correlations based on these plots

Full size image

Stable and unstable manifolds of TAWSS fixed points are computed to identify WSS LCS, a template for near-wall transport. The first step in this approach is the detection of the fixed points of the TAWSS vector field, which can be achieved by locating the triangles whose Poincaré indices are non-trivial (i.e., 1 or \(-1\)) (Tricoche et al. 2001). Next, the vector field is linearized around the fixed points \(\mathbf {x}_0\), i.e., \( \overline{\varvec{\tau } } (\mathbf {x})= \overline{\varvec{\tau } } (\mathbf {x}_0) +J_{\mathbf {x}_0} (\mathbf {x}-\mathbf {x}_0)\), where \(J_{\mathbf {x}_0}=\nabla \overline{\varvec{\tau } } (\mathbf {x}_0)\) is the Jacobian of \( \overline{\varvec{\tau } } \), from which the two eigenvalues/eigenvectors are computed. The fixed points that are of saddle-type (i.e their two eigenvalues are real and have different signs, and the eigenvectors are real) are identified. These fixed points are perturbed along the positive eigenvector (i.e., corresponding to the positive eigenvalue) in two opposite directions to obtain two initial conditions (Gambaruto and João 2012). The WSS trajectories constructed from these initial conditions in forward time will trace out the unstable manifold. Similarly, perturbation along the negative eigenvector (i.e., corresponding to the negative eigenvalue) direction with backward time integration delineates the stable manifold. The trajectory integration is continued until the trajectory reaches another fixed point (typically a source or sink) or leaves the domain. Figure 2 depicts the procedure for computation of TAWSS manifolds and WSSET.

Fig. 8
figure 8

Stable (red line) and unstable (blue line) manifolds of TAWSS vector field for the six abdominal aortic aneurysm patients. The TAWSS vector length is normalized for visualization, and colored based on its magnitude. The unit for TAWSS is \(\frac{{\hbox {dynes}}}{{\hbox {cm}}^2}\). Same view as Fig. 3 is shown

Full size image
Fig. 9
figure 9

Stable (red line) and unstable (blue line) manifolds of TAWSS vector field for the carotid (P7–P8), cerebral aneurysm (P9), and coronary aneurysm (P10) patients. The TAWSS vector length is normalized for visualization and colored based on its magnitude. The unit for TAWSS is \(\frac{\hbox {dynes}}{\hbox {cm}^2}\). The \(\tau _{\hbox {max}}\) value is equal to 10 for P7–P8 and 20 for P9–P10. Same view as Fig. 4 is shown

Full size image

3 Results

Figure 3 and 4 show contour plots of WSSET, RRT, WSSdiv, and surface concentration for the AAA (P1–P6) and the other (P7–P10) models, respectively. It is observed that some of the features in regions of high WSSET and RRT match. However, a comparison of WSSET and RRT to surface concentration reveals that WSSET features are in better agreement with surface concentration. The agreement between RRT and surface concentration is improved for the simpler geometries, due to the simpler flow topology. In general, regions of high WSSET have high RRT and negative WSSdiv. However, this trend does not occur in all regions. The motivation behind the WSSdiv measure shown in the figures is that regions of negative WSSdiv correspond to converging WSS vectors, which can indicate accumulation of near-wall trajectories in these regions.

Scatter plots of the data are shown for a better comparison of the WSS measures. Figure 5 shows scatter plots of WSSdiv vs. RRT colored based on the WSSET value. This figure shows that high WSSET largely occurs where WSSdiv is negative and RRT is higher than a certain threshold. No apparent correlation was observed between RRT and WSSdiv. The reason for this is that RRT is based on the wall shear stress, which is proportional to the tangential velocity component, while WSSdiv is proportional to near-wall normal velocity (Gambaruto et al. 2010; Arzani et al. 2016), and thus these measures represent orthogonal velocity components. Figures 6 and 7 show scatter plots of the data comparing RRT and WSSET measures to surface concentration. The rank of the data are plotted in these figures instead of the values. This was chosen due to the nonlinear nature of the WSSET measure, which produces a wide range of values, thereby restricting any linear correlation between the data. Namely, as the integration time becomes higher, more WSS trajectories accumulate near certain fixed points of the TAWSS vector field, contributing to very high WSSET values in the vicinity of these fixed points. These figures demonstrate that WSSET has a strong correlation with surface concentration. Table 1 shows the Spearman’s rank correlation coefficient between the WSS measures and surface concentration. WSSET and RRT are both correlated with surface concentration; however, the WSSET correlation is stronger. The improvement in the WSSET correlation over RRT is more pronounced in the AAA and cerebral aneurysm models, which have more complex flows. WSSdiv is inversely correlated with surface concentration; however, the correlation is not as strong as the other measures. No correlation is obtained for WSSdiv in the coronary aneurysm case, although as Fig. 4 and 5 demonstrate regions of high surface concentration and WSSET still mostly coincides with negative WSSdiv.

Table 1 Point-wise Spearman’s rank correlation coefficient between surface concentration and the different WSS parameters, relative residence time (RRT), WSS exposure time (WSSET), and WSS divergence (WSSdiv)
Full size table

Figures 8 and 9 show the stable and unstable manifolds of the TAWSS vector field colored by red and blue lines, respectively. The vector lengths are normalized for visualization and colored based on their magnitude. Comparison of these figures with Fig. 3 and 4 shows that unstable manifolds of TAWSS lead to high WSSET and high surface concentration in their surroundings. Near-wall trajectories are attracted to unstable manifolds of TAWSS and accumulate around these manifolds producing high WSSET and high surface concentration. In order to quantify the matching between TAWSS unstable manifolds and regions of high WSSET and surface concentration, Table 2 shows the percentage of the unstable manifold length existing in a region greater than the 80th percentile of these measures.

Figure 10 shows an example of how the intersections of stable and unstable manifolds of TAWSS vector divide the surface into different regions. Regions I and II are the basins of attraction for the first fixed point (F1). WSS trajectories starting in these regions are attracted to this fixed point. Similarly, regions III and IV are the basins of attraction for the second fixed point (F2). WSS trajectories starting in region V leave the aneurysm region, and therefore region V could be regarded as the basin of attraction for a fixed point in infinity.

3.1 Thrombin transport: a case study

In order to compare our results to an example of a precise biochemical transport mechanism, thrombin transport is considered. The problem involves the initiation phase of thrombin production in the coagulation cascade, similar to previous studies (Papadopoulos et al. 2014; Hansen and Shadden 2016). The presence of tissue factor at the prothrombotic wall turns prothrombin into thrombin. Platelets are ignored, as the initiation phase of thrombin production is only considered. The total concentration of thrombin (\(c_{IIa}\)) and prothrombin (\(c_{II}\)) is assumed constant and equal to the prothrombin concentration at the inlet of the domain (\(C_0\)). The reactive boundary condition at the wall is written as \(D\frac{\partial c_{II}}{\partial n} = -kc_{II}\), where \(k = 9.75\times 10^{-6} \frac{\hbox {cm}}{s} \) is the surface reaction rate (Papadopoulos et al. 2014) and \(\mathbf {n}\) is the outward normal vector. Using \(c_{IIa} + c_{II} = C_0 \), the surface boundary condition for thrombin can be written as

$$\begin{aligned} D\frac{\partial c_{IIa}}{\partial n} = k (C_0 - c_{IIa}) \;, \end{aligned}$$
(7)

where \(D = 2\times 10^{-6} \frac{\hbox {cm}^2}{s} \) is set to approximate shear-enhanced diffusivity of thrombin (Sorensen et al. 1999). The advection–diffusion equation with the above surface boundary condition and zero concentration boundary conditions at the inlet and outlet were used to simulate thrombin generation and transport. The above equation is a Robin-type boundary condition, as opposed to the Neumann boundary condition previously used at the wall.

Figure 11 shows the thrombin surface concentration normalized by prothrombin concentration at the inlet for the first patient. The value of \(C_0\) was set to 1 in the simulation. Thrombin surface concentration correlation to the WSS measures is also shown in the figure, demonstrating a good correlation between WSSET and thrombin surface concentration. It should be mentioned that for this patient, the WSSET and RRT correlation to surface concentration was reduced 7 and 14\(\%\), respectively, compared to the previous generic Neumann boundary condition.

Table 2 Percentage of the length of WSS unstable manifolds in the region greater than the 80th percentile of the WSS exposure time (WSSET) and surface concentration
Full size table
Fig. 10
figure 10

Intersection of stable (red line) and unstable (blue line) manifolds of the TAWSS vector divide the aneurysm surface into different regions. WSS trajectories in regions I and II are attracted to one TAWSS vector fixed point (F1), while trajectories in regions III and IV are attracted to another fixed point (F2). The TAWSS manifolds largely influence the WSS exposure time (WSSET). TAWSS vectors are normalized for visualization. Fixed points of TAWSS are marked with gray spheres. Patient 1 is shown in this figure

Full size image
Fig. 11
figure 11

Thrombin surface concentration normalized by the inlet prothrombin concentration (\(C_0\)). The point-wise Spearman’s rank correlation coefficient between thrombin surface concentration and relative residence time (RRT), WSS exposure time (WSSET), and WSS divergence (WSSdiv) is also shown. Patient 1 is shown in this figure. Same view as Fig. 3 is shown

Full size image

4 Discussion

Near-wall transport is of paramount importance in cardiovascular mass transport problems. The reasons for this are twofold. First, hemodynamics directly affects pathophysiology, such as intimal hyperplasia, atherosclerosis or thrombosis, by controlling the transport of chemical and cellular species near the vessel wall. Second, the high Sc numbers encountered in arterial flows leads to the formation of thin concentration boundary layers next to the wall, which marginalizes the direct effect of the core flow on near-wall transport. The explicit modeling and computation of near-wall transport of a chemical species is numerically challenging; however, we demonstrated herein that computation of WSSET can be used to quantify and predict the transport of wall-born species.

In this study, we have proposed WSSET as a novel measure for quantification of near-wall stagnation and concentration. WSSET quantifies the concentration and amount of time that wall-generated species spend near the wall. Consequently, regions of high WSSET typically exhibit negative WSSdiv and elevated RRT. A comparison of WSS measures to surface concentration shows that WSSET has the best correlation with surface concentration. Namely, WSSET measures concentration residence time and hence quantifies what is expected to be a driving mechanism for atherogenic or thrombogenic processes. WSS LCS, computed from stable and unstable manifolds of TAWSS vector field saddle points, provide insight on the near-wall flow topology and help explain WSSET distributions. Unstable manifolds of TAWSS attract the trajectories in their basin of attraction, and thus trajectories accumulate near these manifolds contributing to high WSSET. Stable manifolds of TAWSS repel their nearby trajectories and mark the boundaries of different basins of attraction.

In the context of the endothelial cells (ECs) lining the vessel wall, such cells are known to sense and respond to their environment by direct and indirect mechanisms (Barakat and Lieu 2003). In the direct mechanism, ECs sense and respond to mechanical forces by converting forces to chemical signals (mechanotransduction) and reorganizing their cytoskeleton to affect gene expression or cell functionality (Chien 2007). In the indirect mechanism, agonists in the blood flow interact with ECs to activate various responses (Davies 1995). WSS provides a means to quantify both near-wall mechanisms. For the direct mechanism, WSS measures the frictional force per unit area exerted on the ECs. For the indirect mechanism, WSS is a surrogate for the near-wall transport velocity, and WSSET can be used to quantify the potential for indirect mechanisms on EC response.

While solving the 3D advection–diffusion equation directly quantifies the complete transport of any continuum species, the high computational cost and numerical difficulties involved in accurately resolving the concentration boundary layer make this approach prohibitively expensive in routine image-based hemodynamics applications. Computation of WSSET is far less computationally expensive, but still able to accurately convey and characterize near-wall transport. Due to the quasi-steady nature of near-wall transport, the TAWSS vector can be used as a steady vector to compute WSSET, producing nearly identical results compared to the unsteady WSS vector field (Arzani et al. 2016). We note, however, that RRT can be computed from WSS with trivial computational effort and provides good agreement with WSSET and surface concentration in relatively simple flow environments—making it a preferred measure in such applications. WSS LCS can be computed with minimal computational time and can provide mechanistic insight not conveyed by WSSET or RRT fields. In this study, various arterial domains were considered to characterize different flow conditions in locations known to influence pathology. The results show that RRT mostly holds in laminar scenarios; however, WSSET is predictive over a broader range of flow conditions.

While flow stagnation affects intravascular biological processes, it is more broadly the concentration of near-wall species, and perhaps their origin, that is more directly important. For example, (Chiu et al. 2003) have shown that monocyte adhesion to ECs occurs in regions of high near-wall concentration and long residence time. Near-wall species spend more time in regions of low TAWSS due to the smaller near-wall fluid velocity. This near-wall stagnation is captured by both RRT and WSSET measures. However, the WSSET measure is influenced not only by the amount of time that trajectories spend near the wall, but also the concentration of near-wall trajectories and their origin. In relation, the fixed points of TAWSS that have larger basins of attraction will generate higher WSSET in their vicinity (cf. Fig. 10). The stable manifolds of TAWSS show the boundary of these basins of attraction and could be used to estimate how much an attracting fixed point contributes to high WSSET.

OSI (Ku et al. 1985) is a leading WSS measure that has been widely used to characterize oscillations in the WSS vector field. The main motivation behind this measure is the observation that ECs prefer to align in regions with a well-defined TAWSS vector direction and demonstrate inflammatory response in regions with oscillatory WSS. From a transport perspective, the peak value of OSI = 0.5 corresponds to a TAWSS vector with zero magnitude (infinite RRT). Therefore, in these regions no net tangential convective displacement occurs contributing to high near-wall stagnation. On the other hand, in a region with zero OSI the WSS vector does not change its direction, therefore contributing to a potentially larger TAWSS vector magnitude with a typically well-defined direction. However, the OSI measure by itself does not explain transport. OSI only explains amplification or reduction in effective near-wall transport. This observation is similar to concepts of mobility discussed by McIlhany and Wiggins (2012) in a broader context of Eulerian vector field characterization. Regions of low OSI contribute to a more effective near-wall convective tangential transport, whereas high OSI reduces effective transport due to the rapid temporal change in WSS vector. It should be emphasized though that the WSS vector magnitude needs to be considered to quantify near-wall transport. Recently, the prevailing theory that atherosclerosis is positively correlated with OSI has been challenged (Peiffer et al. 2013). A possible explanation for these inconsistencies may be that many experimental studies impose uniform oscillatory flow in simple settings. This can lead to (exaggeratedly) high near-wall stagnation, promoting atherogenic processes. However, in vivo values of OSI are typically more moderate, and in such contexts the correspondence between locations of higher OSI and the accumulation of near-wall species is less direct. Due to the spatially uniform or less complex flows in experimental studies, this phenomena can be overlooked.

In order to compute WSSET, we seeded trajectories uniformly on the surface. These trajectories represent surface-generated near-wall species. Therefore, regions of high WSSET will represent high near-wall concentration of species if the effective flux of species is coming from the lumen into the fluid domain. In correspondence with the Eulerian advection–diffusion equation, this implies that the flux boundary condition at the wall needs to be inward (into the lumen). In cases where the flux boundary condition at the wall is outward (into the vessel wall) and uniform concentration of species exists at the inlet of the domain (e.g. oxygen), opposite relations would be obtained (see the Appendix). For instance, at a reattachment or impingement point, a source-type fixed point in the WSS vector field can be generated. This source will push wall-generated trajectories away, therefore causing low WSSET in its vicinity. However, if the species are coming from the core flow, high concentration will occur in this region. Therefore, it is important to keep the nature of the transport process in mind when measures such as WSSET or RRT are being studied.

Another important consideration is that WSS and the flux boundary condition at the wall can be interconnected. For example, WSS can affect the permeability of the ECs to certain species, therefore creating a shear-stress-dependent mechanism for the resistance of the surface to mass transfer (Tarbell 2003). WSS can also influence the flux of wall-generated species. For example, high WSS can lead to a higher flux of NO at the vessel wall (Plata et al. 2010). These effects could be accounted for in the WSSET approach by releasing tracers at each location proportional to the non-uniform flux. However, such modifications cannot be integrated in the RRT measure.

We have ignored the effect of diffusion and normal velocity on the WSSET measure. We have previously investigated these effects and observed that the qualitative behavior of WSSET is minimally changed (Arzani et al. 2016). Diffusion causes random near-wall trajectories to escape the near-wall region in long integration times, and therefore the WSSET is generally reduced. Normal velocity is second order in \(\delta n\) and generally small near the wall; however, it is proportional to WSS divergence (Gambaruto et al. 2010) :

$$\begin{aligned} u_{n} = -\frac{1}{2\mu } \nabla \cdot \varvec{\tau } \; \delta n ^2 + \textit{O}(\delta n ^3) \;. \end{aligned}$$
(8)

Significant negative WSS divergence can cause near-wall trajectories to escape the near-wall region. The effect of WSS divergence on WSSET can become important in higher Reynolds numbers where the WSS divergence can become very high. In the present study, we only used one cardiac cycle of WSS data and assumed periodicity to generate WSS trajectories, although cycle-to-cycle variations in WSS exist in some cardiovascular flows such as AAAs (Poelma et al. 2015). However, our aim in this study was to demonstrate the applicability of our approach and comparison to existing methods. In this study, to characterize the near-wall flow topology we computed the stable/unstable manifolds of TAWSS vector. This is based on the observation that the near-wall transport is quasi-steady and the WSS LCS match the TAWSS stable/unstable manifolds (Arzani et al. 2016). However, this quasi-steady behavior can break down if the Reynolds and Womersley numbers are sufficiently increased. For example, exercise in AAA patients creates a more complex flow field (Arzani et al. 2014), with higher WSS values (Les et al. 2010). A preliminary investigation of our methods on AAA exercise data showed that the WSS LCS can slightly fluctuate around the stable/unstable manifolds of TAWSS and demonstrate some time dependence behavior (results not shown). Fortunately, in order to characterize the near-wall stagnation, the WSSET measure can still be applied under these flow conditions, since it is a Lagrangian approach. However, the relevance of RRT as an Eulerian measure becomes questionable, since the TAWSS vector no longer indicates effective near-wall transport. Time-averaged measures like RRT always have the risk of being inaccurate if their averaging time does not capture the flow transients. It should be noted that biological processes occur on the order of days/months, and therefore multiscale simulations are needed to evaluate such long-term processes. Moreover, inclusion of experimental or clinical data, providing a direct link between WSSET and clinical events would be another topic of future studies. Finally, the Newtonian blood rheology assumption might be questionable. This can potentially affect our results in two different ways. First, the WSS vector field obtained from a Newtonian and non-Newtonian assumption can be different, although these differences have been shown to be small in patient-specific AAAs (Marrero et al. 2014). Second, variations in viscosity affect the near-wall fluid velocity in Eq. 4. However, these variations only scale the near-wall fluid velocity and will not change the near-wall velocity direction. Therefore, as long as these changes in the magnitude of the near-wall fluid velocity do not violate the quasi-steady transport behavior, WSS LCS will still be identified from stable/unstable manifolds of the TAWSS vector. Consequently, the same near-wall flow topology will persist and the qualitative aspect of WSSET will not be affected.

5 Conclusion

The transport of chemical and cellular species near the vessel wall (or lumen) directly affects the initiation and progression of most cardiovascular diseases. Hence, the characterization of near-wall transport is a primary concern in hemodynamics research. Directly tracking an advected species in the blood flow domain to understand near-wall transport, through Lagrangian particle-tracking or solving the Eulerian advection–diffusion equations, is computationally difficult because of the disparate spatial and temporal scales between the bulk flow and near-wall regions in high Sc cardiovascular flows. To resolve this challenge, we proposed WSSET as a Lagrangian measure to quantify near-wall transport. This measure is computed from only the WSS vector field, and thus the resolution of the CFD need only be sufficient to solve the Navier–Stokes equation, and the tracking of particles is reduced to only a surface flow. Compared to the traditional RRT measure of near-wall transport, the application of WSSET to six AAA, two carotid artery, one cerebral aneurysm, and one coronary aneurysm models demonstrated improved ability to predict high and low species concentrations at the lumen. In addition, computation of WSS LCS from stable and unstable manifolds of saddle fixed points of the TAWSS vector field was shown to be relevant in the characterization of the near-wall flow topology; that is, unstable manifolds of TAWSS lead to elevated WSSET and surface concentration in their vicinity, whereas stable manifolds of the TAWSS were shown to mark basins of attraction. In summary, WSSET is a new hemodynamic parameter solely based on the WSS vector field that can provide a reasonable approximation of near-wall concentration when compared to full 3D continuum transport.

6 Appendix

6.1 Transport to and from the wall

In this section, an analogy between transport into the wall versus transport from the wall is established. In Sect. 2.3, we considered the problem of continuum transport from the wall into the lumen. However, certain chemicals such as oxygen are transported from the lumen into the wall. Assuming a homogenous concentration at the inlet, such problems can be written as

$$\begin{aligned} \frac{\partial c}{\partial t} + \varvec{u} \cdot \nabla c = D \nabla ^2 c \;, \end{aligned}$$
(9a)
$$\begin{aligned} c = c_0 \; \; \; \hbox {Inlet} \;, \end{aligned}$$
(9b)
$$\begin{aligned} \frac{\partial c}{\partial n} = -A \; \; \;\hbox {Wall.} \end{aligned}$$
(9c)

In order to observe the analogy between this problem and the considerations of Sect. 2.3, let us introduce a new variable \({\widetilde{c}} = c_0 - c \). Substituting this into Eq 9 for c and simplifying gives:

$$\begin{aligned} \frac{\partial {\widetilde{c}}}{\partial t} + \varvec{u} \cdot \nabla {\widetilde{c}} = D \nabla ^2 {\widetilde{c}} \;, \end{aligned}$$
(10a)
$$\begin{aligned} {\widetilde{c}} = 0 \; \; \; \hbox {Inlet} \;, \end{aligned}$$
(10b)
$$\begin{aligned} \frac{\partial {\widetilde{c}}}{\partial n} = A \; \; \; \hbox {Wall.} \end{aligned}$$
(10c)

Note that this is the same problem that is solved in Sect. 2.3. Therefore, referring to the change of the variable introduced, an increase (decrease) in c corresponds to a decrease (increase) in \({\widetilde{c}}\). Therefore, in the regions where WSSET predicts high concentration, a low concentration is actually obtained if the transport is originated from the lumen and travels into the wall. However, this is not an issue as a direct analogy can be established between the two cases. A few remarks follow.

Remark 1

The value of A will have different physical meanings in the two problems, and therefore its value will be different. However, this difference simply shifts the concentration values uniformly.

Remark 2

The above analogy is physically correct as long as \({\widetilde{c}} \le c_0\). The issue arises in the negative flux boundary condition introduced in Eq. 9. The negative flux boundary condition \(\frac{\partial c}{\partial n} = -A\) will be physically wrong if c becomes zero near the wall, and this will lead to erroneous negative values for c at the wall. The requirement for c to be positive leads to \({\widetilde{c}} \le c_0\).

Remark 3

The above issue does not occur if one considers a physically more realistic Robin-type boundary condition \( \frac{\partial c}{\partial n} = -kc \), where k is a constant. It should be mentioned that the incorporation of a Robin-type boundary condition breaks the analogy, although the analogy is expected to hold in some qualitative extent, as demonstrated for thrombin/prothrombin transport (Fig. 11). Future work should investigate this claim for other biochemical transports.