A two-muscle, continuum-mechanical forward simulation of the upper limb

Abstract

By following the common definition of forward-dynamics simulations, i.e. predicting movement based on (neural) muscle activity, this work describes, for the first time, a forward-dynamics simulation framework of a musculoskeletal system, in which all components are represented as continuous, three-dimensional, volumetric objects. Within this framework, the mechanical behaviour of the entire muscle–tendon complex is modelled as a nonlinear hyperelastic material undergoing finite deformations. The feasibility and the full potential of the proposed forward-dynamics simulation framework is demonstrated on a two-muscle, three-dimensional, continuum-mechanical model of the upper limb. The musculoskeletal model consists of three bones, i.e. humerus, ulna, and radius, an one-degree-of-freedom elbow joint, and an antagonistic muscle pair, i.e. the biceps and triceps brachii, and takes into consideration the contact between the skeletal muscles and the humerus. Numerical studies have shown that the proposed upper limb model is capable of predicting realistic moment arms and muscle forces for the entire range of activation and motion. Within the limitations of the model, the presented simulations provide, for the first time, insights into existing contact forces and their influence on the muscle fibre stretch. Based on the presented simulations, the overall change in fibre stretch is typically less than 3%, despite the fact that the contact forces reach up to 71% of the exerted muscle force. Movement-predicting simulations are achieved by minimising a nonlinear moment equilibrium equation. Based on the forward-dynamics simulation approach, an iterative solution procedures for position-driven (inverse dynamics) and force-driven scenarios have been proposed accordingly. Applying these methodologies to time-dependent scenarios demonstrates that the proposed methods can be linked to state-of-the-art control algorithms predicting time-dependent muscle activation levels based on principles of forward dynamics.

1 Introduction

State-of-the-art methods of simulating (parts of) the musculoskeletal system are based on multi-body simulations. They include lumped-parameter models of muscle–tendon complexes for investigating the kinetics of the musculoskeletal system. Multi-body models use a discrete modelling approach, where the components of the musculoskeletal system are typically assumed to be rigid. From a mechanical point of view, they are characterised by discrete mass points and their respective moment of inertia. Hill-type muscle models have gained as lumped-parameter modelling approach acceptance for adequacy representing the muscle–tendon complexes (e.g. Zajac 1989; Winters 1990; Van Soest and Bobbert 1993; Houdijk et al. 2006; Kistemaker et al. 2006; Siebert et al. 2008; Haeufle et al. 2014; Mörl et al. 2012; Millard et al. 2013; Günther et al. 2007). As they have been successfully applied for many decades, they are well validated against experiments (e.g. Günther et al. 2007; Siebert et al. 2008; Van Soest and Bobbert 1993). Geometrically, they are linear objects that span from the muscles’ origin to their insertion points and can hardly represent spatially varying features. The muscle force path can typically only be enhanced by pre-defined wrapping surfaces or via-points to improve muscle force path (Garner and Pandy 2000). The resulting models are not capable of representing detailed heterogeneous material characteristics, but are popular due to the relatively simple representation and relative low computational cost. As a consequence, such computational models can take into account up to more than 200 muscle–tendon units (e.g. Rupp et al. 2015; Christophy et al. 2011).

More recently, further insights into the musculoskeletal system have been attained by exploiting continuum-mechanical principles in order to model skeletal muscle mechanics. Due to a different modelling approach, one can include, at the expense of computational costs, structural properties and local actions. Hence, spatial quantities such as fibre field architecture (e.g. Blemker and Delp 2005), local activation principles (e.g.  Heidlauf et al. 2013; Heidlauf and Röhrle 2013, 2014), complex geometries (e.g. Röhrle and Pullan 2007; Böl et al. 2011), or contact mechanics (e.g. Fernandez and Hunter 2005) can be included in a straight forward way. The drawbacks of continuum-mechanical-based models are (i) the lack of experimental data for validation, (ii) the computational costs, and (iii) an increase in modelling complexity imposing restrictions to the usability. For these reasons, almost all research exploiting continuum-mechanical skeletal muscle models investigating various aspects of skeletal muscles mechanics, for example the mechanical behaviour/influence of tendon tissue (e.g. Lemos et al. 2005), the effect of micro-mechanical features on the overall mechanics (e.g.Sharafi and Blemker 2010; Sharafi et al. 2011), or extension of continuum-mechanical model to include chemo-electrophysiological aspects (e.g. Röhrle et al. 2008; Röhrle 2010; Heidlauf and Röhrle 2014), use skeletal muscle models that do not interact with its surrounding.

While investigating and modelling the mechanical behaviour of a single skeletal muscle in isolation is essential, the ultimate goal must be the use of such continuum-mechanical skeletal models to improve our understanding on how the mechanical and physiological properties impact the musculoskeletal system and, hence, our ability to move. Continuum-mechanical skeletal muscle models investigating the mechanical behaviour within a musculoskeletal setting are rare. The musculoskeletal system is typically overdetermined meaning that the number of muscle actuators acting on a joint is higher than the degrees of freedom (DoFs) of the respective joint. Therefore, further assumptions are needed to solve the redundancy problem. Within simulations, this is achieved by using either an inverse-dynamics or forward-dynamics approach. Since these approaches are typically based on optimising an objective function, the high computational costs for modelling skeletal muscle using three-dimensional continuum-mechanical models would increase even more.

In inverse dynamics, the motion of bones within the musculoskeletal system is captured experimentally and is used as a model input. The aim is to distribute the joint moments among the acting muscles in order to reproduce the given motion. The most frequently used inverse-dynamics modelling approaches for solving the muscle redundancy problem is to introduce physiologically inspired objective functions, e.g. objective functions that aim to minimise the work done, (Seireg and Arvikar 1973), the joint moment (Crowninshield and Brand 1981), or the contact force within the joint (Seireg and Arvikar 1975) while (i) relating the muscle force to the muscle dimension, e.g. the PSCA (Alexander and Vernon 1975), (ii) using experimental data such as EMG for determining muscle activation (Hof and Van Den Berg 1977), or (iii) grouping muscles into agonist and antagonist muscle groups to reduce the number of acting muscles (Morrison 1970; Schipplein and Andriacchi 1991). The solution of the optimisation problem provides estimates of the muscle forces at each time step. Due to the fact that each time step can be solved independently, inverse-dynamics approaches are numerically efficient.

In forward dynamics, the motion is the consequence of the muscle activation. This definition of forward-dynamics is also followed in this work. Hence, muscle forces are considered as the model input and the resulting movements as the model output. Naturally, the muscle forces and, hence, the recruitment strategy leading to a motion or a specific task need to be predicted by a model. It cannot be directly measured experimentally. Possibilities to determine muscle forces are calculating the muscles’ activation state by (i) the use of motor control concepts such as the equilibrium point control (Feldman 1986; Günther and Ruder 2003; Lorussi et al. 2006; Rupp et al. 2015; Kistemaker et al. 2006), (ii) the use of experimental data, e.g. EMG data, to employ activation dynamics, so as to convert EMG signal to muscle activation (Buchanan et al. 2004), or (iii) objective functions. The optimisation problems are typically solved by minimising, for example, the necessary work to carry out a particular task (Pandy et al. 1990; Anderson 1999; Anderson and Pandy 2001).

So far, only a few continuum-mechanical approaches have been used to model the musculoskeletal system. In Fernandez and Hunter (2005), for example, the authors use an inverse-dynamics approach to investigate the wrapping of muscles around the knee joint. For animation purposes, Lee et al. (2009) used an inverse-dynamics approach and a linear mechanical muscle description to visualise the motion of skin. Wu et al. (2013) were the first to prescribe muscle activations to achieve facial expressions. The facial expressions were achieved by using a finite element mapping procedure to embed muscles within the soft tissue. The key difference between modelling facial expressions and modelling a musculoskeletal system such as the upper or lower limb is that movement within the latter example can only be achieved by antagonistic muscle pairs. Unlike the facial simulations, joint moment and joint moment of momentum equilibrium need to be taken into account in order to determine the respective motion of the system.

Forward-dynamics simulations that describe the antagonistic muscles as three-dimensional continuum-mechanical objects do not exist within the literature. This work describes, for the first time, a forward-dynamics model, in which the musculoskeletal system is modelled based on continuum-mechanical principles. To demonstrate the potential of the proposed methodology, a musculoskeletal system consisting of three bones (i.e. humerus, ulna, and radius), of the elbow joint that exhibits one DoF, and of an antagonistic muscle pair consisting of the biceps and triceps brachii is considered. The muscles are modelled as three-dimensional, continuum-mechanical objects that are in contact with rigid bones. Within this work, different solution strategies are investigated to solve for the resulting motion of this musculoskeletal model given different input parameters. Although this work entirely focuses on a two-muscle system, the approach can also be extended to more complex musculoskeletal system. This, however, would lead to a muscle redundancy problem that would need to be solved.

2 Methods

2.1 Finite elasticity fundamentals

As skeletal muscles undergo large deformations, the theory of Finite Elasticity provides an adequate mathematical framework to describe the deformed state of a biological system. The following introduces the fundamentals for using a continuum-mechanical description. The material body, $\mathscr {B}$, is a manifold of connected points $\mathscr {P}$. The points on the boundary of $\mathscr {B}$ define the surface $\varGamma$. Every material point $\mathscr {P}$ in $\mathscr {B}$ has at any time t a unique position defined by the placement function, $\varvec{{x}}={\varvec{\chi }}(\mathscr {P},t)$, called the current configuration. For time $t_0=0$, the reference configuration is defined by $\varvec{{X}} = {\varvec{\chi }}(\mathscr {P},t_0)$. With these definitions, the deformation gradient, $\varvec{{F}}$, is defined by

$$\begin{aligned} \varvec{{F}} := \frac{\partial {\varvec{\chi }} (\varvec{{x}},t)}{\partial \varvec{{X}}} = \frac{\partial \varvec{{x}}}{\partial \varvec{{X}}} . \end{aligned}$$

(1)

Further, the right Cauchy–Green deformation tensor, $\varvec{{C}}$, is introduced by $\varvec{{C}} = \varvec{{F}}^T \,\varvec{{F}}$. More detailed information on the theory of finite elasticity can be found, for example, in Holzapfel (2000) or Bonet and Wood (1997).

To investigate the kinetics of a body $\mathscr {B}$, the linear momentum is balanced. Assuming that no fast motions occur within this work, the inertia terms are neglected. Furthermore, the body forces are neglected since the motion of the investigated forearm is independent of the elevation of the arm and since one can assume that the local muscle forces are much higher than the body forces. Hence, the balance of linear momentum reduces to

$$\begin{aligned} \hbox {div}\,\varvec{T} = \mathbf 0 , \end{aligned}$$

(2)

where $\varvec{T}$ denotes the Cauchy stress, which is the force per squared line element with respect to the actual area element. The Cauchy stress tensor is related to the second Piola–Kirchhoff stress tensor, $\varvec{S}$, by a scaled covariant push forward, $\varvec{T} = (\det \varvec{{F}})^{{-1}} \, \varvec{{F}} \, \varvec{{S}} \, \varvec{{F}}^T$.

2.2 Constitutive modelling

The stress tensor is derived by exploiting a constitutive model. Like within this work, skeletal muscles are typically considered to be hyperelastic, transversely isotropic, and, under physiological loads, incompressible. The stress tensor can be derived from a volume specific strain energy function (or just strain energy function) $\varPsi$ , i.e.

$$\begin{aligned} \begin{aligned} \varvec{{S}}&= 2 \, \frac{\partial \varPsi (I_1, I_2, I_4)}{\partial \varvec{C}} - \frac{\partial \left( p \, \varPsi (I_3)\right) }{\partial \varvec{C}} \\&= 2 \, \frac{\partial \varPsi (I_1, I_2, I_4)}{\partial \varvec{C}} - p \, \varvec{C}^{-1} . \end{aligned} \end{aligned}$$

(3)

For an incompressible material behaviour, p is included as a Lagrangian multiplier to enable the incompressible condition, $\det \varvec{F} -1 = 0$ (cf., Holzapfel 2000), and can be associated with the hydrostatic pressure. The strain energy is formulated with respect to the invariants $I_1 = \mathrm {tr} \,\, \varvec{C}$, $I_2 = \mathrm {tr} \,\, ( \mathrm {cof} \, \varvec{C})$, $I_3 = \det \varvec{{C}}$, and $I_4 = \mathrm {tr} \,(\varvec{{M}} \varvec{{C}})$, in which the structural tensor, $\varvec{{M}}$, is defined by the dyadic product of the fibre direction in the reference configuration, cf. Holzapfel (2000) or Spencer (1971, 1972).

Commonly, the overall strain energy or stress for skeletal muscles is additively split into an isotropic and anisotropic part (cf.,Oomens et al. 2003; Lemos et al. 2005; Blemker et al. 2005; Röhrle et al. 2008). Hence, the overall strain energy function is given by

$$\begin{aligned} \varPsi _\mathrm{muscle}(I_1, I_2, I_4) = \varPsi _\mathrm{iso}(I_1, I_2) + \varPsi _\mathrm{aniso}(I_4) . \end{aligned}$$

(4)

For the isotropic contribution, $\varPsi _\mathrm{iso}(I_1, I_2)$, the following incompressible Mooney–Rivlin material formulation (Mooney 1940; Rivlin 1948) is defined by

$$\begin{aligned} \varPsi _\mathrm{iso}(I_1, I_2) = c_1 \,( I_1 - 3) - c_2 \,( I_2 - 3) , \end{aligned}$$

(5)

where $c_1$ and $c_2$ are two material parameters.

The anisotropic term is split into a passive and an active contribution, where the active part is multiplied with the muscle activation parameter, $\alpha \in [0,1]$. Choosing $\alpha = 0$ describes the purely passive, i.e. inactivated, skeletal muscle behaviour, where $\alpha =1$ describes the mechanical behaviour of a fully activated, i.e. tetanised, skeletal muscle. The anisotropic part of the strain energy function is modelled as

$$\begin{aligned} \varPsi _\mathrm{aniso} (I_4) = \varPsi _\mathrm{passive}(I_4) + \alpha \ \varPsi _\mathrm{active}(I_4) . \end{aligned}$$

(6)

The strain energy function for the passive force–length relation, $\varPsi _\mathrm{passive}(I_4)$, follows a J-shaped material behaviour. It is approximated by a polynomial strain energy function introduced by Markert et al. (2005). The strain energy function meets the requirements of polyconvexity, coercivity, and a stress-free reference state:

$$\begin{aligned} \varPsi _\mathrm{passive} = {\left\{ \begin{array}{ll} \frac{c_3}{c_4} \left( \lambda _f^{c_4} -1 \right) - c_3 \, \mathrm {ln} \lambda _f &{}\quad \text {if }\;\; \lambda _f \ge 1 \\ 0 &{}\quad \text {else}, \end{array}\right. } \end{aligned}$$

(7)

where $c_3$ and $c_4$ are material parameters and $\lambda _f = \sqrt{I_4}$ is the fibre stretch.

The active part of the strain energy function, $\varPsi _\mathrm{active}$, is governed by a so-called force–length relation. It is a product of the maximal stress, $S_\mathrm{max}$, in which a skeletal muscle can produce at optimal length $\lambda _{f}^\mathrm{opt}$ and a dimensionless force–length relation that was adopted from Hatze (1978). Hence, the strain energy function for the active part is given by

$$\begin{aligned} \varPsi _\mathrm{active} = - \frac{S_\mathrm{max}}{\nu _i} \left( \lambda _{f}^\mathrm{opt} \, \Delta W_i\right) ^{-\frac{1}{\nu _i}} \int \limits _{\frac{ \lambda _f^{\nu _i}}{\lambda _{f}^\mathrm{opt} \, \Delta W_i} }^{\infty } \lambda _f^{\frac{1}{\nu _i}-1} e^{-\lambda _f} \, \mathrm {d} \lambda _f , \end{aligned}$$

(8)

where $\nu _i$ and $\Delta W_i$ are two parameters influencing the steepness and the width of the resulting Gaussian bell curve.

Taking the derivative with respect to the right Cauchy–Green deformation tensor, cf., Eq. (3), the respective terms of the second Piola–Kirchhoff tensor can be determined. The isotropic term is given by

$$\begin{aligned} \varvec{{S}}_\mathrm{iso} = 2 \, c_1 \left( \varvec{{I}} - \frac{1}{3} \, I_1 \, \varvec{{C}}^{-1} \right) + 2 \, c_2 \, \left( I_1 \, \varvec{{I}} - \varvec{{C}} - \frac{2}{3} \, I_2 \, \varvec{{C}}^{-1} \right) \, \end{aligned}$$

(9)

and the anisotropic term by

$$\begin{aligned}&\varvec{{S}}_\mathrm{aniso}(\lambda _f) = 2\, \frac{\partial \varPsi _\mathrm{aniso}}{\partial \varvec{{C}}} = 2\, \frac{\partial \varPsi _\mathrm{aniso}}{\partial \lambda _f} \ \frac{\partial \lambda _f}{\partial I_4} \ \frac{\partial I_4}{\partial \varvec{{C}}} \nonumber \\&= \frac{1}{\lambda _f} \frac{\partial \varPsi _\mathrm{aniso}}{\partial \lambda _f} \ \varvec{{M}} = \frac{1}{\lambda _f} P_\mathrm{aniso} \ \varvec{{M}} = \frac{1}{\lambda _f^2} \sigma _\mathrm{aniso} \ \varvec{{M}} , \end{aligned}$$

(10)

where $\varvec{{P}}_\mathrm{aniso}$ refers to the nominal stress acting only along the fibre direction. Note, since the strain-energy function is a scalar, the nominal stress $\varvec{{P}}$ reduces to the scalar-valued function, $P_\mathrm{aniso}$.

Inserting Eq. (7) into Eq. (10), the passive contribution of $\varvec{{S}}$ is given by

$$\begin{aligned} \varvec{{S}}_\mathrm{passive} = {\left\{ \begin{array}{ll} \frac{1}{\lambda _f^{2}} c_3 \left( \lambda _f^{c_4} - 1\right) \varvec{{M}} &{}\quad \text {if }\;\; \lambda _f \ge 1,\\ 0 &{}\quad \text {else}. \end{array}\right. } \end{aligned}$$

(11)

The same holds for the active contribution of $\varvec{{S}}$ such that

$$\begin{aligned} \varvec{{S}}_\mathrm{active} = {\left\{ \begin{array}{ll} \frac{S_\mathrm{max}}{\lambda _f ^2}\,{\text{ exp }} \left( - \left| \frac{ \left( \lambda _f / \lambda _{f}^\mathrm{opt} \right) -1}{\Delta W_\mathrm{asc}} \right| ^{\nu _\mathrm{asc}} \right) \varvec{{M}}, &{}\quad \lambda _f \le \lambda _{f}^\mathrm{opt},\\ \frac{S_\mathrm{max}}{\lambda _f ^2}\,{\text{ exp }} \left( - \left| \frac{ \left( \lambda _f/\lambda _{f}^\mathrm{opt}\right) -1}{\Delta W_\mathrm{desc}} \right| ^{\nu _\mathrm{desc}} \right) \varvec{{M}}, &{}\quad \lambda _f > \lambda _{f}^\mathrm{opt}. \end{array}\right. } \end{aligned}$$

(12)

The resulting curve is $C^1$ continuous. For values smaller than the optimal fibre stretch, the first part of (12) describes the ascending branch of the force–length relation, while the second part of (12), i.e. values larger than the $\lambda _{f}^\mathrm{opt}$, describes the descending branch of the force–length relation. All muscle parameters are listed in Table 1. For uniaxial constraints, the qualitative stress contributions are depicted in Fig. 1.

Table 1 Material parameters for the constitutive laws of the muscle–tendon complex

The constitutive law describing the mechanical behaviour of the skeletal muscle tissue can be extended to a general constitutive law for the entire muscle–tendon complex and its surrounding fat tissue by introducing two further parameters. The first material parameter, $\gamma ^{M}$, determines whether the respective material point is considered to be muscle tissue ($\gamma ^{M}=1$) or tendon tissue ($\gamma ^{M}=0$). The second parameter, $\gamma ^\mathrm{ST}$, allows one to distinguish between muscle or tendon tissue ($\gamma ^\mathrm{ST}=0$) or some other isotropic soft tissue ($\gamma ^\mathrm{ST}=1$) such as fat.

Fig. 1

The Cauchy stress contributions for the triceps’ skeletal muscle tissue in uniaxial direction

Therefore, the strain energy function for an entire muscle–tendon complex, including the surrounding soft tissue, is thus defined within a single strain energy function by

$$\begin{aligned} \varPsi _{\mathrm{MTC}} = \varPsi _{\mathrm{iso}} + \left( \varPsi _{\mathrm{passive}} + \alpha \, \gamma ^{M} \, \varPsi _{\mathrm{active}} \right) \left( 1 - \gamma ^\mathrm{ST} \right) . \end{aligned}$$

(13)

Based on Eq. (3), the second Piola–Kirchhoff stress for the muscle–tendon complex, $\varvec{{S}}_{\mathrm{MTC}}$, is by

$$\begin{aligned} \varvec{{S}}_{\mathrm{MTC}} = \varvec{{S}}_{\mathrm{iso}} + \left( \varvec{{S}}_{\mathrm{passive}} + \alpha \, \gamma ^{M} \, \varvec{{S}}_{\mathrm{active}} \right) \left( 1 - \gamma ^\mathrm{ST} \right) . \end{aligned}$$

(14)

Note, for $\gamma ^\mathrm{ST}=1$, the anisotropic part of the material behaviour vanishes. In case of $\gamma ^\mathrm{ST} > 1$, the material exhibits anisotropic behaviour. For $\gamma ^\mathrm{ST} = 0$ and $\gamma ^{M} = 1$, the material reduces to the material behaviour of the muscle tissue. For $\gamma ^{\mathrm{\mathrm ST}} = 0$ and $\gamma ^{{M}} = 0$, one obtains the stress tensor for the tendon tissue as given in Eq. (14). The different tissue behaviour is enforced by linearly interpolating the material parameters, i.e.

$$\begin{aligned} c_1= & {} \gamma ^{M} \, c_1^{M} + \left( 1-\gamma ^{M}\right) \, c_1^{T} , \nonumber \\ c_2= & {} \gamma ^{M} \, c_2^{M} + \left( 1-\gamma ^{M}\right) \, c_2^{T} , \nonumber \\ c_3= & {} \gamma ^{M} \, c_3^{M} + \left( 1-\gamma ^{M}\right) \, c_4^{T} , \nonumber \\ c_4= & {} \gamma ^{M} \, c_4^{M} + \left( 1-\gamma ^{M}\right) \, c_4^{T} , \end{aligned}$$

(15)

where the material parameters $c_1$ to $c_4$ are those of Eq. (5) and (7). Superscripts M and T denote material-specific parameters, i.e. the material parameters for muscle (M) and tendon tissue (T). All muscle–tendon complex-specific material parameters used within this work are given, together with its source of origin, in Table 1.

2.3 Weak formulation and contact mechanics

The weak form of the governing equations is obtained by multiplying Eq. (2) with a virtual displacement $\delta \varvec{{u}}$, integrating over the whole domain, and using the divergence theorem. Hereby, one obtains the weak formulation of the momentum balance,

$$\begin{aligned} \begin{aligned}&\delta W := \int \limits _{\mathscr {B}}^{}{\varvec{{T}} \cdot \hbox {grad}\,\delta {\varvec{u}}}\mathrm {d}v - \int \limits _{\varGamma _\mathscr {B}}^{}{\varvec{{t}} \cdot \delta \varvec{{u}}}\mathrm {d}a , \\&\varvec{{u}} = \bar{\varvec{{u}}} \quad \mathrm{on} \quad \varGamma ^u , \\&\varvec{{t}} = \bar{\varvec{{t}}} \ \quad \mathrm{on} \quad \varGamma ^\sigma , \end{aligned} \end{aligned}$$

(16)

where $\varvec{{t}} = \varvec{{T}{n}}$ is the traction vector with $\varvec{n}$ being the unit exterior vector normal to the boundary surface and $(\bar{\cdot })$ denote Dirichlet and Neumann relations on the boundaries, $\varGamma ^u$ and $\varGamma ^\sigma$, respectively. Within this work, the displacements are approximated in all three directions with quadratic Lagrange basis functions and the hydrostatic pressure is approximated with linear Lagrange basis functions.

To incorporate the interaction between different tissues during motion, a frictionless contact formulation is incorporated (cf., Chung 2008; Wriggers 2002; Laursen 2002). Since the two muscles considered within this musculoskeletal system, i.e. the biceps brachii and triceps brachii, do not interact with each other, the contact reduces to the muscle–bone interaction. Taking into account contact mechanics between a master $\mathscr {B}^M$ and a slave $\mathscr {B}^S$, the overall virtual work, $\delta W^\mathrm{coupled}$, is defined by

$$\begin{aligned} \delta W^\mathrm{coupled} := \delta W^M + \delta W^S + \delta W^C , \end{aligned}$$

(17)

where $\delta W^M$ and $\delta W^S$ are the virtual work of the master and slave defined by Eq. (16), respectively, and $\delta W^C$ is the contact virtual work coupling the two bodies. Laursen (2002) defines the contact virtual work $\delta W^C$ for the frictionless case as

$$\begin{aligned} \delta W^C = \int \limits _{\varGamma ^C_{\mathscr {B}^M}}^{}{t_N \cdot \delta g_N}\mathrm {d}A , \end{aligned}$$

(18)

where $\varGamma ^C$ is the surface of the master at which contact may occur at specific contact points on the face, $t_N$ is the normal (frictionless) contact pressure, and $\delta g_N$ is the variation of the gap function. Following Wriggers (2002), the gap function $g_N$ and the variation of the gap function $\delta g_N$ are defined by

$$\begin{aligned} g_N&:= -\varvec{{n}} \cdot \left( \varvec{{x}}^S - \varvec{{x}}^M \right) , \end{aligned}$$

(19)

and therefore

$$\begin{aligned} \delta g_N&= -\varvec{{n}} \cdot \left( \delta \varvec{{u}}^S -\delta \varvec{{u}}^M\right) , \end{aligned}$$

(20)

where $\varvec{{n}}$ is the unit outward normal vector defined with respect to the master surface and $\varvec{{x}}$ and $\delta \varvec{{u}}$ are the location and the virtual displaced location on the master and the slave, respectively. Penetration occurs for positive values of $g_N$ and $\delta g_N$.

The regularisation of the frictionless contact description (Kuhn–Tucker condition) is conducted by employing the penalty method. The regularised contact pressure is assumed to be

$$\begin{aligned} t_N = {\left\{ \begin{array}{ll} \epsilon \, g_N \quad &{}\quad \mathrm{if} \quad g_N \ge 0 \\ 0 &{}\quad \mathrm{else} , \end{array}\right. } \end{aligned}$$

(21)

where $\epsilon$ is the penalty factor. The exact solution is obtained as $\epsilon \rightarrow \infty$.

The emerging partial differential equation in space, including frictionless contact between the skeletal muscles and the bone, is defined by Eq. (17). Since the bones are much stiffer than the rest of the soft tissue and since the loads considered within this study are physiological and do not exhibit high accelerations as they might occur, for example, in accidents, the bones are assumed to be rigid within this work. Hence, the master’s virtual work is zero.

The resulting nonlinear system is linearised. The linearisation of the non-contact components is based on computing a numerical tangent, while the frictionless contact formulation uses for linearisation directional derivatives as introduced by Laursen (2002), i.e.

$$\begin{aligned} \Delta t_N = H(g_N) \, \epsilon \, \Delta g_N , \end{aligned}$$

(22)

where $H(\cdot )$ denotes the Heaviside function. The Galerkin finite element method, as implemented within CMISS,¹ has been used to discretise the governing equations.

2.4 Upper limb model

The geometry of the upper limb is based on the visible human male’s data set. The image data of the visible human male were acquired in a supine position, while the arm was resting on the abdominal belt. The arms had an elbow flexion angle of approximately 60$^\circ$. The origin of the chosen coordinate system is the intersection between the mid-sagittal and mid-coronal plane at the most inferior position, where the x-axis points to the right, the y-axis anteriorly, and the z-axis superiorly, see Spitzer et al. (1996).

The humerus, ulna, and radius form the elbow joint. Within this work, the elbow is considered as an ideal hinge joint. As the upper limb model does not account for supination and pronation, the ulna and the radius are united to build the forearm. The bones of the hand are not required for investigating elbow movements and are therefore omitted.

Without involving synergistic muscle effects, at least one single antagonistic muscle pair needs to be chosen to enable the movement of an idealised elbow joint. The most powerful elbow extensor muscle is the triceps brachii. Within the presented upper limb model, the long, lateral, and medial heads of the triceps brachii are not considered as individuals. The two most lateral heads are combined to one strong united head, while the most medial head is separated from the two others. Furthermore, since the triceps’ insertion unites into one wide tendon at the olecranon process, the triceps brachii has been combined to one homogenised, bipennate skeletal muscle. To avoid numerical issue with bad aspect ratios, the gap between the proximal muscle heads is filled by an isotropic soft tissue material, i.e. fat.

One key physiological aspect of bipennate muscles is the existence of an aponeurotic tissue layer (aponeurosis), which often deeply penetrates into the muscle belly. The aponeurosis is a very fine and slim tissue layer which has a strong impact on the mechanical behaviour of the overall muscle–tendon complex. To represent the triceps more realistically, the aponeurotic tissue layer, which connects the proximal and distal ends of the muscle, is modelled by assuming in (14) a $\gamma ^M=0.99$ for the centre elements of the triceps brachii, see Fig. 2a.

Elbow flexion is achieved through multiple synergistically acting muscles, where the flexion strength may additionally depend on the orientation of the hand (supination/pronation). Murray et al. (2000) identified the isometric moment-generating capacity building the product of the physiological cross-section area, the average moment arm, and the cosine pennation angle of the muscles acting on the elbow joint. They pointed out that biceps brachii produces the largest moment capacity followed by brachialis, brachioradialis, extensor carpi radialis longus, and pronator teres. Therefore, and since the focus of this work is on developing a novel methodology to achieve forward-dynamics simulations of antagonistic muscle pairs within a musculoskeletal system, only the biceps brachii has been chosen as flexor within this upper limb model. For the triceps brachii, the geometrical model of the biceps brachii’s two heads is combined to form one fusiform muscle belly with two separate proximal tendon origins. The gap between the two tendon heads is again filled with isotropic soft tissue, see Fig. 2b.

The material properties for the muscles have been chosen according to the respective muscles’ anatomy. The centre of a muscle is defined as muscle tissue, and the elements towards the ends are defined as tendon tissue. The elements in the tapering area form a transition zone, which is modelled using varying $\gamma ^M$ values.

Unlike for muscles in isolation, the choice of pre-stretch is crucial within musculoskeletal systems as wrong pre-stretches can completely alter the mechanical behaviour of the system. Assuming that no physiological muscle length shall cause any compressive force and that one cannot experimentally determine the elbow angle at which the individual muscle produce their largest muscle force, the pre-stretch was chosen such that the muscles exhibited in a non-activated state at its shortest muscle length no muscle force. For the visible human male, the initial resting posture is assumed to be $\theta = 60^\circ$ an averaged fibre stretches of 1.146 and 1.071 for the biceps and triceps brachii, respectively.

The muscle’s origin and insertion define the locations for the boundary conditions. As tendon tissue is compared to muscle tissue relatively stiff, it undergoes only relatively small deformations. Hence, at the tendons’ origin and insertions areas are considered to be spatially fixed with respect to the area on the bone in which the tendons insert or from which they originate.

The mesh for all components is generated within CMISS using the least-square fitting methods described by Chris et al. (1997). The overall model is depicted in Fig. 2. The orientation of the muscles, i.e. the coordinate system, is the same as in Spitzer et al. (1996).

Fig. 2

The muscle tissue is coloured in dark red. Tendon tissue is shown in beige and other soft tissue in white. The transition zone from tendon to muscle tissue is indicated by a colour between dark red and beige. For the triceps, it can be seen that one row of elements along the longitudinal axis exhibits an increased tendon-tissue ratio. This shall represent the aponeurosis sheet of a bipennate muscle. Since the biceps brachii is assumed to be a fusiform skeletal muscle, the fibre orientation is aligned with the longitudinal axis of the muscle. In the case of the triceps brachii, the fibre orientation is defined starting from a fusiform orientation and rotating the muscle fibres located on the medial and lateral side of the aponeurosis by $+15^\circ$ and $-15^\circ$, respectively. a Dorsal view of the triceps brachii. b Lateral view of the biceps brachii

2.5 Equivalent static system

To avoid a large and complex system, in which all components are considered to be deformable and in contact, e.g. bone–bone contact within the joint, a reduced equivalent static system is introduced to investigate equilibrium positions of the upper limb model, see Fig. 3a. It consists of the humerus, forearm bones, a pair of antagonistic upper arm muscles, and an external force F, which is acting at the distal end of the forearm. The humerus is supported in all spatial directions and the forearm rotates around the fulcrum of the elbow joint. The forearm’s rotation matrix is defined by an axis and an angle. The rotation angle is defined to be the elbow flexion angle, $\theta$, and the rotation axis is defined by a vector product of a vector along the humerus and the orientation of a vector from the fulcrum and to the distal end of the forearm.

Fig. 3

Building the equivalent static system. a Equivalent static system. b Definition of the area of interest. c Free body diagram of the forearm. d Defining a moment equilibrium

A free body diagram of the forearm is defined by the black line in Fig. 3b. The forces acting on the forearm (Fig. 3c) are the muscle reaction forces of the triceps brachii, T, of the biceps brachii, B, the elbow contact forces $E_h$ and $E_v$, and a arbitrary chosen external load F, which acts as a perturbing force to the system. As both muscles insert at the forearm, the position of the forearm defines the respective muscle length and lever arm. Hence, the muscles’ kinematics only depends on the elbow angle and a moment balance can be formulated for the forearm with respect to the fulcrum of the elbow, i.e.

$$\begin{aligned} B (\theta , \, \alpha _B) \; l_B (\theta ) + T(\theta , \, \alpha _T) \; l_T (\theta ) + F \; l_F (\theta ) = 0 , \end{aligned}$$

(23)

where $T(\theta ,\alpha )$ and $B(\theta ,\alpha )$ are the exerted muscle forces for a given $\alpha$ and $\theta$ and $l_j$ are the lever arms for $j\in \{T,B,F\}$. The contact forces between humerus and forearm $E_h$ and $E_v$ do not contribute the moment balance as their lever arms are zero. The muscle lengths are defined by the linear distance between the origin and insertion points. The origin is fixed, whereas the location of the insertion point (at the ulna/radius) varies depending on the elbow flexion angle. The chosen nodes on the bone are tracked for the physiologically reasonable range of motion of the forearm. The resulting absolute muscle length is defined as change of the distance between origin and insertion relative to the visible human male’s initial resting position at $\theta _\mathrm{init}=60^\circ$. Then, for each of the muscle’s relative change in length, a separate third-order polynomial has been obtained using MATLAB’s least-squares fitting functionality. The respective relative muscle lengths are depicted in Fig. 4a, b.

Fig. 4

Relative change in length of the biceps and triceps brachii and the associated lever arms for the entire range of motion. a Relative change in length, for triceps brachii. b Relative change in length, for biceps brachii. c Lever arms for triceps, and biceps brachii

The muscle lever arms are determined using the tendon-displacement method described by An et al. (1984). This method is widely used and the related errors are considered to be small. Herein, the lever arms are defined by

$$\begin{aligned} l_j = \displaystyle \frac{\mathrm {d} L_j}{\mathrm {d} \theta } , \end{aligned}$$

(24)

where $j \in \{T,B,F\}$, $L_j$ is the length of muscle j and $l_j$ is the distance from the joint centre to the muscle’s line of action. The resulting muscle lever arms are given by

$$\begin{aligned} l_T&= 9.399 \times 10^{-4} \, \theta ^2 - 0.1126 \, \theta - 22.21 , \end{aligned}$$

(25)

$$\begin{aligned} l_B&= -1.482 \times 10^{-3} \, \theta ^2 + 0.1776 \, \theta + 35.02 , \end{aligned}$$

(26)

$$\begin{aligned} l_F&= - \sin ( \theta ) L_F , \end{aligned}$$

(27)

where $L_F$ is the distance from the elbow fulcrum to the distal end of the forearm and defined to be $L_F = 282.5$  mm. The result for Eqs. (25) and (26) is depicted in Fig. 4c.

2.6 Musculoskeletal system solution schemes

Equation (23) includes four DoFs: the elbow angle, $\theta$, the muscle activation pair, $\alpha _T$ and $\alpha _B$, and the external force, F. The muscle reaction forces are a result of the finite element simulation and depend on the elbow angle as well as on the level of muscle activation. The reaction forces are determined by taking the Euclidean norm after summing the nodal residual vectors at the muscle insertion area.

Based on the four DoFs, the following scenarios are considered: (i) an activation-driven or forward-dynamics scenario, in which one seeks the resulting elbow angle for a set of prescribed activation levels, (ii) a position-driven or inverse-dynamics model, in which one seeks the level of activation given a specific movement, or (iii) a force-driven scenario, in which one seeks the equilibrium of the system after altering the external force. For each scenario, convergence is determined through the resulting elbow moment, i.e. the elbow moment is considered as the system error.

To demonstrate the feasibility of the individual solution schemes, the non-solution variables are fixed. For example, within the activation-driven, forward-dynamics case, all variables except for the level of activation of a muscle (input) and the elbow angle (output) are fixed and denoted with a bar above the variable. Similar in the case of the position-driven, inverse-dynamics scenario, all variables except for elbow angle (input) and the level of activation of a muscle (output) have been kept fixed (denoted by a bar above the variable). For the force-driven scenario, one assumes the external load as input and seeks the elbow angle as an output. Other input–output variable combinations are also feasible.

Note that due to the force–length characteristic within the skeletal muscle constitutive law, a change in elbow angle results in a modified muscle length and hence in a modified exerted muscle force even if the level of activation remains unchanged. The same applies if the muscle length remains unchanged, but the level of activation is modified. Hence, for each modification, one needs to solve the entire continuum-mechanical muscle models including the muscle–bone contact as the contact potentially has an impact on the muscle length and hence the exerted force.

2.6.1 Activation-driven, forward-dynamics solution scenario

For the activation-driven, forward-dynamics solution scenario, one seeks the resulting elbow angle for prescribed activation levels and a given external force. Prescribing arbitrary but fixed levels of activation for the biceps brachii and the triceps brachii, i.e. $\bar{\alpha }_B$ and $\bar{\alpha }_T$, respectively, and choosing an initial angle $\theta ^{(1)} \in [10^\circ ,150^\circ ] \ne \theta ^{(0)}:=60^\circ$, results in a non-equilibrium state and produces a resulting elbow moment (unless $\theta ^{(1)}$ has accidentally be chosen such the system would be in equilibrium). The resulting moment is determined by

$$\begin{aligned} M = B (\theta , \, \bar{\alpha }_B) \; l_B (\theta ) + T(\theta , \, {\bar{\alpha }}_T) \; l_T (\theta ) + \bar{F} \; l_F (\theta ) . \end{aligned}$$

(28)

For the solution process, in which the external force and the muscles’ level of activation are kept constant, a Newton iteration is employed to determine an improved approximation for the elbow angle, i.e. the next iteration step for the elbow angle, $\theta ^{(i+1)}$, is given by

$$\begin{aligned} \theta ^{(i+1)} = \theta ^{(i)} - \frac{M^{(i)}}{\frac{\partial M^{(i)}}{\partial \theta }} , \quad i = 1,\ldots n \, , \end{aligned}$$

(29)

to determine the next iterate for the elbow angle. Should $\theta ^{(i+1)}$ be outside the physiological range, i.e. $\theta ^{(i+1)} < 10^\circ$ or $\theta ^{(i+1)} > 150^\circ$, then the minimal or maximal physiological range value is prescribed. Since computing the analytical derivative of M with respect to $\theta$ is not really feasible and a numerical approximation, e.g. using an appropriate difference scheme, is computationally expensive, (i.e. requires the computation of the respective muscle forces for a perturbed $\theta$), the Newton’s method is replaced by the secant method, i.e. $\frac{\partial M^{(i)}}{\partial \theta }$ is approximated by the following differential quotient,

$$\begin{aligned} \frac{\partial M^{(i)}}{\partial \theta } \approx \frac{\Delta M^{(i)}}{\Delta \theta ^{(i)}} = \frac{M^{(i)} - M^{(i-1)}}{\theta ^{(i)} - \theta ^{(i-1)}} . \end{aligned}$$

(30)

As mentioned above, $\theta ^{(0)}$ is chosen to be $60^\circ$, while $\theta ^{(1)} \ne \theta ^{(0)}$ is chosen arbitrarily.

By prescribing realistic time-dependent activation levels for the respective muscles, one needs to solve at each time step the above equilibrium equations to obtain the activation-induced movement in the forward-dynamics simulation. As inertia terms were neglected, this forward-dynamics simulation approach only holds for relative slow movements.

Fig. 5

The resulting range of motion when considering contact and fully activated muscles. a $\theta = 10^\circ$. b $\theta = 45^\circ$. c $\theta = 80^\circ$. d $\theta = 115^\circ$. e $\theta = 150^\circ$

2.6.2 Position-driven scenario inverse-dynamics scheme

In case of the position-driven scenario/inverse-dynamics scheme, a desired angle $\theta$, and therefore the position of the forearm, the level of activation for one muscle and the external force F are prescribed. The goal of this scenario is to determine the level of activation of the non-prescribed muscle. Without any loss of generality, this section assumes that the level of activation for the biceps brachii is kept constant, while one seeks the level of activation for the triceps. Choosing an initial level of activation for the non-prescribed muscle, e.g. $\alpha _T \in [0,1]$, results in a non-equilibrium state. The resulting moment is determined by

$$\begin{aligned} M = B (\bar{\theta }, \, \bar{\alpha }_B) \; l_B (\bar{\theta }) + T({\bar{\theta }}, \, \alpha _T) \; l_T ({\bar{\theta }}) + F \; l_F ({\bar{\theta }}) . \end{aligned}$$

(31)

For the solution process, in which the external force, the biceps’ level of activation, and the elbow angle are kept constant, (29) is adapted for this scenario to

$$\begin{aligned} \alpha _T^{(i+1)} = \alpha _T^{(i)} - \frac{M^{(i)}}{\frac{\partial M^{(i)}}{\partial \alpha _T}} , \quad i=1,\ldots ,n , \end{aligned}$$

(32)

where $n\in \ \mathbb {N}$. Again, for practical purposes, the Newton’s method is replaced with its differential quotient

$$\begin{aligned} \frac{\partial M^{(i)}}{\partial \alpha _T} \approx \frac{\Delta M^{(i)}}{\Delta \alpha ^{(i)}_{T}} = \frac{M^{(i)} - M^{(i-1)}}{\alpha _{T}^{(i)} - \alpha _{T}^{(i-1)}} = \frac{T^{(i)} - T^{(i-1)}}{\alpha _{T}^{(i)} - \alpha _{T}^{(i-1)}} . \end{aligned}$$

(33)

To determine the differential quotient for $i=1$, the muscle activation, $\alpha _{T}^{(0)}$, is defined as $\alpha _{T}^{(0)}=| \alpha _{T}^{(1)}-0.01|$. Note, $F_T^{(0)}$ needs to be computed based on $\alpha _T^{(0)}$.

2.6.3 Force-driven scenario

Within the force-driven scenario, one assumes that the levels of activation for the biceps and triceps brachii remain constant. Now by varying the external force applied at the distal end of the forearm results in a change of elbow angle, i.e. an increase in F leads to a forearm extension, while a decrease in F leads the forearm to flex. The change of elbow angle resulting due to such a force perturbation can be solved in the same way as described in Sect. 2.6.1.

2.6.4 Stopping criteria

All the above-described iterations aim to find the moment equilibrium of the system. The system is considered to be in equilibrium, if the remaining moment of the system after the iteration, $|M^{(i+1)}|$ is less than a pre-described level of accuracy, $\epsilon$, i.e.

$$\begin{aligned} |\, M^{(i+1)} | \le \epsilon . \end{aligned}$$

(34)

Unless otherwise stated, $\epsilon$ is chosen to be $10^{-5}$ Nmm.

3 Results

3.1 Full range of motion

Due to the large range of motion, which is a result of all combinations of muscle activations and external loads, it is essential that the numerical scheme is solving the muscles’ deformation based on selected material parameters and assumed pre-stretches. To test the upper limb model’s robustness, the first numerical study aims to independently solve for each activation level and elbow angle, i.e. $10^\circ \le \theta \le 150^\circ$ with $\theta = 10^\circ + k\cdot 1^\circ$ and $k=0,\ldots ,140$ and $\alpha _j \in [0,1]$ for $\alpha _j = l\cdot 0.1$, for $l=0,\ldots ,10$ and $j\in \{T,B\}$, the respective deformation of the muscles, the exerted muscle forces, and the resulting contact forces. Snapshots of the selected muscle deformations are depicted in Fig. 5.

For the fully extended forearm, the triceps closely follows the shape of the humerus. At the distal end of the humerus, the gap between humerus and triceps is slightly larger. This is due to the fact that the boundary conditions describing the insertion of triceps brachii follow the circular movement of the olecranon and due to the fact that no boundary constraints are defined, which would pull the triceps towards the humerus, e.g. as the skin would do. While the forearm is flexing, the triceps stretches. Further, for the fully extended forearm, the biceps is fully stretched and forms a long slender muscle. The fully activated biceps is only in contact with the humeral shaft, if the elbow angle $\theta$ is less than $56^\circ$ or more than $139^\circ$. This contact increases the length of the biceps muscle. Flexing the forearm results in a shortened biceps and the belly of the biceps forms. Due to the applied circular movement at the insertion, the distance between the humerus and the biceps brachii increases and contact plays a minor role.

Fig. 6

Muscle reaction forces in the triceps (dashed blue curve) and biceps brachii (solid red curve) for activation $\alpha = 0.1 \cdot i$ with i being an integer and $i={0,\ldots ,10}$. The lowest curve is determined by $\alpha =0$ and the highest by $\alpha =1$

3.1.1 Muscle reaction forces within the overall system

Figure 6 depicts the absolute value of the muscle reaction forces for the biceps and triceps brachii for different activation levels throughout the full range of motion. The blue (dashed) curves denote the triceps reaction forces, while the red (solid) curves denote those of the biceps. The highest curves represent the resulting muscle reaction force for a fully activated muscle ($\alpha _j=1$, $j\in \{B,T\}$), while the lowest curves depict the purely passive mechanical behaviour ($\alpha _j=0$, $j\in \{B,T\}$) of the respective muscles.

The maximum triceps reaction force is reached between 115$^\circ$ and 120$^\circ$ depending on the level of activation. For the fully activated triceps, the maximal value is $T(115^\circ , 1.0)=1123\,$N, while the maximal value for the purely passive behaviour is $T(118^\circ ,0.0)=508.2\,$N. The biceps reaction force is monotonically decreasing and reaches its maximal force values for $B(10^\circ , 1.0)=663.3\,$N and its minimal value for $B(10^\circ , 0.0)=340.2\,$N. Note, the pre-stretch is chosen such that the muscle reaction force is positive for the shortest muscle length.

Fig. 7

Active contribution to the total muscle force for the entire range of motion and activation levels $\alpha _j = 0.1 \cdot i$ with i being an integer between 1 and 10 and $j\in \{T,B\}$. Again, the dashed blue line represents the contributions of the triceps and the red solid line the ones from the biceps

The purely active force contribution of a muscle is obtained by subtracting the passive muscle force from the total one (cf. Fig. 7). Depending on the level of activation, the optimal elbow angle for the triceps brachii ranges between $\theta = 109^\circ$ (for $\alpha _T=$ 0.1 and 0.9) and $\theta = 123^\circ$ (for $\alpha _T=$ 0.8). For the biceps brachii, the optimal elbow angle ranges between $\theta = 51^\circ$ (for $\alpha _T=$ 1.0) and $\theta = 72^\circ$ (for $\alpha _T=$ 0.1). From Fig. 7, one clearly sees that both muscles mainly act for the largest portion of the physiological range of motion on the ascending limb of the force–length relationship, i.e. the muscle force predominantly increases if the muscle is being stretched. Based on these force values, the resulting muscle moments are computed and plotted in Fig. 8.

Fig. 8

The joint moment is a product of the muscle lever arm and the muscle reaction force. The contribution of the triceps and biceps brachii for the entire range of motion and activation levels are depicted in solid red and dashed blue line, respectively. The curve with the lowest absolute value belongs to $\alpha =0$ (passive-only response) and raises in $\Delta \alpha = 0.1$ steps up to $\alpha = 1$ (fully active) for each muscle

The blue (dashed) curves represent the moments for the triceps brachii, and the red (solid) curves those for the biceps brachii. As the two muscles are agonist and antagonist, the resulting moments in Fig. 8 have the opposite sign. The resulting lever arm is dominated by the resulting muscle reaction force because the lever arm is minimally changing for both muscles. For the triceps brachii, a maximal moment of $-26.1 \,$Nm is obtained for $\theta =103^\circ$ and $\alpha _T=1$, while a minimal moment of $-0.88\,$Nm is obtained for $\theta =10^\circ$ and $\alpha _T=0$. The biceps generates its maximal moment ($25.8 \,$Nm) at an elbow angle of $\theta =15^\circ$ and $\alpha _T=1$, while its minimal moment is close to zero and obtained at $\theta =150^\circ$ and $\alpha _T=0$.

3.1.2 Contact forces developing within the overall system

Depending on the elbow angle, the contact forces between the muscles and the bone can be significant. Figure 9 depicts the normalised exerted muscle forces of the biceps and triceps brachii and its contact forces with the bone. For better comparison, the exerted muscle forces have been normalised with respect to the maximal exerted muscle force of the respective muscle. Further, the contact forces, depicted in Fig. 9, have been normalised with respect to the exerted muscle force at the corresponding elbow angle.

Fig. 9

Normalised exerted muscle forces versus contact forces for the entire range of motion assuming fully activated muscles. The muscle reaction force are normalised by the muscle’s maximum muscle force and the contact force is normalised with the exerted muscle force at the corresponding elbow angle

In general, the contact forces increase with increasing elbow angle. For the fully activated triceps brachii, the contact force reaches its maximal value at an elbow angle of $150^\circ$. At this angle, the contact force is 70.4% of the exerted muscle force that is equivalent to a contact force of 710 N. At $\theta =115^\circ$, which is the elbow angle at which the triceps brachii generates under fully activated conditions its highest force, the contact force is still 23.3% of the exerted muscle force.

Since no surrounding tissue was considered within this work, one would expect higher contact forces between the biceps brachii and the bone if further muscles or other surrounding tissue would also be considered. Nevertheless, at small and large elbow angles, i.e. at $10^\circ$ and at $150^\circ$, the contact force is still 41.6 and $11.0\%$ of the respective exerted muscle force.

3.2 Local impact of muscle–bone interaction on fibre distribution

As existing forward-dynamical models almost entirely appeal to Hill-type skeletal muscle models that cannot take into account the heterogeneity of the fibre direction within a muscle and the contact between muscles and bone, little is known about the impact of muscle–bone interactions on these quantities. A suitable possibility to visualise the impact of muscle–bone contact on the muscle fibres is to compare the magnitude of the fibre stretches resulting from simulations that consider contact with those that do not consider contact. To compare the two scenarios with each other, the fibre stretch is determined in each element at each of the 27 integration points of the respective Gauss–Legendre quadrature scheme with 3 Gauss points in each element coordinate direction. Figure 10a–d depicts the differences between the computed fibre stretches, i.e. the differences between the fibre stretches obtained from simulations considering contact and from those that did not include any contact formulation. The aim of Fig. 10 is to provide a spatially distributed view on the impact of the contact formulation on the muscle mechanics.

Fig. 10

The differences in fibre stretch at each integration point obtained from simulations considering contact and from such simulations that did not include any contact formulation. a Fully extended, $\theta =10^\circ$, and $\alpha =0$. b Fully extended, $\theta =10^\circ$, and $\alpha =1$. c Fully flexed, $\theta =150^\circ$, and $\alpha =0$. d Fully flexed, $\theta =150^\circ$, and $\alpha =1$

The impact of muscle–bone contact is most significant when the muscles are fully stretched, i.e. when the triceps and biceps are in the fully flexed or fully extended position. One can observe that the influence of the muscle–bone contact increases with an increase in the level of activation. To prevent penetration of the muscles through the bone, the contact acts as a force boundary condition pushing the muscles outward. Hence, the medial fibres are restrained and the lateral ones are stretched. As a result, the differences in fibre stretches tend to be positive in the lateral region, while they are negative in the medial region.

Figure 10a, b depicts the influence of contact on the fibre stretch for the fully extended arm. In this position, the contact force between the triceps and the bone is less than 5% of the respective muscle reaction force. Therefore, the influence of contact on the fibre stretches of the triceps is minimal. This is not true for the biceps. In the proposed model, the biceps exhibits its strongest contact forces in the fully extended position. Therefore, the influence of contact on the biceps’ fibre stretch is more pronounced. This causes the fibre stretch to decrease in regions far from the bone and to shorten in regions close to the bone/contact. As stated above, the effect increases with increasing activation levels (cf., Fig. 10b).

Figure 10c, d depicts the case in which the triceps is fully stretched and the contact forces between the triceps and bone are at its maximum. The triceps needs to bend around the distal head of the humerus. This bending causes an increase in muscle length. Most effected by this change in length are the regions far from the bone. In these regions, the fibre stretch increases if compared to the fibre stretches resulting from simulations not including contact. In regions close to the bone, the fibre stretch decreases.

3.3 Convergence studies

While the previous sections focused on the mechanical behaviour of the involved muscles for a large range of muscle activities and elbow angles, the next sections focus in determining equilibrium (cf. Sect. 2.6). For this purpose, the equilibrium solution for a particular set of activation parameters $\alpha _T$ and $\alpha _B$, initial angle $\theta$, and applied force F is determined. This equilibrium solution shall serve as reference solution throughout this work. To do so, three of the four DoFs are prescribed in order to solve for the remaining one, i.e. by choosing $\theta ={\bar{\theta }}$, $\alpha _T={\bar{\alpha }}_{T}$, and $\alpha _B={\bar{\alpha }}_B$, one can easily solve for the external force by

$$\begin{aligned} \bar{F} ({\bar{\theta }}) = - \frac{B ({\bar{\theta }}, \, {\bar{\alpha }}_{B}) \; l_B ({\bar{\theta }}) + T({\bar{\theta }}, \, {\bar{\alpha }}_{T}) \; l_T ({\bar{\theta }})}{l_F ({\bar{\theta }})} . \end{aligned}$$

(35)

By choosing ${\bar{\alpha }}_T = 0.29$, ${\bar{\alpha }}_B=0.8858$, and ${\bar{\theta }}= 70.0^\circ$, one obtains exerted muscle forces for the biceps and triceps brachii of $B({\bar{\theta }},{\bar{\alpha }}_{B})=451.9$ N and $T({\bar{\theta }},{\bar{\alpha }}_{T})=483.3$ N, respectively. Based on these computed muscle force values and the respective moment arms, i.e. $l_T({\bar{\theta }})=-25.5$ mm, $l_B({\bar{\theta }})=40.2$ mm, and $l_F({\bar{\theta }})=265.5$ mm, one obtains for the static equilibrium an external force $\bar{F}= 22.0\,$N (cf. Eq. 35). Remember, the four DoFs marked with $({\bar{\cdot }})$ build the reference solution for the subsequent simulations.

3.3.1 Perturbations to the reference solution

The first numerical tests aim to solve for equilibrium after perturbing individual values. In the first case, the level of activation for the triceps is perturbed, while the other DoFs maintain its initial values, i.e. ${\bar{\theta }}$, ${\bar{\alpha }}_{B}$, and $\bar{F}$. Note, any perturbation from the reference solution leads to a nonzero resulting moment. The first numerical test investigates the behaviour of the iteration procedure proposed in Sect. 2.6.2. The aim is to iterate from the perturbed level of activation of the triceps to its level of activation of the initial elbow position, i.e. the position, in which the musculoskeletal system is in equilibrium.

Table 2 Results for the individual iterations necessary for achieving equilibrium after perturbing $\alpha _T$ from 0.29 to 0.20 and keeping the remaining DoFs, i.e. $\bar{F}= 22\,$ N, $\bar{\alpha }_B=0.8858$, $\bar{\theta }=70^\circ$, and ${\epsilon }= 10^{-5}$  Nmm, fixed

To do so, $\alpha _T$ is (randomly) chosen to be 0.20 (instead of $\alpha _T=0.29$, which would provide equilibrium as pre-computed for the reference solution). The results of the iteration process as proposed in Sect. 2.6.2 are shown in Table 2. This particular perturbation (i.e. the perturbation of $\alpha _T$ from 0.29 to 0.20) results in an initial residual moment of −1375 Nmm. After only two iterations, the level of activation of the triceps brachii deviates by less than 1% from its ground truth. After four iteration steps, the resulting moment has decreased to $M=0.17\,$Nmm. The stopping criteria, $\epsilon =10^{-5}$ Nmm in Eq. (34), are reached after seven iteration steps. The system is considered to be in equilibrium. Note, since the elbow position and the level of activation of the biceps have not been changed, the exerted biceps force does remain constant.

In the second scenario, the activation level of the biceps brachii has been perturbed from ${\bar{\alpha }}_B=0.8858$ to $\alpha _B=0.56$. The remaining DoFs are kept fixed, and the iteration process for a position-driven scenario (cf. Sect. 2.6.2) is employed. The results are shown in Table 3. Within this test case, there exists an initial resulting moment of 4.023 Nmm. After five iteration steps, the absolute value of the resulting moment is less than 0.05 Nmm and the level of activation deviates from its exact solution by less than 0.2%. After six iteration steps, the convergence requirement is met. This test case requires one iteration step less than the previous one. However, the relative perturbation of the second test case, $\Delta \alpha _B = 0.3258$, has been much larger than the relative change of the first test case, $\Delta \alpha _t = 0.09$.

Table 3 Results for the individual iterations necessary for achieving equilibrium after perturbing $\alpha _B$ from 0.8858 to 0.56 and keeping the remaining DoFs, i.e. $\bar{F}= 22\,$ N, $\bar{\alpha }_T=0.29$, $\bar{\theta }=70^\circ$, and ${\epsilon } = 10^{-5}$  Nmm, fixed

Similar results are observed, for only perturbing the initial angle and fixing the levels of activation, $\alpha _T$ and $\alpha _B$, and the external force, F. To demonstrate this, the angle $\theta$ is perturbed from ${\bar{\theta }}=70^\circ$ to $\theta =61^\circ$, while the remaining DoFs remain as in the reference solution. The results for employing the iterative procedure described in Sect. 2.6.1 are presented in Table 4.

Table 4 Results for the individual iterations necessary for achieving equilibrium after perturbing $\theta$ from ${\bar{\theta }}$ to $\theta =61^\circ$ and keeping the remaining DoFs, i.e. $\bar{F}= 22$ N, $\bar{\alpha }_T=0.29$, $\bar{\alpha }_B=0.89$, and ${\epsilon } = 10^{-5}$  Nmm, fixed

After perturbing the elbow angle, the resulting moment is −3.784 Nmm. After the first iteration, the angle deviates from the reference solution already by far less than 1$^\circ$. While the absolute difference of the angle $\theta$ between the second iteration and the exact solution is approximately $0.122^\circ$, the stopping criteria based on the moment ($|M^{(i)}|<10^{-5}\,$Nmm) are reached completing the fourth iteration. As the exerted muscle force of both muscles depends on the elbow angle and the contact between the muscle and bone, the muscle forces for both muscles need to be re-computed at every iteration step.

3.3.2 Time-dependent activation levels

In the following, the input to the proposed upper limb model is a time-dependent activation level for the biceps brachii, $\alpha _B(t)$. While the level of activation for the biceps brachii can change with time, the triceps brachii’s level of activation and the external force remain constant: they are $\bar{\alpha }_T(t) \equiv 0.09$ and $\bar{F}(t) \equiv 44\,$N, respectively. To demonstrate the capability of producing activation-driven movements, three distinct levels of activation for the biceps brachii are chosen as input to the activation-driven approach. Within this section, one assumes that evaluating $\alpha _B(t)$ at $t_1$, $t_2$, and $t_3$ (with $t_1< t_2 < t_3$) results in $\alpha _B(t_1)=0.8858$, $\alpha _B(t_2)=0.32$, and $\alpha _B(t_3)=0.65$, see Fig. 11. The initial elbow angle was chosen to be $\theta =60^\circ$. The results of this simulation are presented in Table 5. Note that the converged result of one time step is used as the initial step for the iteration procedure of the next time step.

Fig. 11

Three arbitrarily chosen time incidents ($t_1$, $t_2$, and $t_3$) of an arbitrarily chosen activation dynamics $\alpha _B(t)$ versus time, t

Table 5 Results for the individual iterations by prescribing a time-dependent activation level for the biceps brachii

In this example, a maximum of 7 iterations per time instance were needed to satisfy the stopping criteria, i.e. Eq. (34) with $\epsilon = 10^{-5}$  Nmm. For the initial biceps’ level of activation, $\alpha _B(t_1)=0.8858$, only 4 iterations were necessary to achieve convergence. The resulting elbow angle was $\theta =57.469^\circ$. For the second and third time instance, $t_2$ and $t_3$, convergence was achieved after 6 and 7 iterations, respectively. The resulting elbow angles were $\theta =38.273^\circ$ and $\theta =50.097^\circ$.

Figure 12 depicts the residual moments on the left ordinate (semi-log) and the elbow angle (normal) for each iteration step of the above-described test case.

Fig. 12

Convergence history for the time-dependent activation case. The chosen level of accuracy, $\epsilon =10^{-5}$ Nmm, with respect to the residual moment is indicated by the horizontal red line

4 Discussion

So far, continuum-mechanical investigations of parts of the musculoskeletal system have predominantly focused on investigating bone mechanics or on the mechanical behaviour of skeletal muscles in isolation. Continuum-mechanical models of musculoskeletal systems have been hardly considered due to the significant increase in computational cost and increased model complexity. The proposed framework is the first one that provides the basis for simulations of musculoskeletal systems, in particular for forward-dynamics simulations of musculoskeletal systems, in which all components are represented as volumetric objects and in which the mechanical behaviour of the muscle–tendon complex is modelled using principles of three-dimensional continuum mechanics. This work demonstrates the feasibility of using three-dimensional skeletal muscle models and considering tissue–tissue interaction. This new modelling approach provides the basis for a better understanding of joint loading and, hence, for biomechanically informed implant designs or prosthesis. However, further research is needed to achieve forward-dynamics simulation of multi-muscle musculoskeletal systems. In particular, the ability to couple the proposed framework to other forward-dynamics methodologies capable of predicting time-dependent individual muscle activation levels, e.g. by using state-of-the-art control algorithms, will be needed.

4.1 Pre-stretch, optimal fibre length, and moment arms

4.1.1 Pre-stretch and its influence on optimal fibre length

When using skeletal muscle models in isolation, the pre-stretch, and, hence, the true reference configuration, plays a minor role. For example, the overall conclusion drawn from studies investigating the influence of anatomical or physiological parameters on the mechanical behaviour of the muscles, such as revealing the causes of non-uniform strains in the biceps brachii (Blemker et al. 2005), investigating the muscle–aponeurosis interaction (Chi et al. 2010), exploring micro-mechanical effects of fibre and fascicle geometry (Sharafi and Blemker 2010), or determining the influence of compartmentalisations within skeletal muscles (Heidlauf and Röhrle 2014), would still hold if these studies would have made different assumptions on the pre-stretch. This is no longer the case within models predicting the mechanical loading of musculoskeletal systems. Within a musculoskeletal system, the evaluation of the muscle reaction force does not only depend on the strongly nonlinear skeletal muscle constitutive law, but also on the choice of the initial configuration of the skeletal muscles.

This is due to the well-known force–length relationship of skeletal muscles, which was introduced in Eq. (12). By modifying the initial pre-stretch of one of the muscles, the respective muscle would produce a different force for a particular joint position. This in turn results in a different equilibrium position and would alter the muscle length(s) of the other muscle(s). Hence, modifying the pre-stretch of one muscle leads to an elbow position and ultimately to a different motion. As a consequence of altering the pre-stretch, one might not even be able to achieve the full range of motion for physiological loads. It should be mentioned that a simpler constitutive law for the skeletal muscle tissue, i.e. a neo-Hookean model for the passive part and a quadratic function for the force–length relationship, would have suffice for this study.

For in silico studies, it is essential to appropriately describe the reference configuration of the respective muscles within the musculoskeletal system. One might think that the reference configuration can be deduced from the state at which the musculoskeletal system’s acts in an ”optimal” mechanical sense. However, to the authors’ knowledge, there is no unique definition for describing the state in which a muscle acts on a joint maximally. The muscle’s optimum can be either defined when the muscle reaction force is maximal, when the active contribution of the muscle reaction force is maximal, when the moment of one muscle acting on a joint is maximal, or when the moment of all muscles acting on a joint is maximal.

4.1.2 Moment arm interpretation and calculation

As far as the entire musculoskeletal system is concerned, there exist experimental studies that aim to determine the mechanical behaviour of the entire system. For the upper limb, there exist studies that aim to experimentally determine the elbow angle at which the elbow torques are at its maximum. However, there is quite a large spread. Amis et al. (1980), for example, report an elbow angle of $60^\circ$, while Buchanan et al. (1998) report an angle of $100^\circ$. Moreover, knowing the maximal elbow torque still does not provide any information on the muscles. Computational models, which might be at times subject to quite restrictive assumptions, need to be employed in order to determine muscle-specific properties, albeit for the knee, Lloyd and Besier (2003) use, for example, a Biodex Medical Systems (2006) dynamometer and an EMG-driven musculoskeletal model to determine muscle-specific properties and moment arms.

For the proposed continuum-mechanical upper limb model, the extracted lumped parameters are in good agreement with the literature data. For example, the resulting muscle forces obtained for the full range of motion and for the full range activity levels (cf. Fig. 6) agree well with the data published by Murray et al. (2000). Further, the range of operation for the biceps and triceps brachii is similar. The optimal elbow joint angle for which each of the muscles produces its maximal force is always towards the longest muscle length. For the triceps, this is the case when the forearm is fully flexed and for the biceps when the forearm is fully extended. The presented data also agree well with the in silico studies of Buchanan et al. (1986, 2004) and Manal and Buchanan (2003). Although not a rigorous validation, this comparison provides computational justification that the developed model and the presumed pre-stretches are reasonable.

In addition to determining the optimal fascicle/muscle lengths, the calculation of the muscle lever arms has a strong impact on the resulting muscle moment. This work bases the calculation of the lever arms on the tendon-displacement method published by An et al. (1984). This method is widely used and the resulting lever arms are generally accepted and the lever arms computed based on the proposed continuum-mechanical upper limb model within this work compare well with the literature (An et al. 1989; Murray et al. 1995). The main drawback of the tendon-displacement method, however, is that it cannot take into account dynamically changing mechanical behaviour such as the orientation of the muscle reaction force or the contact-induced alterations of the muscle’s point of action. Since a continuum-mechanical approach provides such data in a natural way, one could have used within the proposed model a more accurate mathematical description of the muscle lever arms. However, by choosing a different lever arm method, one would have unnecessarily complicated the comparison between the proposed model and existing literature data. Moreover, one would have had to carry out a detailed analysis on the impact of using a different muscle lever arm method than the tendon-displacement method. This would have been beyond the scope of this work.

Next to the constitutive laws, lever arms, and a muscle’s pre-stretch and optimal fibre length, the fact that only one antagonistic muscle pair has been considered within this work probably influences the maximal elbow torque the most. Clearly, the maximal elbow torque is due to the interplay of several muscles acting at the same time. Hence, the use of a two-muscle system limits the ability to (rigorously) verify the proposed model with respect to experimentally measured maximal elbow torques.

4.2 Contact

In comparison with a multi-body-dynamics simulation, the proposed continuum-mechanical approach has multiple advantages. One of the major advantages is that contact between muscle and bone is naturally considered. In case that the considered musculoskeletal muscle model would not only consist of an agonist–antagonist muscle pair, e.g. if the proposed upper limb model would be extended by including the brachialis, one could additionally study the influence of the contact between the muscles. The same would apply, if one would extend the upper limb model by considering the other upper limb muscles, the fatty tissue, and the skin. Since this study only considers the biceps muscle, significant contact forces are only obtained for the fully activated muscle and for elbow angles $\theta < 30^\circ$. This result is not further surprising since the biceps is a superficial muscle and no other muscles than the biceps and triceps brachii have been considered. For the triceps brachii, which is considered to be the only extensor muscle, the area, in which the triceps brachii is in contact with the humerus, is considerable. This is particularly true for the area nearby the olecranon. The olecranon acts as a (dynamic) pulley and contact forces reach up to 750 N.

It is obvious that the contact between the muscle and the bone influences the deformation of the respective muscles. As depicted in Fig. 10, the contact causes spatial changes in the muscle fibre stretches. Since the fibre stretch directly influences the force-generating capabilities of the muscle through the force–length relationship, the resulting muscle forces change due to the contact. Although this effect is not deniable (Siebert et al. 2014), the error introduced by assuming a phenomenological constitutive law is most likely more significant.

The influence of the contact probably influences more the muscle force direction than the actual magnitude of the muscle force. This is due to the geometry of the system and due to the muscle attachment areas. The dynamics of changing muscle force directions due to geometrical constraints cannot be captured within multi-body simulations, straightforwardly. The deviations in the muscle force direction can only be taken into account through pulleys.

Another aspect, not yet discussed, is the influence of transversal muscle forces on the joint forces. Through muscle–bone contact, the muscle forces, mainly acting along the bones in longitudinal direction, introduce transversal forces at contact region. This transversal force has the potential to compress adjacent joints, which are crossed by the respective muscles. With that effect, it is plausible that joint stiffness is not only dependent on the longitudinal forces acting over the muscles’ and ligaments’ lever arms on both sides of the joint, but also depend on the transversal force originating from the muscle–bone contact. The proposed model described in this contribution can take that effect into account and is therefore better in representing the biological situation.

4.3 Limitations and opportunities of the upper limb model

4.3.1 The constitutive description

The resulting contact forces depend of course also on the continuum-mechanical descriptions of the involved tissues. The bone is considered to be rigid. Given the difference in the stiffness between the involved tissues, this is certainly a reasonable assumption. One would only expect small errors due to this assumption.

The constitutive law for the muscle tissue is state of the art. Unfortunately, there is hardly any experimental data on whole muscles that would provide a better basis for fitting the material parameters of the proposed constitutive laws, i.e. for a continuum-mechanical model of a skeletal muscle that consists of a tendinous regions, of a tendon–muscle transition zone, and of actively contracting muscle tissue. The major advantage of the proposed constitutive law is that only two more parameters ($\gamma ^{{M}}$ and $\gamma ^{\mathrm{\mathrm ST}}$) are introduced to describe the mechanical behaviour of the muscle, tendon, muscle-tendon transition zone as well as other soft tissue, i.e. fat. While the material parameters have been individually fitted to experimental data, the geometrical demarcation of these three zones is rather abrupt and based on experience rather than imaging data. More research needs to be carried out to improve the overall mechanical descriptions of such models. However, since this work focuses on developing the framework for forward-dynamics simulations, and since the resulting muscle forces are reasonable, no further investigations in improving the constitutive laws have been made within this work.

4.3.2 Modelling muscle recruitment

A similar argument applies to modelling the muscles’ activation. It is presumed to be homogeneous throughout the muscle tissue. Skeletal muscle recruitment, however, is quite complex and heterogeneous. Nevertheless, the framework is set up in such a way that more complex and realistic musculoskeletal muscle models could also be employed. For example, the purely continuum-mechanical model could be replaced with a more detailed chemo-electromechanical model as, for example, proposed by Röhrle et al. (2012) or Heidlauf and Röhrle (2013, 2014). The same also applies, if one would aim to substitute the pre-described levels of activation by biophysical recruitment models (e.g. Heidlauf et al. 2013). One of the key advantages of employing chemo-electromechanical models within such a framework would be the fact that one could predict (surface) EMG in a straight forward fashion (Mordhorst et al. 2015). Since surface EMG can be easily collected and recorded on the biceps, the computed virtual surface EMG data could be used to either validate the (recruitment) model or to drive the model.

4.3.3 Computational cost

Using such detailed multi-scale models to determine the exerted muscle force would significantly increase the computational costs. One would most likely need a significant-sized high-performance computing cluster in order to obtain solutions in acceptable times. The additional computing cost is, however, mainly due to an increase in model complexity for computing the respective muscle reaction forces and not necessarily for determining the equilibrium position. The number of Newton iteration steps per equilibrium is expected to remain similarly.

The overall number of Newton iterations could be significantly reduced by adjusting the level of accuracy. Considering the presented moments within the system, a moment threshold of $\epsilon =10^{-5}$ Nmm could be considered as too excessive. A threshold of $\epsilon$ = 1 Nmm should suffice without introducing too much error within the system.

4.4 Model validation

Model validation will be a very challenging objective for the proposed musculoskeletal system simulations. Just like for multi-body simulations, experimentally measuring mechanical data during motion that could be used to (indirectly) validate the mechanical behaviour of the muscles within a musculoskeletal system hardly exist. However, if the presented continuum-mechanical skeletal muscle model is replaced by an chemo-electromechanical model and if realistic recruitment patterns could be determined (either through motor unit decomposition of high-density EMG signals or through biophysical motor neuron models), one could potentially achieve some validation of the proposed work by linking in silico EMG signals with measured EMG data and arm motion. This, however, would come with a significant increase in computational time. Depending on the number of considered fibres, the chemo-electromechanical models would require significant computational time for a single muscle force calculation. Since the proposed solution strategies, e.g. Sect. 2.6.1, requires for each time step several skeletal muscle force solves, the computational time would significantly increase.

A further possibility of validating such a framework could include a change of musculoskeletal system. If one considers instead of a normal subject a subject with an amputation, new possibilities for validation arise. This is due to the fact that the amputation leads, from a mechanical point of view, to a non-constrained joint at its distal end. Since the bone is no longer constrained, measuring contact pressure, determining the EMG signal and tracking the bone and overall limb movement, could potentially provide an unique set of data to validate a musculoskeletal system model similar to the proposed one. This, however, is beyond the scope of the current work.

Furthermore, since this framework appeals to a three-dimensional framework, potential means of validation could also be by means of cine DENSE dynamic magnetic resonance imaging (MRI) [cf. Fiorentino et al. (2012)], which provides means to determine the strain by means of MRI. However, to the best knowledge of the authors, such data do currently not exist for dynamic movements.

4.5 Outlook and summary

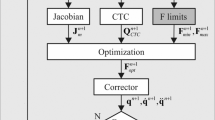
The focus of this work was on establishing an extendable framework that initially focused on a one DoF hinge joint, an antagonistic muscle pair, and a simplified moment equilibrium equation. This setup was chosen such that no muscle redundancy problem needed to be solved. The forward-dynamics simulations are achieved through prescribing time-dependent input variables. To solve the muscle redundancy problem, the proposed framework needs to be coupled to other frameworks that are currently capable of solving the redundancy problem, e.g. rigid-body simulations. Coupling the proposed continuum-mechanical framework with rigid-body simulations can be seen as a predictor–corrector method (Röhrle et al. 2013). In this sense, the multi-body simulations would provide a prediction of the muscle activation and movement, while the continuum-mechanical model would provide the correction due to the geometrical constraints of the model, i.e. the contact between muscle and bone. Moreover, the continuum-mechanical model could provide improved lines of action to the rigid-body simulations in order to improve their model validity. Moreover, the proposed framework has great potential for investigating and hypothesis testing of the mechanical behaviour of different skeletal muscle properties. For example, each phenomena that has so far been studied only skeletal muscles in isolation (essentially all research that has been utilising three-dimensional continuum-mechanical FE skeletal muscle model to investigate mechanical behaviour of skeletal muscles) can now be tested in what-if scenarios within a musculoskeletal system.