1 Introduction

Cancer is a complex disease involving primarily uncontrolled cell proliferation and migration to distant regions of the body (Longo et al. 2011). From the second half of the last century, the scientific community has become more and more aware of the difficulties that arise when treating this illness. Nowadays, it is clear that a combined effort from all the physical sciences is necessary to advance our understanding of the disease and promote the discovery of new cures (Michor et al. 2011; Leder et al. 2014). The pioneering works of Greenspan et al. (1976) paved the way for the development of mathematical models that could investigate the basic principles underlying cancer progression and predict the outcome of therapies. Most continuum models, as the one presented in this work, deal with the avascular phase of tumor growth.

During this stage of cancer progression, a small cluster of cancer cells arises in a healthy tissue due to mutations that alter their biochemical pathways. This small region of abnormal cells grows at the expense of the host counterpart, nourished by oxygen and nutrients that diffuse from the vasculature nearby (Jain 1988; Grantab et al. 2006). At a certain point, the external nutrients are not enough to sustain the expansion of the growing mass, leading to the formation of cell proliferation gradients starting from the outer regions of the tumor. As time passes by, cancer cells at the center of the tumor experience severe hypoxia and critical conditions that lead to the death and consequent necrosis of some of them. Finally, a steady state arises, where cell proliferation at the tumor border balances cell death at the tumor center (Folkman and Hochberg 1973). The subsequent stage of cancer progression is termed the vascular phase, where tumor cells recruit new blood vessels from the host vasculature through tumor angiogenesis. In this second stage, the cancer resumes its previous growth and eventually enters the last stage of the illness, the metastatic phase, where malignant cells evade the tumor area to form metastases at distant regions of the body.

Since the study of the first stage can be performed in a more controlled experimental setting, a large set of literature is devoted to the analysis of avascular tumor growth in vitro. Experiments are usually carried out on tumor spheroids, three-dimensional aggregates of cancer cells that grow in an approximately spherical shape (Sutherland et al. 1971; Kim et al. 2010; Vinci et al. 2012; Mikhail et al. 2013). The investigations on tumor spheroids allow evaluating the extent of the gradients of nutrients and cell proliferation, and more recently, the action of a mechanical stress exerted on the cell aggregates. Helmlinger et al. (1997) grow tumor spheroids in gels with varying stiffness and report a decrease in proliferation for stiffer gels. Another example of spheroids grown in gels with varying stiffness is found in Kaufman et al. (2005). There, cell proliferation and motility are investigated for different concentrations of collagen in the gel matrix. In that work, a positive correlation between increasing concentrations of collagen and cell invasion is reported, followed by an opposite effect on the growth of the spheroids. The original work of Helmlinger is extended in Cheng et al. (2009), where the authors perform similar experiments and introduce new tools to quantify spheroid deformation and variations in cell proliferation and apoptosis. Another set of experiments is presented in Desmaison et al. (2013), where tumor spheroids are subjected to asymmetric stress fields by the use of microstructured substrates. Finally, Montel and Delarue in two subsequent papers (Montel et al. 2011; Delarue et al. 2014) apply mechanical forces on the surface of tumor spheroids through the osmotic effect of Dextran solutions with different concentrations. All these studies report a decrease in tumor cell proliferation as a consequence of the applied stress, even though they are carried out via different experimental configurations.

The earliest continuum models applied to spheroid growth focus on the dependence of cell proliferation on nutrients and other biochemical factors, as reported in the comprehensive reviews of Preziosi and Tosin (2009a), Lowengrub et al. (2010). They are based on mass balance laws for cells and advection–reaction–diffusion equations for nutrient evolution. Later, models include more components and the mechanical interaction between them. For these cases, which are usually defined in the framework of mixture theory or porous media theory, momentum balance equations and constitutive relations are needed for describing the mechanical response of each component (Ambrosi and Mollica 2004; Preziosi and Tosin 2009a; Ehlers et al. 2009; Giverso et al. 2015). Among the first, (Chaplain et al. 2006; Galle et al. 2009) incorporated the effect of mechanical stress on cell proliferation obtaining results matching experimental observations. There followed several papers, where this example of mechanotransduction is investigated with similar approaches (Kim et al. 2011; Ciarletta et al. 2013a, b; Mpekris et al. 2015).

This work arises as an extension of the modeling framework presented in Sciumè et al. (2013b). The model is specialized for tumor spheroids, and the solution procedure is simplified, as all the new equations are formulated in spatial coordinates with no need of a reference configuration.

A set of experiments is carried out on spheroid cultures to validate the equations. The comparison with the experiments is performed both with spheroids growing freely in the culture medium and subjected to increasing mechanical loads, giving in each case a good match. The experiments suggested the presence of a “master curve,” a common growth curve underlying the spheroid growth dynamics. Finally, a new constitutive relation is proposed to describe the inhibitory effect of the stress on cell proliferation, with a better performance in terms of matching the experimental results when compared to the existing laws in the literature.

The rest of the paper is organized as follows. Section 2 introduces the mathematical framework, based on the thermodynamically constrained averaging theory (TCAT), and the differences with the original model. In the last part of that section, the equations are specialized to the case of tumor spheroids. Section 3 presents the experimental setup for the two culturing conditions. Finally, results from the simulations are presented in Sect. 4, and the discussion follows in Sect. 5.

2 A biphasic tumor model

This mathematical model is developed in the framework of the porous media theory, and the governing equations are derived through the TCAT (Gray and Miller 2005, 2014). We start by defining the problem in terms of microscopic relations among the constituents. The TCAT approach is used to transform these microscopic laws into mathematically and physically consistent macroscale relationships, which describe the tumor at the tissue scale. By doing so, the complexity due to the high spatial variability at the microscale is overcome, and equations for average quantities describing the tumor behavior are formulated directly. The closed form of the problem is finally obtained by introducing constitutive relations into the macroscale conservation equations. Detailed information about the mathematical model and its derivation are found in previous work of the authors (Sciumè et al. 2013b, a, 2014). In this work, we describe the behavior of the following constituents or phases: (i) the tumor cells (TCs), which partition into living (LTCs) and necrotic (NTCs) cells, and (ii) the interstitial fluid (IF) (Fig. 1). The extracellular matrix (ECM) is considered together with the tumor cells, and the union of the two entities constitutes the solid skeleton of the tumor. The interstitial fluid phase flows through the pores of this solid matrix, carrying nutrients, growth factors, and waste products. Cell proliferation is related to nutrient concentration, whereby cells stop to proliferate and, after some time, undergo necrosis and lysis, if subjected to low levels of nutrients or high levels of mechanical stress. In the following equations, t will denote the union of the tumor cells and ECM and l the interstitial fluid.

Fig. 1
figure 1

Constituents of the biphasic system

Full size image

2.1 The governing equations

The solid portion of the tumor is modeled as a porous solid with porosity \(\varepsilon ^{l}\), and its volume fraction is defined as \(\varepsilon ^{t}=1-\varepsilon ^{l}\). Hence, the interstitial fluid occupies the rest of the volume, and the sum of all the volume fractions has to be unity:

$$\begin{aligned} \varepsilon ^{t}+\varepsilon ^{l}=1 \end{aligned}$$
(1)

We write the governing equations for the tumor volume fraction \((\varepsilon ^{t})\), the interstitial fluid pressure \((p^{l})\), the nutrient mass fraction \((\omega ^\mathrm{ox})\), and the necrotic mass fraction \((\omega ^\mathrm{Nt})\). These equations are obtained from the general form of the mass and momentum balance equations of phases and species, according to the TCAT derivation.

The mass balance equations for the phases are written as:

$$\begin{aligned}&\frac{\partial \left( {\varepsilon ^{t}\rho ^{t}} \right) }{\partial t}+\nabla \cdot \left( {\varepsilon ^{t}\rho ^{t}{} \mathbf{v}^{t}} \right) -\mathop {M}\limits _\mathrm{growth}^{l\rightarrow t} +\mathop {M}\limits _\mathrm{lysis}^{t\rightarrow l} =0 \end{aligned}$$
(2)
$$\begin{aligned}&\frac{\partial \left( {\varepsilon ^{l}\rho ^{l}} \right) }{\partial t}+\nabla \cdot \left( {\varepsilon ^{l}\rho ^{l}{} \mathbf{v}^{l}} \right) +\mathop {M}\limits _\mathrm{growth}^{l\rightarrow t} -\mathop {M}\limits _\mathrm{lysis}^{t\rightarrow l} =0 \end{aligned}$$
(3)

where \(\rho ^{\alpha }\) is the density and \(\mathbf{v}^{\alpha }\) is the velocity of phase \(\alpha \,(\alpha =t,l)\). The terms \(\mathop {M}\nolimits _\mathrm{growth}^{l\rightarrow t} \) and \(\mathop {M}\nolimits _\mathrm{lysis}^{t\rightarrow l} \) account for the interphase exchange of mass related to cell growth and cell lysis, respectively.

The tumor phase t is composed of two subpopulations, namely necrotic and living cells. The necrotic portion is described by the mass fraction \(\omega ^\mathrm{Nt}\), so that the mass fraction of living cells is \(\omega ^\mathrm{Lt}=1-\omega ^\mathrm{Nt}\). We assume that there is no diffusion for the necrotic and living species, and that necrotic cells exchange mass with the interstitial fluid through the lysis term. The mass fraction of necrotic tumor cells \((\omega ^\mathrm{Nt})\) and living tumor cells \((\omega ^\mathrm{Lt})\) is thus given by:

$$\begin{aligned}&\frac{\partial \left( {\varepsilon ^{t}\rho ^{t}\omega ^\mathrm{Nt}} \right) }{\partial t}+\nabla \cdot \left( {\varepsilon ^{t}\rho ^{t}\omega ^\mathrm{Nt}{} \mathbf{v}^{t}} \right) -\varepsilon ^{t}r^\mathrm{Nt}+\mathop {M}\limits _\mathrm{lysis}^{t\rightarrow l} =0 \end{aligned}$$
(4)
$$\begin{aligned}&\frac{\partial \left( {\varepsilon ^{t}\rho ^{t}\omega ^\mathrm{Lt}} \right) }{\partial t}+\nabla \cdot \left( {\varepsilon ^{t}\rho ^{t}\omega ^\mathrm{Lt}{} \mathbf{v}^{t}} \right) +\varepsilon ^{t}r^\mathrm{Nt}-\mathop {M}\limits _\mathrm{growth}^{l\rightarrow t} =0 \end{aligned}$$
(5)

where \(\varepsilon ^{t}r^\mathrm{Nt}\) represents an intraphase exchange term accounting for the rate of death of living tumor cells.

The evolution of the mass fraction of oxygen \((\omega ^\mathrm{ox})\), the unique nutrient considered here, follows the equation:

$$\begin{aligned} \frac{\partial \left( {\varepsilon ^{l}\rho ^{l}\omega ^\mathrm{ox}} \right) }{\partial t}+\nabla \cdot \left( {\varepsilon ^{l}\rho ^{l}\omega ^\mathrm{ox}{} \mathbf{v}^{l}} \right) -\nabla \cdot \left( {\varepsilon ^{l}\rho ^{l}D^\mathrm{ox}\nabla \omega ^\mathrm{ox}} \right) +\mathop {M}\limits _\mathrm{oxygen}^\mathrm{ox\rightarrow t} =0 \end{aligned}$$
(6)

where \(D^\mathrm{ox}\) is the diffusion coefficient of oxygen in the extracellular space and \(\mathop {M}\nolimits _\mathrm{oxygen}^\mathrm{ox\rightarrow t} \) is a mass exchange term accounting for nutrient consumption by tumor cells metabolism and growth. Note that the mass exchange term in Eq. (6) is included in the reaction term \(\mathop {M}\nolimits _\mathrm{growth}^{l\rightarrow t} \) of Eqs. (2) and (3), since the latter is related to the exchange of mass and nutrients between the two phases (for more details, see Sciumè et al. 2013b and the references therein). Following porous media theory (Lewis and Schrefler 1998; Pinder and Gray 2008), the mechanical stress exerted on the solid phase is described through the effective stress tensor \(\hbox {t}_{\mathrm{eff}}^t \), given by:

$$\begin{aligned} \hbox {t}_{\mathrm{eff}}^t =\hbox {t}^{t}+\alpha p^{l}\hbox {I} \end{aligned}$$
(7)

where \(\hbox {I}\) is the unit tensor, \(\hbox {t}^{t}\) is the total stress tensor in the tissue, \(p^{l}\) is the fluid pressure in the interstitial fluid, and \(\alpha \) is Biot’s coefficient defined by:

$$\begin{aligned} \alpha =1-\frac{K}{K_T } \end{aligned}$$
(8)

with K bulk modulus of the unsaturated skeleton and \(K_T \) bulk modulus of the solid phase. The relative velocity of the interstitial fluid phase is given by a Darcy type equation obtained by TCAT as:

$$\begin{aligned} \varepsilon ^{l}\left( {\mathbf{v}^{l}-\mathbf{v}^{t}} \right) =-\frac{k}{\mu ^{l}}\nabla p^{l} \end{aligned}$$
(9)

where k is the intrinsic permeability of the solid matrix and \(\mu ^{l}\) is the dynamic viscosity of the interstitial fluid. The equations of state for the phases can be approximated as:

$$\begin{aligned}&\frac{1}{\rho ^{l}}\frac{\partial \rho ^{l}}{\partial p^{l}}=\frac{1}{K_L } \end{aligned}$$
(10)
$$\begin{aligned}&\frac{1}{\rho ^{t}}\frac{\partial \rho ^{t}}{\partial \left( {\left\langle {\mathbf{n}_t \cdot \hbox {t}_t \cdot \mathbf{n}_t } \right\rangle } \right) }\simeq \frac{1}{\rho ^{t}}\frac{\partial \rho ^{t}}{\partial p^{l}}=\frac{1}{K_T }; \end{aligned}$$
(11)

here, \(1/K_L \) and \(1/K_T \) are the liquid and solid compressibility, respectively, and \(\left\langle {\mathbf{n}_t \cdot \hbox {t}_t \cdot \mathbf{n}_t } \right\rangle \) is the normal stress at the solid surface averaged over the solid surface. Considering (10), Eq. (2) can be written as:

$$\begin{aligned} \frac{\partial \varepsilon ^{t}}{\partial t}+\frac{\varepsilon ^{t}}{K_T }\frac{\partial p^{l}}{\partial t}+\nabla \cdot \left( {\varepsilon ^{t}{} \mathbf{v}^{t}} \right) +\frac{\varepsilon ^{t}}{\rho ^{t}}{} \mathbf{v}^{t}\cdot \nabla \rho ^{t}-\frac{1}{\rho ^{t}}\left( {\mathop {M}\limits _\mathrm{growth}^{l\rightarrow t} -\mathop {M}\limits _\mathrm{lysis}^{t\rightarrow l} } \right) =0 \end{aligned}$$
(12)

Following the same steps for Eq. (3), it is possible to obtain:

$$\begin{aligned} \frac{\partial \varepsilon ^{l}}{\partial t}+\frac{\varepsilon ^{l}}{K_L }\frac{\partial p^{l}}{\partial t}+\nabla \cdot \left( {\varepsilon ^{l}{} \mathbf{v}^{l}} \right) +\frac{\varepsilon ^{l}}{\rho ^{l}}{} \mathbf{v}^{l}\cdot \nabla \rho ^{l}+\frac{1}{\rho ^{l}}\left( {\mathop {M}\limits _\mathrm{growth}^{l\rightarrow t} -\mathop {M}\limits _\mathrm{lysis}^{t\rightarrow l} } \right) =0 \end{aligned}$$
(13)

and summing (12) and (13) gives:

$$\begin{aligned}&\left( {\frac{\varepsilon ^{t}}{K_T }+\frac{\varepsilon ^{l}}{K_L }} \right) \frac{\partial p^{l}}{\partial t}+\nabla \cdot \left( {\varepsilon ^{t}{} \mathbf{v}^{t}+\varepsilon ^{l}{} \mathbf{v}^{l}} \right) \nonumber \\&\quad -\,\frac{\rho ^{l}-\rho ^{t}}{\rho ^{l}\rho ^{t}}\left( {\mathop {M}\limits _\mathrm{growth}^{l\rightarrow t} -\mathop {M}\limits _\mathrm{lysis}^{t\rightarrow l} } \right) =0 \end{aligned}$$
(14)

where the gradients of the densities have been neglected, and the constrained in (1) has been exploited. Inserting (9) and substituting \(\varepsilon ^{t}=1-\varepsilon ^{l}\) in (14) leads to:

$$\begin{aligned}&\left( {\frac{1-\varepsilon ^{l}}{K_T }+\frac{\varepsilon ^{l}}{K_L }} \right) \frac{\partial p^{l}}{\partial t}+\nabla \cdot \mathbf{v}^{t}-\nabla \cdot \left( {\frac{k}{\mu ^{l}}\nabla p^{l}} \right) \nonumber \\&\quad -\,\frac{\rho ^{l}-\rho ^{t}}{\rho ^{l}\rho ^{t}}\left( {\mathop {M}\limits _\mathrm{growth}^{l\rightarrow t} -\mathop {M}\limits _\mathrm{lysis}^{t\rightarrow l} } \right) =0 \end{aligned}$$
(15)

2.2 The constitutive relationship for the stress

In order to close the system of equations, it is necessary to define a constitutive relation for the stress in the tumor phase. A series of experiments based on single-cell force spectroscopy (Baumgartner et al. 2000; Puech et al. 2005; Helenius et al. 2008; Friedrichs et al. 2013) suggests the following phenomenological description at the microscale. When cells are well separated from each other, they do not experience any interaction. As soon as the distance between two cells is below a certain threshold, they start attracting each other, and once cells are in contact, an adhesive force builds up if they tend to be pulled apart. If the two cells are further pushed together, a repulsive force is observed. This repulsive force tends to high values as cells become more and more packed. Note that, in the context of porous media theory, the volume fraction of tumor cells can be chosen as a surrogate for cell distance. In mathematical terms, this can be written as a pseudo-potential law (Byrne and Preziosi 2003; see Preziosi and Tosin 2009b for qualitative analyses on this kind of nonlinear systems) that describes the stress in the tumor tissue:

$$\begin{aligned} \Sigma \left( {\varepsilon ^{t}} \right) =\left\{ {\begin{array}{l} \alpha \left( {\varepsilon ^{t}-\varepsilon _0^t } \right) ^{2}\left[ {\frac{1-\varepsilon _n^t }{\left( {1-\varepsilon ^{t}} \right) ^{\beta }}-\frac{1}{\left( {1-\varepsilon ^{t}} \right) ^{\beta -1}}} \right] ,\quad \hbox {if }\varepsilon ^{t}>\varepsilon _0^t \\ \\ 0,\quad \hbox {otherwise} \\ \end{array}} \right. \end{aligned}$$
(16)

In Fig. 2, a schematic of cell behavior is provided depicting the behavior of the cellular system for different volume fractions. Note that with this description, the ensemble of tumor cells and ECM behaves like an elastic fluid, and the effective stress follows the relation:

$$\begin{aligned} \hbox {t}^{t}_{\mathrm{eff}} =-\Sigma \left( {\varepsilon ^{t}} \right) \hbox {I} \end{aligned}$$
(17)

with \(\Sigma \) defined in Eq. (16) and positive in compression.

Fig. 2
figure 2

Scheme of the stress function \(\Sigma \left( {\varepsilon ^{t}} \right) \). The two insets represent forces acting on the cells for different degrees of tumor volume fractions. For high-volume fractions, on the right, cells experience a repulsive force. When the volume fractions are low, on the left, cells tend to attract each other

Full size image

2.3 The mass transfer relations

The reaction terms in Eq. (2) represent tumor cell growth and lysis, respectively. In particular, the first term is related to cell proliferation and depends on the exchange of mass between the interstitial fluid and the living portion of the tumor. Its form is given by:

$$\begin{aligned} \mathop {M}\limits _\mathrm{growth}^{l\rightarrow t} =\gamma _g^t G\left( {\omega ^\mathrm{ox}} \right) H\left( {\hbox {t}_{\mathrm{eff}}^t } \right) \omega ^{Lt}\varepsilon ^{t} \end{aligned}$$
(18)

where the coefficient \(\gamma _g^t \) accounts for the nutrient uptake and for the mass of interstitial fluid that becomes tumor due to cell growth. The function G accounts for the effect of nutrient level on cell growth, while H describes the inhibition of cell growth due to the mechanical stress exerted on the cells. Finally, the factor \(\omega ^\mathrm{Lt}\varepsilon ^{t}\) accounts for the volume fraction of viable tumor cells (i.e., only viable cells can proliferate).

The second reaction term in Eq. (2) accounts for cell lysis in the necrotic cell population (NTCs). Its form is given by:

$$\begin{aligned} \mathop {M}\limits _\mathrm{lysis}^{t\rightarrow l} =\lambda _l^t \omega ^\mathrm{Nt}\varepsilon ^{t}; \end{aligned}$$
(19)

here, \(\lambda _l^t \) takes into account the degradation of cellular membranes and the mass conversion into interstitial fluid. Since \(\omega ^\mathrm{Nt}\varepsilon ^{t}\) is the volume fraction of necrotic cells, the lysis term is active only on the dead portion of the tumor tissue.

The rate of death of tumor cells in Eq. (4) is described by the relation:

$$\begin{aligned} \varepsilon ^{t}r^\mathrm{Nt}=\gamma _n^t I\left( {\omega ^\mathrm{ox}} \right) \omega ^{Lt}\varepsilon ^{t} \end{aligned}$$
(20)

where the parameter \(\gamma _n^t \) regulates the rate of cell death. The function I describes cell death by lack of nutrient. By doing so, cell death is considered to solely depend on nutrient concentration. Note that Eq. (20) can be readily modified to include also other effects (i.e., drugs or mechanical pressure).

During the growth of the tumor, nutrients are subtracted from the interstitial fluid, so that the mass exchange term in Eq. (6) takes the form:

$$\begin{aligned} \mathop {M}\limits _\mathrm{oxygen}^\mathrm{ox\rightarrow t} =\gamma _0^t \frac{\omega ^\mathrm{ox}}{\omega ^\mathrm{ox}+c^\mathrm{ox}}\omega ^\mathrm{Lt}\varepsilon ^{t} \end{aligned}$$
(21)

This expression is validated experimentally in Casciari et al. (1992a, b) and takes into account the dependence of nutrient consumption on the local level of nutrient in the tissue. The two oxygen uptake parameters \(\gamma _0^t \) and \(\omega _\mathrm{crit}^\mathrm{ox} \) describe, respectively, the order of magnitude of oxygen uptake in the tumor and the oxygen mass fraction at which oxygen consumption is reduced by half. The functions G, H, and I are derived from phenomenological arguments and are selected to be similar to the available literature on the topic (Byrne and Preziosi 2003; Roose et al. 2007; Wise et al. 2008; Kim et al. 2011; Preziosi and Vitale 2011; Ambrosi et al. 2012; Sciumè et al. 2013b; Mpekris et al. 2015). In particular, the following set is assumed:

$$\begin{aligned}&G\left( {\omega ^\mathrm{ox}} \right) =\left\langle {\frac{\omega ^\mathrm{ox}-\omega _\mathrm{crit}^\mathrm{ox} }{\omega _\mathrm{env}^\mathrm{ox} -\omega _\mathrm{crit}^\mathrm{ox} }} \right\rangle _+ \end{aligned}$$
(22)
$$\begin{aligned}&H\left( {\hbox {t}_{\mathrm{eff}}^t } \right) =1-\delta _1 \frac{\left\langle \Sigma \right\rangle _+ }{\left\langle \Sigma \right\rangle _+ +\delta _2 } \end{aligned}$$
(23)
$$\begin{aligned}&I\left( {\omega ^\mathrm{ox}} \right) =\left\langle {\frac{\omega _\mathrm{crit}^\mathrm{ox} -\omega ^\mathrm{ox}}{\omega _\mathrm{env}^\mathrm{ox} -\omega _\mathrm{crit}^\mathrm{ox} }} \right\rangle _+; \end{aligned}$$
(24)

here, \(\omega _\mathrm{crit}^\mathrm{ox} \) is the oxygen threshold value below which cell growth is inhibited, the constant \(\omega _\mathrm{env}^\mathrm{nl} \) is the environmental mass fraction of oxygen, and the Macaulay brackets \(\left\langle \right\rangle _+ \) indicate the positive value of their argument. Since \(\omega ^\mathrm{ox}\) within the spheroid can only be equal or smaller than \(\omega _\mathrm{env}^\mathrm{ox} \), it follows that the brackets will return a number between one \((\omega ^\mathrm{ox}=\omega _\mathrm{env}^\mathrm{ox} )\) and zero \((\omega ^\mathrm{ox}<\omega _\mathrm{env}^\mathrm{ox} )\) (Sciumè et al. 2013b, 2014). The constants \(\delta _1 \) and \(\delta _2 \) (with \(\delta _1 <1\)) account for the action of mechanical stress on cell proliferation, modeling the inhibitory effect of compression on tumor cell duplication (Helmlinger et al. 1997; Cheng et al. 2009; Montel et al. 2012). Note that the expression for H is different from the usual forms assumed in the literature. However, as it will be shown in the next sections, this relation is able to better describe the experimental results.

2.4 The tumor spheroid case

The mathematical model presented above is extended in view of the comparison with the experiments. In this work, the focus is on modeling tumor spheroids, which are an aggregate of tumor cells approximately of spherical shape. As a starting point, we adapt the equations of the more general model for spherical symmetry. If the constituents are assumed incompressible and the densities of the phases are supposed to be equal \((\rho ^{t}=\rho ^{l}\equiv \rho )\), Eq. (14) becomes:

$$\begin{aligned} \nabla \cdot \left( {\varepsilon ^{t}{} \mathbf{v}^{t}+\varepsilon ^{l}{} \mathbf{v}^{l}} \right) =0 \end{aligned}$$
(25)

In spherical symmetry, Eq. (25) reads:

$$\begin{aligned} \frac{1}{r^{2}}\frac{\partial }{\partial r}\left[ {r^{2}\left( {\varepsilon ^{t}v^{t}+\varepsilon ^{l}v^{l}} \right) } \right] =0 \end{aligned}$$
(26)

which, by symmetry, gives:

$$\begin{aligned} v^{l}=-\frac{\varepsilon ^{t}}{\varepsilon ^{l}}v^{t}=-\frac{\varepsilon ^{t}}{1-\varepsilon ^{t}}v^{t} \end{aligned}$$
(27)

Substituting the new relation in Eq. (9) gives the expression for the phase velocities as:

$$\begin{aligned} v^{t}=\frac{k}{\mu ^{l}}\frac{\partial p^{l}}{\partial r},\quad v^{l}=-\frac{\varepsilon ^{t}}{1-\varepsilon ^{t}}\frac{k}{\mu ^{l}}\frac{\partial p^{l}}{\partial r} \end{aligned}$$
(28)

From the point of view of the motion of the phases, since the hydraulic permeability \(k/\mu ^{l}\) is a positive constant, (28) implies that the interstitial fluid is directed opposite to the pressure gradient while tumor cells move along it. When the interstitial fluid pressure is higher in the tumor center, the interstitial fluid flows toward the boundary of the tumor, whereas tumor cells move in the direction of the tumor center as observed experimentally in Dorie et al. (1982), Jain and Stylianopoulos (2010) and already discussed in Byrne and Preziosi (2003). This mechanism enables the recirculation of interstitial fluid in the tumor tissue: Tumor cells in the inner regions of the tumor become necrotic due to nutrient deprivation and turn into interstitial fluid after lysis. This fluid flows toward tumor periphery and can be employed by proliferating cells. From the equilibrium equation for the total stresses \((\nabla \cdot \hbox {t}^{t}=0)\) and Eqs. (7) and (17), it follows the important relation:

$$\begin{aligned} \frac{\partial p^{l}}{\partial r}=-\frac{\partial \Sigma }{\partial r}=-{\Sigma }'\frac{\partial \varepsilon ^{t}}{\partial r},\quad {\Sigma }'\equiv \frac{\partial \Sigma }{\partial \varepsilon ^{t}} \end{aligned}$$
(29)

The final system of equations for spherical symmetry and with the new expressions for the velocities reads:

$$\begin{aligned}&\frac{\partial \varepsilon ^{t}}{\partial t}-\frac{1}{r^{2}}\frac{\partial }{\partial r}\left( {r^{2}\varepsilon ^{t}\frac{k}{\mu ^{l}}{\Sigma }'\frac{\partial \varepsilon ^{t}}{\partial r}} \right) -\frac{1}{\rho }\left( {\mathop {M}\limits _\mathrm{growth}^{l\rightarrow t} -\mathop {M}\limits _\mathrm{lysis}^{t\rightarrow l} } \right) =0\nonumber \\ \end{aligned}$$
(30)
$$\begin{aligned}&\frac{\partial \left( {\omega ^\mathrm{Nt}\varepsilon ^{t}} \right) }{\partial t}-\frac{1}{r^{2}}\frac{\partial }{\partial r}\left( {r^{2}\varepsilon ^{t}\omega ^\mathrm{Nt}\frac{k}{\mu ^{l}}{\Sigma }'\frac{\partial \varepsilon ^{t}}{\partial r}} \right) \nonumber \\&\quad -\,\frac{1}{\rho }\left( {\varepsilon ^{t}r^\mathrm{Nt}-\mathop {M}\limits _\mathrm{lysis}^{t\rightarrow l} } \right) =0 \end{aligned}$$
(31)
$$\begin{aligned}&\frac{\partial \left[ {\left( {1-\varepsilon ^{t}} \right) \omega ^\mathrm{ox}} \right] }{\partial t}+\frac{1}{r^{2}}\frac{\partial }{\partial r}\left( {r^{2}\varepsilon ^{t}\omega ^\mathrm{ox}\frac{k}{\mu ^{l}}{\Sigma }'\frac{\partial \varepsilon ^{t}}{\partial r}} \right) \nonumber \\&\quad -\,\frac{1}{r^{2}}\frac{\partial }{\partial r}\left[ {r^{2}\left( {1-\varepsilon ^{t}} \right) D^\mathrm{ox}\frac{\partial \omega ^\mathrm{ox}}{\partial r}} \right] +\frac{1}{\rho }\mathop {M}\limits _\mathrm{oxygen}^{ox\rightarrow t} =0 \end{aligned}$$
(32)

The growth of the spheroid is modeled as a free-boundary problem, and the interface constituted by the tumor cells moves with velocity \(v^{t}\):

$$\begin{aligned} \frac{dR}{dt}=v^{t}=-\frac{k}{\mu ^{l}}{\Sigma }'\frac{\partial \varepsilon ^{t}}{\partial r} \end{aligned}$$
(33)

with R being the radius of the spheroid. To close the differential problem in (30)–(32), it is necessary to define a set of boundary and initial conditions. In particular, no-flow boundary conditions are assumed at the spheroid center, while Dirichlet boundary conditions are assumed on the tumor external surface:

$$\begin{aligned}&\frac{\partial \varepsilon ^{t}}{\partial r}=\frac{\partial \omega ^\mathrm{Nt}}{\partial r}=\frac{\partial \omega ^\mathrm{ox}}{\partial r}=0,\quad \hbox {in }r=0, \end{aligned}$$
(34)
$$\begin{aligned}&\varepsilon ^{t}=\varepsilon _\mathrm{ext}^t ,\quad \omega ^\mathrm{Nt}=0,\quad \omega ^\mathrm{ox}=\omega _\mathrm{env}^\mathrm{ox} ,\quad \hbox {in }r=R \end{aligned}$$
(35)

Note that the first condition in (35) implies prescribing an external stress on the tumor surface, since from (16) and (17), we have:

$$\begin{aligned} \Sigma \left( {\varepsilon _\mathrm{ext}^t } \right) =\Sigma _\mathrm{ext} \end{aligned}$$
(36)

In the case of a stress-free growing spheroid, the external volume fraction satisfies:

$$\begin{aligned} \Sigma \left( {\varepsilon _\mathrm{ext}^t } \right) =0,\quad \varepsilon _\mathrm{ext}^t =\varepsilon _n^t \end{aligned}$$
(37)

Finally, the following initial conditions are assumed throughout the domain:

$$\begin{aligned} \varepsilon ^{t}=\varepsilon _\mathrm{ext}^t ,\quad \omega ^\mathrm{Nt}=0,\quad \omega ^\mathrm{ox}=\omega _\mathrm{env}^\mathrm{ox} ,\quad \hbox {on }0<r<R\hbox { at }t=0 \end{aligned}$$
(38)

3 Materials and methods

3.1 Cell culture and spheroid formation

Human multiforme glioblastoma U-87 MG cells (ATCC) are grown at \(37~^{\circ }\hbox {C}\) at 5 % \(\hbox {CO}_{2}\) in EMEM (HyClone) supplemented with 50 U/mL penicillin, 50 \(\upmu \hbox {g/mL}\) streptomycin, and 10 % FBS (v/v). Multicellular U-87 MG spheroids are prepared by the liquid overlay method (Sutherland et al. 1981; Carlsson and Yuhas 1984). Briefly, serum-free EMEM medium with 2 % (w/v) agar is prepared and sterilized; 50 \(\upmu \hbox {l}\) of the agar solution is added to the bottom of each well of the 96-well plates to prevent cell adhesion onto the well surface. Plates are allowed to cool down before use. U-87 MG cells are counted and then seeded at different densities: 1000, 5000, and 10,000 cells/well. Plates are centrifuged for 5 min at 1000\(\times \) g. Spheroid diameter is measured every 2 days using Nikon Eclipse Ti microscope (Nikon) with NIS-Element software. The culture medium is replaced with fresh medium every three days.

3.2 Cell viability test with Dextran solutions and spheroid compression experiments

For the compression experiments, Dextran is added to the culture medium to exert mechanical stress on the spheroids as reported in Montel et al. (2011, 2012), Delarue et al. (2014). Briefly, cell culture medium is mixed with the purified Dextran \((M_w =100\hbox { kDa})\), and the resulting solution is placed at \(37\,^{\circ }\hbox {C}\) to obtain full solubilization. To test the effect of the Dextran solutions on U-87 MG cell viability, XTT assay is performed (Stigliano et al. 2015). In particular, 10,000 cells are plated in each well of 96-well plate. After 24 h, the medium is substituted with different concentrations of Dextran medium (20, 55, and 80 g/l). After 72 h of incubation, the XTT assay is performed according to the manufacturer’s protocol. The same solutions of Dextran at different concentrations are prepared to test the effect of different mechanical pressures on the surface of the spheroids. In particular, 5000 U-87 MG cells are seeded in 48-well plates (day 0), as reported before, and the Dextran medium is added after spheroid formation (day 3) at a concentration of 20 g/l to exert 1 kPa, 55 g/l to exert 5 kPa, and 80 g/l to exert 10 kPa.

The stress acting on the spheroids is estimated as in Montel et al. (2011, 2012), Delarue et al. (2014) via the following mathematical expression:

$$\begin{aligned} p=286c+87c^{2}+5c^{3} \end{aligned}$$

where p is the external mechanical pressure (Pa), and c is the concentration of Dextran (% w/w). This expression was originally derived to describe the osmotic pressure of Dextran solutions in colloidal systems (Bonnet-Gonnet et al. 1994) and then validated to hold also for the spheroid compression experiments (Montel et al. 2012).

Spheroid diameter measurement and medium replacement follow the same procedures described above.

4 Results

4.1 Evolution of the phases

The mathematical framework presented above is applied to analyze the growth of a multicellular tumor spheroid in vitro. In particular, the growth of the tumor mass is investigated, including necrotic tumor cells and the consumption of nutrient (oxygen) over time. The geometry of the problem and the boundary conditions are described in Fig. 3. At the boundary B1, the TC volume fraction \((\varepsilon ^{t})\), the oxygen mass fraction \((\omega ^\mathrm{ox})\), and the necrotic cells mass fraction \((\omega ^\mathrm{Nt})\) are fixed over time. At the symmetry boundaries B2, zero fluxes for all phases are imposed. At the beginning of the simulation, the value of the oxygen and of the other variables are fixed, as indicated in the figure. All other governing parameters are listed in Table 1. Numerical results for the evolution of the three principal variables of the model are shown in Fig. 4. In Fig. 4a, the volume fraction of tumor cells in the system is plotted for different times over the spheroid radius. Initially, the tumor spheroid is composed only by living tumor cells and interstitial fluid. After a few days, necrotic tumor cells appear in the center of the spheroid. Living tumor cells are restricted to the outer portion of the tumor, where there is still enough nutrient to support their growth. At 25 days, necrotic cells occupy the main portion of the spheroid, constituting the “necrotic core,” while the proliferating portion of the tumor is further reduced. Since tumor growth is described by Eqs. (18) and (22), only tumor cells that experience an oxygen level over the critical threshold are allowed to proliferate. This means that the living tumor cells that can actually proliferate are distributed only over a small portion of the radius near the external boundary, called the “proliferative rim.” The remaining portion of living cells are nonproliferating cells that can resume proliferation after an increase in the level of nutrient. Note that the volume fraction of interstitial fluid is approximately constant over time, apart for a small increase at the spheroid center and reduction at the spheroid periphery. These are due, respectively, to the lysis term active at the tumor center and to the fluid consumption induced by cell growth at the boundary.

Table 1 Parameters considered in the simulations
Full size table
Fig. 3
figure 3

Scheme for the geometry of a tumor spheroid immersed in a cell culture medium. The initial and boundary conditions for the differential problem are reported on the right

Full size image
Fig. 4
figure 4

a Volume fraction of tumor cells, plotted as the difference between the volume fraction inside the spheroid and at the spheroid boundary (here, \(\varepsilon _\mathrm{ext}^t =\varepsilon _n^t \) since the spheroids are not compressed). b Mass fraction of oxygen. c Mass fraction of necrotic tumor cells. All the variables are plotted over the spheroid radius with each line drawn every five days from the first

Full size image

The evolution of the oxygen mass fraction, the nutrient species considered here, is shown in Each line is plotted over the spheroid radius, every five days from the first day. As the spheroid grows, gradients of oxygen concentration develop from the tumor boundary to the center of the spheroid. After a few days, the oxygen mass fraction reaches a plateau at the center of the spheroid, with a value below the critical threshold \(\omega _\mathrm{crit}^\mathrm{ox} \). This can be explained by considering that necrotic cells do not consume oxygen, and therefore, a gradient is not observed. Moreover, the oxygen consumption is proportional to the amount of oxygen available through Eq. (21), and this contributes to the shape of the curves.

The evolution of the necrotic mass fraction is presented in the graph of Fig. 4c. The necrotic portion of the tumor develops from the center toward the boundary. As the interface between living tumor cells and necrotic tumor cells is diffused, the separation between the two is smooth, and the model can account for perinecrotic regions.

4.2 Spheroids grown with different initial cell seeding number

The computational model is validated against data from tumor spheroid cultures. U87-MG cells, a human glioblastoma cell line, are cultured with a standard protocol (see Materials and methods). The experimental setup is shown in Fig. 5. The bottom of standard cell culture wells is covered with agarose, in order to prevent tumor cell adhesion. Cells are seeded at different initial numbers (1000, 5000, 10,000) and rapidly form spheroids suspended in standard culture medium. The evolution of the spheroid radii is then recorded over time via optical microscopy, and the resulting growth curves are plotted in Fig. 6a. It is possible to distinguish between the first stages of growth, characterized by an exponential/linear behavior, followed by a phase of growth saturation where the radius reaches a steady value.

Fig. 5
figure 5

Optical images of the growth of U-87 MG spheroids from day 5 to day 21. The scale bar is \(200~\upmu \hbox {m}\), and the spheroids are taken from the 10,000 seeded cells initial condition. The last image represents a scheme of the culture protocol

Full size image
Fig. 6
figure 6

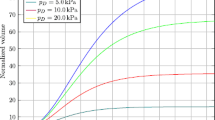
Growth curves recorded from the free growth experiments. a Each curve represents a different initial condition in terms of seeded cells. \(\hbox {N} \ge 4\) spheroids are considered for each condition. Points are experimental data, and error bars are the standard deviations of the measurements. b Solid lines are the results of fits with the mathematical model. c Growth curve obtained by superimposing the evolution of the radii of spheroids grown at different initial cell seeding numbers

Full size image

After recording the curves, a series of simulations is run to reproduce the experimental data. The growth curves corresponding to the best fit of the experimental data are shown in Fig. 6b. The governing parameters are taken from the literature when they are available, and we use the same order of magnitude of the experimental values when they refer to other cell species. Table 1 lists the parameters used in this study together with the ones determined by the fit of the curves. There is a good agreement with the experimental data, for all the three different initial cell seeding numbers. The model captures the growth dynamics both in the first fast-growing phase and in the later phase of growth saturation. Note that the same parameters are used for fitting all the three curves, and only the initial radii of the spheroids are changed, showing a good quality of the fit. This experiment is useful for validating the model and displays a second remarkable result. The different initial seeding of tumor cells affects the initial radius of the tumor spheroid, which increases from \(\approx 100~\upmu \hbox {m}\) to almost \(190~\upmu \hbox {m}\). The data show that, although being constituted by a larger initial number of tumor cells, bigger spheroids reach the same final radius of smaller ones. This result agrees with what is reported in the literature about the existence of a steady radius for growing spheroids (Sutherland et al. 1971; Folkman and Hochberg 1973; Carlsson 1977; Freyer and Sutherland 1986), which in our case takes approximately the value of \(475~\upmu \hbox {m}\).

Interestingly, the model reproduces the same behavior of the experiments with the steady state being reached after 25 days from cell seeding. As the spheroids grow freely in the culture medium, the only mechanism to stop cell proliferation is given by Eq. (22) in the model where it is assumed that cell mitosis and necrosis depend on the local level of nutrient. Therefore, in this modeling framework, the hypothesis of nutrient deprivation is sufficient to explain the phenomenon of growth saturation and the existence of an asymptotic radius for the spheroid.

As a further remark about these results, in Fig. 6c the previous curves are shifted of the proper amount referring to the different initial condition. It is good to see that they coalesce to a single “master curve.” Spheroids grown from a different initial radius follow the same curve, showing that there exists a common dynamics regulating the growth of these cellular aggregates.

4.3 Compression experiments

The application of a constant mechanical stress on the surface of the growing spheroids is investigated in this series of experiments. Addition of Dextran to the cell culture medium produces an osmotic pressure on the outermost layer of cells located on the spheroid surface. The osmotic pressure acts as a network stress directed to decrease the volume occupied by the spheroid (Montel et al. 2011, 2012; Delarue et al. 2014). This compressive force can be calibrated experimentally as in Bonnet-Gonnet et al. (1994), Bouchoux et al. (2009), where an empirical law is given to relate the concentration of Dextran in the solution to the external pressure exerted on the surface of the spheroid. Three pressure conditions are explored following the approach described in the Materials and Methods section, namely 1, 5, and 10 kPa, plus a control experiment with no external pressure. Cell viability is checked as reported in Sect. 3.2, where it is shown that the addition of Dextran does not alter cell death or growth. The results are presented in Fig. 7, where the growth of the spheroids is followed for 18 days after the addition of Dextran. Figure 7a shows optical images of sample spheroids referring to the control and to the most compressed condition for different time instants. Starting from a similar initial radius (about \(200~ \upmu \hbox {m}\)), the two spheroids reach considerable different volumes at 18 days, with the compressed spheroid growing slowly compared to the stress-free case. The growing curves for the other external applied pressures are collected in Fig. 7b. The larger value of the radius is reached for the spheroids grown in the absence of any external compression. When Dextran is added to the medium and the osmotic stress builds up, both the growth rate and the final diameter decrease. If the applied pressure is released, the growth of the aggregates resumes, indicating that the effect of the stress is reversible (Online Resource 1), as shown for the first time in (Helmlinger et al. 1997). The effect of the external pressure on the growth of the spheroid is included in the model through Eq. (23), which describes the inhibition of cell proliferation due to the applied mechanical stress on the tumor cells. The most common mathematical expressions for the inhibiting function H reported in the literature are based on a linear or inversely proportional assumptions (Roose et al. 2003; Byrne and Preziosi 2003; Kim et al. 2011; Mpekris et al. 2015). In Fig. 8, these forms are tested against the experimental data, together with an exponential relation and a Michaelis–Menten-like expression. The data in Table 2 represent the values of the parameters that provide the best fits to the experimental curves. The linear relationship, applied in Fig. 8a, underestimates the inhibition effect for low compressions, leading to larger values of the radius for the 1 and 5 kPa cases. At the same time, for larger compressions the linear relationship gives overestimates for the inhibition, resulting in smaller radii for the 10 kPa curve than experimentally measured. The exponential relationship is applied in Fig. 8b, where it is possible to observe an improvement for high compressions but a similar underestimation for the 1 and 5 kPa curves. Another improvement can be seen in Fig. 8c, referring to the inversely proportional expression. In this case, there is a good agreement with the experimental data for all the curves, except for the 1 kPa case. The best results are obtained with the Michaelis–Menten-like law, represented in Fig. 8d. All the different compression levels are well described by the simulations, together with the final radii reached by the spheroids.

Table 2 Different mathematical expressions for the growth inhibition function in Eq. (23)
Full size table
Fig. 7
figure 7

a Optical images of U-87 MG spheroids grown under the effect of the Dextran solutions. The first row shows the control experiments and the second row a spheroid under the highest compression. The scale bar is \(200~\upmu \hbox {m}\), and the initial seeding is 5000 tumor cells. b Experimental results for the compression experiments. The points are the experimental data, and the error bars represent the standard deviations of the measurements. For each condition, N = 5 spheroids are considered

Full size image
Fig. 8
figure 8

Fit of the experimental data for the compression experiments. Results from the linear a, exponential b, inversely proportional c, and Michaelis–Menten-like d assumptions for the function H in Eq. (23)

Full size image

4.4 Effect of the growth inhibition parameters

The effect of an external stress acting on the cellular component of the spheroid can be evaluated through a parametric study on the growth inhibition parameters \(\delta _1 \) and \(\delta _2 \) of Eq. (23). The growth curves obtained by varying one of the two parameters and keeping the other fixed for the case of an external pressure of 5 kPa are presented in Fig. 9. The two solid lines represent reference values assumed by the parameters. In particular, “zero” indicates the curve obtained by setting both \(\delta _1 \) and \(\delta _2 \) to zero, while “fit” is the curve obtained with the values in Table 2. The effect of different values for \(\delta _1 \) is shown in Fig. 9a. The arrow points in the direction of increasing \(\delta _1 \), while for \(\delta _2 \) the value in Table 2 is selected for all the simulations. From the top curve to the bottom one, we consider values for \(\delta _1 \) that are, respectively, −50, −25, +25, +50 and +75 % of the reference value in Table 2. As \(\delta _1 \) increases, tumor cells sense more the effect of external stresses on their proliferation. This results in smaller final radii of the spheroids and in slower growth rates. If the value of \(\delta _1 \) is sufficiently high, then the tumor starts to shrink, and an equilibrium radius no longer exists. The same investigation, this time for \(\delta _2 \), is reported in Fig. 9b. In this case, the arrow points in the opposite direction, indicating that an increase in \(\delta _2 \) leads to an increase in the final radius. This difference can be easily explained by considering that H in Eq. (23) is directly proportional to \(\delta _1 \) and inversely proportional to \(\delta _2 \), respectively. However, it is possible to note that the effect of varying \(\delta _2 \) is less pronounced on the growth curve, since the reference value in Table 2 is much smaller than the pressures in the compression experiments. These results indicate collectively a double effect of the external environment in limiting the growth of the tumor. Tumor growth may be hindered by nutrient deprivation but also by external stresses exerted by regions close to the tumor.

Fig. 9
figure 9

Parametric study for the growth inhibition parameters in Eq. (23). Effects of \(\delta _1 \) a and of \(\delta _2 \) b on the growth of the spheroids

Full size image

5 Discussion

In the present study, a recent model for tumor growth has been extended to describe the evolution of tumor spheroids. A set of experiments is carried out, and the resulting data are compared to numerical predictions. The experimental growth curves validate the model equations both for the free growth case, where the cells are cultured in three dimensions in standard culture medium, and for the mechanically compressed setup, where the spheroids are subjected to an external pressure. In addition to providing the data for the validation, the first series of experiments highlights the existence of a “master curve” (Fig. 6c). This common growth trend supports the hypothesis of describing the cell aggregates as a dynamical system, which behavior can be predicted, at least as a first approximation, by the laws of mechanics. The results of the model in terms of tumor volume fraction, oxygen mass fraction, and necrotic mass fraction are reported and appear in line with the results of the original model. The second set of experiments about spheroids compression extends the work in Delarue et al. (2014) by adding another cell species (U87-MG) to their study. The observed evolution curves are similar to their findings and confirm the hypothesis of an inhibitory effect of external stress on cancer cell proliferation. Regarding the description of this phenomenon, the experimental data are exploited to design a constitutive relationship that performs better, compared to the existing laws, in describing the evolution of the system.

Several simplifying assumptions are considered in the work, and the model is certainly open to further improvements. In particular, here only one nutrient species, namely oxygen, diffuses in the interstitial fluid and regulates the proliferation of tumor cells. Although the action of other chemicals is implicitly included in the mass transfer term in (18), modeling additional nutrients, growth, and necrosis factors could provide supplementary insights into the evolution of the tumor system (Chauhan and Jain 2013; Jain et al. 2014). Another point that should be addressed is the choice of the constitutive relations used to close the differential system. Most of these laws, as it happens frequently in the literature, are derived from phenomenological arguments and deserve more experimental work to be linked to the biology of what they are describing. In particular, here it is assumed that the compression of the spheroids induces inhibition of cell growth, without modifying the apoptosis rate of the cells. This hypothesis is still a matter of debate in the literature (see, for example, (Montel et al. 2012) and comments therein), and it is adopted here to account for the experimental observations in Delarue et al. (2014) where the experimental setup is similar to the one in this work. A systematic comparison of different compression modalities may improve the understanding of this phenomenon and the design of more accurate constitutive laws.

Finally, here it is considered a very simple mechanical description of the tumor ensemble, function of the volume fraction of the tumor cells. This assumption provides a great simplification of the mechanical equations and describes sufficiently accurately the data; however, it does not take into account several phenomena related to the stress experienced by the cells inside the tumor tissue. For example, viscous effects existing at smaller timescales than cell proliferation are neglected, as well as cellular adhesion bonds breakage and formation during the development of the tumor mass (Ambrosi and Preziosi 2009; Preziosi and Vitale 2011).

Further experiments will be considered in the future that will provide better estimates for the model parameters and new data in terms of quantities that should be compared to the output of the model equations. A part of the future experimental work will be also devoted to the biochemical understanding of the growth inhibition process due to mechanical stress. Even if some work is already present in the literature (Delarue et al. 2014; Fernández-Sánchez et al. 2015), many details remain obscure as well as a proper implementation of the phenomena in the growth equations. A better description of the interactions between the tumor and its external microenvironment (biochemical and mechanical) should offer valuable insights for understanding the progression of the disease and designing new therapeutic treatments.