A phase-field model for fracture in biological tissues

Abstract

This work presents a recently developed phase-field model of fracture equipped with anisotropic crack driving force to model failure phenomena in soft biological tissues at finite deformations. The phase-field models present a promising and innovative approach to thermodynamically consistent modeling of fracture, applicable to both rate-dependent or rate-independent brittle and ductile failure modes. One key advantage of diffusive crack modeling lies in predicting the complex crack topologies where methods with sharp crack discontinuities are known to suffer. The starting point is the derivation of a regularized crack surface functional that ${\varGamma }$-converges to a sharp crack topology for vanishing length-scale parameter. A constitutive balance equation of this functional governs the crack phase-field evolution in a modular format in terms of a crack driving state function. This allows flexibility to introduce alternative stress-based failure criteria, e.g., isotropic or anisotropic, whose maximum value from the deformation history drives the irreversible crack phase field. The resulting multi-field problem is solved by a robust operator split scheme that successively updates a history field, the crack phase field and finally the displacement field in a typical time step. For the representative numerical simulations, a hyperelastic anisotropic free energy, typical to incompressible soft biological tissues, is used which degrades with evolving phase field as a result of coupled constitutive setup. A quantitative comparison with experimental data is provided for verification of the proposed methodology.

1 Introduction

Computational modeling of fracture in soft biological tissues presents a promising research area due to its scope to help improve the understanding behind surgical treatments or injuries involving mechanical stresses, e.g., balloon angioplasty, ruptured aneurysm or ligament tear. An extracellular matrix consisting of networks of elastin and collagen fibers surrounded by smooth muscle cells and fluids constitutes a major part of a tissue; see, e.g., Humphrey (2002). Elastin networks bear long-range reversible small deformations and can endure several million deformation cycles without undergoing fatigue as shown in Gundiah et al. (2007). The triple-stranded helical structure of collagen fibers endows structural integrity to soft tissues at finite deformations due to unraveling of its wavy form (Gelsea et al. 2003). Due to this microstructural composition, soft biological tissues are nearly incompressible with highly nonlinear and anisotropic response to mechanical stimulus where more details can be found in Rhodin (1980) and Chuong and Fung (1984). The constitutive material modeling of biological tissues is a constantly evolving research area. See, e.g., Demiray (1972) and Delfino et al. (1997) where an isotropic strain energy density for soft biological tissues is formulated or Vaishnav et al. (1973), Lanir (1979), Fung et al. (1979) and Billiar and Sacks (2000) which additionally account for material anisotropy. Another set of approaches are based on the structural tensors for incorporating anisotropy into polyconvex free energy functions. See, e.g., Holzapfel et al. (2000), Menzel and Steinmann (2001) and Gasser et al. (2006) where the latter also accounts for fiber dispersion obtained from the orientation distribution function. The conditions of polyconvexity for constructing transversely isotropic or orthotropic free energy functions are shown in Balzani et al. (2006). These material models for soft biological tissues represent a class of phenomenological macroscopic constitutive theories. Another class of models, presumably more physical, takes into account the entropic elasticity of collagen fibers arising due to their nanoscale dimensions. These models are based on the well-known theory of network models for rubber elasticity (see James and Guth (1943), Flory and Rehner (1943), Arruda and Boyce (1993), Miehe et al. (2004)) where a randomly connected network of polymer chains is found cross-linked at the microstructure. The micromechanically motivated network models for soft biological tissues treat the collagen fibers as wormlike chains from the statistical point of view; see Flory (1969) for a detailed description. Some notable applications of network models to soft matter such as biological tissues and fabrics can be found in Bischoff et al. (2002), Kuhl et al. (2005), Alastrué et al. (2009) and Raina and Linder (2014).

The mechanical behavior of soft biological tissues under normal physiological loading conditions can be qualitatively simulated with the aforementioned modeling approaches. The successful applications of the same, particularly with respect to human arterial walls, have been demonstrated in the references mentioned above. However, under certain pathological conditions, the soft biological tissues may undergo fracture which is beyond the scope of modeling capability of those methods. One such disease is atherosclerosis which affects the flow of oxygen-carrying blood through the arteries due to narrowing of the lumen (stenosis). This is caused by accumulation of the extracellular lipids, calcium, foam cells and necrotic tissue forming a plaque-like substance inside the artery wall as shown in Lendon et al. (1991) and Loree et al. (1992). When undiagnosed, it can lead to myocardial infarction, angina or smoker’s leg due to plaque rupture which releases thrombogenic materials into blood stream (Gertz and Roberts 1990; Loree et al. 1991). Upon diagnosis, the treatment of advanced atherosclerosis is generally followed by a stent implantation in the affected artery with the balloon angioplasty procedure. The mechanism of balloon angioplasty requires the concerned artery to be subjected to supra-physiological loading which can possibly lead to tissue degeneration and fracture (Castaneda-Zuniga et al. 1980; Gasser and Holzapfel 2007). One refers to the reviews by Rhodin (1980) and Silver et al. (1989) for a detailed description of the histological and biomechanical features of an artery. The experimental investigations in Schulze-bauer et al. (2002) and Holzapfel et al. (2004) tested layer-specific mechanical properties of the human stenotic iliac arteries up to rupture to identify their strength parameters and confirmed the role of different collagen fiber orientations in different layers yielding anisotropic behavior. Sommer et al. (2008) performed peeling tests on medial layers of abdominal aortas to investigate phenomena of artery dissection during surgical treatment. Given the complexity of material composition and associated deformation mechanisms at hand, the numerical simulations of soft biological tissues in the post-critical range due to fracture are rare. Gasser and Holzapfel (2006) performed numerical simulations of arterial dissection combining transversely isotropic energy density with extended finite element method (Belytschko and Black 1999; Moës et al. 1999) where fracture is modeled by incorporating strong discontinuities via nodal enrichment strategies. Ferrara and Pandolfi (2008, 2010) used the cohesive damage model (Xu and Needleman 1994) by incorporating cohesive interface elements along the edges of bulk finite elements to model tissue failure due to balloon angioplasty and medial dissection under supra-physiological loading conditions. Balzani et al. (2012) resorted to continuum damage mechanics formulation (Govindjee and Simo 1991) by introducing internal damage variables along each fiber direction to simulate angioplasty-induced rupture.

In this paper, our recent advances in the phase-field modeling of fracture (see, e.g., Miehe et al. (2010a, b, 2014), Miehe and Schänzel (2014)) are used to simulate the complex fracture phenomena in soft biological tissues described above. The usual shortcomings of the classical Griffith-type theory of brittle fracture, such as inability to determine branching cracks, can be overcome by variational methods based on energy minimization as suggested by Francfort and Marigo (1998); see also Bourdin et al. (2008), Dal Maso and Toader (2002), Buliga (1999). The regularized setting of their framework considered in Bourdin et al. (2000, 2008) is obtained by convergence inspired by the work of image segmentation by Mumford and Shah (1989). We refer to Ambrosio and Tortorelli (1990) and the reviews of Dal Maso (1993) and Braides (1998, 2002) for details on convergent approximations of free discontinuity problems. The approximation regularizes a sharp crack surface topology in the solid by diffusive crack zones governed by a scalar auxiliary variable. This variable can be considered as a phase field that interpolates between the unbroken and the broken states of the material. Conceptually similar are recently outlined phase-field approaches to brittle fracture based on the classical Ginzburg–Landau-type evolution equation as reviewed in Hakim and Karma (2009). These models may be considered as time-dependent viscous regularizations of the above-mentioned rate-independent theories of energy minimization. The phase-field approach is embedded into the theory of gradient-type materials with a characteristic length scale, as outlined in Capriz (1989), Mariano (2001), Frémond (2002) and Miehe (2011) and conceptually follows the models of continuum damage mechanics; see, e.g., Kachanov (1986) or Frémond and Nedjar (1996). It is to be emphasized here that finite element modeling of fracture such as cohesive zone models (Xu and Needleman (1994), Ortiz and Pandolfi (1999)), configurational-force-driven adaptive remeshing techniques (Ortiz and Quigley (1991), Gürses and Miehe (2009)), element enrichment techniques (Simo et al. (1993), Oliver (1996), Linder and Armero (2007), Linder and Raina (2013)) or nodal enrichment techniques (Belytschko and Black (1999), Moës et al. (1999) Wells and Sluys (2001)) suffer in three-dimensional applications with complex crack topologies. In contrast, the phase-field-type diffusive crack modeling is a spatially smooth continuum formulation that avoids the modeling of discontinuities and can be implemented in a straightforward manner as shown in Miehe et al. (2010a, b, 2014) to model complex crack patterns.

In Sect. 2, a descriptive motivation of a regularized crack topology based on a phase field is presented in a purely geometric setting. As a result, a crack surface functional is defined with a constitutive law that governs the evolution of the crack phase field. This crack functional is considered as the crack surface itself which should stay constant or grow for arbitrary loading processes. For numerical simulations of interest, the crack surface potential is discretized with finite elements with an operator splitting strategy adopted for the evolution of the phase field. In Sect. 3, the local crack driving force, with regard to brittle failure in isotropic and anisotropic materials is introduced. For anisotropy, a general orthotropic failure criterion is developed to model fracture in soft biological tissues. The anisotropic contributions to the free energy with comments on its convexity are given in Sect. 4. Finally, Sect. 5 outlines representative numerical examples of fracture in soft biological tissues which demonstrate the features and algorithmic robustness of the proposed phase-field models of fracture.

Fig. 1

Finite deformation of a solid with a regularized crack. The deformation map ${\varvec{\varphi }}$ maps at time $t\in {\mathcal {T}}$ the reference configuration ${\mathcal {B}}_0\!\in \!{\mathcal {R}}^\delta$ onto the current configuration ${\mathcal {B}}_t$. a The crack phase field $d\in [0,1)$ defines a regularized crack surface functional ${\varGamma }_l(d)$ that converges in the limit $l\!\rightarrow \! 0$ to the sharp crack surface ${\varGamma }$. b The level set ${\varGamma }_c = \{ {\varvec{ X }}\, \vert \, d =c\}$ defines for a constant $c \approx 1$ the crack faces in the regularized setting. Parts of the continuum with $d >c$ are considered to be free space and are not displayed

2 The geometric approach to phase-field fracture

We summarize the basic ingredients of a purely geometric approach to the phase-field modeling of fracture, which was outlined in detail in Miehe et al. (2014).

2.1 Regularization of sharp crack topology

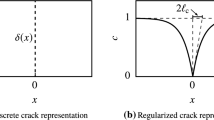
Let ${\mathcal {B}}_0\subset {\mathcal {R}}^\delta$ be the reference configuration of a material body with dimension $\delta \in [2,3]$ in space and $\partial {\mathcal {B}}_0\subset {\mathcal {R}}^{\delta -1}$ its surface as depicted in Fig. 1. We consider the crack phase field $d:{\mathcal {B}}_0\times {\mathcal {T}}\rightarrow [0,1]$ characterizing for $d({\varvec{ X }},t)=0$ the unbroken and for $d({\varvec{ X }},t)=1$ the fully broken state of the material at ${\varvec{ X }}\in {\mathcal {B}}_0$ and time $t\in {\mathcal {T}}$. It governs the regularized crack surface

$$\begin{aligned} {\varGamma }_l(d) = \int _{{\mathcal {B}}_0} \bigg \{\dfrac{1}{2l} d^2 + \dfrac{l}{2} \vert \nabla d \vert ^2\,\bigg \}dV \end{aligned}$$

(1)

that is formulated in terms of the crack surface density function $\gamma _l(d, \nabla d) = d^2/2l + l\vert \nabla d \vert ^2/2$ per unit volume of the solid. It is governed by the length-scale parameter l. Assuming a given sharp crack topology by prescribing the Dirichlet condition $d=1$ on ${\varGamma }\subset {\mathcal {B}}_0$, the regularized crack phase field d in the full domain ${\mathcal {B}}_0$ is obtained by a minimization principle of diffusive crack topology $d = \text{ Arg } \{ \inf _{d} {\varGamma }_l(d) \}$, yielding the second-order Euler equation $d - l^2 \Delta d = 0$ in ${\mathcal {B}}_0$ with an exponential-function-type profile of the phase field d as visualized in Fig. 2b. We refer to Miehe et al. (2010b) for more details.

2.2 Evolution of the regularized crack surface

Based on the global constitutive equation for the evolution of the regularized crack surface functional postulated in Miehe et al. (2014), a local evolution of the phase field is given as

$$\begin{aligned} \underbrace{ \eta \dot{d} }_{\text {evolution}} = \underbrace{ (1-d) {{\mathcal {H}}} }_{\text {driving force}} - \underbrace{ [ \, d - l^2 \Delta d \, ] }_{\text {geometric resistance}} \end{aligned}$$

(2)

in the domain ${\mathcal {B}}_0$, along with the homogeneous Neumann condition $\nabla d \cdot {\varvec{ n }}_0 = 0 \ \ \text{ on }\ \partial {\mathcal {B}}_0$ for the crack phase field. The notation $\dot{(\cdot )}=d/dt(\cdot )$ refers to the time derivative of the underlying field. Here, $(1-d){\mathcal {H}}$ is the local crack driving force and is further assumed to be governed by the constitutive function

$$\begin{aligned} {\mathcal {H}}= \widetilde{{\mathcal {H}}}(state({\varvec{ X }},s),\quad 0\le s\le t))\, , \end{aligned}$$

(3)

where state stands for additional variables determined by the model for the anisotropic bulk response under consideration, such as the local energetic state or the local stress state in the solid. The left-hand side $\eta \dot{d}$ of the local evolution in (2) represents the viscous crack resistance, where $\eta \ge 0$ is a material parameter. The geometric crack resistance is related to the variational derivative of the crack surface density function, i.e., $d - l^2 \Delta d = l \delta _d \gamma _l(d, \nabla d)$. The Eq. (2) makes the evolution of the crack phase field dependent on the difference between the crack driving force and the geometric crack resistance. Note carefully, that the above framework also covers the rate-independent limit for $\eta =0$, where the crack surface is simply defined by an equilibrium for crack driving force and geometric crack resistance.

Fig. 2

Sharp and diffusive crack modeling. a Sharp crack at $x=0$. b Diffusive crack at $x=0$ modeled with the length scale l. Regularized curves obtained from minimization principle of diffusive crack topology $\int _{{\mathcal {B}}_0}\gamma _ldV \rightarrow Min!$ with crack surface density function $\gamma _l$. Thick line crack surface density function $\gamma _l$ (1) with regularization profile $exp[ - \vert x \vert /l ]$ satisfying $d(0)=1$, dotted line higher order regularization approach as suggested in Borden et al. (2014)

2.3 Irreversibility constraint on phase-field evolution

Within this work, we focus on an irreversibility of the crack evolution, governed by the constraint $\dot{\varGamma }_l(d) \ge 0$ on the evolution of the regularized crack surface. This is realized by expressing the local crack driving force ${\mathcal {H}}$ by the maximum value of the associated crack driving state function $\widetilde{D}$

$$\begin{aligned} {{\mathcal {H}}}({\varvec{ X }},t) = \max \limits _{s\in [0,t]} \widetilde{D}(state({\varvec{ X }},s)) \ge 0\, , \end{aligned}$$

(4)

obtained in the full process history $s\in [0,t]$. This function must be a monotonous function that depends on state variables state of the mechanical bulk response, satisfying

$$\begin{aligned} \widetilde{D}\vert ^\mathrm{unbroken}_\mathrm{state} = 0 \quad \text{ and }\quad \widetilde{D}\vert ^\mathrm{broken}_\mathrm{state} = \infty \ . \end{aligned}$$

(5)

Note that the above ansatz is consistent with the local evolution equation

$$\begin{aligned} \dot{d} = \frac{1}{\eta } \left\langle \; (1-d) \widetilde{D} - l \delta _d {\gamma }_l \; \right\rangle \ge 0 \end{aligned}$$

(6)

where $\langle x \rangle := (x + \vert x\vert )/2$ is the Macauley bracket.¹ Hence, a non-smooth evolution of the crack phase field takes place when the driving force exceeds the geometric crack resistance $\delta _d \gamma _l$. For the rate-independent limit $\eta \rightarrow 0$, the associated local evolution equation is

$$\begin{aligned} { \left. \begin{aligned}&\dot{d} \ge 0,\quad [(1-d) \widetilde{D} - l \delta _d {\gamma }_l] \le 0, \\&\dot{d}\, [(1-d) \widetilde{D} - l \delta _d {\gamma }_l] = 0 \end{aligned}\right\} } \end{aligned}$$

(10)

Table 1 Evolution and update of crack surface for given force ${\mathcal {H}}$

2.4 Time integration and operator split

The integration of (2) in the time interval $[t_n,t_{n+1}]$ with increment $\tau =t_{n+1}-t_{n}>0$ gives an update for the regularized crack surface. In what follows, all variables without a subscript are time discrete values at the current solution time $t_{n+1}$. A robust algorithm for the update of the phase field is obtained by an operator splitting, keeping the driving force ${\mathcal {H}}={\mathcal {H}}_n$ constant in the time step $[t_n,t]$. Note that this driving force provides the impact from the bulk response to the crack evolution.

The above assumption covers for the one-path algorithm, a semi-implicit time integration of the phase field, for the multi-path algorithm, where ${\mathcal {H}}$ is corrected, an implicit update scheme with Gauss–Seidel-type iterations between the phase field $d({\varvec{ X }},t)$ and the state variables $state({\varvec{ X }},t)$ of the bulk response. In both cases, ${\mathcal {H}}={\mathcal {H}}_n$ induces an algorithmic decoupling of updates for the phase field and the bulk response in the time interval under consideration, and is the key ingredient of a modular implementation of phase-field fracture. The algorithm in Table 1 provides a crack update module applicable to a wide spectrum of problems. The one-path algorithm for ${\mathcal {H}}= {\mathcal {H}}_n$ adopted here is in line with the treatment of Miehe et al. (2010a).

An incremental quadratic potential is introduced in Miehe et al. (2014) as

$$\begin{aligned} {\varPi }^{\tau }_d(d) = \int _{{\mathcal {B}}_0} \pi ^{\tau }_d({{\mathfrak {c}}}_d) dV = 0 \end{aligned}$$

(11)

in terms of the quadratic potential density per unit of the reference volume

$$\begin{aligned} \pi ^{\tau }_d({{\mathfrak {c}}}_d) =&\frac{\eta }{2\tau } (d-d_n)^2 + l \gamma _l (d, \nabla d) - l \gamma _l(d_n, \nabla d_n) \nonumber \\&\quad - [\, (d-d_n) - \frac{1}{2} (d^2-d^2_n)\, ] {\mathcal {H}} \end{aligned}$$

(12)

that depends on current phase field and its gradient ${{\mathfrak {c}}}_d := \{ d, \nabla d\}$. The potential ${\varPi }^{\tau }_d(d)$ must be stationary, attaining the minimum value zero for the current phase field d. Hence, the phase field is determined by the minimization principle

$$\begin{aligned} d = \text{ Arg }\{\underset{d}{\text{ inf }}\, {\varPi }{}^{\tau }_d ( d)\}. \end{aligned}$$

(13)

The corresponding Euler equation of this minimization principle is the linear update equation for the crack phase field

$$\begin{aligned} \underbrace{ \eta (d-d_n) /\tau }_{\text {crack update}} = \underbrace{ (1-d) {{\mathcal {H}}} }_{\text {driving force}} - \underbrace{ [ \, d - l^2 \Delta d \, ] }_{\text {geometric resistance}} \end{aligned}$$

(14)

in the domain ${\mathcal {B}}_0$, along with the Neumann condition $\nabla d \cdot {\varvec{ n }}_0 = 0$ on $\partial {\mathcal {B}}_0$. Note that this provides in the one-path setting with ${\mathcal {H}}= {\mathcal {H}}_n$ a semi-implicit integration of the continuous Eq. (2). The link to the bulk response is exclusively governed by the driving force ${\mathcal {H}}$. Keeping it constant, fully decouples the update of the crack phase field from the update of the constitutive response of the bulk.

2.5 Finite element discretization of crack phase field

The finite element implementation of the potential ${\varPi }^{\tau }_d$ in (11) is straightforward, yielding the space-discrete formulation

$$\begin{aligned} {\varPi }^{\tau \, h}_d({\varvec{ d }}_d) = \int _{{\mathcal {B}}^h_0} \pi ^{\tau }_d({\varvec{ B }}_d {\varvec{ d }}_d) dV = 0 \end{aligned}$$

(15)

based on the discretization ${{\mathfrak {c}}}^h_d({\varvec{ X }},t) = {\varvec{ B }}_d({\varvec{ X }}) {\varvec{ d }}_d(t)$ in terms of the finite element interpolation matrix ${\varvec{ B }}_d$ and the nodal values ${\varvec{ d }}_d$ of the phase field in a typical finite element mesh. The nodal values follow from the optimization problem

$$\begin{aligned} {\varvec{ d }}_d = \text{ Arg } \{\; \underset{{\varvec{ d }}_d}{\text{ inf }}\, {\varPi }{}^{\tau \, h}_d ( {\varvec{ d }}_d) \; \}, \end{aligned}$$

(16)

for the quadratic space-discrete potential, yielding the closed-form update of the nodal values for the phase field

$$\begin{aligned}&{\varvec{ d }}_d = - \left[ \int _{{\mathcal {B}}^h} {\varvec{ B }}^T_d [\partial ^2_{{{{\mathbf {c}}}}_d {{{\mathbf {c}}}}_d} \pi ^{\tau }_d({\varvec{ B }}_d{\varvec{ d }}_{d\, n}) {\varvec{ B }}_d \, dV \right] ^{-1} \nonumber \\&\quad \int _{{\mathcal {B}}^h} {\varvec{ B }}^T_d [\partial _{{{{\mathbf {c}}}}_d} \pi ^{\tau }_d({\varvec{ B }}_d{\varvec{ d }}_{d\, n})] \, dV \ . \end{aligned}$$

(17)

Reader is referred to Miehe et al. (2010b) for more details on the finite element implementation of the phase-field fracture. Note again that this solution is independent from the finite element updates of bulk response due to the algorithmic decoupling within the time step under consideration. The only interface to the bulk response is provided by the driving force ${\mathcal {H}}_n$ that enters the potential $\pi ^{\tau }_d$ in (12); see Table 1.

3 Driving force for brittle failure and transition rules

The impact from the bulk response on the crack propagation is governed by the crack driving force ${\mathcal {H}}$ that is linked to a constitutive crack driving state function $\widetilde{D}(state)$. Vice versa, the crack phase field enters the state functions of the bulk material via constitutive transition rules $\widehat{{\varvec{ f }}}(state; d)$ from the unbroken to the broken state. This section outlines general structures of these functions, which are specified for a model problem in Sect. 5.

3.1 The maximum principal stress driving force criterion

The key aspect is the modeling of the constitutive function ${\mathcal {H}}$, introduced in (4), that governs the local nominal crack driving force depending on the stress state. A brief summary of the principal stress-based growth function developed in Miehe et al. (2014), that depends on a spectral decomposition of the nominal Cauchy stress of the undamaged solid material is given below

$$\begin{aligned} {\varvec{\sigma }}= \sum _{a=1}^3 {\sigma }_{a}\, {\varvec{ n }}_a\otimes {\varvec{ n }}_a \ , \end{aligned}$$

(18)

where $\{{\sigma }_{a} \}$ are the principal stresses and $\{ {\varvec{ n }}_a \}$ the eigenvectors. The crack driving state function considered is

$$\begin{aligned} \widetilde{D}_\mathrm{iso} = \zeta \left\langle \sum _{a=1}^3 \left( \frac{\langle {\sigma }_{a} \rangle }{\sigma _{\text {crit}}}\right) ^2 - 1 \right\rangle \end{aligned}$$

(19)

and models an isotropic failure surface in the principal stress state. $\sigma _{\text {crit}}>0$ is a critical fracture tensile stress and $\zeta >0$ a material parameter that enforces the slope of the quadratic driving force function. Note that this criterion is characterized by a threshold, that guarantees the existence of non-damaged zones where the crack phase field is zero. To model the failure response in anisotropic biological tissues, the criterion (19) needs to account for the inherent tissue morphology, giving rise to an orthotropic behavior, for accurate prediction of the failure response as presented in the following sections.

Fig. 3

Illustration of the global Cartesian coordinate system spanned by the orthonormal unit vectors $\{{\varvec{ e }}_i\}_{i=1,3}$ with a local orthotropic axes spanned by the orthogonal unit vectors $\{{\varvec{ g }}_i\}_{i=1,3}$. The unit tangents ${\varvec{ a }}^{(1)}$ and ${\varvec{ a }}^{(2)}$ to the two fiber families are inclined at an angle of $2\gamma$ to each other. The 1 and 2 directions span the plane of fiber families (plane of paper) and 3 direction points into the plane of the paper

3.2 Alignment of principal orthotropy axes in soft tissues

The histology of biological tissues makes them ideally an orthotropic material due to the presence of two identical fiber families with different directions ${\varvec{ a }}^{(1)}$ and ${\varvec{ a }}^{(2)}$ inclined at a certain angle as discussed in detail in Sect. 4.2. To incorporate an orthotropic failure criterion, local orthotropy axes ${\varvec{ g }}_i$ are defined in addition to the global Cartesian coordinate axes ${\varvec{ e }}_i$ for $i=1,\ldots ,3$ as follows,

$$\begin{aligned}&{\varvec{ g }}_1 = \dfrac{{\varvec{ a }}^{(1)}+{\varvec{ a }}^{(2)}}{\left| {\varvec{ a }}^{(1)}+{\varvec{ a }}^{(2)}\right| }\,,\quad {\varvec{ g }}_2 = \dfrac{{\varvec{ a }}^{(2)}-{\varvec{ a }}^{(1)}}{\left| {\varvec{ a }}^{(2)}-{\varvec{ a }}^{(1)}\right| }\, \quad \text{ and }\quad \nonumber \\&{\varvec{ g }}_3 = \dfrac{{\varvec{ g }}_1\times {\varvec{ g }}_2}{\left| {\varvec{ g }}_1\times {\varvec{ g }}_2\right| }, \end{aligned}$$

(20)

which are orthonormal with unit magnitude. See Fig. 3 for an illustration of the different coordinate systems. Based on the local orthotropic triad $\{{\varvec{ g }}_i\}_{i=1,3}$, a second-order anisotropy tensor ${\varvec{ A }}$ is introduced as

$$\begin{aligned} {\varvec{ A }}= {{\mathfrak {a}}}_1\,{\varvec{ g }}_1\otimes {\varvec{ g }}_1 + {{\mathfrak {a}}}_2\,{\varvec{ g }}_2\otimes {\varvec{ g }}_2 + {{\mathfrak {a}}}_3\,{\varvec{ g }}_3\otimes {\varvec{ g }}_3 \end{aligned}$$

(21)

where the coefficients $\{{{\mathfrak {a}}}_i\}_{i=1,3}$ are the scaling factors along the orthotropy axes $\{{\varvec{ g }}_i\}_{i=1,3}$, respectively. The tensor ${\varvec{ A }}$ in (21) automatically satisfies the conditions of invariance as imposed in (24). For the plane problems of interest here, the components of the anisotropy tensor ${\varvec{ A }}$ for an arbitrary counterclockwise rotation by angle $\theta$ of orthogonal axes $\{{\varvec{ g }}_i\}_{i=1,2}$ along ${\varvec{ e }}_3$ axis are given as

$$\begin{aligned} A_{ij} = \begin{bmatrix} {{\mathfrak {a}}}_1\cos ^2\theta + {{\mathfrak {a}}}_2\sin ^2\theta&\quad ({{\mathfrak {a}}}_1-{{\mathfrak {a}}}_2)\cos \theta \sin \theta&\quad 0 \\ ({{\mathfrak {a}}}_1-{{\mathfrak {a}}}_2)\cos \theta \sin \theta&\quad {{\mathfrak {a}}}_1\sin ^2\theta + {{\mathfrak {a}}}_2\cos ^2\theta&\quad 0\\ 0&\quad 0&\quad 1 \end{bmatrix}. \end{aligned}$$

(22)

It needs to be emphasized here that the above representation recovers the case of transverse isotropy and isotropy by the following:

• Transverse isotropy: By setting ${{\mathfrak {a}}}_1={{\mathfrak {a}}}_2$.

• Isotropy: By setting ${{\mathfrak {a}}}_1={{\mathfrak {a}}}_2={{\mathfrak {a}}}_3$.

The coefficients $\{{{\mathfrak {a}}}_i\}_{i=1,3}$ enter as the material parameters in the model. However, only two independent coefficients need to be prescribed for a three-dimensional problem and only one for a two-dimensional problem. The remaining coefficient is set to unity for the given direction of the critical fracture tensile stress $\sigma _{\text {crit}}$.

3.3 Anisotropic tensile stress-based driving force criterion

In this section, we derive a general orthotropic failure criterion based on the tensile part of the symmetric Cauchy stress tensor ${\varvec{\sigma }}$. The crack driving state function in (4), alternative to (19), with a threshold is obtained from a scalar-valued tensor function ${\varPhi }({\varvec{\sigma }}^+)$ as

$$\begin{aligned}&\widetilde{D}_\mathrm{ani} = \zeta \big \langle {\varPhi }({\varvec{\sigma }}^+)-1\big \rangle \quad \text{ with }\quad \nonumber \\&{\varvec{\sigma }}^+ = \sum _{a=1}^3 \langle {\sigma }_{a}\rangle \, {\varvec{ n }}_a\otimes {\varvec{ n }}_a. \end{aligned}$$

(23)

The argument ${\varvec{\sigma }}^+$ of function ${\varPhi }$ is characterized by a symmetry group ${\mathcal {R}}{\mathcal {O}}(3)\subset {\mathcal {S}}{\mathcal {O}}(3)$, which is a subset of the special orthogonal group ${\mathcal {S}}{\mathcal {O}}(3)$, and satisfies the following invariance condition

$$\begin{aligned} {\varPhi }({\varvec{\sigma }}^+) = {\varPhi }({\varvec{ R }}\,{\varvec{\sigma }}^+\,{\varvec{ R }}^T) \quad \forall \, {\varvec{ R }}\in {\mathcal {R}}{\mathcal {O}}(3). \end{aligned}$$

(24)

The function ${\varPhi }$ is restricted to quadratic terms in ${\varvec{\sigma }}^+$ by introducing a symmetric fourth-order anisotropy tensor ${{\mathbb {I}}}_A$ (Steinmann et al. 1994) and a specific invariant form of failure surface as

$$\begin{aligned}&{\varPhi }= \dfrac{1}{2\sigma ^2_{\text {crit}}}({\varvec{\sigma }}^+:{{\mathbb {I}}}_A:{\varvec{\sigma }}^+)\, \quad \text{ with }\quad \nonumber \\&{{\mathbb {I}}}_A = \dfrac{1}{2}(A_{ik}A_{jl}+A_{il}A_{jk}){\varvec{ e }}_i\otimes {\varvec{ e }}_j\otimes {\varvec{ e }}_k\otimes {\varvec{ e }}_l\,, \end{aligned}$$

(25)

where $\sigma _{\text {crit}}$ is the reference uniaxial critical fracture tensile stress and $A_{ij}$ are the components of the second-order anisotropy tensor ${\varvec{ A }}$ for $i,j=1,\ldots ,3$ introduced in (21). The symmetry of fourth-order tensor ${{\mathbb {I}}}_A$ with coefficients $\{{{\mathfrak {a}}}_i\}_{i=1,3}>0$ ensures its positive semi-definite form and thereby a convex failure surface resulting from (25). Expansion of the first equation in (25), simplified to the case when orthotropy axes $\{{\varvec{ g }}_i\}_{i=1,3}$ and the principal axes $\{{\varvec{ n }}_i\}_{i=1,3}$ coincide with the global axes $\{{\varvec{ e }}_i\}_{i=1,3}$, reduces to

$$\begin{aligned} {\varPhi }= \bigg (\dfrac{\langle \sigma _1\rangle }{\sigma _{\text {crit}}/{{\mathfrak {a}}}_1}\bigg )^2 + \bigg (\dfrac{\langle \sigma _2\rangle }{\sigma _{\text {crit}}/{{\mathfrak {a}}}_2}\bigg )^2 + \bigg (\dfrac{\langle \sigma _3\rangle }{\sigma _{\text {crit}}/{{\mathfrak {a}}}_3}\bigg )^2. \end{aligned}$$

(26)

Substitution of (26) in (23) yields an expression for an orthotropic crack driving state function, similar to (19), as

$$\begin{aligned} \widetilde{D}_\mathrm{ani} = \zeta \left\langle \sum _{i=1}^3 \left( \frac{\langle {\sigma }_{i} \rangle }{\sigma _{\text {crit}}/{{\mathfrak {a}}}_i}\right) ^2 - 1 \right\rangle . \end{aligned}$$

(27)

An illustration of the failure loci is shown in Fig. 4 where as the corresponding surface of crack driving state function is shown in Fig. 5. Notice that for ${{\mathfrak {a}}}_i=1$ for $i=1,\ldots ,3$, the criterion for isotropic failure surface (19) is retrieved. The simulations presented in Sect. 5 employ the general orthotropic failure criterion (25).

3.4 Transition rules from unbroken to fully broken response

Depending on the crack phase field $d\in [0,1]$, constitutive functions in the bulk undergo a phase transition from the unbroken to the fully broken state. This includes conceptually a degradation, e.g., for the mechanical stresses, but also a growth, e.g., for the non-mechanical fluxes at the crack faces. A general structure of this phase transition for a generic constitutive function $\widehat{\varvec{ f }}$ for the bulk response is provided by a transition rule

$$\begin{aligned} \widehat{{\varvec{ f }}}(state; d) = g^s(d)\, \widetilde{{\varvec{ f }}}{}^s(state) + g^c(d) \, \widetilde{{\varvec{ f }}}{}^c(state) \end{aligned}$$

(28)

that depends on the phase-field and a non-specified set (state) of constitutive state variables for the bulk response. Here, $\widetilde{{\varvec{ f }}}{}^s(state)$ and $\widetilde{{\varvec{ f }}}{}^c(state)$ are effective functions in the unbroken and the fully broken case. The dual weight functions may have the simple form

$$\begin{aligned} g^s(d) = (1-d)^m \quad \text{ and }\quad g^c(d) = d^m\,. \end{aligned}$$

(29)

Here, $g^s(d)$ recovers for $m=1$ the classical $(1-d)$-theory of damage and for $m=2$ the variational theory of brittle fracture in elastic solids outlined in Miehe et al. (2010b).

Fig. 4

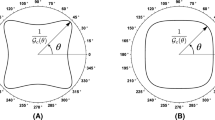
Failure surfaces for orthotropic tensile stress failure criterion (27) in principal plane stress space for different degrees of anisotropies with coefficients a ${{\mathfrak {a}}}_1=2$, ${{\mathfrak {a}}}_2=1$ and b ${{\mathfrak {a}}}_1=1$, ${{\mathfrak {a}}}_2=2$ used in second-order anisotropy tensor (21) for the case when orthotropy axes ${\varvec{ g }}_i$ are coincident with the global axes ${\varvec{ e }}_i$ for $i=1,\ldots ,3$

Fig. 5

The surface of orthotropic crack driving state function $\widetilde{D}_\mathrm{ani}$ is shown in the principal plane stress space by plotting Eq. (27) with scaling coefficients ${{\mathfrak {a}}}_1=2,{{\mathfrak {a}}}_2=1$

Fig. 6

A schematic of primary fields in body ${\mathcal {B}}_0$ undergoing fracture. The deformation field ${\varvec{\varphi }}$, the fracture phase field d and the history field ${\mathcal {H}}$ are defined on the solid domain ${\mathcal {B}}_0$. a The deformation field is constrained by the Dirichlet- and Neumann-type boundary conditions ${\varvec{\varphi }}= \bar{{\varvec{\varphi }}}$ on $\partial {\mathcal {B}}^{\varphi }_{0}$ and ${\varvec{ P }}\cdot {\varvec{ n }}_0 = \bar{{\varvec{ T }}}$ on $\partial {\mathcal {B}}^{T}_{0}$ with $\partial {\mathcal {B}}_0 = \partial {\mathcal {B}}^{\varphi }_{0} \cup \partial {\mathcal {B}}^{T}_{0}$. b The fracture phase field is constrained by the possible Dirichlet-type boundary condition $d = 1$ on ${\varGamma }$ and the Neumann condition $\nabla d\cdot {\varvec{ n }}_0 = 0$ on the full surface $\partial {\mathcal {B}}_0$. c The history field ${\mathcal {H}}$ defined in Eq. (4) is based on the maximum of stress-based criterion in the deformation history. It drives the evolution of the fracture phase field d via Eqs. (19) or (23)

4 Finite elasticity coupled with phase-field fracture

This section focuses on the description of bulk response undergoing fracture which is coupled to the phase field with a constitutive setup of degrading energy. Section 4.1 presents primary field variables and coupled governing equations. Section 4.2 presents a brief overview of the tissue histology concerning human iliac artery. The free energy function characterizing the anisotropic behavior of the tissues is presented in Sect. 4.3.

4.1 Primary fields and governing equations

Consider the motion of a body ${\mathcal {B}}_0$ given by a nonlinear deformation map ${\varvec{\varphi }}$ undergoing finite strains with given body force $\bar{{\varvec{\gamma }}}$ per unit volume. The overall response of the body under fracture is described by the crack phase field d and the deformation field ${\varvec{\varphi }}$ written as

$$\begin{aligned} {\varvec{\varphi }}: {\left\{ \begin{array}{ll} \begin{array}{l} {\mathcal {B}}_0\times {\mathcal {T}}\rightarrow {\mathcal {R}}^\delta \\ ({\varvec{ X }},t) \mapsto {\varvec{ x }}={\varvec{\varphi }}({\varvec{ X }},t). \end{array} \end{array}\right. } \end{aligned}$$

(30)

${\varvec{\varphi }}$ maps at time $t\in {\mathcal {T}}$ the materials points ${\varvec{ X }}\in {\mathcal {B}}_0$ of reference configuration ${\mathcal {B}}_0\in {\mathcal {R}}^{\delta }$ to spatial points ${\varvec{ x }}\in {\mathcal {B}}_t$ in the current configuration ${\mathcal {B}}_t\in {\mathcal {R}}^{\delta }$. The deformation gradient is ${\varvec{ F }}=\nabla {\varvec{\varphi }}({\varvec{ X }},t)\in \text {GL}{(\delta )}$, which is imposed to constraint $J:=\det {[{\varvec{ F }}]}>0$. Furthermore, let ${\varvec{ g }}\in Sym_+(\delta )$ be the standard metric of current configuration ${\mathcal {B}}_t$, the pull back of which yields the right Cauchy-Green tensor ${\varvec{ C }}= {\varvec{ F }}^T{\varvec{ g }}{\varvec{ F }}$. A schematic illustration of the two primary unknowns with the corresponding boundary conditions is shown in Fig. 6. For the soft biological tissue under consideration, the body ${\mathcal {B}}_0$ is assumed to consist of two fiber families denoted by unit vectors ${\varvec{ a }}^{(a)}$ for $a=1,2$ with the corresponding structural tensors given as

$$\begin{aligned} {\varvec{ M }}^{(1)}={\varvec{ a }}^{(1)}\otimes {\varvec{ a }}^{(1)} \quad \text{ and }\quad {\varvec{ M }}^{(2)}={\varvec{ a }}^{(2)}\otimes {\varvec{ a }}^{(2)}. \end{aligned}$$

(31)

In order to construct the constitutive equations for hyperelastic response, an objective anisotropic free energy function is introduced which depends on the deformation gradient ${\varvec{ F }}$ and the structural tensors ${\varvec{ M }}^{(1,2)}$ as

$$\begin{aligned} {\varPsi }= \widehat{{\varPsi }}({\varvec{ F }},{\varvec{ M }}^{(1,2)};d,\nabla d), \end{aligned}$$

(32)

and represents the energy stored per unit reference volume. The dependence on the fracture phase field d and its gradient $\nabla d$ is considered as a geometric property and hence separated by a semicolon. The degradation of the stored energy due to evolving phase field d takes the form

$$\begin{aligned} \widehat{{\varPsi }} = [g^s(d)+k]\widetilde{{\varPsi }}({\varvec{ F }},{\varvec{ M }}^{(1,2)}) \end{aligned}$$

(33)

following the argument in (28). Here, $\widetilde{{\varPsi }}$ is energy stored in undamaged material with a specific form given in Sect. 4.3 and $g^s(d)$ is a monotonically decreasing function defined in (29). At a fully broken state $d=1$, the full degradation of the energy $\widehat{{\varPsi }}$ in (33) is circumvented by the artificial elastic rest energy density $k\widetilde{{\varPsi }}$ for small parameter $k\approx 0$.

The final sets of governing coupled equations of finite elasticity with phase-field fracture are shown in Table 2 in their strong form. The first Piola–Kirchhoff stress tensor is introduced as ${\varvec{ P }}=[g^s(d)+k]\widetilde{{\varvec{ P }}}$ where $\widetilde{{\varvec{ P }}}$ for undamaged material is defined in (38). Following the finite element discretization of crack phase field in Sect. 2.5, the current deformation field ${\varvec{\varphi }}\approx {\varvec{\varphi }}^h$ is approximated from the minimization of discretized potential density $\pi ^{\tau }_\varphi$ as

$$\begin{aligned}&{\varvec{ d }}_\varphi = \text{ Arg } \left\{ \; \underset{{\varvec{ d }}_\varphi }{\text{ inf }} \int _{{\mathcal {B}}^h_0} \pi ^{\tau }_\varphi ({\varvec{ B }}_\varphi {\varvec{ d }}_\varphi )\,dV \; \right\} \quad \text{ with }\quad \nonumber \\&\pi ^{\tau }_\varphi =\widehat{{\varPsi }}({\varvec{ F }}^h,{\varvec{ M }}^{(1,2)};d) - \bar{{\varvec{\gamma }}}\cdot {\varvec{\varphi }}^h \end{aligned}$$

(34)

given in terms of the discretized deformation gradient ${{{\mathbf {c}}}}^h_\varphi :={\varvec{ F }}^h={\varvec{ B }}_\varphi {\varvec{ d }}_\varphi$. Here, ${\varvec{ B }}_\varphi$ is a global strain displacement matrix consisting of shape functions and its derivatives, and ${\varvec{ d }}_\varphi \in {\mathcal {R}}^{\delta }$ is a global array of nodal position vector. A Newton–Raphson iteration scheme is used for the solution of the associated Euler equations of nonlinear elasticity at finite strains as

$$\begin{aligned}&{\varvec{ d }}_\varphi \Leftarrow {\varvec{ d }}_\varphi - \left[ \int _{{\mathcal {B}}^h} {\varvec{ B }}^T_\varphi [\partial ^2_{{{{\mathbf {c}}}}_\varphi {{{\mathbf {c}}}}_\varphi } \pi ^{\tau }_\varphi ] {\varvec{ B }}_\varphi \, dV \right] ^{-1} \nonumber \\&\int _{{\mathcal {B}}^h} {\varvec{ B }}^T_\varphi [\partial _{{{{\mathbf {c}}}}_\varphi } \pi ^{\tau }_\varphi ] \, dV \ , \end{aligned}$$

(35)

which updates the current nodal values of the deformation field at time $t_{n+1}$.

Table 2 Coupled governing equations of finite elasticity with fracture

4.2 Morphology of human iliac artery

One of the most interesting soft biological tissues to study is blood-carrying arteries due to their significance in medical examination of relevant diseases as well as their similarity to other tissues. Among the family of arteries, the elastic iliac artery is discussed here, although other arteries such as aorta or carotid have similar structures. A detailed discussion of the microscopic structure and deformation mechanisms of such tissues can be found in Rhodin (1980) and Silver et al. (1989). For conciseness, only a brief summary is presented here. An artery can be thought of as a composite structure which mainly consists of three different layers: the adventitia, the media and the intima. These layers are made up of collagen fibers of type I, surrounded by a groundmatrix consisting of elastin, endothelial cells, fibroblast and fibrocytes. A schematic illustration of the arterial structure is shown in Fig. 7. The adventitia is the outermost layer whose thickness is not well defined and depends on its topographical site and its physiological function. It is surrounded by loose connective tissue with primary collagen fibers arranged in a double helix structure around the circumferential direction and contributes significantly to the artery strength. The medial layer comes next to adventitial layer and is in the middle of the three aforementioned layers. In the media too, the collagen fibers form a double helix structure, however, with a smaller pitch as compared to the adventitia, and also contributes significantly to the arterial strength. The intima is the innermost layer and mostly consists of endothelial cells. It is observed that intima thickens and stiffens with age and these pathological changes are often associated with the arterial disease called atherosclerosis. It involves deposition of fatty substances, calcium, collagen fibers, cellular waste products and fibrin, generally referred to as atherosclerotic plaque. This changes geometrical and mechanical properties of the arterial wall and affects blood-carrying function by partial blockage of the lumen. A simulation of balloon angioplasty, which is a surgical intervention to treat atherosclerosis, is performed in Sect. 5.3 with a real arterial cross section from Holzapfel et al. (2004) to model tissue rupture.

Fig. 7

Left illustration of the geometrical characteristics of an iliac artery where three concentric layers of intima, media and adventitia form the overall tubular structure. Middle illustration of a dissected adventitial strip for tensile tests where fiber families ${\varvec{ a }}^{(1)}$ and ${\varvec{ a }}^{(2)}$ are inclined at an angle $\gamma$ to the circumferential direction. Right illustration of a medial strip dissected radially for peeling test with a single fiber direction ${\varvec{ a }}$

4.3 Free energy functions for soft biological tissues

The microstructure of arterial walls is composed of wavy collagen fibers embedded in a soft isotropic matrix. These fiber families are predominantly identified by two unit fiber directions ${\varvec{ a }}^{(1)}$ and ${\varvec{ a }}^{(2)}$ aligned at an angle $\gamma$ with respect to circumferential direction as illustrated in Fig. 7. An undamaged hyperelastic constitutive storage function for arterial walls is postulated with the following split

$$\begin{aligned} \widetilde{{\varPsi }}({\varvec{ F }},{\varvec{ M }}^{(1,2)}) =&\underbrace{\dfrac{\mu }{\beta }[(\det {\varvec{ F }})^{-\beta }-1] + \dfrac{\mu }{2}({\varvec{ F }}:{\varvec{ F }}-3)}_{\text {isotropic matrix}} \nonumber \\&+ \underbrace{\sum _{a=1}^{2}\widetilde{{\varPsi }}_{\text {aniso}}^{(a)}({\varvec{ F }},{\varvec{ M }}^{(a)})}_{\text {anisotropic fibers}} \end{aligned}$$

(36)

where the volumetric and deviatoric parts of the isotropic matrix are not necessarily decoupled. The volumetric part of the isotropic matrix assures the weak compressibility of the material in terms of low shear modulus $\mu \ge 0$ and parameter $\beta =2\nu /(1-2\nu )$ given in terms of the Poisson ratio $\nu$. The deviatoric part represents the energy stored in the soft isotropic matrix. The polyconvexity of the free energy contribution corresponding to isotropic matrix in (36) is well understood.

The anisotropic part $\widetilde{{\varPsi }}_{\text {aniso}}^{(a)}$ in (36) is the energy stored in wavy collagen fiber families and has been extensively proposed in the literature. Here, we follow the potential proposed in Billiar and Sacks (2000) for the anisotropic part to write

$$\begin{aligned} \widetilde{{\varPsi }}_{\text {aniso}}^{(a)}({\varvec{ F }},{\varvec{ M }}^{(a)})&= \dfrac{k_1}{k_2}\bigg [\exp {\{k_2({\varvec{ C }}:{\varvec{ M }}^{(a)}-1)\}-1}\bigg ]\nonumber \\&- k_1({\varvec{ C }}:{\varvec{ M }}^{(a)}-1). \end{aligned}$$

(37)

The scalar product ${\varvec{ C }}:{\varvec{ M }}^{(a)}$ of the right Cauchy-Green tensor ${\varvec{ C }}={\varvec{ F }}^T{\varvec{ F }}$ and structural tensor ${\varvec{ M }}^{(a)}$ is the fourth invariant which represents the square of the stretch along the fiber directions ${\varvec{ a }}^{(a)}$ for $a=1,2$. The additional material parameters $k_1>0$ and $k_2>0$ are introduced in (37) where the former represents fiber stiffness and latter a dimensionless constant. The key difference of anisotropic potential in (37) to the potentials introduced in Holzapfel et al. (2000) and Gasser et al. (2006) lies in the energy storage in compression of collagen fibers. Here, a very small compressive stiffness is made available to collagen fibers for better stability of numerical simulations at certain deformations. The convexity of the anisotropic free energy contribution in (37) can be easily established for any general case by simply evaluating its Hessian to be positive semi-definite.

The construction of the overall free energy function (36) automatically fulfills the requirements of polyconvexity, whose results of surface plots and convex contours are shown in Figs. 8 and 9, respectively. A deformation gradient ${\varvec{ F }}=\text {diag}(\lambda _1,\lambda _2,1)$ for $0.5\le \lambda _{1,2}\le 1.5$ is used with material parameters $\mu =10$ kPa, $\nu =0.3$, $k_1=20$ kPa, $k_2=2$ and $\gamma =40^\circ$. The derivate of the storage function (36) with respect to the deformation gradient ${\varvec{ F }}$ gives the undamaged first Piola–Kirchhoff stress $\widetilde{{\varvec{ P }}}$ as

$$\begin{aligned} \widetilde{{\varvec{ P }}}&= -\mu (\det {\varvec{ F }})^{-\beta }{\varvec{ F }}^{-T} + \mu {\varvec{ F }}\, \nonumber \\&\quad \, + \sum _{a=1}^{2}2\,k_1\big [\exp {\{k_2({\varvec{ C }}:{\varvec{ M }}^{(a)}\!-\!1)\}} \!-\! 1\big ] ({\varvec{ F }}{\varvec{ a }}^{(a)}\otimes {\varvec{ a }}^{(a)}). \nonumber \\ \end{aligned}$$

(38)

Fig. 8

For the anisotropic free energy function (36) smoothly continuous surface plot with a softer compressive response is shown in the stretch space $\{\lambda _1,\,\lambda _2\}$

Fig. 9

The locally convex contours of the anisotropic free energy function (36) in the stretch space $\{\lambda _1,\,\lambda _2\}$ is shown

5 Representative numerical simulations

This section presents the modeling capabilities of the framework of phase-field fracture applied to the transversely isotropic biological soft tissues particularly the human iliac artery wall through representative numerical examples shown in Sects. 5.1, 5.2 and 5.3.

Table 3 Material properties for uniaxial tensile tests in adventitial strips

5.1 Uniaxial tensile tests of iliac artery adventitial strips

Strips of artery wall from adventitia layer are dissected along the circumferential and axial directions as shown in Fig. 7 and subjected to monotonic uniaxial loading tests in the experimental investigations of Holzapfel et al. (2004). In the numerical simulations presented in this section, strips of dimensions $10\times 3$ mm$^2$ are used and subjected to a nominal strain of up to $50\,\%$. The material parameters used are given in Table 3 which are in close agreement with the similar parameters used in Gasser et al. (2006). The finite element computation is performed with approximately 30000 displacement-based (Q1) four-noded quadrilateral elements with the plane strain assumption and different values for viscosity $\eta =0, 10^{-6}$ and $10^{-5}$ kNs/mm$^2$ with length scale $l=0.06$ mm. The problem setup is shown on the left of Fig. 10 where a vertical displacement u is applied at top and bottom surfaces in $10^4$ solution steps up to complete failure.The horizontal displacement at these surfaces is not constrained. The resulting load-displacement curves up to complete failure along axial and circumferential loading directions are shown in Fig. 11a, b, respectively.

Fig. 10

Problem setup: geometry and loading conditions for a uniaxial tension test with fiber family ${\varvec{ a }}^{(1,2)}$ orientation separated by angle $2\gamma$ and b peeling test with single fiber family ${\varvec{ a }}$

Fig. 11

Uniaxial tension test: plots of the load at top surface of the specimen against the applied strain for a axial direction and b circumferential direction, with different values of viscosity $\eta$. A comparison with the respective mean experimental load–strain curves from Holzapfel et al. (2004) is provided

Fig. 12

Uniaxial tensile test: Simulation results of loading in the axial direction are shown with a contours of crack phase field d and b contours of principal Cauchy stress $\sigma _2$, at different loading stages

A quantitative comparison of load-displacement curves with the experimental results validates the choice of material parameters used in Table 3. The anisotropic response with lower stiffness along the circumferential direction is very well captured. The crack driving force obtained by the anisotropic failure criterion (23) results in crack initiation from the middle right finite element and propagation toward left as soon as the stresses reach the failure surface. The abrupt loss of stiffness or load-bearing capacity is shown in the numerical load-displacement curves which is in accord with the experimental observation. The influence of viscosity parameter can be seen from the plots in Fig. 11 where the higher viscosity slightly delays crack propagation as expected. The resulting failure contours of crack phase field d and maximum principal Cauchy stress $\sigma _2$ are shown in Fig. 12 for axial direction on the left and right, respectively, where the elements with $d>0.9$ are blanked for visualization. The snapshots are captured at different applied nominal strains to show the evolution of crack phase field and stresses. Starting as a small crack, the failure immediately propagates through the tissue with a similar behavior observed in circumferential direction.

5.2 Peeling test of iliac artery medial strips

Table 4 Material properties for peeling test of medial strips

Fig. 13

Peeling test: contours of a crack phase field d and b maximum principal Cauchy stress $\sigma _2$, shown at different dissection lengths in the deformed configuration

Study of arterial dissection has enormous relevance of surgical interest which involves tear of delicate internal lining of arterial wall. In this section, the experimental investigations of Sommer et al. (2008) are modeled where the strips of medial aorta are peeled in the circumferential direction to study their dissection properties. See Fig. 7 for an illustration of tissue morphology. In the numerical simulations of phase-field fracture presented in this section, a medial strip of dimensions $4\times 1.2$ mm$^2$ is used with an initial vertical notch of size 0.4 mm at the top surface as illustrated on the right of Fig. 10. The bottom surface is fixed, whereas a horizontal displacement $u=4.5$ mm is applied at the two arms on the top surface in $10^3$ solution steps. Contrary to the morphology in Sect. 5.1, the medial strip along the radial direction of the artery in this section possesses a single fiber family ${\varvec{ a }}$ aligned perpendicular to the direction of applied displacement u. The spatial discretization consists of approximately 7000 displacement-based (Q1) four-noded quadrilateral elements with the plane strain assumption and viscosity $\eta =10^{-5}$ kNs/mm$^2$ with length scale $l=0.06$ mm. The transversely isotropic form of anisotropic stress driving force criterion (23) is employed for the evolution of crack phase field as the peeling predominantly takes place in a single radial plane.

The corresponding material parameters used for the peeling simulation are given in Table 4 which agree closely with the parameters in Gasser and Holzapfel (2006). The load per unit width of one of the arms is plotted against the applied displacement and shown on the right of Fig. 14 with a quantitative comparison with experimental data from Sommer et al. (2008). Before the crack starts to propagate from the tip of notch, almost linear response is observed till load per unit width of approximately 23 mN/mm, which agrees well with the experimental results of Sommer et al. (2008) and numerical results from Gasser and Holzapfel (2006) and Ferrara and Pandolfi (2010). At this nearly constant load, the crack continues to develop downwards vertically till the end of simulation. The contours of the crack phase field and the maximum principal Cauchy stress from peeling simulation are shown in Fig. 13a, b, respectively, in the deformed configuration at different stages of loading.

Fig. 14

Peeling test: plot of load per unit width on one side of the notch at top surface against the applied displacement with a comparison to mean experimental value from Sommer et al. (2008)

Fig. 15

Inflation test: cross-sectional view of human atherosclerotic artery with six different material layers, namely adventitia ($m_1$), media ($m_2$), fibrotic media ($m_3$), fibrous cap ($m_4$), lipid pool ($m_5$) and calcification ($m_6$), as given in Holzapfel et al. (2004)

5.3 Inflation test of atherosclerotic iliac artery

The final example of phase-field modeling of fracture in soft biological tissues is presented in this section where the procedure of balloon angioplasty for an atherosclerotic artery is simulated. As discussed in Sect. 1, angioplasty is a surgical intervention to mechanically widen the stenotic lumen by inflating and implanting a stent inside the artery wall. In this section, a two-dimensional cross section of a real atherosclerotic artery, obtained by high-resolution magnetic resonance imaging, from Holzapfel et al. (2004) is taken as the starting point for numerical analysis, which differs from a simplified symmetric tubular structure as shown on the left of Fig. 7. The actual cross section of a diseased artery consists of various layers, such as adventitia $m_1$, media $m_2$, fibrotic media $m_3$, fibrous cap $m_4$, lipid pool $m_5$ and calcifications $m_6$, as marked in Fig. 15. A layer of non-diseased intima is ignored, and fibrotic intima and diseased fibrotic media are treated as single layer, i.e., fibrotic media $m_3$, as followed in Balzani et al. (2012). The overall solution process for the inflation test is divided into two stages. First, a thermal boundary value problem is solved in Sect. 5.3.1 to interpolate fiber orientations in fibrous layers $m_1,\ldots ,m_4$. Based on the computed orientations, a mechanical boundary value problem of angioplasty is solved next in Sect. 5.3.2 to allow for the realistic development of phase-field fracture.

5.3.1 Thermal boundary value problem

The complexity of the morphology of the atherosclerotic artery requires some steps of preprocessing where the fiber orientations inside the material layers $m_1$,$\ldots$, $m_4$ need to be computed from given boundary conditions. In order to do so, a heat-conduction-like problem is solved with the Dirichlet boundary conditions as shown in the following steps.

• 1. The geometry in Fig. 15 is first discretized with 6086 four-noded quadrilateral (Q1) elements with materials tags $m_1,\ldots ,m_6$ corresponding to each layer.

• 2. For all nodes $i=1,\ldots ,n^{a}$ lying on the closed boundaries $\partial _{1}{\mathcal {B}}$, $\partial _{2}{\mathcal {B}}$ and $\partial _{3}{\mathcal {B}}$, compute the x- and y-components of tangent vectors with the line-weighted averaging algorithm, which is similar to area-weighted averaging in Max (1999), as

  $$\begin{aligned}&\bar{\theta }^i_X=\dfrac{\ell _{i-1}\Delta X_i + \ell _{i}\Delta X_{i-1}}{\ell _{i-1}+\ell _{i}} \quad \text{ and }\quad \nonumber \\&\bar{\theta }^i_Y=\dfrac{\ell _{i-1}\Delta Y_i + \ell _{i}\Delta Y_{i-1}}{\ell _{i-1}+\ell _{i}}. \end{aligned}$$

  (39)

  A schematic of the result is shown in Fig. 16a. In Eq. (39), $\Delta (\cdot )_k=(\cdot )_k-(\cdot )_{k+1}$ are the x- and y-components of a vector between nodes k and $k+1$ normalized by its length $\ell _k$. For further calculations, unit tangents are adopted by normalization.

• 3. For the rest of $n^{b}$ nodes inside body ${\mathcal {B}}$ with material tags $m_1,\ldots ,m_4$, compute the tangents by solving the corresponding thermal boundary value problem as

  $$\begin{aligned} \hbox {div}{({\varvec{ K }}\nabla \theta )}+Q=\rho c \dot{\theta }\quad \text{ with }\quad \theta = \bar{\theta } \quad \text {on}\quad \partial {}{\mathcal {B}}. \end{aligned}$$

  (40)

  Steady-state heat conduction $(\dot{\theta }=0)$ is assumed with zero body heat $(Q=0)$. Here, $\rho$ is the mass density and c is the specific heat. For an isotropic constant thermal conductivity ${\varvec{ K }}=K{\varvec{ 1 }}$, the above thermal boundary value problem (40) reduces to the homogeneous Laplacian $\Delta \theta =0$ with Dirichlet boundary conditions $\theta = \bar{\theta }$ on $\partial {}{\mathcal {B}}$ and is solved for x- and y-components separately.

• 4. Project the nodal quantities $\theta _A$ for $A=1,\ldots ,n^a+n^b$ of Step 2 and Step 3 to the integration point I of those finite element with material tags $m_1,\ldots ,m_4$ using the isoparametric projection as

  $$\begin{aligned} \theta _{X,Y}^{I} = \sum _{A=1}^{n^a+n^b} N^A\theta _{X,Y}^A\,, \end{aligned}$$

  (41)

  where $N^A$ are the corresponding shape functions, same as used to define the geometry. Each pair $\{\theta _{X}^{I}$, $\theta _{Y}^{I}\}$ are the components of a unit tangent ${\varvec{ a }}$ defining the fiber orientation at each quadrature point of the discretized body ${\mathcal {B}}$. The resulting distribution of fiber orientations in fibrous layers $m_1,\ldots ,m_4$ arranged circumferentially is shown in Fig. 16b.

The steps (1)–(4) complete the preprocessing step of computing fiber orientation distribution which is followed by the solution of mechanical boundary value problem as shown in the next subsection.

Fig. 16

Inflation test: a boundary $\partial {\mathcal {B}}=\partial _{1}{\mathcal {B}}\cup \partial _{2}{\mathcal {B}}\cup \partial _{3}{\mathcal {B}}$ of fibrous materials used in thermal problem where tangents (39) are applied, b solution of thermal problem (40) in the form of tangents at all nodes representing fiber directions, c zoom of expected zone of failure with finer mesh/fiber density from encircled part in (b)

5.3.2 Mechanical boundary value problem

We start with the same finite element discretization as used in the previous subsection. The layers of adventitia $m_1$, media $m_2$, fibrotic media $m_3$ and fibrous cap $m_4$ are treated as incompressible transversely isotropic fibrous layers where the free energy (36) applies, with the corresponding material parameters given in Table 5, where the critical stress values are chosen from Holzapfel et al. (2004). Only the fiber direction ${\varvec{ a }}^{(1)}:={\varvec{ a }}$, aligned circumferentially, is applicable in (36), which is obtained from Sect. 5.3.1. The lipid pool $m_5$ is treated as a soft incompressible isotropic neo-Hookean material with shear modulus $\mu =0.1$ kPa and Poisson ratio $\nu =0.4$. The calcifications $m_6$ are treated as harder isotropic neo-Hookean solids with shear modulus $\mu =2$ MPa and Poisson ratio $\nu =0.3$. Linear line elements are used on the boundary $\partial _{2}{\mathcal {B}}$ to apply a hydrostatic pressure load of $p=15$ kPa $\approx$ 112.5 mmHg in $10^4$ solution steps, which falls in the range of average physiological pressure. The hydrostatic pressure load is non-conservative which stays normal to the deformed surface, thereby, resulting into an unsymmetrical tangent moduli. To account for the effect of surrounding tissues and fluids, the nodes on the boundary $\partial _{1}{\mathcal {B}}$ of the arterial wall are constrained by linear springs with Young’s modulus $E=0.1$ kPa pointing outwards.

Table 5 Material properties for inflation test of atherosclerotic artery

Fig. 17

Inflation test: contours of crack phase field d are shown at different inflation pressures (zoom in the inset) with the maximum damage obtained in fibrous cap at $p=15$ kPa shown in (d). Elements with $d>0.9$ are blanked out for visualization

In the two-dimensional numerical analysis presented in this section, the effect of circumferential residual stresses (Vaishnav and Vossoughi 1987) is neglected due to its significantly lower values (Balzani et al. 2012). During the simulation, it is observed that peak stresses develop on the outer wall of the fibrous cap $m_4$ where lipid pool $m_5$ lies in contact. The snapshots in Fig. 17 depict the contours of crack phase field at different stages of internal pressures. Depending upon the transversely isotropic form of driving force (23), one can clearly observe the initiation and propagation of fracture from outer wall of fibrous cap toward the inner wall, at its thinnest cross section. The lack of availability of experimental data presents these simulation results merely as a qualitative measure of actual fracture during angioplasty, which can be compared with the simulation results of Ferrara and Pandolfi (2010) and Balzani et al. (2012). It is to be emphasized here that the analysis presented here is only a mechanical simulation of the actual balloon angioplasty procedure and ignores the associated biochemical stimuli, mass transport phenomena and three-dimensional geometrical constraints.

6 Conclusion

We presented an application of recently developed thermodynamically consistent continuum phase-field models for fracture to soft biological tissues with specific focus on human iliac arteries. One of the key characteristics of the phase-field model is the derivation of the regularized crack surface functional, governed by a crack phase field, which converges to sharp crack topology for vanishing length-scale parameter. A rate-dependent incremental variational framework for the evolution of crack phase field is employed, which is driven by the maximum stress-based driving force from the deformation history. In addition, a general orthotropic failure criterion is developed and used to compute the driving forces for phase-field growth in soft biological tissues. The construction of constitutive relations allows the degradation of full anisotropic energy storage function, which takes into account the contribution of collagen fibers embedded in a soft surrounding matrix, with evolving crack phase field. Representative numerical simulations of fracture in soft biological tissues are run which provide quantitative comparisons with experimental data to confirm the accuracy and applicability of phase-field models of fracture.