1 Introduction

Modern three-dimensional muscle models might enable a realistic representation of contractile behaviours. They appear in various domains of our daily routine: from optimised objects like footwear, orthopaedic arch support, prostheses, over films and video games to areas such as medicine, medical device design, surgery simulations, and ergonomics (Herzog 2009; Wrobel et al. 2010; Osth et al. 2011). Also from the scientific point of view, there are several open questions. One key issue, e.g., is the insight into muscle evolution within muscle packages. Over thousands of years, the evolution has formed optimal muscle packages that have the ability to generate highly complex movements. In order to shed light on such evolution processes, the development and utilisation of three-dimensional muscle models can be a remedy. As a precondition, these models need to be validated in such way that they are able to predict correct muscle forces and in particular muscle shapes during contraction periods. However, a crucial point for the validation of such numerical models is the lack of comprehensive data sets including information as muscle properties (force–velocity, force–length and force–strain relations), the active muscle force response or the spatial orientation and alignment of the fibres (in the following refereed to as fascicle orientation) measured from the same muscle.

Mathematical modelling of active muscle properties was pioneered by two concepts: a phenomenological model by Hill (1938) and a micromechanical biophysical-based cross-bridge approach developed by Huxley (1957). The Hill model usually consists of a contractile, a parallel elastic and a series elastic element and has been used in its original and modified form to study different features of muscle contraction (e.g. Lichtwark and Wilson 2005; Houdijk et al. 2006; Günther et al. 2007; Rode et al. 2009a; Lu et al. 2011; Mörl et al. 2012; Siebert et al. 2012b). In contrast, Huxley-type concepts have been mainly used to analyse the properties of the microscopic contractile element (Hill et al. 1975; Oomens et al. 2003; Williams 2011). Indeed, both model types have been used to describe one-dimensional muscle force generation in movement analyses and muscle performance simulations developed around multibody dynamic systems (Pandy 2001; Curtis et al. 2009; Ghafari et al. 2009; Geyer and Herr 2010; Silva et al. 2011; García-Vallejo and Schiehlen 2012). These methods have been recommended as the most practical approaches when focusing on movement analyses of the whole body or parts of it. However, these concepts do not include geometrical information like complex muscle fibre orientation or muscle interaction with other tissues. Consequently, information ranging from fibre characterisation over internal pressure distribution to fibre recruitment strategies get lost. As a consequence, the development of three-dimensional constitutive models has rapidly proceeded in the last years reaching from concepts on the general contractile behaviour (e.g. Johansson et al. 2000; Blemker et al. 2005; Böl and Reese 2008; Hedenstierna et al. 2008; Böl 2010; Chi et al. 2010; Grasa et al. 2011; Böl et al. 2011b; Ehret et al. 2011; Röhrle et al. 2012) over models describing fatigue effects (Tang et al. 2007; Röhrle et al. 2008; Böl et al. 2009, 2011a), growth phenomena (Zöllner et al. 2012) or damage aspects (Ito et al. 2010) to approaches dealing with the electromechanical activation of muscles (Fernandez et al. 2005; Röhrle 2010; Böl et al. 2011c).

Among aforementioned publications, there are several approaches that use three-dimensional muscle shapes in the relaxed state to perform partially complex simulations. However, to the authors’ knowledge, there are only two publications that use the geometry of activated muscles to validate their modelling approaches. In the first contribution by Tang et al. (2007, 2009), two-dimensional silhouettes of the frog gastrocnemius muscle have been measured during tetanic stimulations. As the authors did not determine further geometrical information as fibre orientations or the spatial arrangement of additional tissues (aponeurosis or tendon), a comprehensive validation is hardly possible. Very recently, Böl et al. (2011b) measured the three-dimensional shape of the biceps brachii muscle in vivo. Therefore, magnetic resonance imaging (MRI) data of the human upper arm during isotonic contraction have been utilised. Applying a three-dimensional constitutive muscle model (Böl et al. 2011a; Ehret et al. 2011), it was possible to study the biceps brachii inside the muscle package and thus validate the modelling approach in vivo. The availability of three-dimensional data depicts a clear advantage in contrast to two-dimensional silhouettes (Tang et al. 2007). However, both works Tang et al. (2007) and Böl et al. (2011b) do not record additional information such as, for example, the generated muscle forces, which would enable a more explicit model validation.

Focusing on techniques used to measure geometrical information such as local strains on the surfaces of soft tissues, optical marker tracing methods (OMTMs) are common. The basic strategy of such methods is to fix single optical markers on top of the tissue and trace them during deformation by optical methods like X-ray microscopy or video registration. Thus, multidimensional strain fields can be calculated in a logical step. However, with the exception of Donkelaar et al. (1999) who measured larger regions of the rat gastrocnemius medialis muscle, OMTMs have been used to quantify local tissue deformations of skeletal muscles only (Azizi and Roberts 2009). Very recently, Böl et al. (2012) presented a method to identify the surface of cuboid muscle samples during loading. However, to the authors’ best knowledge, there exists no information about surface deformations of entire muscles during contraction.

Beside the muscles’ shape, its fascicle orientation is crucial when focusing on force development or transmission in skeletal muscle (Azizi et al. 2008). Consequently, it is unavoidable to take the fascicle orientation into account when applying three-dimensional contraction analyses (Böl et al. 2011a; Böl et al. 2011b; Böl et al. 2011c). A very promising method for quantifying the fascicle orientation is the diffusion tensor imaging (DTI)-based fibre tracking method which is rooted on the anisotropic diffusion of water within muscle tissue (cf. Basser et al. 1994). The DTI technique provides a unique way to determine fibre directions in vivo in comparison with manual fibre tracking methods. Thus, the DTI method is an encouraging tool applied in studies on skeletal muscles (Heemskerk et al. 2005; Zhang et al. 2008; Schwenzer et al. 2009; Sinha et al. 2011). Beside many advantages, the DTI method also exhibits some disadvantages such as background noise, movement, distortion from imaging artefacts, assumption of Gaussian diffusion characteristics or crossing fibres leading to limited accuracy and therefore, partially, to questionable results (Tournier et al. 2011; Jeurissen et al. 2012; Jones et al. 2012; Vos et al. 2012). A validated method to determine three-dimensional muscle architectures is the manual digitisation of formalin-embalmed muscles (e.g. Gorb and Fischer 2000; Leon et al. 2006; Kim et al. 2007; Rosatelli et al. 2008; Fung et al. 2009; Mihata et al. 2009; Ravichandiran et al. 2009). The removal of individual muscle fascicles permits the identification and digitisation of successively deeper muscle regions. Due to the examination of cadaveric specimens, the data set is limited to one fixed muscle length. Further, this procedure is highly invasive as the muscle is destroyed while measuring.

As this introduction illustrates, there is a massive need for extensive data sets including geometrical information during muscle contraction combined with the knowledge of the muscles’ force response and its architecture. On that account, to the authors’ knowledge, we, for the first time, present a comprehensive data set of the rabbit soleus muscle. Accordingly, Sect. 2 concerns the outline of the used techniques to determine (i) the specific muscle properties (\(n=11\)), (ii) the muscles’ outer three-dimensional geometry and force data (\(n=3\)) during isometric isotonic and isokinetic contractions, (iii) the spatial arrangement of muscle tissue and aponeurosis–tendon complex (\(n=10\)) and (iv) the muscles’ fascicle orientations (\(n=10\)) at optimal muscle length (\(l_\mathrm{opt}\)), defining the length at which the muscle produces its maximum isometric force. Note, the variable n denotes the number of objects used for the corresponding experiments. Further, in Sect. 3, the results are presented in detail. Before this study is closed with Sect. 5, Sect. 4 is devoted to a critical discussion of the outcomes.

2 Methods

2.1 Ethical approval

Experiments were approved according to Section 8 of the German animal protection law (Tierschutzgesetz, BGBl. I 1972, 1277).

2.2 Muscle force determination

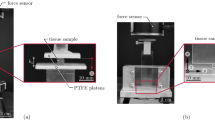
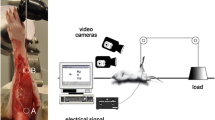
Female New Zealand white rabbits (Oryctolagus cuniculus) with an average weight of 4.12 \(\pm \) 0.69 kg (mean \(\pm \) SD) were anaesthetised with Bupivacain (Jenapharm\(^{\circledR }\), 1 ml, 0.5 %, epidural) after short-term sedation with natrium pentobarbital (Nembutal\(^{\circledR }\), 80 mg/kg BW). Rooted on the dependence of muscle characteristics on temperature, the animal was heated during the entire experimental procedures using a heating pad (Harvard Apparatus, 39.0 \(\pm \) 0.4\(^{\circ }\), mean \(\pm \) SD). After removing the skin of the right hind leg below the knee, the soleus muscle’s surface was frequently sprinkled with heated (39 \(^{\circ }\)C) physiological saline solution during the entire experiment while dissection care was taken to preserve the neurovascular supply. For mounting the muscle in a fixation frame, see Fig. 1, its connection to the head of the fibula was maintained. At the muscles’ distal end, the calcaneus has been removed from the foot but kept connected to the muscle. After dissection, the rabbit was located in a fixation frame and fixed by two pairs of bone pins (Fig. 1a). Note, as optical measurement systems have been used (see Sect. 2.3), a non-constrained view on the muscle has to be assured. For this purpose, the tibia and all other muscles of the hind leg have been removed below the knee, see Fig. 1.

Fig. 1
figure 1

Illustration of the rabbit hind leg mounted in the fixation frame. a Set-up for the measurement of the active muscle characteristics and its geometry (\(p_1\) and \(p_2\) are bone pins used for fixation of the hind leg) and b photograph of the situation in the laboratory

Full size image

A muscle lever (Aurora Scientific 310B-LR) has been used to measure/generate length and force changes. The arm of the muscle lever has been connected with a hook directly to the calcaneus (Fig. 1a). At the beginning of all experiments, the initial muscle length (\(101 \pm 4\) mm, mean \(\pm \) SD) was measured in situ with a micrometre at an ankle joint angle of 90\(^{\circ }\). The soleus muscle was stimulated supramaximal (100 Hz) over the tibial nerve using a bipolar gold electrode. To determine the specific muscle properties, isometric, isotonic and isokinetic contractions have been conducted; for more details, we refer to Siebert et al. (2008). In Fig. 1b, a photograph of the real situation in the laboratory is given.

2.3 Identification of the three-dimensional muscle shape

The commercial measurement system ARAMIS (GOM mbH Braunschweig, Germany), which is based on the so-called grating method (Winter 1993), has been used to capture the shape of the muscle during contraction. Accordingly, the muscles’ surface has been coated with single points of white and black varnish, see also Remark 1. The random pattern sprayed on the muscles’ surface deforms simultaneously with the muscle. This deformation is recorded by four sensors, each of them includes two CCD cameras. The cameras provide 8-bit images with a resolution of 2,352 (horizontal) \(\times \) 1,728 (vertical) pixels (pixel size: 10 \(\upmu \)m \(\times \) 10 \(\upmu \)m) in TIFF format and record at a maximum frame rate of 200 fps. For each of the four sensors, the first post-processing step defines the macro facets in the reference image from one camera compared with the second one. In the following, the coordinates of every facet with respect to the selected start point are allocated automatically. In each successive image, these facets are tracked. While comparing the images, ARAMIS registers any displacement of the muscle surface. This leads to precise three-dimensional coordinates of the surface, from which strains can be derived. In a final post-processing step, the geometrical results of each sensor have been added using a reference frame, for synchronising the four sensors. In Fig. 2,a schematic illustration of the measuring set-up including the four sensors is given.

Fig. 2
figure 2

Idealised illustration of the experimental set-up including the optical measurement systems (sensor 1-4). a Front view in the muscles’ longitudinal direction and b top view on the soleus muscle (sensor 1 is not shown). Due to illustration reasons, the sizes and distances in this figure are not proportional

Full size image

Remark 1

(Influence of varnish on the contraction behaviour) In order to analyse the influence of the varnish sprayed on the muscles’ surface on muscle force generation, a reference experiment has been applied. In doing so, isometric contractions at optimal muscle length using the experimental set-up as described in Sect. 2.2 have been arranged. During these contractions, the pigment content has been increased continuously from 0 to 100 %. In Fig. 3, the influence of the amount of varnish \(A_{v}\) sprayed on the muscles’ surface \(A_{m}\) on the generated muscle force \(F\) related to the maximum isometric muscle force \(F_\mathrm{im}\) is illustrated. During these studies, no significant influence could be detected. The average value of the generated muscle force \(F\) results to be 21.71 \(\pm \) 0.86 N. The calculated standard deviation of 0.86 N is not higher than in appropriate experiments without the use of varnish. Thus, this method seems to be adequate when measuring the muscles’ surface.

Fig. 3
figure 3

Influence of the amount of varnish \(A_{v}\) sprayed on the muscles’ surface \(A_{m}\) on the generated muscle force \(F\), whereby \(F_\mathrm{im}\) denotes the maximum isometric muscle force at optimal muscle length. The subfigures show the uncoated soleus muscle A and the same muscle covered with 80 % of varnish B

Full size image

2.4 Spatial configuration of muscle, aponeurosis and tendon tissue

For a proper construction of a geometrical model, a spatial separation between muscle tissue and aponeurosis–tendon complex is essential. As the aponeurosis–tendon complex is much stiffer than the muscle tissue (e.g. Calvo et al. 2010), we utilise this feature to decide between these tissue types. To this end, the pattern originally applied to determine the muscles’ shape has been used to calculate the strain field \(\varvec{\varepsilon }\) during passive stretching, see Fig. 4b, where \(\varvec{\varepsilon }\) is plotted on the muscles’ surface. Red indicates high and blue low strain values. As expected, high strain values can be detected in region (I) which coincides with the muscles tissue. Very low strains appear on the tendon, in region (III). Due to the high stiffness of the tendon, its deformation is much lower than the one of the muscle tissue. As the aponeurosis acts as interface between tendon and muscle tissue in this region (II), strain values between the two border cases can be found, expressed by mainly green colour.

Fig. 4
figure 4

Differentiation between muscle tissue and aponeurosis–tendon complex. a Isolated soleus muscle before coating with varnish and b calculated strain field \(\varvec{\varepsilon }\). Red characterises high and blue labels low values. The left side is the muscles’ proximal and the right one the distal end. For the determination of the strain field, a grid resolution of \(50\, \upmu \text{ m} \times 50 \,\upmu \text{ m}\) has been chosen

Full size image

2.5 Fascicle orientation

Concerning the drawbacks of the DTI fibre tracking method, in this study, the fascicle orientation has been digitised manually. Immediately after sacrificing the animal with an overdose of natrium pentobarbital (Nembutal\(^{\circledR }\) 800 mg/kg BW), the skin was removed from the lower leg after its amputation. In order to minimise shrinking artefacts, the preparation was fixed in alcoholic Bouins solution for more than 48 h (Gorb and Fischer 2000). Since the preparation has to be stabilised mechanically during digitisation, the isolated soleus muscle, still connected to the bone, was moulded in wax with an ankle joint angle \(\alpha _\mathrm{joint}\) of 80.6 \(\pm \) 4.4\(^{\circ }\), see Fig. 5a, which corresponds to the muscles’ optimal length. In order to record the fascicle orientation, a manual digitiser (MicroScribe\(^{\circledR }\) MLX, measuring accuracy 0.07 mm) with a sampling frequency of 5 Hz has been utilised. During the digitising process of one muscle (average period \(\sim \)5 h), the palm was placed on a holder to minimise movements of the digitise tip, leading to an accuracy of higher than 0.1 mm. However, main idea of the digitising procedure is to take out a single fascicle (Fig. 5a) and digitise the deepening the fascicle consigned, see Fig. 5b. In doing so, highly precise data sets of fascicle orientations have been obtained.

Fig. 5
figure 5

Photographs of the manual digitising procedure. a The isolated soleus muscle has been mechanically fixed in wax and a muscle fascicle is drawn out. b Muscle during the digitisation procedure; some fascicles have been removed and digitised

Full size image

3 Results

Based on the technique described in Sect. 2.4, the spatial arrangement of the muscle, aponeurosis and tendon tissue could be obtained, see Fig. 6a. The muscle is illustrated at its optimal length \(l_\mathrm{opt}\), restricted on its ends by the calcaneus (idealised by a dark grey cylinder) and the head of fibula (idealised by a dark grey sphere). The calcaneus is connected to the tendon (light grey) fading into the aponeurosis (light grey) acting as interface between the tendon and the muscle tissue (red). Note, as anomaly of the soleus muscle, the tendinous adhesion with the gastrocnemius muscle can be identified. On the proximal end, the tendon is connected to the head of the fibula and passes into the aponeurosis. The three-dimensional, spatial orientation of the fascicles is illustrated in Fig. 6b. Further, the classical architectural features have been determined, too, see Table 1.

Fig. 6
figure 6

Exemplary illustration of a typical three-dimensional soleus muscle at its optimal length \(l_\mathrm{opt}=113.0\) mm. a The muscle geometry consisting of muscle, aponeurosis, and tendon tissues and b fascicle orientation. For the sake of clarity, the spatial arrangement of the fascicles has been illustrated separately and enlarged

Full size image
Table 1 Architectural features of the rabbit soleus muscle
Full size table

Specific muscle properties, i.e., force–velocity, force–length as well as force–strain relations, were determined for 11 soleus muscles (Fig. 7). As demonstrated in (a), all experimental force–velocity relationships had the typical hyperbolic shape observed by Hill (1938) and exhibited a characteristic force–length dependency (b) which is attributable to the theoretical sarcomere force–length relationship (Gordon et al. 1966; Rode et al. 2009b). Series and parallel elastic components possess typical (Winters 1990) nonlinear force–strain characteristics, cf. Fig. 7c, d. The standard deviations of the determined muscle properties are small, see (a) to (c), with the exception of the force–strain relation of the parallel elastic component in (d). This is reported for other soleus muscles (Scott et al. 1996; Brown et al. 1999) too and may be related to variations in connective tissues (fascia, epimysium, perimysium, endomysium) or titin-isoforms (e.g. Prado et al. 2005; Rode et al. 2009a).

Fig. 7
figure 7

Muscle properties of soleus muscles (n = 11) determined according to Siebert et al. (2008, 2012b). The black curves indicate mean values, whereas the grey areas depict the standard deviations. a Force–velocity relation, where \(v_\mathrm{max}\) denotes the maximal shortening velocity, \(F_\mathrm{im}\) the maximum isometric muscle force, and \(F_\mathrm{CC}\) is the force of the contractile component. b Force–length relation, herein \(l_\mathrm{CC}\) and \(l_{\mathrm{CC}_\mathrm{opt}}\) (\(21.1 \pm 4.5\) mm) is the length and the optimal length of the contractile component, respectively. c Force–strain relation of the series elastic component. \(\Delta l_\mathrm{sec}\) and \(\Delta l_{\mathrm{sec}_{0}}\) (\(84.8 \pm 4.9\) mm) is the length change and the slack length of the series elastic component. d Force–strain relation of the parallel elastic component characterised by \(\Delta l_\mathrm{pec}\) and \(\Delta l_{\mathrm{pec}_{0}}\) (\(16.2 \pm 2.5\) mm), to be the length change and the slack length of the parallel elastic component

Full size image

Note, in the following subsections, we present the three-dimensional muscle geometries as well as the characteristic force measurements exemplary for one soleus muscle whose muscle properties are representative for all other observed muscles as presented in Fig. 7. Further, for all contraction states, complete data sets including the fascicle orientations (Fig. 6b) and the three-dimensional muscle surfaces during isometric, isotonic and isokinetic contractions (Figs. 9, 11, 13) are provided by the authors and can be found in the supplementary material, see also Sect. 6.

3.1 Isometric contraction

Starting with the simplest contraction type, namely the isometric contraction, characteristic force–time and displacement–time curves are shown in Fig. 8. After the muscle has been elongated to its optimal length, it is activated and reaches its maximal force of \(F_\mathrm{im}=15.8\) N (\(\Box \)D). After a stimulation period of \(t_\mathrm{st}^\mathrm{isom}=1.2\) s the muscle force decreases during \(0.5\) s to a value of \(F=0.7\) N, see \(\Box \mathrm{D} \rightarrow \Box \mathrm{D_1}\). This force value is about \(0.4\) N smaller than before activation at point \(\Box \)C.

Fig. 8
figure 8

Results of an isometric muscle contraction at optimal muscle length. The black curve denotes the generated muscle force and the grey curve describes the elongation \(u\) about \(u_\mathrm{opt}=14.0\) mm to reach the muscles’ optimal length. The discrete points \(\Box \mathrm{A/B/C/D/E/F}= 0/1.5/6.5/7.7/10.7/12.2\) s are associated with the muscle shapes in Fig. 9. The grey bar indicates the period of electrical stimulation

Full size image

Focusing on the reconstructed muscle geometries in Fig. 9, it becomes clear that the largest changes in the muscles’ shape appear first when the muscle is passively stretched to its optimal length (\(\Box \mathrm{A} \rightarrow \Box \mathrm{B}\)) and second when the muscle is activated (\(\Box \mathrm{C} \rightarrow \Box \mathrm{D}\)). During the latter time period, the muscle length is kept constant and the muscle belly changes remarkably due to the stretching of the series elastic components. In Table 2, the percental deflexions \(\delta \mathrm{A}_i^{\Box \mathrm{C} \rightarrow \Box \mathrm{D}}\) of the cross-section areas \(i=1,\ldots ,12\) in situation \(\Box \mathrm{D}\), see Fig. 9, referred to the ones in the non-activated state \(\Box \mathrm{C}\), are given. Rooted on the shortening of the muscle belly (moving of the tapering belly ends together) and the elongation of the distal and proximal tendons, at both muscle ends, a reduction in the cross-sections area can be observed. As expected, the muscle belly thickens and adjustments up to \(\delta A_5^{\Box \mathrm{C} \rightarrow \Box \mathrm{D}} = 41.2\,\%\) can be detected.

Fig. 9
figure 9

Muscle shapes during isometric contraction. The points \(\Box \)A to \(\Box \)F are conform with the points in Fig. 8

Full size image
Table 2 Percentage changes of the cross-section areas \(\delta \mathrm{A}_i^{\Box \mathrm{C} \rightarrow \Box \mathrm{D}}\) in situation \(\Box \mathrm{D}\) referred to the ones in state \(\Box \mathrm{C}\) during isometric contraction
Full size table

3.2 Isotonic contraction

In contrast to an isometric contraction, where the force is measured and the displacement is fixed, for isotonic contractions, the muscle force is held constant, whereas the displacement is measured. Two main effects arise: first, the muscle produces a maximum isotonic force (which is approximately the half of the maximum isometric force \(F_\mathrm{im}\)) during the activation period \({t_\mathrm{st}^\mathrm{isot}=1.2}\) s and second the muscle shortens about \(u_\mathrm{F}=6.0\) mm (Fig. 10). In this regard, a small delay between stimulation (\(\Diamond \mathrm{C}\)) and maximum force generation (\(\Diamond \mathrm{D}\)) as well as deactivation (\(\Diamond \mathrm{F}\)) and the end of force generation (\(\Diamond \mathrm{F}_1\)) can be observed.

Fig. 10
figure 10

Results of an isotonic muscle contraction. The black curve denotes the generated muscle force and the grey one describes the elongation \(u\) about \(u_\mathrm{opt}=14.0\) mm to reach the muscles’ optimal length. The discrete points \(\Diamond \mathrm{A/B/C/D/E/F/G}=0/2.9/7.9/8/8.7/9.1/11.9\) s are associated with the muscle shapes in Fig. 11

Full size image
Fig. 11
figure 11

Muscle shapes during isotonic contraction

Full size image

With regard to the muscle geometries during activation (Fig. 11, \(\Diamond \mathrm{C} \rightarrow \Diamond \mathrm{F}\)), it becomes obvious that the muscle shortens along its longitudinal axis while the muscle belly thickens. This also becomes approved by the percentage changes of the cross-section areas, see Table 3. After the end of the stimulation (Fig. 10, \(\Diamond \mathrm{F}\)), the muscle force drops down to a value of \(0.6\) N (\(\Diamond \mathrm{F}_2\)) while the muscle elongates to 94 % of the optimal length, see point \(\Diamond \mathrm{F}_1\).

Table 3 Percentage changes of the cross-section areas \(\delta \mathrm{A}_i^{\Diamond \mathrm{C} \rightarrow \Diamond \mathrm{E}}\) and \(\delta \mathrm{A}_i^{\Diamond \mathrm{C} \rightarrow \Diamond \mathrm{F}}\) in the situations \(\Diamond \mathrm{E}\) and \(\Diamond \mathrm{F}\) referred to the cross-section areas in state \(\Diamond \mathrm{C}\) during isotonic contraction
Full size table

In order to study the stimulation period \(t_\mathrm{st}^\mathrm{isot}\) in more detail, we consider changes from the initial situation to about two-thirds \(t_\mathrm{st}^\mathrm{isot}\) (\({\Diamond \mathrm{C} \rightarrow \Diamond \mathrm{E}}\)) as well as changes from the initial point to the end of \(t_\mathrm{st}^\mathrm{isot}\) (\({\Diamond \mathrm{C} \rightarrow \Diamond \mathrm{F}}\)). Focusing on the first phase (\({\Diamond \mathrm{C} \rightarrow \Diamond \mathrm{E}}\)), cross-sectional reductions on the tendinous regions (\(\delta \mathrm{A}_{1-5}^{\Diamond \mathrm{C} \rightarrow \Diamond \mathrm{E}}\) and \(\delta \mathrm{A}_{11-12}^{\Diamond \mathrm{C} \rightarrow \Diamond \mathrm{E}}\)) and a thickening of the muscle belly (\(\delta \mathrm{A}_{6-9}^{\Diamond \mathrm{C} \rightarrow \Diamond \mathrm{E}}\)) can be detected. Further shortening (second phase, \({\Diamond \mathrm{C} \rightarrow \Diamond \mathrm{F}}\)) results in an increase in the proximal muscle belly regions (\(\delta \mathrm{A}_{4-5}^{\Diamond \mathrm{C} \rightarrow \Diamond \mathrm{F}}\)) and a simultaneous decrease in the distal muscle belly regions (\(\delta \mathrm{A}_{8-9}^{\Diamond \mathrm{C} \rightarrow \Diamond \mathrm{F}}\)) leading to more homogeneous cross-section increase of the whole muscle belly (\(\delta \mathrm{A}_{4-9}^{\Diamond \mathrm{C} \rightarrow \Diamond \mathrm{F}}\)).

3.3 Isokinetic contraction

The last type of muscle contraction applied on the rabbit soleus muscle is the isokinetic experiment consisting of a sequence of an isometric contraction at optimal muscle length, a concentric muscle shortening with a given constant velocity (5.0 mm/s) and a second isometric contraction at reduced muscle length, see Figs. 12 and 13. According to these three phases, the muscle is stimulated for \(t_\mathrm{st}^\mathrm{isok}=2.7\) s (\(\vartriangle \! \mathrm{C} \rightarrow \vartriangle \! \mathrm{F}\)) thereby generating two isometric force peaks of 15.8 N (at point \(\vartriangle \! \mathrm{D}\)), 10.6 N (at point \(\vartriangle \! \mathrm{F}\)), and a minimum force of 8.6 N (at point \(\vartriangle \! \mathrm{E}\)) at the end of the shortening phase, respectively.

Fig. 12
figure 12

Results of an isokinetic muscle contraction. The black curve denotes the generated muscle force and the grey curve describes the elongation \(u\) about \({u_\mathrm{opt}=14.0}\) mm to reach the muscles’ optimal length as well as a muscle length reduction of \({u_\mathrm{isok}=2.0}\) mm in the shortening phase. The discrete points \(\vartriangle \mathrm{A/B/C/D/}\mathrm{E/F/G/H}=0/1.5/6.5/7.7/7.9/9.2/12/13.3\) s are associated with the muscle shapes in Fig. 13

Full size image
Fig. 13
figure 13

Muscle shapes during isokinetic contraction

Full size image

As the first isometric phase shows the same force characteristics as in the isometric experiment (\(\Box \mathrm{C} \!\rightarrow \!\Box \mathrm{D}\), Fig. 8), the adjustments of the cross-section areas are almost similar (\(\delta A_i^{\Box \mathrm{C} \rightarrow \Box \mathrm{D}}\) in Table 2 versus \(\delta \mathrm{A}_i^{\vartriangle \!\mathrm{C} \rightarrow \vartriangle \! \mathrm{D}}\) in Table 4). As expected, further shortening results in a thickening of the muscle belly, see Table 4, \(\delta \mathrm{A}_{6, 8-9}^{\vartriangle \!\mathrm{C} \rightarrow \vartriangle \! \mathrm{E}}\). In the second isometric phase, a proximal movement of the muscle volume appears resulting in an alteration of the cross-section changes \(\delta \mathrm{A}_{6-10}^{\vartriangle \!\mathrm{E} \rightarrow \vartriangle \! \mathrm{F}}\) (increase) and \(\delta \mathrm{A}_{4-5}^{\vartriangle \!\mathrm{E} \rightarrow \vartriangle \! \mathrm{F}}\) (decrease), respectively.

Table 4 Percentage changes of the cross-section areas \(\delta \mathrm{A}_i^{\vartriangle \!\mathrm{C} \rightarrow \vartriangle \! \mathrm{D}},\,\delta \mathrm{A}_i^{\vartriangle \!\mathrm{C} \rightarrow \vartriangle \! \mathrm{E}}\), and \(\delta \mathrm{A}_i^{\vartriangle \!\mathrm{E} \rightarrow \vartriangle \! \mathrm{F}}\) in the situations \(\vartriangle \)D, \(\vartriangle \)E, and \(\vartriangle \)F related to the reference states \(\vartriangle \)C and \(\vartriangle \)E during isokinetic contraction
Full size table

4 Discussion

Basic motivation for this study is the lack of extensive data sets to validate skeletal muscle models in a three-dimensional way. To this end, we present such a comprehensive data set including (i) the muscles characteristic passive and active force response, its three-dimensional shapes during different contraction experiments, (iii) the spatial arrangement of muscle, aponeurosis and tendon tissues and (iv) the fascicle orientation throughout the muscle. So far, no study has been documented including all four components, at most single aspects have been published.

4.1 Requirement for model validation and impact of this study

For a prosperous model validation, the chosen model needs to fulfil a few requirements. First, as the provided data include the spatial separation of the muscle tissue and the aponeurosis–tendon complex as well as the spatial distribution of the fascicles, the model needs to have the ability to resolve the muscle geometry in a three-dimensional way. Second, since only macro mechanical quantities have been measured, the models has to be aligned to utilise those quantities. A typical example is purely phenomenological models or those, trying to transfer information between different scales (e.g Ehret et al. 2011). Third, beside the ability to describe finite elasticity, mass terms need to include within the governing equations of the model approach as they play a key role in movement analyses. Finally, from the computational point of view, the balance of linear momentum needs to be considered in its unrestricted form what means that dynamic terms have to be considered. Thus, although most models make use of the assumption that contraction can simulated in a quasi-static manner (cf. Sect. 1), this oversimplification does not seem to be appropriate for the gathered data within this study especially in case of isotonic and isokinetic experiments.

Consequently, from the authors perspective, the basic requirement for a satisfying validation process is the availability of three-dimensional geometry measurements and the active force response at the enthesis from the same muscle. Force measurements alone, as frequently published (e.g. Bullimore et al. 2007; Rode et al. 2009a; van Noten and van Leemputte 2011), are insufficient as no statements about the three-dimensional muscle geometry changes (i.e. changes of muscle shape and fascicle orientation) during contraction can be made. But especially in such situations, muscles are subjected to large deformations and thus geometry changes extremely influence the force generation. The combination of both, muscle force and three-dimensional shape measurements during isometric, isotonic and isokinetic contractions, as done in this study, cannot be found in the literature. To the authors’ knowledge, there exists one contribution (Stark and Schilling 2010) that tries to compare the characteristics of the rat soleus muscle in the relaxed and contracted situation for one discrete contracted muscle geometry and one force value, only. However, for an extensive model validation, these information are not adequate, as on the one hand rats have been used instead of rabbits. On the other hand, also qualitative comparison, e.g., of length variations, is hardly feasible as the authors used not the identical muscle when studying the relaxed and contracted muscle.

Rooted on the different stiffnesses of the muscle tissues, we are able to distinguish between the aponeurosis, tendon and contractile tissue. In doing so, it is possible to reconstruct the tissues’ three-dimensional surface arrangement, which is one basic requirement for a proper model validation. There exists two modelling studies that differentiate between these tissue types when reconstructing the rat soleus muscle (Böl et al. 2011a) and the human biceps brachii muscle (Böl et al. 2011b) in order to validate their modelling approach. In comparison with other OMTM where only single markers have been attached to the muscles’ surface (e.g. Donkelaar et al. 1999) in the present study, a dense point pattern has been applied to reflect the surface. Consequently, areal strain fields are measurable indicating an inhomogeneous strain distribution which points to a gradient in tissue stiffness.

Especially, aforementioned strain fields can be used to examine elastic energy storage and release inside the passive muscle components during contraction, referred to as elastic energy flow. Focusing on the hierarchical micro structure of skeletal muscles, it is well known that two layers of elastic connective tissue, the fascia and the epimysium, surround the muscle on the one hand. These tissues may store or release elastic energy during muscle contraction (Siebert et al. 2012a, b), thereby influencing the dynamic of muscle contraction and the metabolic efficiency. On the other hand, aponeurosis exhibits anisotropic stiffnesses in longitudinal and transversal direction (Azizi and Roberts 2009), where, in addition, strains in one direction modulate the stiffness in the other direction. Consequently, in combination with adequate models, the measured three-dimensional muscle deformation as well as the strain fields (cf. Fig. 4) can be used to determine three-dimensional stiffnesses of elastic tissue sheets (Siebert et al. 2012a). Such procedure would improve our understanding of three-dimensional interaction between contractile and elastic structures during contraction. Further, muscle acting as motors, springs or brakes (Wilson et al. 2001; Ahn and Full 2002; Gillis and Biewener 2002) may exhibit not only differences in the fibre type or the ratio of tendon to fibre length (Biewener 1998a) but also in the characteristics of the elastic muscle sheets which can be estimated applying the proposed optical method (Sect. 2.3).

4.2 Comparison with the literature

As it is known from the literature, cf. Sect. 1, the fascicle orientation throughout the muscle volume is essential for the modelling procedure. From the biological perspective, the rabbit soleus muscle is a rather simple one as it features a unipennate fibre orientation (Herbert and Crosbie 1997) and consists of more than 99 % slow twitch fibres (Wank 1996). Comparable measurements of rabbit soleus muscle architecture were taken by Lieber and Blevins (1989). Measuring fibre lengths with a caliper and pennation angles with a protractor on a limited superficial area of the muscle, they obtained a mean fascicle length of 13.8 \(\pm \) 0.8 mm and a mean pennation angle of \(8.5 \pm 1.0^{\circ }\). These results differ slightly from our results (fascicle length: 16.6 \(\pm \) 2.6 mm and pennation angle: \(9.9 \pm 2.8^{\circ }\)) with respect to the mean values, but more pronounced with respect to the standard deviation values. The differences in the mean fascicle lengths can be explained partially by the longer muscle lengths in the present study (65.6 mm) compared to lengths (57.5 mm) measured by Lieber and Blevins (1989). However, the large difference in the standard deviations values cannot be explained by muscle size differences. We suppose that the larger standard deviation values indicate larger heterogeneity in fibre lengths and pennation angles of the unipennate soleus muscle and reveal a more complex architecture than expected. This will be supported by the aforementioned study of Stark and Schilling (2010), demonstrating large heterogeneity for fibre length and pennation angle for relaxed (18.7 \(\pm \) 4.2 mm, \(6.6 \pm 3.1^{\circ }\)) and contracted (15.0 \(\pm \) 3.2 mm, \(8.3 \pm 2.2^{\circ }\)) rat soleus muscles. Focusing further on earlier publications dealing with various muscles of different species, mostly parameters such as pennation angle, fascicle length or fascicle curvature have been studied (e.g. Agur et al. 2003; Fry et al. 2004; Eng et al. 2008). Using more advanced techniques, also spatial fascicle orientation has been measured (Gorb and Fischer 2000; Heemskerk et al. 2005, 2009; Kan et al. 2009; Stark and Schilling 2010). However, muscle regions with different architecture will influence muscle deformation as well as three-dimensional muscle force generation. To that end, the inner muscle architecture of the entire muscle has to be considered in muscle models, as infrequently done (Oomens et al. 2003; Böl et al. 2011a, c; Böl et al. 2011b), instead of mean parameters determined on isolated muscle compartments or entire muscles. This is especially recommended for muscles with more complex fibre organisation as, e.g., the bipennate gastrocnemius muscle or the multipennate plantaris muscle.

Muscle properties determined in this study show satisfying agreement with values observed for slow twitch fibred small mammal muscles. Although the maximum isometric forces are higher than rabbit soleus forces of  Wank (1996), the maximum tension (17.3 \(\pm \) 3.4 \(\mathrm N/cm^2\)) is comparable to values between 15 and 20 \(\mathrm N/cm^2\) determined for isolated soleus muscles of other small mammals (Asmussen and Maréchal 1989; Monti et al. 2003; Stark and Schilling 2010). Maximum shortening velocity (\(v_\mathrm{max}=6.3 \pm 1.2 l_\mathrm{opt}/s\)) and curvature (\(a/F_\mathrm{im}=0.14 \pm 0.06\)) of the force–velocity relation (Winters 1990) are comparable to values reported for slow twitch muscles (maximum velocity: 3–7\(l_\mathrm{opt}/s\), Ranatunga and Thomas (1990); Barclay (1996); Siebert et al. (2008), curvature: 0.1–0.2, Asmussen and Maréchal (1989); Barclay (1996, 2008)).

Finally, the maximum change in volume related to the ones in the initial state of each experiment has been measured to be \(\delta V_\mathrm{max}=4.1\times 10^{-5}\) cm\(^3\). Using a determined wet muscle weight of 3.04 \(\pm \) 0.56 g for \(n=11\), this leads to a relative volume change of \(\delta \bar{V}_\mathrm{max}=1.3\times 10^{-5} \pm 2.5\times 10^{-6}\) cm\(^3\)/g. Existing experiments approve this value as they determine volume changes of \(2.5\times 10^{-6}\) to \(7.6\times 10^{-5}\) cm\(^3\)/g (Abbott and Baskin 1962; Baskin 1967) during active muscle deformation and \(1.0\times 10^{-5}\) cm\(^3\)/g (Baskin and Paolini 1964) for passive muscle loading. These results depend on the muscles’ reference length, temperature and type. However, the calculated volume changes in this work clearly demonstrate two issues. First, the muscle tissue can be seen to be volume-constant, i.e., incompressible. Second, the optical measurement techniques and reconstruction methods applied in this work provide consistent and precise results.

4.3 Limitations of this study

A lack of this study is the determination of muscle architecture using relaxed muscles, only. Measurement of muscle architecture during contraction is possible using, e.g., ultrasound (Ishikawa et al. 2007) which in turn is limited to specific muscle regions and possible in two dimensions, only. Determination of three-dimensional muscle architecture during contraction was performed by Stark and Schilling (2010) for isolated rat soleus muscles which were shock-frozen during isometric contraction and reconstructed from histological sections. This method is limited to small muscles to ensure fast and complete freezing of the whole muscle during stimulation. However, as this method is highly invasive, architectural information of the relaxed and additionally of the activated muscle cannot determined from the same muscle.

Further, in case of modelling soleus muscles of different species, the use of the data gathered in this study is questionable, as muscle properties change with animal size. For example, the maximal shortening velocity of the muscle \(v_\mathrm{max} \sim m^\mathrm{-ks}\) increases with decreasing animal mass (\(m\)), whereas the scaling coefficient ks ranges from 0.125 to 0.33 (Hill 1950; McMahon 1984; Rome et al. 1990). Günther et al. (2012) found that the interaction of muscle inertia and force–velocity relation has strong influence on contraction dynamics. As a consequence, it should be problematic to scale up muscle properties determined on small muscles (as performed usually) to bigger muscles, e.g., to simulate human movement. Further, muscles differ in fibre type and architecture. The ratio of tendon length to the contractile component length increases with animal size and is larger for proximal muscles than distal muscles (Zajac 1989; Biewener 1998b; Biewener 1998a). Thus, it is necessary to determine specific muscle properties and architecture in order to develop realistic muscle models.

A standard procedure to determine muscle characteristics experimentally is the dissection of the selected muscle from all other tissues whereby one end is fixed to the creature and the other one is connected to a muscle lever. In the present study, we also isolate the muscle of interest with the difference that all other tissues have been removed in order to have a \(360^{\circ }\) view on the muscle which, on the other hand requires a quick measurement technique as the removal of the tissue is highly invasive. It is uncontroversial that both scenarios do not reflect the real situation of the muscle inside a body. The major difference in comparison with the situation of the muscle embedded in a muscle package is the lack of surrounding tissues, which influences muscle force generation (Maas et al. 2001; Siebert et al. 2012b). From non-invasive measurement methods, it is well known that non-isolated muscles feature different shapes as in the isolated situations (e.g. Heemskerk et al. 2005; Albracht et al. 2008). However, as the information of the muscle shapes, independent on the experimental method (isolated or non-isolated), are included into the validation process, it is pretty much insignificant whether a model is validated on an isolated or a non-isolated muscle. Quite the contrary, at the current state of experimental techniques, it is, to our best knowledge, impossible to measure a non-isolated muscles’ shape during contraction in combination with its force.

5 Conclusion

In conclusion, we have used different techniques to resolve the muscle shape during contraction, the corresponding active muscle force response, the fascicle orientation at optimal length and the spatial arrangement of the tissue types. In combination with purely passive experiments of the same tissue type (Böl et al. 2012), data are available (see also Sect. 6) to validate muscle models in a broad extensiveness as it is possible, for the first time, to compare virtually active muscle force generation and muscle shape change during a whole contraction period. Thus, with focus on future work, one validation could be to identify first material parameters of a mathematical model by using the force and geometry data of one contraction type, e.g., under isometric conditions. In a second step, these parameters could be used in isotonic and isokinetic analyses which would lead, in case of using a suitable model, to satisfying agreement of the force responses as well as of the muscle shapes when comparing numerical and experimental data. Once a model would perform the experimental findings at least in an appropriate manner, it could be used to intensify the understanding of muscle deformations, functional implications, internal muscle forces and the influence of muscle architecture on contraction dynamics by simulating these scenarios and arbitrary modifications of them in a virtual way.

6 Supplementary materials

For validation reasons supplementary, three-dimensional data can be found in the online version and include the surface coordinates of the muscle geometry during isometric, isotonic and isokinetic contraction according to the illustrations in Figs. 9, 11 and 13 as well as the spatial coordinates of the fascicles as presented in Fig. 6b.