1 Introduction

Shear-driven turbulence induced by wind erodes the stratified oceans to form and deepen the surface mixed layer (ML). The ML deepening has a large impact on the air-sea interaction processes (e.g., Bender et al. 1993; Emanuel et al. 2004; Kataoka et al. 2019), since it causes sea surface cooling through the entrainment of colder water to the ML. The deepening also plays critical roles in the blooming of phytoplankton biomass by supplying nutrients from below the ML (e.g., Obata et al. 1996; Bulusu et al. 2002; Martinez et al. 2000). Thus, quantitative understanding of the ML deepening is important to better understand such upper ocean processes.

The ML deepening is affected by Earth’s rotation because it inhibits the wind-induced shear. Pollard et al. (1973) modeled the ML deepening under the rotation. They assumed that the initial stratification (N0) is constant from the surface, that current speed (U) and buoyancy (B) become uniform in the ML, and that the bulk Richardson number Rb [≡ LMLDΔB/ΔU2, where LMLD is the ML depth (MLD), and ΔB (ΔU) is a difference of B (U) across the ML base] has a critical value (Rbc) when the ML deepens. According to their analytical discussion, the deepening after one-half inertial period (0.5Tf) is arrested by the rotation at the depth

$$ L_\text{MLD} = (8R_{bc})^{1/4} \frac{U_{*}}{\sqrt{N_{0} f}} = (8R_{bc})^{1/4} L_{P73}, $$
(1)

where U∗ is the friction velocity and f is the Coriolis parameter. Here, the deepening of the ML after 0.5Tf is ignored because of the considerable decrease in the deepening speed. This classical model and the scaling of \(L_{P73} (\equiv U_{*}/\sqrt {N_{0} f})\) are widely used (e.g., Zilitinkevich et al. 2002a; Zilitinkevich et al. 2007; Lozovatsky et al. 2005). For example, this model is used as the ocean surface ML model that is attached to atmospheric general circulation models for tropical cyclones (Davis et al. 2008; Nolan et al. 2009), whose intensity and track are affected by the sea surface temperature and hence the MLD (e.g., Bender et al. 1993). The scaling of LP73 was also incorporated in a Nutrient-Phytoplankton-Zooplankton model and used to investigate the biological productivity in the coastal region (Botsford et al. 2006). In these studies, it is implicitly assumed that the ML deepening ceases after 0.5Tf. However, whether the deepening after 0.5Tf actually ceases or whether it is slow enough to be ignored is not well examined. Since the ceasing of the ML deepening causes underestimates of sea surface cooling and nutrient supply, it may affect diagnosing and prognosing tropical cyclones and biological productivity. Therefore, in this study, we investigated the ML deepening in the stratified ocean by using large-eddy simulations (LESs) that can reproduce realistic three-dimensional turbulence and hence the ML deepening.

2 Numerical model and experimental configurations

The LES model used in the present study is the same as the model used in Ushijima and Yoshikawa (2019) except for boundary and initial conditions as described later. The governing equations are the momentum equation, continuity equation, and advection-diffusion equation of buoyancy under the incompressible, f -plane, Boussinesq, and rigid-lid approximations. Sub-grid scale parameterization follows the method described by Deardorff (1980). At the surface, constant wind stress (\(\rho _{0} U_{*}^{2}\)) is imposed while buoyancy flux is set to zero. We also impose sub-grid scale kinetic energy flux due to wave breaking and sub-grid scale shear production at the surface. At the bottom, the free slip condition and the no-buoyancy flux condition are imposed. The lateral boundaries are periodic in both directions. Initially, the buoyancy stratification [\(N_{0} (\equiv \sqrt {\partial B/\partial z})\)] is constant with the surface buoyancy being zero, and the ocean is at rest. Note again that all these configurations are the same as those in Ushijima and Yoshikawa (2019) except for zero surface buoyancy flux and nonzero initial buoyancy stratification.

The governing equations are discretized using the second-order finite-difference scheme and integrated using the second-order Runge-Kutta scheme. The number of grid cells is 128 × 128 × 128 with a uniform grid spacing of LP73/32, where \(L_{P73} \equiv U_{*}/\sqrt {N_{0}f}\). We performed several LESs with half grid spacing and found that these results were similar to those with the original grid spacing (not shown). The inertial sub-range in the kinetic energy spectrum was clearly identified in the ML with the original grid spacing (not shown), indicating a good performance of the present LES model.

The integration was continued for five inertial periods (5Tf = 10π/f). The simulations were run with various momentum fluxes (\(U_{*}^{2} = 5.0 \times 10^{-5}, 1.0 \times 10^{-4}, 2.0 \times 10^{-4} \ \text {m}^{2} \ \text {s}^{-2}\)), initial stratifications (\(N_{0} =5.0 \times 10^{-3}, 1.0 \times 10^{-2}, 2.0 \times 10^{-2} \ \text {s}^{-1}\)), and the Coriolis parameters (f = 2.5 × 10− 5,3.75 × 10− 5,5.0 × 10− 5,7.5 × 10− 5,1.0 × 10− 4 s− 1) (see Table 1). Note that we set the initial stratifications to be much greater than the Coriolis parameters as seen in the realistic ocean surface layer in order to investigate the stratification effects on the MLD. [If N0 ≪ f unlike the present experimental design, the MLD will become proportional to the Ekman length scale (U∗/f).] In the following, we defined MLD as the depth at which stratification (N2), the vertical gradient of horizontally averaged buoyancy, is the strongest. The strongest stratification corresponds to the buoyancy jump at the ML base of Pollard et al. (1973).

Table 1 Dependence of the MLD (LMLD [m]) [normalized MLD (LMLD/LP73)] and ΔSSB [×10− 4 m s− 2] [normalized ΔSSB (\({\Delta } \text {SSB}/{N_{0}^{2}}L_{P73}\))] on \(U_{*}^{2} \ [\times 10^{-4} \ \text {m}^{2}\text {s}^{-2}]\), \(N_{0} \ [\times 10^{-2} \ \text {s}^{-1}]\), and f [×10− 5 s− 1]
Full size table

3 Result

3.1 Time development of mixed layer

To illustrate the temporal variation of the vertical profiles of the properties in the ML, the results of a simulation with \(U_{*}^{2} = 1.0 \times 10^{-4} \ \text {m}^{2} \ \text {s}^{-2}, N_{0} = 1.0 \times 10^{-2} \ \text {s}^{-1}\), and f = 2.5 × 10− 5 s− 1 are described in detail. Note that similar features of the temporal variation of the ML were obtained in the other experiments. Temporal and vertical variations in horizontally averaged current speed and buoyancy are shown in Fig. 1. The current speed near the surface increased at first until around 0.5Tf, and then decreased until Tf (Fig. 1a). Thereafter, the speed oscillated with the inertial period. A layer of the strong current deepened rapidly until 0.5Tf. After that, the deepening slowed down, but it did not stop. The buoyancy near the surface decreased with time (Fig. 1b). The sea surface buoyancy (SSB) reduced in 0.5Tf by 1.5 × 10− 3 m s− 2, but the SSB reduction (ΔSSB) increased by 18 % (ΔSSB = 1.8 × 10− 3 m s− 2), 25 % (ΔSSB = 1.9 × 10− 3 m s− 2), and 56 % (ΔSSB = 2.3 × 10− 3 m s− 2) in Tf, 1.5Tf, and 5Tf, respectively. The ΔSSB at 5Tf corresponds to 1.2 K when the thermal expansion coefficient and acceleration due to gravity are assumed to be 2.0 × 10− 4 K− 1 and 9.8 m s− 2, respectively. As in the layer of the strong current, the MLD increased rapidly until 0.5Tf, and then the ML deepening slowed down, which is consistent with the results of Pollard et al. (1973) (Fig. 1b). Though the ML deepening slowed down, the MLD kept increasing gradually with inertial oscillation. The MLDs at Tf (LMLD = 35 m), 1.5Tf (LMLD = 39 m), and 5Tf (LMLD = 47 m) were greater by 2.0 %, 15 %, and 39 %, respectively, than that at 0.5Tf (LMLD = 34 m). Thus, the ML deepening after 0.5Tf can be as large as the deepening during the first 0.5Tf.

Fig. 1
figure 1

Time-depth variation of the horizontally averaged current speed (U) (a) and buoyancy (B) (b) in the experiment for \(U_{*}^{2} = 1.0 \times 10^{-4} \ \text {m}^{2} \ \text {s}^{-2}, N_{0} = 1.0 \times 10^{-2} \ \text {s}^{-1}\), and f = 2.5 × 10− 5 s− 1. The black solid line is the MLD

Full size image

Through the ML deepening, dense water was entrained to the surface layer. This means the turbulent kinetic energy (TKE) was converted to potential energy. Figure 2 shows the time series of the source and sink terms in the horizontally averaged TKE equation (as below),

$$ \begin{array}{@{}rcl@{}} \frac{\partial}{\partial t}\left( \frac{1}{2} \overline{u_{k}^{\prime} u_{k}^{\prime}} \right) &=& \underbrace{- \overline{u_{k}^{\prime} w^{\prime}} \frac{\partial \overline{u_{k}}}{\partial z}}_{P_{s}} \underbrace{+ \overline{w^{\prime} b^{\prime}}}_{P_{b}}\\ &&\underbrace{- \frac{\partial}{\partial z}\left( \frac{1}{2}\overline{u_{k}^{\prime} u_{k}^{\prime} w^{\prime}} + \frac{\overline{p^{\prime} w^{\prime}}}{\rho_{0}} \right)}_{P_{t}} \underbrace{+ \varepsilon}_{D}. \end{array} $$
(2)

Here, xi (i = 1,2,3) denotes the Cartesian coordinates (x,y,z) with z pointing upward, t is time, ui represents the velocity components (u,υ,w) in the xi direction, b is buoyancy, p is pressure, and \(\rho _{0} (= 1.0 \times 10^{3} \ \text {kg} \ \text {m}^{-3})\) is reference density. The prime means the anomaly from the horizontal mean value, and the overbar represents the horizontal average. Ps, Pb, Pt, and D represent a rate of the shear production, buoyancy production, divergence of vertical transport due to advection and pressure work, and dissipation of the TKE, respectively. The dissipation rate was calculated based on the sub-grid scale parameterization of Deardorff (1980). Note that the negative buoyancy production corresponds to the conversion of the TKE to potential energy. In the ML, the shear production and the dissipation were much greater than the buoyancy production and the divergence of the vertical transport (Fig. 2a–d). The shear production was larger in the upper ML than in the lower ML (Fig. 2a). At the base of the ML, the shear production changed rapidly in the vertical direction to become negligibly smaller below the ML. The buoyancy production decreased almost linearly with the depth in the ML and became smallest at the base of the ML (Fig. 2b). Though the depth of the smallest buoyancy production (LBP) changed with time at the inertial and higher frequencies, its temporal change at frequencies lower than the inertial frequency corresponds well with that of the MLD (say, d〈LBP〉/dt ≈ dLMLD/dt, where 〈 〉 means the average over one inertial period). Figure 2e shows the ratio of the buoyancy production rate to the shear production rate (the flux Richardson number, Rf ≡−Pb/Ps). The flux Richardson number in the ML was small, but it increased rapidly with depth at around the MLD. This indicates the flux Richardson number has a certain critical value at the ML base. Judging from Fig 2e, the depth of the smallest Pb (LBP) roughly coincided with Rf ≈ 10− 0.67 = 0.22, which can be considered as the critical Richardson number.

Fig. 2
figure 2

Time-depth variation of the shear production (Ps) (a), the buoyancy production (Pb) (b), the divergence of vertical transport due to advection and pressure work (c), the dissipation (d), and the flux Richardson number (Rf) (e) in the experiment for \(U_{*}^{2} = 1.0 \times 10^{-4} \ \text {m}^{2} \ \text {s}^{-2}, N_{0} = 1.0 \times 10^{-2} \ \text {s}^{-1}\), and f = 2.5 × 10− 5 s− 1. The black solid line is the MLD, the dashed line in (b) and (e) is the depth of the smallest Pb (LBP), and the red solid line in (b) is averaged LBP for over one inertial period (〈LBP〉)

Full size image

3.2 Parameter dependence of mixed layer deepening

To investigate the ML deepening under parameters other than \(U_{*}^{2} = 1.0 \times 10^{-4} \ \text {m}^{2} \ \text {s}^{-2}, N_{0} = 1.0 \times 10^{-2} \ \text {s}^{-1}\), and f = 2.5 × 10− 5 s− 1 and its scalings, a total of 25 experiments were performed and are shown in this sub-section. (Parameters in these experiments were described in Section 2 and Table 1). Figure 3 shows the time series of the MLDs. Here, time and MLD were normalized by Tf and LP73, respectively. The normalized MLD in all the experiments increased similarly with normalized time. The MLDs gradually increased and became 6.2 %, 16 %, and 40 % larger at t/Tf = 1, 1.5, and 5 than at t/Tf = 0.5, respectively. The ML deepening reduced the SSB, and the SSB reduction (ΔSSB) from t = 0 also increased with time (Fig. 3b). Temporal changes of ΔSSB, normalized by \({N_{0}^{2}} L_{P73}\), were again collapsed to a single line similar to that of the normalized MLD. On average, the normalized ΔSSB at t/Tf = 1, 1.5, and 5 increased by 19 %, 26 %, and 58 % from that at t/Tf = 0.5, respectively. The ΔSSB fluctuated with the inertial frequency as the MLD did, but its amplitude was less than that of the MLD. This smaller amplitude of the ΔSSB caused the difference in the increasing rates from 0.5Tf between ΔSSB and MLD (Fig. 3). Note that if the MLD was defined as the depth at which the buoyancy deviated by 3.0 × 10− 4 m s− 2 from its values at the surface, the amplitude of the inertial oscillation of the MLD was smoothed and the normalized MLD at Tf, 1.5Tf, 5Tf was greater by 22 %, 29 %, and 62 % than that at 0.5Tf, which was almost coincided with the increase of the normalized ΔSSB (not shown). The MLD and ΔSSB are summarized in Table 1.

Fig. 3
figure 3

Temporal variation of the MLD (a) normalized by LP73 (LMLD/LP73) and the SSB reduction (b) normalized by \({N_{0}^{2}} L_{P73}\) (\({\Delta } \text {SSB}/{N_{0}^{2}}L_{P73}\)). Time is also normalized by the inertial period (t/Tf). Solid lines are the averaged value of all the experiments, and shadings show the spread of the results (one standard deviation). The dashed and dotted lines in (a) are the estimated MLD from Eq. 7 with the greatest (f/N = 2.0 × 10− 2) and smallest (f/N = 1.3 × 10− 3) f/N in the parameter range of this study, respectively

Full size image

After t/Tf = 1, the low-frequency (< f) temporal change of the MLD (d〈LMLD〉/dt) roughly coincided with low-frequency change of the depth of the smallest buoyancy production (d〈LBP〉/dt) (Fig. 2b), and the 〈LBP〉 change is related to the buoyancy production (Pb(〈LBP〉)) and the buoyancy jump (ΔB) at 〈LBP〉 as shown below (Niiler and Kraus 1977; Noh et al. 2010),

$$ \begin{array}{@{}rcl@{}} \frac{d\langle L_\text{MLD} \rangle}{dt} {\Delta} B \approx \frac{d\langle L_{BP} \rangle}{dt} {\Delta} B = \langle P_{b}(\langle L_{BP}\rangle) \rangle . \end{array} $$
(3)

Here, the buoyancy jump (ΔB) is estimated as

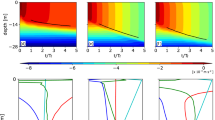
$$ \begin{array}{@{}rcl@{}} {\Delta} B \sim {N_{0}^{2}}\langle L_\text{MLD}\rangle/2 \end{array} $$
(4)

from the mass conservation law. To estimate the scale of 〈Pb(〈LBP〉)〉, we introduce the flux Richardson number (Rf) and relate Pb to the shear production (Ps), Pb = −RfPs. As shown in Fig. 2e, Rf at the base of ML was almost constant, so Pb(LBP) is proportional to Ps(LBP). In general, the value of Ps(〈LBP〉) can be scaled by \(U_{*}^{3}/L_{\text {MLD}}\), but recent studies (Goh and Noh 2013; Zilitinkevich et al. 2002b, 2005) have implied that it also depends on the Rossby number (Ro ≡ U∗/f〈LMLD〉) and the Froude number (Fr ≡ U∗/N0〈LMLD〉). Figure 4a and b show |〈Ps(〈LBP〉)〉| and |〈Pb(〈LBP〉)〉| normalized by \(U_{*}^{3}/\langle L_{\text {MLD}} \rangle \) as a function of the Rossby number (Ro) and the Froude number (Fr). Here, Ps and Pb for t ≥ Tf were only used since they showed high variability when t < Tf. It was found that |〈Ps(〈LBP〉)〉| and |〈Pb(〈LBP〉)〉| depend similarly on Ro and Fr with the Ro dependence being much larger than Fr dependence. (Similarity of |〈Ps(〈LBP〉)〉| and |〈Pb(〈LBP〉)〉| dependencies indicate constant Rf.) Thus, we scale |〈Pb(〈LBP〉)〉| by \(U_{*}^{3}/L_{\text {MLD}} F(\text {Ro, Fr})\), where F(Ro, Fr) is nondimensional function of Ro and Fr. Using this relation and Eqs. 3 and 4, the ML deepening rate becomes

$$ \begin{array}{@{}rcl@{}} \frac{d \langle L_\text{MLD}\rangle}{dt} \approx \frac{\langle P_{b}(\langle L_{BP}\rangle) \rangle}{\Delta B} = U_{*} G(\text{Ro, Fr}), \end{array} $$
(5)

where G(Ro, Fr)[= 2Fr2F(Ro, Fr)] is a function of Ro and Fr. Figure 4c shows the dependence of the ML deepening rate normalized by the friction velocity (d〈LMLD〉/dt/U∗) on the Rossby number and the Froude number. The normalized deepening rate decreased with the Rossby number and increased with the Froude number. From multiple regression of Ro and Fr in the log scale, the ML deepening rate was scaled as

$$ \frac{d \langle L_\text{MLD} \rangle}{dt} = 0.33 U_{*} \text{Ro}^{2.0} \text{Fr}^{2.7} $$
(6)

in this study. This scaling has good agreement with LES results (Fig. 4d). Integrating this scaling, LMLD can be represented as

$$ \langle L_\text{MLD} \rangle = 1.5 L_{P73} \left( \frac{f}{N} \right)^{-2.2 \times 10^{-2}} \left( \frac{t}{T_{f}}\right)^{0.18}. $$
(7)

Note that small factor \((f/N)^{-2.2\times 10^{-2}}\) in the above scaling comes from small deviations of LMLD from LP73, as shown in Fig. 3a. This factor changes the value only by 6.4 % at the largest value in the parameter range. Normalized MLDs (< LMLD > /LP73) at 0.5Tf, Tf, 1.5Tf, and 5Tf were evaluated as 1.5 − 1.6, 1.7 − 1.8, 1.8 − 1.9, and 2.2 − 2.4 from Eq. (7), respectively, while normalized MLDs of the LES results at 0.5Tf, Tf, 1.5Tf, and 5Tf were 1.7, 1.8, 1.9, and 2.3, respectively (Table 1). The scaling well reproduced the low-frequency (< f) temporal change of the MLD (Fig. 3a), which corresponds well with temporal change in the SSB (Fig. 3b).

Fig. 4
figure 4

The Rossby number (Ro) and the Froude number (Fr) dependences of the absolute values of the shear production (|〈Ps(〈LBP〉)〉|) (a) and buoyancy production (|〈Pb(〈LBP〉)〉|) (b) normalized by \(U_{*}^{3}/L_{\text {MLD}}\) at the depth of the smallest buoyancy production (〈LBP〉) and the deepening rate of the ML (d〈LMLD〉/dt) (c) normalized by U∗. d Scatter plots between the ML deepening rate and its scaling (\(0.33 U_{*} \text {Ro}^{2.0} \text {Fr}^{2.7}\))

Full size image

4 Conclusion

In this study, the ML deepening due to wind-induced shear-driven turbulence in the stratified ocean, under influence of the Earth’s rotation, was investigated through LESs. LESs showed that the ML deepens rapidly until 0.5Tf, and then the deepening slows down. This result is consistent with the classical analysis of Pollard et al. (1973). Based on their classical analysis, many previous studies used \(U_{*}/\sqrt {fN} = L_{P73}\), which is the MLD at 0.5Tf, as the scale of the MLD. However, the MLD for t > 0.5Tf keeps increasing (though the deepening speed is slower), resulting in the MLD at Tf, 1.5Tf, and 5Tf being greater by 6.2 %, 16 %, and 40 %, respectively, than at 0.5Tf. Therefore, time-dependent scaling of the MLD is necessary for more quantitative estimates than the classical theory.

To evaluate the time-dependent MLD, TKE budgets were investigated using the LES results. It was found that the buoyancy production is proportional to the shear production at the ML base (because the Richardson number is almost constant there) and that these productions depend on both the Rossby number (Ro) and the Froude number (Fr) though Fr dependence is weak in our parameter range. We then related the ML deepening rate (that is proportional to the buoyancy production) to the shear production that depends on Ro and Fr, to obtain \({d\langle L_{\text {MLD}}\rangle }/{dt} =0.33 U_{*}\text {Ro}^{2.0} \text {Fr}^{2.7}\). This results in \(\langle L_{\text {MLD}} \rangle = 1.5 L_{P73} \left ({f}/{N} \right )^{-2.2\times 10^{-2}}\)\(\left ({t}/{T_{f}}\right )^{0.18}\), which explains well the simulated MLD deepening after 0.5Tf. (Note that the validity of this scaling is lost after the stratification effect disappears).

Some previous studies assumed that ML deepening is arrested after 0.5Tf (e.g., Botsford et al. 2006; Davis et al. 2008; Nolan et al. 2009). This is a good approximation as the first order, but higher-order approximation will be necessary if more quantitative results are required. The present scaling for t > 0.5Tf will be useful for such cases. For example, in Botsford et al. (2006), phytoplankton response to the MLD was calculated with the assumption that LMLD = a + bLP73, where a and b are constants. The present scaling may provide more reliable calculations. The present results may also help estimating the MLD using the bulk Richardson number, because the present scaling (7) and analytical discussion of Pollard et al. (1973) (1) indicate that the critical bulk Richardson number Rbc should change with time; Rbc ∝ (t/Tf)0.71. In fact, Rbc used in previous studies (e.g., Price et al. 1986; Holtslag and Boville 1993; Kiehl et al. 1998) were different. The time-dependent feature of Rbc may be responsible for this difference. Because the bulk Richardson number is used in the KPP scheme (Large et al. 1994) that is widely used as the ML scheme in ocean general circulation models (e.g., Belcher et al. 2012; Huang et al. 2014; Ge et al. 2017), impacts of this time-dependent Rbc on the ML scheme need to be investigated.

In the present study, we ignored, for the sake of simplicity, many processes taking place in the ocean surface boundary layer including heating/cooling at the surface, Langmuir circulation, and temporal variation of wind stress, which also have large impacts on the ML deepening. The simplicity, on the other hand, allows the present results to be applicable to the shear-driven turbulence in the bottom boundary layers of the ocean and the atmosphere (e.g., Zilitinkevich et al. 2007). Note that in these planetary boundary layers, the Coriolis parameter or the effect of the Earth’s rotation itself can suppress the ML deepening (Zilitinkevich et al. 2007; Yoshikawa 2015) when the stratification is weak, although we set the stratifications to be much greater than the Coriolis parameters in this study. These processes need to be examined, so these will be the focus of our future studies.