1 Introduction

It has been noticed for a long time that in tidally dominant shallow seas and estuaries, the long-term mass transport process, which is closely related with the material cycle of the marine ecosystem, is determined by the residual current rather than the periodic tidal current. However, due to a complex nonlinear effect in shallow seas, how to describe the residual current has not yet reached a consensus.

The most straightforward approach to depicting the residual current is the Eulerian residual velocity (ERV), which is defined as the average of the tidal current velocity at a fixed point in space for several tidal periods (e.g., Abbott 1960). However, the ERV was found to violate the law of mass conservation at the sea surface when it was used to study the baroclinic residual circulation in the 3D case by Feng et al. (1984). Furthermore, an annoying term, “tidal dispersion,” appeared in the intertidal transport equation when the ERV acted as the advective transport velocity (Fischer et al. 1979). Despite these disadvantages, the ERV is still widely used as a result of its easy access in practice (e.g., Marinone 1997; Salas-de-León et al. 2003; Lopes and Dias 2007; Carballo et al. 2009; Cheng et al. 2010; Basdurak and Valle-Levinson 2012; Burchard and Schuttelaars 2012).

As a partial modification of the ERV, the Eulerian residual transport velocity (ETV) was proposed in the depth-averaged case by Robinson (1983). Meeting the mass conservation of the residual transport, the ETV has been employed in the research of the residual current by some researchers (e.g., Li and O’Donnell 1997, 2005; Li et al. 2008; Winant 2008). Nevertheless, Zimmerman (1979) pointed out that the ETV was nothing but a velocity vector that could be used to calculate the local residual discharge.

The third approach to describing the residual current is the Lagrangian residual velocity (LRV), which is loosely defined as the mean velocity calculated by dividing the net displacement of a labeled water parcel by one or several tidal periods (Zimmerman 1979). The Lagrangian mean theory was first introduced to the study of the residual mass flux in the time-varying ocean currents by Longuet-Higgins (1969). When able to cope with the disadvantages of both the ERV and the ETV mentioned above, the LRV has been widely used to delineate the residual current in practice (e.g., Cheng and Casulli 1982; Feng et al. 1986a, b; Ridderinkhof and Loder 1994; Delhez 1996; Loder et al. 1997; Jiang and Sun 2002; Wei et al. 2004; Ju et al. 2009; Muller et al. 2009; Liu et al. 2012; Charria et al. 2013).

Since the 1980s, a systematic theory of the LRV has been proposed and developed by Feng and his cooperators (Feng 1986, 1987, 1990; Feng et al. 1986a, b, 2008; Lu 1991; Feng and Lu 1993; Feng and Wu 1995). Recently, it was used in a narrow bay by Jiang and Feng (2011). On the assumption of the weak nonlinearity in the tidal system, Jiang and Feng (2011) deduced the depth-averaged equations for the first-order LRV, i.e., the mass transport velocity (Longuet-Higgins 1969), and obtained the results for a specific bottom profile. In their study, the differences between the various residual velocities were discussed. To make a more quantitative comparison, a 2D numerical model is employed in this paper to complete the work. In view of the weak nonlinearity in which Jiang and Feng’s (2011) results strongly depended, the feasibility of the analytic solutions in the case of a general nonlinearity will also be examined. Moreover, the Coriolis effect and the quadratic bottom friction, both of which were neglected or modified by the analytic solutions, will be taken into consideration, and their effects on the LRV will be discussed in the present work.

This paper consists of five sections. Subsequent to the section of introduction is section 2, which presents the methodology of the present study, including the definitions of the various residual velocities (section 2.1), the introduction of the numerical model setup (section 2.2), and the method to compute the LRV (section 2.3). Section 3 makes a comparison of the various residual velocities (section 3.1), followed by a detailed discussion about the feasibility of the mass transport velocity (MTV) with a general nonlinearity in the system (section 3.2). The influences of the Coriolis effect and the bottom friction in different forms on the LRV are studied in section 4.1 and section 4.2, respectively. The major conclusions are summarized in section 5.

2 Methodology

2.1 Definitions of the various residual velocities

Before computing the different residual velocities mentioned above, it is necessary to define them first. Discussions in this paper are only conducted in the depth-averaged case.

Fixed at a point in space, the ERV can be defined as follows:

$$ {\overset{\rightharpoonup }{u}}_{\mathrm{E}}=<\overset{\rightharpoonup }{u}\left({\overset{\rightharpoonup }{x}}_0,t\right)>, $$
(1)

where the tidal average operator is defined as

$$ <\psi >=\frac{1}{ mT}{\displaystyle {\int}_{t_0}^{t_0+ mT}\psi \left(\overset{\rightharpoonup }{x},t\right) dt}, $$
(2)

and \( {\overset{\rightharpoonup }{x}}_0\left({x}_0,{y}_0\right) \), \( \overset{\rightharpoonup }{u}=\left(u,v\right) \) are the initial position of the water parcel at time t 0, the velocity, and its components in x and y directions, respectively. T is the tidal period and m is the number of tidal periods used to compute the average.

As a partial modification of the ERV, the ETV is expressed by taking the surface elevation ζ into consideration, i.e.,

$$ {\overset{\rightharpoonup }{u}}_T={\overset{\rightharpoonup }{u}}_{\mathrm{E}}+\frac{<\overset{\rightharpoonup }{u}\left({\overset{\rightharpoonup }{x}}_0,t\right)\cdot \zeta \left({\overset{\rightharpoonup }{x}}_0,t\right)>}{h} $$
(3)

where h refers to the water depth at \( {\overset{\rightharpoonup }{x}}_{{}_0} \) when the water is static.

With a specific physical meaning, the LRV, which focuses on a labeled water parcel rather than just a fixed point in space, can be defined as the ratio of the net displacement \( {\overset{\rightharpoonup }{\xi}}_{mT} \) after m tidal periods to the corresponding temporal interval, namely

$$ {\overset{\rightharpoonup }{u}}_{\mathrm{LR}}=<\overset{\rightharpoonup }{u}\left(\overset{\rightharpoonup }{x},t\right)>=\frac{{\overset{\rightharpoonup }{\xi}}_{mT}}{ mT}, $$
(4)

where \( \overset{\rightharpoonup }{x}=\left(t;{\overset{\rightharpoonup }{x}}_0,{t}_0\right) \) denotes the position of the labeled water parcel at time t, with \( \left({\overset{\rightharpoonup }{x}}_0,{t}_0\right) \) being its initial position. In Feng et al. (2008), the LRV was further expressed as the differentiation of the water parcel displacement \( \overset{\rightharpoonup }{\xi } \) with respect to another independent time variable τ, which can be used to describe the intertidal process associated with the time–mean water circulation, i.e.,

$$ {\overset{\rightharpoonup }{u}}_{\mathrm{LR}}=\frac{\partial \overset{\rightharpoonup }{\xi }}{\partial \tau } $$
(5)

where \( \overset{\rightharpoonup }{\xi }=\overset{\rightharpoonup }{\xi}\left(\tau; {t}_0\right) \).

In the case of a weak nonlinearity, the MTV can be taken as the first-order approximation of the LRV, i.e.,

$$ {\overset{\rightharpoonup }{u}}_{{}_{\mathrm{L}\mathrm{R}}}={\overset{\rightharpoonup }{u}}_{\mathrm{L}}+\kappa {\overset{\rightharpoonup }{u}}_{\mathrm{ld}}+o\left({\kappa}^2\right), $$
(6)

where \( {\overset{\rightharpoonup }{u}}_{\mathrm{L}} \) is the MTV and \( {\overset{\rightharpoonup }{u}}_{\mathrm{ld}} \) is the Lagrangian drift velocity (LDV). The MTV can be further written as the sum of the ERV and the Stokes drift velocity (SDV), namely,

$$ {\overset{\rightharpoonup }{u}}_{\mathrm{L}}={\overset{\rightharpoonup }{u}}_{\mathrm{E}}+{\overset{\rightharpoonup }{u}}_{\mathrm{S}}, $$
(7)

where \( {\overset{\rightharpoonup }{u}}_{\mathrm{S}} \) is the SDV obtained by the zeroth-order astronomic tide (denoted by the subscript “0”) in light of Feng et al. (1986a)

$$ {\overset{\rightharpoonup }{u}}_{\mathrm{S}}=<{\displaystyle \kern-.6em {\int}_{t_0}^t{\overset{\rightharpoonup }{u}}_0\left({\overset{\rightharpoonup }{x}}_0,{t}^{\prime}\right)d{t}^{\prime }}\cdot \nabla {\overset{\rightharpoonup }{u}}_0\left({\overset{\rightharpoonup }{x}}_0,t\right)>. $$
(8)

For comparison with Eq. 3, the SDV can also be rewritten by using the continuity equation (Eq. 15) and < ξ 0 u 0 > = < η 0 v 0 > = 0 to the lowest order, as

$$ {\overset{\rightharpoonup }{u}}_{\mathrm{S}}=\left({u}_{\mathrm{S}},{v}_{\mathrm{S}}\right)=\frac{1}{h}\left(<{u}_0{\zeta}_0>,<{v}_0{\zeta}_0>\right)\kern-14.5em +\frac{1}{h}\left(\frac{\partial <h{u}_0{\eta}_0>}{\partial y},\frac{\partial <h{v}_0{\xi}_0>}{\partial x}\right), $$
(9)
$$ {\xi}_0=\kern-.5em {\displaystyle {\int}_{t_0}^t{u}_0}\left({\overset{\rightharpoonup }{x}}_0,{t}^{\prime}\right)d{t}^{\prime }, $$
(10)
$$ {\eta}_0=\kern-.5em {\displaystyle {\int}_{t_0}^t{v}_0}\left({\overset{\rightharpoonup }{x}}_0,{t}^{\prime}\right)d{t}^{\prime }. $$
(11)

The Lagrangian drift velocity, which is the second-order term in the LRV, was defined by Feng et al. (1986a) as

$$ \begin{array}{l}{\overset{\rightharpoonup }{u}}_{\mathrm{ld}}=<{\overset{\rightharpoonup }{\xi}}_0\cdot \nabla {\overset{\rightharpoonup }{u}}_1>+<{\overset{\rightharpoonup }{\xi}}_1\cdot \nabla {\overset{\rightharpoonup }{u}}_0>\hfill \\ {}\kern-14.8em +\left[<\left(\frac{\partial^2{\overset{\rightharpoonup }{u}}_0}{\partial {x}^2}\right){\xi}_0^2>+2<\left(\frac{\partial^2{\overset{\rightharpoonup }{u}}_0}{\partial x\partial y}\right){\xi}_0{\eta}_0>+<\left(\frac{\partial^2{\overset{\rightharpoonup }{u}}_0}{\partial {y}^2}\right){\eta}_0^2>\right]/2\hfill \end{array} $$
(12)
$$ {\xi}_1=\kern-.5em {\displaystyle {\int}_{t_0}^t\left[{u}_1\left({\overset{\rightharpoonup }{x}}_0,{t}^{\prime}\right)+{\xi}_0\frac{\partial {u}_0}{\partial x}+{\eta}_0\frac{\partial {u}_0}{\partial y}\right]}d{t}^{\prime }, $$
(13)
$$ {\eta}_1=\kern-.5em {\displaystyle {\int}_{t_0}^t\left[{v}_1\left({\overset{\rightharpoonup }{x}}_0,{t}^{\prime}\right)+{\xi}_0\frac{\partial {v}_0}{\partial x}+{\eta}_0\frac{\partial {v}_0}{\partial y}\right]}d{t}^{\prime }, $$
(14)

where the variables with a subscript “1” denote the first-order terms in the instantaneous motion. Compared with the MTV’s independence of time, the LDV is a function of the initial tidal phase which can vary continuously from 0 to 2π in a tidal cycle.

2.2 Numerical model and configurations

A depth-averaged 2D numerical model in light of Flather and Heaps (1975) is adopted in the present study for a better focus and simplification of the physical problem. The governing equations are modified to keep the same forms as those used by Jiang and Feng (2011), which can be shown as follows:

$$ \frac{\partial \zeta }{\partial t}+\frac{\partial \left(h+\zeta \right)u}{\partial x}+\frac{\partial \left(h+\zeta \right)v}{\partial y}=0 $$
(15)
$$ \frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}- fv=-g\frac{\partial \zeta }{\partial x}-\frac{\beta }{h+\zeta }u $$
(16)
$$ \frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+ fu=-g\frac{\partial \zeta }{\partial y}-\frac{\beta }{h+\zeta }v $$
(17)
$$ \overset{\rightharpoonup }{u}\cdot \overset{\rightharpoonup }{n}=0,\mathrm{at}\ \mathrm{the}\ \mathrm{fixed}\ \mathrm{boundary} $$
(18)
$$ {\zeta}_{\mathrm{OB}}={\zeta}_c \sin \left(\omega \cdot t+{\phi}_0\right), $$
(19)

where u, v, ζ, and h follow the same meanings as mentioned above. g, f, and β are the gravitational acceleration, the Coriolis parameter, and the bottom fiction coefficient, respectively. \( \overset{\rightharpoonup }{n} \) refers to the outer normal direction of the fixed boundary. ζ OB denotes the surface elevation at the open boundary. ζ c, ω, and φ 0 are the amplitude, the angular frequency, and the phase lag, respectively.

Relevant computations are carried out in a semi-enclosed bay where a Cartesian coordinate system is set up with the x-axis along the bay (with the open boundary at x = 0) and the y-axis across the bay. In view of some typical estuaries and bays around the world, such as the Hudson River estuary (70 km long and ∼1 km wide), the York River estuary (55 km long and ∼4 km wide), the San Francisco Bay (97 km long and 5 ∼ 20 km wide), and the Xiangshan Bay in China (70 km long and ∼10 km wide), the model bay is set to be 100-km long and 10 km wide. The topography varies only in the y direction and the lateral depth profile is expressed as:

$$ h(y)={h}_1+{h}_2\cdot {e}^{-{\left[\frac{B}{\alpha}\cdot \left(\frac{y}{B}-\frac{1}{2}\right)\right]}^2}, $$
(20)

where B is the breadth of the bay and h 1, h 2, and α are all constants. Let B = 10 km, h 1 = 5 m, h 2 = 10 m, and α = 1, 750 m, respectively. In this way, a nondimensional depth profile identical to that in Jiang and Feng’s (2011) study can be obtained when B and the mean depth h c (8.1 m) are taken as scales (Fig. 1). As a result, the Rossby deformation radius \( {R}_{\mathrm{d}}=\sqrt{g{h}_{\mathrm{c}}}\cdot {f}^{-1} \) (about 90 km since f = 10− 4s− 1 in the current situation) is much longer than B. Hence, the Coriolis effect can be neglected. Meanwhile, the velocity component in the y direction will also be greatly limited.

Fig. 1
figure 1

The nondimensional depth profile across the bay (see from the bay head)

Full size image

The other parameters in this paper are all kept identical to those adopted by Jiang and Feng (2011) to make the results comparable. Correspondingly, g and β are 9.8 m s−2 and 1.76 × 10−3 m s−1, respectively. Here, a tidal wavelength \( \lambda =T\cdot \sqrt{g{h}_{\mathrm{c}}} \) about 400 km is taken as the length scale in the x direction when a semidiurnal tidal period T is adopted.

The model grid is 200 (in the x direction) by 1,000 (in the y direction) cells with a spatial resolution of 500 m × 10 m (the minimum in the y direction to ensure the numerical stability). Therefore, the time step is set as 0.2 s. Only the tidal constituent M 2 (T = 12.4 h, ζ c = 1 m, φ 0 = 0) is imposed at the open boundary to drive the model.

2.3 Computation of the Lagrangian residual velocity

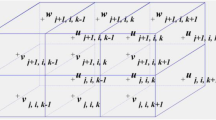
A method named “labeled particle tracking” is employed to calculate the LRV on the basis of the definition in Eq. 4. Taking the elevation as the center of the grid (the size of which is still 500 m × 10 m), components u and v are located at the east–west and north–south boundaries of the grid, respectively (Fig. 2). By taking the lower left corner of the grid as the origin, another independent coordinate system is embedded in a united coordinate system for the entire bay for each grid. Thus, the components u and v can only vary along the x and y directions separately. For instance, the component u on the east and the west boundaries of the grid can be separately expressed as u e and u w. Expand u into series and just keep the first-order approximation as

Fig. 2
figure 2

Illustration for the net displacement of a labeled particle during an interval Δt in a grid

Full size image
$$ u={u}_{\mathrm{w}}+x\frac{\partial u}{\partial x}. $$
(21)

In a local coordinate system of the grid, the west side is considered to be at x = 0. The east–west gradient of the component u is

$$ \frac{\partial u}{\partial x}=\frac{u_{\mathrm{e}}-{u}_{\mathrm{w}}}{\varDelta x}=\mathrm{const}, $$
(22)

where Δx is the length of the grid. Assuming that a labeled particle moves from position x 1 to x 2 after an interval Δt, it is easy to acquire

$$ {\displaystyle {\int}_{x_1}^{x_2} dx}=\kern-.5em {\displaystyle {\int}_{t_0}^{t_0+\varDelta t}\left({u}_{\mathrm{w}}+x\frac{\partial u}{\partial x}\right) dt}. $$
(23)

Eq. 23 can be rewritten into

$$ \varDelta \xi ={x}_2-{x}_1=\left(\frac{u_{\mathrm{w}}}{\partial u/\partial x}+{x}_1\right)\cdot \left({e}^{\frac{\partial u}{\partial x}\varDelta t}-1\right), $$
(24)

where Δξ is the displacement of the particle in the x direction during Δt. u e and u w will be updated in time when the particle strides over the grids. If Δξ is accumulated during each Δt for m tidal cycles, the net displacement ξ mT will be obtained. Thus, the component of the LRV in the x direction can be acquired as

$$ {u}_{\mathrm{LR}}=\frac{\xi_{mT}}{ mT}. $$
(25)

The other component v LR can also be gained likewise.

3 Discussions on the various residual velocities

To address the controversy over the description of the residual current, the validity of each residual velocity mentioned above will be discussed in this section.

3.1 Comparisons among the various residual velocities

In this study, the model ran for 30 tidal cycles, and the labeled particles were released at the beginning of the 29th cycle. The instantaneous velocities of the particles were recorded in real time from which the various residual velocities were separately derived according to their definitions in Eqs. 1, 3, 4, and 7 in subsection 2.1. In order to ensure the comparability between these residual velocities and the analytic solutions (Jiang and Feng 2011), the corresponding results were normalized in this paper. The scales for the different variables were taken as t c = T, x c = λ, y c = B, \( {u}_{\mathrm{c}}=\sqrt{g/{h}_{\mathrm{c}}}{\zeta}_{\mathrm{c}} \), and v c = Bζ c/(h c T).

The flow patterns, which are almost identical to those in Jiang and Feng’s (2011) study when the same extents from the bay head are compared, are presented in Fig. 3. In the flow field of the LRV, there are a couple of gyres at the head of the bay (Fig. 3a). At the open boundary, water flows into the bay from the shoal and flows out along the deep channel. The flow pattern of the MTV (Fig. 3b), which is exactly the analytic results obtained by Jiang and Feng (2011), is well consistent with the flow pattern of the LRV except for the difference at the open boundary, where the water flows into the bay from both the shoal and the deep channel but flows out just along the slope of the bay. In spite of the size of the gyres at the head of the bay, the flow pattern of the ETV (Fig. 3c) shares the same features with that of the LRV. By contrast, the flow field of the ERV seems to be much simpler in which the exchange flow exhibits a violation of the law of mass conservation because the water all flows out of the bay (Fig. 3d).

Fig. 3
figure 3

The nondimensional form streamline of the LRV (a), the MTV (b), the ETV (c), and the ERV (d) in the model bay

Full size image

Now that the qualitative differences have been illustrated, a quantitative comparison seems to be much more necessary. Since the long-term mass transport is determined by the residual current, whether the various residual velocities could exactly reflect the process should be taken as a convincible examination of their validities. Therefore, 20 particles (Fig. 4) were selected to get retracked for two tidal cycles by using the different residual velocities. The displacements of the particles by retracking are compared with those in the actual flow field which includes both the tidal and the residual currents. The relative errors in the magnitude and the absolute errors in the direction (limited to 0∼180°) have been listed in Table 1. With a small mean error of 1.56 % in the magnitude and 0.55° in the direction, the results obtained by the LRV perfectly coincide with the reality. However, both the ETV and the ERV are far from the real situation since the mean errors are both more than 50 % in the magnitude and 40° in the direction. To give a better illustration, the results of no. 5, 6, 14, and 17 particles are picked out and demonstrated in Fig. 5. The terminal points of the particles computed by the LRV and the actual velocity almost overlap each other. Nevertheless, those based on the ETV and the ERV tend to deviate from the actual results greatly in space. Therefore, it is confirmed that the long-term transport of a labeled particle in the actual flow field can be directly calculated by the residual velocity. It is also verified that the LRV rather than the ERV or the ETV is a more appropriate description of the residual current.

Fig. 4
figure 4

The initial positions of the selected particles in the model bay

Full size image
Table 1 Errors between the displacements of the particles retracked by the different residual velocities for two tidal cycles and those in the actual flow field
Full size table
Fig. 5
figure 5

The starting and terminal points of the no. 5 (a), no. 6 (b), no. 14 (c), and no. 17 (d) particles by integrating for two tidal cycles with the actual velocity (denoted by the exaggerated black dots), the LRV (denoted by the red dots), the MTV (denoted by the green dots), the ETV (denoted by the orange dots), and the ERV (denoted by the blue dots), respectively. The dots, all of which overlap with each other, denote the starting points otherwise denote the terminal points. The thinner crosses in the picture represent the trajectories of the particles corresponding to different velocities mentioned above

Full size image

As to the results based on the MTV, the mean errors in the magnitude and the direction are found to be 15.78 % and 7.89°, respectively. Thereinto, the particles with a prominent deviation (M > 10 %, D > 10°) mainly exist in the center and on the border of the gyres, where the currents vary so dramatically in space that it is difficult to conduct a precise computation with such a limited resolution. Meanwhile, it is easy to introduce a considerable error to the MTV due to the complex numerical discretization of the gradient terms in the SDV. Moreover, an additional error comes from the error accumulation during the particle retracking. In spite of these errors, the corresponding displacement vectors in Fig. 5 show a good consistency with the actual situation. Therefore, despite the inevitable discrepancy induced by the numerical computation, the closeness between the results of the MTV and the reality is satisfactory. In other words, the MTV can be a reasonable approximation of the LRV in this case.

3.2 Feasibility of the MTV with a general nonlinearity in the system

The achievement of the analytic solutions based on the MTV by Jiang and Feng (2011) is strongly dependent on a weak nonlinearity in the system. It is necessary to figure out whether the MTV can keep an effective approximation of the LRV when it comes to a generally nonlinear problem. Therefore, a nondimensional parameter κ = ζ c/h c, which is considered to be a conservative estimation of the nonlinearity in the system, is modified by enhancing ζ c from 1 to 3.5 m (the maximum restricted by the numerical stability) with an interval of 0.5 m. Moreover, it was found by Jiang and Feng (2011) that more differences among the various residual velocities can be revealed if the length of the bay is extended to a tidal wavelength. In order to ensure a better comparability with the analytic results, the geometry of the model bay was modified to make it identical to that in Jiang and Feng (2011), namely with a length of 400 km and a breadth of 2 km. Then, a comprehensive comparison between the MTV and the LRV will be made in this subsection.

Figure 6 presents the flow patterns of the MTV and the LRV with an increasing κ. There is only a slight discrepancy between the two patterns when κ < 0.185. However, the two patterns tend to be more and more different when κ becomes considerably large. With significant deviations mainly concentrated in the region x < 0.6, which implies a notable difference in the exchange flow at the mouth of the bay. For the LRV, the couple of semi-gyres in the deep channel gets restrained and tend to vanish with the increase of κ. Consequently, the inflow gradually takes over the region and confines the outflow only to the deep channel. As to the MTV, the water still flows into the bay both from the shoal and the deep channel and flows out from the slope region. The most noteworthy change in the pattern of the MTV is that a new couple of eddies appear over the slope region when κ > 0.370.

Fig. 6
figure 6

The nondimensional form streamline of the MTV (left panel with the suffix “1”) and the LRV (right panel with the suffix “2”) when κ is equal to 0.123 (a), 0.185 (b), 0.247 (c), 0.309 (d), 0.370 (e), and 0.432 (f), respectively

Full size image

Since the qualitative difference has been clearly exhibited, a quantification should be sequentially carried out. The spatially averaged errors between the MTV and the LRV in the entire bay are shown in Fig. 7. It is found that the discrepancies do increase both for the magnitude and for the direction when κ gets enhanced. Moreover, the curves tend to rise rapidly when κ > 0.185. Thus, a rough estimation of κ for the validity of the MTV can be acquired here. In order to further highlight the relationship between the error and the nonlinearity in space, the regions with a prominent discrepancy (more than 50 % in the magnitude and more than 30° in the direction) are shaded in Fig. 8. Meanwhile, the distributions of the local κ, which is defined as the ratio of the local tidal amplitude to the depth, are displayed in Fig. 9. Besides those located in the center and on the border of the gyres mentioned above, significant errors are found in the regions where the local κ is considerably big and varies rapidly in space by comparing Figs. 8 and 9. In view of the strong current and the large topographic gradient in these regions, the nonlinear advection will become very significant both in its magnitude and in its spatial variation. The considerable κ in such regions results in the invalidity of the perturbation method used by Feng et al. (1986a) to compute the MTV. Actually, this is exactly the main source of the growing error mentioned above. As a result, the MTV in such regions will fail to approximate the LRV without any doubt. Considering the effect of the local scale on the nonlinearity, another nondimensional parameter ε proposed by Ju et al. (2009), i.e.,

Fig. 7
figure 7

Spatially averaged relative error in the magnitude (a) and absolute error in the direction (b) with an increasing κ

Full size image
Fig. 8
figure 8

Regions with a prominent relative error more than 50 % in the magnitude (shaded in red with the suffix “1”) and absolute error more than 30° in the direction (shaded in blue with the suffix “2”) between the MTV and the LRV when κ is separately equal to 0.123 (a), 0.185 (b), 0.247 (c), 0.309 (d), 0.370 (e), and 0.432 (f). The nondimensional form streamlines in the pictures describe the flow patterns of the LRV with the varying κ

Full size image
Fig. 9
figure 9

Distributions of the local κ corresponding to the cases in Fig. 8

Full size image
$$ \varepsilon =\kappa \cdot \left(\frac{\lambda }{L}\right), $$
(26)

where L is the horizontal scale of the current field can be a better indicator of the nonlinearity for a realistic ocean with a more complex topography and geometry. However, for the context of the theoretical study in this paper with a simple topography, κ is still an effective indicator to distinguish the various residual velocities conceptually.

It is pointed out by Feng et al. (1986a) that the MTV is independent of time, while the LDV included in the LRV is a function of the initial tidal phase when the particles are released. In light of Feng et al. (1986a), the LDV was considered to be one order of magnitude smaller than the MTV when the nonlinearity of the system was weak. In fact, the LDV in the present study is found to be only 0.001 % of the MTV when κ = 0.123. It means that the LRV in this case is insensitive to the initial tidal phase since the LDV is negligibly small. However, with the growth of κ, it is revealed in Fig. 10 that the dots (the LRV) with different initial tidal phases are scattered on the hodograph plane in contrast to the overlapped triangles (the MTV). Although the difference is slight, it does indicate that an additional error between the MTV and the LRV will come from the various initial tidal phases when the Lagrangian drift velocity cannot be ignored in the case of a general nonlinearity.

Fig. 10
figure 10

Scatter diagram of the nondimensional MTV (denoted by triangles) and LRV (denoted by dots) on a hodograph plane for the no. 5 (a), no. 6 (b), no. 14 (c), and no. 17 (d) particles in Fig. 4 when κ = 0.247. Symbols in red denote the initial tidal phase of 0 when the particles are released. Similarly, those in black, orange, and green denote the initial tidal phases of π/2, π, and 3π/2, respectively (Since the symbols are very close to each other, different scales of the coordinates are used for each subgraph to clearly distinguish the symbols in space. For the same purpose, the origin (u, v) = (0, 0) is not shown in the figure as well.)

Full size image

4 Discussions on the factors affecting the LRV

Now that the LRV has been proven to be an appropriate description of the residual current, it is necessary to focus on the factors affecting its generation and variation. Because the Coriolis effect was neglected by Jiang and Feng (2011), its effect on the LRV will be discussed in the present work. In addition, the bottom friction linearized by Jiang and Feng (2011) will also return to the quadratic form to examine its effect on the LRV.

4.1 Coriolis effect on the LRV

In the previous section, the model bay was so narrow that the Coriolis effect, which is significant in geophysical fluid dynamics, could be neglected. Hence, it is necessary to find out what will happen to the LRV if the Coriolis effect is taken into consideration. In order to do this, four contrast experiments were conducted in the present study. The breadth of the bay is extended to 20 km, and the parameter α in Eq. 16 is correspondingly modified to keep the mean depth invariant. In this way, a laterally uniform elevation can still be imposed at the open boundary due to a relatively small aspect ratio. All the other parameters in the model remain unchanged for comparability with the previous study. Then, two main variables, the Coriolis force and the topography, are separately manipulated in the contrast experiments to define their roles in the LRV.

The flow patterns of the LRV in different cases are displayed in Fig. 11. There is a slight difference in the symmetry between a and b of Fig. 11, indicating that the Coriolis effect is weak but does affect the LRV under the current circumstances. For further illustration, the topography is firstly turned into a flat bottom with a constant depth h c = 8.1 m, and only the Coriolis effect is taken into consideration. It can be seen that an anticlockwise residual circulation comes into being (Fig. 11c). Then, the Coriolis effect is removed, and the residual current is found to disappear with it (not shown here). For the sake of quantification, the total tidally averaged kinetic energy of the whole bay and the component related to the LRV are calculated at the same time (Table 2). The ratio of the latter to the former is found to just decrease a little when the Coriolis effect is ignored. By contrast, the ratio tends to reduce by one order of magnitude when the flat bottom is adopted. However, it is almost zero if the Coriolis effect and the varying topography are both excluded. On the basis of the qualitative and quantitative results, the Coriolis effect is confirmed to be important to the generation of the Lagrangian residual circulation, although it is obscured by the effect of the topography in the present case.

Fig. 11
figure 11

The nondimensional form streamline of the LRV with the Coriolis effect and the varying topography (a), with the varying topography but without the Coriolis effect (b), and with the Coriolis effect and a constant depth (c)

Full size image
Table 2 The total tidally averaged kinetic energy in the entire bay and its component related to the LRV in different cases
Full size table

In view of the weak nonlinearity here, the MTV is considered to be a good approximation of the LRV. Thus, a depth-averaged residual vorticity equation based on the MTV is obtained for a dynamic diagnosis (see Appendix 1 for the derivation):

$$ \beta {\omega}_{\mathrm{L}}=f{\overset{\rightharpoonup }{u}}_{\mathrm{L}}\cdot \nabla h+\frac{\beta }{h}\nabla h\times {\overset{\rightharpoonup }{u}}_{\mathrm{L}}\cdot \overset{\rightharpoonup }{k}-\frac{1}{h}\nabla h\times \overset{\rightharpoonup }{\varPi}\cdot \overset{\rightharpoonup }{k}+\nabla \times \overset{\rightharpoonup }{\varPi}\cdot \overset{\rightharpoonup }{k} $$
(27)
$$ {\omega}_{\mathrm{L}}=\nabla \times {\overset{\rightharpoonup }{u}}_{\mathrm{L}}\cdot \overset{\rightharpoonup }{k} $$
(28)
$$ \begin{array}{l}{\Pi}_x=- gh\frac{\partial }{\partial x}<\frac{1}{2}{\overset{\rightharpoonup }{\xi}}_0\cdot \nabla {\zeta}_0>+\frac{\beta }{h}<{u}_0{\zeta}_0>\hfill \\ {}\kern-18em +\beta \left(\frac{1}{h}\frac{\partial <h{u}_0{\eta}_0>}{\partial y}+<{\xi}_0\nabla \cdot {\overset{\rightharpoonup }{u}}_0>+<{\eta}_0\cdot \nabla \times {\overset{\rightharpoonup }{u}}_0>\right)\hfill \end{array} $$
(29)
$$ \begin{array}{l}{\varPi}_y=- gh\frac{\partial }{\partial y}<\frac{1}{2}{\overset{\rightharpoonup }{\xi}}_0\cdot \nabla {\zeta}_0>+\frac{\beta }{h}<{v}_0{\zeta}_0>\hfill \\ {}+\beta \left(\frac{1}{h}\frac{\partial <h{v}_0{\xi}_0>}{\partial x}+<{\eta}_0\nabla \cdot {\overset{\rightharpoonup }{u}}_0>+<{\xi}_0\cdot \nabla \times {\overset{\rightharpoonup }{u}}_0>\right)\hfill \end{array} $$
(30)

where ω L is the residual vorticity, \( \overset{\rightharpoonup }{k} \) is the unit vector along the z-axis, and \( \overset{\rightharpoonup }{\varPi } \), which was termed as the “tidal stress” by Feng (1991), is the integral of the tidal body force along the water column; the other variables all follow the same meanings as mentioned above. The term on the left-hand side of Eq. 27 represents the dissipation of the residual vorticity due to the bottom friction, while the four terms on the right-hand side stand for four types of mechanisms with which the residual vorticity is induced. The first mechanism is due to the cross-isobath flow induced by the Coriolis force. The second mechanism is the result of the slope-induced bottom stress torque (Lee et al. 2001). The third mechanism is the interaction between the varying topography and the tidal stress. The fourth one is the curl of the tidal stress. Different from the first two mechanisms well discussed by many researchers (e.g., Zimmerman 1978; Robinson 1981), the last two mechanisms, which exactly epitomize the nonlinear effect of the tidal system to connect the astronomic tide with the residual current, have rarely been studied. In order to figure out the role of each term in Eq. 27, the time series of the instantaneous velocity for the five particles released at section x = 0.4 are exhibited in Fig. 12 for an illustration.

Fig. 12
figure 12

The time series of the instantaneous velocity (u in the left panel and v in the right panel) of the particles released at the same positions as those (no. 6∼10) in Fig. 4 (separately denoted by the lines in mauve, red, green, blue, and black) for the case with the Coriolis effect and a constant depth (a), with the varying topography but without the Coriolis effect (b), with the Coriolis effect and the varying topography (c), and with a constant depth but without the Coriolis effect (d)

Full size image

When the Coriolis effect is taken into consideration and the depth is set as a constant, the first three terms on the right-hand side of Eq. 27 are all zero. Although the Coriolis parameter f is not explicitly expressed in the residual vorticity equation, it should be noted that a shear of the u component and a weak v component to ensure a nonzero fourth term on the right-hand side of Eq. 27 have been induced by the combination of the rotation and the lateral boundaries (Fig. 12a). As a result, the Coriolis effect will still generate the residual vorticity through the curl of the tidal stress.

When the Coriolis effect is neglected and only the varying topography is taken into consideration, the first term on the right-hand side of Eq. 27 can be eliminated. Analogous to the Coriolis effect, the topography with a lateral variation can also cause a shear of the u component and a weak v component (Fig. 12b). Therefore, the other three terms on the right-hand side of Eq. 27 are all nonzero. The residual vorticity finally results from the slope-induced bottom stress torque, the interaction between the varying topography, and the tidal stress, as well as the curl of the tidal stress.

When the Coriolis effect and the varying topography are both included, the residual vorticity will arise from the combination of the first two cases (Fig. 12c). Moreover, the first term on the right-hand side of Eq. 27 starts to work since the cross-isobath flow is induced by the Coriolis effect. Consequently, a more complicated pattern of the residual circulation comes into being in Fig. 11a.

By contrast, when the Coriolis effect and the varying topography are both excluded, the first three terms on the right-hand side of Eq. 27 are firstly eliminated. The tidal current retreats to a simple reversing style without the lateral variation (Fig. 12d). As a result, the fourth term also vanishes since the constituents including v 0, η 0, and ∂/∂y are all equal to zero. In this case, there is no residual vorticity.

It was verified by Feng et al. (1986a) that the velocity shear was not a necessary condition for the existence of the LRV in an infinite domain. However, for a semi-enclosed bay, the velocity shear is important for the formation of a Lagrangian residual circulation to meet the law of mass conservation on a long-time scale. According to Eq. 27, any mechanism which can introduce the velocity shear will make a great contribution to inducing the residual vorticity. Therefore, the Coriolis effect works on the residual vorticity in a similar way as the varying topography since both of them can cause the tidally averaged nonzero velocity shear with the help of the nonlinear effect in the tidal system. For the Coriolis effect, the process operates mainly through the curl of the tidal stress. It is interesting that the Coriolis effect, which does no work at all, will be of great importance to the energy transfer from the astronomical tide to the residual current.

4.2 Sensitivity of the LRV to the bottom friction in different forms

In the last subsection, the Coriolis effect was confirmed to play an important role in inducing the residual vorticity. In fact, the effect of the bottom friction on the LRV seems to be much more significant. If the fluid is inviscid, Eq. 27 will be reduced to an equation for some geostrophic motions (see Appendix 2 for the derivation), which has been discussed by Moore (1970) and Feng (1987). Since the model bay is laterally bounded and contains no closed geostrophic contours, the residual current will vanish everywhere even if the Coriolis effect is taken into consideration. Therefore, the bottom friction is essential to the generation of the LRV and should be further studied. In Moore (1970) or Feng (1987), the LRV cannot be determined if no bottom friction is assumed. Huthnance (1981) made this kind of geostrophic motion soluble by introducing a weak bottom friction. He found that the type of the friction is important in the control of the LRV, and the magnitude is not of importance. Yet the situation is different in this paper with the bottom friction being dominant in the momentum balance which is similar to the case of Ianniello (1977) and Feng (1987). So, the sensitivity of the LRV to the bottom friction in different forms will be discussed here.

The term of the bottom friction, which was linearized in the previous section to make the numerical results comparable with the analytic solutions in Jiang and Feng (2011), will return to the quadratic form in light of Proudman (1953):

$$ -\frac{C_{\mathrm{d}}\left|\overset{\rightharpoonup }{u}\right|\cdot \overset{\rightharpoonup }{u}}{h+\zeta }, $$
(31)

where \( {C}_{\mathrm{d}}=\frac{3\pi \beta}{8U} \) denotes the bottom drag coefficient and U is the mean amplitude of the tidal current in the entire bay. In order to ensure the same energy dissipation during a tidal cycle, C d is set to be 2.59 × 10− 3. This subsection will focus on the effect of the quadratic bottom friction on the LRV.

The nondimensional streamline of the LRV with the quadratic bottom friction is shown in Fig. 13. A significant difference can be seen in Fig. 13 in comparison with Fig. 3a. There is a change in the position of the gyre centers at the head of the bay. The gyres located at x = 0.6 get extended and are completely independent. Moreover, a new couple of gyres appear at x = 0.4 and push the semi-gyres towards the mouth of the bay. The exchange flow pattern remains unchanged except for a restriction of the inflow in the deep channel.

Fig. 13
figure 13

The nondimensional form streamline of the LRV with the quadratic bottom friction

Full size image

To figure out the difference, the distribution of the local κ is checked in Fig. 14. In contrast with those in Fig. 9a, all of the local κ in the region x > 0.3 tend to increase due to an enhancement of the elevation amplitude. This indicates that the nonlinearity of the system has been significantly changed. This can be explained by the fact that \( {C}_{\mathrm{d}}\left|\overset{\rightharpoonup }{u}\right| \) in the quadratic bottom friction is continuously modified by the local instantaneous velocity in comparison with the constant β. Therefore, the instantaneous energy dissipation will be very different despite the same accumulation during a tidal cycle. As a result, a greater complexity is brought in the LRV through the nonlinear effect of the tidal currents, which have become much stronger with a more complicated spatiotemporal variation. Therefore, researchers should be careful to choose the scheme of the bottom friction for the numerical computation of the LRV.

Fig. 14
figure 14

The distribution of the local κ when the quadratic bottom friction is adopted

Full size image

5 Conclusions

In this paper, the tidally induced Lagrangian residual current in a model bay was studied with a depth-averaged numerical model. The correctness of the LRV in physics and the feasibility of its first-order approximation (i.e., the MTV) are examined in succession. In addition, two factors affecting the LRV are discussed in detail.

The LRV is proven to be a more suitable description of the residual current than any other residual velocity. Besides a qualitative difference in the flow pattern, there is a quantitative discrepancy among the LRV, the ERV, and the ETV. The results of the particle retracking indicates that only the LRV can perfectly reflect the process of the long-term mass transport, whereas both the ERV and the ETV are far from the reality due to their defects in physics.

The validity of the MTV to approximate the LRV is found to strongly depend on the nonlinear effect of the system, which can be indicated by a parameter κ. In spite of the numerical error, the MTV is very close to the LRV when the nonlinearity is weak. However, with the growth of κ, the perturbation method to obtain the MTV is broken, which results in an increasing error between the MTV and the LRV. Moreover, in the case of a general nonlinearity, the effect of the initial tidal phase on the LRV cannot be ignored anymore. In consequence, a time-dependent error is also appended when κ remains the same.

The Coriolis effect is verified to make a contribution to the generation of the Lagrangian residual vorticity. In view of the weak nonlinear effect in the system, a residual vorticity equation based on the MTV is obtained for a dynamic diagnosis. It is found that the Coriolis effect can induce the residual vorticity by causing a velocity shear in the nonlinear tidal system, which is finally embodied in the curl of the tidal stress.

The LRV seems to be sensitive to the bottom friction in different forms. With the same energy dissipation in a tidal cycle, the LRV tends to be more complex when the quadratic bottom friction rather than the linear one is adopted. It may be caused by the varying \( {C}_{\mathrm{d}}\left|\overset{\rightharpoonup }{u}\right| \) in the quadratic bottom friction in comparison with the constant β in the linear one.

Because of the 3D nature of the LRV, the 2D model employed in the present work is inadequate. Hence, research will be extended to a 3D case in the future.