1 Introduction

Sea water level is a dynamic variable and its variations are controlled by many environmental forcing, such as lunar and solar gravitational attraction, ocean waves and currents, atmospheric pressure and wind forcing, as well as the shape of the continental shelf. Thus, the values of sea water level are affected by several, sometimes interconnected and nonlinear, physical variables. Their predictions in near-shore environments are often required for design purposes, and their knowledge is used as management information necessary for reducing risk along coastal and low-lying regions or for monitoring and predicting changes in fishery and marine ecosystems. Different models of time series analysis include fuzzy logic (Zadeh 1965), neurofuzzy (Lee and Han 2005), genetic programming (GP), artificial neural networks (ANN) (Makarynskyy et al. 2004) and recently chaos theory. This paper is focussed on chaos theory and GP.

A low-dimensional chaotic system largely behaves in a deterministic manner, but its behaviour is sensitive to small changes in the initial conditions leading to a completely different behaviour in the future. Since its first presentation by Lorenz (Wilks 1991), chaotic behaviours have been observed in diverse systems by many researchers. The applicability of the chaos theory has been widened to a large class of problems in many areas of natural sciences. Notwithstanding this, the presence of chaotic signals is not obvious in irregular time series in the first place, and therefore, this is a motivation for researchers to identify their presence by applying chaos theory. The identification of chaotic signals is still a novel approach in ocean-related problems.

The focus of research on the identification of the presence of low-dimensional deterministic chaotic behaviours is more on river flow time series than that on sea water level. For a review on river applications, see, e.g. Sivakumar (2009).

Chaotic signals have also been identified in time series of coastal water and investigations as follows: (1) Frison et al. (1999) use data at 6-min intervals from seven ‘tide’ stations with different water level characteristics operated in the USA, measuring ocean surface motions, and they find chaos theory to be an attractive real-time forecasting tool for its simple data requirements, low computational burden and the need far few decisions on the parameters. (2) Zaldivar et al. (2000) use chaos theory in Venice, Italy, for tidal data at an hourly interval and report a predictability between 8 and 13 h ahead using the Lyapunov dimension, though they identify chaotic signals but find that chaos theory fails to forecast the ‘high water’ phenomenon more than 2–3 h ahead. (3) Solomatine et al. (2000) model the surge time series in the North Sea in itself using nonlinear chaos models, identify the presence of chaotic signals and produce quite accurate results for the short-term prediction. There seems to be no investigation for identifying chaotic signals in sea level time series over longer time horizon such as a month and this makes the focus of this investigation.

Since the 1990s, time series analysis methods employing GP have become viable, and this paper uses GP for comparisons with the performance of chaos theory. The GP methods, first proposed by Koza (1992), are wide ranging, similar to genetic algorithms (Goldberg 1989). Generally, GP techniques are robust applications of optimisation algorithms and represent one way of mimicking natural selection. The techniques have the capability for deriving a set of mathematical expressions to describe the relationship between the independent and dependent variables using such operators as mutation, recombination (or crossover) and evolution. These are operated in a population evolving in generations through a definition of fitness and selection criteria, where the subsequent techniques are data driven. GP techniques are particularly applicable to cases where: (1) the interrelationships among the relevant variables are poorly understood or suspected to be wrong; (2) finding the size and shape of the ultimate solution is itself a major part of the problem; (3) conventional mathematical analyses are constrained by restrictive assumptions but approximate solutions are acceptable; (4) small improvements in performance are routinely measured, easily measurable and highly prized; and (5) the amount of data is large (e.g. satellite observation data), which requires examination, classification and integration (Banzhaf et al. 1998).

Borelli et al. (2006) introduced an approach based on the GP for extracting the trend in noisy data series. Kalra and Deo (2007) applied the GP for the completion of missing data in wave records along the west coast of India. Ustoorikar and Deo (2008) used the GP for filling up gaps in datasets of wave heights. Gaur and Deo (2008) applied the GP for real-time wave forecasting. Ghorbani et al. (2010) apply GP for modelling sea level at Hillarys Boat Harbour and compare its performance with observed and that of artificial neural networks. Their results indicate an edge for GP compared with ANN and hence the GP performance is used for comparison in this paper.

Sea level variations are subject to combined influences of tides as well as to other hydrometeorological factors such as barometric pressure, sea water temperature, wind forcing and wave setup. The non-tidal signals are generally referred to as residuals (computed as observations minus tidal predictions) and can contribute up to 30% of the measured values at the Hillarys tide gauge (Makarynskyy et al. 2004). Therefore, the proposed chaos theory and GP models for sea level variations cannot be compared to any other tide prediction method (e.g. harmonic analysis) in any meaningful way. As such, the results obtained here may not necessarily be applicable to other locations on the Western Australian coast, where independent site-specific studies should be performed.

This paper aims at investigating the possible presence of chaotic signals in sea water level time series at Hillarys Boat Harbour. Section 2 presents the methodology for chaos theory, which is implemented by four techniques: the phase space reconstruction is carried out by average mutual information (AMI) and the false nearest neighbours technique; the correlation dimension method; Lyapunov exponent and local prediction but only the latter is implemented for prediction purposes; and this is compared with the GP model. Section 3 outlines the gauging site and specifies the data. Section 4 presents the results in terms of identifying chaotic signals in the data and predicting future values by both chaos theory and GP. Section 5 discusses the results and their implied issues.

2 Methodology of the models used

2.1 Chaos theory

Chaos theory is a method of nonlinear time series analysis. It involves a host of methods, essentially based on the phase space reconstruction of the process, from scalar or multivariate measurements of physical observables. This study uses four of these techniques, described next, and this is normal in chaos theory modelling practices, as a way of avoiding spurious results.

2.1.1 Phase space reconstruction

One way of characterising dynamical systems is by the concept of phase space, according to which given a set of physical variables and an analytical model describing their interactions, the dynamics of the system can be represented geometrically by a single point moving along a trajectory, where each of its points corresponds to a state of the system. The delay-embedding method reconstructs phase space from a univariate or multivariate time series (Takens 1981), which is assumed to be generated by a deterministic dynamical system. The Takens theorem states that the underlying dynamics can be fully recovered by building an m-dimensional space wherein the components of each state vector \( \overrightarrow {{Y_t}} \) are defined through the delay coordinates:

$$ \overrightarrow {{Y_t}} = \left( {{X_t},{X_{{t - \tau }}},{X_{{t - 2\tau }}},...,{X_{{t - (m - 1)\tau }}}} \right) $$
(1)

where m is known as embedding dimension, τ as delay time and X t  = {x 1, x 2, …x N } with N-observed values. If the dynamics of the system can be reduced to a set of deterministic laws, trajectories converge towards a subset of the phase space with fractional dimension, called attractor. This delay-embedding method is sensitive to both embedding parameters of τ and m, which are unknown a priori. As suggested by Cellucci et al. (2003), AMI is used to estimate τ; and the minimisation of the false nearest neighbours to do that of the optimal values for the embedding dimension, m.

AMI (Fraser and Swinney 1986) defines how the measurements X(t) at time t are related, from an information theoretic point of view, to measurements X(t + τ) at time t + τ. The average mutual information is defined as:

$$ I\left( \tau \right) = \sum\limits_{{X(i),X\left( {i + \tau } \right)}} {P\left( {X(i),X\left( {i + \tau } \right)} \right)\log } \left[ {\frac{{P\left( {X(i),X\left( {i + \tau } \right)} \right)}}{{P\left( {X(i)} \right)P\left( {X\left( {i + \tau } \right)} \right)}}} \right] $$
(2)

where the sum is extended to the total number of samples in the times series. P(X(i)) and P(X(i + τ)) are the marginal probabilities for measurements X(i) and X(i + τ), respectively, whereas P(X(i), X(i + τ)) is their joint probability. The optimal delay time τ minimises the function I(τ): for t = τ, X(i +  τ) adds the maximum information on X(i).

The false nearest neighbours procedure (Kennel et al. 1992) is a method to obtain the optimum embedding dimension for phase space reconstruction. By checking the neighbourhood of points embedded in projection manifolds of increasing dimension, the algorithm eliminates 'false neighbours': This means that points apparently lying close together due to projection are separated in higher embedding dimensions. When the ratio between the number of false neighbours at the dimension m + 1 and m is below a given threshold, generally smaller than 5%, each m' > m + 1 is an optimal embedding. However, if m' is too large, a poor reconstruction of few embedding states with several components is obtained and the next analyses should not be performed.

2.1.2 Correlation dimension

Correlation dimension is a nonlinear measure of the correlation between pairs lying on the attractor. For time series whose underlying dynamics is chaotic, the correlation dimension gets a finite fractional value, whereas for stochastic systems it is infinite. For an m-dimensional phase space, the correlation function C m(r) is defined as the fraction of states closer than r, (Grassberger and Procaccia 1983; Theiler 1986):

$$ {C_{\text{m}}}(r) = \mathop{{\lim }}\limits_{{N \to \infty }} \frac{2}{{\left( {N - w} \right)\left( {N - w - 1} \right)}}\sum\limits_{{i = 1}}^N {\sum\limits_{{j = i + 1 + w}}^N {H\left( {r - \left| {{{\vec{Y}}_i} - {{\vec{Y}}_j}} \right|} \right)} } $$
(3)

where C is the correlation dimension, r is the radius of hypersphere within phase space, H is the Heaviside step function, \( \overrightarrow {{Y_i}} \),\( \overrightarrow {{Y_j}} \) are the ith and jth state vectors defined by Eq. 1, and N is the number of points on the reconstructed attractor. The number w is called Theiler window and it is the correction needed to avoid spurious results due to temporal correlations instead of dynamical ones. For stochastic time series C m(r)∝r m holds, whereas for chaotic time series the correlation function scales with r as:

$$ {C_{\text{m}}}(r) \propto {r^{{{D_2}}}} $$
(4)

where D 2, correlation exponent, quantifies the degrees of freedom of the process, and defined by:

$$ {D_2} = \mathop{{\lim }}\limits_{{r \to 0}} \frac{{\ln {C_{\text{m}}}(r)}}{{\ln r}} $$
(5)

and can be reliably estimated as the slope in the lnC m(r) versus ln(r) plot.

2.1.3 Lyapunov exponents

Lyapunov exponents is a measure of exponential divergence of nearby trajectories in the phase space, along a given direction. Given two nearby states and their Euclidean distance d(t 0) at time t 0, the largest Lyapunov exponent λ max, corresponding to the dominant divergence direction, is defined as:

$$ {\lambda_{{\max }}} = \mathop{{\lim }}\limits_{{t \to \infty }} \frac{1}{{t - {t_0}}}\log \frac{{d(t)}}{{d\left( {{t_0}} \right)}} $$
(6)

In the present work, the method proposed by Rosenstein et al. (1993) was adopted for the estimation of λ max, which makes use of stretching factor, defined as:

$$ S(t) = \frac{{\Delta t}}{t}\sum\limits_{{i = 1}}^{{t/\Delta t}} {\log \left[ {\frac{1}{{\left| {{\Omega_i}} \right|}}\sum\limits_{{j \in {\Omega_i}}}^N {\left| {{{\vec{Y}}_i} - {{\vec{Y}}_j}} \right|} } \right]} $$
(7)

along an orbit of Δt/t time steps, where |Ω i | is the number of neighbours in the neighbourhood Ω i of the reference state \( \overrightarrow {{Y_i}} \), and Δt is the sampling time of measurements. For a chaotic dynamics, the stretching factor S(t) is expected to be proportional to time, the largest Lyapunov exponent λ max being the proportionality constant.

2.1.4 Local predictions

Local prediction techniques are generally adopted for predicting/forecasting the future states of the process under investigation, with no explicit use of an analytical model. The first method of local prediction was suggested by Lorenz (1969). In this approach, if the value of the measurement x t is known at time t, the prediction of the measurement x t + 1 at time t + 1 is given by x T + 1, where x T is the nearest neighbour to x t in the phase space. This method is called first-order approximation (Farmer and Sidorowich 1987a). Another popular method is to choose a collection of k nearest neighbours and to use the average value of their images for forecasting. However, a more sophisticated local prediction method was suggested by Farmer and Sidorowich (1987b), who approximated the local mapping of successive states with higher-order polynomials, whose coefficients should be determined by means of nearest neighbours and fitting procedures. In an m-dimensional space, prediction is thus performed by estimating the trajectory changes with time. Let us assume that the relationship between two embedding states \( \overrightarrow {{X_t}} \) and \( {\overrightarrow X_{{t + p}}} \) on the attractor, delayed by a time p, can be approximated by the mapping \( \overrightarrow F \) as

$$ {\vec{X}_{{t + p}}} \cong \vec{F}\left( {{{\vec{X}}_t}} \right) $$
(8)

and the evolving dynamics of the state \( \overrightarrow {{X_t}} \) is that one of the nearby states. In the present study, the future state \( {\overrightarrow X_{{t + p}}} \) is determined by the first-order polynomial mapping \( \overrightarrow f \) (Itoh 1995) as follows:

$$ {\vec{X}_{{t + p}}} \cong \vec{F}\left( {{{\vec{X}}_t}} \right) = \vec{a} + \vec{f}\left( {{{\vec{X}}_t},{{\vec{X}}_{{t - \tau }}},...,{{\vec{X}}_{{t - \left( {m - 1} \right)\tau }}}} \right) $$
(9)

Although this mapping is linear, the prediction is nonlinear because, during the prediction procedure, every state on the trajectory corresponds to a different neighbourhood, therefore to a different expression for \( \overrightarrow F \) and the linear map \( \overrightarrow f \) (Porporato and Ridolfi 1997).

2.2 Genetic programming

This study employs GP to reference the performance of the low-dimensional dynamic model. GP is selected as it makes no assumption on the structure of the relationship between the independent and dependent variables but an appropriate relationship is identified for any given time series. The mathematical form of such a relation can be shown as below:

$$ {H_{{t + \delta { }\Delta t}}} = f\left( {{H_t},{H_{{t - \Delta t}}},...{H_{{t - \omega \Delta t}}}} \right) $$
(10)

where f is a function, H is the height of sea water level with respect to a reference point and δ(δ = 0, 1, 2, 3,…ω) describes the time step (Δt) used for the forecast water level. Implementation of GP models involves a number of preliminary decisions including a set of basic operators such as \( \left\{ { + , - ,*,/, \wedge ,\sqrt {{}} ,\log ,a\log ,\sin ,a\sin ,\exp ,...} \right\} \) to construct the function, f.

The GP modelling programmes provide operators like crossover and mutation to the winners, ‘children’ or ‘offspring’ to emulate natural selection, in which crossovers are responsible for maintaining identical features from one generation to another but mutations cause random changes. The evolution starts from an initially selected random population of models, where the relationship, f, between the independent and dependent variables is often referred to as the ‘model’, the ‘programme’, or the ‘solution’. The population is allowed to evolve through generations by the virtue of a selected fitness criterion by replacing old models with new ones when performing better. For further details of GP, see Ghorbani et al. (2010).

3 Study area and data

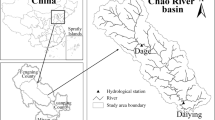
In this study, sea level data were recorded by a SEA-level Fine Resolution Acoustic Measuring Equipment station deployed at Hillarys Boat Harbour (Fig. 1) at latitude 31.82° South and longitude 115.73° East (GDA94). The accuracy resolution of the gauge is 1 mm and the data have been collected since 1991 by the National Tidal Centre, Australia, where the Centre specialises in sea level monitoring and analysis. The purpose for collecting the data is to derive trends in absolute sea level and produce national tide predictions, tide streams and related information and hence its high level accuracy. Hillarys Boat Harbour is the first major marina in the north metropolitan region of Perth with the primary function of accommodating yachts and small boats.

Fig. 1
figure 1

Location of the gauge site (star) at Hillarys Boat Harbour (Makarynskyy et al. 2004)

Full size image

The raw measurements demonstrate a prominent seasonal variability with annual minima during the Southern Hemisphere summers and maxima in the winters, which occur mainly due to the astronomical forcing of the Sun’s and Moon’s gravitational attractions. The observed values oscillate between −140 mm (December 1993) and 1,680 mm (July 1995) with respect to the unspecified local datum on this decadal time scale, while in a usual year, the range of variations does not exceed 1,200 mm. The quasi-diurnal (K1, O1 and P1) and quasisemidiurnal (M2) tide waves are the dominant ones in the area of Hillarys Boat Harbour (e.g. Australian National Tide Tables 2003). The data used in this study cover 30 months of observations from January 2000 to June 2002 and are measured at hourly intervals with some of their important statistics presented in Table 1.

Table 1 Statistics of hourly sea level data—Hillarys Harbour
Full size table

For the present investigation, sea level data observed over a period of 30 months (January 2000–June 2002) are considered. Figure 2 shows the variations of hourly data series. The entire dataset of 30 months was divided into two parts. The first 29 months of data was used in training for the phase space reconstruction, but the subsequent 1 month of data was used as observed data in the prediction phase.

Fig. 2
figure 2

Hourly sea level time series at the Hillarys Boat Harbour

Full size image

4 Results

In this study, the characterisation of the sea level dynamics employs the following methods: the correlation integral analysis together with the false nearest neighbours algorithm, where the appropriateness and accuracy of such a reconstruction depends on the delay time, τ; correlation dimension, as well as the Lyapunov exponent to estimate the predictability of the data into the future and the local prediction method to predict the future values. These predicted time series are compared with those by GP, in running which its default values are given in Table 2. The following software applications were used: the TISEAN package (Hegger et al. 1999) is used for the implementation of chaos theory but local prediction was run, as in Koçak (1997), and GP was implemented using GeneXPro software application (Ferreira 2001a, b).

Table 2 Default values in running the GP model
Full size table

4.1 Characterisation of sea level dynamics

Phase space reconstructions for the sea level time series are presented in Fig. 3a–d through examples. These figures show reconstructions in two dimensions, i.e. the projection of the attractor on the plane {X i , X i + τ } and with delay time τ = 1, 50, 100, 200. A reasonably clear attractor is present for τ = 1, 50 but those for τ = 100 and 200 occupy larger space in the phase space diagram. An appropriate τ of the phase space reconstruction is used in the prediction stage to separate neighbouring trajectories within the minimum embedding phase space.

Fig. 3
figure 3

Reconstruction of phase space by using four different delay time values for sea level time series: a τ = 1—sharper attractor; b τ = 50—somewhat diffused attractor; c τ = 100—the attractor is noisy; d τ = 200—the attractor is very noisy

Full size image

The AMI method may be used to compute τ by varying delay time in the range of 1–100 h. The value of delay time is calculated as the first (local) minimum in the variation of AMI against varying delay time from 1 to 100 h. As shown in Fig. 4, this method shows well-defined first minima at delay time of 12 h, which is then used for the determination of the sufficient embedding dimension using the percentage of false nearest neighbours for the time series. Figure 5 shows the results of the false nearest neighbours method for embedding dimension so that the value of embedding dimension is 6.

Fig. 4
figure 4

Average mutual information (AMI) function of the sea level time series

Full size image
Fig. 5
figure 5

Percentage of false nearest neighbours of the sea level time series in embedding dimension

Full size image

4.2 Estimation of correlation dimension

The correlation function is calculated for the dataset using the delay times (τ = 12), determined by the AMI method in the previous section, and embedding dimensions, m, by allowing it to vary from 1 to 20. The presence of chaotic signals in the data is further confirmed by the correlation dimension method. Figure 6 shows the relationship between correlation function C(r) and radius r (i.e. lnC(r) versus ln(r)) for increasing m, whereas Fig. 7 shows the relationship between the correlation dimension values D 2(m) and the embedding dimension values m. It can be seen from Fig. 7 that the value of correlation exponent increases with the embedding dimension up to a certain value and then saturates beyond it. The saturation of the correlation exponent is an indication of the existence of deterministic dynamics. The saturated correlation dimension is ∼6.45, (D 2 = 6.45). The value of correlation dimension also suggests the possible presence of chaotic behaviour in the dataset. The nearest integer above the correlation dimension value (D 2 = 7) is taken as the minimum dimension of the phase space.

Fig. 6
figure 6

Convergence of logC(r) versus log(r) for hourly sea level data—signifying chaotic signals

Full size image
Fig. 7
figure 7

Saturation of correlation dimension D 2(m) with embedding dimension m—saturation signifies chaotic signals

Full size image

4.3 Estimation of the largest Lyapunov exponent

The curves for the stretching factor versus the number of points N show the expected linear increase and flat regions (Fig. 8) with some fluctuations superimposed on the linear part of the curve. The slope value corresponding to the largest Lyapunov exponent is obtained after the least-squares line fit for the sea level time series and is found to be 0.0023. The inverse of this parameter value defines the maximum predictability, and for this time series, it is equal 1/0.0023 or less than 437 h (18 days) into the future.

Fig. 8
figure 8

Estimating the largest Lyapunov exponent using the method by Rosenstein et al. (1993)

Full size image

4.4 Sea level prediction

The local prediction technique explained in Section 2.1.4 is employed to study the possible presence of chaotic signals in sea level in the data (the first 29 months used as the training data). The embedding dimension is varied systematically from 2 to 10 until they identify the optimum value of the dimension corresponding to the highest R 2 and possibly the lowest root mean square error (RMSE). Statistics in Table 3 indicate that reasonably good predictions (with R 2  > 0.94) were overall achieved for all 10 embedding dimensions. A closer look at the statistics however reveals that the best predictions were achieved when the embedding dimension was m opt  = 9 (i.e. highest R 2 and lowest RMSE and delay time = 12 h). With these training parameter values, the model is run in the prediction mode to produce future values. Figure 9 compares visually the predicted sea water levels with their corresponding observed values, which also displays their scatter plot. Whilst the results will be discussed in the next section, the successful performance of the local prediction method clearly complements those in Figs. 3, 4, 5, 6, 7 and 8 that (a) there is a clear deterministic chaotic signal in the dataset at the Hillarys Boat harbour, and (b) using this information, chaos theory is also a versatile prediction tool.

Table 3 Values of R 2 and RMSE for different embedding dimensions—local prediction method
Full size table
Fig. 9
figure 9

Performance of local prediction: a comparison of predicted and observed time series and b their scatter diagram

Full size image

For comparison with the results of the local prediction model, the GP model was run for the same data using GeneXpro software. A number of combinations of inputs (sea level with different lead times) were tested. The best combination was selected with RMSE = 55.8 mm and R 2 = 0.94. Figure 10 presents the recorded and simulated values and their scatter plot.

Fig. 10
figure 10

Performance of GP: a comparison of predicted and observed time series and b their scatter diagram

Full size image

5 Discussion

A visual comparison of the results by the local prediction model with that of the GP model demonstrates that both these models explain the data adequately. The model performances are estimated in terms of RMSE and R 2 and presented in Table 4, according to which the RMSE value of the local prediction model is smaller and R 2 is higher than those of the GP model for the prediction period. The performance of the local prediction model is slightly better than that of the GP model.

Table 4 Statistical analysis of performances of both local prediction and GP
Full size table

The significance of the difference between the results of the respective models is not obvious, as the minimum and maximum differences produced by both the local prediction and GP models are approximately ±150 mm, and these differences do not arise on the peak values but on the rising or falling limbs. Using a time scale of 3 h rather than 1 h slightly deteriorates the results and more fluctuating but the performances of both models remain robust.

There are two issues, which require explanation. (1) The presence of chaotic signals in the data reveals that site-specific sea levels undergo a sudden loss of temporal correlation in response to small perturbations in initial conditions. The likely causes for this sudden loss of correlation include the harbour site geomorphology, where either there is a sudden expansion or funnelling at a given water level, there can be specific local wave/current and/or reflection/refraction patterns at such sea level and/or specific meteorological conditions contributing to this. Based on engineering judgement, such complexity is quite likely in a harbour situation. (2) Contrary to chaos theory stipulating a sudden loss of temporal correlation, GP is essentially a regression model and assumes continuity in the functional relationship. However, modelling experience accumulating since the 1950s is indicative that models are not exact replica of the real systems but surrogate representations. Each model is likely to unravel a certain feature that otherwise is not obvious without applying the particular model. The emerging consensus is to use different modelling techniques in a pluralistic modelling culture and draw a consensus from them rather than rule in or rule out a single model as superior to the others.

Application of chaos theory to sea level predictions provides another technique adding to the pluralistic modelling capabilities. The capabilities are diverse depending on a range of factors including the data availability, the time horizon and the required lead time for the predictions. Both chaos theory and GP are used for time series analysis to make use of the information within the time series, and as such, they differ from distributed models capable of modelling hydraulic processes.

Time series are datasets with a natural temporal ordering, and as such, they are quite different than event data describing a dynamic situation of change created by a meteorological, hydrological or hydraulic event within a specific time period. Time series normally cover long periods of time, e.g. from a month to years, or to centuries, but event data cover a period normally less than a month and can be a few hours. The time horizon for the prediction into the future is referred to as lead time and its different ranges have given rise to different management practices, including:

  • Nowcasting: these are confined to a very short-range weather forecasting for say the impending12-h period, using data for a very specific geographic area based on very detailed observational data.

  • Real-time forecasting: these types of modelling are widespread and normally cover full events of periods in the range of a few hours to a few weeks, which are normally based on detailed distributed models but their lead time for flood warning may be in the range of a few hours to not more than a few days. The lead time may be enhanced with near real-time forecasting capabilities integrating satellite and radar imagery with hydrological, hydraulic and meteorological models and telemetric capabilities.

  • Early warning capabilities: these modelling capabilities seek a lead time of 3–10 days to aid the management of impending flooding incidents and they employ distributed models with coarser resolutions compared with real-time modelling. For longer lead times, modelling capabilities include seasonal forecasting and long-term predictions.

Generally, the longer the lead time, the greater inherent uncertainty and less useful the results are but even such noisy predictions are vital for resource management. Notably, the above time horizons of lead time are based on distributed models, although transfer functions and stochastic time series analysis may also be used by modelling researchers and practitioners. Time series analysis based on GP and chaos theory has not penetrated coastal modelling practices. For instance, a survey of coastal flood forecasting techniques by the Environment Agency has no mention of such techniques, see Khatibi et al. (2003), Hawkes et al. (2004) and EA (2004). So there is a gap in knowledge on the suitability of such techniques as GP and chaos theory to aid practical problems.

Arguably, as time series measure local information, their applicability is confined to the measurement locations and not beyond. The time horizon for the prediction of time series into the future has not been adequately discussed in the past but normally time series has a long tail back into the past. Depending on the time scale of the data, the prediction model can be formulated within the lead time of real-time forecasting, early warning and seasonal forecasting or even predicting over annual cycles. The lead time of chaos theory is estimated by the Lyapunov exponent, which provides the information into the future predictability of the time series, but there is no such a technique available for the other time series techniques.

Research approaches on time series normally implement a technique by dividing the available dataset into two training and prediction data and studying its predictability by such parameters as the coefficient of correlation and RMSE or other parameters. The literature review presented above shows that chaos theory is applied to a storm surge event as well as sparse applications to long-term records of data, including this study. However, the authors are not aware of any systematic study through systematically varying the future time horizon of lead time. Such a study will undoubtedly help the uptake of these modelling capabilities from research to practice.

As the trends in policymaking are towards both basin management and local management, the availability of capabilities for both types of management is necessary. Management strategies normally require proactively constructed models and an insight into possible future patterns. Arguably, both models offer versatile, compact and less resource incentive capabilities for nowcasting, forecasting and seasonal forecasting of site-specific sea level. In particular, such capabilities make it feasible to implement cloud computing facilities to enable a diverse range of stakeholders to look after their interests by having access to predicted sea levels for taking timely actions to protect human health and lives, materials and investments. This study addressed sea level, but a host of other water quality variables can be modelled in a similar way by these emerging modelling capabilities to facilitate the following services:

  • Navigations in and out of harbours or along coasts

  • Managing stormy waters or flooding incidents, particularly boat owners concerned with the safety of their boats

  • Managing legal obligations toward bathing water directives/policies

  • Providing appropriate services to fish farmers to ensure optimum feeding of the fish depending on the variation of salt and temperature or to anglers concerned with locating cold water where the salmon may be plentiful

  • Ecological information including timely warnings on noxious algae

  • Reliable prediction of sea level variations, which affect both groundwater tables in low-lying coastal areas and hydrological regimes of coastal rivers

6 Conclusions

This paper references the performance of a low-dimensional dynamic model, known as the deterministic chaos model, with a genetic programming model. Both techniques are applied to the sea water level time series observed at the Hillarys Boat Harbour over 30 months (January 2000–June 2002). In the study, the dynamic model was implemented by using the TISEAN package (Hegger et al. 1999) and GeneXPro to implement GP. The existence of chaotic signals in the data was identified by the reconstruction of the phase space of the data and the delay time was quantified by using the mutual information function and the embedding dimension by the false nearest neighbours, where their values were identified to be 12 and 9, respectively. The presence of chaotic signals in the data was further confirmed by (1) the correlation dimension method, according to which the finite correlation dimension is 6.45, and (2) by Lyapunov exponent, in which the positive largest Lyapunov exponent is 0.0023 and this means that the predictability of the results into the future is 437 h or 18 days.

A local prediction model has been applied to sea level time series. The dynamics of the system are described step by step locally in the phase space. The predicted values are in good agreement with the observations. The correlation coefficient and root mean square error have values of 0.95 and 48.2 mm, respectively. These model results were further referenced with the performance of the GP model, and the intercomparison of their results indicates that in this case the local prediction model has a slight edge over the performance of GP but both can be used, each having their own strengths and weaknesses.

The paper raised issues on the applicability of both techniques and explained them recommending a pluralistic modelling culture, in which each modelling technique might offer a specific insight into the data, helping consensus to be drawn for better implementation of modelling results.