1 Introduction

Estuarine and coastal sediment transport is characterised by the transport of both sand-sized particles (of diameter greater than 63 μm) and muddy fine-grained sediments (silt, diameter less than 63 μm; clay, diameter less than 2 μm). The first of these fractions is termed non-cohesive, whilst the latter fractions are generally referred to as cohesive (although non-cohesive silt does exist naturally in some coastal areas) or more simply as “mud”. The cohesive nature of mud is partly due to the chemical forces that act between grains on the micro-scale. Clay particles in particular are subject to both electrostatic and molecular attraction with each other (Whitehouse et al. 2000) and so aggregate together to form flocs. In contrast, particles over 60 μm in diameter (i.e. sand particles) appear to display very little physico-chemical cohesion (Migniot 1968).

However, the flocculation of sediment particles is not only caused by physico-chemical attraction. Cohesivity of sediment is also caused by biology. Epipelic diatoms (diatoms which live freely on muddy sediment surfaces) can secrete sticky extra-cellular polymeric substances (EPS; Tolhurst et al. 2002). These EPSs act as biostabilisers, thus increasing the collision efficiency (Edzwald and O’Melia 1975) of flocculating particles and increasing the potential for cohesive and also non-cohesive sand grains to adhere to mud sediments. The dominance of biology over physico-chemical processes for flocculation was shown in laboratory experiments undertaken by Gratiot and Manning (2007) which compared the flocculation of natural muds with purely inorganic material. In addition to the binding effect of EPS for cohesive particles, Manning et al. (2009) point out that epipsammic diatoms (which are bound to sand particles) also produce strong adhesion (Harper and Harper 1967). Thus, biological activity is a mechanism by which sand particles can be incorporated into flocs in spite of the lack of physico-chemical cohesion described above.

In many estuaries, both the sand and fine sediment fractions are transported in significant quantities. Historically, to investigate the potential impacts of engineering applications in these estuaries, there was a pragmatic approach which consisted of the separate use of mud transport and sand transport models. Whilst this approach is often still adequate, the increasing need for a better understanding of potential changes in morphology and substrate has driven the use of combined mud-sand transport models. Examples of the use of these combined mud and sand models are Ockenden and Chesher (1994) in the Mersey Estuary, van Ledden et al. (2006) in the Wadden Sea and Waeles et al. (2007) in the Seine Estuary. Many of the more common sediment transport modelling suites (e.g. Delft-3D, MIKE and TELEMAC) now have the capability to combine mud and sand transport. However, in all of these modelling approaches, the modelling of mixed sediment transport has still essentially separated the modelling of sand and mud fractions assuming that these different fractions do not interact except at the bed. Even when considering hindered settling of mixed sediment, the scientific emphasis has been that sand and silt or clay particles only affect each other through their contribution to the volume concentration rather than any more direct interaction (Dankers et al. 2008; Cuthbertson et al. 2008).

Recent developments in the tools that are available for examination of floc processes and structure have allowed the direct and detailed examination of floc structure (e.g. Spencer et al. 2007; Manning et al. 2009) via use of electron microscope. One of the outcomes of such studies has been the identification of the range and micro-structure of materials that comprise both the large macrofloc structures and the constituent microfloc structures that form the building blocks for the macroflocs, including inorganic particles, algae, bacteria, extra-cellular polymers, and pore water spaces. Accompanying this notable step forward have been improvements in the quality (and quantity) of reliable and accurate measurements of settling velocity. The use of in situ video techniques (e.g. Fennessy et al. 1994; van Leussen and Cornelisse 1996; Manning 2006), which do not compromise the floc structure and which are not vulnerable to error induced by secondary circulation in settling columns (Dearnaley 1996), has greatly enhanced the reliability of settling velocity measurements.

Manning (2008) undertook a combination of field-based and laboratory experiments to show that the flocculation of cohesive sediments could be well described by a set of empirically derived algorithms which include the effects of turbulent shear stress and concentration. In the first part of this paper, Manning et al. (submitted) extend this approach to sediment mixtures of mud and sand. Measurements of the settling velocity of varying mud-sand mixtures are described, and empirical algorithms governing the variation of settling velocity with turbulence, suspended sediment concentration and mud-sand content are derived. The second part of this paper continues the theme of examination of the effects of mud-sand interaction on flocculation. However, whilst the accompanying paper concentrates on experimental measurement and analysis of the results, this paper focuses on the use of numerical modelling. A 1DV mixed transport model is used to reproduce both the measurement experiments and a further set of measurements undertaken in the Outer Thames Estuary. The results of this modelling are used to further evaluate the evidence for the flocculation of sand and the validity of the developed empirical relationships.

2 Description of 1DV numerical model

2.1 Flow equations

The 1DV model used in this paper is based on work undertaken during the COSINUS project (Violeau et al. 2000) and is similar to 1DV sediment transport models which have been used successfully by other authors (e.g. Winterwerp 1999; Winterwerp and van Kesteren 2004; Violeau et al. 2000). The model distributes current velocity and suspended sediment concentration through the vertical.

The 1DV equation for horizontal momentum, ignoring inter-particle stresses, is as follows (Winterwerp 1999):

$$ \frac{{\partial u}}{{\partial t}} + \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} = \frac{\partial }{{\partial z}}\left[ {\left( {{D_s} + {\nu_T}} \right)\frac{{\partial u}}{{\partial z}}} \right] + \frac{1}{\rho }\frac{{2{\tau_{sf}}}}{b} $$
(1)

where

u :

is the horizontal flow velocity;

p :

is the pressure;

ρ :

is the water density;

x :

is the horizontal distance;

z:

is the vertical height;

t :

is time;

D s and ν T :

are the molecular and eddy viscosity, respectively;

τsf :

is the side wall friction (to be included when modelling a flume as in Section 4), and b is the width of the flume.

The solution of this equation is undertaken in two steps. Firstly, Eq. 1 is approximated by the following equation which is solved for \( \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} \)to maintain the desired depth-averaged velocity, U 0,

$$ \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} = \frac{{{\tau_s} - {\tau_b}}}{{\rho h}} + \frac{{U(t) - {U_0}(t)}}{{{T_{rel}}}} $$
(2)

where

τ s and τ b :

is the shear stress imparted on the surface and bed, respectively;

h :

is the water depth;

U :

is the actual computed depth-averaged flow velocity;

U 0 :

is the desired depth-averaged flow velocity; and

T rel :

is a relaxation time (Winterwerp 1999 suggests a value of twice the value of the time step for this parameter).

Secondly, the computed value of \( \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} \) is used in Eq. 1 to calculate the values of velocity throughout the water depth. To do this, Eq. 1 is written in the matrix form,

$$ {{\bf A}}u = {{\bf B}} $$
(3)

where A is a tridiagonal matrix with components, A i,j , which are given as follows,

$$ \matrix{ {i = 1} \hfill \cr {\quad \quad {A_{i - 1,i}} = 0} \hfill \cr {\quad \quad {A_{i + 1,i}} = vis{c_i}dt/\left[ {\left( {{z_{i + 1}} - {z_1}} \right)\left( {{z_{i + 1}} - {z_{i - 1}}} \right)/2} \right]} \hfill \cr {\quad \quad {A_{i,i}} = 1 + {C_d}dt\left| {{u_i}\left( {{z_{i + 1}} - {z_i}} \right)} \right|} \hfill \cr }<!end array> $$
(4)

where C d is the drag coefficient.

$$ \matrix{ {i = 2,n - 1} \hfill \cr {\quad \quad {A_{i - 1,i}} = vis{c_{i1}}dt/\left[ {\left( {{z_{i + 1}} - {z_i}} \right)\left( {{z_i} - {z_{i - 2}}} \right)/2} \right]} \hfill \cr {\quad \quad {A_{i + 1,i}} = 1 + vis{c_i}dt/\left[ {\left( {{z_{i + 1}} - {z_i}} \right)\left( {{z_{i + 1}} - {z_{i - 2}}} \right)/2} \right]} \hfill \cr {\quad \quad {A_{i,i}} = 1 + vis{c_{i - 1}}dt/\left[ {\left( {{z_{i + 1}} - {z_i}} \right)\left( {{z_i} - {z_{i - 2}}} \right)/2} \right] + vis{c_i}dt/\left[ {\left( {{z_{i + 1}} - {z_i}} \right)\left( {{z_{i + 1}} - {z_{i - 1}}} \right)/2} \right]} \hfill \cr {i = n} \hfill \cr {\quad \quad {A_{i - 1,i}} = vis{c_{i - 1}}dt/\left[ {\left( {{z_{i + 1}} - {z_i}} \right)\left( {{z_i} - {z_{i - 2}}} \right)/2} \right]} \hfill \cr {\quad \quad {A_{i + 1,i}} = 0} \hfill \cr {\quad \quad {A_{i,i}} = 1 + vis{c_{i - 1}}dt/\left[ {\left( {{z_{i + 1}} - {z_i}} \right)\left( {{z_i} - {z_{i - 2}}} \right)/2} \right]} \hfill \cr }<!end array> $$

and where

z i :

are the values of vertical height and current speed at the ith layer in the model;

visc i :

are the values of viscosity (the sum of the molecular and eddy contributions) at the ith layer in the model;

n :

is the total number of layers in the model, and dt is the time step.

$$ {{\bf B}}\,{\hbox{is the single column matrix given by }}{{\bf B}} = {{\bf U}} - dt\,{{\bf dpdx}}{ } $$
(5)

where

U :

is the single column matrix with components u i ; and

dpdx :

is the single column matrix with each component equal to \( \frac{{\partial p}}{{\partial x}} \).

2.2 Calculation of suspended sediment profile

The distribution of suspended sediment in the vertical is modelled with the advection–diffusion equation (Winterwerp 1999)

$$ \frac{{\partial {c^k}}}{{\partial t}} - \frac{\partial }{{\partial z}}\left\{ {w_s^k{c^k}} \right\} - \frac{\partial }{{\partial z}}\left\{ {\left( {{D_s} + {\Gamma_T}} \right)\frac{{\partial {c^k}}}{{\partial z}}} \right\} = 0 $$
(6)

where

c k :

is the suspended sediment concentration of the kth sediment fraction;

w ks :

is the settling velocity of the kth sediment fraction; and

D s and Γ T :

are the molecular and eddy diffusivity.

For each of the sediment fractions, Eq. 6 is solved in matrix form,

$$ {{\bf F}}{{\hbox{c}}^{\rm{k}}} = {{\bf G}} $$
(7)

where F is a tridiagonal matrix with components, F i,j , which are given as follows:

$$ \matrix{ {i = 1} \hfill \cr {\quad \quad {F_{i - 1,i}} = 0} \hfill \cr {\quad \quad {F_{i + 1,i}} = {\Gamma_T}_idt/\left[ {\left( {{z_{i + 1}} - {z_i}} \right)\left( {{z_{i + 1}} - {z_{i - 1}}} \right)/2} \right]} \hfill \cr {\quad \quad {F_{i,i}} = 1 + dt{\Gamma_T}_i/\left[ {\left( {{z_{i + 1}} - {z_i}} \right)\left( {{z_{i + 1}} - {z_{i - 1}}} \right)/2} \right]} \hfill \cr {i = 2,n - 1} \hfill \cr {\quad \quad {F_{i - 1,i}} = {\Gamma_T}_{i - 1}dt/\left[ {\left( {{z_{i + 1}} - {z_i}} \right)\left( {{z_i} - {z_{i - 2}}} \right)/2} \right]} \hfill \cr {\quad \quad {F_{i + 1,i}} = {\Gamma_T}_idt/\left[ {\left( {{z_{i + 1}} - {z_i}} \right)\left( {{z_{i + 1}} - {z_{i - 1}}} \right)/2} \right]} \hfill \cr {\quad \quad {F_{i,i}} = 1 + {\Gamma_T}_{i - 1}dt/\left[ {\left( {{z_{i + 1}} - {z_i}} \right)\left( {{z_i} - {z_{i - 2}}} \right)/2} \right] + {\Gamma_T}_idt/\left[ {\left( {{z_{i + 1}} - {z_i}} \right)\left( {{z_{i + 1}} - {z_{i - 1}}} \right)/2} \right]} \hfill \cr {i = n} \hfill \cr {\quad \quad {F_{i - 1,i}} = {\Gamma_T}_{i - 1}dt/\left[ {\left( {{z_{i + 1}} - {z_i}} \right)\left( {{z_i} - {z_{i - 2}}} \right)/2} \right]} \hfill \cr {\quad \quad {F_{i + 1,i}} = 0} \hfill \cr {\quad \quad {F_{i,i}} = 1 + {\Gamma_T}_{i - 1}dt/\left[ {\left( {{z_{i + 1}} - {z_i}} \right)\left( {{z_i} - {z_{i - 2}}} \right)/2} \right]} \hfill \cr }<!end array> $$
(8)

and where ΓTi is the value of eddy diffusivity at the ith layer in the model and ΓT is calculated by Eqs. 12, 13, 14 and 15.

G is the single column matrix given by,

$$ {G_i} = c_i^k + \left[ {c_i^kw_{si}^kdt} \right]/\left( {{z_{i + 1}} - {z_i}} \right) - \left[ {c_{i - 1}^kw_{si - 1}^kdt} \right]/\left( {{z_{i + 1}} - {z_i}} \right) $$
(9)

where G i is the ith row of the matrix G; c k i is the concentration of the kth fraction at the ith layer and w ks i is the settling velocity of the kth fraction at the ith layer.

2.3 Unhindered settling

The settling velocity of sand and mud fractions in the model was derived using the algorithms developed by Manning (2008) and Manning et al. (submitted, part 1 of this paper). These algorithms are presented in Section 3.

2.4 Hindered settling

The settling velocities calculated using the algorithms presented in Section 3 were adjusted for hindered settling using approach of van Rhee (2002) which utilises the formula of Richardson and Zaki (1954) with an adjustment to account for the effect of return currents in poly-disperse scenarios,

$$ w\prime_s^k = w_s^k{\left( {1 - \frac{c}{\phi }} \right)^n} - \sum {\frac{{{c^k}w_s^k}}{{{\rho_s}}}} $$
(10)

where

w s k and w' s k :

are the settling velocities for the kth fraction before and after hindered settling effects have been taken into account;

c :

is the (total) suspended sediment concentration;

c k :

is the suspended sediment concentration of the kth fraction;

∅ :

is the gelling concentration;

ρ s :

is the density of sediment (2,650 kg/m3); and

n :

is given by the formula of Rowe (1987) which is a convenient approximation to the results of Richardson and Zaki,

$$ n = \frac{{4.7 + 0.41{R^{0.75}}}}{{1 + 0.175{R^{0.75}}}} - 1\quad {\hbox{where}}\quad R = \frac{{w_s^kd}}{\nu } $$
(11)

Note that the value of n used here is one less than the value proposed by Rowe (1987) because the effect of the return current from settling particles is included explicitly by the second term on the right hand side of Eq. 10 (Smith 1966; van Rhee 2002). This type of poly-disperse approach was identified by Cuthbertson et al. (2008) as taking better account of the volumetric interaction in hindered environments.

2.5 Turbulence

The turbulence model within the 1DV model is a mixing layer model with the classic parametric calculation of eddy viscosity,

$$ {\nu_T} = 0.16\mathop z\nolimits^2 \left( {1 - \frac{z}{h}} \right)\frac{{\partial u}}{{\partial z}} $$
(12)

The eddy diffusivity is given by,

$$ {\Gamma_T} = \frac{{{\nu_T}}}{\sigma }\quad \quad {\hbox{where }}\sigma {\hbox{ is the Schmidt number }}\left( {{\hbox{in this study the value is set to 1}}.0} \right) $$
(13)

The eddy viscosity and eddy diffusivity are then modified to take account of the damping of turbulence by the density gradient using the following damping functions (Toorman 2000),

$$ {F_{vis}} = {\left( {1 + 100{R_g}} \right)^{ - 1/3}} $$
(14)

and

$$ {F_{diff}} = {F_{vis}}{\left( {1 + 21{R_g}} \right)^{ - 0.8}} $$
(15)

where R g is the gradient Richardson Number given by, \( {R_g} = \frac{{ - g\frac{{d\rho }}{{dz}}}}{{\rho {{\left( {\frac{{du}}{{dz}}} \right)}^2}}} \)

3 Suspended sediment settling velocity algorithms

3.1 Macrofloc fraction

An appraisal of floc data in an earlier study (Manning 2001) identified that 160 μm provided the optimum separation point between macrofloc and microfloc fractions; in particular, the settling velocity and dry mass, of each floc sub-population, were consistently and significantly different for a wide range of turbulent shear stresses and suspended sediment concentrations. Following this result, the macrofloc size fraction is here defined as those flocs with diameter greater than 160 μm.

To predict macrofloc settling velocity, empirical equations for 100% mud (Manning 2008), 75% mud, 50% mud, 25% mud (Manning et al., submitted, part 1 of this paper) and 0% mud (Soulsby 1997) are used. In the model, the settling velocity for macroflocs is interpolated from these results based on mud-sand content.

The macrofloc settling velocity, Ws macro_EM , (units of mm s−1) is given by the following equation:

$$ {\hbox{W}}{{\hbox{s}}_{macro\_ EM}} = A + B\tau --C{\tau^2} + D{\hbox{SPM}} $$
(16)

where

A, B, C and D :

are constants which vary with the proportion of mud-sand content and shear stress as given in Table 1;

τ:

is the turbulent shear stress at elevation z above the bed (units of N m−2); and

SPM:

is the suspended particulate matter at elevation z above the bed (units of mg l−1).

Table 1 Coefficients used in Eq. 16 for calculation of macrofloc settling velocity for different values of shear stress and percentage mud-sand
Full size table

The nature of the form of Eq. 1 and the experiments on which it is based (which include values of shear stress less than or equal to 0.9 N m−2) mean that the uncertainty of the equation increases as the shear stress increases above 0.9 N m−2. The annular flume tests (Section 4) do not exceed this value, but the example from the Thames in Section 5 experiences shear stresses which are greater than 0.9 N m−2. As the form of Eq. 16, i.e. the slow reduction in macrofloc settling velocity, is qualitatively correct, Eq. 16 was implemented for higher stresses for the Thames example. However, the form of Eq. 16 means that Ws macro_EM will start to increase when shear stress approaches 2 N m−2 which is not physically correct as higher stresses will cause the increasing break up of macroflocs (e.g. van Leussen 1988). Thus, τ ≈ 2 N m−2 forms a limit to the applicability of Eq. 16. For values of shear stress higher than this, the settling velocity of macroflocs was calculated assuming τ = 2 N m−2.

For pure sand, the settling velocity estimate of Soulsby (1997) is used.

$$ W{s_{macro\_ EM}} = \frac{\nu }{D}\left[ {\left( {{{10.36}^2} + 1.049{D_* }^3} \right) - 10.36} \right] $$
(17)

where υ is the kinematic viscosity, D * is the non-dimensional particle diameter given by \( {D_* } = D{\left[ {\frac{{g\left( {{\rho_s} - \rho } \right)}}{{{\upsilon^2}}}} \right]^{\left( {1/3} \right)}} \),ρ s is the particle density (here assumed to be 2,650 kg m−3), and ρ is the water density.

3.2 Microflocs

The microfloc size fraction is here defined as those flocs with diameter less than 160 μm. Equations for 100% mud (Manning 2008), 75% mud, 50% mud, 25% mud (Manning et al., submitted, part 1 of this paper) and 0% mud (Soulsby 1997) are used. In the model, the settling velocity for microflocs is interpolated from these results based on mud-sand content.

The microfloc settling velocity, Ws micro_EM , (units of mm s−1) is given by the following equation:

$$ {\hbox{W}}{{\hbox{s}}_{micro\_ EM}} = E + F\tau --G{\tau^2} + H{\hbox{SPM}} $$
(18)

where E, F, G and H are constants which vary with the proportion of mud:sand content and the shear stress as given in Table 2. As discussed in Section 3.1, the uncertainty in Eq. 18 increases as the shear stress increases above 0.9 N m−2. For reasons of continuity with Eq. 16, Eq. 18 was used for values of shear stress up to τ = 2 N m−2. For values of shear stress higher than this, the settling velocity of macroflocs was calculated assuming τ = 2 N m−2.

Table 2 Coefficients used in Eq. 18 in calculation of microfloc settling velocity for different values of shear stress and percentage mud-sand
Full size table

As before, for pure sand, the settling velocity estimate of Soulsby (1997) is used (Eq. 17).

3.3 Macrofloc–microfloc distribution

To parameterise the distribution of particulate matter throughout the macrofloc and microfloc sub-populations, a dimensionless SPM ratio (SPM ratio_EM ) is used. This was calculated by dividing the percentage of SPMmacro by the percentage of SPMmicro for each floc population:

$$ {\hbox{SP}}{{\hbox{M}}_{ratio\_ EM}} = \% {\hbox{SP}}{{\hbox{M}}_{\rm{macro}}}/\% {\hbox{SP}}{{\hbox{M}}_{\rm{micro}}} $$
(19)

If the value of SPM ratio_EM is known, then the macro/micro floc distribution is found from:

$$ \% {\hbox{SP}}{{\hbox{M}}_{\rm{micro}}} = 100/\left( {1 + {\hbox{SP}}{{\hbox{M}}_{ratio\_ EM}}} \right) $$
(20)

and

$$ \% {\hbox{SP}}{{\hbox{M}}_{\rm{macro}}} = 100 - \% {\hbox{SP}}{{\hbox{M}}_{\rm{micro}}} $$
(21)

Manning et al. (submitted, part 1 of this paper) derived empirical formulae for the mean SPM ratio value based on SPM concentration for a variety of shear stress levels. In the model, the macrofloc/microfloc distribution is interpolated from these results based on mud-sand content. The SPM ratio_EM equations are of the form:

$$ {\hbox{SP}}{{\hbox{M}}_{ratio\_ EM}} = \alpha + \beta {\hbox{SPM}}--\gamma {\hbox{SP}}{{\hbox{M}}^2} $$
(22)

where α, β and γ are empirical constants varying with the proportion of mud-sand as given in Table 3.

Table 3 Coefficients used for Eq. 22 in calculation of the SPM ratio (SPM ratio_EM ) for different values of percentage mud-sand
Full size table

Equation 22 is valid for the entire experimental total SPM concentration and shear stress ranges (i.e. 200 to 5,000 mg l−1 and 0.06–0.9 N m−2, respectively). For pure sand, for particle sizes less than 160 μm, the entire population will be microflocs.

3.4 Distribution of mud-sand across sub-fractions

In the end, the sediment transport modeller needs to know the settling velocities of the mud and sand fractions rather than the settling velocities of the microfloc and macrofloc components, and hence, it is necessary to know how much mud and sand is in the microfloc and macrofloc components. If the concentration of sand and mud is already known, then it suffices to know the micro/macrofloc distribution of the sand only as the mud distribution can then be derived from the other information. The relative distribution of the total sand content, present within a mixed suspension, across the two sub-fractions, M:S _mi:MA _EM , is given by:

$$ {\hbox{M}}:{{\hbox{S}}_{\_ mi:MA\_ EM}} = \% {\hbox{san}}{{\hbox{d}}_{\rm{micro}}}/\% {\hbox{san}}{{\hbox{d}}_{\rm{macro}}} $$
(23)

where

$$ \% {\hbox{san}}{{\hbox{d}}_{\rm{macro}}} = 100{/}\left( {{1} + {\hbox{M}}:{{\hbox{S}}_{\_ mi:MA{ }\_ EM}}} \right) $$
(24)

and

$$ \% {\hbox{san}}{{\hbox{d}}_{\rm{micro}}} = 100 - \% {\hbox{san}}{{\hbox{d}}_{\rm{macro }}} $$
(25)

Regression analysis (Manning et al., submitted, part 1 of this paper) produced a series of M:S _mi:MA _EM equations representing each ratio of mud and sand, for each shear stress and SPM concentration range. In the model, the sand macrofloc/microfloc distribution is interpolated from these results based on mud-sand content. The SPM ratio_EM equations are of the form:

$$ {\hbox{M}}:{{\hbox{S}}_{\_ mi:MA{ }\_ EM}} = \delta --\varepsilon \tau + \zeta {\tau^2}--\theta {\hbox{SPM}} + \lambda {\hbox{SP}}{{\hbox{M}}^2} + \mu {\hbox{SPM}}\tau --\xi {\hbox{SPM}}{\tau^2} $$
(26)

where δ, ε, ζ, θ, λ, τ, μ, and ξ are empirical constants varying with the proportion of mud-sand as given in Table 4.

Table 4 Coefficients used for Eq. 26 in calculation of the sand macrofloc/microfloc distribution (M:S _mi:MA _EM ) for different values of percentage mud-sand
Full size table

4 Model implementation—annular flume tests

4.1 Introduction

The model described above in Sections 1 and 2 was first utilised to reproduce the measurements of settling velocity in the annular flume where they were derived. To do this, the 1DV model described in Section 2 was set up to reproduce the 1DV flow and concentration structure in the flume. It is recognised in this process that the 1DV model will not be able to reproduce the secondary currents generated in the annular flume, but a detailed evaluation of the annular flume performance (Manning and Whitehouse 2010) showed that the secondary currents were in the region of 11–14% of the streamwise velocity, giving an error in the calculated magnitude of current speed in the 1DV model of around 1% percent, and thus, it is considered that this application leads to firm conclusions regarding the interaction of sand and mud in flocculation.

The model was run both using the empirical algorithms presented in Section 3 and, additionally, to test the null hypothesis, using an assumption of no interaction between sand and mud particles (see the discussion regarding Eq. 28 below). For this, the sand particles were assumed to settle according to Soulsby’s equation (Soulsby 1997), and the mud was assumed to fall at the rates described by Mannings “mud only” equations (See Eqs. 16 and 18 and Tables 1 and 2).

The following brief description of the experiments is summarised from Manning et al. (submitted, part 1 of this paper). The annular flume used to derive the mud-sand algorithms has an outer diameter of 1.2 m, a channel width of 0.1 m and a maximum depth of 0.15 m, along with a detachable roof 10 mm thick. An adjustable annular ring, which has six 15-mm deep wooden paddles on the underside, was rigidly suspended from the roof. The annular ring fits into the channel, and is set to the height of the fluid 0.13 m above the channel base. A detailed description of the mini-annular flume operation is reported by Manning and Whitehouse (2010). The flume hydrodynamics, in terms of velocity and turbulent kinetic energy, were measured by a Nortek mini-acoustic Doppler velocimeter (ADV) at a distance of 22 mm above the flume channel base, which was also the floc extraction height.

The video-based LabSFLOC—Laboratory Spectral Flocculation Characteristics—instrument (Manning 2006) was used to measure floc/aggregate properties from each population. Sampling comprised careful extraction of a suspension from a distance of 22 mm above the flume channel base. The sample was then quickly transferred to a Perspex column containing clear water with the same salinity as used in the flume runs (salinity of 20 ± 0.2), and then, each floc/aggregate was observed using a high resolution miniature underwater video camera as they were settling in the column.

The laboratory experiments primarily utilised pre-determined mixed sediments, which were a combination of natural Tamar Estuary (UK) mud mixed with sand, in order to produce the desired mud-sand ratio. The sand used in these experiments was Redhill 110, which is a closely graded silica sand with a d50 of about 110 μm, and this value was used in the model.

4.2 Application of model

The model was applied to the annular flume using a 28-layer model with resolution near the bed and surface of 0.2 mm and resolution at mid-depth of around 0.5 mm. Owing to the shallow depths and small size of the flume, no velocity profiles were available for calibration through depth, but information about measured current speed and turbulence at the measurement point was available, and this was used to calibrate the model. The model was initially calibrated, in a similar manner to the annular flume, with clear water. The physical roughness value for bed friction was found through calibration to be in the range 10−5 to 10−6 which compares well with values derived from a similar calibration exercise by Winterwerp (1999). Side wall friction was included in the model using the formula

$$ {\tau_{sf}} = \lambda \rho {u^2} $$
(27)

where λ is the side wall roughness (set to 5 × 10−4 m in this case).

To calibrate the velocities and turbulent shear stress within, the model was used to reproduce the measured turbulent shear stress at 22 mm above the bed for measured current speeds (at this depth) of 0.14, 0.30, 0.39, 0.54, 0.60 and 0.75 m/s (Manning and Whitehouse 2010), without sediment in the flow. The measured and predicted turbulent shear stress are plotted against each other in Fig. 1. The agreement is good (with an R 2 value of 0.98 and a gradient close to unity), and it is considered that the model forms a good basis for examining the distribution of suspended sediment concentration and turbulent shear stress and hence settling velocity in the flume. The model was run with two fractions: cohesive mud and 110 μm sand.

Fig. 1
figure 1

Comparison of predicted and measured turbulent shear stress at 22 mm above the bed in the annular flume. The measured shear stress presented is a mean value. Error bars are shown where the estimated error in the measured shear stress is greater than 0.01 N m−2

Full size image

The model was used to repeat every experiment from the annular flume. The resulting predictions of suspended settling concentrations are compared with the corresponding observations from Manning et al. (submitted, part 1 of this paper) in Table 5 and Fig. 2. The root-mean-square error in the prediction of macrofloc settling velocity was ±1.2 mm/s which corresponds to around 59% of the mean measured macrofloc settling velocity. The root-mean-square error in the prediction of microfloc settling velocity was ±0.56 mm/s which corresponds to around 24% of the mean measured microfloc settling velocity. Figure 2 shows an R 2 value of 0.74 and 0.40, respectively, for the microfloc and macrofloc predictions and the best fit for linear regression passing through the origin has slopes of 0.89 and 0.75, respectively. In Fig. 2, there are two particular outliers at observed macrofloc settling velocities of 7.2 and 5.4 mm/s occur. These measurements occur for a mud percentage of 75% and 50%, respectively, and relatively high suspended sediment concentration of 5,000 mg/l and a shear stress of 0.35 N m−2. The observations in these two cases are significantly under-predicted by the model (the model predicts 2.9 mm/s in both cases). The most likely reason for this is the under-estimation of settling velocity by the empirical equations compared to the measurements for shears stress of 0.35 N m−2 and concentrations of 5,000 mg/l (Manning et al., submitted, part 1 of this paper), although this error in the empirical model does not account for all of the error in these outliers.

Table 5 Predicted and observed settling velocity in the annular flume using the empirical flocculation algorithms
Full size table
Fig. 2
figure 2

Comparison of predicted and observed settling velocity in the annular flume using the empirical flocculation algorithms. Error bars are shown where the estimated error in the measured settling velocity is greater than 0.1 mm/s

Full size image

The exercise was then repeated but this time assuming no interaction between sand and mud particles. The resulting predictions of suspended settling concentrations are compared with the corresponding observations in Fig. 3 and Table 6. The root-mean-square error in the prediction of macrofloc settling velocity was ±1.4 mm/s which corresponds to around 67% of the mean measured macrofloc settling velocity. The root-mean-square error in the prediction of microfloc settling velocity was ±2.0 mm/s which corresponds to around 89% of the mean measured microfloc settling velocity. Figure 3 shows an R 2 value of 0.25 and −1.9, respectively, for the microfloc and macrofloc predictions, and the best fit for linear regression passing through the origin has slopes of 1.4 and 0.58, respectively. These results are significantly worse than the results using the empirical model.

Fig. 3
figure 3

Comparison of predicted and observed settling velocity in the annular flume assumption mud and sand are independent. Error bars are shown where the estimated error in the measured settling velocity is greater than 0.1 mm/s

Full size image
Table 6 Predicted settling velocity in the annular flume assuming no interaction between sand and mud
Full size table

The Brier Skill Score (BSS) for the predictions for the proposed equations was derived from the formula

$$ BSS = 1 - \frac{{\sum {{{\left( {{x_i} - {y_i}} \right)}^2}} }}{{\sum {{{\left( {{x_i} - {z_i}} \right)}^2}} }} $$
(28)

where x i is the ith observation, y i is the ith model prediction using the proposed empirical equations and z i is the ith model prediction using the null hypothesis that there is no interaction between sand and mud: flocculation occurs only for mud, and sand particles settle at rates given by Eq. 17 regardless of concentration or shear stress. A positive BSS score indicates an improvement using the empirical equations compared to use of the null hypothesis model, with a score of 1 indicating a perfect fit. A negative score indicates that the empirical model reproduces the data less well than the null hypothesis. The BSS for the prediction of macroflocs was 0.27 whilst that for prediction of microflocs was 0.91. These results indicate strongly that the flocculation behaviour of the mud and sand particles is much more akin to that described by the empirical equations rather than treating the mud and sand as independent.

5 Model implementation—comparison with field data

5.1 Description of field measurements

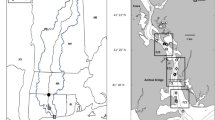
The 1DV model was also used to reproduce the observed (mixed) suspended sediment concentrations from measurements in the Outer Thames in 1971/1972 (Whitehouse and Thorn 1997). The measurements were located in the deep water channels in water depths of 14–19 m (see Fig. 4). The tidal conditions modelled were a little smaller than a mean spring tide with peak current speeds of around 1 m/s. The measurements were taken during relatively calm conditions with little wave action, and so, waves are ignored in this comparison. The bed surface was composed of fine sand (d50 of 162 μm) with sand ripples.

Fig. 4
figure 4

Location of Outer Thames measurements (reproduced from the original, Whitehouse and Thorn 1997). Location of data utilised in this paper is shown by thick circle

Full size image

Suspended solids and current measurements were taken from a moored vessel using a combination of miniature current meters and water sample nozzles mounted on a bed frame and a wire-suspended current meter and sampling nozzle which could be raised and lowered through the water column. The number of revolutions of the Braystoke current meters was recorded over 50–100 s at each measurement height. The number of revolutions was converted to a current speed on the basis of towing tank calibrations. At each measurement height, a pump sampler was used to sample between 10 and 40 l of the water/sediment over the same sampling period as the current metering. The pumped water/sediment was passed through a filtration unit which retained the solids exceeding 40 μm in diameter, whilst bottles samples were taken of the filtrate. The filter papers and the filtrate samples were analysed in the laboratory to determine the concentration of suspended sediment in the pumped samples. The concentrations of the following fractions were derived: D < 40 μm, 40–60 μm, 60–75 μm, 75–100 μm, 100–150 μm, D > 150 μm. Whitehouse and Thorn (1997) state that the error in the measured concentrations (for each fraction) was in the range 0.25–1.0 mg l−1.

The measurements consisted of through-depth profiles taken every half hour over a tide, at distances of 0.05, 0.1, 0.15, 0.3, 0.6, 0.9, 1.8, 3.6, 7.3, 11.0, and 14.6 m above the bed. At each point of the profile, the velocity was measured, and water samples were collected and analysed. An example of the measured results for 0.3 m above the bed is shown in Fig. 5.

Fig. 5
figure 5

Example of Outer Thames measurements at 0.3 m above the bed (reproduced from the original, Whitehouse and Thorn 1997)

Full size image

The model was run using the measurements of location 1 as shown in Fig. 4.

5.2 Implementation of model

As in Section 4, the model was implemented using the empirical algorithms presented in Section 3. In addition, a similar model was run but this time using the null hypothesis assumption that mud and sand do not interact and that sand particles settle at their still water velocities. In both cases, the model was run with the following five fractions represented: cohesive sediment of less than 40 μm (assumed to be fully cohesive “mud”), 50 μm, 67 μm, 87 μm, and 125 μm. The aim of the modelling was to reproduce the measured concentrations of these fractions.

The model was used to predict the distribution of sediment through the water column but was not used to predict deposition and erosion of the bed. This approach was used by Winterwerp (1999) to examine many facets of mud transport dynamics and was utilised in this study for four reasons: (a) the object of the study was to investigate flocculation rather than erosion/deposition and removing this process from the model removed a potential source of uncertainty; (b) at a single location point, the sediment flux advected from other sources is orders of magnitude higher than the local exchange with the bed; (c) the nature of the suspended material (d50 of 70–88 μm, Whitehouse and Thorn 1997) is different from that characterising the bed, indicating little real exchange between the two; (d) there is no information governing the nature of any thin surficial layer that might temporally occur at slack water. As a result of these considerations, the depth-averaged suspended sediment concentrations (and depth-averaged velocity) were proscribed on each time step (based on the field measurements), and the model was used to distribute this concentration (and velocity) over the water depth. The resulting predicted concentrations were then compared with those measured in the Outer Thames.

The model was run with 34 layers. Larger numbers of layers were tried, but the model results were relatively insensitive to increased resolution by this point (see Fig. 6). The layers were distributed so that resolution near the bed was greatest which was set at 0.02 m or approximately 0.1% of water depth. The physical roughness length in the model was set to 6 mm which is representative of rippled sands (Soulsby 1997).

Fig. 6
figure 6

Sample results of 1DV model applied to the Thames dataset at 0.3 and 1.83 m above the bed, with 34 and 56 layers. Times of high and low water are marked as HW and LW

Full size image

5.3 Extrapolation of the derived empirical algorithms to other sand fractions

The empirical algorithms developed by Manning et al. (submitted, part 1 of this paper) were developed using Redhill sand (with a d50 of 110 μm), and so, it is necessary to adjust the algorithms for sands with a different d50 or to model the behaviour of specific fractions.

A comparison of the settling velocity measurements undertaken on the mixed mud-sand mixture from Portsmouth (Manning et al., submitted, part 1 of this paper) with those mixtures made using the finer sand presented in Section 3 allows some insights into how settling velocity varies with different sand fractions. The equations derived for the Portsmouth material are of the same form as Eqs. 16 and 18 but with different coefficients. The coefficients for Eqs. 16 and 18 are presented in Tables 7 and 8, respectively.

Table 7 Coefficients used in Eq. 16 for calculation of macrofloc settling velocity for Portsmouth material for different values of shear stress and percentage mud-sand
Full size table
Table 8 Coefficients used in Eq. 18 for calculation of microfloc settling velocity for Portsmouth material for different values of shear stress and percentage mud-sand
Full size table

The Portsmouth empirical equations are measured for different mud-sand proportions than the fine silica sand equations but through interpolation, the results of each can be compared for mixtures (mud-sand percentages) of 70:30, 50:50 and 38:62. When the two sets of equations are compared, the following conclusions are obtained:

  • The predicted macrofloc settling velocities are broadly similar for the two sets of equations for a mixture with high sand content, although the predicted Portsmouth macrofloc settling velocities are considerably higher for the measurements with lower sand content;

  • The predicted Portsmouth microfloc settling velocities are always higher than the predicted laboratory-derived microfloc settling velocities; and

  • The proportional difference between the Portsmouth and the finer sand microfloc settling velocities appears relatively insensitive to mud-sand content of the flocs or concentration.

As a result of these considerations, it would seem that any initial first order addition to the algorithms presented in Section 3 to incorporate the effect of different sand particle size should relate to the microfloc population but should not involve mud-sand content.

The empirical algorithms were initially applied without revision to the field dataset described in detail in Section 5.4 below. The results were found to exhibit the following behaviour (see for instance Fig. 7):

  • The peak concentrations were consistently over-estimated in the upper and middle part of the water column and under-estimated in the lower part of the water column; and

  • During times of slack water, the concentrations were predicted within an error of 10 mg/l or less.

Fig. 7
figure 7

Initial results of 1DV model applied to the Thames dataset, predicted suspended sediment concentrations at 0.3 and 7.32 m above bed. Times of high and low water are marked as HW and LW

Full size image

However, application of the results without the empirical algorithms (assuming sand fractions fall according to the equation of Soulsby (1997)) showed the opposite tendencies (see for instance Fig. 7):

  • The peak concentrations were consistently over-estimated in the lower part of the water column; and

  • During times of slack water, the concentrations were predicted to reduce to zero through much of the water column.

On this basis, a modification to the empirical microfloc equations was sought which tended to increase the (average) microfloc settling velocities for higher levels of turbulent shear stress (but not to the level of those associated with pure sand) and tended to leave the microfloc velocities unaltered for lower values of shear stress. A rationale for this might be that, since sand particles are more susceptible to breaking up than mud particles (the bonds between particles being less strong in general), at higher levels of shear stress, the population of sand particles which are not involved in the flocculation process increases, so raising the average microfloc settling velocity. The laboratory measurements (Manning et al. 2009) identified individual sand-size particles settling at speeds in excess of 10 mm/s.

Application of the model to the field measurements described in Section 5.1 indicated that estimating the proportion of the sand population, which is involved in flocs as exp(-τ), where τ is the turbulent shear stress, gave the best fit. The re-application of the revised algorithms to the annular flume model, but this time modelling the sand population as five separate fractions, resulted in a root-mean-square error in the prediction of macrofloc settling velocity of ±1.1 mm/s, and of the microfloc of settling velocity was ±0.80 mm/s. These errors are (overall) slightly larger than the results presented in Section 4 (which presents results for the modelling of a single mud and a single sand fraction), but still considerably smaller than the corresponding results for a many-fraction model assuming no mud-sand interaction (which gave errors of macrofloc ±1.4 mm/s and microfloc ±2.0 mm/s). On this basis, it was concluded that the revision to the algorithms, whilst not perfect, represented an improvement in that it allowed the representation of many fractions in the flocculation model without compromising the (measurable) accuracy of the model as a whole.

5.4 Comparison of model predictions against observations

The revised model, incorporating the relationship for the proportion of the sand population which form macroflocs, was used to reproduce the observed concentrations of the six different fractions D < 40 μm, 40–60 μm, 60–75 μm, 75–100 μm, 100–150 μm, and D > 150 μm for the Thames dataset. The performance of the revised model in reproducing the observations was compared to the model results assuming no interaction between sand and mud in flocculation in two ways: by evaluating the root-mean-square error of the model predictions and by calculating the Brier Skill Score (with the null hypothesis being that the “no sand/mud interaction” (NSMI) model describes the observed behaviour). Some examples of the model predictions of concentration for some of the sediment fractions are shown in Figs. 8, 9 and 10. Figure 11 shows a comparison of the predicted vertical profile of total suspended sediment concentration at HW +3.5 h and HW −4 h using the empirical model equations.

Fig. 8
figure 8

Results of revised 1DV model, predicted suspended sediment concentrations at 0.1 m above bed. Times of high and low water are marked as HW and LW

Full size image
Fig. 9
figure 9

Results of revised 1DV model, predicted suspended sediment concentrations at 1.83 m above bed. Times of high and low water are marked as HW and LW

Full size image
Fig. 10
figure 10

Results of revised 1DV model, predicted suspended sediment concentrations at 10.97 m above bed. Times of high and low water are marked as HW and LW

Full size image
Fig. 11
figure 11

Measured and predicted through-depth profiles at HW +3.5 h and HW −4 h, revised 1DV model applied to Thames dataset

Full size image

Figure 8 shows the predicted suspended sediment concentrations for the 40–60-, 75–100- and 100–150-μm fractions at 0.1 m above the bed. The 40–60-μm predictions (top of Fig. 8) are fairly similar for both the revised empirical and the NSMI models, except for the peaks just after slack water at 14:30 and 20:30 where the NSMI model predicts concentrations of 210 and 118 mg/l, respectively, compared to the empirical model predictions of 89 and 50 mg/l and the measured values of 20 and 23 mg/l. The over-prediction of concentrations near the bed by the NSMI model indicates over-prediction of settling velocity higher in the water column during slack water. The 75–100-μm results (centre of Fig. 8) show the empirical model correctly predicting the range of variation of concentration of this fraction but also shows the NSMI model over-predicting by as much as 300 mg/l (80%) at mid-tide (16:30). The 100–150-μm results (bottom of Fig. 8) show the empirical model more closely predicting the range of variation of concentration than the NSMI model with the empirical model over-predicting the peak concentration by up to 20% (compared to 50% for the NSMI). In all these examples, there is a noticeable phase difference in the model prediction of suspended sediment concentration after the slack water at 14:00 which is not present after the later slack water at 20:30.

Figure 9 shows the predicted suspended sediment concentrations for the 60–75-, 75–100- and 100–150-μm fractions at 1.83 m above the bed. The 60–75-μm predictions (top of Fig. 9) show that the empirical model (RMS error = 5 mg/l) predicts the suspended sediment concentration better than the NSMI model (RMS error = 7 mg/l) and predicts both the peaks and troughs of the tidal signal more appropriately. The 75–100-μm results (centre of Fig. 9) suggest that the empirical model prediction is more similar to that of the NSMI model (= 15 mg/l), but the RMS error is still lower (RMS error = 12 mg/l for the empirical model and 15 mg/l for the NSMI model) partly because the NSMI model predicts zero concentration for this fraction at slack water. Both models over-predict the peak concentrations by 25–30 mg/l (around 40–50%). The 100–150-μm results (bottom of Fig. 9) show a similar model performance for the empirical and NSMI models (RMS error = 8 mg/l in both cases). The first peak is predicted within 2–8 mg/l, whilst the error in the second peak is 26 mg/l (80%) for both models.

Figure 10 shows the predicted suspended sediment concentrations for the 0–40-, 75–100- and 100–150-μm fractions at 10.97 m above the bed. The 0–40-μm predictions (top of Fig. 10) show similar results for both models (RMS error = 3 mg/l in both cases). The 75–100-μm results (centre of Fig. 9) show that the NSMI model (RMS error = 5 mg/l or around 30% of the peak concentration) under-predicts the concentration of this fraction compared to the empirical model (RMS error = 2 mg/l or around 12% of the peak concentration). The 100–150-μm results (bottom of Fig. 10) again show that the NSMI model (RMS error = 2 mg/l or around 40% of the peak concentration) under-predicts the concentration of this fraction compared to the empirical model (RMS error = 1 mg/l or around 20% of the peak concentration).

Examples of measured and predicted through-depth profiles at HW +3.5 h and HW −4 h are presented in Fig. 11. The profiles show that the assumption of no interaction between mud and sand can result in considerable inaccuracy.

The RMS error was computed for each fraction for all of the data (i.e. all of the through-tide measurements at 0.1, 0.3, 0.6, 0.91, 1.83, 3.66, 7.32 and 10.97 m above the bed). The results are summarised in Table 9. It can be seen that overall, there is a significant reduction in error in the modelling using the empirical equations (of between 22% and 41%, with an overall 24% reduction in RMS error). Using Eq. 28, the Brier Skill Score for the use of the empirical equations as a whole is equivalent to 0.42, again indicating a significant benefit to use of the revised empirical model.

Table 9 Summary of the RMS error (mg/l) in the predicted concentrations
Full size table

Figures 8, 9, 10 and 11 and Table 9 provide evidence that the refined empirical model represents an improvement over a model which assumes no interaction between sand and mud in flocculation. In general, the improvement consists of a reduction in near bed concentrations and an increase in concentrations in the upper water column. The improvement in the model arises mainly because the inclusion of sand particles in flocs reduces the settling velocity of the sand particles leading to higher concentrations in the upper water column and lower concentrations near the bed, more in line with the observed variation in suspended sediments. The remaining error in the empirical model is exhibited most strongly by the finest fraction (0–40 μm). Whilst the examination of flocculation processes in this fraction was not a focus of the present study, the further refinement of the flocculation model for muddy sediment is highlighted as an area for future research.

6 Summary and conclusions

Manning et al. (2009) discussed the biological causes of sand flocculation and presented evidence for sand flocculation from laboratory measurements of settling velocity in mixed muds and sands. In part one of this paper (Manning et al., submitted), the results of the same laboratory tests were used to development empirical equations which described the flocculation of the mixtures used in the laboratory. In the present paper, these equations were used in combination with a 1DV model to (a) reproduce the laboratory measurements themselves and (b) with a small modification, to reproduce detailed measurements in the Outer Thames Estuary. In both applications of the 1DV model, the results of use of the empirical mud-sand flocculation formulae significantly out-performed the results assuming that there is no interaction between sand and mud in flocculation. This numerical modelling provides further evidence that this interaction is a real and observable phenomenon.

This improvement in the understanding of how sand and mud can interact in flocculation allows the possibility of enhanced accuracy in sediment transport models, potentially leading to improvements in the prediction of dredging maintenance requirement, and wider changes in morphology and substrate following development in mixed sediments. This work complements the present focus of mud-sand interaction which considers how mud and sand interact at the sea bed surface.

This study has also identified the strong possibility that, as well as the macrofloc–microfloc interaction that is satisfactorily described by the empirical algorithms, there is a varying population of sand particles engaging in the flocculation which appears to be principally affected by turbulent shear stress. This aspect of the mud-sand flocculation is crudely described by the addition to the empirical model presented in this paper, and it is recommended that further measurements be undertaken with mud-sand mixtures of differing sand distributions and sand mud content to provide further data for subsequent development of the empirical model.

The empirical model developed in part 1 of this paper (Manning et al., submitted) and utilised in the present study represents a first, but important, step towards establishing a physically based, scale-independent model which can be utilised more widely in mixed sediment transport models.