Abstract
We deal with a notion of weak binormal and weak principal normal for non-smooth curves of the Euclidean space with finite total curvature and total absolute torsion. By means of piecewise linear methods, we first introduce the analogous notion for polygonal curves, where the polarity property is exploited, and then make use of a density argument. Both our weak binormal and normal are rectifiable curves which naturally live in the projective plane. In particular, the length of the weak binormal agrees with the total absolute torsion of the given curve. Moreover, the weak normal is the vector product of suitable parameterizations of the tangent indicatrix and of the weak binormal. In the case of smooth curves, the weak binormal and normal yield (up to a lifting) the classical notions of binormal and normal. Finally, the torsion force is introduced: similarly as for the curvature force, it is a finite measure obtained by performing the tangential variation of the length of the tangent indicatrix in the Gauss sphere.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In classical differential geometry, it sometimes happens that the geometry of a proof can become obscured by analysis. This statement by Penna [11], which may be referred, e.g., to the classical proof of the Gauss-Bonnet theorem, suggests to apply piecewise linear methods in order to make the geometry of a proof completely transparent.
For this purpose, by using the geometric description of the torsion of a smooth curve, Penna [11] gave in 1980 a suitable definition of torsion for a polygonal curve of the Euclidean space \({{\mathbb {R}}}^3\), and used piecewise linear methods and homotopy arguments to produce an illustrative proof of the well-known property that the total torsion of any closed unit speed regular curve of the unit sphere \({{{\mathbb {S}}}^2}\) is equal to zero.
Differently to the smooth case, the polygonal torsion is a function of the segments. His definition, in fact, relies on the notion of binormal vector at the interior vertices. Since the angle between consecutive discrete binormals describes the movements of the “discrete osculating planes” of the polygonal, binormal vectors naturally live in the projective plane \({\mathbb {RP}}^2\), see Sect. 2.
We recall here that Milnor [8] defined the tangent indicatrix, or tantrix, of a polygonal P as the geodesic polygonal \({{\mathfrak {t}}}_P\) of the Gauss sphere \({{{\mathbb {S}}}^2}\) obtained by connecting with oriented geodesic arcs the consecutive points given by the direction of the oriented segments. Therefore, the total curvature \(\mathrm{TC}(P)\), i.e., the sum of the turning angles of the polygonal, agrees with the length \(\mathcal{L}_{{{{\mathbb {S}}}^2}}({{\mathfrak {t}}}_P)\) of the tantrix, and the total absolute torsion \(\mathrm{TAT}(P)\) agrees with the sum of the shortest angles between the geodesic arcs in \({{{\mathbb {S}}}^2}\) meeting at the edges of \({{\mathfrak {t}}}_P\).
From another viewpoint, Fenchel [6] in the 1950’s exploited the spherical polarity of the tangent and binormal indicatrix in order to analyze the differential geometric properties of smooth curves in \({{\mathbb {R}}}^3\). In his survey, Fenchel proposed a general method that gathers several results on curves in a unified scheme. We point out that Fenchel deals with \(C^4\) rectifiable curves (parameterized by arc length) such that at each point it is well defined the osculating plane, that is, a plane containing the linearly independent vectors \({{\mathfrak {t}}}:=\dot{c}\) and \(\ddot{c}\), such that its suitably oriented normal unit vector \({{\mathfrak {b}}}\), the binormal vector, is of class \(C^2\), and the two vectors \({\dot{{{\mathfrak {t}}}}}\) and \({\dot{{{\mathfrak {b}}}}}\) never vanish simultaneously. He then defines the principal normal by the vector product
Since the derivatives of \({{\mathfrak {t}}}\) and \({{\mathfrak {b}}}\) are perpendicular to both \({{\mathfrak {t}}}\) and \({{\mathfrak {b}}}\), the curvature \(\mathbf{{k}}\) and torsion \({\varvec{\tau }}\) are well defined through the formulas:
As a consequence, one has
and hence the Frenet–Serret formulas hold true, but Fenchel allows both curvature and torsion to be zero or negative. Related arguments have been treated in [2, 4, 5, 7, 14].
Content of the paper We deal with curves in the Euclidean space \({{\mathbb {R}}}^3\) with finite total curvature and total absolute torsion. We address to Sullivan [13] for the analysis of curves with finite total curvature, and also to our paper [10] for the \(\mathop {\mathrm{BV}}\nolimits \)-properties of the unit normal of planar curves.
By melting together the approaches by Penna and Fenchel previously described, in this paper we firstly define the binormal indicatrix \({{\mathfrak {b}}}_P\) of a polygonal P in \({{\mathbb {R}}}^3\) as the arc-length parameterization \({{\mathfrak {b}}}_P\) of the polar in \({\mathbb {RP}}^2\) of the tangent indicatrix \({{\mathfrak {t}}}_P\), see Definition 2 and Fig. 1. Therefore, the total absolute torsion \(\mathrm{TAT}(P)\) of P is equal to the length of the curve \({{\mathfrak {b}}}_P\). We remark that a similar definition has been introduced by T. F. Banchoff in his paper [2] on space polygons.
However, differently from what happens for the length and the total curvature, the monotonicity formula fails to hold. More precisely, if \(P'\) is a polygonal inscribed in P, by the triangular inequality we have \(\mathcal{L}(P')\le \mathcal{L}(P)\) and \(\mathrm{TC}(P')\le \mathrm{TC}(P)\), compare, e.g., [13, Cor. 2.2], but it may happen that \(\mathrm{TAT}(P')>\mathrm{TAT}(P)\), see Example 1.
For that reason, the total absolute torsion \(\mathrm{TAT}(c)\) of a curve c in \({{\mathbb {R}}}^3\) is defined by following the approach due to Alexandrov and Reshetnyak [1] that involves the notion of modulus \(\mu _c(P)\) of a polygonal P inscribed in c, see (3.1).
As a consequence, by means of a density argument, a good notion of weak binormal indicatrix \({{\mathfrak {b}}}_c\) for a non-smooth curve with finite total curvature and absolute torsion is obtained in our first main result, see Theorem 1. In fact, we infer that for any sequence \(\{P_h\}\) of inscribed polygonals with \(\mu _c(P_h)\rightarrow 0\), one has \(\mathrm{TAT}(P_h)\rightarrow \mathrm{TAT}(c)\), see Proposition 1, and hence that the weak binormal \({{\mathfrak {b}}}_c\) only depends on the curve c.
For smooth curves, the total absolute torsion, which agrees with the length in the Gauss sphere of the smooth binormal curve \({{\mathfrak {b}}}\), actually agrees with the total geodesic curvature of the smooth tantrix \({{\mathfrak {t}}}\) in \({{{\mathbb {S}}}^2}\).
In fact, on account of the density result from [11, Prop. 4], by Proposition 1 one readily obtains that
where \({\varvec{\tau }}(s)\) is the torsion of the smooth curve c. This property is checked in Example 2, referring to a helicoidal curve, where we exploit piecewise linear methods in the computation.
In Theorem 1, we show the existence of a curve \({{\mathfrak {b}}}_c\) of \({\mathbb {RP}}^2\), parameterized by arc length, whose length is equal to the total absolute torsion:
The hypothesis \(\mathrm{TC}(c)<\infty \) in Theorem 1 may sound a bit unnatural, and actually a technical point, since it allows us to prove that \({{\mathfrak {b}}}_c\) has constant velocity one, so that (1.3) holds true.
To this purpose, we recall that the definition of complete torsion \(\mathrm{CT}(P)\) of polygonals P given by Alexandrov and Reshetnyak [1], who essentially take the distance in \({{{\mathbb {S}}}^2}\) between consecutive discrete binormals, implies that planar polygonals may have positive torsion at “inflections points”. Defining the complete torsion \(\mathrm{CT}(c)\) of curves c in \({{\mathbb {R}}}^3\) as the supremum of the complete torsion of the inscribed polygonals, they obtain in [1, p. 244] that any curve with finite complete torsion and with no points of return must have finite total curvature.
With our definition of torsion, the above implication clearly fails to hold, see Remark 9. On the other hand, equality (1.2) is violated if one considers the complete torsion from [1], since for a smooth planar curve with inflection points, one has \(\mathrm{CT}(c)>0\).
We finally notice that a curve with finite total curvature and total absolute torsion may have infinite complete torsion in the sense of [1]: just take a smooth planar curve with a countable set of inflection points.
In Theorem 2, we show that for smooth curves whose torsion \({\varvec{\tau }}\) (almost) never vanishes, the weak binormal \({{\mathfrak {b}}}_c\) obtained in Theorem 1, when lifted to \({{{\mathbb {S}}}^2}\), agrees with the arc-length parameterization of the smooth binormal \({{\mathfrak {b}}}\).
Similar features concerning the tantrix are collected in Propositions 2 and 3. Our curve \({{\mathfrak {t}}}_c\) satisfies \(\mathcal{L}_{{{{\mathbb {S}}}^2}}({{\mathfrak {t}}}_c)=\mathrm{TC}(c)\) and hence it is strictly related with the complete tangent indicatrix in the sense of Alexandrov and Reshetnyak [1].
Now, when looking for a possible weak notion of principal normal, a drawback appears. In fact, in Penna’s approach [11], the curvature of an open polygonal P is a nonnegative measure \(\mu _P\) concentrated at the interior vertices, whereas the torsion is a signed measure \(\nu _P\) concentrated at the interior segments, see Remark 5. Since these two measures are mutually singular, in principle there is no way to extend Fenchel’s formula (1.1) in order to define the principal normal.
To overcome this problem, in Sect. 5 we proceed as follows. Firstly, we choose two suitable curves \( \widetilde{{\mathfrak {t}}}_P,\widetilde{{\mathfrak {b}}}_P:[0,C+T]\rightarrow {\mathbb {RP}}^2\), where \(C=\mathrm{TC}(P)\) and \(T=\mathrm{TAT}(P)\), that on one side inherit the properties of the tangent and binormal indicatrix \({{\mathfrak {t}}}_P\) and \({{\mathfrak {b}}}_P\), respectively, and on the other side take account of the order in which curvature and torsion are defined along P. More precisely, one of the two curves is constant when the other one parameterizes a geodesic arc, whose length is equal to the curvature or to the (absolute value of the) torsion at one vertex or segment of P, respectively. As in Fenchel’s approach, by exploiting the polarity of the curves \(\widetilde{{\mathfrak {t}}}_P\) and \(\widetilde{{\mathfrak {b}}}_P\), the weak normal of the polygonal is well defined by the inner product
compare Remark 16 and Fig. 2. Notice that by our Definition 3 we have:
As a consequence, in our second main result, see Theorem 3, using again an approximation procedure, the weak principal normal of a curve c with finite total curvature and finite complete torsion is well defined as a rectifiable curve \({{\mathfrak {n}}}_c\) in \({\mathbb {RP}}^2\). We recall that condition \(\mathrm{CT}(c)<\infty \) is stronger than the more natural assumption \(\mathrm{TAT}(c)<\infty \). It turns out that the product formula (1.1) continues to hold in a suitable sense, and we also have:
In particular, for smooth curves whose curvature (almost) never vanishes, the principal normal \({{\mathfrak {n}}}\) agrees with a lifting of a suitable parameterization of the weak normal \({{\mathfrak {n}}}_c\). More precisely, in Proposition 4 we obtain that
where s(t) is the inverse of the increasing and bijective function
In Sect. 6, we make use of an analytical approach in order to define the binormal and principal normal of smooth regular curves with inflection points. In fact, if \(|\dot{c}(s_0)|=1\) but \(\ddot{c}(s_0)=0_{{{\mathbb {R}}}^3}\), the first nonzero higher-order derivative \(c^{(n)}(s_0)\) of c at \(s_0\) satisfies \(\dot{c}(s_0)\perp c^{(n)}(s_0)\) and hence it plays a role in the definition of the binormal. Therefore, following Fenchel [6] in order to define the normal as in (1.1), in Proposition 5 we get:
In general, the binormal and the normal fail to be continuous at inflection points, see Example 3. However, according to Proposition 5, it turns out that they are both continuous when seen as functions in \({\mathbb {RP}}^2\).
This feature confirms that the natural ambient of definition for both the binormal and principal normal is indeed the projective plane \({\mathbb {RP}}^2\).
Finally, in Sect. 7, we define a measure \(\mathcal{T}\), that we call torsion force, that is obtained by performing the tangential variation of the length of the tangent indicatrix \({{\mathfrak {t}}}_c\) that we have built up in Proposition 2. Our torsion force may be compared with the curvature force \(\mathcal K\) introduced in [3], that comes into the play by computing the first variation of the length of curves with finite total curvature. In fact, in the smooth case we have:
where in the second formula we have set \(k(s):=\int _0^s\mathbf{{k}}(\lambda )\,d\lambda \), the primitive of the curvature of the curve.
In general, the curvature force \(\mathcal K\) is a finite measure when the curve c has finite total curvature \(\mathrm{TC}(c)\), i.e., when the tantrix \({{\mathfrak {t}}}=\dot{c}\) is a function of bounded variation. The torsion force \(\mathcal{T}\), instead, is a finite measure when the arc-length derivative of the tantrix \({{\mathfrak {t}}}_c\) from Proposition 2 is a function with bounded variation. We shall see that this condition is satisfied if the curve c has finite complete torsion \(\mathrm{CT}(c)\) in the sense of Alexandrov and Reshetnyak [1].
2 Weak binormal and total torsion of polygonals
In this section, we introduce a weak notion of binormal indicatrix \({{\mathfrak {b}}}_P\) for a polygonal P in \({{\mathbb {R}}}^3\), see Definition 2. It is a rectifiable curve in the projective plane \({\mathbb {RP}}^2\) whose length is equal to the total absolute torsion of P.
Let P be a polygonal curve in \({{\mathbb {R}}}^3\) with consecutive vertices \(v_i\), \(i=0,\ldots ,n\), where \(n\ge 3\) and P is not closed, i.e., \(v_0\ne v_n\). Without loss of generality, we assume that every oriented segment \(\sigma _i:=[v_{i-1},v_{i}]\) has positive length \(\mathcal{L}(\sigma _i):=\Vert v_{i}-v_{i-1}\Vert \), for \(i=1,\ldots ,n\), and that two consecutive segments are never aligned, i.e., the vector product \(\sigma _{i}\times \sigma _{i+1}\ne 0_{{{\mathbb {R}}}^3}\) for each \(i=1,\ldots ,n-1\).
Remark 1
If \(\sigma _{i}\times \sigma _{i+1}= 0_{{{\mathbb {R}}}^3}\), we replace \(\sigma _{i+1}\) with the oriented segment \([v_{i},v_{j+1}]\), where j is the first index greater than i such that \(\sigma _{j}\times \sigma _{j+1}\ne 0_{{{\mathbb {R}}}^3}\). If \(\sigma _{j}\times \sigma _{j+1}= 0_{{{\mathbb {R}}}^3}\) for each \(j>i\), we set \(b_i=b_{i-1}\) in Definition (2.1).
Binormal vectors and torsion In the definition by Penna [11], the discrete unit binormal is the unit vector given at each interior vertex \(v_{i}\) of P by the formula:
The torsion of P is a function \({\varvec{\tau }}(\sigma _i)\) of the interior oriented segments \(\sigma _i\) defined as follows. Let \(i=2,\ldots ,n-1\). If the three segments \(\sigma _{i-1},\,\sigma _i,\,\sigma _{i+1}\) are coplanar, i.e., if the vector product \(b_{i-1}\times b_i=0_{{{\mathbb {R}}}^3}\), one sets \({\varvec{\tau }}(\sigma _i)=0\). Otherwise, one sets
where \(\theta _i\) denotes the angle between \(-\pi /2\) and \(\pi /2\) whose magnitude is the undirected angle between the binormals \(b_{i-1}\) and \(b_i\), and whose sign is equal to the sign of the scalar product between the linearly independent vectors \(b_{i-1}\times b_i\) and \(\sigma _i\). Penna then defined the total torsion of P through the sum:
In a similar way, we define the total absolute torsion of P by:
Remark 2
In the above definitions, one considers angles between unoriented osculating planes. In fact, it may happen that the planes \({\text {span}\,}(\sigma _{i-1},\,\sigma _i)\) and \({\text {span}\,}(\sigma _i,\,\sigma _{i+1})\) are almost parallel, but the directed angle between the binormal vectors \(b_i\) and \(b_{i+1}\) is equal to \(\pi -\varepsilon \) for some small \(\varepsilon >0\). However, one gets \(|\theta _i|=\varepsilon \). In facts, denoting by \(\bullet \) the scalar product, in general one obtains
An equivalent definition In the classical approach by [1, 8], one considers the tangent indicatrix of P, i.e., the polygonal \({{\mathfrak {t}}}_P\) in the Gauss sphere \({{\mathbb {S}}}^2\) obtained by letting \(t_i:=\sigma _i/\mathcal{L}(\sigma _i)\in {{\mathbb {S}}}^2\), for \(i=1,\ldots ,n\), and connecting with oriented geodesic arcs \(\gamma _i\) the consecutive points \(t_{i}\) and \(t_{i+1}\), for \(i=1,\ldots ,n-1\). Therefore, one has \(\mathcal{L}(\gamma _i)=d_{{{\mathbb {S}}}^2}(t_i,t_{i+1})\), where \(d_{{{\mathbb {S}}}^2}\) denotes the geodesic distance on \({{{\mathbb {S}}}^2}\).
Remark 3
The total curvature \(\mathrm{TC}(P)\) of P is the sum of the turning angles \(\alpha _i\) at the interior vertices of P, compare, e.g., [13], and it is therefore equal to the length of \({{\mathfrak {t}}}_P\), i.e.,
In particular, the arc-length parameterization \({{\mathfrak {t}}}_P:[0,C]\rightarrow {{\mathbb {S}}}^2\), where \(C:=\mathcal{L}({{\mathfrak {t}}}_P)=\mathrm{TC}(P)\), is Lipschitz continuous and piecewise smooth, with \(|{\dot{{{\mathfrak {t}}}}}_P|=1\) everywhere except to a finite number of points, the edges of the tangent indicatrix \({{\mathfrak {t}}}_P\), which correspond to the interior segments of the polygonal P.
Remark 4
With the previous assumptions on P, see Remark 1, the total absolute torsion of P can be equivalently defined through the formula:
where \(\widetilde{\theta }_i\in [0,\pi /2]\) is the shortest angle in \({{\mathbb {S}}}^2\) between the unoriented geodesic arcs \(\gamma _{i-1}\) and \(\gamma _i\) meeting at the edge \(t_i\) of \({{\mathfrak {t}}}_P\).
In fact, the geodesic arcs \(\gamma _{i}\) are unique, as the consecutive points \(t_i\) and \(t_{i+1}\) are not antipodal. Moreover, we have \(\widetilde{\theta }_i=0\) exactly when \(b_{i-1}\times b_i= 0_{{{\mathbb {R}}}^3}\), i.e., when \(b_{i-1}=b_i\) or \(b_{i-1}=-b_i\), so that \({\varvec{\tau }}(\sigma _i)=0\). Otherwise, we now check that \(\widetilde{\theta }_i=|\theta _i|\) for each \(i=1,\ldots ,n-1\). By similarity, and up to a rotation, we can assume that \(\sigma _i=(1,0,0)\). Setting \(\sigma _{i-1}=(\alpha _1,\beta _1,\delta _1)\) and \(\sigma _{i+1}=(\alpha _2,\beta _2,\delta _2)\), one has \(\sigma _{i-1}\times \sigma _i=(0,\delta _1,-\beta _1)\) and \(\sigma _{i}\times \sigma _{i+1}=(0,-\delta _2,\beta _2)\), so that
where \(\sigma _{i-1},\,\sigma _i,\,\sigma _{i+1}\) are not coplanar provided that \(b_{i-1}\times b_i\ne 0_{{{\mathbb {R}}}^3}\). Now, the shortest angle \(\widetilde{\theta }_i\) between the geodesic arcs \(\gamma _{i-1}\) and \(\gamma _i\) meeting at \(t_i\) is equal to the angle between the planes \(\pi _i^-\) and \(\pi _i^+\) spanned by the vectors \((\sigma _{i-1},\sigma _i)\) and \((\sigma _{i},\sigma _{i+1})\), respectively. But the corresponding unit normals are \(b_{i-1}\) and \(b_i\), whence \(\widetilde{\theta }_i=|\theta _i|\), where \(|\theta _i|\) is given by (2.2), as required.
Remark 5
In an analytical approach, it turns out that the total curvature and absolute torsion of a polygonal P can be seen as the total variation of mutually singular Radon measures \(\mu _P\) and \(\nu _P\) in \({{\mathbb {R}}}^3\). In fact, with the above notation we have:
where

\(\delta _{v_i}\) being the unit Dirac mass at the vertex \(v_i\) and  the restriction to the segment \(\sigma _i\) of the one-dimensional Hausdorff measure \(\mathcal{H}^1\).
the restriction to the segment \(\sigma _i\) of the one-dimensional Hausdorff measure \(\mathcal{H}^1\).
Remark 6
If the polygonal P is closed, i.e., \(v_0=v_n\), the above notation is modified in a straightforward way: the torsion is defined at all the n segments \(\sigma _i\), whereas the tangent indicatrix \({{\mathfrak {t}}}_P\) is a closed polygonal curve in \({{\mathbb {S}}}^2\), so that n angles are to be considered in both the equivalent definitions of \(\mathrm{TAT}(P)\).
The projective plane We have seen that the torsion is computed in terms of angles between undirected unit normal vectors \(b_i\) of \({{\mathbb {R}}}^3\), see Remarks 2 and 4. This implies that any reasonable notion of binormal (for non-smooth curves) naturally lives in the real projective plane \({\mathbb {RP}}^2\).
For this purpose, we recall that \({\mathbb {RP}}^2\) is defined by the quotient space \({\mathbb {RP}}^2:={{\mathbb {S}}}^2/\sim \), the equivalence relation being \(y\sim \widetilde{y}\iff y=\widetilde{y}\) or \(y=-\widetilde{y}\), and hence the elements of \({\mathbb {RP}}^2\) are denoted by [y]. The projective plane \({\mathbb {RP}}^2\) is naturally equipped with the induced metric
Similarly to \(({{{\mathbb {S}}}^2},d_{{{{\mathbb {S}}}^2}})\), the metric space \(({\mathbb {RP}}^2,d_{{\mathbb {RP}}^2})\) is complete, and the projection map \(\Pi :{{{\mathbb {S}}}^2}\rightarrow {\mathbb {RP}}^2\) such that \(\Pi (y):=[y]\) is continuous. Let \(u:A\rightarrow {\mathbb {RP}}^2\) be a continuous map defined on an open set \(A\subset {{\mathbb {R}}}^{n}\). If \(A\subset {{\mathbb {R}}}^{n}\) is simply connected, by the lifting theorem, see, e.g., [12, p. 34], there are exactly two continuous functions \(v_i:A\rightarrow {{{\mathbb {S}}}^2}\) such that \([v_i]:=\Pi \circ v_i=u\), for \(i=1,2\), with \(v_2(x)=-v_1(x)\) for every \(x\in A\).
The manifold \({\mathbb {RP}}^2\) is non-orientable. Moreover, the mapping \(g:{{{\mathbb {S}}}^2}\rightarrow {{\mathbb {R}}}^6\)
induces an embedding
Notice that \({\mathrm{RP}}^{2}\) is a non-orientable, smooth, compact, connected submanifold of \({{\mathbb {R}}}^6\) without boundary, such that \(|z|=\sqrt{2}/2\) for every \( z \in {\mathrm{RP}}^{2} \). Also, g maps the equator \({{{\mathbb {S}}}^2}\cap \{y^3=0\}\) into a circle C of radius 1/2, covered twice, with constant velocity equal to one. The circle C is a minimum length generator of the first homotopy group \( \pi _1({\mathrm{RP}}^{2})\simeq {{\mathbb{Z}}}_2 \). We also have \( \mathcal{H}^2({\mathrm{RP}}^{2})=2\pi \), where \(\mathcal{H}^2\) is the two-dimensional Hausdorff measure, compare, e.g., [9, Prop. 2.3]. Moreover, g is an isometric embedding. If, e.g., a map \(u:A\rightarrow {\mathrm{RP}}^{2}\) is given by \(u=g\circ v\) for some smooth map \(v:A\rightarrow {{{\mathbb {S}}}^2}\), we in fact have
for each partial derivative \(D_i\). Therefore, since \(\Vert v\Vert =1\) and \(2\,(v\bullet D_iv)=D_i\Vert v\Vert ^2=0\) a.e. for every i, we infer that \(\Vert Du\Vert =\Vert Dv\Vert \).
Polar curve Using the above notation, and following Fenchel’s approach [6], we now introduce the polar of the tangent indicatrix \({{\mathfrak {t}}}_P\), a curve supported in the projective plane \({\mathbb {RP}}^2\), in such a way that the length in \({\mathbb {RP}}^2\) of the polar is equal to the total absolute torsion \(\mathrm{TAT}(P)\).
For this purpose, we recall that the support of \({{\mathfrak {t}}}_P\) is the union of \(n-1\) geodesic arcs \(\gamma _i\), where \(\gamma _i\) has initial point \(t_i\) and end point \(t_{i+1}\), for \(i=1,\ldots ,n-1\). Since we assumed that consecutive segments of P are never aligned, each arc \(\gamma _i\) is non-trivial and well defined. According to Definition (2.1), it turns out that the discrete unit binormal \(b_i\in {{\mathbb {S}}}^2\) is the “north pole” corresponding to the great circle passing through \(\gamma _i\) and with the same orientation as \(\gamma _i\).
For any \(i=2,\ldots ,n-1\), we denote by \(\Gamma _i\) the geodesic arc in \({\mathbb {RP}}^2\) with initial point \([b_{i-1}]\) and end point \([b_{i}]\). Then, \(\Gamma _i\) is degenerate when \(b_{i-1}=\pm b_i\), i.e., when the three segments \(\sigma _{i-1},\,\sigma _i,\,\sigma _{i+1}\) are coplanar. We thus have \(\mathcal{L}_{{\mathbb {RP}}^2}(\Gamma _i)=\widetilde{\theta }_i=|\theta _i|\) for each i, and hence that
Also, for \(i<n-2\) the end point of \(\Gamma _i\) is equal to the initial point of \(\Gamma _{i+1}\). Finally, if \(\mathrm{TAT}(P)=0\), i.e., if the polygonal P is coplanar, all the arcs \(\Gamma _i\) degenerate to a point \([b]\in {\mathbb {RP}}^2\), which actually identifies the binormal to P.
Definition 1
Polar of the tangent indicatrix \({{\mathfrak {t}}}_P\) is the oriented curve in \({\mathbb {RP}}^2\) obtained by connecting the consecutive geodesic arcs \(\Gamma _i\), for \(i=2,\ldots ,n-1\).
Weak binormal Therefore, the polar of \({{\mathfrak {t}}}_P\) connects by geodesic arcs in \({\mathbb {RP}}^2\) the consecutive discrete binormals \([b_i]\) of the polygonal P, and its length is equal to the total absolute torsion \(\mathrm{TAT}(P)\) of P. In particular, it is a rectifiable curve. This property allows us to introduce a suitable weak notion of binormal.
Definition 2
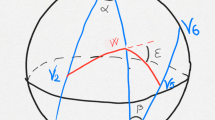
We denote binormal indicatrix of the polygonal P the arc-length parameterization \({{\mathfrak {b}}}_P\) of the polar in \({\mathbb {RP}}^2\) of the tangent indicatrix \({{\mathfrak {t}}}_P\) (see Fig. 1).
An example of a polygonal curve with tangent indicatrix moving as in the left figure. The weak binormal indicatrix moves as in the right figure. Since the weak binormal indicatrix lives in the projective space \({\mathbb {R}}{\mathbb {P}}^2\), in the figure we have drawn one of its two possible liftings into the sphere \({\mathbb {S}}^2\)
We thus have \({{\mathfrak {b}}}_P:[0,T]\rightarrow {\mathbb {RP}}^2\), where \(T:=\mathcal{L}_{{\mathbb {RP}}^2}({{\mathfrak {b}}}_P)=\mathrm{TAT}(P)\). Moreover, \({{\mathfrak {b}}}_P\) is Lipschitz continuous and piecewise smooth, with \(|{\dot{{{\mathfrak {b}}}}}_P|=1\) everywhere except to a finite number of points.
Remark 7
Differently from what happens for the length and the total curvature, the monotonicity formula fails to hold. More precisely, if \(P'\) is a polygonal inscribed in P, by the triangular inequality we have \(\mathcal{L}(P')\le \mathcal{L}(P)\) and \(\mathrm{TC}(P')\le \mathrm{TC}(P)\), but it may happen that \(\mathrm{TAT}(P')>\mathrm{TAT}(P)\). This is due to the fact that the total absolute torsion of a polygonal P can be computed as the sum of \(\min \{\theta _i,\pi -\theta _i\}\), where \(\theta _i\) is the turning angle of the tantrix \({{\mathfrak {t}}}_P\) at the i-th vertex.
Example 1
Let P be a polygonal made of six segments \(\sigma _i\), for \(i=1,\ldots ,6\), where the first three ones and the last three ones lay on two different planes \(\Pi _1\) and \(\Pi _2\). Then, the tantrix \({{\mathfrak {t}}}_P\) connects with geodesic arcs in \({{{\mathbb {S}}}^2}\) the consecutive points \(t_i:=\sigma _i/\mathcal{L}(\sigma _i)\), for \(i=1,\ldots , 6\), where the triplets \(t_1,t_2,t_3\) and \(t_4,t_5,t_6\) lay on two geodesic arcs, which are inscribed in the great circles corresponding to the vector spaces spanning the planes \(\Pi _1\) and \(\Pi _2\), respectively. If both the angles \(\alpha \) and \(\beta \) of \({{\mathfrak {t}}}_P\) at the points \(t_3\) and \(t_4\) are small, then \(\mathrm{TAT}(P)=\alpha +\beta \).
Let \(P'\) be the inscribed polygonal obtained by connecting the first point of \(\sigma _3\) with the last point of \(\sigma _4\). The tantrix \({{\mathfrak {t}}}_{P'}\) connects with geodesic arcs the consecutive points \(t_1,t_2,w,t_5,t_6\), where the point w lays in the minimal geodesic arc between \(t_3\) and \(t_4\). Now, assume that the turning angle \(\varepsilon \) of \({{\mathfrak {t}}}_{P'}\) at the point \(t_5\) satisfies \(\alpha<\varepsilon <\pi /2\), and that the two geodesic triangles with vertices \(t_2,t_3,w\) and \(w,t_4,t_5\) have the same area. By suitably choosing the position of the involved vertices, and by using the Gauss-Bonnet theorem in the computation, it turns out that \(\mathrm{TAT}(P')-\mathrm{TAT}(P)=2(\varepsilon -\alpha )>0\).
Remark 8
For future use, we finally check the following inequality:
In fact, for closed polygonals in the Gauss sphere such that three consecutive vertices never lie on the same geodesic, it turns out that polarity is an involutive transformation. Therefore, the polar of (a lifting of) the binormal indicatrix \({{\mathfrak {b}}}_P\) agrees with the polygonal in \({{{\mathbb {S}}}^2}\) obtained by replacing any chain of consecutive geodesic segments \(\gamma _i\) of \({{\mathfrak {t}}}_P\) which lay on some maximum circle, with a single geodesic arc obtained by connecting the end points of the chain. In particular, the total curvature of \({{\mathfrak {b}}}_P\) in \({\mathbb {RP}}^2\) is bounded by the length of \({{\mathfrak {t}}}_P\).
3 Curves with finite total absolute torsion
In this section, we collect some notation concerning the total absolute torsion of curves in \({{\mathbb {R}}}^3\). We thus let c be a curve in \({{\mathbb {R}}}^3\) parameterized by \(c:I\rightarrow {{\mathbb {R}}}^3\), where \(I:=[a,b]\).
Any polygonal curve P inscribed in c, say \(P \ll c\), is obtained by choosing a finite partition \(\mathcal{D}:=\{a=\lambda _0<\lambda _1<\cdots<\lambda _{n-1}<\lambda _{n}=b\}\) of I, say \(P=P(\mathcal{D})\), and letting \(P:I\rightarrow {{\mathbb {R}}}^3\) such that \(P(\lambda _i)=v_i:=c(\lambda _i)\) for \(i=0,\ldots ,n\), and \(P(\lambda )\) is affine on each interval \(I_i:=[\lambda _{i-1},\lambda _i]\) of the partition, so that \(P(I_i)=\sigma _i=[v_{i-1},v_i]\). The mesh of the polygonal is defined by \(\mathop {\mathrm{mesh}}\nolimits P:=\sup \{\mathcal{L}(\sigma _i)\mid i=1,\ldots ,n \}\).
The length \(\mathcal{L}(c)\) and the total curvature \(\mathrm{TC}(c)\) are, respectively, defined through the formulas:
Let c be a curve in \({{\mathbb {R}}}^3\) with finite total curvature, i.e., \(\mathrm{TC}(c)<\infty \). Then it is rectifiable, too, see, e.g., [13]. Assume that \(c:[0,L]\rightarrow {{\mathbb {R}}}^3\) is its arc-length parameterization, whence \(L=\mathcal{L}(c)<\infty \). Since c is a Lipschitz-continuous function, by Rademacher’s theorem it is differentiable a.e. in [0, L].
As a consequence, the tangent indicatrix \({{\mathfrak {t}}}:[0,L]\rightarrow {{\mathbb {S}}}^2\) is well defined by setting \({{\mathfrak {t}}}(s):=\dot{c}(s)\) for a.e. \(s\in [0,L]\). It is well-known that \({{\mathfrak {t}}}\) is a function with bounded variation (see [10] for the notation on BV functions) and moreover that its essential variation in \({{\mathbb {S}}}^2\) agrees with the total curvature of c, i.e., \(\mathop {\mathrm{Var}}\nolimits _{{{\mathbb {S}}}^2}({{\mathfrak {t}}})=\mathrm{TC}(c)\). Notice that \({{\mathfrak {t}}}\) is not continuous, as can be seen by taking a piecewise \(C^1\) curve: a discontinuity point of \({{\mathfrak {t}}}\) appears at any edge point of c.
Moreover, by taking any sequence \(\{P_h\}\) of inscribed polygonal curves such that \(\mathop {\mathrm{mesh}}\nolimits P_h\rightarrow 0\), on account of Remark 7, and by using a continuity argument, compare [13], one infers that \(\mathcal{L}(P_h)\rightarrow \mathcal{L}(c)\) and \(\mathrm{TC}(P_h)\rightarrow \mathrm{TC}(c)\).
Total absolute torsion Due to the lack of monotonicity described in Example 1, we define the total absolute torsion \(\mathrm{TAT}(c)\) of c by means of the approach due to Alexandrov and Reshetnyak [1].
For this purpose, we recall that the modulus \(\mu _c(P)\) of a polygonal P inscribed in c is the maximum of the diameter of the arcs of c determined by the consecutive vertices in P.
We also notice that if c is a polygonal curve itself, there exists \(\varepsilon >0\) such that any polygonal P inscribed in c and with modulus \(\mu _c(P)<\varepsilon \) satisfies \({{\mathfrak {t}}}_P={{\mathfrak {t}}}_c\), whence \({{\mathfrak {b}}}_P={{\mathfrak {b}}}_c\) and definitely we get \(\mathrm{TAT}(P)=\mathrm{TAT}(c)\). It suffices indeed to take \(\varepsilon \) lower than half of the mesh of the polygonal c, so that in every segment of c there are at least two vertices of P.
The above facts motivate the following definition:
Therefore, if \(\mathrm{TAT}(c)<\infty \), for any sequence \(\{P_h\}\) of polygonal curves inscribed in c and satisfying \(\mu _c(P_h)\rightarrow 0\), one has \(\sup _h\mathrm{TAT}(P_h)<\infty \), and one can find an optimal sequence as above in such a way that \(\mathrm{TAT}(P_h)\rightarrow \mathrm{TAT}(c)\).
Let now c be a curve with finite total curvature and total absolute torsion. In the next section, we shall see that it is possible to give a suitable weak notion of binormal indicatrix, a curve \({{\mathfrak {b}}}_c\) in \({\mathbb {RP}}^2\) such that its length agrees with the total absolute torsion \(\mathrm{TAT}(c)\), see (4.1).
As a consequence of Theorem 1, see Remark 11, we also obtain:
Proposition 1
Let c be a curve in \({{\mathbb {R}}}^3\) with both finite total curvature \(\mathrm{TC}(c)\) and total absolute torsion \(\mathrm{TAT}(c)\). Then for any sequence \(\{P_h\}\) of inscribed polygonal curves such that \(\mu _c(P_h)\rightarrow 0\), one has \(\mathrm{TAT}(P_h)\rightarrow \mathrm{TAT}(c)\).
For this purpose, we first discuss here the regular case, i.e., when curvature and torsion are defined as in the usual way.
The smooth case Let c be a smooth regular curve in \({{\mathbb {R}}}^3\) defined through the arc-length parameterization (so that \(|\dot{c}|=1\) a.e.). Assuming \(\ddot{c}\ne 0\) everywhere, and letting \({{\mathfrak {t}}}:=\dot{c}\), \({{\mathfrak {n}}}:={\dot{{{\mathfrak {t}}}}}/|{\dot{{{\mathfrak {t}}}}}|\), \(\mathbf{{k}}:=|{\dot{{{\mathfrak {t}}}}}|\), \({{\mathfrak {b}}}:={{\mathfrak {t}}}\times {{\mathfrak {n}}}\), the classical Frenet–Serret formulas for the spherical frame \(({{\mathfrak {t}}},{{\mathfrak {n}}},{{\mathfrak {b}}})\) of c give:
where \(\mathbf{{k}}\) is the (positive) curvature and \({\varvec{\tau }}\) the torsion of the curve.
By Proposition 1, and on account of the density result from [11, Prop. 4], one readily obtains:
Corollary 1
If c is a smooth regular curve in \({{\mathbb {R}}}^3\) , then
Remark 9
Notice that a rectifiable curve may have unbounded total curvature but zero torsion (just consider a planar curve). Conversely, by taking \(s\in [0,1]\) and letting \(\mathbf{{k}}(s)\equiv 1\) and \({\varvec{\tau }}(s)=(1-s)^{-1}\), solutions to the Frenet–Serret system (3.2) are rectifiable curves c such that \(\int _c \mathbf{{k}}\,ds=1\) but \(\int _c|{\varvec{\tau }}|\,ds=+\infty \).
As the following example shows, the (absolute value of the) torsion may be seen as the curvature of the tantrix, when computed in the sense of the spherical geometry.
Example 2
Given \(R>0\) and \(K\ge 0\), we let \(c:[-L/2,L/2]\rightarrow {{\mathbb {R}}}^3\) denote the helicoidal curve
where we denote \(v:=(R^2+(K/2\pi )^2)^{1/2}\) and choose \(L:=2\pi v\), so that \(|\dot{c}|\equiv 1\) and the length \(\mathcal{L}(c)=L\). Moreover, \(c(\pm L/2)=(\pm R,0,\pm K/2)\), and \(c(0)=(R,0,0)\). We thus have
so that both curvature and torsion are constant, \(\mathbf{{k}}\equiv Rv^{-2}\), \({\varvec{\tau }}\equiv v^{-2}(K/2\pi )\). Therefore, the integral of the curvature and of the torsion of c are readily obtained:
We now compute the spherical curvature \(\mathbf{{k}}_{{{\mathbb {S}}}^2}({{\mathfrak {t}}})\) of the tantrix \({{\mathfrak {t}}}\), a closed curve embedded in the Gauss sphere \({{\mathbb {S}}}^2\) and parameterizing (when \(K>0\)) a small circle whose radius depends on R and K. We consider a sequence of (strongly converging) polygonal curves \(\{{{\mathfrak {t}}}_n\}\) in \({{\mathbb {S}}}^2\) inscribed in the tantrix \({{\mathfrak {t}}}\). The total curvature of \({{\mathfrak {t}}}_n\) is equal to the sum of the width in \({{\mathbb {S}}}^2\) of the angles between consecutive segments. When \(n\rightarrow \infty \), by uniform convergence we obtain the total curvature of \({{\mathfrak {t}}}\) in \({{\mathbb {S}}}^2\). Actually, it agrees with the integral of the absolute torsion of c, i.e.,
To this purpose, for each \(n\in {{\mathbb {N}}}^+\), we let \(t_n(i):={{\mathfrak {t}}}(s_i)\), where \(s_i=(L/n)i\) and \(i\in {{\mathbb {Z}}}\cap [-n,n]\), and we consider the closed spherical polygonal generated by the consecutive points \(t_n(i)\in {{\mathbb {S}}}^2\).
The turning angle in \({{\mathbb {S}}}^2\) of two consecutive geodesic segments \(t_n(i-1)t_n(i)\) and \(t_n(i)t_n(i+1)\) agrees with the angle between the two planes in \({{\mathbb {R}}}^3\) spanned by \(0_{{{\mathbb {R}}}^3}\) and the end points of the above segments, i.e., between the normals \(t_n(i-1)\times t_n(i)\) and \(t_n(i)\times t_n(i+1)\). By symmetry, such an angle \(\theta _n\) does not depend on the choice of i, and will be computed at \(i=0\). The total spherical curvature of the polygonal being equal to \(n\cdot \theta _n\), we check:
In fact, in correspondence to the middle point we have
so that we get
Denoting for simplicity
and setting \(N^\pm _n:=\pm (t_n(0)\times t_n(\pm 1))/M_n\), we compute
By symmetry, the turning angle of the geodesic arcs connecting two consecutive points \(t_n(i)\) does not depend on the choice of i and is equal to
Since for \(n\rightarrow \infty \) we have \(2(1-\cos (2\pi /n))\sim (2\pi /n)^2\) and \(\sin (2\pi /n)\sim 2\pi /n\), we get \(M_n\sim R (2\pi /n) v\) and finally \(n\cdot \theta _n\sim n\,\Vert N^+_n \times N^-_n\Vert \rightarrow K/v\) where, we recall, \(\int _c|{\varvec{\tau }}|\,ds =K/v\).
Remark 10
In the previous example, we have considered a sequence \(\{{{\mathfrak {t}}}_n\}\) of polygonal curves in \({{\mathbb {S}}}^2\) inscribed in the tantrix \({{\mathfrak {t}}}\) of c and converging to \({{\mathfrak {t}}}\) in the sense of the Hausdorff distance. In general, each \({{\mathfrak {t}}}_n\) is not the tangent indicatrix of a polygonal inscribed in c. However, the total spherical curvature \(n\cdot \theta _n\) of \({{\mathfrak {t}}}_n\) clearly agrees with the length in \({\mathbb {RP}}^2\) of the polar of \({{\mathfrak {t}}}_n\), which is constructed as in Sect. 2, see Definition 1.
Now, one may similarly consider a sequence \(\{P_h\}\) of polygonals inscribed in c, each one made of h segments with the same length, so that \(\mathop {\mathrm{mesh}}\nolimits P_h\rightarrow 0\). The total absolute torsion \(\mathrm{TAT}(P_h)\) of \(P_h\) agrees with the length in \({\mathbb {RP}}^2\) of the binormal indicatrix \({{\mathfrak {b}}}_{P_h}\), see Definition 2. By means of a similar computation (that we shall omit), one can show that \(\mathcal{L}_{{\mathbb {RP}}^2}({{\mathfrak {b}}}_{P_h})\rightarrow K/v\) as \(h\rightarrow \infty \), in accordance with the formula in Corollary 1.
4 Weak binormal of a non-smooth curve
In this section, we consider rectifiable curves c in \({{\mathbb {R}}}^3\) with finite total curvature \(\mathrm{TC}(c)\) and finite (and nonzero) total absolute torsion \(\mathrm{TAT}(c)\). Using a density approach by polygonals, in Theorem 1 we show that a weak notion of binormal indicatrix of c is well defined. For smooth curves, we shall recover the classical binormal, see Theorem 2 and Remark 12. Finally, similar properties concerning the tangent indicatrix are discussed in Propositions 2 and 3.
More precisely, we shall define a Lipschitz-continuous function \({{\mathfrak {b}}}_c:[0,T]\rightarrow {\mathbb {RP}}^2\), where \(T=\mathrm{TAT}(c)\), satisfying \(|{\dot{{{\mathfrak {b}}}}}_c|=1\) a.e. in [0, T]. Therefore, \({{\mathfrak {b}}}_c\) is a curve in \({\mathbb {RP}}^2\) with length equal to the total absolute torsion of c, i.e.,
This is the content of our first main result:
Theorem 1
Let c be a curve in \({{\mathbb {R}}}^3\) with finite total curvature \(\mathrm{TC}(c)\) and finite (and nonzero) total absolute torsion \(T:=\mathrm{TAT}(c)\). There exists a rectifiable curve \({{\mathfrak {b}}}_c:[0,T]\rightarrow {\mathbb {RP}}^2\) parameterized by arc length, so that \(\mathcal{L}_{{\mathbb {RP}}^2}({{\mathfrak {b}}}_c)=\mathrm{TAT}(c)\), satisfying the following property. For any sequence \(\{P_h\}\) of inscribed polygonal curves, let \(b_h:[0,T]\rightarrow {\mathbb {RP}}^2\) denote for each h the parameterization with constant velocity of the binormal indicatrix \({{\mathfrak {b}}}_{P_h}\) of \(P_h\) , see Definition 2. If \(\mu _c(P_h)\rightarrow 0\), then \(b_h\rightarrow {{\mathfrak {b}}}_c\) uniformly on [0, T] and \(\mathcal{L}_{{\mathbb {RP}}^2}(b_h)\rightarrow \mathcal{L}_{{\mathbb {RP}}^2}({{\mathfrak {b}}}_c)\).
Remark 11
Recalling that \(\mathcal{L}_{{\mathbb {RP}}^2}(b_h)=\mathrm{TAT}(P_h)\), Proposition 1 readily follows.
Furthermore, we shall see that if c is smooth in the sense of the previous section (so that the Frenet–Serret formulas (3.2) hold), the binormal \({{\mathfrak {b}}}(s)\) of c agrees with the value of a suitable lifting of the weak binormal \({{\mathfrak {b}}}_c\) in \({{\mathbb {S}}}^2\), when computed at the expected point.
Theorem 2
Let \(c:[0,L]\rightarrow {{\mathbb {R}}}^3\) be a rectifiable curve of class \(C^3\) parameterized in arc length, so that \(L=\mathcal{L}(c)\). Assume that \(\ddot{c}(s)\ne 0\) for each \(s\in [0,L]\), so that the spherical frame \(({{\mathfrak {t}}},{{\mathfrak {n}}},{{\mathfrak {b}}})\) of c is well defined. Let \({{\mathfrak {b}}}_c:[0,T]\rightarrow {\mathbb {RP}}^2\) be the rectifiable curve in \({\mathbb {RP}}^2\) defined in Theorem 1, so that \(T=\mathrm{TAT}(c)\). Then, for each \(s\in ]0,L[\) there exists \(t(s)\in [0,T]\) such that
for a unique lifting \(\widetilde{{\mathfrak {b}}}_c\) of \({{\mathfrak {b}}}_c\) in \({{{\mathbb {S}}}^2}\). Moreover, t(s) is equal to the total absolute torsion \(\mathrm{TAT}(c_{\vert [0,s]})\) of the curve \(c_{\vert [0,s]}:[0,s]\rightarrow {{\mathbb {R}}}^3\). In particular, we have:
where \({\varvec{\tau }}(\lambda )\) is the torsion of the curve c at the point \(c(\lambda )\).
Remark 12
Notice that if the torsion \({\varvec{\tau }}\) of c (almost) never vanishes, the function \(t(s):[0,L]\rightarrow [0,T]\) in equation (4.2) is strictly increasing, and its inverse \(s(t):[0,T]\rightarrow [0,L]\) gives
Therefore, in this case, the weak binormal \({{\mathfrak {b}}}_c\) in \({\mathbb {RP}}^2\), when suitably lifted to \({{{\mathbb {S}}}^2}\), agrees with the arc length parameterization of the binormal \({{\mathfrak {b}}}\) of c.
Tangent indicatrix Similarly to Theorems 1 and 2, we also obtain the following properties concerning the tantrix.
Proposition 2
Let c be a curve in \({{\mathbb {R}}}^3\) with finite total curvature \(C:=\mathrm{TC}(c)\) and with no points of return. Then, there exists a rectifiable curve \({{\mathfrak {t}}}_c:[0,C]\rightarrow {{{\mathbb {S}}}^2}\), parameterized by arc length, so that \(\mathcal{L}_{{{{\mathbb {S}}}^2}}({{\mathfrak {t}}}_c)=\mathrm{TC}(c)\), satisfying the following property. For any sequence \(\{P_h\}\) of inscribed polygonal curves such that \(\mathop {\mathrm{mesh}}\nolimits P_h\rightarrow 0\), denoting by \(t_h:[0,C]\rightarrow {{{\mathbb {S}}}^2}\) the parameterization with constant velocity of the tangent indicatrix \({{\mathfrak {t}}}_{P_h}\) of \(P_h\), then \(t_h\rightarrow {{\mathfrak {t}}}_c\) uniformly on [0, C] and \(\mathcal{L}_{{{{\mathbb {S}}}^2}}(t_h)\rightarrow \mathcal{L}_{{{{\mathbb {S}}}^2}}({{\mathfrak {t}}}_c)\).
Remark 13
If c has points of return, i.e., if, e.g., for some \(s\in ]0,L[\) we have \({{\mathfrak {t}}}(s-)=-{{\mathfrak {t}}}(s+)\), then the curve \({{\mathfrak {t}}}_c\) is uniquely determined up to the choice of the geodesic arc in \({{{\mathbb {S}}}^2}\) connecting \({{\mathfrak {t}}}(s-)\) and \({{\mathfrak {t}}}(s+)\).
Proposition 3
Let \(c:[0,L]\rightarrow {{\mathbb {R}}}^3\) be a curve of class \(C^2\) parameterized in arc length, so that \(L=\mathcal{L}(c)\), and let \({{\mathfrak {t}}}_c:[0,C]\rightarrow {{{\mathbb {S}}}^2}\) be the rectifiable curve in \({{{\mathbb {S}}}^2}\) defined in Proposition 2, so that \(C=\mathrm{TC}(c)\). Then, for each \(s\in ]0,L[\) there exists \(k(s)\in [0,C]\) such that the tangent indicatrix \({{\mathfrak {t}}}:=\dot{c}\) satisfies
Moreover, k(s) is equal to the total curvature \(\mathrm{TC}(c_{\vert [0,s]})\) of the curve \(c_{\vert [0,s]}:[0,s]\rightarrow {{\mathbb {R}}}^3\), whence:
where \(\mathbf{{k}}(\lambda ):=\Vert \ddot{c}(\lambda )\Vert \) is the curvature of c at the point \(c(\lambda )\).
Remark 14
As before, if the curvature \(\mathbf{{k}}\) of c (almost) never vanishes, the function \(k(s):[0,L]\rightarrow [0,C]\) in equation (4.3) is strictly increasing, and its inverse \(s(k):[0,C]\rightarrow [0,L]\) gives
Proof
We now give the proofs of the previous results.
Proof of Theorem 1
It is divided into four steps.
Step 1. Choose an optimal sequence \(\{P_h\}\) of polygonal curves inscribed in c such that \(\mu _c(P_h)\rightarrow 0\) and \(T_h\rightarrow T\), where \(T_h:=\mathrm{TAT}(P_h)\) and \(T=\mathrm{TAT}(P)\). For h large enough so that \(T_h>0\), the binormal indicatrix of \(P_h\) has been defined by the arc-length parameterization \({{\mathfrak {b}}}_{P_h}:[0,T_h]\rightarrow {\mathbb {RP}}^2\) of the curve in \({\mathbb {RP}}^2\) given by the polar of the tangent indicatrix \({{\mathfrak {t}}}_{P_h}\), see Definition 2. Whence it is a rectifiable curve such that \(\mathcal{L}_{{\mathbb {RP}}^2}({{\mathfrak {b}}}_{P_h})=T_h\) and \(\Vert {\dot{{{\mathfrak {b}}}}}_{P_h}\Vert =1\) a.e. on \([0,T_h]\).
Define \(b_h:[0,T]\rightarrow {\mathbb {RP}}^2\) by \(b_h(s):={{\mathfrak {b}}}_{P_h}((T_h/T)s)\), so that \(\Vert \dot{b}_h(s)\Vert = T_h/T\) a.e., where \(T_h/T\rightarrow 1\). By Ascoli-Arzela’s theorem, we can find a subsequence \(\{b_{h_k}\}\) that uniformly converges in [0, T] to some Lipschitz-continuous function \(b:[0,T]\rightarrow {\mathbb {RP}}^2\), and we denote \(b={{\mathfrak {b}}}_c\).
Step 2. We claim that \(\dot{b}_h\rightarrow \dot{b}={\dot{{{\mathfrak {b}}}}}_c\) strongly in \(L^1\). As a consequence, we deduce that \(\Vert \dot{{\mathfrak {b}}}_c\Vert =1\) a.e. on [0, T], and hence that
In order to prove the claim, recalling from Sect. 2 that \(\widetilde{g}:{\mathbb{RP}}^2\rightarrow {\mathrm{RP}}^{2}\subset {{\mathbb{R}}}^6\) is the isometric embedding of the projective plane, we shall denote here \(\underline{f}:=\widetilde{g}\circ f\), for any function f with values in \({\mathbb {RP}}^2\), and we consider the tantrix \(\tau _{h}\) of the curve \({\underline{b_h}}:[0,T]\rightarrow {\mathrm{RP}}^{2}\), i.e., \(\tau _{h}(s)=\dot{\underline{b_h}}(s)/\Vert \dot{\underline{b_h}}(s)\Vert \). We have \(\mathcal{L}_{{\mathbb {RP}}^2}(b_h)=\mathrm{TAT}(P_h)\) and \(\Vert \dot{\underline{b_h}}(s)\Vert =T_h/T\), whereas by Remark 8
Therefore, it turns out that the essential total variation of \(\tau _h\) in \({\mathrm{RP}}^{2}\) is lower than the sum \(\mathrm{TC}(P_h)+\mathrm{TAT}(P_h)\). We thus get:
As a consequence, by compactness, a subsequence of \(\{\dot{\underline{b_h}}\}\) converges weakly-* in the \(\mathop {\mathrm{BV}}\nolimits \)-sense to some \(\mathop {\mathrm{BV}}\nolimits \)-function \(v:[0,T]\rightarrow {\mathrm{RP}}^{2}\).
We show that \(v(s)=\dot{\underline{b}}(s)\) for a.e. \(s\in [0,T]\). This yields that the sequence \(\{\dot{b}_{h}\}\) converges strongly in \(L^1\) (and hence a.e. on [0, T]) to the function \(\dot{b}\).
In fact, using that by Lipschitz-continuity
and setting
by the weak-* \(\mathop {\mathrm{BV}}\nolimits \) convergence \(\dot{\underline{b_h}}\rightharpoonup v\), which implies the strong \(L^1\) convergence, we have \({\underline{b_h}}\rightarrow V\) in \(L^\infty \), hence \(\dot{\underline{b_h}}\rightarrow \dot{V}=v\) a.e. on [0, T]. But we already know that \({\underline{b_h}}\rightarrow {\underline{b}}\) in \(L^\infty \), thus we get \(v=\dot{\underline{b}}\).
Step 3. Let now \(\{\widetilde{P}_h\}\) denote any sequence of polygonal curves inscribed in c such that \(\mu _c(\widetilde{P}_h)\rightarrow 0\). We claim that possibly passing to a subsequence, the binormals \({{\mathfrak {b}}}_{\widetilde{P}_h}\) converge uniformly (up to reparameterizations) to the curve \({{\mathfrak {b}}}_c\).
In fact, we recall that the polar of the tantrix \({{\mathfrak {t}}}_{P}\) to a polygonal curve P is defined in terms of vector products of couples of consecutive points of its geodesic segments, the vector product being continuous. Moreover, the Frechét distance (see, e.g., [13, Sec. 1]) between the two sequences \(\{{{\mathfrak {t}}}_{P_h}\}\) and \(\{{{\mathfrak {t}}}_{\widetilde{P}_h}\}\) goes to zero. This property follows from the equiboundedness of the total curvatures. Whence, the polars of \({{\mathfrak {t}}}_{P_h}\) and of \({{\mathfrak {t}}}_{\widetilde{P}_h}\) must converge uniformly (up to reparameterizations) to the same limit function. Therefore, the sequence \({{\mathfrak {b}}}_{\widetilde{P}_h}\) converges in the Frechét distance to the curve \({{\mathfrak {b}}}_c\) obtained in Step 1.
Step 4. Now, if \(\{\widetilde{P}_h\}\) is the (not relabeled) subsequence obtained in Step 3, by repeating the argument in Step 1 we infer that the limit function \(b={{\mathfrak {b}}}_c\) is unique. As a consequence, a contradiction argument yields that all the sequence \(\{b_{h}\}\) uniformly converges to \({{\mathfrak {b}}}_c\) and that the limit curve \({{\mathfrak {b}}}_c\) does not depend on the choice of the sequence \(\{P_h\}\) of inscribed polygonals satisfying \(\mu _c(P_h)\rightarrow 0\). Therefore, the curve \({{\mathfrak {b}}}_c\) is identified by c. Arguing as in Step 2, we finally infer that \(\mathcal{L}_{{\mathbb {RP}}^2}(b_h)\rightarrow \mathcal{L}_{{\mathbb {RP}}^2}({{\mathfrak {b}}}_c)\), as required. \(\square \)
Proof of Theorem 2
For any given \(s\in ]0,L[\), since \(\Vert \dot{c}(s)\Vert =1\) and \(\ddot{c}(s)\ne 0\), the binormal is defined by \({{\mathfrak {b}}}(s):={{\mathfrak {t}}}(s)\times {{\mathfrak {n}}}(s)\), with \({{\mathfrak {t}}}(s):=\dot{c}(s)\) and \({{\mathfrak {n}}}(s):=\ddot{c}(s)/\Vert \ddot{c}(s)\Vert \), so that \(\dot{c}(s)\times \ddot{c}(s)\ne 0\) and
We thus may and do choose a sequence of polygonals \(\{P_h\}\) inscribed in c such that \(\mu _c(P_h)\rightarrow 0\) and (with the notation from Sect. 2 for \(P=P_h\)) the following properties hold for any \(h\in {{\mathbb {N}}}^+\) large enough :
-
(1)
the four points \(v_{i-2}=c(s-2h)\), \(v_{i-1}=c(s-h)\), \(v_i=c(s+h)\), \(v_{i+1}=c(s+2h)\) are consecutive (and interior) vertices of \(P_h\);
-
(2)
the three segments \(\sigma _{i-1}=v_{i-1}-v_{i-2}\), \(\sigma _i=v_{i}-v_{i-1}\), \(\sigma _{i+1}=v_{i+1}-v_{i}\) satisfy \(\sigma _{i-1}\times \sigma _i\ne 0_{{{\mathbb {R}}}^3}\) and \(\sigma _{i}\times \sigma _{i+1}\ne 0_{{{\mathbb {R}}}^3}\).
By taking the second-order expansions of c at s, we get
and hence
On account of (2.1), we thus get for any h large:
so that in particular \(b_i(h)\rightarrow -{{\mathfrak {b}}}(s)\) as \(h\rightarrow \infty \).
Now, consider the polygonal \(P_h(s)\) given by the union of the segments \(\sigma _1,\ldots ,\sigma _{i-1},\sigma _i\) of \(P_h\). It turns out that the total absolute torsion of \(P_h(s)\) satisfies \(\mathrm{TAT}(P_h(s))=t_h(s)\) for some number \(t_h(s)\in [0,\mathrm{TAT}(P_h)]\). Since \(\mathrm{TAT}(P_h)\rightarrow \mathrm{TAT}(c)\in {{\mathbb {R}}}^+\), possibly passing to a subsequence, the sequence \(\{t_h(s)\}\) converges to some number \(t(s)\in [0,T]\). By Theorem 1, we thus infer that \(b_i(h)\rightarrow {{\mathfrak {b}}}_c(t(s))\) as \(h\rightarrow \infty \), whence we obtain \({{\mathfrak {b}}}(s)=-{{\mathfrak {b}}}_c(t(s))\).
Moreover, since both the end points of the segment \(\sigma _i\) of \(P_h\) converge to c(s) as \(h\rightarrow \infty \), whereas \(\mu _c(P_h)\rightarrow 0\), by Proposition 1 we deduce that \(\mathrm{TAT}(P_h(s))\rightarrow \mathrm{TAT}(c_{\vert [0,s]})\), which yields the equality \(t(s)=\mathrm{TAT}(c_{\vert [0,s]})\). Since by smoothness of the curve c
recalling that \({\dot{{{\mathfrak {b}}}}}(\lambda )=-{\varvec{\tau }}(\lambda )\,{{\mathfrak {n}}}(\lambda )\), we finally obtain the equality (4.2). \(\square \)
Proof of Proposition 2
Following the proof of Theorem 1, we choose h large enough so that \(C_h:=\mathrm{TC}(P_h)>0\), and we denote by \({{\mathfrak {t}}}_{P_h}:[0,C_h]\rightarrow {{{\mathbb {S}}}^2}\) the arc-length parameterization of the tantrix \({{\mathfrak {t}}}_{P_h}\), so that \(C_h=\mathcal{L}_{{{{\mathbb {S}}}^2}}({{\mathfrak {t}}}_{P_h})\) and \(\Vert {\dot{{{\mathfrak {t}}}}}_{P_h}\Vert =1\) a.e. on \([0,C_h]\). Since \(\mathop {\mathrm{mesh}}\nolimits P_h\rightarrow 0\), we have \(C_h\rightarrow C^-\), where \(C:=\mathrm{TC}(c)\). Setting \(t_h:[0,C]\rightarrow {{{\mathbb {S}}}^2}\) by \(t_h(s):={{\mathfrak {t}}}_{P_h}((C_h/C)s)\), as in Step 1 we can find a subsequence \(\{t_{h_k}\}\) that uniformly converges in [0, C] to some Lipschitz-continuous function \(t:[0,C]\rightarrow {{{\mathbb {S}}}^2}\). Moreover, as in Steps 3-4 we deduce that t does not depend on the choice of \(\{P_h\}\), and that all the sequence \(\{t_{h}\}\) uniformly converges to t, so that the curve \({{\mathfrak {t}}}_c:=t\) is identified by c.
We claim that \(\mathcal{L}_{{{\mathbb {S}}}^2}({{\mathfrak {t}}}_c)=C\). As a consequence, since the equality \(\Vert \dot{t}_h\Vert =C_h/C\) a.e. yields that \(\Vert \dot{{\mathfrak {t}}}_c\Vert \le 1\) a.e., whereas \(\mathcal{L}_{{{\mathbb {S}}}^2}({{\mathfrak {t}}}_c)=\int _0^C \Vert {\dot{{{\mathfrak {t}}}}}_c(s)\Vert \,ds\), we infer that \(\Vert {\dot{{{\mathfrak {t}}}}}_c\Vert =1\) a.e., as required.
It remains to prove the claim. Since \({{\mathfrak {t}}}=\dot{c}\) is a function of bounded variation, for each h we can find a partition \(\mathcal{D}_h\) of [0, L] in \(2^h\) intervals \(I^h_i=[s^h_{i-1},s^h_i]\), for \(i=1,\ldots ,2^h\), satisfying the following properties:
-
(1)
\(\mathcal{D}_{h+1}\) is a refinement of \(\mathcal{D}_h\), and \(\mathop {\mathrm{mesh}}\nolimits \mathcal{D}_h\rightarrow 0\) as \(h\rightarrow \infty \) ;
-
(2)
for each i, the end points of the intervals \(I^h_i\) are Lebesgue points of \({{\mathfrak {t}}}\), with Lebesgue values \({{\mathfrak {t}}}(s^h_{i-1})\) and \({{\mathfrak {t}}}(s^h_i)\) ;
-
(3)
if \(f_h:[0,L]\rightarrow {{{\mathbb {S}}}^2}\) is the piecewise constant function with \(f_h(s)={{\mathfrak {t}}}(s^h_i)\) for each \(s\in ]s^h_{i-1},s^h_i[\) and each i, then \(\mathop {\mathrm{Var}}\nolimits _{{{\mathbb {R}}}^3}(f_h)\rightarrow \mathop {\mathrm{Var}}\nolimits _{{{\mathbb {R}}}^3}({{\mathfrak {t}}})\) .
Let now \(\gamma _h\) denote the spherical polygonal in \({{{\mathbb {S}}}^2}\) obtained by connecting the consecutive vertices \({{\mathfrak {t}}}(s^h_i)\). Then, \(\mathcal{L}_{{{\mathbb {S}}}^2}(\gamma _h)=\mathop {\mathrm{Var}}\nolimits _{{{\mathbb {S}}}^2}(\gamma _h)\rightarrow \mathop {\mathrm{Var}}\nolimits _{{{\mathbb {S}}}^2}({{\mathfrak {t}}})=\mathrm{TC}(c)\). On the other hand, the Frechét distance between the two sequences \(\{{{\mathfrak {t}}}_{P_h}\}\) and \(\{\gamma _h\}\) goes to zero. Therefore, \(\gamma _h\) converges to \({{\mathfrak {t}}}_c\) in the Frechét distance. As a consequence, each polygonal \(\gamma _h\) is inscribed in \({{\mathfrak {t}}}_c\), which yields that \(\mathcal{L}_{{{\mathbb {S}}}^2}(\gamma _h)\rightarrow \mathcal{L}_{{{\mathbb {S}}}^2}({{\mathfrak {t}}}_c)\), and hence that \(\mathcal{L}_{{{\mathbb {S}}}^2}({{\mathfrak {t}}}_c)=\mathrm{TC}(c)\), which completes the proof. \(\square \)
Remark 15
It turns out that the essential total variation in \({{{\mathbb {S}}}^2}\) of the tantrix \(\tau _h\) of \(t_h\) is lower than the complete torsion \(\mathrm{CT}(P_h)\) in the sense of [1]. Therefore, if in addition the curve c has finite complete torsion in the sense of [1], \(\mathrm{CT}(c)<\infty \), as in Step 3 of the proof of Theorem 1 we infer that the derivative \({\dot{{{\mathfrak {t}}}}}_c\) is a function of bounded variation, and that \(\dot{t}_h\) converges to \({\dot{{{\mathfrak {t}}}}}_c\) weakly-* in the \(\mathop {\mathrm{BV}}\nolimits \)-sense, and hence a.e. in [0, C]. We finally recall that a curve with finite total curvature and total absolute torsion may have infinite complete torsion.
Proof of Proposition 3
Similarly to the proof of Theorem 2, for any \(s\in ]0,L[\) we choose \(\{P_h\}\) inscribed in c such that \(\mathop {\mathrm{mesh}}\nolimits P_h\rightarrow 0\) and for any \(h\in {{\mathbb {N}}}^+\) the two points \(v_{i-1}=c(s-h)\) and \(v_{i}=c(s+h)\) are consecutive (and interior) vertices of \(P_h\). We thus get \(\sigma _i:=v_{i}-v_{i-1}=2\dot{c}(s)\,h+o(h)\), whence \(t_i(h):=\sigma _i/\Vert \sigma _i\Vert \rightarrow \dot{c}(s)={{\mathfrak {t}}}(s)\) as \(h\rightarrow \infty \). Also, denoting again by \(P_h(s)\) the polygonal corresponding to the segments \(\sigma _1,\ldots ,\sigma _{i-1},\sigma _i\) of \(P_h\), we have \(\mathrm{TC}(P_h(s))=k_h(s)\in [0,\mathrm{TC}(P_h)]\), where \(\mathrm{TC}(P_h)\rightarrow C\in {{\mathbb {R}}}^+_0\), whence a subsequence of \(\{k_h(s)\}\) converges to some \(k(s)\in [0,C]\). Proposition 2 yields that \(t_i(h)\rightarrow {{\mathfrak {t}}}_c(k(s))\) as \(h\rightarrow \infty \), whence we get \({{\mathfrak {t}}}(s)={{\mathfrak {t}}}_c(k(s))\). We clearly have \(\mathrm{TC}(P_h(s))\rightarrow \mathrm{TC}(c_{\vert [0,s]})\), which implies that
Recalling that \({\dot{{{\mathfrak {t}}}}}=\mathbf{{k}}\,{{\mathfrak {n}}}\), we finally obtain the equality (4.3). \(\square \)
5 Weak normal of a non-smooth curve
We have seen that the curvature of an open polygonal P is a nonnegative measure \(\mu _P\) concentrated at the interior vertices of P, whereas the torsion is a signed measure \(\nu _P\) concentrated at the interior segments, see Remark 5. Since these two measures are mutually singular, in principle there is no analogous to the classical formula by Fenchel for the (principal) normal of smooth curves in \({{\mathbb {R}}}^3\), namely
In this section, following Banchoff [2], a weak notion of normal indicatrix of a polygonal is introduced, see Definition 3, in such a way that formula (5.1) continues to hold. As a consequence, according to the cited Fenchel’s approach, the principal normal of a curve with finite total curvature and absolute torsion is well defined in a weak sense, see Theorem 3.
Weak normal of polygonals Let P be an open polygonal in \({{\mathbb {R}}}^3\) with non-degenerate segments. Denoting \(C=\mathrm{TC}(P)\) and \(T=\mathrm{TAT}(P)\), we first choose two suitable curves
which on one side inherit the properties of the tangent indicatrix and of the binormal indicatrix of P, respectively, and on the other side take account of the order in which curvature and torsion are defined along P. More precisely, we shall recover the properties
(where all equalities hold in the case of closed polygonals), which are satisfied (up to a lifting) by the curves \({{\mathfrak {t}}}_P\) and \({{\mathfrak {b}}}_P\) defined in Sect. 2. Moreover, in accordance with the mutual singularities of the measures \(\mu _P\) and \(\nu _P\), see Remark 5, one curve is constant when the other one parameterizes a geodesic arc, whose length is equal to the curvature or to the (absolute value of the) torsion at one vertex or segment of P, respectively.
Recalling the notation from Sect. 2, we let \(v_i\), \(i=0,\ldots ,n\), denote the vertices, and \(\sigma _i:=[v_{i-1},v_{i}]\), \(i=1,\ldots ,n\), the oriented segments of P. Also, we let \(t_i:=\sigma _i/\mathcal{L}(\sigma _i)\in {{\mathbb {S}}}^2\), for \(i=1,\ldots ,n\), and \(\gamma _i\) is a minimal geodesic arc in \({{{\mathbb {S}}}^2}\) connecting the consecutive points \(t_{i}\) and \(t_{i+1}\), for \(i=1,\ldots ,n-1\). Notice that \(\gamma _i\) is unique when \(t_{i+1}\ne -t_i\), and it is trivial when \(t_{i+1}= t_i\). Finally, \(\Gamma _i\) is the geodesic arc in \({\mathbb {RP}}^2\) with initial point \([b_{i-1}]\) and end point \([b_{i}]\), for any \(i=2,\ldots ,n-1\), where \(b_i\) is the discrete binormal (2.1). Therefore, \(\Gamma _i\) is trivial when \(b_i=\pm b_{i-1}\). We thus have
Remark 16
In order to explain our construction below, let us choose a lifting \(\widehat{{\mathfrak {b}}}_P:[0,T]\rightarrow {{\mathbb {S}}}^2\) of the (continuous) curve \({{\mathfrak {b}}}_P\) from Definition 2, and let \(\widehat{b}_i\) and \(\widehat{\Gamma }_i\) denote the points and geodesic arcs corresponding to \([b_i]\) and \(\Gamma _i\). For \(i=1,\ldots ,n-1\), we let \(\widetilde{\gamma }_i=\widehat{b}_i\times \gamma _i\), i.e., \(\widetilde{\gamma }_i\) is the oriented geodesic arc in \({{\mathbb {S}}}^2\) obtained by means of the vector product of the lifted discrete binormal \(\widehat{b}_i\) with each point in the support of the arc \(\gamma _i\). For \(i=2,\ldots ,n-1\), we also let \(\widetilde{\Gamma }_i=\widehat{\Gamma }_i\times t_{i+1}\), i.e., \(\widetilde{\Gamma }_i\) is the oriented geodesic arc in \({{\mathbb {S}}}^2\) obtained by means of the vector product of each point in the support of the lifted arc \(\widehat{\Gamma }_i\) with the direction \(t_{i+1}\).
It turns out that for \(i=1,\ldots ,n-2\), the final point of \(\widetilde{\gamma }_i\) agrees with the initial point of \(\widetilde{\Gamma }_{i+1}\), and that the final point of \(\widetilde{\Gamma }_{i+1}\) agrees with the initial point of \(\widetilde{\gamma }_{i+1}\). Using this order to join the geodesic arcs, one obtains a rectifiable curve in \({{\mathbb {S}}}^2\) whose total length is equal to the sum of the lengths of \({{\mathfrak {t}}}_P\) and of \({{\mathfrak {b}}}_P\), i.e., to \(\mathrm{TC}(P)+\mathrm{TAT}(P)\). However, since the curve depends on the chosen lifting of the binormal, it is more natural to work in the projective plane. Therefore, we shall consider the geodesic arcs \([\gamma _i]:=\Pi (\gamma _i)\) with end points \([t_i]:=\Pi (t_i)\), where \(\Pi :{{{\mathbb {S}}}^2}\rightarrow {\mathbb {RP}}^2\) is the canonical projection.
Recalling that \(C:=\mathrm{TC}(P)\) and \(T=\mathrm{TAT}(P)\), we shall denote for brevity \(C_0:=0\), \(T_1:=0\), and
Notice that \(C_i=C_{i-1}\) if \(\gamma _i\) is trivial, i.e., when \(t_{i+1}=t_i\), and that \(T_i=T_{i-1}\) when \(\Gamma _i\) is trivial, i.e., when \(b_i=\pm b_{i-1}\).
We define \(\widetilde{{\mathfrak {t}}}_P:[0,C+T]\rightarrow {\mathbb {RP}}^2\) and \(\widetilde{{\mathfrak {b}}}_P:[0,C+T]\rightarrow {\mathbb {RP}}^2\) as follows:
-
(1)
\(\widetilde{{\mathfrak {t}}}_P\) parameterizes with velocity one the oriented geodesic arc \([\gamma _i]\) on the interval \([C_{i-1}+T_i,C_i+T_i]\), for \(i=1,\ldots , n-1\) such that \(\gamma _i\) is non-trivial;
-
(2)
\(\widetilde{{\mathfrak {t}}}_P\) is constantly equal to \([t_i]\) on the interval \([C_{i-1}+T_{i-1},C_{i-1}+T_{i}]\), for \(i=2,\ldots , n-2\) ;
-
(3)
\(\widetilde{{\mathfrak {b}}}_P\) is constantly equal to \([b_i]\) on the interval \([C_{i-1}+T_i,C_i+T_i]\), for \(i=1,\ldots , n-1\) ;
-
(4)
\(\widetilde{{\mathfrak {b}}}_P\) parameterizes with velocity one the oriented geodesic arc \(\Gamma _i\) on the interval \([C_{i-1}+T_{i-1},C_{i-1}+T_{i}]\), for \(i=2,\ldots , n-2\) such that \(\Gamma _i\) is non-trivial.
The functions \(\widetilde{{\mathfrak {t}}}_P\) and \(\widetilde{{\mathfrak {b}}}_P\) are both continuous, and property (5.2) is readily checked. Furthermore, it turns out that the unit vectors \(\widetilde{{\mathfrak {t}}}_P(s)\) and \(\widetilde{{\mathfrak {b}}}_P(s)\) are orthogonal, for a.e. \(s\in [0,C+T]\). As a consequence, we are able to define the weak normal according to the formula (5.1).
Definition 3
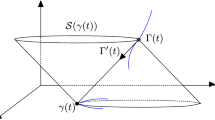
Normal indicatrix of the polygonal P is the curve \({{\mathfrak {n}}}_P:[0,C+T]\rightarrow {\mathbb {RP}}^2\) (see Fig. 2) given by the pointwise vector product
For closed polygonals, the above notation is modified in a straightforward way, arguing as in Remark 6.
The weak normal indicatrix of the curve whose tangent and binormal indicatrix are those in Fig. 1. Again, for the sake of the illustration we consider one of the two liftings of the normal indicatrix into the sphere \({{\mathbb {S}}}^2\)
Remark 17
By the definition, it turns out that
Notice that, the curvature and torsion of P being mutually singular measures, see Remark 5, the above equality is the analogous in the category of polygonals to the integral formulas
for smooth curves c, which clearly follow from the Frenet–Serret formulas (3.2).
Moreover, we have \(\Vert {\dot{{{\mathfrak {n}}}}}_P(s)\Vert =1\) for a.e. \(s\in [0,C+T]\). In fact, by the definition of \(\widetilde{{\mathfrak {t}}}_P\) and \(\widetilde{{\mathfrak {b}}}_P\), we get:
-
(1)
for \(i=1,\ldots , n-1\) and \(s\in ]C_{i-1}+T_i,C_i+T_i[\), we have \(\widetilde{{\mathfrak {b}}}_P(s)\equiv [b_i]\in {\mathbb {RP}}^2\) and hence \({\dot{{{\mathfrak {n}}}}}_P(s)= [b_i]\times \dot{\widetilde{{\mathfrak {t}}}}_P(s)\), where \(\Vert \dot{\widetilde{{\mathfrak {t}}}}_P(s)\Vert =1\) and \([b_i]\) is orthogonal to \(\dot{\widetilde{{\mathfrak {t}}}}_P(s)\), if \(\gamma _i\) is non-trivial;
-
(2)
for \(i=2,\ldots , n-2\) and \(s\in ]C_{i-1}+T_{i-1},C_{i-1}+T_{i}[\) we have \(\widetilde{{\mathfrak {t}}}_c(s)\equiv [t_i]\) and hence \({\dot{{{\mathfrak {n}}}}}_P(s)= \dot{\widetilde{{\mathfrak {b}}}}_P(s)\times [t_i]\), where \(\Vert \dot{\widetilde{{\mathfrak {b}}}}_P(s)\Vert =1\) and \([t_i]\) is orthogonal to \(\dot{\widetilde{{\mathfrak {b}}}}_P(s)\), if \(\Gamma _i\) is non-trivial.
Remark 18
Notice that the turning angle in \({\mathbb {RP}}^2\) of the curve \({{\mathfrak {n}}}_P\) is equal to \(\pi /2\) at each “non-trivial” vertex of \({{\mathfrak {n}}}_P\). Indeed, from a vertex of \({{\mathfrak {n}}}_P\) we move by rotating either around \({{\mathfrak {t}}}_\alpha \) or \({{\mathfrak {b}}}_\beta \) (\(\beta =\alpha \) or \(\beta =\alpha -1\)), where \({{\mathfrak {t}}}_\alpha \perp {{\mathfrak {b}}}_\beta \), hence the two curves are orthogonal. More precisely, for \(i=1,\ldots , n-1\), if both the geodesic arcs \([\gamma _i]\) and \(\Gamma _{i+1}\) are non-degenerate, they meet orthogonally at the vertex \({{\mathfrak {n}}}_P(C_i+T_i)\) of \({{\mathfrak {n}}}_P\). Similarly, for any \(i=2,\ldots , n-2\) such that both the geodesic arcs \(\Gamma _{i+1}\) and \([\gamma _{i+1}]\) are non-degenerate, they meet orthogonally at the vertex \({{\mathfrak {n}}}_P(C_i+T_{i-1})\).
Weak normal of curves In the same spirit as in Theorem 1, for non-smooth curves (that may have points of return or planar pieces) we now obtain our second main result. In view of Remark 15, we need the stronger assumption that the curve has finite complete torsion \(\mathrm{CT}(c)\) in the sense of [1]. To this purpose, we recall that the implication \(\mathrm{CT}(c)<\infty \Longrightarrow \mathrm{TAT}(c)<\infty \) holds true in general, whereas the implication \(\mathrm{CT}(c)<\infty \Longrightarrow \mathrm{TC}(c)<\infty \) is satisfied provided that the curve has no points of return.
Theorem 3
Let c be a curve in \({{\mathbb {R}}}^3\) with finite total curvature \(C:=\mathrm{TC}(c)\), finite complete torsion \(\mathrm{CT}(c)\), and finite total absolute torsion \(T:=\mathrm{TAT}(c)\). There exists a rectifiable curve \({{\mathfrak {n}}}_c:[0,C+T]\rightarrow {\mathbb {RP}}^2\) parameterized by arc length, so that \(\mathcal{L}_{{\mathbb {RP}}^2}({{\mathfrak {n}}}_c)=C+T\), satisfying the following property. For any sequence \(\{P_h\}\) of inscribed polygonal curves, let \(n_h:[0,C+T]\rightarrow {\mathbb {RP}}^2\) denote the parameterization with constant velocity of the normal indicatrix \({{\mathfrak {n}}}_{P_h}\) of \(P_h\), see Definition 3. If \(\mu _c(P_h)\rightarrow 0\), then \(n_h\rightarrow {{\mathfrak {n}}}_c\) uniformly on \([0,C+T]\) and \(\mathcal{L}_{{\mathbb {RP}}^2}(n_h)\rightarrow \mathcal{L}_{{\mathbb {RP}}^2}({{\mathfrak {n}}}_c)\).
Proof
We clearly may and do assume that each \(P_h\) has non-degenerate segments. By Definition 3, setting \(C_h=\mathrm{TC}(P_h)\) and \(T_h=\mathrm{TAT}(P_h)\), the normal indicatrix of \(P_h\) is the curve \({{\mathfrak {n}}}_{P_h}:[0,C_h+T_h]\rightarrow {\mathbb {RP}}^2\) given by \( {{\mathfrak {n}}}_{P_h}(s):=\widetilde{{\mathfrak {b}}}_{P_h}(s)\times \widetilde{{\mathfrak {t}}}_{P_h}(s)\), so that \( \mathcal{L}_{{\mathbb {RP}}^2}({{\mathfrak {n}}}_{P_h})=C_h+T_h\), and \(\Vert {\dot{{{\mathfrak {n}}}}}_{P_h}\Vert =1\) a.e. on \([0,C_h+T_h]\). Also, condition \(\mu _c(P_h)\rightarrow 0\) yields that \(C_h\rightarrow C\) and \(T_h\rightarrow T\).
Setting \(n_h:[0,C+T]\rightarrow {\mathbb {RP}}^2\) by \(n_h(s):={{\mathfrak {n}}}_{P_h}((C_h+T_h)s/(C+T))\), as before we deduce that possibly passing to a subsequence, \(\{n_{h}\}\) uniformly converges to some Lipschitz-continuous function \({{\mathfrak {n}}}_c:[0,C+T]\rightarrow {\mathbb {RP}}^2\).
We claim that \(\Vert {\dot{{{\mathfrak {n}}}}}_c\Vert = 1\) a.e. in \([0,C+T]\). This yields that
For this purpose, we note that by Definition 3 we have \(n_h(s)=\widetilde{b}_h(s)\times \widetilde{t}_h(s)\) for each \(s\in [0,T+C]\), where
As in Theorem 1 and Proposition 2, using that (by Remark 8) we again have:
we deduce that (possibly passing again to a subsequence) \(\widetilde{b}_h\rightarrow \widetilde{b}\) and \(\widetilde{t}_h\rightarrow \widetilde{t}\) strongly in \(L^1\) (and uniformly) to some continuous functions with bounded variation \(\widetilde{b},\widetilde{t}:[0,C+T]\rightarrow {\mathbb {RP}}^2\), and that the approximate derivatives \(\dot{\widetilde{b}_h}\rightarrow \dot{\widetilde{b}}\) and \(\dot{\widetilde{t}_h}\rightarrow \dot{\widetilde{t}}\) a.e. on \([0,C+T]\), see Remark 15. This yields that \({{\mathfrak {n}}}_c(s)=\widetilde{b}(s)\times \widetilde{t}(s)\) and hence:
for a.e. \(s\in [0,C+T]\). But we already know that \(\Vert \dot{n}_h(s)\Vert =(C_h+T_h)/(C+T)\) for a.e. s, where \(C_h\rightarrow C\) and \(T_h\rightarrow T\), whence the claim is proved.
We now show that the limit function \({{\mathfrak {n}}}_c\) does not depend on the initial choice of the approximating sequence \(\{P_h\}\). As a consequence, as before we conclude that the weak normal \({{\mathfrak {n}}}_c\) only depends on c, and that the whole sequence \(\{n_{h}\}\) converges to \({{\mathfrak {n}}}_c\).
In fact, if we choose another sequence of polygonals \(\{P^{(1)}_h\}\), we know that the sequences \(\{\widetilde{b}_{P^{(1)}_h}\}\) and \(\{\widetilde{t}_{P^{(1)}_h}\}\) take the same limit as the one of the sequences \(\{\widetilde{b}_{P_h}\}\) and \(\{\widetilde{t}_{P_h}\}\), respectively. Moreover, the corresponding limit function \({{\mathfrak {n}}}_c^{(1)}\) has length equal to the length of \({{\mathfrak {n}}}_c\) on each interval \(I\subset [0,C+T]\), and hence the same property holds true for the corresponding couples of functions \(\widetilde{b}\), \(\widetilde{b}^{(1)}\) and \(\widetilde{t}\), \(\widetilde{t}^{(1)}\), respectively. These facts imply that \({{\mathfrak {n}}}_c^{(1)}={{\mathfrak {n}}}_c\), as required. \(\square \)
Remark 19
On account of Remark 18, denoting by \(\tau _h\) the tantrix of the curve \(\underline{n}_h:=\widetilde{g}(n_h)\) in \({\mathrm{RP}}^{2}\), in general we do not have \(\sup _h \mathop{\mathrm{Var}}\nolimits _{{\mathrm{RP}}^{2}}(\tau _h)<\infty \). Therefore, we cannot argue as in Theorem 1 to conclude that the sequence \(\dot{n}_h\) converges weakly in the \(\mathop {\mathrm{BV}}\nolimits \)-sense (and hence strongly in \(L^1\)) to the function \({\dot{{{\mathfrak {n}}}}}_c\). Actually, the derivative \({\dot{{{\mathfrak {n}}}}}_c\) of the weak normal \({{\mathfrak {n}}}_c\) is not a function with bounded variation, in general.
The case of smooth curves We finally have:
Proposition 4
Let \(c:[0,L]\rightarrow {{\mathbb {R}}}^3\) be a smooth curve satisfying the hypotheses of Theorem 2, so that \(L=\mathcal{L}(c)\), \(C=\mathrm{TC}(c)\), and \(T=\mathrm{TAT}(c)\) are finite. Let \(s:[0,C+T]\rightarrow [0,L]\) be the inverse of the increasing and bijective function \(t:[0,L]\rightarrow [0,C+T]\) given by
where \(\mathbf{{k}}(\lambda )\) and \({\varvec{\tau }}(\lambda )\) are the curvature and torsion of the curve c at the point \(c(\lambda )\). Then the principal normal \({{\mathfrak {n}}}\) in \({{{\mathbb {S}}}^2}\) of the curve c, and the curve \({{\mathfrak {n}}}_c\) in \({\mathbb {RP}}^2\) given by Theorem 1, are linked by the formula:
Proof
For any given \(s\in ]0,L[\), we choose a sequence \(\{P_h\}\) as in the proof of Theorem 2, and we correspondingly denote:
Letting \(t_h(s):=\mathrm{TC}(P_h(s))+\mathrm{TAT}(P_h(s))\), this time we infer that (possibly passing to a subsequence) \(t_h(s)\rightarrow t(s):=\mathrm{TC}(c_{\vert [0,s]})+\mathrm{TAT}(c_{\vert [0,s]})\), so that t(s) satisfies the formula (5.3). As a consequence, arguing as in the proofs of Theorem 2 and Proposition 3, on account of Theorem 3 this time we get:
Since \(b_i(h)\rightarrow {{\mathfrak {b}}}(s)\) and \(t_i(h)\rightarrow {{\mathfrak {t}}}(s)\), we also have \(b_i(h)\times t_i(h)\rightarrow {{\mathfrak {n}}}(s)\), so that formula (5.4) holds. We omit any further detail. \(\square \)
6 On the spherical indicatrices of smooth curves
The trihedral \(({{\mathfrak {t}}},{{\mathfrak {n}}},{{\mathfrak {b}}})\) is well defined everywhere in the case of regular curves \(\gamma \) in \({{\mathbb {R}}}^3\) of class \(C^2\) such that \(\gamma '(t)\) and \(\gamma ''(t)\) are always independent vectors, and the Frenet–Serret formulas (3.2) hold true if in addition \(\gamma \) is of class \(C^3\).
Fenchel [6] used a geometric approach in order to define (under weaker hypotheses on the curve) the osculating plane. He chooses the binormal \({{\mathfrak {b}}}\) as a smooth function. Therefore, the principal normal is the smooth function given by \({{\mathfrak {n}}}={{\mathfrak {b}}}\times {{\mathfrak {t}}}\). The Frenet–Serret formulas continue to hold, but this time the curvature may vanish and even be negative. He also calls \(\mathbf{{k}}\)-inflection or \({\varvec{\tau }}\)-inflection a point of the curve where the curvature or the torsion changes sign, respectively.
By using an analytical approach, we recover some of the ideas by Fenchel in order to define the binormal (and principal normal). In general, it turns out that the binormal and normal fail to be continuous at the inflection points (see Example 3). However, both the binormal and normal are continuous when seen as functions in the projective plane \({\mathbb {RP}}^2\).
For this purpose, in the sequel we shall assume that \(\gamma :[a,b]\rightarrow {{\mathbb {R}}}^3\) satisfies the following properties:
-
(1)
\(\gamma \) is differentiable at each \(t\in [a,b]\) and \(\gamma '(t)\ne 0_{{{\mathbb {R}}}^3}\), i.e., \(\gamma \) is a regular curve;
-
(2)
for each \(t_0\in ]a,b[\), the function \(\gamma \) is of class \(C^n\) in a neighborhood of \(t_0\), for some \(n\ge 2\), and \(\gamma ^{(n)}(t_0)\ne 0_{{{\mathbb {R}}}^3}\), but \(\gamma ^{(k)}(t_0)=0_{{{\mathbb {R}}}^3}\) for \(2\le k\le n-1\), if \(n\ge 3\).
We thus denote by \(c(s):=\gamma (t(s))\) the arc-length parameterization of the curve \(\gamma \), i.e., \(t(s)=s(t)^{-1}\), with \(s(t):=\int _a^t\Vert {\dot{\gamma }}(\lambda )\Vert \,d\lambda \in [0,L]\), where \(L:=\mathcal{L}(\gamma )\).
Proposition 5
Under the above assumptions, the Frenet–Serret frame \(({{\mathfrak {t}}},{{\mathfrak {b}}},{{\mathfrak {n}}})\) is well defined for each \(s_0\in [0,L]\) by:
where \(s_0=s(t_0)\) and \(n\ge 2\) is given as above. Furthermore, \(\ddot{c}(s_0)=0_{{{\mathbb {R}}}^3}\) at a finite or countable set of points, and if \(\ddot{c}(s_0)\ne 0_{{{\mathbb {R}}}^3}\), then \({{\mathfrak {n}}}(s_0)=\ddot{c}(s_0)/\Vert \ddot{c}(s_0)\Vert \). Finally, \([{{\mathfrak {b}}}]\) and \([{{\mathfrak {n}}}]\) are continuous functions with values in \({\mathbb {RP}}^2\).
Proof
We set \({{\mathfrak {t}}}(s):=\dot{c}(s)\) for each s. If \(\ddot{c}(s_0)=0_{{{\mathbb {R}}}^3}\), then for some \(n\ge 3\) and for h small (and nonzero) we have
This implies that \(\ddot{c}(s)=0_{{{\mathbb {R}}}^3}\) only at isolated points \(s\in [0,L]\), hence at an at most countable set.
If \(\ddot{c}(s_0)\ne 0_{{{\mathbb {R}}}^3}\), one defines as usual \({{\mathfrak {n}}}(s_0):=\ddot{c}(s_0)/\Vert \ddot{c}(s_0)\Vert \) and \({{\mathfrak {b}}}(s_0):=\dot{c}(s_0)\times \ddot{c}(s_0)/\Vert \ddot{c}(s_0)\Vert \). In fact, the orthogonality property \(\dot{c}(s_0)\bullet \ddot{c}(s_0)=0\) yields that \((\dot{c}(s_0)\times \ddot{c}(s_0))\times \dot{c}(s_0)=\ddot{c}(s_0)\).
If \(\ddot{c}(s_0)=0_{{{\mathbb {R}}}^3}\), for h small we have \(\dot{c}(s_0+h)\bullet \ddot{c}(s_0+h)=0_{{{\mathbb {R}}}^3}\). Letting \(h\rightarrow 0\), we obtain that \(\dot{c}(s_0)\bullet c^{(n)}(s_0)=0_{{{\mathbb {R}}}^3}\), whence \(\dot{c}(s_0)\times c^{(n)}(s_0)\ne 0_{{{\mathbb {R}}}^3}\) and \(\Vert \dot{c}(s_0)\times c^{(n)}(s_0)\Vert =\Vert c^{(n)}(s_0)\Vert >0\). As a consequence, the binormal is well defined at \(s_0\) such that \(\ddot{c}(s_0)=0_{{{\mathbb {R}}}^3}\) by the limit
and the principal normal is then defined by letting \( {{\mathfrak {n}}}(s_0):={{\mathfrak {b}}}(s_0)\times {{\mathfrak {t}}}(s_0)\), where this time the orthogonality property \(\dot{c}(s_0)\bullet c^{(n)}(s_0)=0_{{{\mathbb {R}}}^3}\) yields that
Finally, we observe that where \(\ddot{c}\ne 0_{{{\mathbb {R}}}^3}\), both \({{\mathfrak {n}}}\) and \({{\mathfrak {b}}}\) are continuous (as functions valued in \({\mathbb {S}}^2\), hence also as functions valued in \({\mathbb {RP}}^2\)). Therefore, the problematic points are where \(\ddot{c}=0_{{{\mathbb {R}}}^3}\), which is a set of isolated points. At one of these point, \({{\mathfrak {n}}}(s_0)\) is ideally given by the limit of \(\ddot{c}(s_0+h)/\Vert \ddot{c}(s_0+h)\Vert \), as \(h\rightarrow 0\). Using equation (6.2), it is easy to see that, depending on the parity of the derivative order n, either the right and left limits coincide (thus the limit exists, and \({{\mathfrak {n}}}\) is continuous at \(s_0\)) or they are opposite to one another. Hence, \({{\mathfrak {n}}}\) and \({{\mathfrak {b}}}\) may not be continuous as sphere-valued functions, but they are continuous as projective-valued function, since their directions are well defined and continuous. \(\square \)
Remark 20
If in addition we assume that \(\gamma \) is of class \(C^3\), it turns out that the Frenet–Serret formulas (3.2) hold true outside the at most countable set of inflection points. In fact, we have seen that \(\ddot{c}(s)=0_{{{\mathbb {R}}}^3}\) only at isolated points \(s\in [0,L]\).
Example 3
Let \(c:[-1,1]\rightarrow {{\mathbb {R}}}^3\) be a regular curve with derivative
so that \(\Vert \dot{c}(s)\Vert \equiv 1\) and hence \({{\mathfrak {t}}}(s)=\dot{c}(s)\). For \(s\in ]-1,1[\), we compute
Therefore, if \(0<|s|<1\) we have \(\ddot{c}(s)\ne 0_{{{\mathbb {R}}}^3}\) and hence
In particular, the normal and binormal can be extended by continuity at \(s=\pm 1\) by letting \({{\mathfrak {n}}}(\pm 1):=(0,0,\mp 1)\) and \({{\mathfrak {b}}}(\pm 1):=2^{-1/2}(\mp 1,\pm 1,0)\).
Furthermore, for \(0<|s|<1\) we get:
and hence \(\mathbf{{k}}(s)\rightarrow 0\) and \({\varvec{\tau }}(s)\rightarrow 0\) as \(s\rightarrow 0\), whereas both \(\mathbf{{k}}\) and \({\varvec{\tau }}\) are summable functions in \(L^1(-1,1)\). Moreover, the Frenet–Serret formulas (3.2) hold true in the open intervals \(]-1,0[\) and ]0, 1[.
Since \({{\mathfrak {t}}}(0)=2^{-1/2}(1,0,1)\), \(\ddot{c}(0)=0_{{{\mathbb {R}}}^3}\), and \(c^{(3)}(0)=2^{-1/2}(0,1,0)\), by using the formulas in (6.1) we get:
and hence both the unit normal and binormal are not continuous at \(s=0\). However, since \([{{\mathfrak {n}}}(s)]\rightarrow [{{\mathfrak {n}}}(0)]\) and \([{{\mathfrak {b}}}(s)]\rightarrow [{{\mathfrak {b}}}(0)]\) as \(s\rightarrow 0\), they are both continuous as functions with values in \({\mathbb {RP}}^2\).
We finally compute the total curvature and the total absolute torsion of c. With \(t=s^2\), we have:
and similarly
In fact, c is regular at \(s=0\), so that there is no turning angle at c(0), whereas \({{\mathfrak {b}}}(0-)=-{{\mathfrak {b}}}(0+)\), so that also the total absolute torsion is zero at c(0). On the other hand, due to the occurrence of an inflection point at c(0), the complete torsion in the sense of Alexandrov and Reshetnyak [1] yields a contribution equal to \(\pi \) at c(0), so that \(\mathrm{CT}(c)=\mathrm{TAT}(c)+\pi \).
Remark 21
We finally point out that with the above assumptions, the statements of Theorem 2, Proposition 3, and Proposition 4 continue to hold. More precisely, using that the nonnegative curvature \(\mathbf{{k}}(\lambda )\) and the torsion \({\varvec{\tau }}(\lambda )\) may vanish only at a negligible set of inflection points, with our previous notation one readily obtains the following relations concerning the trihedral \(({{\mathfrak {t}}},{{\mathfrak {b}}},{{\mathfrak {n}}})\) from Proposition 5:
-
(1)
\({{\mathfrak {t}}}(s_1(k))={{\mathfrak {t}}}_c(k)\in {{{\mathbb {S}}}^2}\) for \(k\in [0,C]\), where \(s_1:[0,C]\rightarrow [0,L]\) is the inverse of the function
$$ k(s):=\int _0^s\mathbf{{k}}(\lambda )\,d\lambda \,,\qquad s\in [0,L] \,; $$(6.3) -
(2)
\([{{\mathfrak {b}}}(s_2(t))]={{\mathfrak {b}}}_c(t)\in {\mathbb {RP}}^2\) for \(t\in [0,T]\), where \(s_2:[0,T]\rightarrow [0,L]\) is the inverse of the function
$$ t(s):=\int _0^s|{\varvec{\tau }}(\lambda )|\,d\lambda \,, \qquad s\in [0,L]\,; $$(6.4) -
(3)
\([{{\mathfrak {n}}}(s_3(\rho ))]={{\mathfrak {n}}}_c(\rho )\in {\mathbb {RP}}^2\) for \(\rho \in [0,C+T]\), where \(s_3:[0,C+T]\rightarrow [0,L]\) is the inverse of the function
$$ \rho (s):=\int _0^s(\mathbf{{k}}(\lambda )+|{\varvec{\tau }}(\lambda )|)\,d\lambda \,, \qquad s\in [0,L]. $$
Example 4
Going back to Example 3, we compute
and hence \(s_1(k)=|\cos (\sqrt{2}k)|^{1/2}\), where \(k\in [0,C]\), with \(C=\pi /\sqrt{2}\), so that
with \(k(0)=\pi /(2\sqrt{2})\) and \({{\mathfrak {t}}}_c(k(0))=2^{-1/2}(1,0,1)\). Notice moreover that
so that \({\dot{{{\mathfrak {t}}}}}_c(k(0)\pm )=(0,\pm 1,0)\). We also get
where \(t(0)=\pi /(2\sqrt{2})\) and \({{\mathfrak {b}}}_c(t(0))=\bigl [2^{-1/2}\,(-1,0,1) \bigr ]\). Finally,
so that \({\dot{{{\mathfrak {b}}}}}_c(t(0)+)={\dot{{{\mathfrak {b}}}}}_c(t(0)-)=[(0,1,0)]\), whence \({{\mathfrak {b}}}_c\) has no corner points.
7 Torsion force
The curvature force was introduced in [3], see also [13], as the distributional derivative of the tangent indicatrix of curves in \({{\mathbb {R}}}^{N}\) with finite total curvature. It comes into the play when one computes the first variation of the length.
More precisely, a rectifiable curve c has finite total curvature if and only if the tantrix \({{\mathfrak {t}}}\) is a function with bounded variation, i.e., the distributional derivative \(D{{\mathfrak {t}}}\) is equal to a finite measure, the curvature force \(\mathcal{K}\). Also, this property is equivalent to the requirement that the first variation \(\delta _\xi \mathcal{L}(c)\) of the length has distributional order one.
In this section, we shall see that a torsion force measure can be similarly obtained by means of the tangential variation of the length \(\mathcal{L}_{{{{\mathbb {S}}}^2}}({{\mathfrak {t}}}_c)\) of the tangent indicatrix \({{\mathfrak {t}}}_c\) that we built up in Proposition 2 for any curve c with finite total curvature.
In fact, the first variation \(\delta _\xi \mathcal{L}_{{{{\mathbb {S}}}^2}}({{\mathfrak {t}}}_c)\) has distributional order one if and only if the arc-length derivative \({\dot{{{\mathfrak {t}}}}}_c\) of the tantrix \({{\mathfrak {t}}}_c\) is a function of bounded variation, see (7.1). By the way, we recall that this condition is satisfied if in addition the curve c has finite complete torsion, \(\mathrm{CT}(c)<\infty \), see Remark 15.
In this case, there exists a finite measure, the torsion force \(\mathcal{T}\), such that \(\langle \mathcal{T},\xi \rangle =\langle D{\dot{{{\mathfrak {t}}}}}_c,\xi \rangle \) for each smooth tangential vector field \(\xi \) along \({{\mathfrak {t}}}_c\).
Finally, the tangential variation of the length of the weak binormal \({{\mathfrak {b}}}_c\) from Theorem 1 is briefly discussed.
Curvature force Let \(c:[0,L]\rightarrow {{\mathbb {R}}}^{N}\) denote a rectifiable curve parameterized in arc length s. Suppose that \(c_\varepsilon \) is a variation of c under which the motion of each point c(s) is smooth in time and with initial velocity \(\xi (s)\), where \(\xi :[0,L]\rightarrow {{\mathbb {R}}}^{N}\) is a Lipschitz-continuous function of arc length. The first variation formula gives
where \({{\mathfrak {t}}}(s)=\dot{c}(s)\) and \({\dot{\xi }}(s)\) are defined for a.e. s, by Rademacher’s theorem.
If c is of class \(C^2\), integrating by parts one gets
where in terms of the (positive) first curvature \(\mathbf{{k}}\) and first unit normal \({{\mathfrak {n}}}(s)\) one has \({\dot{{{\mathfrak {t}}}}}(s)=\mathbf{{k}}(s)\,{{\mathfrak {n}}}(s) \), see (3.2) for the case \(N=3\).
More generally, if c is a curve with finite total curvature, then \({{\mathfrak {t}}}\) is a function of bounded variation, the right and left limits \({{\mathfrak {t}}}(s\pm ):=\displaystyle \lim _{\lambda \rightarrow s^\pm }{{\mathfrak {t}}}(\lambda )\in {\mathbb {S}}^{N-1}\) are well defined for each \(s\in ]0,L[\), and the distributional derivative \(D{{\mathfrak {t}}}\) is a finite vector-valued measure. Therefore, if in addition \(\xi (0)=\xi (L)=0\) one obtains
The measure \(\mathcal{K}:=D{{\mathfrak {t}}}\) is called in [3] the curvature force, and in the smooth case one has \(\mathcal{K}=\mathbf{{k}}\,{{\mathfrak {n}}}\,ds\). If c is a piecewise smooth function, one has the decomposition \(\mathcal{K}=\mathcal{K}^a+\mathcal{K}^s\), where the absolutely continuous component \(\mathcal{K}^a\) is equal to  , whereas the singular component \(\mathcal{K}^s\) is given by a sum of Dirac masses concentrated at the corner points of the curve c.
, whereas the singular component \(\mathcal{K}^s\) is given by a sum of Dirac masses concentrated at the corner points of the curve c.
More precisely, taking for simplicity \(N=3\), if \(s\in ]0,L[\) is such that \({{\mathfrak {t}}}(s-)\ne {{\mathfrak {t}}}(s+)\), then \(\mathcal{K}(\{c(s)\})=({{\mathfrak {t}}}(s+)-{{\mathfrak {t}}}(s-))\,\delta _{c(s)}\). Therefore, if \(\theta \in ]0,\pi ]\) is the shortest angle in the Gauss sphere \({{{\mathbb {S}}}^2}\) between \({{\mathfrak {t}}}(s\pm )\), so that \(d_{{{\mathbb {S}}}^2}({{\mathfrak {t}}}(s+),{{\mathfrak {t}}}(s-))=\theta \), one has \(|\mathcal{K}|(\{c(s)\})=\Vert {{\mathfrak {t}}}(s+)-{{\mathfrak {t}}}(s-)\Vert =2\sin (\theta /2)\).
As a consequence, comparing [13], denoting by \(\mathrm{TC}^*(c)\) the total variation of the curvature force \(\mathcal{K}\), in general one has \(\mathrm{TC}^*(c)\le \mathrm{TC}(c)\), and the strict inequality holds true as soon has the curve c has an interior corner point. More precisely, by the previous computation one has
First variation of total curvature In Proposition 2, for any curve c in \({{\mathbb {R}}}^3\) with finite total curvature \(C:=\mathrm{TC}(c)\) we have constructed a rectifiable curve \({{\mathfrak {t}}}_c:[0,C]\rightarrow {{{\mathbb {S}}}^2}\) parameterized in arc length that is strictly related with the complete tangent indicatrix in the sense of [1]. We wish to compute the tangential variation of the length \(\mathcal{L}_{{{{\mathbb {S}}}^2}}({{\mathfrak {t}}}_c)\) of \({{\mathfrak {t}}}_c\), by considering in particular the smooth case.
For this purpose, we assume that \({{\mathfrak {t}}}_{c,\,\varepsilon }\) is a variation of \({{\mathfrak {t}}}_c\) under which the motion of each point \({{\mathfrak {t}}}_c(k)\) is smooth in time and with initial velocity \(\xi (s)\), where this time \(\xi :[0,C]\rightarrow {{\mathbb {R}}}^3\) is a Lipschitz-continuous function of arc length k, with \(\xi (0)=\xi (C)=0\). Since we deal with tangential variations, we assume in addition that \(\xi (k)\in T_{{{\mathfrak {t}}}_c(k)}{{{\mathbb {S}}}^2}\) for each k. The first variation formula gives:
where \({\dot{{{\mathfrak {t}}}}}_c(k)\) and \({\dot{\xi }}(k)\) are defined for a.e. k. Therefore, by the definition of distributional derivative, in general we obtain:
Assume now that c is of class \(C^3\) and \(\ddot{c}(s)\ne 0_{{{\mathbb {R}}}^3}\) for each \(s\in ]0,L[\). In point (1) of Remark 21, we have seen that \({{\mathfrak {t}}}_c(k)={{\mathfrak {t}}}(s_1(k))\) for each \(k\in [0,C]\), where \({{\mathfrak {t}}}(s)=\dot{c}(s)\) and \(s_1:[0,C]\rightarrow [0,L]\) is the inverse of the function k(s) in (6.3), so that
for each \(k\in [0,C]\), by the first Frenet–Serret formula in (3.2). Therefore, by the second formula in (3.2) we compute for each k
Now, the tangential component to \({{{\mathbb {S}}}^2}\) of the second derivative \(\ddot{{\mathfrak {t}}}_c(k)\), i.e., the geodesic curvature of \({{\mathfrak {t}}}_c\) at the point \({{\mathfrak {t}}}_c(k)\), agrees with the quotient between the torsion and the scalar curvature of the initial curve c at the point \(c(s_1)\), where \(s_1=s_1(k)\).
In fact, the Darboux frame along \({{\mathfrak {t}}}_c\) is the triad \((\mathbf{T},{{\mathbf {N}}},{{\mathbf {U}}})\), where \(\mathbf{T}(k):={\dot{{{\mathfrak {t}}}}}_c(k)\), \({{\mathbf {N}}}(k):=\nu ({{\mathfrak {t}}}_c(k))\), \(\nu (p)\) being the unit normal to the tangent 2-space \(T_p{{{\mathbb {S}}}^2}\), and \({{\mathbf {U}}}(k):={{\mathbf {N}}}(k)\times \mathbf{T}(k)\) is the unit conormal. The curvature vector \(\mathbf{K}(k):={\dot{\mathbf{T}}}(k)=\ddot{{\mathfrak {t}}}_c(k)\) is orthogonal to \(\mathbf{T}(k)\), and thus decomposes as
where \({{\mathfrak {K}}}_g:=\mathbf{K}\bullet {{\mathbf {U}}}\) and \({{\mathfrak {K}}}_n:=\mathbf{K}\bullet {{\mathbf {N}}}\) denote the geodesic and normal curvature of \({{\mathfrak {t}}}_c\), respectively. By changing variable, we get
and hence we obtain for each \(k\in [0,C]\)
As a consequence, integrating by parts in (7.1) we get
where, we recall, \(\xi (k)\in T_{{{\mathfrak {t}}}_c(k)}{{{\mathbb {S}}}^2}\) for each k. Therefore, by changing variable \(s=s_1(k)\), since \(ds=\mathbf{{k}}(s_1(k))^{-1}\,dk\) we recover the expected formula:
Torsion force Denoting by \({\mathcal{T}}\) the “tangential” component of the distributional derivative of \({\dot{{{\mathfrak {t}}}}}_c\), so that \(\langle \mathcal{T},\xi \rangle =\langle D{\dot{{{\mathfrak {t}}}}}_c,\xi \rangle \) for each smooth tangential vector field along \({{\mathfrak {t}}}_c\), we have just seen that if c is smooth, then

i.e., \(\mathcal T\) is the push forward of the measure  by the function k(s) defined in (6.3), and its total mass is equal to \(\int _c|{\varvec{\tau }}|\,ds\). For that reason, the measure \({\mathcal{T}}\) may be called the torsion force.
by the function k(s) defined in (6.3), and its total mass is equal to \(\int _c|{\varvec{\tau }}|\,ds\). For that reason, the measure \({\mathcal{T}}\) may be called the torsion force.
More generally, it turns out that the torsion force \(\mathcal{T}\) is a finite measure provided that the derivative \({\dot{{{\mathfrak {t}}}}}_c\) is a function of bounded variation. To this purpose, see Remark 15, we recall that this sufficient condition is satisfied if in addition the curve c has finite complete torsion, \(\mathrm{CT}(c)<\infty \).
If c is piecewise smooth, we obtain again the decomposition \(\mathcal{T}=\mathcal{T}^a+\mathcal{T}^s\). By Proposition 3, it turns out that the absolutely continuous component \( \mathcal{T}^a \) takes the same form as in the right-hand side of the formula (7.2), where this time \(k(s):=\mathrm{TC}(c_{\vert [0,s]})\). Moreover, using that \({{\mathfrak {t}}}(s)={{\mathfrak {t}}}_c(k(s))\), if c is smooth at s we have \({{\mathfrak {t}}}'(s)={\dot{{{\mathfrak {t}}}}}_c(k(s))\cdot k'(s)\), with \(k'(s)=\mathbf{{k}}(s)\), hence by the first formula in (3.2) we get \({\dot{{{\mathfrak {t}}}}}_c(k(s))={{\mathfrak {n}}}(s)\).
If c has a point of return at c(s), we have \({{\mathfrak {t}}}(s-)=-{{\mathfrak {t}}}(s+)\). In this case, see Remark 13, the curve \({{\mathfrak {t}}}_c\) (and hence the torsion force \(\mathcal{T}\)) depends on the choice of the geodesic arc connecting the antipodal points \({{\mathfrak {t}}}(s\pm )\). However, the total mass of \(\mathcal{T}\) is finite and it does not depend on the choice of the geodesics.
If c has no points of return, the torsion force \(\mathcal{T}\) only depends on c. In fact, the singular component \(\mathcal{T}^s\) is a sum of Dirac masses concentrated at the corner points \(x={{\mathfrak {t}}}_c(k)\) of the curve \({{\mathfrak {t}}}_c\), with weight \({\dot{{{\mathfrak {t}}}}}_c(k+)-{\dot{{{\mathfrak {t}}}}}_c(k-)\). If \(\theta \) is the turning angle of \({{\mathfrak {t}}}_c\) at x, then \(\Vert {\dot{{{\mathfrak {t}}}}}_c(k+)-{\dot{{{\mathfrak {t}}}}}_c(k-)\Vert =2\sin (\theta /2)\).
In Example 4, at \(x={{\mathfrak {t}}}_c(k(0))=2^{-1/2}(1,0,1)\) we have \({\dot{{{\mathfrak {t}}}}}_c(k(0)\pm )=(0,\pm 1,0)\), so that \(\theta =\pi \) and \(\Vert {\dot{{{\mathfrak {t}}}}}_c(k(0)+)-{\dot{{{\mathfrak {t}}}}}_c(k(0)-)\Vert =2\).
First variation of total torsion In Theorem 1, we defined the weak binormal \({{\mathfrak {b}}}_c:[0,T]\rightarrow {\mathbb {RP}}^2\), that satisfies \(|{\dot{{{\mathfrak {b}}}}}_c|=1\) a.e. and \(\mathcal{L}_{{\mathbb {RP}}^2}({{\mathfrak {b}}}_c)=\mathrm{TAT}(c)\), and it turns out that the derivative \({\dot{{{\mathfrak {b}}}}}_c\) is a function of bounded variation.
Moreover, in point (2) of Remark 21, we have seen that if c is smooth as above, then \({{\mathfrak {b}}}_c(t)=[{{\mathfrak {b}}}(s_2(t))]\) for each \(t\in [0,T]\), where \(s_2:[0,T]\rightarrow [0,L]\), with \(T=\mathrm{TAT}(c)\), is the inverse of the function t(s) in (6.4). We have
for each t, by the third Frenet–Serret formula in (3.2). Therefore, by the second formula in (3.2) we get
Arguing as above, the tangential variation of the length \(\mathcal{L}_{{\mathbb {RP}}^2}({{\mathfrak {b}}}_c)\) yields to the “tangential” component of the distributional derivative \(D{\dot{{{\mathfrak {b}}}}}_c\). In the smooth case, its lifting gives the measure  , with total mass \(\int _c|\mathbf{{k}}|\,ds\). If c is piecewise smooth, the singular component \(\mathcal{T}^s\) is a sum of Dirac masses concentrated at the corner points \(x={{\mathfrak {b}}}_c(t)\) of the curve \({{\mathfrak {b}}}_c\) in \({\mathbb {RP}}^2\), i.e., at the points where \({\dot{{{\mathfrak {b}}}}}_c(t+)\ne {\dot{{{\mathfrak {b}}}}}_c(t-)\) in \({\mathbb {RP}}^2\). Notice however that in Example 4, at \(x={{\mathfrak {b}}}_c(t(0))=\bigl [2^{-1/2}\,(-1,0,1) \bigr ]\) we have \({\dot{{{\mathfrak {b}}}}}_c(t(0)+)={\dot{{{\mathfrak {b}}}}}_c(t(0)-)=[(0,1,0)]\), whence \({{\mathfrak {b}}}_c\) has no corner points and the measure \(D{\dot{{{\mathfrak {b}}}}}_c\) has no singular part.
, with total mass \(\int _c|\mathbf{{k}}|\,ds\). If c is piecewise smooth, the singular component \(\mathcal{T}^s\) is a sum of Dirac masses concentrated at the corner points \(x={{\mathfrak {b}}}_c(t)\) of the curve \({{\mathfrak {b}}}_c\) in \({\mathbb {RP}}^2\), i.e., at the points where \({\dot{{{\mathfrak {b}}}}}_c(t+)\ne {\dot{{{\mathfrak {b}}}}}_c(t-)\) in \({\mathbb {RP}}^2\). Notice however that in Example 4, at \(x={{\mathfrak {b}}}_c(t(0))=\bigl [2^{-1/2}\,(-1,0,1) \bigr ]\) we have \({\dot{{{\mathfrak {b}}}}}_c(t(0)+)={\dot{{{\mathfrak {b}}}}}_c(t(0)-)=[(0,1,0)]\), whence \({{\mathfrak {b}}}_c\) has no corner points and the measure \(D{\dot{{{\mathfrak {b}}}}}_c\) has no singular part.
References
Alexandrov, A.D., Reshetnyak, YuG: General Theory of Irregular Curves. Mathematics and Its Applications. Soviet Series. Kluwer Academic Publishers, Dordrecht (1989)
Banchoff, T.F.: Global geometry of polygons.III. Frenet frames and theorems of Jacobi and Milnor for space polygons. Rad Jugoslav. Akad. Znan. Umjet. 396, 101–108 (1982)
Cantarella, J., Fu, J.H.G., Kusner, R., Sullivan, J.M., Wrinkle, N.C.: Criticality for the Gehring link problem. Geom. Topol. 10, 2055–2116 (2006)
Enomoto, K., Itoh, J.-I.: The total mixed curvature of open curves in \({\mathbb{E}}^3\). Geom. Dedicata 194, 131–140 (2018)
Enomoto, K., Itoh, J.-I., Sinclair, R.: The total absolute curvature of open curves in \({\mathbb{E}}^3\). Ill. J. Math. 52(1), 47–76 (2008)
Fenchel, W.: On the differential geometry of closed space curves. Bull. Am. Math. Soc. 57, 44–54 (1951)
McRae, A.S.: The Milnor–Totaro theorem for space polygons. Geom. Dedicata 84(1–3), 321–330 (2001)
Milnor, J.W.: On the total curvature of knots. Ann. Math. 52, 248–257 (1950)
Mucci, D.: Maps into projective spaces: liquid crystals and conformal energies. Discrete Contin. Dyn. Syst. Ser. B 17(2), 597–635 (2012)
Mucci, D., Saracco, A.: Bounded variation and relaxed curvature of surfaces. Milan J. Math. (2020). https://doi.org/10.1007/s00032-020-00311-w
Penna, M.A.: Total torsion. Am. Math. Mon. 87, 452–461 (1980)
Spanier, E.H.: Algebraic Topology. Springer, Berlin (1981). (Corrected reprint)
Sullivan, J.M.: Curves of finite total curvature. In: Bobenko, A., Schröder, P., Sullivan, J.M., Ziegler, G. (eds.) Discrete Differential Geometry. Oberwolfach Seminars, vol. 38. Birkäuser, Basel (2008)
Totaro, B.: Space curves with nonzero torsion. Int. J. Math. 1(1), 109–117 (1990)
Acknowledgements
D.M. wishes to thank his seventeen-year-old son, Giovanni Mucci, for his useful help in pointing out to us some interesting phenomena concerning spherical geometry that he learned by himself. We also thank the referee for his/her suggestions that allowed us to improve the first version of the paper and to obtain the results contained in the last section. The research of D.M. was partially supported by the GNAMPA of INDAM. The research of A.S. was partially supported by the GNSAGA of INDAM.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Mucci, D., Saracco, A. The weak Frenet frame of non-smooth curves with finite total curvature and absolute torsion. Annali di Matematica 199, 2459–2488 (2020). https://doi.org/10.1007/s10231-020-00976-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10231-020-00976-5