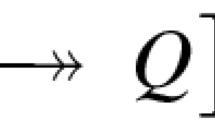Abstract
We describe new components of the Gieseker–Maruyama moduli scheme \({\mathcal {M}}(n)\) of semistable rank 2 sheaves E on \({\mathbb {P}^{3}}\) with \(c_1(E)=0\), \(c_2(E)=n\) and \(c_3(E)=0\) whose generic point corresponds to nonlocally free sheaves. We show that such components grow in number as n grows, and discuss how they intersect the instanton component. As an application, we prove that \({\mathcal {M}}(2)\) is connected, and identify a connected subscheme of \({\mathcal {M}}(3)\) consisting of seven irreducible components.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let \({\mathcal {M}}(c_1;c_2;c_3)\) denote the Gieseker–Maruyama moduli scheme of semistable rank 2 sheaves on \({\mathbb {P}^{3}}\) with the first, second and third Chern classes equal to \(c_1\), \(c_2\) and \(c_3\), respectively. We will be particularly concerned with \({\mathcal {M}}(n):={\mathcal {M}}(0;n;0)\). In addition, we also define \({\mathcal {B}}(n)\) to be the open subset of \({\mathcal {M}}(n)\) consisting of stable locally free sheaves, and let \({\mathcal {R}}(c_1;c_2;c_3)\) denote the open subset of \({\mathcal {M}}(c_1;c_2;c_3)\) consisting of stable reflexive sheaves.
The study of stable rank 2 locally free sheaves on \({\mathbb {P}^{3}}\) in the past 40 years has been mostly concentrated on instanton bundles, that is, those stable rank 2 locally free sheaves E on \({\mathbb {P}^{3}}\) satisfying \(c_1(E)=0\) and \(h^1(E(-2))=0\). Let \({\mathcal {I}}(n)\) denote the moduli space of instanton bundles E with \(c_2(E)=n\), regarded as an open subset of \({\mathcal {M}}(n)\); the basic questions about its geometry have been settled just recently: it is an irreducible [24, 25], nonsingular [16], affine [5] variety of dimension \(8n-3\). However, \(\overline{{\mathcal {I}}(n)}\), the closure of \({\mathcal {I}}(n)\) within \({\mathcal {M}}(n)\), is not the only irreducible component of \({\mathcal {M}}(n)\) for \(n\ge 2\); in fact, Ein showed in [7] that \({\mathcal {B}}(n)\) has several irreducible components as soon as \(n\ge 3\) and that the number of irreducible components of \({\mathcal {B}}(n)\) is not bounded as n grows.
In addition, the closure \(\overline{{\mathcal {B}}(n)}\) of \({\mathcal {B}}(n)\) within \({\mathcal {M}}(n)\) does not exhaust \({\mathcal {M}}(n)\) already for \(n\ge 2\), as it was observed by Le Potier [17, Chapter 7], Trautmann [26] and Miró-Roig [19]. In other words, for each \(n\ge 2\), \({\mathcal {M}}(n)\) possesses entire irreducible components whose generic point corresponds to a stable rank 2 torsion free sheaf which is not locally free. Such components are the main focus of the present paper.
To be more precise, let E be a rank 2 torsion free sheaf on \({\mathbb {P}^{3}}\) with \(c_1(E)=0\), \(c_2(E)=n\) and \(c_3(E)=0\). Clearly, \(c_1(E^{\vee \vee })=0\); we denote \(m:=c_2(E^{\vee \vee })\) and \(l=c_3(E^{\vee \vee })/2\). Setting \(Q_E:=E^{\vee \vee }/E\), one has the fundamental sequence
from which one can check that \(c_2(Q_E)=-(n-m)\) and \(c_3(Q_E)=2l\). If E is not locally free, then \(Q_E\ne 0\) and there are three possibilities:
-
(i)
\(\dim Q_E=0\); in this case, \(n=m\) and \(E^{\vee \vee }\) is not locally free; we say that E has 0-dimensional singularities;
-
(ii)
\(Q_E\) has pure dimension 1; in this case, \(n>m\) and we say that E has 1-dimensional singularities;
-
(iii)
\(\dim Q_E=1\), but it contains 0-dimensional subsheaves; in this case, we say that E has mixed singularities.
Note that in general \({\text {Supp}}(Q_E)\subseteq {\text {Sing}}(E)\), with equality if \(E^{\vee \vee }\) is locally free. Remark that \({\text {Sing}}(E)\) may contain 0-dimensional components even when \(Q_E\) has pure dimension one.
We present a systematic construction of irreducible components of \({\mathcal {M}}(n)\) whose generic point corresponds to stable rank 2 torsion free sheaves with 0- and 1-dimensional singularities, see Theorems 7 and 17 below, respectively. Furthermore, we also show that the number of such components grows as n grows, cf. Theorem 9, for the 0-dimensional case, and Theorem 19, for the 1-dimensional case, below.
These results raise the questions of whether it is possible to enumerate all of the irreducible components of \({\mathcal {M}}(n)\), at least for low values of n, and whether \({\mathcal {M}}(n)\) is connected. Indeed, it is not difficult to check that \({\mathcal {M}}(1)\) is irreducible (see Sect. 6), while Le Potier [17] and Trautmann [26] showed that \({\mathcal {M}}(2)\) has precisely three irreducible components, \(\overline{{\mathcal {I}}(2)}\) plus two additional ones. In Sect. 6, we show, in addition, that the generic point of each of the two so-called Trautmann components identified by Le Potier corresponds to a sheaf with 0-dimensional singularities, and that \({\mathcal {M}}(2)\) is connected.
Finally, we show in Sect. 7 that \({\mathcal {M}}(3)\) has at least seven irreducible components. In addition, we provide a discussion on how these various components intersect each other, showing that their union forms a connected subscheme of \({\mathcal {M}}(3)\).
2 Torsion free sheaves with 0-dimensional singularities
Let us begin by fixing some basic facts about torsion free sheaves E with 0-dimensional singularities. Given any coherent sheaf G on \({\mathbb {P}^{3}}\), one has \({\mathcal {E}}{} { xt}^3(E,G)=0\) and \({\mathcal {E}}{} { xt}^2(E,G)\simeq {\mathcal {E}}{} { xt}^3(Q_E,G)\) due to the reflexivity of \(E^{\vee \vee }\). It follows that torsion free sheaves E with 0-dimensional singularities have homological dimension equal to 2; in other words, E admits a resolution of the form
with each \(L_k\) (\(k=0,1,2\)) being a locally free sheaf.
Note that \({\mathcal {E}}{} { xt}^1(E,E)\) and \({\mathcal {E}}{} { xt}^2(E,E)\) are 0-dimensional sheaves, while \({\mathcal {E}}{} { xt}^3(E,E)\) vanishes. Thus using the spectral sequence of local-to-global Ext’s, we obtain:
-
(i)
\({{\mathrm{Ext}}}^1(E,E) = H^1({\mathcal {H}}{} { om}(E,E)) \oplus \ker d^{01}_2\)
-
(ii)
\({{\mathrm{Ext}}}^2(E,E) = \ker d^{02}_3 \oplus {{\mathrm{coker}}}d^{01}_2\)
-
(iii)
\({{\mathrm{Ext}}}^3(E,E) = {{\mathrm{coker}}}d^{02}_3\)
where \(d^{01}_2\) and \(d^{02}_3\) are the spectral sequence maps
It then follows that
Remark 1
Observe that for a reflexive sheaf F (so that \({\mathcal {E}}{} { xt}^2(F,F)=0\)) the previous expressions for \({{\mathrm{Ext}}}^j(F,F)\) simplify to
-
\({{\mathrm{Ext}}}^1(F,F) = H^1({\mathcal {H}}{} { om}(F,F)) \oplus \ker d^{01}_2\);
-
\({{\mathrm{Ext}}}^2(F,F) = {{\mathrm{coker}}}d^{01}_2\);
-
\({{\mathrm{Ext}}}^3(F,F) = H^3({\mathcal {H}}{} { om}(F,F))\),
where \(d^{01}_2\) is the spectral sequence map \(d^{01}_2 : H^0({\mathcal {E}}{} { xt}^1(F,F)) \rightarrow H^2({\mathcal {H}}{} { om}(F,F))\). Note as well that (5) simplifies to
Lemma 2
If E is a rank 2 torsion free sheaf with 0-dimensional singularities and \(c_1(E)=0\), then
Proof
The strategy is to show that
The desired equality will follow from (5), (6), and
see [12, Prop. 3.4].
Indeed, applying the functor \({\mathcal {H}}{} { om}(\cdot ,E)\) to the fundamental sequence (1) we obtain the isomorphism \({\mathcal {E}}{} { xt}^2(E,E)\simeq {\mathcal {E}}{} { xt}^3(Q_E,E)\) plus the exact sequence
since \({\mathcal {E}}{} { xt}^2(E^{\vee \vee },E)=0\) because \(E^{\vee \vee }\) is reflexive. Next, apply the functor \({\mathcal {H}}{} { om}(E^{\vee \vee },\cdot )\) to the fundamental sequence (1), obtaining
Comparing Euler characteristics of these last two sequences, we conclude that
Thus, since \(\chi ({\mathcal {E}}{} { xt}^2(E,E))=\chi ({\mathcal {E}}{} { xt}^3(Q_E,E))\), it is now enough to show that
noticing that \({\mathcal {H}}{} { om}(Q_E,E)=0\) and \({\mathcal {E}}{} { xt}^j(E^{\vee \vee },Q_E)=0\) for \(j=2,3\).
We first consider the left-hand side of (11). One can break a locally free resolution of E as in (2) into short exact sequences
Applying the functor \({\mathcal {H}}{} { om}(Q_E,\cdot )\) to the first sequence, we obtain
with all the other sheaves vanishing. Passing to Euler characteristics, we obtain
But \({\mathcal {E}}{} { xt}^3(Q_E,L_k)={\mathcal {E}}{} { xt}^3(Q_E,{\mathcal {O}}_{\mathbb {P}^{3}})\otimes L_k\), hence \(\chi ({\mathcal {E}}{} { xt}^3(Q_E,L_k))={{\mathrm{{rk}}}}(L_k)\cdot \chi (Q_E)\). Therefore
Next, apply the functor \({\mathcal {H}}{} { om}(Q_E,\cdot )\) to the second part of (2) to obtain the isomorphism \({\mathcal {E}}{} { xt}^1(Q_E,E)\simeq {\mathcal {E}}{} { xt}^2(Q_E,T)\) and the exact sequence
Passing to Euler characteristics, we obtain
Subtracting \({\mathcal {E}}{} { xt}^1(Q_E,E)\) from the left-hand side and \({\mathcal {E}}{} { xt}^2(Q_E,T)\) from the right-hand side and then substituting for (12), we obtain
Finally, we compute the right-hand side of (11) in a similar way. Take a locally free resolution of \(E^{\vee \vee }\):
Applying the functor \({\mathcal {H}}{} { om}(\cdot ,Q_E)\) and passing to Euler characteristics, we obtain
as desired.
Next, we consider semistable rank 2 torsion free sheaves with 0-dimensional singularities.
Lemma 3
Let E be a rank 2 torsion free sheaf on \({\mathbb {P}^{3}}\) with \(c_1(E)=0\), \(c_2(E)=n\), \(c_3(E)=0\), and with 0-dimensional singularities. If E is semistable, then \(E^{\vee \vee }\) is stable.
We remark that the vanishing of the third Chern class is an essential hypothesis: the sum of the ideal sheaves \(I_{x/{\mathbb {P}^{3}}}\oplus I_{y/{\mathbb {P}^{3}}}\) of two points \(x,y\in {\mathbb {P}^{3}}\) is semistable and with 0-dimensional singularities, but \((I_{x/{\mathbb {P}^{3}}}\oplus I_{x/{\mathbb {P}^{3}}})^{\vee \vee }\) is not stable. Recall also that the Hilbert polynomial of a rank 2 torsion free sheaf on \({\mathbb {P}^{3}}\) with \(c_1(E)=0\), \(c_2(E)=n\), \(c_3(E)=0\) is given by
Proof
If \(E^{\vee \vee }\) is not \(\mu \)-stable (or, equivalently, stable), then it has a section \(\sigma \). We can then form the following diagram

where \(\Delta \) is a 0-dimensional scheme contained in the support of \(Q_E\) and \(I_{\Delta /{\mathbb {P}^{3}}}\) is its ideal sheaf. Notice that one cannot have \(\varphi \sigma =0\) because \(h^0(E)=0\) by semistability.
Let d denote the length of \(\Delta \); it follows that
thus \(I_\Delta \) would destabilize E, contradicting our hypothesis. \(\square \)
We remark that the only properly semistable torsion free sheaf E with \(c_1(E)=c_3(E)=0\) and with 0-dimensional singularities is \(2\cdot {\mathcal {O}}_{\mathbb {P}^{3}}\). Indeed, assume that \(Q_E\ne 0\); if E is semistable, then \(E^{\vee \vee }\) is \(\mu \)-stable by Lemma 3 above; hence, E is also \(\mu \)-stable and thus stable. When \(Q_E=0\), this claim is just [12, Remark 3.1.1].
In addition, Hartshorne provides in [12, Thm. 8.2(b)] a bound for the third Chern class of a stable rank 2 reflexive sheaf on \({\mathbb {P}^{3}}\). Translating this bound to our context, we have the following statement.
Corollary 4
If E is a semistable rank 2 sheaf on \({\mathbb {P}^{3}}\) with \(c_1(E)=0\), \(c_2(E)=n\), \(c_3(E)=0\), and with 0-dimensional singularities, then \(c_3(E^{\vee \vee })\le n^2-n+2\).
Lemma 5
Let E be a rank 2 torsion free sheaf on \({\mathbb {P}^{3}}\) with \(c_1(E)=0\), \(c_2(E)=n\), \(c_3(E)=0\), and with 0-dimensional singularities. If E is stable, then
-
(a)
\({{\mathrm{Ext}}}^1(E,E) = H^1({\mathcal {H}}{} { om}(E,E)) \oplus \ker d^{01}_2\);
-
(b)
\({{\mathrm{Ext}}}^2(E,E) = H^0({\mathcal {E}}{} { xt}^2(E,E)) \oplus {{\mathrm{coker}}}d^{01}_2\);
-
(c)
\({{\mathrm{Ext}}}^3(E,E) = 0\);
-
(d)
\(\dim {{\mathrm{Ext}}}^1(E,E) = 8n - 3 + \dim {{\mathrm{Ext}}}^2(E,E)\).
Proof
The stability of E implies that
and, by Serre duality,
Item (c) now follows, and item (d) is then immediate from Lemma 2.
Item (a) coincides with item (i) in page 2, so it only remains for us to establish item (b).
Since \({\mathcal {E}}{} { xt}^1(Q_E,E)\) has dimension zero, we get from sequence (7) that
Similarly, since \({\mathcal {E}}{} { xt}^1(E^{\vee \vee },E)\) has dimension zero, we get from sequence (9) that
Putting the isomorphisms above, we get
In particular, \(H^3({\mathcal {H}}{} { om}(E,E))\simeq {{\mathrm{Ext}}}^3(E^{\vee \vee },E^{\vee \vee })=0\) since \(E^{\vee \vee }\) is stable. Thus, the spectral sequence map \(d^{02}_3\) in (4) vanishes. Item (b) now follows from item (ii) in page 3. \(\square \)
2.1 Components of sheaves with 0-dimensional singularities
In this section, we will show how to produce irreducible components of \({\mathcal {M}}(n)\) whose generic point corresponds to a sheaf with 0-dimensional singularities.
Start by considering the following ingredients:
-
(i)
A stable rank 2 reflexive sheaf F on \({\mathbb {P}^{3}}\) with \(c_1(F)=0\), \(c_2(F)=n\) and \(c_3(F)=2l\);
-
(ii)
A 0-dimensional sheaf Q of length l on \({\mathbb {P}^{3}}\);
-
(iii)
An epimorphism \(\varphi : F \rightarrow Q\).
Now let \(E:=\ker \varphi \). Clearly, this is a (\(\mu \)-)stable rank 2 torsion free sheaf with \(c_1(E)=0\), \(c_2(E)=n\) and \(c_3(E)=0\) such that \(E^{\vee \vee }=F\) and \(E^{\vee \vee }/E=Q\); in particular, \({\text {Sing}}(E)\) has dimension 0.
Proposition 6
Let F be a stable rank 2 reflexive sheaf with \(c_1(F)=0\), \(c_2(F)=n\) and \(c_3(F)=2l\) such that \({{\mathrm{Ext}}}^2(F,F)=0\). Take l distinct points \(q_1,\dots ,q_l\) such that \(\{q_1,\dots ,q_l\}\cap {\text {Sing}}(F)=\emptyset \), and set \(Q:=\oplus _{j=1}^{l}{\mathcal {O}}_{q_j}\). Then, the kernel E of any epimorphism \(\varphi : F \twoheadrightarrow Q\) satisfies \(\dim {{\mathrm{Ext}}}^1(E,E)=8n-3+4l\).
Proof
Since E is stable, it is enough to show, by Lemma 5(d), that \(\dim {{\mathrm{Ext}}}^2(E,E)=4l\). The first step is to show that the spectral sequence map (3) is surjective. Indeed, one has the commutative diagram

where vertical arrow in the left is the natural map coming from the exact sequence
while the vertical arrow in the right is the natural isomorphism obtained as in (14). Applying \({{\mathrm{Hom}}}(F,\cdot )\) to the sequence (17), we get
To see that \({{\mathrm{Ext}}}^1(F,Q)=0\), note that \(H^i({\mathcal {E}}{} { xt}^j(F,Q))=0\) if \(i,j\ne 0\): indeed, \({\mathcal {E}}{} { xt}^j(F,Q)=0\) for \(j=2,3\) because F is reflexive; \({\mathcal {E}}{} { xt}^1(F,Q)=0\) because the singular locus of F is disjoint from the support of Q; and \({\mathcal {H}}{} { om}(F,Q)\) has dimension 0. It follows from the spectral sequence of local-to-global Ext’s that \({{\mathrm{Ext}}}^j(F,Q)=0\) for \(j>0\). Since, by hypothesis, \({{\mathrm{Ext}}}^2(F,F)=0\), it follows that \({{\mathrm{Ext}}}^2(F,E)=0\). Since \({{\mathrm{Ext}}}^2(F,E)\) coincides with the cokernel of top horizontal map in diagram (16), it follows that the bottom horizontal map, which is precisely the spectral sequence map \(d^{01}_2\) in (3), is also surjective.
It then follows from Lemma 5(b) that \(\dim {{\mathrm{Ext}}}^2(E,E)=h^0({\mathcal {E}}{} { xt}^2(E,E))\). To compute this, note that
where \({\text {Sing}}(E)={\text {Sing}}(F)\cup \{q_1,\dots ,q_l\}\).
First, take \(p\in {\text {Sing}}(F)\); since \(p\notin {\text {Supp}}(Q)\), we get \(E_p\simeq F_p\). However, \({\mathcal {E}}{} { xt}^2_{{\mathcal {O}}_{{\mathbb {P}^{3}},p}}(F_p,F_p)={\mathcal {E}}{} { xt}^2(F,F)_p=0\) because F, being reflexive, has cohomological dimension 1.
Next, take \(p=q_j\) for some \(1\le j\le l\); restricting the sequence (17) to an open affine subset U of \({\mathbb {P}^{3}}\) containing p but none of the other singularities of F, we have the following short exact sequence of sheaves on U:
where \(I_{p/U}\) denotes the ideal sheaf of the point \(p\in U\) and \({\mathcal {O}}_{p/U}\) denotes the structure sheaf of the point p as a subscheme of U. It follows that
We argue that the first summand has length 1, while the second one has length 3. Indeed, we might as well perform the calculation globally, using the ideal sheaf \(I_{p/{\mathbb {P}^{3}}}\) of the point \(p\in {\mathbb {P}^{3}}\) and its structure sheaf \({\mathcal {O}}_{p/{\mathbb {P}^{3}}}\).
From the exact sequence
we obtain that \({\mathcal {E}}{} { xt}^2(I_{p/{\mathbb {P}^{3}}},{\mathcal {O}}_{\mathbb {P}^{3}})\simeq {\mathcal {E}}{} { xt}^3({\mathcal {O}}_{p/{\mathbb {P}^{3}}},{\mathcal {O}}_{\mathbb {P}^{3}})\simeq {\mathcal {O}}_{p/{\mathbb {P}^{3}}}\), so it has length 1.
Now use the resolution of \(I_{p/{\mathbb {P}^{3}}}\) by locally free sheaves:
Applying the functor \({\mathcal {H}}{} { om}(\cdot ,I_{p/{\mathbb {P}^{3}}})\) to the sequence
we obtain that \({\mathcal {E}}{} { xt}^2(I_{p/{\mathbb {P}^{3}}},I_{p/{\mathbb {P}^{3}}})\simeq {\mathcal {E}}{} { xt}^1(G,I_{p/{\mathbb {P}^{3}}})\). Applying the same functor to the exact sequence
we obtain the sequence
Note that the cokernel of the first arrow is just \(I_{p/{\mathbb {P}^{3}}}\otimes {\mathcal {O}}_{p/{\mathbb {P}^{3}}}\simeq 3\cdot {\mathcal {O}}_{p/{\mathbb {P}^{3}}}\); thus, \({\mathcal {E}}{} { xt}^1(G,I_{p/{\mathbb {P}^{3}}})\) has length 3.
Thus, the points of \({\text {Sing}}(F)\) do not contribute to (18), while each of the l points in \({\text {Supp}}(Q)\) contributes with a sheaf of length 4. We conclude that \(\dim {{\mathrm{Ext}}}^2(E,E)=4l\), as desired. \(\square \)
Now let \({\mathcal {S}}(n,l)\) denote an irreducible, open subset of \({\mathcal {R}}(0;n;2l)\) whose points correspond to stable reflexive sheaves F satisfying \({{\mathrm{Ext}}}^2(F,F)=0\); in particular, \({\mathcal {S}}(n,l)\) must be the nonsingular locus of an irreducible component of \({\mathcal {R}}(0;n;2l)\) of expected dimension \(8n-3\). In the product \({\mathcal {S}}(n,l)\times ({\mathbb {P}^{3}})^l\), we consider the open subset
Clearly, a point in \(\left( {\mathcal {S}}(n,l)\times ({\mathbb {P}^{3}})^l \right) ^0\) can be regarded as a pair of sheaves \(([F],Q:=\oplus _{j=1}^{l}{\mathcal {O}}_{q_j})\) which fulfills the condition of Proposition 6. Next, with \(([F],Q)\in \left( {\mathcal {S}}(n,l)\times ({\mathbb {P}^{3}})^l \right) ^0\) as above, consider the open set \({{\mathrm{Hom}}}(F,Q)_e\) of \({{\mathrm{Hom}}}(F,Q)\) consisting of epimorphisms \(\varphi : F\twoheadrightarrow Q\); the group \({{\mathrm{Aut}}}(Q)\) of automorphisms of the sheaf Q acts on \({{\mathrm{Hom}}}(F,Q)_e\) just by homotheties on each factor \({\mathcal {O}}_{q_j}\) of Q.
Putting all these data together, we construct the set of triples
By construction, \({\mathcal {T}}(n,l)\) is an irreducible, quasi-projective variety of dimension \(8n-3+4l\). Indeed, one has the surjective projection
onto an irreducible base variety of dimension \(8n-3+3l\), with fibers given by
which have dimension \(2l-l=l\).
To each point \(\mathbf {t}:=([F],Q,\varphi )\in {\mathcal {T}}(n,l)\), one associates the sheaf
which defines a point \([E(\mathbf {t})]\) in \({\mathcal {M}}(n)\). Proposition 6 tells us that, for each \(\mathbf {t}\in {\mathcal {T}}(n,l)\),
therefore, the image of \({\mathcal {T}}(n,l)\) into \({\mathcal {M}}(n)\) is a dense open subset of an irreducible component of \({\mathcal {M}}(n)\); to simplify notation, we denote such component by \(\overline{{\mathcal {T}}(n,l)}\), the closure of the image of \({\mathcal {T}}(n,l)\) within \({\mathcal {M}}(n)\).
We summarize the considerations above into the following result.
Theorem 7
For every nonsingular irreducible component \({\mathcal {F}}\) of \({\mathcal {R}}(0;n;2l)\) of expected dimension \(8n-3\), there exists an irreducible component \(\overline{{\mathcal {T}}(n,l)}\) of dimension \(8n-3+4l\) in \({\mathcal {M}}(n)\) whose generic point [E] satisfies \([E^{\vee \vee }]\in {\mathcal {F}}\) and \({\text {length}}(Q_E)=l\).
2.2 An Ein-type result for sheaves with 0-dimensional singularities
Recall that Ein has shown in [7, Proposition 3.6] that the number of irreducible components of \({\mathcal {B}}(n)\) is unbounded as n grows. We now prove a similar statement for those irreducible components of \({\mathcal {M}}(n)\) whose generic points correspond to sheaves with 0-dimensional singularities.
We begin by considering morphisms
whose degeneracy locus
is 0-dimensional. It follows that the cokernel of \(\alpha \) is a rank 2 reflexive sheaf on \({\mathbb {P}^{3}}\), which we normalize as to fit into the short exact sequence:
with \(a,b,c\ge 0\) and such that \(3a+2b+c\) is nonzero and even; we set \(k:=(3a+2b+c)/2\), so that \(c_1(F)=0\).
For simplicity of notation, let
The dimension of the family of rank 2 reflexive sheaves constructed as in Eq. (19) is given by
One easily checks for that \(h^0(F)=0\) for every F given by (19); thus, F is always stable. In addition, it is not hard to check that \({{\mathrm{Ext}}}^2(F,F)=0\). Indeed, applying the functor \({{\mathrm{Hom}}}(\cdot ,F(k))\) to the sequence (19), we obtain
The group on the left vanishes because \(H^1(F(t))=0\) for every \(t\in {\mathbb {Z}}\), while the group on the right vanishes because \(H^2(F(k))=0\). We conclude from [12, Prop. 3.4] that \(\dim {{\mathrm{Ext}}}^1(F,F)=8c_2(F)-3\), matching the dimension of the family as computed in the previous paragraph. It follows that the family of sheaves given by (19) provides a component of the moduli space of stable rank 2 reflexive sheaves on \({\mathbb {P}^{3}}\).
Summarizing the results obtained so far, we have the following theorem.
Theorem 8
For each triple (a, b, c) of positive integers such that \(3a+2b+c\) is nonzero and even, the rank 2 reflexive sheaves given by (19) fill out an irreducible, nonsingular, component \({\mathcal {S}}(a,b,c)\) of \({\mathcal {R}}(0;n;m)\) of expected dimension \(8n-3\), where n and m are given by the expressions:
More precisely, let \(\widetilde{{\mathcal {S}}}(a,b,c)\subset {{\mathrm{Hom}}}\left( G_{(a,b,c)},(a+b+c+2)\cdot {\mathcal {O}}_{\mathbb {P}^{3}}\right) \) be the open subset consisting of monomorphisms with 0-dimensional degeneracy loci; then,
Two particular cases deserve special attention, as they were previously considered by Chang [4]. First, we set \(a=b=0\) and \(c=2\), so that \(n=2\) and \(m=4\) and (19) reducing to
It is shown in [4, Lemma 2.9] that every stable rank 2 reflexive sheaf F with \(c_2(F)=2\) and \(c_3(F)=4\) admits a resolution of the form (20); in other words, \({\mathcal {S}}(0,0,2)={\mathcal {R}}(0;2;4)\).
The second case considered by Chang corresponds to \(a=c=0\) and \(b=1\), so that \(n=3\) and \(m=8\) and (19) reducing to
One can check that every stable rank 2 reflexive sheaf F with \(c_2(F)=3\) and \(c_3(F)=8\) admits a resolution of the form (21), cf. [4, proof of Theorem 3.9]; in other words, \({\mathcal {S}}(0,1,0)={\mathcal {R}}(0;3;8)\).
Finally, we are ready to establish the result promised in the beginning of the section.
Theorem 9
Let \(\zeta _n\) denote the number of irreducible components of \({\mathcal {M}}(n)\) whose generic points correspond to sheaves with 0-dimensional singularities. Then, \(\lim \sup _{n\rightarrow \infty }\zeta _n=\infty \).
Proof
For any integer \(q\ge 1\) set \(n_q=9q^2-6q-1\) and for any integer \(i,\ 0\le i\le q-1,\) set \(a_{q,i}=i,\ b_{q,i}=3q-3i-3,\ c_{q,i}=3i+2\). Then, according to Theorem 8, the sheaf F defined by (19) for the triple of integers \((a,b,c)=(a_{q,i},b_{q,i},c_{q,i})\) belongs to an irreducible component \({\mathcal {S}}_{q,i}={\mathcal {S}}(a_{q,i},b_{q,i},c_{q,i})\) of \({\mathcal {R}}(0;n_q,m_{q,i})\), where \(m_{q,i}=m(a_{q,i},b_{q,i},c_{q,i})\) is an even integer given by the second formula of Theorem 8. Now by Theorem 7, to each \({\mathcal {S}}_{q,i}\) there corresponds an irreducible component \(\overline{{\mathcal {T}}(n_q,\frac{m_{q,i}}{2})}\) of dimension \(8n_q-3+2m_{q,i}\) in \({\mathcal {M}}(n_q)\) whose generic point is a sheaf with 0-dimensional singularities. Since \(0\le i\le q-1\), we therefore obtain q distinct irreducible components of \({\mathcal {M}}(n_q)\) with this property. In other words, in the notation of this theorem, \(\zeta _{n_q}\ge q\). Hence, \(\lim \sup _{n\rightarrow \infty }\zeta _n=\infty \). \(\square \)
3 Components of sheaves with 1-dimensional singularities
Let E be a rank 2 torsion free sheaf with 1-dimensional singularities, that is, the quotient sheaf \(Q_E=E^{\vee \vee }/E\) has pure dimension one. Given any coherent sheaf G on \({\mathbb {P}^{3}}\), one has \({\mathcal {E}}{} { xt}^3(E,G)=0\) and \({\mathcal {E}}{} { xt}^2(E,G)\simeq {\mathcal {E}}{} { xt}^3(Q_E,G)=0\) due to the reflexivity of \(E^{\vee \vee }\). Therefore, torsion free sheaves E with 1-dimensional singularities have homological dimension equal to 1; in other words, E admits a locally free resolution of the form
Lemma 10
If E is a rank 2 torsion free sheaf on \({\mathbb {P}^{3}}\) with \(c_1(E)=0\), and with 1-dimensional singularities, then
Proof
In this case, the spectral sequence of local-to-global Ext’s converges in the third page, and it yields
-
(i)
\({{\mathrm{Ext}}}^1(E,E) = H^1({\mathcal {H}}{} { om}(E,E))\oplus \ker d^{01}_2\);
-
(ii)
\({{\mathrm{Ext}}}^2(E,E) = {{\mathrm{coker}}}d^{01}_2 \oplus \ker d^{11}_2\);
-
(iii)
\({{\mathrm{Ext}}}^3(E,E) = {{\mathrm{coker}}}d^{11}_2\)
where \(d^{01}_2\) and \(d^{11}_2\) are the spectral sequence maps
The first equality is then an immediate consequence.
As for the last equality, the same proof of [12, Prop. 3.4] applies here, since E has homological dimension 1.
Remark 11
We observe that the proof of the first equality does not depend on the hypotheses \({{\mathrm{{rk}}}}(E)=2\) and \(c_1(E)=0\), being valid for any torsion free sheaf with 1-dimensional singularities.
Recall that a rank 2 instanton sheaf on \({\mathbb {P}^{3}}\) is a rank 2 torsion free sheaf E with \(c_1(E)=0\) such that
These are precisely the sheaves obtained as cohomology of linear monads of the form (cf. [15])
The second Chern class of E is called the charge of E. An instanton bundle is simply a locally free instanton sheaf. Let \({\mathcal {I}}(n)\) denote the moduli space of instanton bundles of charge n; since every instanton bundle is \(\mu \)-stable, \({\mathcal {I}}(n)\) can be regarded as an open subset of \({\mathcal {M}}(n)\). Moreover, for each \(n\ge 1\), \({\mathcal {I}}(n)\) is an irreducible [24, 25], nonsingular [16], affine [5] variety of dimension \(8n-3\). The trivial sheaf \(2\cdot {\mathcal {O}}_{\mathbb {P}^{3}}\) is considered the instanton bundle of charge 0; with this in mind, \({\mathcal {I}}(0)\) consists of a single point. \({\mathcal {I}}(n)\) is known to be rational for \(n\le 3\).
For \(n>0\), denote by \({\mathcal {L}}(n)\) the union of those irreducible components of \({\mathcal {M}}(n)\) whose generic points F satisfy the condition
We call \({\mathcal {L}}(n)\) the instanton stratum of \({\mathcal {M}}(n)\).
In this section, we study the sheaves from \({\mathcal {M}}(n)\) with 1-dimensional singularities obtained from the instanton bundles of charge \(n-d\) by elementary transformations, in the sense of [14, Section 3], along complete intersection curves of degree d in \({\mathbb {P}^{3}}\).
Let \(d_1\le d_2\) be positive integers, and for \(i=1,2\) let \(S_{d_i}\) be a surface of degree \(d_i\) in \({\mathbb {P}^{3}}\). If the scheme \(C_{d_1,d_2}:=S_{d_1}\cap S_{d_2}\) has pure dimension 1, we call it a complete intersection curve. The degree, the arithmetic genus and the Hilbert polynomial of the curve \(C=C_{d_1,d_2}\) are given by the formulas
Let \({\mathrm {Hilb}}_{d_1,d_2}\) be an open subset of the Hilbert scheme \({\mathrm {Hilb}}_{H(t)}\) consisting of reduced complete intersection curves \(C_{d_1,d_2}\). This is a smooth irreducible scheme of dimension
where \(C\in {{\mathrm {Hilb}}}_{d_1,d_2}\). Besides, the \(h^1\)-cohomology of the sheaf \(N_{C/{\mathbb {P}^{3}}}\) is given by
Let \({\mathcal {H}}\) be an open dense subset of \({\mathrm {Hilb}}_{d_1,d_2}\) defined as
Note that \({\mathcal {H}}\) contains a dense open subset
Let
be the universal family of curves over \(\mathcal {H}\). For any \(C\in {\mathcal {H}}\), denote \(g:=p_a(C)\) and let
be the Hilbert polynomial of \(\mathcal {O}_C((g-1)\mathrm {pt})\) with respect to the sheaf \({\mathcal {O}}_{{\mathbb {P}^{3}}}(1)\).
Consider the relative Jacobian functor \(\mathbf {J}=\mathbf {J}^P:(Schemes/{\mathcal {H}})^o\rightarrow (Sets)\) defined as
where \(F_1\sim F_2\) if there exists an invertible sheaf N on T such that \(F_1\simeq F_2\otimes p^*N\), for \(p:{\mathcal {Z}}\times _{{\mathcal {H}}}T\rightarrow T\) the projection. Let \(\mathbf {P}\) be the étale sheaf associated with \(\mathbf {J}\). It is known (see [1], [9, 0.2]) that \(\mathbf {P}\) is represented by an algebraic space \(\mathbb {P}\), locally of finite type over \({\mathcal {H}}\). Furthermore, according to [9, Theorem B] there exists an étale base change
such that the functor \(\widehat{\mathbf {J}}=\mathbf {J}\times _{{\mathcal {H}}}\widetilde{{\mathcal {H}}}\) is represented by a \(\widetilde{{\mathcal {H}}}\)-scheme
together with the universal (Poincaré) line bundle
where \(\widetilde{{\mathcal {Z}}}:={\mathcal {Z}}\times _{{\mathcal {H}}}{\widetilde{{\mathcal {H}}}}\). Consider an open subfunctor \(\mathbf {J}^{ss}\) of \(\mathbf {J}\) defined as
The functor \(\widetilde{\mathbf {J}}=\mathbf {J}^{ss}\times _{{\mathcal {H}}} \widetilde{{\mathcal {H}}}\) is represented by a \(\widetilde{{\mathcal {H}}}\)-scheme
of finite type over \(\widetilde{{\mathcal {H}}}\), which is an open subscheme of \(\widehat{\mathbb {J}}\) endowed with the universal (Poincaré) line bundle
On the other hand, \(\mathbf {J}^{ss}\) is an open subfunctor of the moduli functor \(\mathbf {M}=\mathbf {M}^P:(Schemes/{\mathcal {H}})^o\rightarrow (Sets)\),
where by Simpson [23] (see also [13, Section 4]) \(\mathbf {M}\) is corepresented by a projective \({\mathcal {H}}\)-scheme
respectively, \(\mathbf {J}^{ss}\) is corepresented by a quasi-projective \({\mathcal {H}}\)-scheme
which is an open subscheme of \(\mathbb {M}\) and \(\pi '= \pi |_{\mathbb {M}'}\). Note that set-theoretically the schemes \(\widetilde{\mathbb {J}}\) and \(\mathbb {M}'\) are described as
where \([L]_S\) denotes S-equivalence class of L with respect to \({\mathcal {O}}_{{\mathbb {P}^{3}}}(1)|_C\). Under this description, the corepresentability of \(\mathbf {J}^{ss}\) by \(\mathbb {M}'\) implies that there exists a surjective morphism of schemes
Note that, since every invertible sheaf on a smooth (hence irreducible) curve \(C\in {\mathcal {H}}_s\) is \({\mathcal {O}}_{{\mathbb {P}^{3}}}(1)|_C\)-stable, it follows that the functors \(\mathbf {J}_s=\mathbf {J}^{ss}\times _{{\mathcal {H}}}{\mathcal {H}}_s\) and \(\mathbf {M}\times _{{\mathcal {H}}}{\mathcal {H}}_s\) are isomorphic, and they are represented by the scheme
where \(\pi _s=\pi |_{\mathbb {M}_s}\). Hence, the functor \(\widetilde{\mathbf {J}}_s= \mathbf {J}_s\times _{{\mathcal {H}}_s}\widetilde{{\mathcal {H}}}_s\) is represented by the scheme
of finite type over \(\widetilde{{\mathcal {H}}}_s\), which is an open subscheme of \(\widetilde{\mathbb {J}}\). Note that, by construction, \(\pi _s\) is a fibration
where \({\mathrm {Pic}}^{g-1}(C)=\{[L]\in {\mathrm {Pic}}(C)\ |\ \deg L=g-1\}\). This implies that \(\mathbb {M}_s\) is smooth and irreducible, since \({\mathcal {H}}_s\) is clearly smooth and irreducible. In addition,
is also a fibration with fiber \({\mathrm {Pic}}^{g-1}(C)\) which is smooth since \(\widetilde{{\mathcal {H}}}_s\) is smooth as an étale cover of \({\mathcal {H}}_s\).
Now consider the closure
of the scheme \(\mathbb {M}_s\) in \(\mathbb {M}\). In the next section (see the proof of Lemma 20 (iv)), we will make use of the following lemma.
Lemma 12
\(\mathbb {M}'\subset \mathbb {M}^0\).
Proof
It is known (see, e.g., [9, Section 0.2], [18, Fact 4.4]) that the algebraic space \(\mathbb {P}\) representing the functor \(\mathbf {P}\) is formally smooth over \({\mathcal {H}}\). This implies that the scheme \(\widehat{\mathbb {J}}\), hence also the schemes \(\widetilde{\mathbb {J}}\) and \(\widetilde{\mathbb {J}}_s\), is formally smooth over \(\widetilde{{\mathcal {H}}}\).
Take a point \(x=(C,[L]_S)\in \mathbb {M}'\). By definition, L is an invertible sheaf on C. We have to show that \(x\in \mathbb {M}^0\). For this, let \(\tilde{x}\in \widetilde{\mathbb {J}}\) be any point in the fiber \(\varphi ^{-1}(x)\) where \(\varphi \) is defined in (40) and let \(w=\tilde{\pi }(\tilde{x})\). Refining the étale base change \(\sigma \), we may assume \(\widetilde{{\mathcal {H}}}=\sqcup \widetilde{U}_i\), where each \(\widetilde{U}_i=\sigma ^{-1}(U_i)\) is irreducible and \(\cup U_i\) is an open cover of \({\mathcal {H}}\). The point \(w\in \widetilde{{\mathcal {H}}}\) lies in some \(\widetilde{U}_i\), and let X be any irreducible component of \(\tilde{\pi }^{-1}(U_i)\) containing \(\tilde{x}\). Since \({\mathcal {H}}_s\) is an irreducible dense open subset of \({\mathcal {H}}\), it follows that \(U_{is}=U_i\cap {\mathcal {H}}_s\) is a dense open subset of \(U_i\). Hence, \(\widetilde{U}_{is}=\sigma ^{-1}(U_{is})\) is a dense open subset.
Next, as \(\tilde{\pi }:\widetilde{\mathbb {J}}\rightarrow \widetilde{{\mathcal {H}}}\) is formally smooth, \(\tilde{\pi }|_X:X\rightarrow \widetilde{U}_i\) is dominant. Hence, \(X'=X\cap \tilde{\pi }^{-1}(\widetilde{U}_{is})\) is dense open in both X and \(\tilde{\pi }^{-1}(\widetilde{U}_{is})\). Thus, \(\varphi (X')\) is dense in \(\varphi (X)\) and, by construction [see (42)–(44)], \(\varphi (X')\) lies in \(\mathbb {M}_s\) and contains a nonempty open subset of \(\mathbb {M}_s\). Since \(\mathbb {M}_s\) is irreducible, \(\mathbb {M}^0=\overline{\mathbb {M}}_s=\overline{\varphi (X')}=\overline{\varphi (X)}\), and, by construction, \(x\in \overline{\varphi (X)}\). \(\square \)
Note that, since \(\widetilde{\mathbb {J}}\) is formally smooth over \(\widetilde{{\mathcal {H}}}\), it follows that \(\widetilde{\mathbb {J}}_s\) is dense and open in \(\widetilde{\mathbb {J}}\); hence, (44) implies that
where \(\dim {\mathcal {H}}\) is given by (26).
Take any curve \(C\in {\mathcal {H}}_s\). Then, the set \(U_C:=\{[L]\in {\mathrm {Pic}}^{g-1}(C)\ |\ h^0(L)=h^1(L)=0\}\) is dense and open in \({\mathrm {Pic}}^{g-1}(C)\) since it is the complement of the divisor \(\Theta ={{\mathrm{im}}}(a)\), where \(a:S^{g-1}C\rightarrow {\mathrm {Pic}}^{g-1}(C),\ D\mapsto {\mathcal {O}}_C(D)\) is the Abel–Jacobi map. Therefore, denoting
we obtain that \(\mathbb {J}\) is a nonempty and, by semicontinuity, open subset of \(\mathbb {M}_s\), which is dense and smooth as \(\mathbb {M}_s\) is smooth and irreducible. Similarly, \(\widetilde{\mathbb {J}}_0\) is smooth, dense and open in \(\widetilde{\mathbb {J}}_s\). Note also that by (35), \({\widetilde{\mathbb {J}}_0\times _{\widetilde{{\mathcal {H}}}}{\widetilde{{\mathcal {Z}}}}}\) carries a universal (Poincaré) line bundle, which is
Next, for \(c\ge 0\) and any point \(([F],C,[L])\in {\mathcal {I}}(c)\times \mathbb {J}\), set
Recall that \({\mathcal {I}}(0)=\{{\mathrm {pt}}\}\).
Lemma 13
For each \(c\ge 0\), there is a smooth, dense and open subset \(({\mathcal {I}}(c)\times \mathbb {J})_e^0\) of \({\mathcal {I}}(c)\times \mathbb {J}\) such that, for any \(([F],C,[L])\in ({\mathcal {I}}(c)\times \mathbb {J})_e^0\), one has:
-
(i)
\(h^i(L)=h^i(L^{-1}\otimes \omega _C)=0,\ i=0,1;\)
-
(ii)
\(h^1(F\otimes L(2)) = h^1(F\otimes (L^{-1}\otimes \omega _C)(2))=0\);
-
(iii)
\(\mathbb {P}{\mathrm {Hom}}(F,C,L)_e\) is a dense open subset of \(\mathbb {P}({\mathrm {Hom}}(F,L(2)))\);
-
(iv)
$$\begin{aligned} \dim \mathbb {P}{\mathrm {Hom}}(F,C,L)_e=4d_1d_2-1. \end{aligned}$$(48)
-
(v)
There is a smooth, dense and open subset \(({\mathcal {I}}(c)\times \mathbb {J})_e\) of \({\mathcal {I}}(c)\times \mathbb {J}\) containing \(({\mathcal {I}}(c)\times \mathbb {J})_e^0\) and such that, for any \(([F],C,[L])\in ({\mathcal {I}}(c)\times \mathbb {J})_e\), the statements (iii) and (iv) and the equalities \(h^0(L)=h^1(L)=h^1(F\otimes L(2))=0\) from (i) and (ii) above are true.
Proof
Take a point \((C,[L])\in \mathbb {J}_0\cap \mathbb {J}_s\), so that
We first consider the case \(c=0\), so that \(F\otimes L(2) \simeq 2\cdot L(2)\) and \({\mathrm {Hom}}(F,L(2)) \simeq H^0(2\cdot L(2))\). Items (ii), (iii) and (v) follow immediately. As for item (iv), just note that \(\chi (L(k))=d_1d_2\cdot k\) (since \(\chi (L)=0\) and \(\deg C=d_1d_2\)); thus, \(h^0(L(2))=\chi (L(2))=2d_1d_2\).
Next, let \(c>0\); take a \({}^{,}\)t Hooft bundle \([F]\in {\mathcal {I}}(c)\), i.e., a bundle fitting in an exact triple
where Y is a union of \(c+1\) disjoint lines in \({\mathbb {P}^{3}}\). Choose Y in such a way that \(Y\cap C=\emptyset \). Then, tensoring the above triple with L(2), we obtain exact triples
The equalities (49) imply
so that (50) yields
for the above chosen point \(([F],C,[L])\in {\mathcal {I}}(c)\times \mathbb {J}\). Since, by semicontinuity, the vanishing of \(h^1(F\otimes L(2))\) and \(h^1(F\otimes (L^{-1}\otimes \omega _C)(2))\) is an open condition on \(([F],C,[L])\in {\mathcal {I}}(c)\times \mathbb {J}\), it follows that the set
is a nonempty (hence dense) open subset of \({\mathcal {I}}(c)\times \mathbb {J}\). Next, from (49) and (50) we obtain the exact sequence
Since the sheaves \({\mathcal {O}}_{{\mathbb {P}^{3}}}(1)\) and \({\mathcal {O}}_{{\mathbb {P}^{3}}}(3)\) are very ample, it follows from (49) that the linear series |L(1)| and |L(3)| on C have no fixed points. This implies that there exist such sections \(s_i\in H^0(L(i)),\ i=1,3,\) that
Take any section \(s'\in \varepsilon ^{-1}(s_3)\), where \(\varepsilon \) is the epimorphism in (53). Then, the last equality implies that the section \(s:=s'+s_1\in H^0(F\otimes L(2))\) has no zeroes. Hence, its transpose \(\varphi ={}^{\sharp }s:F\simeq F^{\vee }\rightarrow L(2)\) is an epimorphism, i.e.,
Since \(\mathbb {P}{\mathrm {Hom}}(F,C,L)_e\) is an open subset of the irreducible space \(\mathbb {P}({\mathrm {Hom}}(F,L(2)))\), it is dense in \(\mathbb {P}({\mathrm {Hom}}(F,L(2)))\). Moreover, (54) is an open condition on the point ([F], C, [L]) in \(({\mathcal {I}}(c)\times \mathbb {J})'\). Thus in view of (52), there exists a dense open subset \(({\mathcal {I}}(c)\times \mathbb {J})_e\) of \(({\mathcal {I}}(c)\times \mathbb {J})'\) (hence of \({\mathcal {I}}(c)\times \mathbb {J}\)) for which the statements (i)–(iii) of Lemma hold. Besides, the smoothness of \(({\mathcal {I}}(c)\times \mathbb {J})_e\) follows from that of \({\mathcal {I}}(c)\) (see [16]) and of \(\mathbb {J}\).
Next, since \(F\simeq F^{\vee }\), we have
Note that
where the first equality follows from the exact sequence (51), while the second equality follows from (53). Putting the last two equations together, we obtain (48).
At last, the statement (v) is clear by semicontinuity. \(\square \)
In particular, note that \(({\mathcal {I}}(0)\times \mathbb {J})_e=\mathbb {J}\).
Next, using Lemma 13 consider, for each \(c\ge 1\) and \(d_2\ge d_1\ge 1\), the set
and the surjective projection
with fiber
When \(c=0\), one must also quotient out by the action of GL(2) on the trivial sheaf \(2\cdot {\mathcal {O}}_{\mathbb {P}^{3}}(2)\) in order to obtain a family of isomorphism classes of torsion free sheaves. Therefore, we define:
Also denote
Remark 14
Note that \(\widetilde{W}(d_1,d_2,c)\) with \(c\ge 1\) is a dense open subset of a Severi–Brauer variety fibered over \(\mathcal {B}:=({\mathcal {I}}(c)\times \mathbb {J})_e\) with fibers, given by \({\mathbb {P}}^{4d_1d_2-1}\) via the projection \(\pi \).
Indeed, let \(\widetilde{\mathbf {V}}:=\mathcal {B}\times _{\mathcal {H}} \widetilde{\mathcal {H}}\rightarrow \mathcal {B}\) be an étale covering induced by (32). According to [13, Section 4], over \({\mathcal {I}}(c)\) there exists (locally in the étale topology) a universal rank-2 vector bundle. This means that there exists an open étale covering \(\Phi :W\rightarrow {\mathcal {I}}(c)\) and a rank 2 vector bundle \(\mathbf {E}\) over \({\mathbb {P}^{3}}\times W\) such that, for any \(w\in W\), \(\mathbf {E}|_{{\mathbb {P}^{3}}\times w}\simeq E_t\), where \(t=\Phi (w)\in {\mathcal {I}}(c)\) and \(E_t\) denotes the instanton bundle whose isomorphism class is represented by t. Let \(\widetilde{\mathbf {U}}:=W\times _{{\mathcal {I}}(c)} \widetilde{\mathbf {V}}\), and let \(\widetilde{\mathbf {\Gamma }}:=\widetilde{\mathbf {U}}\times _{\widetilde{\mathcal {H}}}\widetilde{\mathcal {Z}}\); let \(\varvec{\iota }:\widetilde{\mathbf {\Gamma }}\hookrightarrow \widetilde{\mathbf {U}}\times {\mathbb {P}^{3}}\) be the lift into \(\widetilde{\mathbf {U}}\times {\mathbb {P}^{3}}\) of the universal family of curves \(\mathcal {Z}\). Let also \(\mathbf {E}_{\widetilde{\mathbf {U}}}\) be the lift into \(\widetilde{\mathbf {U}}\times {\mathbb {P}^{3}}\) of the sheaf \(\mathbf {E}\) and let \(\mathbf {L}\) be the lift onto \(\widetilde{\mathbf {\Gamma }}\) of the sheaf \(\widetilde{\mathbb {L}}_0\) defined in (47). We thus obtain a vector bundle \(\varvec{\tau }:= \mathcal {H}om_{\widetilde{\mathbf {\Gamma }}/\widetilde{\mathbf {U}}} (\mathbf {E}_{\widetilde{\mathbf {U}}},\varvec{\iota }_*\mathbf {L}(2))\) over \(\widetilde{\mathbf {U}}\), the fiber of which over a point \(u\in \widetilde{\mathbf {U}}\) lying over a point \(([F],C,[L])\in \mathcal {B}\) is by construction isomorphic to \({\mathrm {Hom}}(F,L(2))\). Hence, by (48) the associated projective bundle \(\mathbf {P}\varvec{\tau }\rightarrow \widetilde{\mathbf {U}}\) is a \({\mathbb {P}}^{4d_1d_2-1}\)-fibration. Applying to it the argument from the proof of Proposition 6.4 from [14], we obtain that this fibration descends to a Severi–Brauer variety \(\mathbf {p}_{\mathcal {B}}:\mathbf {P}_{\mathcal {B}}\rightarrow \mathcal {B}\) with fibers \({\mathbb {P}}^{4d_1d_2-1}\) over \(\mathcal {B}\) such that, by the above, for any point \(([F],C,[L])\in \mathcal {B}\) one has
This, together with (57), shows that the variety \(\mathbf {P}_{\mathcal {B}}\) contains \(\widetilde{W}(d_1,d_2,c)\) as a dense open subset.
Finally, for the case \(c=0\), note that although the fibers of the projection \(\pi :\widetilde{W}(d_1,d_2,0)\rightarrow \mathbb {J}^0\) are not open subsets of a projective space, they are still smooth.
From the previous remark and the smoothness of \(({\mathcal {I}}(c)\times \mathbb {J})_e\) (see Lemma 13), we obtain the following statement.
Theorem 15
For each \(c\ge 0\) and \(d_2\ge d_1\ge 1\), \(\widetilde{W}(d_1,d_2,c)\) has a natural structure of a smooth integral scheme of dimension
where \(\dim {\mathcal {H}}\) is given by (26), and, for \(c\ge 1\), the map
defined in (56) is a morphism. Respectively, \(\widetilde{W}(d_1,d_2,c)^0\) is a dense open subscheme of \(\widetilde{W}(d_1,d_2,c)\).
Proof
It is enough to prove (61). For \(c\ge 1\), since \(\dim {\mathcal {I}}(c)=8c-3\), (61) follows from (46) and (48). For \(c=0\), one easily sees from (58) and (46) that
as desired.
Now for any point \(\mathbf {w}=([F],C,[L],\mathbf {k}\varphi )\in \widetilde{W}(d_1,d_2,c)\) set
By definition, we have an exact triple
One easily checks, using the irreducibility of C, that \(E(\mathbf {w})\) is a stable sheaf (see [14, Corollary 4.2 and Lemma 4.3]) and, in fact, \([E(\mathbf {w})]\in {\mathcal {M}}(c+d_1d_2)\). Moreover, Lemma 13(i) and the triple (62) twisted by \({\mathcal {O}}_{{\mathbb {P}^{3}}}(-2)\) yield
Given a point \((C,[L])\in \mathbb {J}\), we call the invertible \({\mathcal {O}}_C\)-sheaf L a theta -characteristic on C if
Consider a subset of \(\mathbb {J}\) defined as
It is a locally closed subset of \(\mathbb {J}\). (Indeed, \(\Theta _{\mathbb {J}}\) is a fixed point set of an involution \(\mathbb {J}\rightarrow \mathbb {J},\ (C,[L])\mapsto (C,[\omega _C\otimes L^{-1}])\).)
Denote
where \(\overline{\Theta }_{\mathbb {J}}\) is the closure of \(\Theta _{\mathbb {J}}\) in \(\mathbb {J}\). By definition, \(W(d_1,d_2,c)\) is an open subset of \(\widetilde{W}(d_1,d_2,c)\). Since for \(p_a(C)>0\) the set \(\overline{\Theta }_{\mathbb {J}}\) is clearly a proper closed subset of \(\mathbb {J}\), it follows that for \(p_a(C)>0\) the set \(W(d_1,d_2,c)\) is a dense open subset of \(\widetilde{W}(d_1,d_2,c)\).
Proposition 16
For an arbitrary closed point \(\mathbf {w}=([F],C,[L],\mathbf {k}\varphi )\in W(d_1,d_2,c)\) with \(c\ge 0\), and \((d_1,d_2)\ne (1,1)\), \((d_1,d_2)\ne (1,2)\), the sheaf \(E=E(\mathbf {w})\) satisfies the relations:
where \(p_a(C)\) and \(h^1(N_{C/{\mathbb {P}^{3}}})\) are given by (25) and (27), respectively.
Proof
The conditions \((d_1,d_2)\ne (1,1)\), \((d_1,d_2)\ne (1,2)\) imply that \(p_a(C)>0\), so that \(W(d_1,d_2,c)\) is nonempty. Apply the functor \({\mathrm {Hom}}(L(2),-)\) to the triple (62):
Next, apply the functor \(\mathcal {H}om(L(2),-)\) to (62). Using the vanishing of the sheaves \({\mathcal {H}}{} { om}(L(2),F)\), \({\mathcal {E}}{} { xt}^1(L(2),F)\) and \({\mathcal {E}}{} { xt}^i(F,L(-2)),\ i=1,2,\) (note that \(\dim L(2)=1\) and F is locally free on \({\mathbb {P}^{3}}\)), we obtain an isomorphism \(\partial _1:\mathcal {H}om(L(2),L(2))\overset{\simeq }{\rightarrow } {\mathcal {E}}{} { xt}^1(L(2),E)\) and an exact sequence
Respectively, applying the functor \({\mathcal {H}}{} { om}(\cdot ,L(-2))\) to the triple (62) yields an isomorphism
The isomorphisms \(h^1(\partial ):\ H^1(\mathcal {H}om(L(2),L(2)))\overset{\simeq }{\rightarrow }H^1({\mathcal {E}}{} { xt}^1(L(2),E))\), the homomorphism \(\delta \) in (67) and the monomorphism \(h^0(\partial _2):\ H^0({\mathcal {E}}{} { xt}^1(L(2),L(2)))\rightarrow H^0({\mathcal {E}}{} { xt}^2(L(2),E))\) induced by (68) fit in the commutative diagram

in which the vertical exact triples come from the spectral sequences
respectively. Now restrict the triple (62) onto the curve C. Using the relation \(\det F\otimes {\mathcal {O}}_C \simeq {\mathcal {O}}_C\), we obtain an exact triple \(0\rightarrow L^{-1}(-2)\rightarrow F\otimes {\mathcal {O}}_C\rightarrow L(2)\rightarrow 0\). Tensoring this triple with the invertible \({\mathcal {O}}_C\)-sheaf \({\mathcal {E}}{} { xt}^2(L(2),{\mathcal {O}}_C)\) and using the isomorphisms \({\mathcal {E}}{} { xt}^2(L(2),{\mathcal {O}}_C)\otimes L^{-1}(-2)\simeq {\mathcal {E}}{} { xt}^2(L(2),L^{-1}(-2))\), \({\mathcal {E}}{} { xt}^2(L(2),{\mathcal {O}}_C)\otimes F\simeq {\mathcal {E}}{} { xt}^2(L(2),F)\), \({\mathcal {E}}{} { xt}^2(L(2),{\mathcal {O}}_C)\otimes L(2)\simeq {\mathcal {E}}{} { xt}^2(L(2),L(2))\), we obtain the exact triple
This triple together with (68) yields an exact triple
Note that, since L is not a theta-characteristic on C, it follows that the sheaf
is an invertible \({\mathcal {O}}_C\)-sheaf of degree 0, nonisomorphic to \({\mathcal {O}}_C\); hence, it has no sections. Thus, the above triple gives an isomorphism
This is the lower horizontal isomorphism in the diagram (70) from which it follows that the homomorphism \(\delta \) is an isomorphism:
Next, from Lemma 13(i) and the triple (50) twisted by \({\mathcal {O}}_{{\mathbb {P}^{3}}}(-4)\) it follows easily that \(H^0(F\otimes L(-2))=0\), and the Serre–Grothendieck duality together with the isomorphism \(F\simeq F^{\vee }\) implies
Similarly, since \(\dim C=1\), it follows that \({\mathrm {Ext}}^1(L(2),F(-4))\simeq H^2(F\otimes L(-2))=0\). Thus, the exact sequence
together with the equality \({\mathrm {Hom}}(F,F(-4))=0\) (note that F is stable) yields \({\mathrm {Hom}}(E,F(-4))=0\), and again by Serre–Grothendieck duality we obtain
Next, twisting the triple (62) with \(F^{\vee }\simeq F\) and passing to cohomology, we obtain an exact sequence \(H^1(F\otimes L(2))\rightarrow H^2(F^{\vee }\otimes E)\rightarrow H^2(F^{\vee }\otimes F)\). Using the vanishing of \(H^2(F^{\vee }\otimes F)\) (see [16]) and of \(H^1(F\otimes L(2))\) (Lemma 13(ii)), we get since F is locally free:
Now apply the functor \({\mathrm {Hom}}(-,E)\) to the triple (62) and use (76) and (77) to obtain the isomorphism
The sequence (67) together with (74), (75) and (78) yields an exact sequence
Next, since \(F\simeq F^{\vee }\) is locally free, the Serre–Grothendieck duality on \({\mathbb {P}^{3}}\) and on C yields:
On the other hand, Riemann–Roch for the sheaf \(F\otimes (L^{-1}\otimes \omega _C)(2)\) and item (ii) of Lemma 13 imply \(h^0(F\otimes (L^{-1}\otimes \omega _C)(2))^{\vee }=4d_1d_2\), hence (78) and (80) yield
Next, using the fact that \(H^2({\mathcal {E}}{} { xt}^2(L,L))=0\) since \(\dim {\mathcal {E}}{} { xt}^2(L,L)=1\), we obtain that the spectral sequence \(H^p({\mathcal {E}}{} { xt}^q(L,L))\Rightarrow {\mathrm {Ext}}^{\bullet }(L,L)\) yields an exact triple
Note that, in view of the isomorphisms
and of Serre duality \(h^1({\mathcal {O}}_C(d_1+d_2))=h^0({\mathcal {O}}_C(-4))=0\), we obtain by Riemann–Roch
This, together with the above triple, yields
Now (65) follows by substituting the last equality in (81) and using (25). The equality (66) follows from here in view of the relation
(see Lemma 10 above). \(\square \)
Consider the map
Using Remark 14 and Theorem 15, one easily sees that f is a morphism.
Theorem 17
For any point \(\mathbf {w}\in W(d_1,d_2,c)\) with \(c\ge 0\), and \((d_1,d_2)\ne (1,1)\), \((d_1,d_2)\ne (1,2)\), one has
In addition, the morphism \(f|_{W(d_1,d_2,c)}\) is an open embedding. Thus,
is a dense smooth open subset of an irreducible component
of \({\mathcal {L}}(c+d_1d_2)\), hence also of \({\mathcal {M}}(d_1d_2+c)\).
Proof
Equality (83) follows by comparing formulas (61) and (66) and using (25)–(27).
As for the second claim, note that \(f|_{W(d_1,d_2,c)}\) is an injective morphism by construction. Its Kodaira–Spencer map \(df|_{\mathbf {w}}:\ T_{\mathbf {w}}W(d_1,d_2,c)\rightarrow T_{f(\mathbf {w})}\mathcal {M}(d_1d_2+c)= {\mathrm {Ext}}^1(E(\mathbf {w}),E(\mathbf {w}))\) is an isomorphism by (83) for any \(\mathbf {w}\in W(d_1,d_2,c)\). The assertion follows. \(\square \)
Remark 18
The cases \((d_1,d_2)=(1,1)\), and \((d_1,d_2)=(1,2)\), in which C is either a line or a conic, respectively, were studied in [14], where elementary transformations of instanton bundles by smooth rational curves of arbitrary degree are considered. In fact, for \(k=1,2\), \(\overline{\mathcal {C}(1,k,c)}\) coincides with the variety \(\overline{{\mathcal {D}}(k,c+k)}\) introduced in [14, Section 6]. It turns out that \(\overline{{\mathcal {D}}(k,c+k)}\) are irreducible projective varieties of dimension \(8(c+k)-4\) lying in the closure \(\overline{{\mathcal {I}}(c+k)}\) of \({\mathcal {I}}(c+k)\) within \({\mathcal {M}}(c+k)\). In particular, for \(k=1,2\), \(\overline{\mathcal {C}(1,k,c)}\) does not define a new irreducible component of \({\mathcal {M}}(c+k)\), differently from the conclusion of Theorem 17.
We conclude this section with a result in the same spirit of [7, Proposition 3.6] and Theorem 9 above, showing that the number of irreducible components of \({\mathcal {M}}(n)\) whose generic points correspond to sheaves with 1-dimensional singularities becomes arbitrarily large as n grows.
Theorem 19
Let \(\eta _n\) denote the number of irreducible components of \({\mathcal {M}}(n)\) whose generic points correspond to sheaves with 1-dimensional singularities. Then, \(\lim _{n\rightarrow \infty }\eta _n=\infty \).
Proof
Indeed, the number of ways in which a given positive integer n can be represented as a sum \(n=c+d_1d_2\), where \(c,\ d_1\) and \(d_2\) are positive integers and \((d_1,d_2)\ne (1,1),\ (d_1,d_2)\ne (1,2)\), is unbounded as n grows. Thus, the result follows from Theorem 17.
4 Nonemptiness of the intersection \(\overline{\mathcal {C}(d_1,d_2,c)}\cap \overline{{\mathcal {I}}(n)}\)
In this section, we will perform an inductive procedure showing that each irreducible component \(\overline{\mathcal {C}(d_1,d_2,c)}\) of \({\mathcal {M}}(d_1d_2+c)\) (with \(c\ge 0\), and \((d_1,d_2)\ne (1,1)\), \((d_1,d_2)\ne (1,2)\)), constructed in Theorem 17, has a nonempty intersection with the closure of the instanton component \(\overline{{\mathcal {I}}(d_1d_2+c)}\).
We start with a construction of a reduced curve \(C\in {\mathcal {H}}={\mathcal {H}}_{d_1,d_2}\) completely decomposable into a union of projective lines and satisfying some additional properties. Namely, we prove the following lemma.
Lemma 20
For any \(1\le d_1\le d_2\), there exists a curve \(C\in {\mathcal {H}}\) which is completely decomposable into a union of \(d_1d_2\) projective lines
such that
-
(i)
The \({\mathcal {O}}_C\)-sheaf
$$\begin{aligned} L_0=\underset{j=1}{\overset{d_1d_2}{\bigoplus }} {\mathcal {O}}_{\ell _j}(-1) \end{aligned}$$(86)is \({\mathcal {O}}_{\mathbb {P}^{3}}(1)|_C\)-semistable.
-
(ii)
There exists a curve Y with a marked point \(0\in Y\), a morphism \(f:Y\rightarrow {\mathcal {H}}\) and a sheaf \(\mathbf {L}\) on \(Y\times _{{\mathcal {H}}}{\mathcal {Z}}\), flat over Y and such that, for \(C_t:=pr^{-1}(f(t)),\ t\in Y\), where \(pr:{\mathcal {Z}}\rightarrow {\mathcal {H}}\) is the projection, one has
$$\begin{aligned} \mathbf {L}|_{C_0}\simeq L_0, \end{aligned}$$(87)where \(C_0\) is the curve C from (85), and
$$\begin{aligned} \mathbf {L}|_{C_t}\ \mathrm {is}\, \mathrm {locally}\, \mathrm {free},\ \ \ t\in Y^*:=Y\setminus \{0\}. \end{aligned}$$(88)
Proof
Let \(x_i=(\mathbb {P}_{i1}^2,\ldots ,\mathbb {P}_{id_i}^2)\in ({\mathbb {P}}^{3\vee })^{\times d_i},\ \ \ i=1,2,\) be two collections of hyperplanes in \({\mathbb {P}^{3}}\), and set \(\ell _{j_1j_2}:=\mathbb {P}_{1j_1}^2\cap \mathbb {P}_{2j_2}^2,\ 1\le j_1\le d_1,\ 1\le j_2\le d_2\). It is clear that, for a general choice of the points \(x_i\in ({\mathbb {P}}^{3\vee })^{\times d_i},\ i=1,2\), the curve \(C={\cup }_{j_1,j_2=1}^{d_1,d_2}\ell _{j_1j_2}\) satisfies the statement of Lemma. We re-enumerate the lines \(\ell _{j_1j_2}\) as the lines \(\ell _j\) in (85).
Next, the sheaf \(L_0\) in (86) is polystable as a direct sum of stable \({\mathcal {O}}_{\mathbb {P}^{3}}(1)\)-sheaves \({\mathcal {O}}_{\ell _j}(-1)\). Hence, it is \({\mathcal {O}}_{\mathbb {P}^{3}}(1)|_C\)-semistable.
For the second item, set \(C_1:=\ell _1\) and, for \(2\le k\le d_1d_2-1\), consider a sub-curve \(C_k:={{\cup }_{j=1}^{k}}\ell _j\) of C and a subscheme \(D_k:=\ell _{k}\cap C_{k-1}\) of \(\ell _{k}\). Since \(C\in {\mathcal {H}}\), it follows that \(D_k\) is a reduced divisor on \(C_k\); let, say, \(D_k=a_{k1}+\cdots +a_{km_k}\). Consider a sequence of \({\mathcal {O}}_{C_k}\)-sheaves \(L_{k}\), where \(L_{1}:={\mathcal {O}}_{\ell _1}(-1)\) and for \(2\le k\le d_1d_2-1\) the sheaf \(L_k\) is defined inductively as an extension
Each such extension is given by an element of the group \({\mathrm {Ext}}^1({\mathcal {O}}_{\ell _k}(-1),L_{k-1})\), and an easy calculation (cf. [9, proof of Lemma 4]) shows that
Furthermore, for any point \(\tau _k\in \mathbb {A}^{m_k*}:=\{(t_1,\ldots ,t_{m_k})\in \mathbb {A}^{m_k}\ |\ t_j\ne 0,\ j=1,\ldots , m_k\}\), the sheaf \(L_k\) is locally free at the points of \(D_k\). Hence, the last extension \(L_{d_1d_2}=L_{d_1d_2}(\mathbf {t})\) in the sequence (89) defined by the element \(\mathbf {t}=(\tau _1,\ldots ,\tau _{d_1d_2})\in \mathbf {A}^*:= \mathbb {A}^{m_1*}\times \cdots \times \mathbb {A}^{m_{d_1d_2}*}\) is a locally free \({\mathcal {O}}_C\)-sheaf. In addition, from (89) it follows immediately that, for this point \(\mathbf {t}\), the sequence of sheaves \(0\subset L_1\subset L_2\subset \cdots \subset L_{d_1d_2}(\mathbf {t})\) is a Jordan–Hölder filtration of \(L_{d_1d_2}(\mathbf {t})\) with the associated graded sheaf \(L_0\) in (86). Thus,
Hence, since \(L_{d_1d_2}(\mathbf {t})\) is a locally free \({\mathcal {O}}_C\)-sheaf, it follows that, in the notation of Lemma 12,
Now, recall the construction of the moduli space \(\mathbb {M}\) containing \(\mathbb {M}^0\) as a closed subscheme (see, e. g., [13, Thm 4.3.7]). Namely, \(\mathbb {M}\) is obtained as a GIT-quotient \(p:R\rightarrow R/\!\!\!\!/GL(N)=\mathbb {M}\) for an appropriately chosen open subset R of the Quot-scheme \({\mathrm {Quot}}_{{\mathcal {Z}}/{\mathcal {H}}}(\mathcal {V},P)\), where P is the Hilbert polynomial defined in (31), \(\mathcal {V}={\mathcal {O}}_{{\mathcal {Z}}/{\mathcal {H}}}(-m)^{\oplus N},\ N= P(m)\) and m large enough. Now, for the point \(s=[L_0]_S\in \mathbb {M}^0\), there exists a point \([\rho :\mathcal {V}_s\twoheadrightarrow L_0]\in R\) such that \(p([\rho ])=s\). Consider the closed subscheme \(R_0=p^{-1}(\mathbb {M}^0)\) of R. Since \(R_0\) is quasi-projective over \(\mathbb {M}^0\) and \(\mathbb {M}^s\) is open dense in \(\mathbb {M}^0\), it follows that there exists a curve Y in \(R_0\) passing through the point \(0=[\rho ]\) and such that
By the definition of \(\mathbb {M}^s\), the last inclusion means that the universal quotient sheaf on \(R_0\times _{{\mathcal {H}}}{\mathcal {Z}}\) being restricted onto \({\mathcal {Z}}_Y=Y\times _{{\mathcal {H}}}{\mathcal {Z}}\) becomes a sheaf \(\mathbf {L}\) such that, for \(t\in Y^*\), the sheaf \(\mathbf {L}|_{C_t}\) is locally free, where \(C_t=pr^{-1}(f(t))\), and \(f=p|_Y:Y\rightarrow {\mathcal {H}}\) and \(pr:{\mathcal {Z}}\rightarrow {\mathcal {H}}\) is the projection. Besides, by the above, \(\mathbf {L}|_{C_0}\simeq L_0\). \(\square \)
Lemma 21
For any \(c\ge 0\), \(1\le d_1\le d_2\), and any \([F]\in {\mathcal {I}}(c)\), there exists a curve \(C\in {\mathcal {H}}\) satisfying the properties of Lemma 20, and, in addition, the following ones:
Proof
Both (92) and (93) are immediate when \(c=0\).
Since every instanton bundle of charge \(c>0\) is stable, there is, by the Grauert–Müllich Theorem (see [2, 13]), a divisor \(D_{F}\) in the Grassmannian \(Gr=Gr(1,{\mathbb {P}^{3}})\) such that, for any line \({\mathbb {P}^{1}}\in Gr\setminus D_{F}\), \(F|_{\mathbb {P}^1_i}\simeq 2{\mathcal {O}}_{\mathbb {P}^1_i}\). Thus, for a general choice of the points \(x_i\in ({\mathbb {P}}^{3\vee })^{\times d_i},\ i=1,2\), the condition (92) above holds.
From (92) and (86), it follows immediately that
Since \(\mathbf {L}\) is flat over Y, the rest is clear by semicontinuity (after possibly shrinking the curve Y). \(\square \)
In the notation of Lemma 20, let \(p_Y:{\mathcal {Z}}_Y={\mathcal {Z}}\times _{{\mathcal {H}}}{\mathcal {Z}}\rightarrow Y\) and \(\varvec{\iota }_Y:{\mathcal {Z}}\hookrightarrow Y\times {\mathbb {P}^{3}}\) be the natural projections; let \(\varvec{F}:=F\boxtimes {\mathcal {O}}_Y\), \(\varvec{\iota }_{Y*}\mathbf {L}(2):=\varvec{\iota }_{Y*} \mathbf {L}\otimes {\mathcal {O}}_{{\mathbb {P}^{3}}}(2)\boxtimes {\mathcal {O}}_Y\), and \(\varvec{\tau }_Y:={\mathcal {H}}{} { om}_{{\mathcal {Z}}_Y/Y}(\varvec{F}, \varvec{\iota }_{Y*}\mathbf {L}(2))\). In addition, consider the projections \(\mathbf {p}_Y:{\mathbb {P}}\varvec{\tau }_Y\rightarrow Y\), and \(\mathbf {p}_Y:{\mathbb {P}}\varvec{\tau }_Y^*:={\mathcal {P}}\varvec{\tau }_Y\times _YY^*\rightarrow Y^*\); by construction, \(\mathbf {p}_Y\) is a projective bundle over Y such that,
By Lemma 21, one has a morphism
and from (60) and (95), it follows that
Moreover, using Lemma 13, (iii)–(v), consider the open dense subset \(\widetilde{W}_Y\) of \({\mathcal {P}}\varvec{\tau }_Y\) defined as
Comparing (97) with (55) and using (96), we obtain the relation
On the other hand, consider the morphism
From (82) and (98), it follows that \(f_Y|_{\widetilde{W}_{Y^*}}\) coincides with the composition
In view of Theorem 17, this implies that \(f_Y(\widetilde{W}_{Y^*})\subset \overline{\mathcal {C}(d_1,d_2,c)}\). Since \(\overline{\mathcal {C}(d_1,d_2,c)}\) is projective, this implies that also
In particular, since by (97)
where \(C_0\) is the curve C defined in (85) and \(\overline{\mathcal {C}(d_1,d_2,c)}\) is a projective scheme, we obtain the following result.
Theorem 22
In the conditions and notation of Lemma 20 and of Lemma 21, there is a morphism
Now, take a point
and, as above, denote
Next, using (86), set
so that
and we have splitting exact triples
where each \(\varepsilon _{(k)}\) is the projection onto a direct summand. Set \(\varphi _{(d_1d_2)}:=\varphi \) and, using (101), define the epimorphisms \(\varphi _{(k)}\) as the composition
Set \(E_{(k)}:=\ker \varphi _{(k)}\), so that, by the above,
and, for \(2\le k\le d_1d_2\), there is a commutative diagram

in which the right vertical triple is the triple (102) twisted by the sheaf \({\mathcal {O}}_{\mathbb {P}^{3}}(2)\).
We are going to show, by induction on k, that
First, in the case \(k=1\) we have the exact triple
which by Jardim et al. [14, Proposition 7.2] yields (105) for \(k=1\).
Next, given \(k\ge 2\), assume that (105) is true for \(k-1\), i. e., in the diagram (104),
This implies that there exists a curve T with a marked point \(0\in T\) and a sheaf \(\mathbf {E}'\) on \({\mathbb {P}^{3}}\times T\), flat over T and such that
and, for \(t\in T^*=T\smallsetminus \{0\}\), the sheaf \(E'_t:=\mathbf {E}'|_{{\mathbb {P}^{3}}\times \{t\}}\) is an instanton bundle from \({\mathcal {I}}(c+k-1)\):
Now one easily sees that, after possibly shrinking the curve T, the epimorphism \(\theta \) in the diagram (104) extends to an epimorphism \(\varvec{\Theta }:\ \mathbf {E}'\twoheadrightarrow {\mathcal {O}}_{\ell _k}(1)\boxtimes {\mathcal {O}}_T\), and we denote \(\mathbf {E}=\ker \varvec{\Theta }\). By construction, the \({\mathcal {O}}_{\mathbb {P}^3\times T}\)-sheaf \(\mathbf {E}\) is flat over T, so that, restricting the exact triple \(0 \rightarrow \mathbf {E} \rightarrow \mathbf {E}' \rightarrow {\mathcal {O}}_{\ell _k}(1)\boxtimes {\mathcal {O}}_T \rightarrow 0\) onto \({\mathbb {P}^{3}}\times \{t\}, \ t\in T,\) we obtain an exact triple
where \(E_t=\mathbf {E}|_{{\mathbb {P}^{3}}\times \{t\}}\). By Jardim et al. [14, Proposition 7.2], this triple together with (108) implies that
On the other hand, by the construction, the triple (109) for \(t=0\) coincides with the left vertical triple in (104), so that
Besides, in the case \(c>0\), since F is \(\mu \)-stable, the upper horizontal triple in diagram (104) easily shows that the sheaf \(E_0\) is (\(\mu \)-)stable as well. When \(c=0\) and \(F=2\cdot {\mathcal {O}}_{\mathbb {P}^{3}}\) in diagram (104), we again proceed by induction on k. For \(k=1\), triple (106) and [14, Lemma 4.3] implies that \(E_{(1)}\) is stable. Now assume that \(E_{(k-1)}\) is stable; the first column of diagram (104) immediately implies that \(E_{(k)}\) is also stable, since any sheaf that would destabilize \(E_{(k)}\) would also destabilize \(E_{(k-1)}\).
Thus, in view of (110) and (111) we obtain a modular morphism
Since \(\overline{{\mathcal {I}}(c+k)}\) is closed in \({\mathcal {M}}(c+k)\), it follows that \([E_{(k)}]=f(0)\in \overline{{\mathcal {I}}(c+k)}\), i.e., we obtain (105).
In particular, (103) and (105) yield
Since by construction \([E(\mathbf {w})]\in {{\mathrm{im}}}f_0\), it follows from Theorem 22 that \([E(\mathbf {w})]\in \overline{{\mathcal {I}}(c+d_1d_2)}\cap \overline{\mathcal {C}(d_1,d_2,c)}\).
Finally, note that each \(E_{(k)}\), and hence \(E_0\), is actually an instanton sheaf. Indeed, since F is a locally free instanton sheaf, one easily checks from triple (106) that \(E_{(1)}\) is an instanton sheaf. Assuming that \(E_{(k-1)}\) is an instanton sheaf, one can use the first column of diagram (104) to check that so is \(E_{(k)}\).
Summing it all up, we obtain the following theorem.
Theorem 23
For any \(c\ge 0\) and \(1\le d_1\le d_2\),
In addition, the above intersection contains instanton sheaves.
5 Intersection of \(\overline{\mathcal {C}(d_1,d_2,c)}\) with the Ein components
For any three integers \(c>b\ge a\ge 0\), consider the monad
with morphisms given by
where
do not vanish simultaneously. Ein showed in [7, Proposition 1.2(a)] that the cohomology of such a monad is stable if and only if \(c>a+b\); in this case, there exists an irreducible component \({\mathcal {N}}(a,b,c)\) of \({\mathcal {B}}(c^2-b^2-a^2)\) whose generic point corresponds to a locally free sheaf given as cohomology of (112). Such components are called Ein components.
Let \(\overline{{\mathcal {N}}(a,b,c)}\) denote the closure of \({\mathcal {N}}(a,b,c)\) within \({\mathcal {M}}(c^2-b^2-a^2)\). The main goal of this section is to establish the following result.
Proposition 24
The components \(\overline{{\mathcal {N}}(0,b,c)}\) and \(\overline{\mathcal {C}(c-b,c+b,0)}\) intersect within \({\mathcal {M}}(c^2-b^2)\) along a subvariety of codimension \(1+(c^2-b^2)(c-2)\) in \(\overline{\mathcal {C}(c-b,c+b,0)}\).
Proof
Given a parameter \(t\in \mathbb {A}^1\), consider the following family of monads
where \(\alpha _t\) is given by
while \(\beta \) is given as in (113). Clearly, for each \(t\ne 0\), the sheaf \(E_t=:\ker \beta /{{\mathrm{im}}}\alpha _t\) defines a point \([E_t]\in {\mathcal {N}}(0,b,c)\); we thus obtain a modular morphism
whose image lies within \({\mathcal {N}}(0,b,c)\).
Next, we show that \(E_0\) fits into the following exact triple:
where \(\Gamma \) is the complete intersection curve defined by \(\{\sigma _1=\sigma _4=0\}\); we may assume that \(\Gamma \) is irreducible since this is an open condition. Note also that \({\mathcal {O}}_{\Gamma }(c-2)\) is a theta-characteristic on \(\Gamma \).
Indeed, consider the following short exact sequence of complexes:

where the complex in the middle line is (114) for \(t=0\) and the morphisms \(\tilde{\alpha }\) and \(\tilde{\beta }\) are given by
Passing to cohomology, we obtain precisely the triple (115).
By Jardim et al. [14, Lemma 4.3], (115) implies that \(E_0\) is stable; hence, it follows that \([E_0]\in \overline{{\mathcal {N}}(0,b,c)}\). On the other hand, one clearly sees from (115) and from the definition of \({\mathcal {C}}(c-b,c+b,0)\) in Theorem 17 that \([E_0]\in \overline{{\mathcal {C}}(c-b,c+b,0)}\).
Finally, note that a generic point [E] in the intersection
will be precisely of the form (115), fixing the choice of a line bundle in \({\mathrm {Pic}}^{g-1}(\Gamma )\), where \(g=1+(c^2-b^2)(c-2)\) is the genus of \(\Gamma \). It is then easy to see that such sheaves form a family of codimension g in \(\overline{{\mathcal {C}}(c-b,c+b,0)}\). \(\square \)
6 Connectedness of \({\mathcal {M}}(2)\)
As mentioned in Introduction, it is not difficult to check that \({\mathcal {M}}(1)\) is irreducible; this fact is probably well known to specialists, but for lack of a suitable reference, we present a brief argument here.
The key point is to show that every semistable rank 2 sheaf E on \({\mathbb {P}^{3}}\) with \(c_1(E)=0\), \(c_2(E)=1\) and \(c_3(E)=0\) is a nullcorrelation sheaf in the sense of [6], that is, given by an exact sequence of the form
It follows that E is uniquely determined by the section \(\sigma \in H^0(\Omega ^1_{{\mathbb {P}^{3}}}(2))\) up to scalar multiples, so that \({\mathcal {M}}(1)\simeq \mathbb {P}H^0(\Omega ^1_{{\mathbb {P}^{3}}}(2))\).
Indeed, semistability implies that \(h^0(E)=0\). If E is locally free, then E is stable and it follows from Barth’s theory of spectra, see [3] or [12, Section 7], that E is an instanton bundle of charge 1, and these are precisely the locally free nullcorrelation sheaves. On the other hand, if E is not locally free, then \(E^{\vee \vee }\) is a \(\mu \)-semistable rank 2 reflexive sheaf with \(c_1(E^{\vee \vee })=0\) and \(c_2(E^{\vee \vee })=0,1\). If \(c_2(E^{\vee \vee })=1\), so that E has 0-dimensional singularities, then \(E^{\vee \vee }\) must be stable by Lemma 3; it follows from [4, Lemma 2.1] that \(c_3(E^{\vee \vee })=0\), so \(E^{\vee \vee }/E=0\), contradicting the hypothesis of E not being locally free. Therefore, we must have \(c_2(E^{\vee \vee })=0\), hence \(E^{\vee \vee }\simeq 2\cdot {\mathcal {O}}_{\mathbb {P}^{3}}\) and
where \(\ell \) is a line. One can then check that E satisfies the cohomological conditions of [6, Proposition 1.1], so that E is a nullcorrelation sheaf.
Next, we recall the description of \({\mathcal {M}}(2)\) given by Hartshorne [11], Le Potier [17] and Trautmann [26]. By Hartshorne [11, Section 9], the scheme \({\mathcal {B}}(2)\) coincides with the instanton component \({\mathcal {I}}(2)\) of dimension 13, so its closure \(\overline{{\mathcal {I}}(2)}\) is an irreducible component of \({\mathcal {M}}(2)\). According to [17, Thm. 7.12], \({\mathcal {M}}(2)\) contains two additional irreducible components, which are given by the closures of the subschemes
within \({\mathcal {M}}(2)\); furthermore, \(\dim \overline{{\mathcal {P}}(2)_l}=13+4l\). Le Potier calls these the Trautmann components.
Note that these actually coincides with the components \(\overline{{\mathcal {T}}(2,l)}\) described in Section 2.1 above. Indeed, note that if \([E]\in {\mathcal {T}}(2,l)\), then
However, the length of \(Q_E\) is half of \(c_3(E^{\vee \vee })\), which means that \([E]\in {\mathcal {P}}(2)_l\), thus \({\mathcal {T}}(2,l)\subset {\mathcal {P}}(2)_l\).
In addition, Chang proved in [4, Section 2] that, for each \(l=1,2\), \({\mathcal {R}}(0;2;2l)\) is irreducible, nonsingular of dimension 13. It follows from Theorem 7 that, for each \(l=1,2\), \(\overline{{\mathcal {T}}(2,l)}\) is an irreducible component of \({\mathcal {M}}(2)\) of dimension \(13+4l\); therefore, we must have that \(\overline{{\mathcal {T}}(2,l)}=\overline{{\mathcal {P}}(2)_l}\).
Consequently, Le Potier’s result can be restated in the following form, see also [26]:
The main goal of this section is to show that \({\mathcal {M}}(2)\) is connected.
Recall from Sect. 2.1 that a generic sheaf E from \(\overline{{\mathcal {T}}(2,1)}\) is obtained as the kernel of an epimorphism \(\epsilon :\ F\twoheadrightarrow {\mathcal {O}}_q\) where F is a generic reflexive sheaf from \({\mathcal {R}}(0;2;2)\) and \(q\not \in {\text {Sing}}(F)\):
Every \([F]\in {\mathcal {R}}(0;2;2)\) satisfies \(h^0(F(1))=3\), cf. [4, Table 2.8.1]; moreover, the zero scheme \(Y=(s)_0\) of a generic section \(s\in H^0(F(1))\) is a disjoint union of a line \(\ell \) and a nonsingular conic C [4, Lemma 2.7], i.e., there is an exact triple
In addition, a generic sheaf E from \(\overline{{\mathcal {T}}(2,4)}\) is obtained as the kernel of an epimorphism \(\epsilon :\ F\twoheadrightarrow {\mathcal {O}}_{q_1}\oplus {\mathcal {O}}_{q_2}\) where F is a generic reflexive sheaf from \({\mathcal {R}}(0;2;4)\) with \(q_1,q_2\not \in {\text {Sing}}(F)\), and \(q_1\ne q_2\):
Every \([F]\in {\mathcal {R}}(0;2;4)\) satisfies \(h^0(F(1))=4\), cf. [4, Table 2.12.2]; the zero scheme \(Y=(s)_0\) of a generic section \(s\in H^0(F(1))\) is a nonsingular twisted cubic curve [4, Lemma 2.13], i.e., there is an exact triple
We are finally in position to prove the main result of this section.
Theorem 25
Both components \(\overline{{\mathcal {T}}(2,1)}\) and \(\overline{{\mathcal {T}}(2,2)}\) have nonempty intersection with the instanton component \(\overline{{\mathcal {I}}(2)}\). In particular, \({\mathcal {M}}(2)\) is connected.
Proof
We first consider the case \(l=1\). Recall from [11] that a generic locally free sheaf G from \({\mathcal {I}}(2)\) is a ’t Hooft bundle, fitting in an exact triple
where \(\ell _0,\ell _1,\ell _2\) are disjoint lines in \({\mathbb {P}^{3}}\). We include Z as a generic fiber \(Z_t,\ t\ne 0,\) into a 1-dimensional flat family \({\mathcal {Z}}\) of curves in \({\mathbb {P}^{3}}\):
with base \(U\ni 0\) which is an open subset of \(\mathbb {A}^1\), such that
-
(a)
for \(t\ne 0\) the fiber \(Z_t=\pi ^{-1}(t)\) of the family \({\mathcal {Z}}\) is a disjoint union of three lines in \({\mathbb {P}^{3}}\);
-
(b1)
the zeroth fiber \(Z_0\) of this family, being reduced, is a union of lines
$$\begin{aligned} (Z_0)_\mathrm{red}=\ell _0\sqcup (\ell _1\cup \ell _2),\ \ \ w:=\ell _1\cap \ell _2=\{{\mathrm {pt}}\}. \end{aligned}$$(123)and as a scheme \(Z_0\) has an embedded point w:
$$\begin{aligned} 0\rightarrow {\mathcal {O}}_w\rightarrow {\mathcal {O}}_{Z_0}\rightarrow {\mathcal {O}}_{(Z_0)_\mathrm{red}}\rightarrow 0. \end{aligned}$$(124)
The sheaf G from (121) can then be included into the family \(\varvec{G}\) of sheaves on \({\mathbb {P}^{3}}\) with base U fitting in the exact triple
We thus obtain a modular morphism
Moreover, in view of (125), the sheaf \(G_0\) fits into the exact triple
composing the morphism r in the previous equation with the standard monomorphism \(G_0 \rightarrow G_0^{\vee \vee }\) we obtain, using the triple (124), the following exact triples for \(G_0^{\vee \vee }\):
Now (123) and (128) show that s is a section of a reflexive sheaf \(G_0^{\vee \vee }\) having a disjoint union \((Z_0)_\mathrm{red}\) of a line and a reducible conic as the zero scheme. Note that \(G_0^{\vee \vee }\) is \(\mu \)-stable, since Y is not contained in a plane (cf. [12, Proposition 4.2]); it follows that \(G_0\) is stable. Since, by construction, \(\Phi (U\setminus \{0\})\subset {\mathcal {I}}(2)\), we conclude that
By the description of \({\mathcal {R}}(0;2;2)\) above, it follows that the triple (128) is a specialization of the triple (118) within a flat family of triples in which the conic C specializes into a reducible conic \(\ell _1\cup \ell _2\), so that Y in (118) specializes to \((Z_0)_\mathrm{red}\). It follows that the triple (127) is a flat specialization of the triple (117), so that
Finally, (129) and (130) imply that \(\overline{{\mathcal {T}}(2,1)}\cap \overline{{\mathcal {I}}(2)}\ne \emptyset \), as desired.
Next, consider the case \(l=2\); one takes a family \({\mathcal {Z}}\) as in (122) satisfying property (a) above and replacing property (b1) by the following one:
-
(b2)
the zeroth fiber \(Z_0\) of this family, being reduced, is a (connected) chain of three lines not lying in a plane:
$$\begin{aligned} (Z_0)_\mathrm{red}=\ell _0\cup \ell _1\cup \ell _2 ,\ \ \ q_1:=\ell _0\cap \ell _1=\{{\mathrm {pt}}\},\ q_2:=\ell _1\cap \ell _2=\{{\mathrm {pt}}\},\ q_1\ne q_2. \end{aligned}$$(131)and as a scheme \(Z_0\) has two embedded points \(q_1\) and \(q_2\):
$$\begin{aligned} 0\rightarrow {\mathcal {O}}_{q_1}\oplus {\mathcal {O}}_{q_2}\rightarrow {\mathcal {O}}_{Z_0}\rightarrow {\mathcal {O}}_{(Z_0)_\mathrm{red}}\rightarrow 0. \end{aligned}$$
Then, as above, the ’t Hooft bundle G from (121) is included into the family \(\varvec{G}\) of sheaves on \({\mathbb {P}^{3}}\) given by the exact triple (125). In this case, instead of the triple (127), one has an exact triple
Besides, the triple (128) holds as before; thus, in view of (131), the morphism s in (128) is a section of a reflexive sheaf \(G_0^{\vee \vee }(1)\) having the chain of lines \((Z_0)_\mathrm{red}\) in (131) as its zero scheme. Note that \(G_0^{\vee \vee }\) is \(\mu \)-stable, since Y is not contained in a plane (cf. [12, Proposition 4.2]); it also follows that \(G_0\) is stable, so that \([G_0]\in \overline{{\mathcal {I}}(2)}\), where, as before, \(G_0=:\varvec{G}|_{{\mathbb {P}^{3}}\times \{0\}}\).
Hence, from the above description of \({\mathcal {R}}(0;2;4)\), it follows that the triple (128) is a specialization of the triple (120) within a flat family of triples in which the twisted cubic Y specializes to the chain of lines \((Z_0)_\mathrm{red}\) in (131). It follows that the triple (132) is a flat specialization of the triple (119), so that
Now \(\overline{{\mathcal {T}}(2,2)}\cap \overline{{\mathcal {I}}(2)}\ne \emptyset \) follows from (129) and (133). \(\square \)
Remark 26
It follows from [14, Theorem 7.8], (116) and Theorem 25 that the boundary of charge 2 instanton bundles
has exactly four components, divided into two types:
-
(I)
\(\overline{{\mathcal {C}}(1,1,1)}\) and \(\overline{{\mathcal {C}}(1,2,0)}\), which corresponds to \({\mathcal {D}}(1,2)\) and \({\mathcal {D}}(2,2)\), respectively, in the notation of [14, Theorem 7.8]; and
-
(II)
\(\overline{{\mathcal {T}}(2,l)}\cap \overline{{\mathcal {I}}(2)}\) for \(l=1,2\).
Indeed, either \([E]\in \partial {\mathcal {I}}(2)\) is an instanton sheaf, so [E] lies in one of the components of type (I), or [E] is not an instanton sheaf, in which case [E] lies in one of the components of type (II). In addition, by Jardim et al. [14, Proposition 6.4], the components of type (I) are irreducible and divisorial.
The fact that \(\partial {\mathcal {I}}(2)\) has exactly 4 components was first observed by Narasimhan and Trautmann [20]; they also showed that all four components are irreducible and divisorial. Therefore, it is quite reasonable to conjecture that the components of type (II) above are both irreducible and divisorial. \(\square \)
7 Irreducible components of \({\mathcal {M}}(3)\)
Ellingsrud and Stromme showed in [8] that \({\mathcal {B}}(3)\) has precisely two irreducible components, both nonsingular, rational and of the expected dimension 21; these can be described as follows:
-
The instanton component \({\mathcal {I}}(3)\), whose points are the cohomology of monads of the form
$$\begin{aligned} 0\rightarrow 3\cdot {\mathcal {O}}_{\mathbb {P}^{3}}(-1) \rightarrow 8\cdot {\mathcal {O}}_{\mathbb {P}^{3}} \rightarrow 3\cdot {\mathcal {O}}_{\mathbb {P}^{3}}(1) \rightarrow 0; \end{aligned}$$ -
The Ein component \({\mathcal {N}}(0,1,2)\), following the notation of Sect. 5 above, whose points are the cohomology of monads of the form
$$\begin{aligned} 0\rightarrow {\mathcal {O}}_{\mathbb {P}^{3}}(-2) \rightarrow {\mathcal {O}}_{\mathbb {P}^{3}}(-1) \oplus 2\cdot {\mathcal {O}}_{\mathbb {P}^{3}} \oplus {\mathcal {O}}_{\mathbb {P}^{3}}(1) \rightarrow {\mathcal {O}}_{\mathbb {P}^{3}}(2) \rightarrow 0. \end{aligned}$$
Recall also that Chang [4, Section 3] proved that \({\mathcal {R}}(0;3;l)\) is, for each \(l=1,\dots ,4\), irreducible and of expected dimension 21; in addition, \({\mathcal {R}}(0;3;4)\) and \({\mathcal {R}}(0;3;8)\) are rational, while \({\mathcal {R}}(0;3;6)\) is unirational. Therefore, we can apply Theorem 7 to show that there are four irreducible components \(\overline{{\mathcal {T}}(3,l)}\) of dimensions \(21+4l\), for each \(l=1,\dots ,4\) within \({\mathcal {M}}(3)\).
Furthermore, Theorem 17 provides one additional irreducible component whose generic point corresponds to sheaves with 1-dimensional singularities, labeled \(\overline{\mathcal {C}(1,3,0)}\) in Sect. 3.
We therefore conclude that \({\mathcal {M}}(3)\) has at least seven irreducible components, divided into three types, as below:
-
(I)
\(\overline{{\mathcal {I}}(3)}\) and \(\overline{{\mathcal {N}}(0,1,2)}\), both of dimension 21, whose generic point corresponds to a locally free sheaf;
-
(II)
\(\overline{\mathcal {C}(1,3,0)}\), of dimension 21, whose generic point corresponds to a sheaf which is singular along smooth plane cubic;
-
(III)
\(\overline{{\mathcal {T}}(3,l)}\) for \(l=1,2,3,4\), of dimension \(21+4l\), whose generic point corresponds to a sheaf which is singular along 3l distinct points.
In this section, we prove the following.
Theorem 27
The union
is connected.
Remark 28
It seems likely that \({\mathcal {M}}(3)\) has no other irreducible components whose generic point corresponds either to a locally free sheaf, or to a sheaf with pure 0- or 1-dimensional singularities. But \({\mathcal {M}}(3)\) might possess other irreducible components whose generic point corresponds to a sheaf with mixed singularities.
First, note that Theorem 23 guarantees, in particular, that \(\overline{{\mathcal {I}}(3)}\cap \overline{\mathcal {C}(1,3,0)}\ne \emptyset \), something that has also been remarked by Perrin [21, Thm 0.1]. In addition, Proposition 24 for \(c=2\) and \(b=1\) guarantees that \(\overline{\mathcal {C}(1,3,0)}\) also intersects the closure of \({\mathcal {N}}(0,1,2)\). Therefore, the proof of Theorem 27 is completed by proving the following result.
Proposition 29
For each \(l=1,2,3,4\), we have \(\overline{{\mathcal {T}}(3,l)}\cap \overline{{\mathcal {I}}(3)}\ne \emptyset \).
Proof
We begin by recalling the description of \(\overline{{\mathcal {T}}(3,l)},\ l=1,2,3,4,\) from Sect. 2.1. A generic sheaf E from \(\overline{{\mathcal {T}}(3,l)}\) is defined as the kernel of an epimorphism \(\epsilon :\ F\twoheadrightarrow \oplus _{i=1}^l{\mathcal {O}}_{q_j}\), where \([F]\in {\mathcal {R}}(0;3;2l)\) and \(q_j\not \in {\text {Sing}}(F),\ j=1,\ldots ,l\):
According to Chang [4, Section 3], for each \(l=1,\ldots ,l\) there exist sheaves F in \({\mathcal {R}}(0;3;l)\) such that \(h^0(F(1))>0\), and whose zero scheme \(Y=(s)_0\) of a nontrivial section \(s\in H^0(F(1))\) can be described as follows:
-
(i)
For \(l=1\), the scheme Y is a disjoint union \(\ell _1\sqcup \ell _2\sqcup C\) of two lines \(\ell _1,\ell _2\) and a nonsingular conic C;
-
(ii)
For \(l=2\), the scheme Y is a disjoint union \(\ell \sqcup C\) of a line \(\ell \) and a nonsingular twisted cubic C, cf. [4, proof of Thm. 3.4];
-
(iii)
For \(l=3\), the scheme Y is a nonsingular rational quartic curve, cf. [4, proof of Thm. 3.5];
-
(iv)
For \(l=4\), the scheme Y is a nonsingular space elliptic quartic curve, cf. [4, proof of Lemma 3.8].
In addition, such sheaves are generic for \(l=2,3,4\), but special in the case \(l=1\).
Let us first consider the case \(l=1\). We repeat with minor modifications the argument from Sect. 6; more precisely, compare with Eqs. (117), (120)–(130). First, similar to (118) the sheaf \(F=E^{\vee \vee }\) fits in an exact triple
Next, according to [11] there exists a ’t Hooft vector bundle H in \({\mathcal {I}}(3)\) given by an exact triple
where \(\ell _1,\ldots ,\ell _4\) are disjoint lines in \({\mathbb {P}^{3}}\) of which \(\ell _1\) and \(\ell _2\) are taken from (i) above. We now include Z as a generic fiber \(Z_t,\ t\ne 0,\) into a 1-dimensional flat family \({\mathcal {Z}}\) of curves in \({\mathbb {P}^{3}}\) as in (122), with base \(U\ni 0\) being an open subset of \(\mathbb {A}^1\), such that
-
(a)
For \(t\ne 0\) the fiber \(Z_t=\pi ^{-1}(t)\) of the family \({\mathcal {Z}}\) is a disjoint union of four lines in \({\mathbb {P}^{3}}\);
-
(b)
The zeroth fiber \(Z_0\) of this family, being reduced, is a union of lines
$$\begin{aligned} (Z_0)_\mathrm{red} = \ell _1\sqcup \ell _2\sqcup (\ell _3\cup \ell _4),\ \ \ q=\ell _3\cap \ell _4=\{{\mathrm {pt}}\}. \end{aligned}$$(137)and as a scheme \(Z_0\) has an embedded point \(q_1\):
$$\begin{aligned} 0\rightarrow {\mathcal {O}}_{q} \rightarrow {\mathcal {O}}_{Z_0} \rightarrow {\mathcal {O}}_{(Z_0)_\mathrm{red}} \rightarrow 0. \end{aligned}$$(138)
The sheaf H defined in (136) is then included into the family \(\varvec{H}\) of sheaves on \({\mathbb {P}^{3}}\) with base U given by the exact triple
Thus as in (126) we obtain a modular morphism \(\Phi _U:\ U\rightarrow \overline{{\mathcal {I}}(3)},\ t\mapsto [H_t]\), where \(H_t=\varvec{H}|_{{\mathbb {P}^{3}}\times \{t\}}\). In particular,
In view of (139), the sheaf \(H_0\) fits into the exact triple
composing the morphism r in the previous equation with the standard monomorphism \(H_0\rightarrow H_0^{\vee \vee }\), we obtain, using the triple (138), the following exact triples for \(H_0^{\vee \vee }\):
Now (137) and (142) show that s is a section of a reflexive sheaf \(F_0^{\vee \vee }(1)\) having a disjoint union \((Z_0)_\mathrm{red}\) of two lines and a reducible conic as its zero scheme. Hence, from the description of \({\mathcal {R}}(0;3;2)\) given in item (i) above, it follows that the triple (142) is a specialization of the triple (135) within a flat family of triples in which the nonsingular conic C specializes into a reducible conic \(\ell _3\cup \ell _4\), so that Y specializes to \((Z_0)_\mathrm{red}\). It follows that the triple (141) is a flat specialization of the triple (134), so that
Finally, the case \(l=1\) follows from (140) and (143).
For \(l=2,3,4\), the above argument goes through with the following modifications.
For \(l=2\), instead of (137) one takes \((Z_0)_\mathrm{red}=\ell _1\sqcup (\ell _2\cup \ell _3\cup \ell _4)\) with points \(q_1=\ell _2\cap \ell _3\) and \(q_2=\ell _3\cap \ell _4\), and consider it as a flat degeneration of a disjoint union of a line \(\ell \) plus a smooth twisted cubic C item (ii) above.
For \(l=3\), one takes \((Z_0)_\mathrm{red}=\ell _1\cup \ell _1\cup \ell _2\cup \ell _3)\) to be a chain of lines with three distinct points \(q_1=\ell _1\cap \ell _2\), \(q_2=\ell _2\cap \ell _3\), and \(q_2=\ell _3\cap \ell _4\), considered as a flat degeneration of a nonsingular rational quartic curve C from item (iii) above.
For \(l=4\), one takes \((Z_0)_\mathrm{red}=\ell _1\cup \ell _2\cup \ell _3\cup \ell _4\), to be a space union of lines with distinct intersection points \(q_1=\ell _1\cap \ell _2\), \(q_2=\ell _2\cap \ell _3\), \(q_3=\ell _3\cap \ell _4\), \(q_4=\ell _4\cap \ell _1\), considered as a flat degeneration of the nonsingular space elliptic quartic from item (iv) above. \(\square \)
Remark 30
Gruson and Trautmann conjectured that the boundary of charge 3 instanton bundles
has exactly 8 divisorial irreducible components, which can be divided into 2 types, cf. [21, Remarque 3.6.8]:
-
(I)
4 Components whose generic point corresponds to an instanton sheaf which is singular along a line, a smooth conic, a smooth twisted cubic or a smooth plane cubic;
-
(II)
4 Components whose generic point corresponds to a (noninstanton) sheaf which is singular along 2, 4, 6 or 8 points.
The components of type (I) are, in the notation of [14], \({\mathcal {D}}(m,3)\) for \(m=1,2,3\) and \(\overline{{\mathcal {C}}(1,3,0)}\cap \overline{{\mathcal {I}}(3)}\); all of these are known to be irreducible and divisorial, see [10, 14], [21, Théorème 0.1], and [22].
The components of type (II) are, in the notation of this paper, \(\overline{{\mathcal {T}}(3,l)}\cap \overline{{\mathcal {I}}(3)}\) for \(l=1,2,3,4\). Perrin showed in [21] that \(\overline{{\mathcal {T}}(3,1)}\cap \overline{{\mathcal {I}}(3)}\) is an irreducible divisor within \({{\mathcal {I}}(3)}\).
Therefore, completing the proof of the Gruson–Trautmann conjecture amounts to showing that \(\overline{{\mathcal {T}}(3,l)}\cap \overline{{\mathcal {I}}(3)}\) are irreducible and divisorial within \({{\mathcal {I}}(3)}\) for \(l=2,3,4\) and that \(\partial {\mathcal {I}}(3)\) has no other divisorial components.
Remark 31
It is interesting to note that the argument in Proposition 29 can be adapted to show that \(\overline{{\mathcal {T}}(3,1)}\cap \overline{{\mathcal {N}}(0,1,2)}\ne \emptyset \).
Indeed, consider a 1-dimensional flat family \({\mathcal {Z}}\) of curves in \({\mathbb {P}^{3}}\) as in (122), with base \(U\ni 0\) being an open subset of \(\mathbb {A}^1\), such that
-
(a)
For \(t\ne 0\), the fiber \(Z_t=\pi ^{-1}(t)\) of the family \({\mathcal {Z}}\) is a disjoint union of a nonsingular elliptic cubic \(C_t\) with a nonsingular space elliptic quartic \(Q_t\);
-
(b)
The zeroth fiber \(Z_0\) of this family, being reduced, is the union a nonsingular elliptic cubic \(C_0\) with a nonsingular space elliptic quartic \(Q_0\) meeting a point q
$$\begin{aligned} (Z_0)_\mathrm{red} = C_0\cup Q_0,\ \ \ q := C_0\cap Q_0 = \{{\mathrm {pt}}\} \end{aligned}$$and as a scheme \(Z_0\) has q as an embedded point:
$$\begin{aligned} 0\rightarrow {\mathcal {O}}_{q} \rightarrow {\mathcal {O}}_{Z_0} \rightarrow {\mathcal {O}}_{(Z_0)_\mathrm{red}} \rightarrow 0. \end{aligned}$$(144)
Next, consider the family \(\varvec{H}\) of sheaves on \({\mathbb {P}^{3}}\) with base U given by the exact triple
As before, set \(H_t:=\varvec{H}|_{{\mathbb {P}^{3}}\times \{t\}}\). As observed by Hartshorne [11, Example 3.1.3], the sheaves \(H_t\) for \(t\ne 0\) are stable locally free sheaves with \(c_1(H_t)=0\), \(c_2(H_t)=3\) and \(\alpha \) invariant equal to 1; since instanton bundles have \(\alpha =0\), it follows that \([H_t]\in {\mathcal {N}}(0,1,2)\) when \(t\ne 0\).
On the other hand, the reflexive sheaf F defined by the exact triple
yields a point in \({\mathcal {R}}(0;3;2)\), since \((Z_0)_\mathrm{red}\) is not contained in a hypersurface of degree 2, so that F is \(\mu \)-stable; note, however, that the sheaves obtained in this way are not generic in \({\mathcal {R}}(0;3;2)\), cf. [4, proof of Lemma 3.6]. Since \(H_0\) fits into the exact triple
it then follows from (144) that \(H_0\) and F are related via the exact triple
The stability of F implies that \(H_0\) is also stable. Now, (145) implies that \([H_0]\in \overline{{\mathcal {N}}(0,1,2)}\); on the other hand, (146) implies that \([H_0]\in \overline{{\mathcal {T}}(3,1)}\), proving our claim.
We conjecture that \(\overline{{\mathcal {T}}(3,l)}\cap \overline{{\mathcal {N}}(0,1,2)}\ne \emptyset \) also for \(l=2,3,4\).
References
Artin, M.: Algebraization of formal moduli, I. In: Spencer, DC., Iyanaga, S. (eds.) Global Analysis, Papers in Honor of K. Kodaira, pp. 21–71. University of Tokyo Press, Tokyo (1969)
Barth, W.: Some properties of stable rank-2 vector bundles on \({\mathbb{P}}_n\). Math. Ann. 226, 125–150 (1977)
Barth, W.: Stable vector bundles on \({\mathbb{P}}_3\), experimental data. Astérisque 71–72, 205–218 (1980)
Chang, M.-C.: Stable rank 2 reflexive sheaves on \({\mathbb{P}}^{3}\) with small \(c_2\) and applications. Trans. Am. Math. Soc. 284, 57–89 (1984)
Costa, L., Ottaviani, G.: Nondegenerate multidimensional matrices and instanton bundles. Trans. Am. Math. Soc. 355, 49–55 (2003)
Ein, L.: Some stable vector bundles on \({\mathbb{P}}^4\) and \({\mathbb{P}}^5\). J. Reine Angew. Math. 337, 142–153 (1982)
Ein, L.: Generalized null correlation bundles. Nagoya Math. J. 111, 13–24 (1988)
Ellingsrud, G., Stromme, S.A.: Stable rank 2 vector bundles on \({\mathbb{P}}^3\) with \(c_1 = 0\) and \(c_2 = 3\). Math. Ann. 255, 123–135 (1981)
Esteves, E.: Compactifying the relative Jacobian over families of reduced curves. Trans. Am. Math. Soc. 353, 3045–3095 (2001)
Gruson, L., Skiti, M.: 3-Instantons et réseaux de quadriques. Math. Ann. 298, 253–273 (1994)
Hartshorne, R.: Stable vector bundles of rank 2 on \({\mathbf{P}}^3\). Math. Ann. 254, 229–280 (1978)
Hartshorne, R.: Stable reflexive sheaves. Math. Ann. 254, 121–176 (1980)
Huybrechts, D., Lehn, M.: The Geometry of Moduli Spaces of Sheaves, 2nd edn. Cambridge Math. Lib., Cambridge University Press, Cambridge (2010)
Jardim, M., Markushevich, D., Tikhomirov, A.S.: New divisors in the boundary of the instanton moduli space. Preprint arXiv:1501.00736 [math.AG]
Jardim, M.: Instanton sheaves on complex projective spaces. Collect. Math. 57, 69–91 (2006)
Jardim, M., Verbitsky, M.: Trihyperkähler reduction and instanton bundles on \({\mathbb{P}}^3\). Compos. Math. 150, 1836–1868 (2014)
Le Potier, J.: Systèmes cohérents et structures de niveau. Astérisque 214, 1–143 (1993)
Melo, M., Rapagnetta, A., Viviani, F.: Fine compactified Jacobians of reduced curves. Trans. Am. Math. Soc. Preprint arXiv:1406.2299v2 [math.AG]
Miró-Roig, R.M.: Construction of rank 2 semistable torsion free sheaves which are not limit of vector bundles. Manuscr. Math. 80, 89–94 (1993)
Narasimhan, M.S., Trautmann, G.: Compactification of \(M_{{\mathbb{P}}_3}(0,2)\) and Poncelet pairs of conics. Pac. J. Math. 145, 255–365 (1990)
Perrin, N.: Deux composantes du bord de \(I_3\). Bull. Soc. Math. Fr. 130, 537–572 (2002)
Perrin, N.: Déformations de fibrés vectoriels sur les variétés de dimension 3. Manuscr. Math. 116, 449–474 (2005)
Simpson, C.: Moduli of representations of the fundamental group of a smooth projective variety I. Publ. Math. IHES 79, 47–129 (1994)
Tikhomirov, A.S.: Moduli of mathematical instanton vector bundles with odd \(c_2\) on projective space. Izv. Math. 76, 991–1073 (2012)
Tikhomirov, A.S.: Moduli of mathematical instanton vector bundles with even \(c_2\) on projective space. Izv. Math. 77, 1331–1355 (2013)
Trautmann, G.: Components of \(M_{{\mathbb{P}^{3}}}(2;0,2,0)\). Private communication of unpublished notes
Acknowledgements
MJ is partially supported by the CNPq Grant Number 303332/2014-0 and the FAPESP Grant Number 2014/14743-8. DM was partially supported by Labex CEMPI (ANR-11-LABX-0007-01). AST was supported by Grant Number 16-01-0028 in the framework of the Academic Fund Program at the National Research University Higher School of Economics (HSE) in 2016-2017 and by a subsidy to the HSE from the Government of the Russian Federation for the implementation of Global Competitiveness Program. Part of this paper was written while AST visited the University of Campinas under the FAPESP Grant Number 2014/22807-6. AST also acknowledges the support from the Max Planck Institute for Mathematics in Bonn, where some of the main ideas of this work were conceived during the winter of 2014.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Jardim, M., Markushevich, D. & Tikhomirov, A.S. Two infinite series of moduli spaces of rank 2 sheaves on \({\mathbb {P}}^3\) . Annali di Matematica 196, 1573–1608 (2017). https://doi.org/10.1007/s10231-016-0630-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10231-016-0630-3