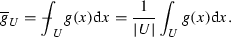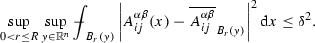Global $W^{1,p}$ estimates for elliptic systems in homogenization problems in Reifenberg domains

Abstract

In this paper, we examine an elliptic system of divergence form in a homogenization problem in order to obtain a global $W^{1,p}$ estimate for $1<p<\infty$. Throughout our study, the coefficients are assumed to have a small bounded mean oscillation seminorm, and the boundary of the domain is assumed to be flat in the Reifenberg sense, which is a natural generalization of a Lipschitz domain with a small Lipschitz constant. As a consequence, an optimal $W^{1,p}$ regularity is determined.

1 Introduction

This study aims to produce Calderón–Zygmund type estimates for the weak solution to a Dirichlet problem of a divergence-form elliptic system in a homogenization problem :

$$\begin{aligned} \left\{ \begin{array}{rclcc} D_{\alpha } \left( A_{ij}^{\alpha \beta , \epsilon }(x)D_{\beta }u_{\epsilon }^{j}(x) \right) &{} = &{} D_{\alpha } f_{\alpha }^{i}(x) &{} {\text { in }} &{} \varOmega \\ u_{\epsilon }^{i}(x) &{} = &{} 0 &{} {\text { on }} &{} \partial \varOmega \end{array}\right. \end{aligned}$$

(1.1)

for $1 \le \alpha , \beta \le n$ and $1\le i,j \le m$ with $m \ge 2$, where the nonhomogeneous term $F = \{ f_{\alpha }^{i} \}$ is given by a matrix-valued function. Here, $\Omega$ is a bounded domain in $\mathbb {R}^n$ with $n \ge 2$ and $0<\epsilon \le 1$. Also, the coefficients $A^\epsilon =\{A_{ij}^{\alpha \beta ,\epsilon }\}$ for $0<\epsilon \le 1$ from $A=\{A_{ij}^{\alpha \beta }\}$, $A_{ij}^{\alpha \beta }:\mathbb {R}^{n} \rightarrow \mathbb {R}$, are defined to be

$$\begin{aligned} A_{ij}^{\alpha \beta }(x)=A_{ij}^{\alpha \beta ,1}(x) \quad {\text {and}} \quad A_{ij}^{\alpha \beta ,\epsilon }(x)=A_{ij}^{\alpha \beta }\left( \frac{x}{\epsilon }\right) . \end{aligned}$$

(1.2)

The coefficients are assumed to have uniform ellipticity and uniform boundedness. In other words, we assume that there exist positive constants $\nu$ and L such that

$$\begin{aligned} \nu |\xi |^{2} \, \le \, A_{ij}^{\alpha \beta }(x)\xi _{\alpha }^{i}\xi _{\beta }^j \quad {\text { and }} \quad \Vert A \Vert _{L^{\infty }(\mathbb {R}^{n},\mathbb {R}^{mn\times mn})} \ \le \ L, \end{aligned}$$

(1.3)

for every matrix $\xi \in \mathbb {R}^{mn}$ and for almost every $x\in \mathbb {R}^{n}$.

The primary question that $W^{1,p}$ regularity theory poses for (1.1) is : what are the minimal requirements for coefficient $A_{ij}^{\alpha \beta }$ and the boundary condition of $\Omega$, which are related by

$$\begin{aligned} F\in L^p(\Omega ,\mathbb {R}^{mn}) \Longrightarrow Du_\epsilon \in L^p(\Omega ,\mathbb {R}^{m}) \quad {\text { for every }}\quad 1<p<\infty ? \end{aligned}$$

(1.4)

When $\epsilon =1$, meaning there is no homogenization issue, $W^{1,p}$ regularity theory for elliptic equations and systems has been extensively studied by investigating the regularity requirements for the coefficients and smoothness of the domain’s boundary. We refer to [2, 4–7, 9–11, 16] and the references therein for related results. In [15], we see that the coefficients must not be measurable in two variables. Also, as it relates to the domain, $W^{1,p}$ regularity does not hold even for Poisson’s equation when $\Omega$ is a bounded Lipschitz domain [13].

Homogenization theory of partial differential equations studies equations that have rapidly oscillating coefficients. Therefore, this theory has many applications in multiple fields, such as mechanics and physics. One of the goals of this theory is to find a macroscopic, or effective, description, even when the microscopic structure is irregular. In this study, we examine the global $W^{1,p}$ theory of the homogenization problem (1.1). Hence, our goal is to produce a uniform result of (1.4) that is independent of $\epsilon$ for $0<\epsilon \le 1$. Namely, if $F\in L^p(\Omega ,\mathbb {R}^{mn})$, we want to derive the following estimate for $1<p<\infty$ :

$$\begin{aligned} \Vert Du_\epsilon \Vert _{L^p(\Omega )}\le c \Vert F\Vert _{L^p(\Omega )}, \end{aligned}$$

(1.5)

where the constant c is independent of $F {\text { and }} \epsilon$.

Much research has been devoted to the globalization of the homogenization problem. In [1], a uniform $W^{1,p}$ regularity for (1.1) was proved when the coefficients are Hölder continuous and the boundary of the domain is $C^{1,\alpha }$. Following this, given continuous coefficients, the interior $W^{1,p}$ regularity for linear elliptic equations was established in [9]. Also, the estimate (1.5) of a linear elliptic equation for $1<p<3+\delta _1$ when $n\ge 3$, and for $1<p<4+\delta _1$ when $n=2$ under the conditions that the coefficients are in the vanishing mean oscillation (VMO) class and the domain is a general Lipschitz domain was established [19]. Contrary to the result in [19], we want to prove (1.5) for all p, in which $1<p<\infty$.

Study of global $W^{1,p}$ regularity of the homogenization problem (1.1) has been limited to Lipschitz domains. However, we want to extend the previous results of $W^{1,p}$ regularity to an irregular domain : the Reifenberg-flat domain, which is not contained in the Lipschitz domain category. A Reifenberg-flat domain was introduced in [17] and a typical example of this kind of domain is a Van Koch curve, which allows for fractal structures. Even though this domain has a sufficiently irregular structure on its boundary, its beneficial properties help address the partial differential equations over a Reifenberg-flat domain, such as a scaling invariance. In this domain, some regularity results when there is no homogenization [4–7]. Also, we assume that the coefficients are in the bounded mean oscillation (BMO) class with small BMO seminorms. It should be noted that for $\epsilon =1$, $W^{1,p}$ regularity was established under the weaker condition for coefficients than that for a BMO [4, 7]. However, in order to remain consistent with the conditions between the coefficients in the homogenization and the domain, we provide a BMO condition for the coefficients.

Throughout this paper, we address periodic homogenization. In particular, we assume the following periodicity condition on $\left\{ A_{ij}^{\alpha \beta }(x) \right\}$ :

$$\begin{aligned} A_{ij}^{\alpha \beta }(x+z)=A_{ij}^{\alpha \beta }(x) \quad (x\in \mathbb {R}^n , z\in \mathbb {Z}^n). \end{aligned}$$

(1.6)

In general, we say that $u_\epsilon =(u_\epsilon ^{1},\ldots ,u_\epsilon ^{m})\in H^1_0(\Omega ,\mathbb {R}^m)$ is a weak solution of (1.1) if

$$\begin{aligned} \int _{\Omega }A_{ij}^{\alpha \beta ,\epsilon } D_{\beta }u_\epsilon ^{j}D_{\alpha }\phi ^{i}\mathrm{d}x=\int _{\Omega }f_{\alpha }^{i}D_{\alpha }\phi ^{i}\mathrm{d}x, ~\quad \forall \phi =(\phi ^1,\ldots ,\phi ^m) \in H_{0}^{1}(\Omega ,\mathbb {R}^{m}). \end{aligned}$$

(1.7)

In order to understand the periodic homogenization problem (1.1), we must recall some basic facts. First, (1.1) is considered to be well posed if $F\in L^2(\Omega ,\mathbb {R}^{mn})$. The Lax-Milgram lemma implies the existence and uniqueness of the solutions $u_\epsilon \in H_0^1(\Omega , \mathbb {R}^m)$ with the estimate

$$\begin{aligned} \Vert Du_\epsilon \Vert _{L^2(\Omega )}\le c \Vert F\Vert _{L^2(\Omega )}, \end{aligned}$$

(1.8)

where the constant c does not depend on $\epsilon$. The matrix of correctors $\chi =\left\{ \chi ^{ij}_{\alpha } \right\}$, with $1\le i,j\le m$ and $1\le \alpha \le n$, is the weak solution of the following cell problem:

$$\begin{aligned} \left\{ \begin{array}{rclcc} - D_{\alpha } \left( A_{ij}^{\alpha \beta }(x)D_{\beta }\chi ^{jk}_{\gamma }(x) \right) &{} = &{} D_{\alpha } A_{ik}^{\alpha \gamma }(x) &{} {\text { in }} &{} \mathbb {R}^n \\ \int _{[0,1]^n} \chi _{\gamma }^{jk} &{}=&{} 0 \\ \chi _{\gamma }^{jk} &{} \mathbb {Z}^n {\text { periodic}}, \end{array}\right. \end{aligned}$$

(1.9)

in which the $L^{\infty }$ estimate is defined by

$$\begin{aligned} \Vert \chi \Vert _{L^{\infty }(\mathbb {R}^n)}\le c(\nu , L, m, n). \end{aligned}$$

(1.10)

Let

$$\begin{aligned} A_{ij}^{\alpha \beta ,0}=\int _{[0,1]^n}\left( A_{ij}^{\alpha \beta } + A_{ik}^{\alpha \gamma } D_{\gamma } \chi _{\beta }^{kj}\right) . \end{aligned}$$

Then the linear elliptic system

$$\begin{aligned} \left\{ \begin{array}{rclcc} D_{\alpha } \left( A_{ij}^{\alpha \beta ,0}D_{\beta }u_0^{j}(x) \right) &{} = &{} D_{\alpha } f_{\alpha }^{i}(x) &{}{\text { in }}&{} \varOmega \\ u_0^{i}(x) &{} = &{} 0 &{} {\text { on }} &{} \partial \varOmega \end{array} \right. \end{aligned}$$

(1.11)

is the homogenized problem of (1.1), whose weak solution $u_0$ of (1.11) is the weak limit of the weak solutions $u_\epsilon$ in $H_0^1 (\Omega , \mathbb {R}^m)$ as $\epsilon \rightarrow 0$, see [3].

This paper is organized as follows. Section 2 introduces some basic notations and states our main result. Section 3 addresses analytic and geometric tools used to determine the global $W^{1,p}$ regularity. Section 4 establishes the uniform $W^{1,p}$ estimate.

2 Main results

We begin this section with some notations.

• 1. An open ball in $\mathbb {R}^{n}$ with center y and radius $r>0$ is defined to be

  $$\begin{aligned} B_{r}(y)=\{x\in \mathbb {R}^{n} : |x - y|<r\}. \end{aligned}$$

  If the center is the origin, we denote $B_{r}(0)$ by $B_{r}$ for simplicity.

• 2. The integral average of $g\in L^{1}(U)$ over bounded domain U in $\mathbb {R}^{n}$ is denoted

  

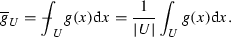
• 3. $B_{r}^{+}=B_{r}\cap \{x_{n}>0\},\quad T_{r}=B_{r} \cap \{x_{n}=0\}.$

• 4. $\Omega _r=B_{r}\cap \Omega , \quad \partial \Omega _r=\partial (B_{r} \cap \Omega ).$

• 5. $\partial _{w}\Omega _r=B_{r} \cap \partial \Omega$ : the wiggled part of $\partial \Omega _r$.

Hereafter, $\delta$ is a small positive constant to be determined later. On the other hand, the constant R can be 1 or any other constant greater than 1 to be determined by our purpose, since our primary problem (1.1) has a scaling invariance property.

Definition 2.1

Let U be a bounded domain in $\mathbb {R}^n$.

• 1. We say that $A_{ij}^{\alpha \beta }$ is $(\delta ,R)$ -vanishing if

  

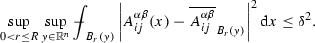  (2.1)

• 2. We also say that U is $(\delta ,R)$ -Reifenberg flat if for every $x \in \partial \Omega$ and every $r \in (0,R]$, there exists a coordinate system $\{ y_1, \dots , y_n\}$ dependent on r and x so that $x=0$ in this coordinate system and

  $$\begin{aligned} B_{r} \cap \left\{ y_n > \delta r \right\} \subset B_{r} \cap \Omega \subset B_{r} \cap \left\{ y_n > - \delta r \right\} . \end{aligned}$$

  (2.2)

Remark 2.2

Recall that the class of vanishing mean oscillation functions VMO consists of functions whose integral oscillation over balls shrinking to a point converges uniformly to zero, see [18]. In fact, (2.1) holds true if the term on the left-hand side of (2.1) vanishes as $R\rightarrow 0$. This means that the small BMO assumption (2.1) generalizes the case of VMO coefficients.

Remark 2.3

This definition prompts a few comments. The constant $\delta$ is a small, positive constant that is still invariant under scaling. This small number will be selected later. In fact, Reifenberg flatness (2.2) is meaningful when $0<\delta <\frac{1}{8}$ [21], and a small $\delta$ allows the deviation of $\partial \Omega$, an $(n-1)$-dimensional affine space, to be sufficiently small for each scale $r>0$.

Theorem 2.4

Suppose $F \in L^{p}(\Omega ,\mathbb {R}^{mn})$ for some $2<p<\infty$. Then there exists a small positive constant $\delta =\delta (\nu , L,m,n,p)$ such that if $A_{ij}^{\alpha \beta }$ is $(\delta ,R)$-vanishing and $\Omega$ is $(\delta ,R)$-Reifenberg flat, then for the weak solution $u_\epsilon \in H_0^1(\Omega ,\mathbb {R}^m)$ of (1.1), we have

$$\begin{aligned} Du_\epsilon \in L^p(\Omega ,\mathbb {R}^{mn}) \end{aligned}$$

(2.3)

with estimate

$$\begin{aligned} \Vert Du_\epsilon \Vert _{L^p(\Omega )}\le c \Vert F\Vert _{L^p(\Omega )}, \end{aligned}$$

(2.4)

where the positive constant $c=c(|\Omega |,\nu , L,m,n,p)$ is independent of $\epsilon$.

Remark 2.5

When $p=2$, the estimate is a classical one. After the estimate has been determined for $2<p<\infty$, the estimate for the $1<p<2$ case follows using a duality argument.

3 Preliminary tools

In this section, we introduce analytic and geometric tools that will be used later in the proof of our main theorem. Our approach is based on the Hardy-Littlewood maximal function, classical measure theory, and a Vitali-type covering argument.

First, let us recall the Hardy-Littlewood maximal function and its basic properties. If we suppose g is a locally integrable function on $\mathbb {R}^{n}$, then the Hardy-Littlewood maximal function is given by

$$\begin{aligned} (\mathcal {M} g)(x)=\sup _{r>0}\frac{1}{|B_{r}(x)|}\int _{B_{r}(x)} |g(y)| \mathrm{d}y. \end{aligned}$$

If g is defined only on a bounded subset of $\mathbb {R}^n$, then we define

$$\begin{aligned} \mathcal {M}g = \mathcal {M} \overline{g}, \end{aligned}$$

where $\overline{g}$ is the zero extension of g from the bounded set to $\mathbb {R}^n$. This maximal function satisfies the weak 1-1 estimate and strong p-p estimate as follows :

For $g\in L^{1}(\mathbb {R}^{n})$, there is a constant $c=c(n)>0$ such that

$$\begin{aligned} |\{x\in \mathbb {R}^{n} : (\mathcal {M}g)(x)>t\}|\le \frac{c}{t}\Vert g \Vert _{L^{1}(\mathbb {R}^{n})}, \quad \forall t > 0. \end{aligned}$$

Also, given $g \in L^{p}(\mathbb {R}^{n})$ for some $p \in (1, \infty )$, $\mathcal {M}g \in L^{p}(\mathbb {R}^{n})$ holds with the estimate

$$\begin{aligned} \frac{1}{c}\Vert g\Vert _{L^{p}(\mathbb {R}^{n})}\le \Vert \mathcal {M}g\Vert _{L^{p}(\mathbb {R}^{n})}\le c\Vert g\Vert _{L^{p}(\mathbb {R}^{n})} \end{aligned}$$

(3.1)

for some constant $c=c(n,p)>0$ [20].

In order to apply it later, we need to review some classical measure theory.

Lemma 3.1

[8] Assume g is a nonnegative, measurable function defined on the bounded domain $\Omega \subset \mathbb {R}^{n}$, and let $\theta >0$ and $\lambda >1$ be constants. Then for $0<q<\infty$, we have

$$\begin{aligned} g \in L^{q}(\Omega ) \quad \Longleftrightarrow \quad S = \sum _{k\ge 1} \lambda ^{qk} \left| \left\{ x \in \Omega : g(x) > \theta \lambda ^{k} \right\} \right| < \infty \end{aligned}$$

and

$$\begin{aligned} \frac{1}{c} S\le \Vert g\Vert ^{q}_{L^{q}(\Omega )}\le c(|\Omega |+S). \end{aligned}$$

(3.2)

The positive constant c depends only on $\theta$, $\lambda$, and q.

In addition, we will use the following version of the Vitali-type covering lemma for the proof of our main theorem.

Lemma 3.2

[5, 22] Assume that C and D are measurable sets with $C\subset D\subset \Omega$ and $\Omega$ being $(\delta ,1)$-Reifenberg flat. Also assume there exists a small $\eta >0$ such that

$$\begin{aligned} |C|<\eta |B_{1}| \end{aligned}$$

(3.3)

and that for each $x\in \Omega$ and $r\in (0,1]$ with $|C\cap B_{r}(x)| > \eta |B_{r}(x)|$, we have

$$\begin{aligned} B_{r}(x)\cap \Omega \subset D. \end{aligned}$$

(3.4)

Then

$$\begin{aligned} |C|\le \left( \frac{10}{1-\delta } \right) ^{n}\eta |D|. \end{aligned}$$

(3.5)

4 Global $W^{1,p}$ estimate

Because the proof of the interior case is essentially the same as that of the boundary case, we briefly introduce some counterparts to the boundary case of the interior case without proof. In order to do this, let us suppose $B_5 \subset \Omega$ and that $u_\epsilon \in H^1(B_5,\mathbb {R}^m)$ is a weak solution of

$$\begin{aligned} D_{\alpha }(A_{ij}^{\alpha \beta ,\epsilon }D_{\beta }u_\epsilon ^{j}) \ = \ D_{\alpha }f_{\alpha }^{i} \qquad {\text { in }} \quad B_5 \end{aligned}$$

(4.1)

for each $i=1,\ldots ,m$. Then we consider the following homogeneous problem.

$$\begin{aligned} \left\{ \begin{array}{rclcc} D_{\alpha } \left( A_{ij}^{\alpha \beta , \epsilon }(x)D_{\beta }v_\epsilon ^{j}(x) \right) &{} = &{} 0 &{} {\text { in }} &{} B_4 \\ v_\epsilon ^{i}(x) &{} = &{} u_\epsilon ^{i}(x) &{} {\text { on }} &{} \partial B_4 \end{array}\right. \end{aligned}$$

(4.2)

In order to solve this problem, we need the following higher integrability lemma for the weak solution $v_\epsilon \in H^1(B_4, \mathbb {R}^m)$ of (4.2).

Lemma 4.1

[19] Let $v_\epsilon$ be the weak solution of (4.2). Then for any $2<q<\infty$, there exists $\delta =\delta (\nu , L, m, n, q)$ such that if $A_{ij}^{\alpha \beta }$ is $(\delta ,5)$-vanishing, then we have

$$\begin{aligned} |Dv_\epsilon | \in L^q (B_1, \mathbb {R}^m) \end{aligned}$$

with the estimate

(4.3)

for some positive constant $c=c(\nu , L, m, n, q)$, independent of $\epsilon$.

Remark 4.2

In [19], the author proved interior $W^{1,p}$ regularity with VMO coefficients using a blow-up argument. Using the same argument, we can prove Lemma 4.1 for our situation by using the interior $W^{1,p}$ regularity for coefficients with small BMO seminorms which was already established, [6].

With these lemmas established, we are able to return to the boundary case. In order to address this problem, we must first assume that

$$\begin{aligned} B_{5}^{+}\subset \Omega _5\subset B_{5}\cap \{x_{n}>-10\delta \}. \end{aligned}$$

(4.4)

Let us suppose that $u_\epsilon \in H^{1}(\Omega _5,\mathbb {R}^{m})$ is a weak solution of

$$\begin{aligned} \left\{ \begin{array}{rclcc} D_{\alpha } \left( A_{ij}^{\alpha \beta ,\epsilon }(x) D_{\beta }u_\epsilon ^{j}(x) \right) &{} = &{} D_{\alpha } f_{\alpha }^{i}(x) &{} {\text { in }} &{} \Omega _5 \\ u_\epsilon ^{i}(x) &{} = &{} 0 &{} {\text { on }} &{} \partial _{w}\Omega _5, \end{array}\right. \end{aligned}$$

(4.5)

in which

$$\begin{aligned} \frac{1}{|B_5|}\int _{\Omega _5}|Du_\epsilon |^{2} \mathrm{d}x \le 1. \end{aligned}$$

(4.6)

Then we can consider the homogeneous problem :

$$\begin{aligned} \left\{ \begin{array}{rclcc} D_{\alpha } \left( A_{ij}^{\alpha \beta ,\epsilon }(x)D_{\beta }w_\epsilon ^{j}(x) \right) &{} = &{} 0 &{} {\text { in }} &{} \Omega _4 \\ w_\epsilon ^{i}(x) &{} = &{} u_\epsilon ^{i}(x) &{} {\text { on }} &{} \partial \Omega _4. \end{array}\right. \end{aligned}$$

(4.7)

This leads us to the following regularity result.

Lemma 4.3

[12, 14] Let $w_\epsilon$ be the weak solution of (4.7). Then there exist small positive constants $\sigma _1$ and c, which depend only on $\nu , L, m$ and n, such that

$$\begin{aligned} \Vert Dw_\epsilon \Vert _{L^{2+\sigma _1}(\Omega _3)} \le c. \end{aligned}$$

(4.8)

However, a higher integrability is required—an integrability up to the flat boundary for the following homogeneous problem on the flat boundary :

$$\begin{aligned} \left\{ \begin{array}{rclcc} D_{\alpha } \left( A_{ij}^{\alpha \beta ,\epsilon }(x)D_{\beta }v_\epsilon ^{j} \right) &{} = &{} 0 &{} {\text { in }} &{} B_{3}^{+} \\ v_\epsilon ^{i} &{} = &{} 0 &{} {\text { on }} &{} T_{3}. \end{array}\right. \end{aligned}$$

(4.9)

Lemma 4.4

[19] Let $v_\epsilon \in H^1(B_3^+,\mathbb {R}^m)$ be a weak solution of (4.9). Then for any $2<q<\infty$, there exists $\delta =\delta (\nu ,L,m,n,q)$ such that if $A_{ij}^{\alpha \beta }$ is $(\delta ,50)$-vanishing, then we have

(4.10)

for some positive constant $c=c(\nu ,L,m,n,q)$, independent of $\epsilon$.

Remark 4.5

In [19], Lemma 4.4 was proved for VMO coefficients and a general Lipschitz domain but not for all q in which $2<q<\infty$ because the author dealt with a general Lipschitz domain. In our case, we only control the flat boundary, and our results still hold for all $2<q<\infty$. Also, the proof of the case involving BMO coefficients with small BMO seminorms is similar to that involving VMO coefficients, see [2].

Therefore, we need the following lemma in order to justify our argument in a Reifenberg domain.

Lemma 4.6

Let $u_\epsilon \in H^1(\Omega _5,\mathbb {R}^{m})$ be a weak solution of (4.5) satisfying (4.6), and let $w_\epsilon \in H^1(\Omega _4,\mathbb {R}^{m})$ be the weak solution of (4.7). Then for any fixed $\kappa >0$, there exists a small $\delta =\delta (\kappa ,\nu ,L,m,n)>0$ such that if

$$\begin{aligned} B_{5}^{+}\subset \Omega _5 \subset B_{5}\cap \{x_{n}>-10\delta \} \end{aligned}$$

(4.11)

holds for $\delta$, then there exists a weak solution $v_\epsilon \in H^1(B^+_3,\mathbb {R}^{m})$ of (4.9) with

(4.12)

for some positive constant $c=c(\nu ,L,m,n)$ such that

(4.13)

Proof

We argue this by contradiction. To do this, we assume there exist $\kappa _0 > 0$, $\left\{ u_{\epsilon ,k} \right\} _{k=1}^{\infty }$, and $\left\{ \Omega _5^k \right\} _{k=1}^{\infty }$ such that $u_{\epsilon ,k}$ is a weak solution of

$$\begin{aligned} \left\{ \begin{array}{rclcc} D_{\alpha } \left( A_{ij}^{\alpha \beta ,\epsilon }(x) D_{\beta } (u_{\epsilon ,k})^{j} \right) &{} = &{} 0 &{} {\text { in }} &{} \Omega _5^k \\ (u_{\epsilon ,k})^{i} &{} = &{} 0 &{} {\text { on }} &{} \partial _w \Omega _5^k \end{array}\right. \end{aligned}$$

(4.14)

with

(4.15)

and

$$\begin{aligned} B_{5}^{+}\subset \Omega _5^k \subset B_5 \cap \left\{ x_{n}> - \frac{10}{k} \right\} . \end{aligned}$$

(4.16)

However,

(4.17)

for any weak solution $v_\epsilon$ of

$$\begin{aligned} \left\{ \begin{array}{rclcc} D_{\alpha } \left( A_{ij}^{\alpha \beta ,\epsilon }(x)D_{\beta } v_\epsilon ^{j} \right) &{} = &{} 0 &{} {\text { in }} &{} B_3^+ \\ v_\epsilon ^{i} &{} = &{} 0 &{} {\text { on }} &{} T_3, \end{array}\right. \end{aligned}$$

(4.18)

where

(4.19)

for the same positive constant c as in (4.12) and $w_{\epsilon ,k}$ is the weak solution of

$$\begin{aligned} \left\{ \begin{array}{rclcc} D_{\alpha } \left( A_{ij}^{\alpha \beta ,\epsilon }(x)D_{\beta }w_{\epsilon ,k}^{j}(x) \right) &{} = &{} 0 &{} {\text { in }} &{} \Omega _4^k \\ w_{\epsilon ,k}^{i}(x) &{} = &{} u_{\epsilon ,k}^{i}(x) &{} {\text { on }} &{} \partial \Omega _4^k. \end{array}\right. \end{aligned}$$

(4.20)

Applying (4.15) and the standard $L^2$-estimate for (4.20), we know that

$$\begin{aligned} \frac{1}{|B_4|}\int _{\Omega _4^k}|Dw_{\epsilon ,k}|^2 \mathrm{d}x \le c\frac{1}{|B_5|}\int _{\Omega _5^k}|Du_{\epsilon ,k}|^2 \mathrm{d}x\le c. \end{aligned}$$

(4.21)

Also, using the fact that $w_{\epsilon , k} = 0$ on $\partial _w \Omega _3^k$ and (4.16), we apply Poincaré’s inequality to find that

$$\begin{aligned} \frac{1}{|B_3|}\int _{B_3^+} |w_{\epsilon ,k}|^2 \mathrm{d}x\le & {} \frac{1}{|B_3|}\int _{\Omega _3^k} |w_{\epsilon ,k}|^2 \mathrm{d}x \le \frac{c}{|B_3|}\int _{\Omega _3^k} |Dw_{\epsilon ,k}|^2 \mathrm{d}x \nonumber \\\le & {} \frac{c}{|B_5|}\int _{\Omega _5^k}|Du_{\epsilon ,k}|^2 \mathrm{d}x \le c \end{aligned}$$

(4.22)

for some positive constant $c=c(\nu ,L,m,n)$. If we apply the zero extension of $w_{\epsilon ,k}$ from $\Omega _3^k$ to $B_3$, say, $\bar{w}_{\epsilon ,k}$, then (4.21) and (4.22) imply that $\left\{ \bar{w}_{\epsilon , k} \right\} _{k=1}^{\infty }$ is uniformly bounded in $H^1(B_3,\mathbb {R}^{m})$. Thus, there exists a subsequence, which we will continue to denote as $\left\{ \bar{w}_{\epsilon ,k} \right\}$, and $\bar{w}_{\epsilon , 0} \in H^1(B_3,\mathbb {R}^{m})$ such that

$$\begin{aligned} \left\{ \begin{array}{ccc} D\bar{w}_{\epsilon ,k} \rightharpoonup D\bar{w}_{\epsilon ,0} &{} {\text { weakly in }} &{} L^2(B_3,\mathbb {R}^{mn}) \\ \bar{w}_{\epsilon ,k} \rightarrow \bar{w}_{\epsilon ,0} &{} {\text { strongly in }} &{}L^2(B_3,\mathbb {R}^m) \end{array} \right. \end{aligned}$$

(4.23)

as $k \rightarrow \infty$. We define $w_{\epsilon ,0}$ on $B_3^+\cup T_3$ by $w_{\epsilon ,0}(x)=\bar{w}_{\epsilon ,0}(x)$ for all $x\in B_3^+\cup T_3$. Hence, $w_{\epsilon ,0}$ is a weak solution of

$$\begin{aligned} \left\{ \begin{array}{rclcc} D_{\alpha } \left( A_{ij}^{\alpha \beta ,\epsilon }(x)D_{\beta } w_{\epsilon ,0}^{j} \right) &{} = &{} 0 &{} {\text { in }} &{} B_3^+ \\ w_{\epsilon ,0}^{i} &{} = &{} 0 &{} {\text { on }} &{} T_3. \end{array}\right. \end{aligned}$$

(4.24)

From (4.21) and the lower semicontinuity with respect to weak convergence, we see that

(4.25)

Thus, we derive a contradiction by showing that

$$\begin{aligned} Dw_{\epsilon ,k} \rightarrow Dw_{\epsilon ,0} {\text { strongly in }} L^2(B_1^+, \mathbb {R}^{mn}). \end{aligned}$$

In order to do this, we begin with the cut-off function $\phi \in C^\infty _0(B_3)$ that satisfies

$$\begin{aligned} 0\le \phi \le 1, ~ \ \phi = 1 ~ {\text { on }}~ B_1, ~ \ \phi = 0 ~{\text { on }} B_3 \backslash B_2, ~ {\text { and }}~ |D \phi | \le 2. \end{aligned}$$

(4.26)

Then,

$$\begin{aligned} \int _{B_1^+}|D(w_{\epsilon ,k}-w_{\epsilon ,0})|^2\mathrm{d}x\le & {} \int _{B_1}|D(\bar{w}_{\epsilon ,k}-\bar{w}_{\epsilon ,0})|^2 \mathrm{d}x \\\le & {} c\int _{B_1} A_{ij}^{\alpha \beta ,\epsilon }D_{\beta }(\bar{w}_{\epsilon ,k}-\bar{w}_{\epsilon ,0})^{j}D_{\alpha }(\bar{w}_{\epsilon ,k}-\bar{w}_{\epsilon ,0})^{i} \mathrm{d}x\\\le & {} c\int _{B_3} A_{ij}^{\alpha \beta ,\epsilon }D_{\beta }(\bar{w}_{\epsilon ,k})^{j}D_{\alpha }(\bar{w}_{\epsilon ,k}-\bar{w}_{\epsilon ,0})^{i} \phi ^2\mathrm{d}x\\&-\,c\int _{B_3} A_{ij}^{\alpha \beta ,\epsilon }D_{\beta }(\bar{w}_{\epsilon ,0})^{j}D_{\alpha }(\bar{w}_{\epsilon ,k}-\bar{w}_{\epsilon ,0})^{i} \phi ^2 \mathrm{d}x\\\le & {} c\int _{B_3} A_{ij}^{\alpha \beta ,\epsilon }D_{\beta }(\bar{w}_{\epsilon ,k})^{j}D_{\alpha }(\phi ^2(\bar{w}_{\epsilon ,k}-\bar{w}_{\epsilon ,0}))^{i}\mathrm{d}x\\&-\,c\int _{B_3} A_{ij}^{\alpha \beta ,\epsilon }D_{\beta }(\bar{w}_{\epsilon ,k})^{j}(2\phi D_{\alpha }\phi )(\bar{w}_{\epsilon ,k}-\bar{w}_{\epsilon ,0})^{i}\mathrm{d}x\\&-\,c\int _{B_3} A_{ij}^{\alpha \beta ,\epsilon }D_{\beta }(\bar{w}_{\epsilon ,0})^{j}D_{\alpha }(\bar{w}_{\epsilon ,k}-\bar{w}_{\epsilon ,0})^{i} \phi ^2\mathrm{d}x\\\rightarrow & {} 0 \end{aligned}$$

as $k\rightarrow \infty$ by applying (4.20) and (4.23). This completes the proof. $\square$

Now we are ready to prove the following lemma, which is a key ingredient in our argument.

Lemma 4.7

Let $2<p<\infty$. Suppose that $u_\epsilon \in H_0^1(\Omega ,\mathbb {R}^m)$ is the weak solution of (1.1). Then there exists a universal constant $\eta =\eta (\nu , L, m,n,p)$ so that one can select a small $\delta =\delta (\nu ,L,m,n,p)>0$ such that if $A_{ij}^{\alpha \beta }$ is $(\delta ,50)$-vanishing, $\Omega$ is $(\delta ,50)$-Reifenberg flat, and for $0<r\le 1$ and $y\in \Omega$, then the ball $B_r(y)$ satisfies

$$\begin{aligned} \left| \left\{ x \in \Omega : \mathcal {M}(|Du_\epsilon |^{2}) > N^{2} \right\} \cap B_r(y) \right| > \eta \left| B_r(y) \right| , \end{aligned}$$

(4.27)

where

$$\begin{aligned} \left( \frac{80}{7} \right) ^n N^p \eta =\frac{1}{2}, \end{aligned}$$

(4.28)

and the following condition holds

$$\begin{aligned} \Omega \cap B_r(y) \subset \left\{ x \in \Omega : \mathcal {M}(|Du_\epsilon |^{2}) > 1 \right\} \cup \left\{ x \in \Omega : \mathcal {M}(|F|^{2} ) > \delta ^{2} \right\} . \end{aligned}$$

(4.29)

Proof

Our argument is one of contradiction. Using a scaling argument, it suffices to prove this lemma for the $r=1$ case. Therefore, assume (4.27) holds, but (4.29) is false. Then there is a point $x_{1} \in \Omega \cap B_1(y)$ such that

$$\begin{aligned} \frac{1}{|B_{\rho }(x_{1})|} \int _{\Omega _{\rho }(x_{1})} |Du_\epsilon |^{2} \mathrm{d}x \le 1 \quad {\text {and}} \quad \frac{1}{|B_{\rho }(x_{1})|} \int _{\Omega _{\rho }(x_{1})} |F|^{2} \mathrm{d}x \le \delta ^{2} \end{aligned}$$

(4.30)

for all $\rho >0$.

We divide this into the two cases : an interior case when $B_5(y)\subset \Omega$ and a boundary case where $B_5(y)\not \subset \Omega$. Here, we only consider the boundary case because the proof for the interior case is similar to that of the boundary case. Because $\Omega$ is $(\delta ,50)$-Reifenberg flat, there exists an appropriate coordinate system such that

$$\begin{aligned} B_5(y)\cap \Omega \subset B_{10} \cap \Omega \end{aligned}$$

(4.31)

and

$$\begin{aligned} B_{50}^{+}\subset \Omega _{50} \subset B_{50}\cap \{x_{n}>-100\delta \}. \end{aligned}$$

(4.32)

It directly follows from (4.30) that

$$\begin{aligned} \frac{1}{|B_{50}|}\int _{\Omega _{50}} |Du_\epsilon |^{2} \mathrm{d}x \le \frac{|B_{100}(x_1)|}{|B_{50}|} \frac{1}{|B_{100}|}\int _{\Omega _{100}(x_1)} |Du_\epsilon |^2 \mathrm{d}x \le 2^{n} \end{aligned}$$

(4.33)

because $B_{50} \subset B_{100}(x_1)$. Similarly, we have

$$\begin{aligned} \frac{1}{|B_{50}|}\int _{\Omega _{50}} |F|^{2} \mathrm{d}x \le 2^{n} \delta ^{2}. \end{aligned}$$

(4.34)

The rescaled maps are defined as:

$$\begin{aligned} \tilde{u}_{\epsilon }(z)=\frac{u_{\epsilon }(10z)}{10 \sqrt{2^n}}, \quad \tilde{F}(z)=\frac{F(10z)}{\sqrt{2^n}}, \quad \tilde{A}_{ij}^{\alpha \beta ,\epsilon }(z)=A_{ij}^{\alpha \beta , \epsilon }(10z) \quad (z\in \Omega _5). \end{aligned}$$

(4.35)

Therefore, $\tilde{u}_\epsilon \in H^{1}(\Omega _5,\mathbb {R}^{m})$ is a weak solution of

$$\begin{aligned} \left\{ \begin{array}{rclcc} D_{\alpha } \left( \tilde{A}_{ij}^{\alpha \beta ,\epsilon }(z) D_{\beta }\tilde{u}_\epsilon ^{j}(z) \right) &{} = &{} D_{\alpha } \tilde{f}_{\alpha }^{i}(z) &{} {\text { in }} &{} \Omega _5 \\ \tilde{u}_\epsilon ^{i}(z) &{} = &{} 0 &{} {\text { on }} &{} \partial _{w}\Omega _5 \end{array}\right. \end{aligned}$$

(4.36)

with

$$\begin{aligned} \frac{1}{|B_5|}\int _{\Omega _5}|D\tilde{u}_\epsilon |^{2}dz \le 1 \quad {\text { and }} \quad \frac{1}{|B_{5}|}\int _{\Omega _5}|\tilde{F}|^{2}dz \le \delta ^2. \end{aligned}$$

(4.37)

Let $\tilde{w}_\epsilon \in H^1(\Omega _4, \mathbb {R}^m)$ be the weak solution of

$$\begin{aligned} \left\{ \begin{array}{rclcc} D_{\alpha } \left( \tilde{A}_{ij}^{\alpha \beta , \epsilon }(z)D_{\beta }\tilde{w}_\epsilon ^{j}(z) \right) &{} = &{} 0 &{} {\text { in }} &{} \Omega _4 \\ \tilde{w}_\epsilon ^{i}(z) &{} = &{} \tilde{u}_\epsilon ^{i}(z) &{} {\text { on }} &{} \partial \Omega _4. \end{array}\right. \end{aligned}$$

(4.38)

Then $\tilde{u}_\epsilon - \tilde{w}_\epsilon \in H^1_0(\Omega _4, \mathbb {R}^m)$ is the weak solution of

$$\begin{aligned} \left\{ \begin{array}{rclcc} D_{\alpha } \left( \tilde{A}_{ij}^{\alpha \beta , \epsilon }(z)D_{\beta }(\tilde{u}_\epsilon ^{j}(z)-\tilde{w}_\epsilon ^{j}(z) \right) &{} = &{} D_{\alpha } \tilde{f}_{\alpha }^{i}(z) &{} {\text { in }} &{} \Omega _4, \\ \tilde{u}_\epsilon ^{i}(z)-\tilde{w}_\epsilon ^{i}(z) &{} = &{} 0 &{} {\text { on }} &{} \partial \Omega _4. \end{array}\right. \end{aligned}$$

(4.39)

Applying a standard $L^2$ estimate to (4.39) and (4.37), we obtain

$$\begin{aligned} \frac{1}{|B_4|}\int _{\Omega _4}|D\tilde{u}_{\epsilon }-D\tilde{w}_{\epsilon }|^2 dz \le \frac{c}{|B_4|}\int _{\Omega _4}|\tilde{F}|^2 dz \le c\delta ^2 \end{aligned}$$

(4.40)

for some positive constant $c=c(\nu , L,m,n)$.

In addition, if we apply Lemma 4.6, then for any fixed $\kappa >0$, there exists a small $\delta =\delta (\kappa ,\nu ,L,m,n)>0$ such that a weak solution $\tilde{v}_\epsilon \in H^1(B^+_3,\mathbb {R}^{m})$ exists for

$$\begin{aligned} \left\{ \begin{array}{rclcc} D_{\alpha } \left( \tilde{A}_{ij}^{\alpha \beta ,\epsilon }(z)D_{\beta }\tilde{v}_\epsilon ^{j} \right) &{} = &{} 0 &{} {\text { in }} &{} B_{3}^{+} \\ \tilde{v}_\epsilon ^{i} &{} = &{} 0 &{} {\text { on }} &{} T_{3}, \end{array}\right. \end{aligned}$$

(4.41)

with

(4.42)

for some constant $c=c(\nu ,L,m,n)$ such that

(4.43)

Applying Lemma 4.4 to (4.41) with $q=p+1$, we know there is a small $\delta =\delta (\nu ,L,m,n,p)$ so that

(4.44)

for some constant $c=c(\nu , L,m,n,p)$. Therefore, for the zero extension $\bar{\tilde{v}}_\epsilon$ of $\tilde{v}_\epsilon$ from $B_3^+$ to $B_3$ we have

Estimate of $I_1$ : the inequality (4.40) gives us

$$\begin{aligned} I_1\le \frac{c}{N^2}\delta ^2 \end{aligned}$$

(4.45)

for some positive constant $c=c(\nu ,L,m,n)$.

Estimate of $I_2$ : applying Lemma 4.3, Hölder’s inequality, and (4.43), we see that

$$\begin{aligned} I_2\le & {} \frac{c}{N^2}\left( \frac{1}{|B_1|}\int _{B_1^+}|D\tilde{w}_\epsilon -D\tilde{v}_\epsilon |^{2}dz + \frac{1}{|B_1|}\int _{\Omega _1 \backslash B_1^+} |D\tilde{w}_\epsilon |^{2}dz\right) \nonumber \\\le & {} \frac{c}{N^2}\left( \kappa ^2 + \left( \int _{\Omega _3}|D\tilde{w}_\epsilon |^{2+\sigma _1}dz \right) ^{\frac{2}{2+\sigma _1}}\left( \int _{\Omega _1\backslash B_1^+} dz \right) ^{\frac{\sigma _1}{2+\sigma _1}}\right) \nonumber \\\le & {} \frac{c}{N^2}\left( \kappa ^2 + \delta ^{\frac{\sigma _1}{2+\sigma _1}}\right) \end{aligned}$$

(4.46)

for some positive constant $c=c(\nu ,L,m,n)$.

Estimate of $I_3$ : from (4.42) and (4.44) we can conclude

(4.47)

for some positive constant $c=c(\nu ,L,m,n,p)$.

Therefore, if we combine (4.45), (4.46), and (4.47), we see that

$$\begin{aligned}&\frac{1}{|B_1|}|\{x\in \Omega : \mathcal {M}(|Du_\epsilon |)^2 > N^2\} \cap B_1(y)| \nonumber \\&\quad \le I_1+I_2+I_3 \nonumber \\&\quad \le \frac{c}{N^{p+1}}+\frac{c}{N^2}\left( \kappa ^2+\delta ^2+\delta ^{\frac{\sigma _1}{2+\sigma _1}}\right) \nonumber \\&\quad \le c\eta ^{\frac{p+1}{p}}+c\eta ^{\frac{2}{p}}\left( \kappa ^2+\delta ^2+\delta ^{\frac{\sigma _1}{2+\sigma _1}}\right) \nonumber \\&\quad = \eta \left( c\eta ^{\frac{1}{p}}+ c\eta ^{\frac{2}{p}-1}\left( \kappa ^2+\delta ^2+\delta ^{\frac{\sigma _1}{2+\sigma _1}}\right) \right) \end{aligned}$$

for some constant $c=c(\nu ,L,m,n,p)$. Finally, if we select $\eta$ so that it satisfies $c \eta ^{\frac{1}{p}}=\frac{1}{3}$ and $\delta$ so that it satisfies $c \eta ^{\frac{2}{p}-1} \kappa ^2 \le \frac{1}{3}$ and $c\eta ^{\frac{2}{p}-1}\left( \delta ^2+\delta ^{\frac{\sigma _1}{2+\sigma _1}}\right) \le \frac{1}{3}$, then given this $\eta$ and $\delta$ we can conclude that

$$\begin{aligned} |\{x\in \Omega : \mathcal {M}(|Du_\epsilon |)^2 > N^2\} \cap B_1(y)| \le \eta |B_1|. \end{aligned}$$

(4.48)

This contradicts (4.27) and completes the proof. $\square$

After establishing the preceding lemmas, we are ready to verify the required $W^{1,p}$ estimate for the homogenization problem. Henceforth, we will fix constants $\eta$ and N given by Lemma 4.7. The letter c denotes the constant that can be explicitly computed in terms of the known quantities: $|\Omega |,\nu , L, m, n, \text{ and } p$.

Proof of Theorem 2.4

Given any p with $2<p<\infty$, assume that $F\in L^p(\Omega , \mathbb {R}^{mn})$ and $A_{ij}^{\alpha \beta }$ is $(\delta ,50)$-vanishing. Also let $u_\epsilon \in H_0^{1}(\Omega ,\mathbb {R}^m)$ be the weak solution of (1.1).

We can further suppose that

$$\begin{aligned} \Vert F \Vert _{L^{p}(\Omega )} \le \delta \end{aligned}$$

(4.49)

by replacing $u_\epsilon$ and F with $\frac{u_\epsilon }{\frac{1}{\delta }\Vert F \Vert _{L^{p}(\Omega )} +\sigma }$ and $\frac{F}{\frac{1}{\delta } \Vert F \Vert _{L^{p}(\Omega )} +\sigma }$ for $\sigma >0$, respectively. We want to show that

$$\begin{aligned} \Vert \mathcal {M}(|Du_\epsilon |^2) \Vert _{L^{\frac{p}{2}}(Q_1)}\le c \end{aligned}$$

for some universal constant $c>0$ when $\sigma \rightarrow 0$.

In order to do this, we write

$$\begin{aligned} C= \left\{ x \in \Omega : \mathcal {M}(|Du_\epsilon |^{2}) > N^{2} \right\} \end{aligned}$$

and

$$\begin{aligned} D= \left\{ x \in \Omega : \mathcal {M}(|Du_\epsilon |^{2}) > 1 \right\} \cup \left\{ x \in \Omega : \mathcal {M}(|F|^{2} ) > \delta ^{2} \right\} . \end{aligned}$$

If we use the weak 1-1 estimate, the standard $L^2$ estimate, and Hölder’s inequality, we see that

$$\begin{aligned} |C|\le & {} \frac{c}{N^{2}} \int _{\Omega } |Du_\epsilon |^{2} \mathrm{d}x \le \frac{c}{N^{2}} \int _{\Omega } |F|^{2} \mathrm{d}x \nonumber \\\le & {} \frac{c}{N^{2}} |\Omega |^{\frac{p-2}{p}}\Vert F \Vert ^2_{L^{p}(\Omega )} \le \frac{c \delta ^2}{N^2} < \eta |B_{1}|, \end{aligned}$$

(4.50)

in which $\delta >0$ is sufficiently small. This confirms the first condition of Lemma 3.2. Moreover, the second condition of Lemma 3.2 directly follows from Lemma 4.7. Applying Lemma 3.2, we see that

$$\begin{aligned} |C| < \eta _{1} |D|, \qquad {\text { where }} \quad \eta _{1}= \left( \frac{10}{1-\delta } \right) ^{n}\eta \le \left( \frac{80}{7}\right) ^n \eta , \end{aligned}$$

when $\delta <\frac{1}{8}$ [21].

On the other hand, because (1.1) has the invariance property under normalization, we obtain the same results for $(\frac{u_\epsilon }{N}, \frac{F}{N}), \, (\frac{u_\epsilon }{N^2}, \frac{F}{N^2}), \, (\frac{u_\epsilon }{N^3}, \frac{F}{N^3}),\ldots$ inductively. Using this iteration argument, the following power decay estimates of $\mathcal {M}(|Du_\epsilon |^{2})$ are produced :

$$\begin{aligned}&\left| \left\{ x \in \Omega : \mathcal {M}(|Du_\epsilon |^{2}) > N^{2k} \right\} \right| \\&\quad \le \, \eta _{1}^{k} \left| \left\{ x \in \Omega : \mathcal {M}(|Du_\epsilon |^{2}) > 1 \right\} \right| + \sum _{i=1}^{k} \eta _{1}^{i} \left| \left\{ x \in \Omega : \mathcal {M}(|F|^{2} ) > \delta ^{2} N^{2(k-i)} \right\} \right| . \end{aligned}$$

If we apply Lemma 3.1 to

$$\begin{aligned} g= \mathcal {M}(|Du_\epsilon |^2), \quad \lambda =N^2, \quad \theta =1, ~{\text { and }}~ q=\frac{p}{2}, \end{aligned}$$

then a direct computation yields

$$\begin{aligned} \Vert \mathcal {M}( |Du_\epsilon |^2) \Vert ^{\frac{p}{2}}_{L^{\frac{p}{2}}(\Omega )}\le & {} c \left( |\Omega | + \sum _{k\ge 1} N^{2k\frac{p}{2}} \left| \left\{ x \in \Omega : \mathcal {M}(|Du_\epsilon |^{2}) > N^{2k} \right\} \right| \right) \\\le & {} c \left( 1 + \sum _{k\ge 1} N^{kp} \eta _{1}^{k} \left| \left\{ x \in \Omega : \mathcal {M}(|Du_\epsilon |^{2}) > 1 \right\} \right| \right. \\&+ \sum _{k\ge 1} N^{kp} \sum _{i=1}^{k}\eta _{1}^{i} \left| \left\{ x \in \Omega : \mathcal {M}(|F|^{2} ) > \delta ^{2} N^{2(k-i)} \right\} \right| \Bigg ) \\=: & {} S_1 ~ + ~ S_2.\\ \end{aligned}$$

$$\begin{aligned} S_1\le & {} c \left( 1 + \sum _{k\ge 1} N^{kp} \eta _{1}^{k} \left| \left\{ x \in \Omega : \mathcal {M}(|Du_\epsilon |^{2}) > 1 \right\} \right| \right) \\\le & {} c \left( 1 + |\Omega | \sum _{k\ge 1} N^{kp} \eta _{1}^{k} \right) .\\ S_2\le & {} c \sum _{k\ge 1} N^{kp} \sum _{i=1}^{k}\eta _{1}^{i} \left| \left\{ x \in \Omega : \mathcal {M}(|F|^{2} ) > \delta ^{2} N^{2(k-i)} \right\} \right| \\= & {} c \sum _{i\ge 1} \left( N^{p} \eta _{1} \right) ^{i} \sum _{k\ge i}(N^{p})^{k-i} \left| \left\{ x \in \Omega : \mathcal {M}(|F|^{2} ) > \delta ^{2} N^{2(k-i)} \right\} \right| \\= & {} c \sum _{i\ge 1} \left( N^{p} \eta _{1} \right) ^{i} \sum _{j\ge 0}(N^{p})^{j} \left| \left\{ x \in \Omega : \mathcal {M} \left( \left| \frac{F}{\delta }\right| ^2 \right) > N^{2j} \right\} \right| \\\le & {} c \sum _{i\ge 1} \left( N^{p} \eta _{1} \right) ^{i} \left\| \mathcal {M} \left( \left| \frac{F}{\delta } \right| ^2 \right) \right\| _{L^{\frac{p}{2}}(\Omega )} \\\le & {} c \sum _{i\ge 1} \left( N^{p} \eta _{1} \right) ^{i} \frac{\Vert F \Vert _{L^p(\Omega )}^2}{\delta ^2} ~ \le ~ c \sum _{i\ge 1} \left( N^{p} \eta _{1} \right) ^{i} . \end{aligned}$$

Therefore, we have

$$\begin{aligned} \Vert \mathcal {M}( |Du_\epsilon |^2) \Vert ^{\frac{p}{2}}_{L^{\frac{p}{2}}(\Omega )} ~ \le ~ c \left( 1 + \sum _{k\ge 1} \left( N^{p} \eta _{1} \right) ^{k} \right) \le c \end{aligned}$$

because we know $N^{p} \eta _{1} = N^p \left( \frac{10}{1-\delta } \right) ^{n}\eta \le N^p \left( \frac{80}{7}\right) ^n \eta =\frac{1}{2}$ from (4.28). Hence, we can select a corresponding small $\delta =\delta (\nu ,L,m,n,p)>0$ from Lemmas 4.7 and (4.50). Using the strong p-p estimate of (3.1), we have

$$\begin{aligned} \Vert Du_\epsilon \Vert _{L^{p}(\Omega )} \le c \end{aligned}$$

for some constant $c>0$. This completes the proof. $\square$