Researchers have consistently demonstrated that studying multiple examples is more effective than studying one example to facilitate learning because the comparison evoked by multiple examples facilitates schema construction and is thus beneficial for learning (Catrambone and Holyoak 1989; Cooper and Sweller 1987; Gibson and Gibson 1955; Gick and Paterson 1992; Reed 1993; Rittle-Johnson and Star 2009; Schwartz and Bransford 1998; Silver et al. 2005; Sweller and Cooper 1985; Tennyson 1973). As Gentner (2005) noted, “Comparison is a general learning process that can promote deep relational learning and the development of theory-level explanations” (p. 251).

However, it remains unclear how similar or different examples should be in order to promote learning (for a review, see Guo et al. 2012). For example, should we present students with high-variability examples or low-variability examples? Is the effectiveness of multiple examples the same for all students or moderated by students’ prior knowledge? In the current study, we experimentally evaluated the effects of different comparisons on the learning of multistep linear equation solving and their interaction effects with students’ prior knowledge.

In the introduction, we briefly review literature on learning from comparing multiple examples and discuss limitations in existing research. Next, we elaborate the “critical aspects/features” and “patterns of variation and invariance” from variation theory that guided this investigation of unresolved issues in example comparison research. Finally, we introduce the two critical aspects of problem type and solution method for learning equation solving according to which the experimental conditions were designed.

Experimental research on learning from comparing multiple examples

Studies on learning comparing from multiple examples have shown that the impact of comparison on learning depends on the variability of multiple examples being compared and the prior knowledge of the students. However, still unclear is the role of example variability and students’ prior knowledge in learning from comparing examples.

First, it is unclear how similar or different examples should be in order to promote learning (Renkl et al. 1998; Rittle-Johnson and Star 2009). Examples are generally analyzed from surface (irrelevant) features and structural (relevant) features (Gick and Holyoak 1980, 1983; Holyoak and Koh 1987; Paas and Van Merrienboer 1994; Quilici and Mayer 1996; Reed 1989; Ross 1989b, 1997; Ross and Kennedy 1990; VanderStoep and Seifert 1993). Example variability consists of differences in the surface and structural aspects among the examples. Holyoak and Koh (1987) distinguished surface features, such as names, objects, numbers, and story lines, as irrelevant to goal attainment and structural features, such as underlying mathematical procedures, rules, solutions, and principles, as relevant to goal attainment.

Researchers have reported contradictory findings regarding how similar multiple examples should be in terms of surface and structural features (Renkl et al. 1998; Rittle-Johnson and Star 2009). Considerable evidence on concept learning and procedural learning indicated that providing positive examples differing in surface features should help learners focus on structural features rather than relying on surface features, which might facilitate structure-based schema formation and develop a more accurate understanding of the concept (Hammer et al. 2008; Merrill and Tennyson 1978; Ranzijn 1991; Tennyson 1973) or the procedure (Paas and Van Merrienboer 1994; Quilici and Mayer 1996; Rittle-Johnson and Star 2009). Given superficially similar examples, the learner might consider surface features as relevant, which might interfere with schema construction and future problem solving (Quilici and Mayer 1996; Reed 1989). The reverse, however, seems to be true as well. Providing superficially similar examples might help the learner discern and align the structural features and form the schema; highly variable examples might make the structural features difficult to discern (e.g., Gentner and Namy 1999; Gick and Holyoak 1980, 1983; Namy and Clepper 2010; Namy and Gentner 2002; Richland et al. 2004; Ross 1989a; Ross and Kennedy 1990).

Second, the literature is unclear with respect to the role of students’ prior knowledge in learning from multiple examples (Rittle-Johnson et al. 2009). Some researchers found that (a) students with low prior knowledge did not benefit from comparing multiple examples, especially complex and unfamiliar examples (e.g., Holmqvist et al. 2007; Schwartz and Bransford 1998); (b) students with high prior knowledge benefited from comparing any example variability, whereas students with low prior knowledge benefited from comparing only highly variable examples (e.g., Quilici and Mayer 1996); (c) students with higher prior knowledge benefited more from comparing high-variability examples, whereas students with lower prior knowledge benefited more from comparing low-variability examples (e.g., Große and Renkl 2006, 2007); and (d) there was no interaction between students’ prior knowledge and example variability (e.g., Renkl et al. 1998). In short, as noted by Guo and Pang (2011), it remains unclear what type of example variability should be provided to students with different levels of prior knowledge.

Rittle-Johnson and colleagues (Rittle-Johnson and Star 2007, 2009; Rittle-Johnson et al. 2009; Star and Rittle-Johnson 2009) explored these issues in the context of mathematics learning. Rittle-Johnson and Star (2007, 2009) found that students who compared the same equations solved with different solution methods learned better than those who (a) compared the same solution methods one at a time, (b) compared equivalent equations solved with the same solution method, or (c) compared different equations solved with the same solution method. Rittle-Johnson et al. (2009) carried these findings a step further to investigate whether students’ prior knowledge of solution methods impacted the effectiveness of comparison for supporting equation learning. Results showed that students with lower prior knowledge benefited most from studying examples sequentially or comparing problem types, whereas students with higher prior knowledge benefited more from comparing solution methods.

However, students in research conducted by Rittle-Johnson and colleagues either compared the same equations solved with different solution methods or compared different equations solved with the same solution method. In other words, only solution method or problem type was varied for students to learn equation solving; they did not experience the variation of both problem type and solution method in the intervention. Because both problem type and solution method are crucial for learning equation solving, it is necessary for researchers to examine how to introduce the variation of both problem type and solution method to students and the effectiveness of different types of example variability.

The present study continues to investigate the role of example variability and students’ prior knowledge in mathematics learning. We chose the topic of equation solving that had been examined by Rittle-Johnson and colleagues because only one critical aspect (problem type or solution method) was manipulated in their studies. Our aim in the present study was to explore the relative effectiveness of separately and simultaneously varying the two critical aspects of problem type and solution method in equation solving. Our findings can thus contribute to the effective use of comparison in the classroom.

Critical aspects/features and patterns of variation and invariance

Our research was based on the variation theory which holds variation to be epistemologically fundamental for all learning to happen (for details, see Marton and Booth 1997; Marton and Tsui 2004). Different from cognitive theories that consider learning as the construction of mental representations, the variation theory interprets learning as the creation of new individual-world relations through our experiences and thus as a new way of seeing something (Marton and Booth 1997). The new way of seeing amounts to discerning certain critical features and focusing on them simultaneously (Marton 1999). In particular, the notions of “critical aspects/features” and “patterns of variation and invariance” from the variation theory guided the present study to address unresolved issues in example variability research.

Critical aspects/features of the object of learning

In the variation theory, aspects and features of a phenomenon and its examples are analyzed as critical or uncritical to students’ understanding and learning, rather than as surface or structural to the objective disciplinary knowledge. Critical aspects are aspects that cause difficulty for students in the process of learning; they might be superficial or structural to the objective knowledge. For example, if a child believes that fruit can only be round, then the surface aspect (shape) and feature (round) become critical for the child to learn the concept of fruit. In order to help the child realize that fruit could be in different shapes, we should show him/her different examples (e.g., an apple, a banana, and a carambola) that have different shapes. Here, the surface aspect of shape is the critical aspect for learning the concept of fruit. As such, other surface aspects of fruit such as size and color also become critical aspects for students who wrongly associate fruit to a specific size or color. As Marton and Pang (2008) argued, both the disciplinary knowledge and the students’ understanding should be taken into account when identifying the critical aspects of a learning object.

Patterns of variation and invariance

According to the variation theory, to learn a phenomenon means to simultaneously discern the critical aspects/features of the phenomenon. To discern, a learner must experience variation. When an aspect of a phenomenon varies while other aspects remain invariant, the varied aspect will be discerned (Pang and Marton 2005). In particular, Marton and his colleagues (e.g., Marton and Pang 2006; Marton and Tsui 2004) defined four patterns of variation and invariance to facilitate the discernment of critical aspects: contrast, separation, fusion, and generalization.

Contrast occurs when a learner experiences variation of different values or features in an aspect of a phenomenon. To experience something, the learner must experience something else in order to make a comparison. The pattern of contrast focuses on a particular value or feature of an aspect. Separation happens when a learner focuses on an aspect of a phenomenon. To experience a certain aspect of something separately from other aspects, it must vary while other aspects remain invariant. In this pattern, the varied aspect is discerned by the learner. Contrast and separation occur when two or more objects have a varying aspect while other aspects remain invariant. Fusion takes place when a learner wants to discern several aspects of a phenomenon that vary simultaneously. To experience a phenomenon, the learner must discern all critical aspects at the same time when different critical aspects vary simultaneously. Students will grasp a concept if they can simultaneously discern all critical aspects of the concept. Generalization occurs when a learner wants to apply his/her previous discernment to various contexts. To fully understand an object of learning, the learner must experience many other examples to generalize the meaning (for a more detailed discussion, see Guo et al. 2012). Researchers have suggested that contrast and separation should be used first to help students discern each critical aspect separately, followed by fusion that simultaneously varies all critical aspects (Ki 2007; Marton and Tsui 2004; Pang 2002). Generalization can be used after students have simultaneously discerned all critical aspects to generalize the discernment to other contexts.

In the current study, we analyzed multistep linear equation solving and its worked examples based on the two critical aspects for learning equation solving and investigated the effectiveness of patterns of variation and invariance in helping students discern these critical aspects. We expected that this way of analyzing equation solving and designing its multiple examples would help to clarify ambiguous issues in research on example comparison.

Two critical aspects for the learning of equation solving

Rittle-Johnson and colleagues (Rittle-Johnson and Star 2007, 2009; Rittle-Johnson et al. 2009) identified two critical aspects for the learning of equation solving: problem type and solution method. As shown in Table 1, three types of multistep linear equations were identified: divide composite, combine composite, and subtract composite; these three equation types were three values of the critical aspect of problem type. For each type of equation, there were two types of solution methods. The first method was a conventional and distribute-first method that could be used to solve most equations. This method first distributed the parentheses, then combined like terms, subtracted constants and variables from both sides, and finally divided both sides by the coefficient. The second method of solving equations was a nonconventional and shortcut method that considered expressions such as (χ + 3) a composite variable. The nonconventional method was more efficient because it involved fewer steps and fewer computations. These two methods were two values of the critical aspect of solution method.

Table 1 Alternative solution methods for the three types of equations
Full size table

Rittle-Johnson et al. (2009) indicated that only 20 % of seventh-grade and eighth-grade students could correctly use the distribute-first method, 4 % attempted to use shortcut methods, and 41 % of students never used an algebraic approach to solve an equation at pretest. Even after instruction, only about 20 % of items were solved via the shortcut method. To completely master multistep linear equation solving, students need to simultaneously discern the two critical aspects of problem type and solution method. In other words, they should understand that there are three types of equations and that each equation can be solved by two methods.

Present study

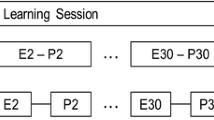
We evaluated four types of comparison for supporting seventh-grade students’ learning about equation solving. The four conditions differed in how the problem type and solution method varied within an example pair (see Fig. 1 and Table 3). Students were randomly assigned to first compare separate variation of problem types and solution methods and then compare simultaneous variation of these two aspects (compare types, compare methods, compare types + methods; abbreviated as T_M_T + M), to first compare separate variation of solution methods and then compare simultaneous variation of problem types and solution methods (compare methods, compare methods, compare types + methods; abbreviated as M_M_T + M), to first compare separate variation of problem types and then compare simultaneous variation of problem types and solution methods (compare types, compare types, compare types + methods; abbreviated as T_T_T + M), or to compare separation variation of problem types and solution methods but not compare simultaneous variation of these two aspects (compare types, compare methods, compare types or methods; abbreviated as T_M_T/M).

Fig. 1
figure 1

Three types of comparison

Full size image

Comparison of T_M_T + M with M_M_T + M permitted the assessment of the effects of separate variation of problem type, comparison of T_M_T + M with T_T_T + M permitted the assessment of the effects of separate variation of solution method, and comparison of T_M_T + M with T_M_T/M permitted the assessment of the effects of simultaneous variation of problem type and solution method.

Students in this study were expected to vary in their prior knowledge of equation solving. According to the curriculum, students had previously learned about solving a multistep linear equation using the conventional method. However, they had not been taught the composite-variable shortcut method in the classroom, although some teachers might have mentioned the shortcut method to some extent. Students thus varied in their knowledge of solving equations. As a result, the present study investigated the possible interaction effect between students’ prior knowledge and condition to examine the role of students’ prior knowledge in learning from examples. We hypothesized that the effect of condition would interact with students’ prior knowledge of equation solving.

Method

Participants

Participants were 274 seventh-grade students from an urban public high school in Xiamen, China that was considered at above average level. The students were drawn from six classes and their mean age was 14.2 years (range, 12.1 to 16.2). Of these students, seven were absent for the pretest and four were absent for the posttest and were dropped from the analysis. In previous lessons, students had learned about distributive property, simplifying expressions, and solving multistep equations by a conventional method. However, they had not been taught how to solve equations by a shortcut method.

Design

We employed a pretest–intervention–posttest design. A pretest and a posttest were used to evaluate students’ procedural knowledge, flexibility knowledge, and conceptual knowledge of equation solving. Students were randomly assigned to T_M_T + M (n = 66), M_M_T + M (n = 64), T_T_T + M (n = 65), or T_M_T/M (n = 68). The intervention occurred during three consecutive mathematics classes. During the 3-day intervention, students studied a corresponding intervention packet of worked-example pairs, answered explanation prompts, and solved practice problems.

To explore the possible interaction effect of prior equation solving knowledge and intervention condition, we assessed students’ prior knowledge based on whether they used or did not use a shortcut method to solve equations at pretest. We did not categorize students as using algebra or not using algebra as in Rittle-Johnson and colleagues’ studies because most students in the present study showed mastery of algebraic methods at pretest.

Materials

Intervention

Packets of worked examples were created for each condition as follows: compare types, compare methods, compare types + methods, and compare types or methods. The primary difference between the packets was how the worked examples were paired, as shown in Fig. 1 and Table 2. In the compare types packets, each worked-example pair contained two different types of equations, each solved with the same method; the critical aspect of problem type was separately varied while the critical aspect of solution method was kept invariant. In the compare methods packets, each worked-example pair contained the same equation solved with the conventional and the shortcut methods; the critical aspect of solution method was separately varied while the critical aspect of problem type was kept invariant. In the compare types + methods packets, each worked-example pair contained two different types of equations solved with the conventional and the shortcut methods; the two critical aspects of problem type and solution method were simultaneously varied. In the compare types or methods packets, worked-example pairs were similar to those from compare types packets or compare methods packets; the two critical aspects were varied separately rather than simultaneously.

Table 2 Difference among four packets of worked examples
Full size table

Except for the difference in how the worked examples were paired, the packets were as similar as possible. Both the compare types packets and the compare methods packets contained 4 instances of each of the 3 equation types for a total of 12 worked examples. Both the compare types + methods packets and the compare types or methods packets contained six worked examples. Half of the worked examples illustrated the conventional solution method and half illustrated the composite-variable shortcut method.

The four conditions consisted of different packets as shown in Table 3. The T_M_T + M condition contained one compare types packet, one compare methods packet, and one compare types + methods packet; the M_M_T + M condition contained two compare methods packets and one compare types + method packet; the T_T_T + M condition contained two compare types packets and one compare types + method packet; and the T_M_T/M condition contained one compare types packet, one compare methods packet, and one compare types or method packet.

Table 3 Comparison among four conditions
Full size table

The packets were distributed to students over three intervention sessions. As a result, students in the T_M_T + M condition first compared equations that had different problem types and the same solution method, then compared the same equations that had different solution methods, and finally compared equations that had different problem types and solution methods. Those students first separately compared each of the two critical aspects (i.e., problem type and solution method) and then experienced simultaneous variation of these two critical aspects. Students in the M_M_T + M condition compared the same equations that had different solution methods in the first two intervention sessions and then compared equations that had different problem types and solution methods. Those students separately compared the critical aspect of solution method and then experienced simultaneous variation of these two critical aspects; they did not separately compare the critical aspect of problem type. Students in the T_T_T + M condition compared equations that had different problem types and the same solution method in the first two intervention sessions. Then, they compared equations that had different problem types and solution methods. Those students separately compared the critical aspect of problem type and then experienced simultaneous variation of these two critical aspects; they did not separately compare the critical aspect of the solution method. Students in the T_M_T/M condition separately compared each of the two critical aspects in the first two sessions. In the third session, they did not simultaneously compare variation of these two aspects but compare equations similar to those in the first two sessions (compare types or compare methods).

Therefore, the four conditions were different with respect to whether critical aspects of equation solving were compared first separately and then simultaneously. Except for the difference of how examples were paired, other components of the four conditions were as similar as possible. At the end of the third session, students were asked to solve four practice problems each in two different ways. Answers for these practice problems were provided on the next page of the packet for students to self-evaluate their understanding.

Assessment

A test of 19 items was developed to measure the students’ procedural knowledge, flexibility knowledge, and conceptual knowledge at pretest and posttest, as suggested by Rittle-Johnson et al. (2009). The pretest and posttest were paper-and-pencil assessments. Sample items are included in Table 4.

Table 4 Sample items and coding scheme for assessing procedural, flexibility, and conceptual knowledge at the pretest and the posttest
Full size table

To make our results comparable to those from studies by Rittle-Johnson and colleagues (Rittle-Johnson and Star 2007, 2009; Rittle-Johnson et al. 2009), we replicated their assessment of students’ performance. Procedural knowledge was measured by seven items assessing students’ ability to solve familiar, near transfer, and far transfer problems. The familiar problems were the same types of problems as those used in the intervention packets. The near transfer problems included additional terms inside the parentheses and new operators. The far transfer problems required using the equation knowledge to solve practical problems. Flexibility knowledge was independently measured in three ways: (a) recognize appropriate first solution steps for a particular problem (two items); (b) generate different solutions to an equation (two items); and (c) evaluate novel solution steps for accuracy and efficiency (two items). Conceptual knowledge was assessed by six items measuring students’ verbal and nonverbal knowledge of equivalence, like terms, and composite variables. Items measuring flexibility knowledge and conceptual knowledge were designed to mainly evaluate students’ discernment of solution methods, i.e., whether they were able to consider expressions such as (χ + 1) a composite variable. It should be noted that, although the critical aspect of problem type might also affect how students solved the problems, we did not design items to evaluate students’ familiarity with different types of equations.

Procedure

All data collection occurred over five class sessions. On day 1, all of the students were asked to take a 45-min pretest to determine their prior knowledge of equation solving. One week after the pretest, students were assigned to T_M_T + M, M_M_T + M, T_T_T + M, or T_M_T/M conditions and were given a corresponding intervention packet to study for 45 min. An instructor gave a brief (10 min) scripted introduction to students before the intervention. All instructors were our research assistants and followed a script. The instructor reminded students when 10 min remained in a session. The packets were collected after the intervention was completed for that session. The next 2 days of instruction followed the same format. At the end of day 4, the instructor provided an 8-min wrap-up lesson to explain that (a) there is more than one way to solve an equation, (b) any way is OK if the two sides of the equation are kept equal, and (c) some ways of solving equations are better or easier than others.

On day 5, students were given 45 min to complete the posttest, which was equivalent to the pretest. Before the pretest and posttest, the instructor also gave a brief scripted introduction of the tests, explaining the task to the students. They were told to justify their answers and to feel free to elaborate on their ideas as much as possible. The students were told that their answer sheets would not be rated or reviewed by their teachers. They were also reminded when 10 min remained. To ensure fidelity of condition, the authors did not administer any test or intervention, but gave direction and provided assistance to instructors when necessary, as well as observed classrooms.

Coding

As shown in Table 4, the seven equations on the procedural knowledge assessment were scored for response accuracy. In addition, students’ solution methods for the seven procedural knowledge items and two generate methods items were coded, based on whether the first step was or was not a shortcut step. Different from Rittle-Johnson and colleagues who considered students’ use of algebraic methods at pretest as an index of prior knowledge of algebraic methods, we considered students’ use of shortcut method at pretest to differentiate students’ prior knowledge. This is because most students in the present study demonstrated their mastery of algebraic methods at pretest. The flexibility and conceptual knowledge assessment were scored according to the guidelines in Table 4. The tests were coded by two independent raters. The agreement was 93 % for coding the solution methods and 95 % for coding the explanations; disagreements were resolved through consensus.

Data analysis

Seven students did not complete the pretest and four did not complete the posttest. These missing values were deleted in the following data analyses. We used two-way analyses of covariance (ANCOVA) models to examine the effects of different conditions and students’ prior knowledge on learning equation solving. The posttest scores were compared among the conditions and shortcut use at pretest using the pretest scores on each measure and mathematics ability scores as covariates.

Results

In this section, we first overview students’ knowledge at pretest. We then report the effects of intervention condition and students’ use of a shortcut method at pretest on students’ learning performance. We first compared the conditions of T_M_T + M and M_M_T + M, then compared T_M_T + M and T_T_T + M, and finally compared T_M_T + M and T_M_T/M.

Pretest knowledge

At pretest, students had some prior procedural, flexibility, and conceptual knowledge of equation solving. Some students even received full credits on some questions, perhaps because the interventions occurred after students had completed relevant classroom lessons. Most students, however, had only a partial understanding of the topic. Less than 1 % of procedural knowledge items at pretest were solved by shortcut methods. Fifty-nine percent of the students used a shortcut method at least once at pretest and were categorized as Use Shortcut, while other students who never used a shortcut method were categorized as No Shortcut. Students in the No Shortcut group scored 8.1 of 24 points on flexibility knowledge and 3.3 of 7 points on conceptual knowledge. This indicated that those students were unable to consider expressions such as (χ + 1) a composite variable and mainly used the conventional and distribute-first method to solve equations. In other words, they did not discern the critical aspect of solution method at pretest. Even for students in the Use Shortcut group who attempted composite-variable shortcut methods to solve equations, they certainly were not proficient equation solvers; they scored 13.2 points on flexibility knowledge and 5.2 points on conceptual knowledge.

Procedural knowledge correlated with both flexibility knowledge, r(263) = 0.549, p < 0.001, and conceptual knowledge, r(263) = 0.584, p < 0.001. Flexibility knowledge correlated with conceptual knowledge, r(263) = 0.585, p < 0.001. Students significantly improved from the pretest to the posttest on all outcome measures (ps < 0.01). No significant differences between conditions in procedural, flexibility, and conceptual knowledge were found (ps > 0.05). Boys and girls did not differ in performance on the pretest measures.

Effect of condition (T_M_T + M and M_M_T + M) and prior knowledge on students’ performance

Students’ posttest performance on all measures was summarized in Table 5. To determine the possible interaction effect between condition and prior knowledge, we conducted separate two-way ANCOVAs for each outcome, with students’ shortcut use at pretest and condition as between-subjects factors. Students’ pretest scores on each measure and mathematics ability (based on students’ midterm and final mathematics exam scores in the previous semester) were included as covariates to control for prior knowledge differences. When there was an interaction effect for condition and shortcut use at pretest, tests of simple effect were carried out to further investigate the effects of conditions. We also explored the possible interaction effect between students’ mathematics ability and condition, but no interaction effect was found. Therefore, we did not include the interaction term in the final models.

Table 5 Students’ posttest performance on outcome measures by condition and pretest use of shortcut
Full size table

Procedural knowledge

As shown in Table 6 and Fig. 2a, there was a significant interaction effect between the experimental condition (T_M_T + M and M_M_T + M) and shortcut use at pretest (p = 0.01). There was not an overall main effect for condition (p = 0.503) but a main effect for shortcut use at pretest (p < 0.05). The significant interactions suggested that the most effective condition depended on whether students used a shortcut at pretest.

Table 6 Analysis of covariance results for learning outcomes (T_M_T + M and M_M_T + M)
Full size table
Fig. 2
figure 2

Interaction between condition and pretest use of shortcut on a procedural knowledge, b flexibility knowledge, and c conceptual knowledge. Covariates of pretest procedural, flexibility, conceptual knowledge, and mathematics ability appear in the models

Full size image

After the significant interactions had been determined, tests of the simple effects were carried out. A significant effect was found for students who did not use a shortcut at pretest, F(1, 122) = 4.406, MSE = 1.704, p < 0.05; students in the M_M_T + M condition performed significantly better than those in the T_M_T + M condition. For students who used a shortcut at pretest, no significant differences were found among conditions, F(1, 122) = 2.483, MSE = 1.704, p = 0.118. Students’ prior procedural knowledge and mathematics ability also had significant influences on procedural knowledge at posttest (ps < 0.001).

Flexibility knowledge

As shown in Table 6 and Fig. 2b, there was a significant interaction effect between condition and shortcut use at pretest (p < 0.01). There were no overall main effects for shortcut use at pretest and condition (ps > 0.05). Tests of simple effects showed a significant effect for students who did not use a shortcut at pretest, F(1, 122) = 7.312, MSE = 11.207, p < 0.01; students in the T_M_T + M condition scored significantly lower than those in the M_M_T + M condition. For students who used a shortcut at pretest, condition had minimal influence on flexibility knowledge (p > 0.05). Students’ prior flexibility knowledge, conceptual knowledge, and mathematics ability also had significant influences on flexibility knowledge at posttest (ps < 0.01).

Conceptual knowledge

Finally, we considered students’ conceptual knowledge. As shown in Table 6 and Fig. 2c, there was no significant interaction effect between condition and shortcut use at pretest (p = 0.208). There were no main effects for condition and shortcut use at pretest (ps > 0.05). Students’ conceptual knowledge at posttest was also predicted by their prior conceptual knowledge and mathematics ability (ps < 0.01).

Effect of condition (T_M_T + M and T_T_T + M) and prior knowledge on students’ performance

Procedural knowledge

As shown in Table 7 and Fig. 3a, there was a significant interaction effect between the experimental condition (T_M_T + M and T_T_T + M) and shortcut use at pretest (p < 0.05). There was no overall main effect for condition (p = 0.088), but there was a main effect for shortcut use at pretest (p < 0.05).

Table 7 Analysis of covariance results for learning outcomes (T_M_T+M and M_M_T+M)
Full size table
Fig. 3
figure 3

Interaction between condition and pretest use of shortcut on a procedural knowledge, b flexibility knowledge, and c conceptual knowledge. Covariates of pretest procedural, flexibility, conceptual knowledge, and mathematics ability appear in the models

Full size image

After the significant interactions had been determined, tests of the simple effects were carried out. A significant effect was found for students who did not use a shortcut at pretest, F(1, 123) = 6.147, MSE = 1.789, p < 0.05; students in the T_T_T + M condition performed significantly better than those in the T_M_T + M condition. For students who used a shortcut at pretest, no significant differences were found among conditions, F(1, 123) = 0.050, MSE = 1.789, p = 0.823. Students’ mathematics ability also had significant influences on procedural knowledge at posttest (ps < 0.001).

Flexibility knowledge

As shown in Table 7 and Fig. 3b, there was a significant interaction effect between condition and shortcut use at pretest (p < 0.01). There was no overall main effect for shortcut use at pretest (p = 0.270), but there was a main effect for condition (p < 0.05). Tests of simple effects showed a significant effect for students who did not use a shortcut at pretest, F(1, 123) = 7.310, MSE = 11.092, p < 0.01; students in the T_M_T + M condition scored significantly lower than those in the T_T_T + M condition. For students who used a shortcut at pretest, condition had minimal influence on flexibility knowledge (p > 0.05). Students’ prior flexibility knowledge, conceptual knowledge, and mathematics ability also had significant influences on flexibility knowledge at posttest (ps < 0.01).

Conceptual knowledge

As shown in Table 7 and Fig. 3c, there was no significant interaction effect between condition and shortcut use at pretest (p > 0.05). There were no overall main effects for shortcut use at pretest and condition (ps > 0.05). Students’ conceptual knowledge at posttest was predicted by their prior conceptual knowledge and mathematics ability (ps < 0.01).

Effect of condition (T_M_T + M and T_M_T/M) and prior knowledge on students’ performance

Procedural knowledge

As shown in Table 8 and Fig. 4a, there was a significant interaction effect between the experimental condition (T_M_T + M and T_M_T/M) and shortcut use at pretest (p < 0.05). There was no overall main effect for condition (p = 0.229), but there was a main effect for shortcut use at pretest (p < 0.05). Tests of simple effects showed a significant effect for students who did not use a shortcut at pretest, F(1, 126) = 6.046, MSE = 1.590, p < 0.05; students in the T_M_T/M condition had greater procedural knowledge than those in the T_M_T + M condition. For students who used shortcuts at pretest, T_M_T + M and T_M_T/M did not have significant difference (p > 0.05). Students’ prior procedural knowledge and mathematics ability also had significant influences on procedural knowledge at posttest (ps < 0.005).

Table 8 Analysis covariance results for learning outcomes (T_M_T + M and T_M_T/M)
Full size table
Fig. 4
figure 4

Interaction between condition and pretest use of shortcut on a procedural knowledge, b flexibility knowledge, and c conceptual knowledge. Covariates of pretest procedural, flexibility, conceptual knowledge, and mathematics ability appear in the models

Full size image

Flexibility knowledge

As shown in Table 8 and Fig. 4b, there was a marginal condition × shortcut use interaction effect (p = 0.062). There was no main effect for shortcut use at pretest (p = 0.141), but there was a main effect for condition (p < 0.05). Tests of simple effects showed a significant effect for students who did not use a shortcut at pretest, F(1, 126) = 7.738, MSE = 10.770, p < 0.01; students in the T_M_T/M condition scored significantly higher than those in the T_M_T + M condition. For students who used a shortcut at pretest, no significant differences were found among conditions (p = 0.733). Students’ flexibility knowledge at posttest was also predicted by their prior flexibility knowledge, conceptual knowledge, and mathematics ability (ps ≤ 0.001).

Conceptual knowledge

As shown in Table 8 and Fig. 4c, there was no significant interaction effect between condition and shortcut use at pretest (p = 0.392). There was no main effect for condition (p = 0.09), but there was a main effect for shortcut use at pretest (p < 0.05). Students’ conceptual knowledge at posttest was also predicted by their prior conceptual knowledge and mathematics ability (ps < 0.005).

Discussion

As predicted, students’ prior knowledge of equation solving impacted the effectiveness of example design in the intervention conditions. In particular, students who did not use a shortcut method at pretest benefited least if they first separately compared the two critical aspects of problem type and solution method and then simultaneously compared the two aspects. In this section, we first summarize the major research findings. Next, we discuss the current findings in relation to what, how, and when comparison is effective. Finally, we consider the instructional implications of the study.

Summary of major findings

The results of the present study indicated that comparing the two critical aspects of problem type and solution method first separately and then simultaneously (T_M_T + M) led to less procedural knowledge and flexibility knowledge than separately comparing only one of the two critical aspects (M_M_T + M and T_T_T + M) or comparing the two critical aspects separately but not simultaneously (T_M_T/M) for students who did not use shortcuts at pretest. The different effectiveness of conditions, however, was absent for students who used shortcuts at pretest; those students did not show any preference for either condition.

A plausible explanation may lie in the different prior knowledge that students possessed. Students who did not use shortcuts at pretest benefited either from separately comparing one of the two critical aspects or from separately comparing two critical aspects without the simultaneous variation of the two; they likely became overwhelmed when first separately comparing the two critical aspects and then simultaneously comparing them. According to the variation theory, separately discerning each critical aspect is necessary for the later simultaneous discernment of all critical aspects. Although the T_M_T + M condition first separately varied the two critical aspects followed by the simultaneous variation of the two aspects, it seemed that students could not separately discern each of the two critical aspects within a single intervention session. Therefore, they encountered difficulty when comparing examples that simultaneously varied both problem type and solution method. Separately varying one of the two critical aspects or separately varying the two critical aspects without the simultaneous variation of the two was more beneficial for those students.

In contrast, students who used shortcuts at pretest learned equally from the conditions. This may be because those students had discerned the critical aspect of solution method and thus were not overwhelmed by T_M_T + M as students who did not use shortcuts were. Students who used shortcuts at pretest might have learned so much that example pairings did not matter; they learned regardless. This explains the insignificant differences among conditions in promoting those students’ learning.

It should be noted that, with respect to conceptual knowledge, we did not find an interaction effect between condition and shortcut use, nor did we find a main effect for condition. This may be because participants in the present study had been taught how to solve multistep equations by a conventional method and, therefore, had acquired considerable conceptual knowledge before the intervention. As a result, all types of comparison were sufficient and equally effective for learning conceptual knowledge of equivalence, like terms, and composite variables.

The what, when, and how of comparison

First, our findings suggested that what aspects to be focused on in example design depended on students’ prior knowledge or what aspects they had discerned. The aspect of solution method was important for students who did not use shortcuts at pretest. Thus, comparing solution methods (M_M_T + M) that helped students to discern the critical aspect of the solution method led to greater knowledge. However, for students who used shortcuts at pretest, the aspect of solution method had been discerned and was thus not important for their learning. This explains the reason why the advantage of comparing solution methods disappeared for students who used shortcuts at pretest.

Students with different levels of prior knowledge might discern and perceive different aspects as critical for their learning and thus benefited differently from the same instruction; novices should have more critical aspects than more experienced learners. The present study differentiated the prior knowledge of students based on their shortcut use at pretest. Those who used shortcuts at pretest had discerned the critical aspect of solution method, whereas those who did not use shortcuts at pretest had not discerned this aspect. It should be noted that our measure focused on knowledge of solution methods rather than familiarity with different types of equations. Measures that capture students’ familiarity with different problem types may be used in future study to identify the discernment of problem types.

Next, the results of the present study suggested the necessity of the stage of separate discernment. It is important to make sure students have separately discerned each critical aspect before simultaneously varying all critical aspects. In the present study, simultaneous variation of problem type and solution method was found to be harmful for learning if students had not separately discerned the two critical aspects (T_M_T + M). When provided with equations simultaneously varying in problem type and solution method, they were likely overwhelmed by too much variation. Future research should investigate the effect of simultaneous variation on learning after confirming that each critical aspect has been separately discerned. Also, other effective ways of determining the variability of examples besides those used in our study warrant further investigation.

Consequently, we conclude that comparing examples is effective when students’ critical aspects are focused on and varied in a suitable way. Instruction or examples are ineffective and inefficient if students do not have an opportunity to compare their critical aspects or if they are asked to compare aspects that have already been mastered.

Future directions and conclusion

The present study indicated that comparing the two critical aspects of problem type and solution method first separately and then simultaneously was harmful for students who did not use shortcuts at pretest. A possible interpretation might be the fact that these students did not have sufficient time to separately discern the two aspects in such a short intervention period, which made the T_M_T + M condition ineffective. Future research should be conducted to extend the intervention time to ensure that problem type and solution method are separately discerned. This would help to identify a more effective instructional approach. We expect that teacher-led whole-class verbal instructional studies will further illuminate this issue.

Future studies should also be conducted to examine the effectiveness of different patterns of variation and invariance in promoting learning from examples with a variety of topics and with a wider range of ages and disciplinary prior knowledge. For example, most students in the present study had mastered the algebraic method of solving an equation; they had ample prior knowledge about equation solving before the intervention. It is important to examine the effects of comparison with students with lower prior topic knowledge. For those who are not familiar with the algebraic method, what are their critical aspects for learning and which condition would be most beneficial? In addition, results of the present study showed that conditions were not particularly beneficial for students who used shortcuts at pretest. There may be other critical aspects for learning equation solving that need to be discerned. Additional research could investigate ways of facilitating more experienced students’ learning. Finally, more research should be conducted to generalize these findings to different domains and to more typical classroom contexts.

In conclusion, comparison of examples should focus on students’ critical aspects for learning. For those who do not discern the critical aspect of solution method, examples should be provided to help them separately discern this aspect. Without having separately discerned each critical aspect, students cannot benefit from simultaneous variation of all critical aspects. The what, when, and how of comparison should be taken into consideration when designing multiple examples for learning.