Abstract
We develop in this paper a theoretical framework for the topological study of time series data. Broadly speaking, we describe geometrical and topological properties of sliding window embeddings, as seen through the lens of persistent homology. In particular, we show that maximum persistence at the point-cloud level can be used to quantify periodicity at the signal level, prove structural and convergence theorems for the resulting persistence diagrams, and derive estimates for their dependency on window size and embedding dimension. We apply this methodology to quantifying periodicity in synthetic data sets and compare the results with those obtained using state-of-the-art methods in gene expression analysis. We call this new method SW1PerS, which stands for Sliding Windows and 1-Dimensional Persistence Scoring.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Signal analysis is an enormous field. There are many methods to study signals and many applications of that study. Given its importance, one might conclude that there is little opportunity left for the development of totally new approaches to signals. Yet in this paper we provide a new way to find periodicity and quasiperiodicity in signals. The method is based on sliding windows (also known as time-delay reconstruction), which have been used extensively in both engineering applications and in dynamical systems. But the approach presented here adds a new element not applied before, which comes from the new field of computational topology [12].
Persistent homology is a topological method for measuring the shapes of spaces and the features of functions. One of the most important applications of persistent homology is to point clouds [3], where shape is usually interpreted as the geometry of some implicit underlying object near which the point cloud is sampled. The simplest nontrivial example of this idea is a point cloud that has the shape of a circle, and this shape is captured with one-dimensional (1D) persistence. The challenge in applying the method is that noise can reduce the persistence, and not enough points can prevent the circular shape from appearing. It is also a challenge to deal with the fact that features come on all scale levels and can be nested or in more complicated relationships. But this is what persistent homology is all about.
The idea of applying 1D persistence to study time series arose in our study of gene expression data [11, 23]. The first of these papers studied a variety of existing methods for finding periodicity in gene expression patterns. The motivation of that work was the search for gene regulatory networks (more precisely, possible nodes of gene regulatory networks) that control periodic processes in cells such as the cell division cycle, circadian rhythms, metabolic cycles, and periodic patterning in biological development (lateral roots and somites). The methods studied in [11] were derived from a number of fields, including astronomy, geometry, biology, and statistics, and all were based on a direct study of the underlying signal in either physical or frequency space. The most successful methods are based on finding cosinelike behavior, a rather limited definition of periodicity.
In this paper and in [23] we look instead at the shape of the sliding window point cloud, a totally different approach. Of course, the geometry of point clouds derived from other kinds of data like images has been studied [4, 16], but the current approach is quite different. Our method understands periodicity as the repetition of patterns, whatever these may be, and quantifies this recurrence as the degree of circularity/roundness in the generated point-cloud. Thus, it is fundamentally agnostic.
1.1 Previous Work
The sliding window, or time-delay embedding, has been used mostly in the study of dynamical systems to understand the nature of their attractors. Takens’ theorem [28] gives conditions under which a smooth attractor can be reconstructed from the observations of a function, with bounds related to those of the Whitney embedding theorem. This methodology has in turn been employed to test for nonlinearity and chaotic behavior in the dynamics of Electroencephalogram, Electrocardiogram, and Electromyogram [25, 26].
It was recently demonstrated by [10] that combining time-delay embeddings with topological methods provides a framework for parameterizing periodic systems.
[16] provide in their Chap. 1 a good source of examples of time-delay embeddings used in real-world data sets.
1.2 Our Contribution
In the aforementioned applications, little of the topology and none of the geometry of the resulting sliding window embedding have ever been used. The novelty of our approach lies in our use of this geometry and topology through persistent homology. We make this possible by showing that maximum persistence, as a measure of the roundness of the point cloud, occurs when the window size corresponds to the natural frequency of the signal. This means that 1D persistence is an effective quantifier of periodicity and quasiperiodicity and can be used to infer properties of the signal.
1.3 Outline
In Sect. 2 we show a motivating example to illustrate our perspective. In Sect. 3 we give a general introduction to persistent homology. More on this topic can be found in [12]. In Sect. 4 we show that sliding windows behave well under approximations, and we give explicit estimates at the point-cloud level. Section 5 is devoted to studying the geometric structure of sliding-window embeddings from truncated Fourier series and their dependency on embedding dimension and window size. In Sect. 6 we prove results describing the structure of persistent diagrams from sliding-window embeddings. Some examples of how our method applies in the problem of quantifying periodicity in time series data are given in Sect. 7.
2 Definitions and Motivation
Suppose that \(f\) is a function defined on an interval of the real numbers. Choose an integer \(M\) and a real number \(\tau \), both greater than \(0\). The sliding-window embedding of \(f\) based at \(t \in \mathbb {R}\) into \(\mathbb {R}^{M+1}\) is the point
Choosing different values of \(t\) gives a collection of points called a sliding-window point cloud for \(f\). A critical parameter for this embedding is the window size \(M\tau \).
2.1 Motivation
To motivate the approach we take in the paper, let us begin with the following example.
Example. Let \(L\in \mathbb {N}\) and \(f(t) = \cos (Lt)\). Then
and therefore \(t \mapsto SW_{M,\tau } f(t)\) describes a planar curve in \(\mathbb {R}^{M+1}\), with winding number \(L\), whenever \(\mathbf {u}\) and \(\mathbf {v}\) are linearly independent. One can in fact see how the shape of this curve changes as a function of \(L\), \(M\), and \(\tau \). Indeed, let
which can be computed using Lagrange’s trigonometric formulae
It follows that \(A\) is positive semidefinite (both its determinant and trace are nonnegative). This means the eigenvalues of \(A\) are nonnegative and real, \(\lambda _1\ge \lambda _2\ge 0 \), and there is a \(2\times 2\) orthogonal matrix \(B\) such that
Therefore, if \(\mathbf {x}(t) = {\begin{bmatrix}\cos (Lt)&\sin (Lt)\end{bmatrix}}^\prime \) (here \(\prime \) denotes transpose), then
Since \(B\) is a rotation matrix, say by an angle \(\alpha \), then the map
is an isometry.
In summary, for \(f(t) = \cos (Lt)\), the embedding \(t\mapsto SW_{M,\tau } f(t)\) describes an ellipse on the plane \(Span\{\mathbf {u},\mathbf {v}\}\) whose shape (minor and major axes) is determined by the square roots of the eigenvalues of \(A\). These eigenvalues can be computed explicitly as
It follows that the ellipse is roundest when \(\lambda _2\) attains its maximum, which occurs if and only if \(L(M+1)\tau \equiv 0 \mod \pi \). One such instance is
which is when the window-size approximates the length of the period of \(f(t)\). In other words, the roundness of the sliding-window point cloud for \(f(t)=\cos (Lt)\) is maximized when the window size is close to resonating with its natural frequency.
The previous example provides the following intuition: for a generic function \(f\), the degree to which the image of \(SW_{M,\tau }f\) traces a closed curve in \(\mathbb {R}^{M+1}\) reflects how periodic \(f\) is. Moreover, if \(f\) is periodic, then the roundness of \(SW_{M,\tau }f\) defined as the largest radius of a ball in \(\mathbb {R}^{M+1}\) so that the curve
is tangent to at least two points of its equator is maximized when the window size \(M\tau \) approaches the period length. The goal of this paper is to understand these relations.
The geometry of the curve \(t\mapsto SW_{M,\tau }f(t)\) can be quite complicated, as shown in Fig. 1. The 1D persistence diagram for the Vietoris–Rips filtration on a finite sample \(\{SW_{M,\tau }f(t_1),\ldots , SW_{M,\tau } f(t_S)\}\), on the other hand, is readily computable [29, 30], and its maximum persistence is a measure of roundness as defined in the previous paragraph. We will review in Sect. 3 the basic concepts behind persistent homology and devote the rest of the paper to understanding how the geometry of \(SW_{M,\tau } f\) reflects properties of \(f\) such as periodicity and period.
2.2 Approach
With this motivation in mind, we now describe our approach: as we have seen, understanding the algebraic properties of trigonometric functions allows one to characterize the geometry of \(SW_{M,\tau } f\) when \(f\) is a trigonometric polynomial. This understanding, in turn, can be bootstrapped using Fourier analysis and the stability of persistence diagrams in an approximation step toward \(SW_{M,\tau }\) of a generic periodic function. In what follows, we will establish the appropriate continuity results for approximation and the necessary structural results for persistence diagrams from sliding-window point clouds.
3 Background: Persistent Homology
In this section we define the key concepts that underlie the theory of persistent homology for filtered simplicial complexes. We give a terse introduction to simplicial homology, but more information can be found in [14] and [21].
3.1 Homology of Simplicial Complexes
Let \(K\) be a simplicial complex and \(p\) a prime number. Recall that this means that \(K\) is a finite set of simplices that is closed under the face relation and that two simplices of \(K\) are either disjoint or intersect in a common face. Let \(\mathbb {F}_p \) be the finite field with \(p\) elements; the \(\mathbb {F}_p \) vector space generated by the \(k\)-dimensional simplices of \(K\) is denoted by \(C_k(K)\). It consists of all \(k\)-chains, which are finite formal sums \(c = \sum _j \gamma _j x_j\), with \(\gamma _j \in \mathbb {F}_p \) and each \(x_j\) a \(k\)-simplex in \(K\). The boundary \(\partial (x_j)\) is the alternating formal sum of the \((k-1)\)-dimensional faces of \(x_j\), and the boundary of the chain \(c\) is obtained by extending \(\partial \) linearly:
It is not difficult to check that \(\partial \circ \partial = \partial ^2 = 0\). The \(k\)-chains that have boundary \(0\) are called \(k\)-cycles; they form a subspace \(Z_k\) of \(C_k\). The \(k\)-chains that are the boundary of \((k+1)\)-chains are called \(k\)-boundaries and form a subspace \(B_k\) of \(C_k\). The fact that \(\partial ^2 = 0\) tells us that \(B_k \subset Z_k\). The quotient group \(H_k (K) = Z_k / B_k\) is the \(k\)th simplicial homology group of \(K\) with \(\mathbb {F}_p\)-coefficients. The rank of \(H_k (K)\) is the \(k\)th mod \(p\) Betti number of \(K\) and is denoted by \(\beta _k (K)\). Since the prime \(p\) will be clear from the context, we do not include it in the notation.
When we have two simplicial complexes \(K\) and \(K'\), a simplicial map \(f: K \rightarrow K'\) is a continuous map that takes simplices to simplices and is linear on each. A simplicial map induces a homomorphism on homology, \(f_*: H_k(K) \rightarrow H_k(K')\), and homotopic maps induce the same homomorphism. Homotopy equivalences of spaces induce isomorphisms on homology. The simplicial approximation theorem tells us that a continuous map of simplicial complexes can be approximated by a simplicial map, so that it makes sense to talk about continuous maps inducing homomorphisms on homology.
3.1.1 Persistence
We next define persistence, persistent homology, and the persistence diagram for a simplicial complex \(K\). A subcomplex of \(K\) is a subset of its simplices that is closed under the face relation. A filtration of \(K\) is a nested sequence of subcomplexes that starts with an empty complex and ends with a complete complex,
A homology class \(\alpha \) is born at \(K_i\) if it is not in the image of the map induced by the inclusion \(K_{i-1} \subset K_i\). If \(\alpha \) is born at \(K_i\), then we say that it dies entering \(K_j\) if the image of the map induced by \(K_{i-1} \subset K_{j-1}\) does not contain the image of \(\alpha \) but the image of the map induced by \(K_{i-1} \subset K_j\) does. The persistence of \(\alpha \) is \(j-i\).
We code birth and death information in persistence diagrams, one for each dimension. The diagram \(\mathsf dgm (k)\) has a point \((i,j)\) for every \(k\)-homology class that is born at \(K_i\) and dies entering \(K_j\). For most of the paper the homological dimension \(k\) will be clear from the context or unimportant for the discussion. To ease notation, we will simply write \(\mathsf dgm \) instead of \(\mathsf dgm (k)\) and let \(\mathsf dgm _1\) and \(\mathsf dgm _2\) denote two \(k\)-persistence diagrams to be compared. Sometimes we have a function \(h\) that assigns a height or distance to each subcomplex \(K_i\), and in that case we use the pair \((h(i),h(j))\). Each diagram is now a multiset since classes can be born simultaneously and die simultaneously. We adjoin the diagonal \(\Delta = \{(x,x): x\ge 0 \}\) to each diagram and endow each point \((x,x)\in \Delta \) with countable multiplicity.
The bottleneck distance between two persistence diagrams \(\mathsf dgm _1\) and \( \mathsf dgm _2\) is defined by
where the infimum is taken over all bijections \(\phi :\mathsf dgm _1 \rightarrow \mathsf dgm _2\). Note that such \(\phi \) exist even if the number of points of \(\mathsf dgm _1\) and \(\mathsf dgm _2\) are different since we have included the diagonal.
3.1.2 Rips Complex
Let \(X \subset \mathbb {R}^n\) be a compact set, for example, a finite point cloud. We define \(d_X(y)\) as the distance from the point \(y \in \mathbb {R}^n\) to \(X\). We are interested in how the homology of the sublevel sets \(X_r = d_X^{-1}([0,r])\) changes as we increase \(r\). To make this computationally feasible, we replace the continuous family of spaces \(X_r\) with a discrete family of approximations called the Rips complexes defined as follows. Fix \(r \ge 0\); \(R_r(X)\) is the simplicial complex whose vertices are the points of \(X\) and whose \(k\)-simplices are the \(k+1\) tuples \([x_0, \ldots , x_k]\) such that the pairwise distances \(||x_i - x_j||\) are less than or equal to \(r\) for all \(0 \le i < j \le k\). Note that the edges determine the simplices of \(R_r(X)\), that a higher-dimensional simplex is added if and only if all its edges have been added, and that the Rips construction makes sense for any metric space.
Since \(R_r(X) \subset R_s(X)\) whenever \(r < s\), the Rips complexes form a filtration of \(R_{\infty }\), which denotes the largest simplicial complex having \(X\) as its vertex set. Changes occur at the finite set of \(r\) values that are pairwise distances between points, so we can work with just these \(r_j\) to get the filtration
where \(R_j= R_{r_j}(X)\) and \(R_{m} = R_{\infty }\). We will use this filtered complex to study the persistence and the persistence diagrams of the point cloud \(X\). We thus denote by \(\mathsf dgm (X)\) the persistence diagram of the homology filtration induced from the Rips filtration on \(X\), where we use homology with coefficients in \(\mathbb {F}_p\).
A key property of persistence is that it is stable [6]. In our context this means that if \(X,Y\) are two point clouds and \(d_\mathrm{{H}}\), \(d_{GH}\) are the Hausdorff and Gromov–Hausdorff distances, then
4 Approximation Theorem
In this section we show that one can study \(SW_{M,\tau } f\) and the persistence of the point cloud it generates for a generic function \(f\in L^2(\mathbb {T}= \mathbb {R}/ 2\pi \mathbb {Z})\) by using its Fourier series approximation. While it seems quite difficult to study \(SW_{M,\tau } f\) directly, it is not hard to understand \(SW_{M,\tau } \cos (nt)\) and \(SW_{M,\tau } \sin (nt)\), so we will build our understanding of the geometry of a general \(SW_{M,\tau } f\) from these special cases using the Fourier series of \(f\). To do this, we will need to show that \(SW_{M,\tau }\) behaves well under approximations and that these approximations work in the context of stability for persistence diagrams.
Let \(C(X,Y)\) denote the set of continuous functions from \(X\) to \(Y\) equipped with the sup norm. The sliding-window embedding induces a mapping
The first fact about this map that we need is the following proposition.
Proposition 4.1
Let \(\mathbb {T}= \mathbb {R}/ 2\pi \mathbb {Z}\). Then for all \(M\in \mathbb {N}\) and \(\tau >0\), the mapping \(SW_{M,\tau }: C(\mathbb {T},\mathbb {R}) \longrightarrow C(\mathbb {T},\mathbb {R}^{M+1})\) is a bounded linear operator with norm \(\Vert SW_{M,\tau }\Vert \le \sqrt{M+1}\).
Proof
The linearity of \(SW_{M,\tau }\) follows directly from its definition. To see that it is bounded, notice that for every \(f\in C(\mathbb {T},\mathbb {R})\) and \(t \in \mathbb {T}\) we have
\(\square \)
We now consider approximating a function \(f\) by its Fourier polynomials and study how the sliding windows behave in this context. In particular, let
where
is the \(N\)-truncated Fourier series expansion of \(f\), \(R_N f\) is the remainder, and
We can easily compute that
where
The vectors \(\mathbf {u}_n\) and \(\mathbf {v}_n\) form a fundamental basis out of which we can build our understanding of the structure of the point clouds that sliding windows create. We introduce the notation
for the sliding-window embedding for \(S_N f(t)\). Also, when \(f\), \(M\), and \(N\) are clear from the context, we will simply write \(\phi _\tau = SW_{M,\tau } S_N f\).
The next step is to find a bound on the term \(SW_{M,\tau } R_N f(t)\). We will actually find a series of bounds, one for each of the derivatives \(f^{(k)} = \frac{d^k f}{dt^k}\), whenever they exist and are continuous.
Proposition 4.2
Let \(k\in \mathbb {N}\). If \(f\in C^k(\mathbb {T},\mathbb {R})\), then for all \(t\in \mathbb {T}\)
Proof
If \(k\in \mathbb {N}\) and \(f\in C^k(\mathbb {T},\mathbb {R})\), then integration by parts yields the well-known identity
for the length of \(\widehat{f^{(k)}}(n)\), the \(n\)th complex Fourier coefficient of \(f^{(k)}\), \(n\in \mathbb {Z}\). Thus, for all \(t\in \mathbb {T}\) the Cauchy–Schwartz inequality, Young’s inequality and Parseval’s theorem together imply that
and hence, by Proposition 4.1,
\(\square \)
These bounds readily imply estimates for the Hausdorff distance between the sliding-window point clouds of \(f\) and \(S_N f\). Indeed, let \(X\) and \(Y\) be the images of \(T\subset \mathbb {T}\) through \(SW_{M,\tau } f\) and \(\phi _\tau \), respectively. It follows that if \(f\in C^k(\mathbb {T},\mathbb {R})\) and
then \(X \subset Y^\epsilon \), \(Y\subset X^\epsilon \), and, therefore, \(d_\mathrm{{H}}(X,Y) \le \epsilon \). Letting \(\epsilon \) approach its lower bound and using the stability of \(d_\mathrm{{B}}\) with respect to \(d_\mathrm{{H}}\) (Eq. 1), we obtain the relation
As described in the introduction, the maximum persistence of \(\mathsf dgm (X)\) will serve to quantify the periodicity of \(f\) when measured with sliding windows of length \(M\tau \). By the maximum persistence of a diagram \(\mathsf dgm \), we mean the following.
Definition 4.3
Let \((x,y)\in \mathsf dgm \), and define \(\mathsf pers (x,y) = y-x\) for \((x,y) \in \mathbb {R}^2\), and as \(\infty \) otherwise. We let
denote the maximum persistence of \(\mathsf dgm \).
Remark 4.4
If \(\mathsf dgm _\Delta \) denotes the diagram with the diagonal as underlying set, each point endowed with countable multiplicity, then
Indeed, for any bijection \(\phi : \mathsf dgm \longrightarrow \mathsf dgm _\Delta \) and every \(\mathbf {x}\in \mathsf dgm \)
with equality if and only if \(\phi (x,y) = \left( \frac{x+y}{2},\frac{x+y}{2}\right) \). Thus,
and therefore \( d_\mathrm{{B}}(\mathsf dgm , \mathsf dgm _\Delta ) = \min \limits _{\phi } \max \limits _{\mathbf {x}\in \mathsf dgm } \Vert \mathbf {x}- \phi (\mathbf {x})\Vert \ge \frac{1}{2}mp(\mathsf dgm )\). For the reverse inequality, notice that the map
extends to a bijection \(\phi _0 : \mathsf dgm \longrightarrow \mathsf dgm _\Delta \) of multisets such that for all \(\mathbf {x}\in \mathsf dgm \) one has \( \Vert \mathbf {x}- \phi _0(\mathbf {x})\Vert _\infty = \frac{1}{2} \mathsf pers (\mathbf {x})\).
We summarize the results of this section in the following theorem.
Theorem 4.5
(Approximation) Let \(T\subset \mathbb {T}\), \(f\in C^k(\mathbb {T},\mathbb {R})\), \(X = SW_{M,\tau } f(T)\), and \(Y = SW_{M,\tau }S_N f(T)\). Then
-
(1)
$$\begin{aligned} d_\mathrm{{H}}(X,Y) \le \sqrt{4k -2}\left\| R_N f^{(k)}\right\| _{2} \frac{\sqrt{M+1}}{(N+1)^{k - \frac{1}{2}}}, \end{aligned}$$
-
(2)
$$\begin{aligned} \left| mp\big (\mathsf dgm (X)\big ) - mp\big (\mathsf dgm (Y)\big )\right| \le 2d_\mathrm{{B}}\big (\mathsf dgm (X),\mathsf dgm (Y)\big ), \end{aligned}$$
-
(3)
$$\begin{aligned} d_\mathrm{{B}}\Big (\mathsf dgm (X),\mathsf dgm (Y)\Big ) \le 2\sqrt{4k -2}\left\| R_N f^{(k)}\right\| _{2} \frac{\sqrt{M+1}}{(N+1)^{k - \frac{1}{2}}}. \end{aligned}$$
It follows that the persistent homology of the sliding-window point cloud of a function \(f\in C^k(\mathbb {T},\mathbb {R})\) can, in the limit, be understood in terms of that of its truncated Fourier series.
Remark 4.6
Regarding the hypothesis of \(f\) being at least \(C^1\), Proposition 4.2 (which is the basis of the approximation theorem, Theorem 4.5) only uses that \(f^{\prime } \in L^2(\mathbb {T})\); thus, everything up to this point (and, in fact, for the rest of the paper) holds true for functions in the Sobolev space \(W^{1,2}(\mathbb {T})\). The reason why we have phrased the results in terms of the spaces \(C^k(\mathbb {T})\) is because it provides the following interpretation: if the function \(f\) has a certain degree of niceness, then one should expect the approximation of the persistence diagrams from \(SW_{M,\tau } f\) by those of \(SW_{M,\tau } S_N f\) to improve at an explicit rate. Moreover, the nicer the function, the better the rate.
Another function space for which our arguments apply is the set of Hölder-continuous functions with exponent \(\alpha \in \left( \frac{1}{2},1\right) \). Indeed, if for such an \(f\) one considers the Fejér approximation
then [see Theorem 1.5.3 in [22]]
where \(K_\alpha \) is the Hölder constant of \(f\) and \(C_\alpha \) is a constant depending solely on \(\alpha \). Hence, one obtains the following version of Proposition 4.2: for every \(t\in \mathbb {T}\)
and the corresponding version of the approximation theorem follows. Later on (e.g., in Theorem 6.8) we will use some bounds in terms of \(\Vert f^\prime \Vert _2\) and \(\Vert S_N f^\prime \Vert _2\). Adapting the results involving such bounds to the Hölder-continuous setting requires some work: one can use the fact that every Hölder function has a Lipschitz approximation and then invoke Rademacher’s theorem. We leave the details to the interested reader.
5 Geometric Structure of \(SW_{M,\tau } S_N f\)
We now turn our attention to the sliding-window construction applied to the truncated Fourier series of a periodic function. More specifically, we study the geometric structure of the sliding-window point cloud and its dependency on \(\tau \), \(N\), and \(M\).
Our focus on geometry contrasts with the methods used by others to determine \(\tau \) and \(M\). Traditionally, \(M\tau \), the window size, is estimated using the autocorrelation function [17], while \(M\) is sometimes estimated directly using the method of false nearest neighbors [16].
5.1 Dimension of Embedding
One way of interpreting the embedding dimension, \(M+1\), is as the level of detail (from the function) one hopes to capture with the sliding-window representation. Given the advantages of a description that is as detailed as possible, it can be argued that large dimensions are desirable. From a computational perspective, however, this is a delicate point as our ultimate goal is to compute the persistent homology of the associated sliding-window point cloud. Indeed, as the dimension of the embedding grows, it follows that the point cloud needs to be (potentially) more densely populated. This causes the size of the Rips complex to outweigh the computational resources, making the persistent homology calculation unfeasible.
While there has been considerable progress on dealing with the size problem of the Rips complex [20], it is important to have a sense of the amount of retained information given the computational constraints on the embedding dimension. Fortunately, when dealing with trigonometric polynomials, the answer is clear: one loses no information if and only if the embedding dimension is greater than twice the maximum frequency. Indeed, recall the linear decomposition
where
and \(a_n,b_n\) are as defined in Eq. 2. Since the angles between the \(\mathbf {u}_n\) and the \(\mathbf {v}_m\), as well as their norms, can be determined from \(M\) and \(\tau \) (see example in Sect. 2.1), \(S_N f\) can be recovered from \(SW_{M,\tau } S_N f\) if the \(\mathbf {u}_n\) and the \(\mathbf {v}_m\) are linearly independent. This is the sense in which we say that there is no loss of information.
Proposition 5.1
Let \(M\tau < 2\pi \). Then \(\mathbf {u}_0,\mathbf {u}_1,\mathbf {v}_1,\ldots , \mathbf {u}_N,\mathbf {v}_N\) are linearly independent if and only if \(M \ge 2N\).
Proof
If \(2N + 1\) vectors in \(\mathbb {R}^{M+1}\) are linearly independent, it readily follows that \(2N \le M\). Let us assume now that \(\mathbf {u}_0,\mathbf {u}_1,\mathbf {v}_1,\ldots ,\mathbf {u}_N,\mathbf {v}_N\) are linearly dependent, and let us show that \(2N > M\) or, equivalently, that \(2N \ge M+1\). Indeed, let \(\gamma _0,\beta _0,\ldots ,\gamma _N,\beta _N \in \mathbb {R}\) be scalars not all zero (set \(\beta _0 = 0\)), so that
That is, for all \(m = 0,\ldots , M\) we have
Let \(\xi _m = e^{im\tau }\), \(p(z) = \sum \limits _{n=0}^N (\gamma _n + i\beta _n)z^n\), \(\bar{p}(z) = \sum \limits _{n=0}^N (\gamma _n - i\beta _n)z^n\), and
It follows that \(q(z)\) is a nonconstant complex polynomial of degree at most \(2N\) and that for \(m=0,\ldots ,M\) we have \(0 = Re(\bar{p}(\xi _m))\). This implies that
and therefore \(\xi _0,\ldots , \xi _M\) are roots of \(q(z)\). Since \(M\tau < 2\pi \), then \(\xi _0,\xi _1,\ldots , \xi _M\) are distinct, and we have that
\(\square \)
It is useful to contrast Proposition 5.1 with two important results in signal analysis: Takens’ theorem from dynamical systems [28] and the Nyquist–Shannon sampling theorem from information theory [27]. Takens’ theorem gives sufficient conditions on the length of a sequence of observation, so that the resulting embedding recovers the topology of a smooth attractor in a chaotic dynamical system. The aforementioned condition is that the dimension of the embedding should be greater than twice (an appropriate notion of) that of the attractor. The Nyquist–Shannon sampling theorem, on the other hand, contends that a band-limited signal can be recovered (exactly) from a sequence of observations whenever the sampling frequency is greater than twice the position, in the frequency domain, of the limiting band. The conclusion: in the case of trigonometric polynomials and the sliding-window construction, the usual sufficient condition on the dimension of the embedding and maximum frequency is also necessary.
Important assumption unless otherwise stated, given \(N\in \mathbb {N}\), we will always set \(M = 2N\) and require \(\tau > 0\) to be such that \(M\tau < 2\pi \).
5.2 Window Size and Underlying Frequency
As we saw in Sect. 2 on definitions and motivation, the sliding window point cloud for \(\cos (Lt)\) describes a planar ellipse that is roundest when \(\Vert \mathbf {u}\Vert - \Vert \mathbf {v}\Vert = \langle \mathbf {u},\mathbf {v}\rangle =0\) or, equivalently, when
This uncovers a fundamental relation between window size, 1D persistence, and underlying frequency: the maximum persistence of the sliding-window point cloud from \(\cos (Lt)\) is largest when the window size \(M\tau \) is proportional to the underlying frequency \(\frac{2\pi }{L}\), with proportionality constant \(\frac{M}{M+1}\).
For the case of the truncated Fourier series \(S_N f\) from a periodic function \(f\), we will see shortly that if the same proportionality relation between window size and underlying frequency holds, then
is a linear decomposition into mutually orthogonal vectors. We begin with the now familiar case of the restriction to \(Span\{\mathbf {u}_n , \mathbf {v}_n\}\).
Proposition 5.2
For \(n\ge 1\), \(\langle \mathbf {u}_n, \mathbf {v}_n\rangle = \Vert \mathbf {u}_n\Vert ^2 - \Vert \mathbf {v}_n\Vert ^2 =0\) if and only if
Proof
and therefore
It follows that \(\langle \mathbf {u}_n,\mathbf {v}_n\rangle = \Vert \mathbf {u}_n\Vert ^2 - \Vert \mathbf {v}_n\Vert ^2 = 0 \) if and only if \(z_{2n(M+1)\tau } =1\), which holds if and only if \(n(M+1)\tau \equiv 0\) (mod \(\pi \)). \(\square \)
It can be checked that \(nM\tau \equiv 0\) (mod \(\pi \)) also yields \(\langle \mathbf {u}_n,\mathbf {v}_n\rangle = 0\), but letting \(n(M+1)\tau \equiv 0\) (mod \(\pi \)) implies that \(a_n \mathbf {u}_n + b_n \mathbf {v}_n\) is perpendicular to \(b_n \mathbf {u}_n - a_n \mathbf {v}_n\) for all \(a_n,b_n \in \mathbb {R}\). Now, to extend the perpendicularity results to components from different harmonics, we will use the following definition.
Definition 5.3
We say that a function \(f\) is \(L\)-periodic on \([0,2\pi ]\), \(L\in \mathbb {N}\), if
for all \(t\).
Remark 5.4
If \(f\) is an \(L\)-periodic function, \(a_n\) and \(b_n\) are its \(n\)th real Fourier coefficients (see Eq. 2), and we let \(a_n + ib_n = r_n e^{i\alpha _n}\), with \(\alpha _n = 0\) whenever \(r_n = 0\), then \(r_n \ne 0\) implies \(n \equiv 0\) (mod \(L\)). Indeed, \(g(t) = f(t/L)\) is a 1-periodic function and therefore has a Fourier series expansion
with equality almost everywhere. Thus,
for almost every \(t\), and the result follows from the uniqueness of the Fourier expansion in \(L^2(\mathbb {T})\).
We are now ready to see that the potentially nonzero terms in the linear decomposition of \(SW_{M,\tau } S_N f\) (Eq. 3) can be made mutually orthogonal by choosing the window size proportional to the underlying frequency, with proportionality constant \(\frac{M}{M+1}\).
Proposition 5.5
Let \(f\) be \(L\)-periodic, and let \(\tau = \frac{2\pi }{L(M+1)}\). Then the vectors in
are mutually orthogonal, and we have \(\Vert \mathbf {u}_n\Vert = \Vert \mathbf {v}_n\Vert = \sqrt{\frac{M+1}{2}}\) for \(n\equiv 0\) (mod \(L\)).
Proof
Let \(k = pL\) and \(n = qL\). If \(k=n\), then it follows from Proposition 5.2 that \(\langle \mathbf {u}_n,\mathbf {v}_n\rangle = 0 \) and
Let us assume now that \(p\ne q\). If we let \(z_\theta = e^{i \theta }\), \(\theta \in \mathbb {R}\), then
Notice that
implies that the denominators are never zero. Similarly,
\(\square \)
When computing persistent homology it is sometimes advantageous to pointwise center and normalize the set of interest. The next theorem describes the result of such operations on the sliding-window point cloud for \(SW_{M,\tau } S_N f\) when \(f\) is \(L\)-periodic and \(L(M+1)\tau = 2\pi \).
Theorem 5.6
(Structure) Let \(C: \mathbb {R}^{M+1} \longrightarrow \mathbb {R}^{M+1}\) be the centering map
If \(f\) is \(L\)-periodic, \(L(M+1)\tau = 2\pi \) and \(\phi _\tau = SW_{M,\tau } S_N f\), then
-
(1)
$$\begin{aligned} \phi _\tau (t)= \widehat{f}(0)\cdot \mathbf {1} + C(\phi _\tau (t)); \end{aligned}$$
-
(2)
$$\begin{aligned} \left\| C\big (\phi _\tau (t)\big )\right\| = \sqrt{M+1}\left( \left\| S_N f\right\| _2^2 - \widehat{f}(0)^2\right) ^{1/2}; \end{aligned}$$
-
(3)
There exists an orthonormal set
$$\begin{aligned} \left\{ \widetilde{\mathbf {x}}_n , \widetilde{\mathbf {y}}_n \in \mathbb {R}^{M+1}\; \Big |\; 1\le n \le N, \; n\equiv 0 \;(\text{ mod } L)\right\} \end{aligned}$$such that
$$\begin{aligned} \varphi _\tau (t) = \frac{C\left( \phi _\tau (t)\right) }{\Vert C\left( \phi _\tau (t)\right) \Vert }= \sum _{ \begin{array}{c} n=1\\ n \equiv 0 (mod L) \end{array}}^N \widetilde{r}_{n}\big (\cos (nt)\widetilde{\mathbf {x}}_{n} + \sin (nt)\widetilde{\mathbf {y}}_{n}\big ), \end{aligned}$$(4)where
$$\begin{aligned} \widetilde{r}_n = \frac{2\left| \widehat{f}(n)\right| }{\sqrt{\Vert S_N f\Vert ^2_2 - \widehat{f}(0)^2}}. \end{aligned}$$
Proof
If \(f\) is an \(L\)-periodic function on \([0,2\pi ]\) and \(L(M+1)\tau = 2\pi \), then Remark 5.4 and Proposition 5.5 imply that for all \(t\in \mathbb {R}\)
is a linear combination of the mutually orthogonal vectors \(\mathbf {x}_n = \cos (\alpha _n)\mathbf {u}_n + \sin (\alpha _n)\mathbf {v}_n\) and \(\mathbf {y}_n = \sin (\alpha _n)\mathbf {u}_n - \cos (\alpha _n)\mathbf {v}_n\).
Moreover, from Proposition 5.5 we have that if \(n\ge 1\) is such that \(n \equiv 0\) (mod \(L\)), then \(\Vert \mathbf {x}_n\Vert = \Vert \mathbf {y}_n\Vert = \sqrt{\frac{M+1}{2}}\). It follows that if
then
is a linear decomposition of \(\phi _\tau (t)\) in terms of the orthonormal set
Hence, \(C\big (\phi _\tau (t)\big ) \;\;\;= \sum \limits _{\begin{array}{c} n=1\\ n\equiv 0 \, (mod L) \end{array}}^N\sqrt{\frac{M+1}{2}}r_n\big (\cos (nt)\widetilde{\mathbf {x}}_n + \sin (nt) \widetilde{\mathbf {y}}_n\big )\), and therefore
which we write as
The result follows from the identities \(r_n = 2\left| \widehat{f}(n)\right| = \left| \widehat{f}(n)\right| + \left| \widehat{f}(-n)\right| \), \(n\ge 1\). \(\square \)
Theorem 5.6 allows us to paint a very clear geometric picture of the centered and normalized sliding-window point cloud for \(S_N f\) (see Eq. 4). Indeed, if \(S^1(r)\subset \mathbb {C}\) denotes the circle of radius \(r\) centered at zero, then \(t\mapsto \varphi _\tau (t)\) can be regarded as the curve in the \(N\)-torus
which when projected onto \(S^1(\widetilde{r}_n)\), \(\widetilde{r}_n >0\), goes around \(n\) times at a constant speed. Another interpretation, in terms of flat (polar) coordinates, is as the image through the quotient map
of the line segment in \(\mathbb {R}^N\) joining \((0,0,\ldots , 0)\) and \((\widetilde{r}_1,2\widetilde{r}_2,\ldots ,N\widetilde{r}_N)\). Figure 2 depicts \(\varphi _\tau (t)\) inside \(\mathcal {T}\) for \(N=3\).
The curve \(\varphi _\tau (t)\), in colors, with respect to its flat coordinates \((t,2t,3t)\in (\mathbb {R}/\widetilde{r}_1\mathbb {Z})\times (\mathbb {R}/\widetilde{r}_2\mathbb {Z})\times (\mathbb {R}/\widetilde{r}_3\mathbb {Z})\). Please refer to the electronic version for colors. Bottom right \(\varphi _\tau (t)\) in fundamental domain \([0,\widetilde{r}_1)\times [0,\widetilde{r}_2)\times [0,\widetilde{r}_3)\). Top left Projection onto \(xy\)-plane. Top right Projection onto \(xz\)-plane. Bottom left Projection onto \(yz\)-plane
6 Persistent Homology of \(\varphi _\tau \hbox { and } SW_{M,\tau }f\)
The structural observations from the previous section, as well as the approximation results from Sect. 4, set the stage for understanding the persistent homology of the image of \(\phi _\tau \) (or rather of \(\varphi _\tau \)) and how it relates to that of \(SW_{M,\tau } f\).
6.1 Some Convergence Results
Let \(T\subset \mathbb {T}\), and let \(SW_{M,\tau }f(T)\) and \(\phi _\tau (T)\) be the images of \(T\) through \(SW_{M,\tau }f\) and \(\phi _\tau \), respectively. An immediate consequence of Proposition 4.2 is that as \(N\) (and thus \(M =2N\)) gets larger, \(\phi _\tau (T)\) gets closer to \(SW_{M,\tau } f(T)\) with respect to the Hausdorff metric on subspaces of \(\mathbb {R}^\infty \). Here \(\mathbb {R}^\infty \) denotes the set of sequences \(x= (x_k)_{k\in \mathbb {N}}\), \(x_k \in \mathbb {R}\), such that \(x_n = 0\) for all \(n\ge N_0\) and some \(N_0 = N_0(x) \in \mathbb {N}\). We endow \(\mathbb {R}^\infty \) with the \(L^2\) metric and regard \(SW_{M,\tau }f(t)\), \(t\in T\), as an element of \(\mathbb {R}^\infty \) by identifying it with
Notice, however, that while increasing the dimension \(M+1\) of the sliding-window embedding yields better approximations
the object being approximated, \(SW_{M,\tau } f(T)\), is changing. Since \((\mathbb {R}^\infty ,\Vert \cdot \Vert _2)\) is not complete, there is no reason to believe this process converges or stabilizes, even with a sensible way of comparing, say, \(SW_{M,\tau } f(t)\) and \(SW_{2M,\frac{\tau }{2}}f(t)\). This is the case since they are samplings at different rates from the same window. Perhaps considering the Gromov–Hausdorff distance instead of the Hausdorff distance would yield such a comparison, but at least at the moment we do not have a natural embedding to make this case. In addition, even when the metric completion \(\overline{\mathbb {R}^\infty }= \ell ^2(\mathbb {R})\), the space of square-summable sequences, is well understood, it is also large enough that tracking global geometric features requires some work. It is in situations like this that a succinct and informative summary, such as persistence diagrams, is critical.
It is known that the space of persistence diagrams is not complete with respect to the bottleneck distance but that it can be completed by allowing diagrams with countably many points with at most countable multiplicity, satisfying a natural finiteness condition. [See Theorem 3.4 in [2] and Theorem 6 in [19]]. Moreover, features such as maximum persistence can be easily tracked, and there is no ambiguity on how to compare the diagrams from, say, \(SW_{M,\tau } f(T)\) and \(SW_{2M,\frac{\tau }{2}} f(T)\).
Proposition 6.1
Let \(f\) be \(L\)-periodic, \(N< N'\), \(M = 2N\), \(M' = 2N'\), and
If \(T\subset \mathbb {T}\) is finite, \(Y = SW_{M,\tau } S_N f(T)\), and \(Y' = SW_{M',\tau '}S_{N'}f(T)\), then
where \(\lambda \cdot \mathsf dgm (Z)\) is defined as \(\left\{ (\lambda x, \lambda y)\,|\, (x,y) \in \mathsf dgm (Z)\right\} \) for \(\lambda \ge 0\).
Proof
Let us fix the notation \(\mathbf {u}_n = \mathbf {u}_n(M,\tau )\), \(\mathbf {v}_n = \mathbf {v}_n(M,\tau )\), \(\mathbf {u}'_n = \mathbf {u}_n(M',\tau ')\), and \(\mathbf {v}'_n = \mathbf {v}_n(M',\tau ')\) in order to specify the dependencies of \(\mathbf {u}_n\) and \(\mathbf {v}_k\) on \(M\) and \(\tau \). Then we have the linear maps
which are well defined by Proposition 5.1. Moreover, Proposition 5.5 implies that \(P\) can be interpreted as an orthogonal projection when restricted to \(Y'\) and that \(Q\) is an isometry on \(P(Y')\). Notice that for every \(y' \in Y'\)
where \(r_n\) is as defined in Remark 5.4, and therefore
Finally, since \(Q\,\circ P(Y^{\prime }) = \sqrt{\frac{M^{\prime }+1}{M+1}}Y\) and \(\mathsf dgm (\;\cdot \;)\) is invariant under isometries, then
and the result follows from the identity \(r_n = 2\left| \widehat{f}(n)\right| = \left| \widehat{f}(n)\right| + \left| \widehat{f}(-n)\right| \), \(n\ge 1\). \(\square \)
This result, paired with the fact that \(\Vert f - S_N f\Vert _2 \rightarrow 0\) as \(N\rightarrow \infty \) and the Structure Theorem 5.6 (1), (2), implies the following corollary.
Corollary 6.2
Let \(f\in L^2(\mathbb {T})\) be \(L\)-periodic, \(N\in \mathbb {N}\), \(\tau _N = \frac{2\pi }{L(2N +1)} \), \(T\subset \mathbb {T}\) finite, and let \(\bar{Y}_N\) be the set resulting from pointwise centering and normalizing the point cloud
Then for any field of coefficients, the sequence \(\mathsf dgm (\bar{Y}_N)\) of persistence diagrams is Cauchy with respect to \(d_\mathrm{{B}}\).
Completeness of the set of (generalized) diagrams [2, Theorem 3.4], allows one to state the following definition.
Definition 6.3
Let \(w = \frac{2\pi }{L}\), and denote by \(\mathsf dgm _\infty (f,T,w)\) the limit in the bottleneck distance of the sequence \(\mathsf dgm (\bar{Y}_N)\).
We hope the notation \(\mathsf dgm _\infty (f,T,w)\) is suggestive enough to evoke the idea that there exists a limiting diagram from the sequence of pointwise-centered and normalized versions of \(SW_{M,\tau }f(T)\), as \(M\rightarrow \infty \), and while keeping the window size \(M\tau = \frac{M}{M+1}w\approx w\). The first convergence theorem (Theorem 6.6) below asserts the validity of this notation. Before presenting the proof, we start with a technical result.
Proposition 6.4
Let \(f\in C(\mathbb {T})\) be \(L\)-periodic, \(N\in \mathbb {N}\), and \(\tau _N = \frac{2\pi }{L(2N+1)}\). Then
uniformly in \(t\in \mathbb {T}\).
Proof
Since the result is trivially true if \(f\) is constant, let us assume \(f \ne \widehat{f}(0)\), and let
It follows that \(g\in C(\mathbb {T})\) is \(L\)-periodic,
Using the identity \(L(2N+1)\tau _N= 2\pi \), a Riemann sums argument, and the fact that \(g\) is \(L\)-periodic, it follows that if
then for all \(t\in \mathbb {T}\)
We contend that the convergence \(c_N (t)\rightarrow 0\) is uniform in \(t\in \mathbb {T}\). Indeed, the fact that \(g\) is uniformly continuous implies that the sequence \(c_N(t)\) is uniformly equicontinuous. This means that for every \(\epsilon >0\) there exists \(\delta >0\) independent of \(N\) such that for every \(t,t'\in \mathbb {T}\) and all \(N\in \mathbb {N}\)
Let \(N_t\in \mathbb {N}\), for \(t\in \mathbb {T}\), be such that \(N\ge N_t\) implies \(|c_N(t)| <\frac{\epsilon }{2}\). These two inequalities together imply that if \(N\ge N_t\) and \(|t-t'| < \delta \), then \(|c_N(t')| < \epsilon \).
By choosing a finite open cover of \([0,2\pi ]\) with intervals of length \(\delta \) and letting \(N_0\) be the maximum of the \(N_t\) corresponding to their centers, we get that \(N\ge N_0\) implies \(|c_N(t)| <\epsilon \) for all \(t\in \mathbb {T}\). Thus, the convergence \(c_N(t)\rightarrow 0\) is uniform. A similar argument shows that
uniformly in \(t\in \mathbb {T}\), and replacing \(g\) by \(\frac{f -\widehat{f}(0)}{\left\| f - \widehat{f}(0)\right\| _2}\) yields the result. \(\square \)
Remark 6.5
Notice that an alternative proof of Proposition 6.4 follows from combining the Structure Theorem 5.6 (2), Parseval’s Theorem, and the fact that
Theorem 6.6
(Convergence I) Let \(f\in C^1(\mathbb {T})\) be an \(L\)-periodic function, \(N\in \mathbb {N}\), \(\tau _N = \frac{2\pi }{L(2N +1)}\), \(T\subset \mathbb {T}\) finite, and let \(\bar{Y}_N\) be as in Corollary 6.2. Let \(\bar{X}_N\) be the set resulting from pointwise centering and normalizing the point cloud
Then for any field of coefficients, the sequence \(\mathsf dgm (\bar{X}_N)\) of persistence diagrams is Cauchy with respect to \(d_\mathrm{{B}}\), and
Proof
To prove Theorem 6.6, we will use the Approximation Theorem 4.5 to show that
and combine this with Corollary 6.2 to obtain the result.
Assume without loss of generality that \(f\) satisfies \(\widehat{f}(0)=0\) and \(\Vert f\Vert _2 =1\). Let \(X_N \) and \(Y_N \) be the resulting sets from pointwise centering the point clouds \(SW_{2N,\tau _N} f(T)\) and \(SW_{2N,\tau _N} S_Nf(T)\), respectively. Using the uniform convergence in Eq. 5 we get that
and moreover, since \(\lim \limits _{N\rightarrow \infty } \Vert S_N f\Vert _2 = \Vert f\Vert _2 =1\), then
Now, from the Structure Theorem 5.6 (2) we have the identity
and using the Approximation Theorem 4.5 (1), along with the fact that \(C\) is distance nonincreasing, we conclude that
The triangular inequality then implies that \(\lim \limits _{N\rightarrow \infty } d_\mathrm{{H}}(\bar{X}_N,\bar{Y}_N)=0\), and the result follows from combining the stability of \(d_\mathrm{{B}}\) with respect to \(d_\mathrm{{H}}\) and Corollary 6.2. \(\square \)
The first convergence theorem asserts that for each choice of discretization \(T\subset \mathbb {T}\) one obtains a limiting diagram \(\mathsf dgm _\infty (f,T,w)\) by letting \(N\rightarrow \infty \) in the pointwise centered and normalized versions of either \(SW_{2N,\tau _N} S_N f(T)\) or \(SW_{2N,\tau _N} f(T)\). Next we will show that there is also convergence when \(T\) tends to \(\mathbb {T}\) with respect to the Hausdorff distance on subspaces of \(\mathbb {T}\).
Theorem 6.7
(Convergence II) Let \(T,T^\prime \subset \mathbb {T}\) be finite, and let \(f\in C^1(\mathbb {T})\) be \(L\)-periodic with modulus of continuity \(\omega :[0,\infty ]\longrightarrow [0,\infty ]\). If \(w = \frac{2\pi }{L}\), then
and thus there exists a persistence diagram \(\mathsf dgm _\infty (f,w)\) so that
Proof
Fix \(t\in T \) and \(t^\prime \in T^\prime \). If we let \(\mathbf {x}_N = SW_{2N,\tau _N} f(t)\), \(\mathbf {x}_N^\prime = SW_{2N,\tau _N} f(t^\prime )\), \(\tau _N = \frac{2\pi }{L(2N+1)}\), and \(\lambda =\left\| f - \widehat{f}(0) \right\| _2\), then
It follows from Proposition 6.4 that both the summand
and its version with \(\mathbf {x}^\prime _N\) go to zero as \(N\rightarrow \infty \). Thus, given \(\epsilon > 0\), there exists \(N_0 \in \mathbb {N}\) such that \(N\ge N_0\) implies
Let \(\bar{X}_N\) and \(\bar{X^\prime }_N\) be the sets resulting from pointwise centering and normalizing \(SW_{2N,\tau _N} f(T)\) and \(SW_{2N,\tau _N} f(T^\prime )\), respectively. Since the preceding estimates are uniform in \(t\) and \(t^\prime \) (by Proposition 6.4), it follows that whenever \(N\ge N_0\),
Notice that the Hausdorff distance on the left-hand side is for subspaces of \(\mathbb {R}^{2N+1}\), while that on the right-hand side is between subspaces of \(\mathbb {T}\).
Applying the stability theorem for persistence diagrams yields
which, by letting \(N\rightarrow \infty \) and applying the first convergence theorem (Theorem 6.6), implies
Since this is true for any \(\epsilon >0\), letting \(\epsilon \downarrow 0\) yields the first part of the theorem. The existence of \(\mathsf dgm _\infty (f,w)\) follows from the fact that the set of generalized persistence diagrams is complete with respect to \(d_\mathrm{{B}}\). \(\square \)
6.2 A Lower Bound for Maximum Persistence
The structure theorem, Theorem 5.6 (3), and the fact that orthogonal projections are distance nonincreasing allow us to now prove the following theorem.
Theorem 6.8
Let \(f\in C^1(\mathbb {T})\) be an \(L\)-periodic function, \(N\in \mathbb {N}\), \(M\ge 2N\), \(L(M+1)\tau = 2\pi \), and let \(T\subset \mathbb {T}\) be finite. Furthermore, assume that \(d_\mathrm{{H}}(T,\mathbb {T}) <\delta \) for some [see Theorem 5.6 (3)]
Let \(\bar{Y} = \bar{Y}_N\) be the set resulting from pointwise centering and normalizing the point cloud
and let \(p>N\) be a prime. If \(\mathsf dgm (\bar{Y})\) denotes the 1D \(\mathbb {F}_p\)-persistence diagram for the Rips filtration on \(\bar{Y}\), then \(\varphi _\tau \) yields an element \(\mathbf {x}_\varphi \in \mathsf dgm (\bar{Y})\), with
-
(1)
\(\mathsf birth (\mathbf {x}_\varphi ) \le \delta \kappa _N\),
-
(2)
\(\mathsf death (\mathbf {x}_\varphi ) \ge \sqrt{3} \max \limits _{1\le n \le N} \widetilde{r}_n\),
and therefore
Proof
Given the linear decomposition
of \(\varphi _\tau (t)\) with respect to the orthonormal set \(\big \{\widetilde{\mathbf {x}}_n,\widetilde{\mathbf {y}}_n\;|\; 1\le n\le N, \; n\equiv 0 \;(\text{ mod } L)\big \}\) described in the proof of Theorem 5.6 (3), it follows that
can be regarded as the restriction to \(\bar{Y}\) of the orthogonal projection from \(\mathbb {R}^{M+1}\) onto \(Span\{\widetilde{\mathbf {x}}_n,\widetilde{\mathbf {y}}_n\}\). Since orthogonal projections are linear and norm-non-increasing, then \(\Vert P_n(\mathbf {x}) - P_n(\mathbf {y})\Vert \le \Vert \mathbf {x}- \mathbf {y}\Vert \) for every \(\mathbf {x},\mathbf {y}\in \bar{Y}\). Thus, if
then it follows that \(P_n\) induces simplicial maps
for every \(\epsilon >0\), which in turn yield homomorphisms
of \(\mathbb {F}_p\)-vector spaces at the homology level. What we contend is that, via the homomorphisms \(P_{n_*}\), the maximum 1D persistence of \(\bar{Y}\) can be bounded below by that of \(S^1(\widetilde{r}_n)\). Indeed, let \(\epsilon _1,\epsilon _2>0\) be such that
where \(m = \arg \max \;\{\widetilde{r}_n\;|\; 1\le n \le N\}\). If we write
then it follows from \(d_\mathrm{{H}}(T,\mathbb {T})< \delta \) that \(|t_{j} - t_{j-1} | < 2\delta \) for all \(j= 1, \ldots , J\), and therefore
The first inequality is a consequence of the Taylor expansion for \(\cos (x)\) around zero, and \(f^\prime \) denotes the first derivative of \(f\).
Therefore,
is a 1D cycle on \(R_{\epsilon _1}(\bar{Y})\), and we obtain the homology class
Let \( \{\theta _0 < \theta _1 <\cdots < \theta _{J_m}\} = \left\{ t \text{ mod } \frac{2\pi }{m}\;|\; t\in T\right\} \) and let \(c_j = \widetilde{r}_m e^{im \theta _j}\). It follows from a similar calculation that
and therefore the 1-cycle
is such that its homology class \([\mu ] \in H_1\left( R_{\epsilon _1}\left( S^1(\widetilde{r}_m)\right) ;\mathbb {F}_p\right) \) satisfies \(i_*([\mu ]) \ne 0\), where \(i_*\) is the homomorphism induced by the inclusion
Since \(P_{m_*}([\nu ]) = m[\mu ]\), and given that \(1\le m\le N < p\) implies that \(m\) is invertible in \(\mathbb {F}_p\), \(i_*\circ P_{m_*}([\nu ]) \ne 0\). From the commutativity of the diagram

we conclude that \(i_*([\nu ]) \ne 0\), and thus \([\nu ]\) yields an element \(\mathbf {x}_\varphi \in \mathsf dgm (\bar{Y})\) such that
Given that this is true for every \(\epsilon _1> \delta \kappa _N\) and every \(\epsilon _2 < \sqrt{3}\widetilde{r}_m\), letting \(\epsilon _1 \downarrow \delta \kappa _N \) and \(\epsilon _2 \uparrow \sqrt{3}\widetilde{r}_m\) concludes the proof. \(\square \)
Remark 6.9
It is worth noting that in the proof of Theorem 6.8 one can replace \(\mathbb {F}_p\), \(p> N\), by the field of rational numbers \(\mathbb {Q}\). That is, the estimated bound for maximum persistence is valid for all \(N\in \mathbb {N}\) and homology with \(\mathbb {Q}\) coefficients.
Equation 6, together with the Convergence Theorems I (Theorem 6.6) and II (Theorem 6.7), implies the following corollary.
Corollary 6.10
Let \(f\in C^1(\mathbb {T})\) be an \(L\)-periodic function such that \(\widehat{f}(0)= 0\) and \(\Vert f\Vert _2 = 1\). Let \(T\subset \mathbb {T}\) be finite and such that \(d_\mathrm{{H}}(T,\mathbb {T}) < \delta \) for some
Then with \(\mathbb {Q}\) coefficients, the 1D persistence diagram \(\mathsf dgm _\infty (f,T,w)\) satisfies
and therefore
6.3 Field of Coefficients
One question worth asking is whether the lower bound for maximum persistence presented in Theorem 6.8 is in fact dependent on the field of coefficients. More generally, one would like to determine whether the full persistence diagram has such a dependency. To this end, let us consider the functions
We construct their associated sliding-window point clouds, \(SW_{M,\tau } g_1(T)\) and \(SW_{M,\tau }g_2(T)\), using \(M=4\), \(\tau = 2\pi /5\), and \(T = \left\{ \frac{2\pi k}{150}\;|\; k=0,1,\ldots , 150\right\} \). After pointwise centering and normalizing, we compute their 1D persistent homology with coefficients in \(\mathbb {F}_2\) and \(\mathbb {F}_3\). For this we use a fast implementation of the 1D persistent homology, based on the Union–Find algorithm and the work of Mischaikow and Nanda [20]. Details of this implementation will appear in [23].
We summarize the results in Fig. 3.
This example shows that, at least in low dimensions, the persistent homology of sliding-window point clouds is coefficient-dependent. Let us see why this is so. If \((r_1,r_2) \in \mathbb {R}^2\) is such that \(r_1^2 + r_2^2 = 1\) and \(r_1r_2 \ne 0\), it follows from the Structure Theorem 5.6 (3) that if \(\alpha _1,\alpha _2 \in [0,2\pi ]\) and
then for every \(t\in [0,2\pi ]\) and \(M\ge 4\), \(\tau = \frac{2\pi }{M+1}\), one has that
can be isometrically identified with
Let us use \(\widetilde{\varphi }\) instead of \(\varphi _\tau \) for the persistent homology computation. The first thing to notice is that the image of \(\widetilde{\varphi }\) can be realized as the boundary of a Möbius strip. Indeed, consider the map
It follows that \(\mathcal {M}\) is a continuous injection on \([0,\pi )\times [-1,1)\), since \(r_1r_2 \ne 0\), and that it descends to an embedding of the quotient space
where \((0,s) \sim (\pi ,-s)\) for every \(s\in [-1,1]\). Notice that \([0,\pi ]\times [-1,1]/\sim \) serves as the usual model for the Möbius strip and that \(\partial \Big (Img(\widetilde{\mathcal {M}})\Big ) = Img(\widetilde{\varphi })\).
Let \(T = \{t_0 < t_2 < \cdots < t_J\}\) be a \(\delta \)-dense subset of \([0,2\pi ]\), \(X = \widetilde{\varphi }(T)\), and let
for \(r > 4\delta \), be the homology class of the 1-cycle
It can be readily verified that if we let
then there exists a triangulation of \(Img(\widetilde{\mathcal {M}})\) having \(\widetilde{\mathcal {M}}(V)\) as vertex set, and so if we take coefficients in \(\mathbb {F}_2\), then the formal sum of its triangles yields a 2-chain \(\Sigma \) with \(\partial _2 (\Sigma ) = \nu \). Moreover, since \(T\) is \(\delta \)-dense in \([0,2\pi ]\) and for all \(t\in [0,\pi ]\)
if \(\delta > 0\) is small, then we can choose \(\Sigma \) such that
In summary, if
then the death time of the class \([\nu ]\) is less than or equal to \(r_1 \sqrt{4 - 5\delta ^2} + 2\delta \), with coefficients in \(\mathbb {F}_2\), but larger than \(\sqrt{3}\,r_2\) (by Theorem 6.8), with coefficients in \(\mathbb {F}_p\) for any prime \(p \ge 3\). Moreover, with coefficients in \(\mathbb {F}_2\) and provided Eq. 7 holds (e.g., for \(g_1\)), the first edge across the Möbius band prompts the birth of a new class corresponding to the equator
of the embedded Möbius strip. This class in turn survives up to \(\sqrt{3}r_2\). With coefficients in \(\mathbb {F}_3\), on the other hand, the equatorial and boundary classes will be in the same persistence class once all the 2-simplices in the Möbius band have been added. This results in the death of the class that was born later, i.e., the one represented by the equator.
7 Examples: Quantifying Periodicity of Sampled Signals
We present in this section two experiments to test our ideas: first, the ranking of signals by periodicity alone, in a way that is invariant to the shape of the periodic pattern, and second, the accurate classification of a signal as periodic or nonperiodic at different noise levels. A detailed description of our methods is provided below, but roughly speaking, we associate to each sampled signal \(S = [s_1,\ldots , s_J]\) a real-valued function \(f_S\) by cubic spline interpolation, construct its centered and normalized sliding-window point cloud \(X_S\), and let
be its periodicity score. We then compare it to those obtained with the JTK_CYCLE [15], Lomb–Scargle [13, 18, 24], and total persistent homology [7] algorithms.
7.1 Shape Independence
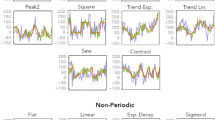
For this experiment we construct ten different shapes: a 2-periodic pure cosinelike curve, a 2-periodic cosinelike function plus three levels of gaussian noise (variances at 25, 50, and 75 % of signal amplitude), a noisy sawtooth (noise level at 25 % of signal amplitude), a function of the form \(\cos (\phi (t))\) for \(\phi (t) = e^{at +b}\), a noisy and damped cosinelike curve with three periods, a spiky signal with three periods, a noisy square wave with two periods, and a 1-periodic function of the form \(Re\left( \sum \limits _{n=1}^5 \widehat{f}(n)e^{2int} \right) \) for \(\widehat{f}(n)\) drawn randomly and uniformly from the unit disk in \(\mathbb {C}\). Each function is then evaluated at 50 evenly spaced time points, yielding the sampled signals \([s_1,\ldots , s_{50}]\) that we input into the algorithms. For the construction of the sliding-window point clouds we use \(N=10\), coefficients in \(\mathbb {F}_{11}\), \(L=2,3,4\), and report the best score. In all the other algorithms we set the parameters to their suggested or default values. The results are summarized in Fig. 4.
Two things are worth noting. First, except for the sliding-window method (SW1PerS), all other algorithms have clear preferences for the type of shape they consider to be most periodic. These biases are of course part of the wiring of the algorithms and were to be expected. The second thing to notice has to do with the distribution of scores and their relative differences. Methods such as JTK or Lomb–Scargle define their periodicity score in terms of \(p\)-values, which are extremely difficult to interpret. Our scoring method, by way of contrast, has a clear geometric interpretation and a reasonable distribution.
7.2 Classification Rates
We compare the different algorithms by their ability to separate periodic from nonperiodic signals. The performance of this type of binary classification can be visualized using a receiver operating characteristic (ROC) plot, which compares the true positive rate (TPR) to the false positive rate (FPR) as a cutoff on the scores is varied. Here the TPR is the proportion of correctly identified positive cases out of all positives, and FPR is the proportion of negative cases incorrectly identified as positives out of all the negatives. The line TPR = FPR is the performance of random guessing; the higher the ROC curve is above this line, the better its classification performance. An algorithm that is able to perfectly separate all positive from negative test cases would have a ROC curve that passes through the point TPR = 1 and FPR = 0. It follows that a reasonable measure of classification success for a particular method is the area under its ROC curves.
The synthetic data are generated as follows: the periodic signals (positive cases) span two periods and include a cosine, cosine with trending, cosine with damping, and cosine with increased peak steepness. The nonperiodic signals (negative cases) include a constant and a linear function. We generate 100 profiles from each shape by adjusting its phase. For instance, in the case of the cosine shape we let
be the profiles. We sample each of the 600 profiles at 50 evenly spaced time points \(t\in [0,2\pi ]\) and add gaussian noise with standard deviation at 0, 25, and \(50~\%\) of signal amplitude. Please refer to Fig. 5 for examples.
Remark 7.1
There are two reason why we regard constant functions as nonperiodic. On the one hand, the intended application for SW1PerS (Sliding Windows and 1-Persistence Scoring) is to identify genes that are both relevant and exhibit a periodic expression pattern with respect to time. Relevance in this case means that changes in expression level translate into physiological phenomena. The second reason has to do with the philosophy of the proposed method: we quantify periodicity as the prominence of 1-homology classes in the sliding-window point cloud. Since this point cloud for a constant function is only a point, it does not have 1-homology and hence is interpreted as coming from a nonperiodic function.
For the Sliding Windows + 1D \(\mathbb {F}_p\)-Persistence computation we let \(N=10\), \(L=2\), and \(p=11\). To address noise, we include a layer of (simple) moving average at the sampled signal level and one iteration of mean shift [8] at the sliding-window point cloud level. For the moving average we fix a window size with seven data points and use a cubic spline of this denoised signal to populate the point cloud. Mean shift on a pointwise centered and normalized point cloud \(X_S\) was implemented as follows: given a point \(x\in X_S\), we let \(\bar{x}\) be the mean of the set
where \(\epsilon = \cos \left( \frac{\pi }{16}\right) \) and \(x\cdot y\) denotes the Euclidean inner product of \(x\) and \(y\). In other words, \(\bar{x}\) is the mean of the \(\epsilon \)-neighbors of \(x\) if distance is measured by cosine similarity. We obtain the mean-shifted point cloud
which we now use for the persistent-homology computation. We report our results in Fig. 6.
ROC curves: true positive rate versus false positive rate. We compare the classification success of each algorithm on the synthetic data set using the area under its ROC curves. Curves are colored according to the type of periodic shape, and the area under the curve (AUC) is reported. Please refer to electronic version for colors
The Lomb–Scargle periodogram is considered to be one of the best methods for detecting periodicity, and its ROC curves support this belief. The fact that it is attuned to favoring cosinelike curves makes it very resilient to dampening, trending, and noise. It was thus a great surprise to see that our method performs comparably well in all cases, except for trended cosines and cosines, and that outperforms it for peaked and damped profiles at high noise levels.
A final point we would like to make is that denoising really is a crucial element of the SW1PerS pipeline. We show in Fig. 7 the results of quantifying periodicity on raw synthetic data, i.e., without applying denoising. As one can see, in the absence of preprocessing, the results degrade considerably.
ROC curves for SW1PerS analysis on raw synthetic data, that is, we do not apply moving average or mean shift. For a comparison on the effect of denoising, please refer to the rightmost column in Fig. 6
8 Final Remarks
In this paper we proved results that describe the structure of persistence diagrams obtained by sliding-window embeddings of time series. The main tools for the analysis were a Fourier series approximation argument and the stability theorem for persistence diagrams. The results we obtained, provide explicit information about how diagrams from sliding-window point clouds depend on the embedding dimension, window size, and field of coefficients. We then presented examples of the effectiveness of our method for quantifying periodicity of time series data. The experimental side of this framework will be explored in more depth in future work.
This paper also presented the first full theoretical analysis of the use of persistent homology in finding structure in time series data. Time-delay embeddings as a means to analyze signals is not new; rather, it is a well-established method in dynamical systems and in image analysis. In addition, the use of computational topology methods to find structure in transformed data has already been considered experimentally, notably in [4] and [10]. This paper, however, is the first to provide a theoretical analysis of the dependency of persistence on the embedding dimension and window size.
There are some interesting new aspects of the use of persistence in this method. It provides one of the first examples where persistent homology with coefficients other than \(\mathbb {F}_2\) is required. Other notable examples include [4], where coefficients in \(\mathbb {F}_3\) were essential to discovering the embedded Klein bottle, and [9] and [10], where the authors start with a 1D persistent cohomology class mod \(\mathbb {F}_p\) and lift it to an integer 1D class to obtain a map to the circle. They do this by choosing \(p\) such that the relevant homomorphism in the Bockstein long exact sequence is surjective. Their approach to real data is to choose a prime \(p\) at random and evaluate whether \(H^2(X,\mathbb {Z})\) has \(p\)-torsion. If it does, they then choose another prime. By contrast, we have established exactly how to determine which primes could be problematic, which allows us to avoid them in advance.
It was highlighted in Remark 4.4 that maximum persistence, the main feature for periodicity studied in this paper, satisfies \(mp(\mathsf dgm ) = 2d_\mathrm{{B}}(\mathsf dgm ,\mathsf dgm _\Delta )\). This is in fact part of a bigger picture. Indeed, the \(q\)-Wasserstein distance between two persistence diagrams \(\mathsf dgm _1\) and \( \mathsf dgm _2\) is defined by
where \(\phi :\mathsf dgm _1 \rightarrow \mathsf dgm _2\) is a matching of \(\mathsf dgm _1\) with \(\mathsf dgm _2\). As with the bottleneck distance (Remark 4.4), one can show that
and since \(W_q \rightarrow d_\mathrm{{B}}\) as \(q\rightarrow \infty \), \(2W_q(\mathsf dgm ,\mathsf dgm _\Delta )\) can be regarded as a smoother version of \(mp(\mathsf dgm )\). When \(\mathsf dgm \) comes from a sliding-window point cloud, \(2W_q(\mathsf dgm ,\mathsf dgm _\Delta )\) can be interpreted as a sequence of signatures, or features, for periodicity and other phenomena at the signal level. Here the parameter \(q\) serves as the level of smoothing, and as it gets larger, the emphasis in what \(W_q(\mathsf dgm ,\mathsf dgm _\Delta )\) measures shifts from topological noise and fine attributes to large topological events.
The ring of algebraic functions on persistence diagrams, as a source of features for machine learning purposes, was recently studied by [1]. We believe these and other signatures, such as \(W_q(\mathsf dgm ,\mathsf dgm _\Delta )\), should uncover nontrivial signal properties captured by their sliding-window point clouds. We devoted this paper to exploring the use of \(mp(\mathsf dgm )\), but we hope that in future work the list of useful features from persistence diagrams on sliding-window point clouds can be extended.
We also mention that Sect. 6.3 is the first explicit computation of the persistence diagram of a parameterized space. The method of Fourier approximation presented here is one of the first in a much-needed toolbox for explicit computations of persistence diagrams.
Our final comment is to point out that the fact that the size of the sliding window should match the period searched for was not obvious in advance. Knowing this provides powerful information on sampling density to scientists planning an experiment that looks for periodic data and lays the groundwork for the use of SW1PerS as a filter for time series data.
In future work we plan to establish our conjecture that \(mp(\mathsf dgm )\) is maximized by our choice of window size, and the main ingredient will be strengthening the lower bound presented in Theorem 6.8. We also plan to establish the filtering properties of SW1PerS and apply it to a variety of data, including biological data like those from gene expression and physiology, astronomical data, and weather. Finally, we plan to extend these methods using other tools from topological data analysis to find structure and features in time series.
References
A. Adcock, E. Carlsson and G. Carlsson, The Ring of Algebraic Functions on Persistence Bar Codes, Preprint http://comptop.stanford.edu/u/preprints/multitwo, 2012
A. J. Blumberg, I. Gal, M. A. Mandell and M. Pancia, Persistent homology for metric measure spaces, and robust statistics for hypothesis testing and confidence intervals, arXiv preprint http://arxiv.org/pdf/1206.4581, 2012
G. Carlsson, Topology and Data, Bulletin of the American Mathematical Society, vol 46(2), pp. 255–308, 2009.
G. Carlsson, T. Ishkhanov, V. de Silva and A. Zomorodian, On the local behavior of spaces of natural images, International Journal of Computer Vision, vol 7(1), pp. 1–12, 2008.
F. Chazal, D. Cohen-Steiner, M. Glisse, L. J. Guibas, and S. Y. Oudot, Proximity of persistence modules and their diagrams, In SCG, pp. 237–246, 2009.
D. Cohen-Steiner, H. Edelsbrunner and J. Harer, Stability of persistence diagrams, Discrete and Computational Geometry, vol 37(1), pp. 103–120, 2007.
D. Cohen-Steiner, H. Edelsbrunner, J. Harer and Y. Mileyko, Lipschitz Functions Have \(L^p\)-Stable Persistence, Foundations of Computational Mathematics, vol 10(2), pp. 127–139, 2010.
D. Comaniciu and P. Meer, Mean shift: A robust approach toward feature space analysis, Pattern Analysis and Machine Intelligence, vol 24(5), pp. 603–619, 2002.
V. de Silva, D. Morozov and M. Vejdemo-Johansson, Persistent Cohomology and Circular Coordinates, Discrete & Computational Geometry, vol 45(4), pp. 737–759, 2011.
V. de Silva, P. Skraba and M. Vejdemo-Johansson, Topological Analysis of Recurrent Systems, Workshop on Algebraic Topology and Machine Learning, NIPS 2012, Preprint available at url: http://sites.google.com/site/nips2012topology/contributed-talks
A. Deckard, R. Analfi, D. Orlando, J. Hogenesch, S. Haase and J. Harer, Design and Analysis of Large-Scale Biological Rhythm Studies: A Comparison of Algorithms for Detecting Periodic Signals in Biological Data, Bioinformatics, btt541v1-btt541, 2013.
H. Edelsbrunner and J. Harer Computational Topology, an Introduction, American Mathematical Society, (2010) (241 pages).
E. F. Glynn, J. Chen and A. Mushegian, Detecting periodic patterns in unevenly spaced gene expression time series using Lomb-Scargle periodograms, Bioinformatics, vol 22(3), pp. 310–316, 2006.
A. Hatcher Algebraic Topology. Cambridge Univ. Press, England, 2002.
M. E. Hughes, J. B. Hogenesch and K. Kornacker, JTK-CYCLE: An Efficient Nonparametric Algorithm for Detecting Rhythmic Components in Genome-Scale Data Sets, Journal of Biological Rhythms, vol 25(372), pp. 372–380, 2010.
H. Kantz and T. Schreiber, Nonlinear Time Series Analysis, Cambridge University Press, 2003.
H. S. Kim, R. Eykholt and J. D. Salas, Nonlinear dynaimcs, delay times, and embedding windows, Physica D: Nonlinear Phenomena, vol 127(1), pp. 48–60, 1999.
N. R. Lomb, Least-squares frequency analysis of unequally spaced data, Astrophysics and Space Science, vol 39, pp. 447–462, 1976.
Y. Mileyko, S. Mukherjee, and J. Harer, Probability measures on the space of persistence diagrams, Inverse Problems, 27(12), p.p. 124007, 2011.
K. Mischaikow and V. Nanda, Morse Theory for Filtrations and Efficient Computation of Persistent Homology, To appear on Discrete and Computational Geometry, 2013.
J. R. Munkres Elements of Algebraic Topology. Addison-Wesley, Redwood City, California, 1984.
M. A. Pinsky, Introduction to Fourier Anlysis and Wavelets, The Brooks/Cole Series in Advanced Mathematics, USA, 2003.
J. A. Perea, A. Deckard, S. B. Haase and J. Harer, SW1PerS: Sliding Windows and 1-Persistence Scoring; Discovering Periodicity in Gene Expression Time Series Data, preprint (2013).
J. D. Scargle, Studies in astronomical time series analysis. II-Statistical aspects of spectral analysis of unevenly spaced data, Astrophysical Journal, vol 263, pp. 835–853, 1982.
C. J. Stam, Nonlinear dynamical analysis of EEG and MEG: Review of an emerging field, Clinical Neurophisiology, 116, pp. 2266–2301, 2005.
N. Hundewale, The application of methods of nonlinear dynamics for ECG in Normal Sinus Rythm, Int. J. of Computer Science, 9, pp. 458–467, 2012.
C. E. Shannon, Communication in the presence of noise, Proc. Inst. Radio Eng., vol. 37, no. 1, pp. 10–21, 1949.
F. Takens, Detecting strange attractors in turbulence. in D. A. Rand and L. -S. Young. Dynamical Systems and Turbulence, Lecture Notes in Mathematics, vol. 898. Springer-Verlag. pp. 366–381.
A. Tausz, M. Vejdemo-Johansson and H. Adams, JavaPlex: A research software package for persistent (co)homology, 2011, Software available at url: http://code.google.com/p/javaplex
A. Zomorodian and G. Carlsson, Computing Persistent Homology, Discrete & Computational Geometry, vol 33(2), pp. 249–274, 2005.
Acknowledgments
Both authors were supported in part by DARPA under Grants D12AP00001 and D12AP00025-002 and by the AFOSR under Grant FA9550-10-1-0436.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Herbert Hedelsbrunner.
Rights and permissions
About this article
Cite this article
Perea, J.A., Harer, J. Sliding Windows and Persistence: An Application of Topological Methods to Signal Analysis. Found Comput Math 15, 799–838 (2015). https://doi.org/10.1007/s10208-014-9206-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10208-014-9206-z