Markets with random lifetimes and private values: mean reversion and option to trade

Abstract

We consider a market in which traders arrive at random times, with random private values for the single-traded asset. A trader’s optimal trading decision is formulated in terms of exercising the option to trade one unit of the asset at the optimal stopping time. We solve the optimal stopping problem under the assumption that the market price follows a mean-reverting diffusion process. The model is calibrated to experimental data taken from Alton and Plott (Principles of continuous price determination in an experimental environment with flows of random arrivals and departures. Working paper, Caltech, 2010), resulting in a very good fit. In particular, the estimated long-term mean of the traded prices is close to the theoretical long-term mean at which the expected number of buys is equal to the expected number of sells. We call that value long-term competitive equilibrium, extending the concept of flow competitive equilibrium of Alton and Plott (Principles of continuous price determination in an experimental environment with flows of random arrivals and departures. Working paper, Caltech, 2010).

1 Introduction

This paper models optimal trading of individuals at a microstructure level, by formulating the decision to trade as an optimal stopping problem. We adopt the setting of Alton and Plott (2010) of a market with a single asset, in which buyers and sellers arrive at random times, with random private values for one unit of the asset. While this may not be an accurate depiction of real markets, it is a natural benchmark model, in which we can solve for the optimal strategies of the traders and test whether those strategies are in agreement with data obtained in a controlled experimental setting.

A trader has an option to exchange the private value of the asset for the market price (or vice-versa), at time of her choosing, during a time interval of random length after which the option expires. Thus, assuming the traders is risk neutral, the decision problem is the one of choosing the optimal stopping time at which the trade will take place, during a time interval of random length (exponentially distributed for tractability). This makes it equivalent to the problem of optimally exercising an American option over a random horizon, with the market price as the underlying asset. The option is of the put type for the traders who consider buying the asset and of the call type for the traders who consider selling the asset.

If the underlying asset follows the geometric Brownian motion (GBM) process, solving such problems is standard in the option pricing theory; see, for example, Carr (1998) and Shreve (2004). Extensions of the GBM model and/or different optimization objectives when looking for the optimal time to sell or buy a stock have been considered, among others, by Guo and Zhang (2005), Peskir and Toit (2009), Shiryaev et al. (2008), and Zhang (2001). However, while exponential growth that the GBM process exhibits on average may be appropriate for long-term horizons, it is not realistic for very short-term, tick-by-tick trading. Instead, a process which exhibits mean reversion is much more appropriate, and we model the market log price as a mean-reverting Ornstein–Uhlenbeck process. The same model is used by Zhang and Zhang (2008) for the problem of optimal buying and selling in the presence of transaction costs. Moreover, the paper Song et al. (2009) develops numerical methods for such problems for general mean-reverting processes, and Zervos et al. (2013) solve such problems analytically for general one-dimensional homogeneous diffusion processes.

Mean reversion makes the optimal stopping problem harder than in the GBM case, but we are able to solve our problem semi-analytically, in terms of parabolic cylinder functions and up to one-dimensional integration.¹

Using the fact that we can compute the optimal trading strategies for the traders, and in the second part of the paper, we calibrate this model to the price data generated in trading experiments by Alton and Plott (2010). More precisely, we do the following: we estimate all the parameters of the mean-reverting process using (a part of) the price data, except for the long-term mean parameter. Then, we compute the value of the long-term mean for which the expected number of optimal buys is equal to the expected number of optimal sells in the model. We call this value long-term competitive equilibrium, or LTCE. We find that this value is close to the estimated value of the long-term mean, and that the price data is concentrated around it. Alton and Plott (2010) also introduce a notion of a long-term equilibrium price value called flow competitive equilibrium (FCE), at which there is a clearing of the market in the expected value sense. Our LTCE value can be thought of as an analog of FCE in a model that accounts for the mean-reversion feature of the price formation process, and assumes rational, rather than random behavior of the traders. The mean squared error of FCE and LTCE for our experimental data is similar, thus not favoring either of the equilibrium notions over the other.

While LTCE seems to be a good measure for the equilibrium price, it has the disadvantage, relative to FCE, that its value depends on how exactly one estimates the remaining parameters of the price process, and that the numerical procedure for computing is much more involved than for computing FCE. In particular, FCE does not involve using past data to compute it. Nevertheless, we find it worthwhile developing a definition of an equilibrium price that arises from optimal behavior of the traders in a plausible model. That is, while FCE assumes completely random behavior of traders, LTCE is based on a model of rational traders. Moreover, even though LTCE depends on parameter estimation using historical data, with our data set the computed value of LTCE is very stable relative to the part of the data sample chosen to compute it. More precisely, it does not make a big difference in the computed value of the LTCE whether we use a quarter, a half, or the full sample of our data points for parameter estimation. This is to be contrasted with the estimated value of the long-term mean, which is very sensitive to the chosen sample. Overall, perhaps we pose more questions than we answer, and in particular, whether or not it is possible to determine what drives the traders behavior just from looking at the long-term price average. In the experimental data we use, this is not possible.

Trading a single asset using market orders or limit orders has been modeled by a number of papers in the literature. Most of those construct equilibrium strategies when trading is performed by different types of traders, such as market makers, informed traders, noise traders, patient and impatient traders. This approach is taken in Back and Baruch (2007), Biais et al. (2000), Biais and Weill (2009), Foucault (1999), Foucault et al. (2005), Goettler et al. (2005), Rosu (2009), Parlour (1998), Parlour and Seppi (2003), and Biais et al. (2010) among others. Then, there are partial equilibrium models like those of Avellaneda and Stoikov (2008), Kuhn and Stroh (2009), and Cont et al. (2009), that, like this paper, take the price process as given and find the best strategy for the single trader. Perhaps most similar in spirit to the theoretical part of our paper is Pagnotta (2010), who, in a different and more complex model, also assumes that there is a given price for the asset, and what the traders decide on is the frequency of their trades. However, in that model, there is a “true asset value” about which the traders have asymmetric information, and they also decide whether to submit market or limit orders. In contrast, in our model the optimal strategy is to place a limit order at an optimal level, with the additional option to exercise a market order at the end of the trader value’s “lifetime.” Moreover, there is no single true asset value, instead, the traders differ by their private values, not by the information they have. We abstract from specifying how the private values are formed, as they may be influenced by factors outside of the model, such as hedging trades in other markets, for example. Instead, we model them as randomly drawn from one distribution for buyers and one distribution for sellers.

Our aim is different than that of the latter papers. We are not interested in providing sophisticated algorithms for a trader to follow, or in finding how the limit order book features depend on the level of information traders have. Rather, as mentioned above, we examine whether a relatively simple model with mean reversion and optimal timing of trade describes well, at least in aggregate, the price formation in an experimental market designed to mimic the model.²

We present the theoretical model in Sect. 2, compute the value of the option to trade and the probability of exercising that option in Sect. 3, calibrate the model in Sect. 4 and conclude in the last section.

2 Model

There is a single asset to be traded in single units, and buyers/sellers decide at what time $t$ to buy/sell, submitting orders at the market price $P_t$. Let $v_B^i$ denote the “private value” for buyer $i$, who lives during a random interval $I_i^B=[s_i^B,t_i^B]$, where $s_i^B$ and $t_i^B-s_i^B$ are independent and exponentially distributed. Similarly, for the sellers, it is assumed that the private values $v_B^i,v_S^j$ are assigned randomly, in an iid manner to the traders, independent of everything else.³

By private value, we mean that (risk-neutral) buyer $i$’s problem is

$$\begin{aligned} \max _{\tau _i\in I_i^B} E\left[ \left. e^{-r^i_B\tau _i}\left( v_B^i-P_{\tau _i}\right) ^+ \right| v_B^i\right] \end{aligned}$$

(2.1)

and (risk-neutral) seller $j$’s problem is

$$\begin{aligned} \max _{\tau _j\in I_j^S} E\left[ \left. e^{-r^j_S\tau _j}\left( P_{\tau _j}-v_S^j\right) ^+ \right| v_S^j\right] \end{aligned}$$

(2.2)

where $r^i_B$ and $r^j_S$ are the traders’ discount rates, and $\tau _k,\,k=i,j$ is the trader-specific time of trade.

The above optimization problems are equivalent to the problem of pricing American options with random maturity. For each buyer (seller), $v_B^i\,(v_S^j)$ is a fixed value, but those values randomly vary across buyers/sellers because they are chosen in an iid manner. We assume that the price process $P$ of the asset is mean reverting (as is consistent with tick-by-tick trading data). More precisely, let $X_t$ be the log price of this asset, $X_t=\log P_t$, then $X_t$ is an Ornstein–Uhlenbeck process, given as the solution to the stochastic differential equation

$$\begin{aligned} \mathrm{d}X_t=\kappa (\theta -X_t)\mathrm{d}t+\sigma \mathrm{d}W_t, \end{aligned}$$

(2.3)

where $\kappa >0$ and $W_t$ is a standard Brownian motion process. Process $X_t$ is a well-known Gaussian process used in finance to model economic variables which tend to fluctuate around a long-term mean $\theta$. Parameter $\kappa$ measures the speed of mean reversion, and $\sigma$ is the variance parameter.

The above optimal stopping problem can be solved for such $P_t=e^{X_t}$, and we will compute below the optimal time to trade for each buyer/seller. Moreover, to calibrate the model to the experimental data of Alton and Plott (2010), in addition to optimal exercise levels, we will also compute the probabilities that the buyer/seller will make a transaction during her lifetime interval $I_i^k$ given the initial price $P_0$.

Remark 2.1

Strictly speaking, the mean-reverting process $P_t$ is not the true price process, but the traders’ estimate of the price process. It might be more satisfying not to impose the price process exogenously, but to derive it endogenously from market clearing between our buyers and sellers. However, that is a hard problem, outside of the scope of the paper. Our interpretation (assumption) is that the buyers and the sellers use a mean-reverting process for modeling the trading prices, whose parameters are common knowledge. Thus, the mean-reverting price process is not the actual price process resulting from trading, but a common belief (or estimate) by the traders about the price process. Put differently, any given trader does not have enough information to predict the price process in equilibrium; instead, she uses the Ornstein–Uhlenbeck model as the best guess for the price process, estimates its parameters, and solves her individual optimization problem, without solving the equilibrium problem.

3 Random maturity American options with mean-reverting underlying

Before starting computations needed to solve the model, let us present a brief outline of the model’s timeline and of what we want to do in the rest of the paper:

• A trader with a private value arrives.

• She computes the optimal level at which to trade, assuming an OU price process.

• Based on these levels, we compute the expected numbers (averaged over varying private values) of buy transactions and of sell transactions.

• We find the long-term mean $\theta$ that makes those two numbers equal.

The latter value of $\theta$ is called the LTCE.

3.1 Put and call values

We first solve the American put problem (2.1), and solving the problem (2.2) is analogous. For a fixed buyer with value $v$, which we re-denote to $K$ using the standard option pricing notation for strike price, we can write the problem (2.1) as

$$\begin{aligned} \max _{0\le \tau \le T} E\left[ e^{-r\tau }\left( K-P_{\tau }\right) ^+\right] \end{aligned}$$

(3.1)

where $T$ is an exponential random variable with intensity $\lambda$, and independent of everything else.

As noted in Carr (1998) (in which paper $P$ was a geometric Brownian motion), the function in (3.1) is a Laplace transform of the standard American put option price, and as a function $P(X)$ of the initial log price $X_0=X$, it satisfies the ordinary differential equation (ODE)

$$\begin{aligned} \frac{\sigma ^2}{2}P''(X)+\kappa (\theta -X)P'(X)-rP(X)=\lambda \left[ P(X)-\left( K-e^X\right) ^+\right] ,\quad X>\underline{X}\nonumber \\ \end{aligned}$$

(3.2)

with appropriate boundary conditions, listed in “Appendix.” Here, $\underline{X}$ is the optimal level at which to exercise the option (that is, to buy the asset).

In order to present the solution, we need to introduce some notation first. Let $D_{-\nu }(z)$ denote the parabolic cylinder functions.⁴ Also introduce⁵

$$\begin{aligned} \phi (x)&= \phi (x,\nu ):=e^{z_x^2/4}D_{-\nu }(z_x)\end{aligned}$$

(3.3)

$$\begin{aligned} \psi (x)&= \psi (x,\nu ):=e^{z_x^2/4}D_{-\nu }(-z_x), \end{aligned}$$

(3.4)

where

$$\begin{aligned} z_x:=\frac{\sqrt{2\kappa }(x-\theta )}{\sigma } \end{aligned}$$

(3.5)

Moreover, let the Wronskian of $\phi$ and $\psi$ be denoted as

$$\begin{aligned} W(x):=\phi (x)\psi '(x)-\phi '(x)\psi (x) \end{aligned}$$

Let $P(X)$ denote the value (3.1) of the American put option, where $X$ is the initial value of $X_t=\log P_t$. We have

Proposition 3.1

The value $P(X)$ of the random maturity American put with mean-reverting underlying is given by

$$\begin{aligned} P(X)=\left\{ \begin{array}{ll} C\phi (X),&{}\quad \text {if } \ X\ge \underline{X_0}\equiv \log K\\ A\phi (X)+Q(X),&{}\quad \text {if } \ X\in (\underline{X},\underline{X_0})\\ K-e^X, &{} \quad \text {if } \ X\le \underline{X} \end{array}\right. \end{aligned}$$

(3.6)

where $\phi (X)$ and $\psi (X)$ are defined in (3.3) and (3.4) with

$$\begin{aligned} \nu =\frac{\lambda +r}{\kappa } \end{aligned}$$

(3.7)

and

$$\begin{aligned} Q(X)&= \phi (X)\int \limits _{\underline{X}}^X\frac{2\psi (s)}{\sigma ^2 W(s)}\lambda (K-e^s)\hbox {d}s+\psi (X)\int \limits _X^{\underline{X_0}}\frac{2\phi (s)}{\sigma ^2 W(s)}\lambda (K-e^s)\hbox {d}s,\qquad \end{aligned}$$

(3.8)

$$\begin{aligned} A&= \frac{(K-e^{\underline{X}})\psi '(\underline{X})+e^{\underline{X}}\psi (\underline{X})}{W(\underline{X})}\end{aligned}$$

(3.9)

$$\begin{aligned} C&= A+\int \limits _{\underline{X}}^{\underline{X_0}}\frac{2\psi (s)}{\sigma ^2W(s)}\lambda (K-e^s)\hbox {d}s \end{aligned}$$

(3.10)

and the critical value $\underline{X}$ satisfies

$$\begin{aligned} \frac{(K-e^{\underline{X}})\phi '(\underline{X})+ e^{\underline{X}}\phi (\underline{X})}{W(\underline{X})}=-\int \limits _{\underline{X}}^{\underline{X_0}}\frac{2\phi (s)}{\sigma ^2W(s)}\lambda (K-e^s)\hbox {d}s \end{aligned}$$

(3.11)

Similarly, the random maturity American call value $C(X)$ in (2.2), with mean-reverting underlying, is given by

$$\begin{aligned} C(X)=\left\{ \begin{array}{ll} E\psi (X), &{} \quad \text {if}\quad X\le \overline{X_0}\equiv \log K\\ B\psi (X)+S(X), &{}\quad \text {if}\quad X\in (\overline{X_0},\overline{X})\\ e^X-K, &{}\quad \text {if}\quad X\ge \overline{X} \end{array}\right. \end{aligned}$$

(3.12)

where

$$\begin{aligned} S(X)&= \phi (X)\int \limits _{\overline{X_0}}^X\frac{2\psi (s)}{\sigma ^2 W(s)}\lambda (e^s-K)\hbox {d}s+\psi (X)\int \limits _X^{\overline{X}}\frac{2\phi (s)}{\sigma ^2 W(s)}\lambda (e^s-K)\hbox {d}s\qquad \qquad \end{aligned}$$

(3.13)

$$\begin{aligned} B&= \frac{e^{\overline{X}}\phi (\overline{X})-(e^{\overline{X}}-K)\phi '(\overline{X})}{W(\overline{X})}\end{aligned}$$

(3.14)

$$\begin{aligned} E&= B+\int \limits _{\overline{X_0}}^{\overline{X}}\frac{2\phi (s)}{\sigma ^2W(s)}\lambda (e^s-K)\hbox {d}s \end{aligned}$$

(3.15)

and the critical value $\overline{X}$ satisfies

$$\begin{aligned} \frac{(e^{\overline{X}}-K)\psi '(\overline{X})-e^{\overline{X}}\psi (\overline{X})}{W(\overline{X})}=\int \limits _{\overline{X_0}}^{\overline{X}}\frac{2\psi (s)}{\sigma ^2W(s)}\lambda (e^s-K)\hbox {d}s \end{aligned}$$

(3.16)

3.2 Probability of exercising options to trade

In order to be able to compute the expected number of trades in a given interval, we need to compute the probability that a trader will submit an order during her lifetime. In this regard, consider the process $X_t$ with $X_0=x$. Introduce the minimum and maximum values of $X$ up-to-date,

$$\begin{aligned} m(x,t)&:= \inf _{0\le s\le t}\{ X(s)~|~X(0)=x\}\end{aligned}$$

(3.17)

$$\begin{aligned} M(x,t)&:= \sup _{0\le s\le t}\{ X(s)~|~X(0)=x\} \end{aligned}$$

(3.18)

Also introduce the densities

$$\begin{aligned} p(x~|~y,t)=\frac{\partial }{\partial y}Pr\{X_t\le y~|~X_0=x\} \end{aligned}$$

(3.19)

and

$$\begin{aligned} f_y(x~|~t)=\frac{\partial }{\partial t}Pr\{M(x,t)\ge y~|~X_0=x\} \end{aligned}$$

(3.20)

Denote by $\hat{f}$ the Laplace transform of $f$. We have the following “Laplace transform variation” of a classical result by Darling and Siegert (1953).

Proposition 3.2

The probabilities that $m(x,t)\,(M(x,t))$ is less than $\underline{X}$ (greater than $\overline{X}$) during the exponentially distributed period with mean length $1/\lambda$ are given by, respectively,

$$\begin{aligned} P_{min}(x~|~\underline{X},\lambda )&= \hat{f}_{\underline{X}}(x~|~\lambda )=\frac{\phi (x)}{\phi (\underline{X})}, ~~ x\ge \underline{X}\end{aligned}$$

(3.21)

$$\begin{aligned} P_{max}(x~|~\overline{X},\lambda )&= \hat{f}_{\overline{X}}(x~|~\lambda )=\frac{\psi (x)}{\psi (\overline{X})}, ~~ x\le \overline{X}~, \end{aligned}$$

(3.22)

where $\phi (x)$ and $\psi (x)$ are defined in (3.3) and (3.4) with $\nu$ equal to $\lambda /\kappa$.

3.3 Probability of exercising options to trade with random starting time

The above result is still not sufficient for computing the probability that a trader will submit an order during her lifetime that is assumed to be random. We now extend the result to random lifetimes.

Recall that $p(x~|~y,t)$ denotes the transition density of $X$. Assuming the buyers/sellers live during a random interval $[\tau ,~\tau +\Delta \tau ]$ with

$$\begin{aligned} Pr\{\tau \in \hbox {d}t\}&= \lambda _B e^{-\lambda _Bt} \hbox {d}t, \quad \quad Pr\{\Delta \tau \in \hbox {d}t\}= \rho _B e^{-\rho _Bt} \hbox {d}t\end{aligned}$$

(3.23)

$$\begin{aligned} Pr\{\tau \in \hbox {d}t\}&= \lambda _S e^{-\lambda _St} \hbox {d}t, \quad \quad Pr\{\Delta \tau \in \hbox {d}t\}= \rho _S e^{-\rho _St} \hbox {d}t \end{aligned}$$

(3.24)

we have

Proposition 3.3

The probability that the minimum of $X(t)$ is less than $\underline{X}$ during a buyer’s lifetime is given by, in the notation of the previous sections, and given that $X_0=x$,

$$\begin{aligned} \mathbf {P}_{min}(x~|~\underline{X},\lambda _B,\rho _B)&= \int \limits _{\underline{X}}^\infty \lambda _BP_{min}(y~|~\underline{X},\rho _B)\hat{p}(x~|~y,\lambda _B)~\hbox {d}y\nonumber \\&+\int \limits _{-\infty }^{\underline{X}} \lambda _B\hat{p}(x~|~y,\lambda _B)~\hbox {d}y, \end{aligned}$$

(3.25)

where

$$\begin{aligned} P_{min}(y~|~{\underline{X}},\rho _B)=\frac{\phi (y,\rho _B)}{\phi (\underline{X},\rho _B)}, \end{aligned}$$

(3.26)

with

$$\begin{aligned} \phi (x,\lambda )=e^{z_x^2/4}D_{-\lambda /\kappa }(z_x),\quad \quad z_x\equiv \frac{\sqrt{2\kappa }(x-\theta )}{\sigma } \end{aligned}$$

(3.27)

Similarly, the probability that the maximum of $X(t)$ is higher than $\overline{X}$ during a seller’s lifetime is given by

$$\begin{aligned} \mathbf {P}_{max}(x~|~\overline{X},\lambda _S,\rho _S)&= \int \limits _{-\infty }^{\overline{X}}\lambda _SP_{max}(y~|~\overline{X},\lambda _S)\hat{p}(x~|~y,\lambda _S)~\hbox {d}y\nonumber \\&+\int \limits _{\overline{X}}^\infty \lambda _S\hat{p}(x~|~y,\lambda _S)~\hbox {d}y, \end{aligned}$$

(3.28)

where

$$\begin{aligned} P_{max}(y~|~{\overline{X}},\lambda )=\frac{\psi (y,\lambda )}{\psi (\overline{X},\lambda )} \end{aligned}$$

(3.29)

with

$$\begin{aligned} \psi (x,\lambda )=e^{z_x^2/4}D_{-\lambda /\kappa }(-z_x),\quad \quad z_x\equiv \frac{\sqrt{2\kappa }(x-\theta )}{\sigma } \end{aligned}$$

(3.30)

Moreover, the Laplace transform $\hat{p}$ in these expressions is given by

$$\begin{aligned}&\hat{p}(x~|~y,\lambda ) =\Gamma (\lambda /k)\sqrt{\frac{1}{\pi \kappa \sigma ^2}}e^{\frac{z_x^2-z_y^2}{4}}\\&\quad \times \left[ \Theta (x-y)D_{-\lambda /k}(z_x)D_{-\lambda /k}(-z_y)+\Theta (y-x)D_{-\lambda /k}(-z_x)D_{-\lambda /k}(z_y)\right] \end{aligned}$$

where $\Theta (x)$ is Heaviside theta function.

We now have all the equations needed to compute the expected number of buys and sells during a given interval of time. We use those equations on experimental data in the following section.

4 Long-term competitive equilibrium and calibration to experimental data

In this section, we first define the long-term competitive equilibrium (LTCE), and then, we calibrate our model to experimental data of Alton and Plott (2010).

Definition 4.1

Given a fixed interval of time, the LTCE price is the value of the long-term mean for which the expected number of buys is equal to the expected number of sells during that interval when the traders submit their orders optimally according to the model of the previous sections.

The LTCE price can be interpreted as an analog of the FCE price that Alton and Plott (2010) introduced as the value at which the expected number of buys is equal to the expected number of sells in the market in which the traders do not behave strategically, but immediately submit their private values as buy and sell orders. That is, given the distributions of incoming buyers’ and sellers’ private values $G_S$ and $G_b$, the intensities of their lifetimes $\lambda _b$ and $\lambda _s$, and the number of buyers and sellers $n_b$ and $n_s$, implicitly assuming that the private values are immediately submitted as trade orders, FCE is defined by the equation

$$\begin{aligned} n_s\lambda _sG_S(\mathrm{FCE})=n_b\lambda _b(1-G_b(\hbox {FCE})) \end{aligned}$$

Alton and Plott (2010) also define temporal equilibrium (TE) price, which is the price at which the market clears at the present time. TE changes from one moment to another, while FCE and LTCE are constant across time, serving as predictors of the long-term average price. Our LTCE price is based on a more sophisticated behavior of traders, in the sense that it takes into account the traders’ optimization and the mean-reverting nature of the price, rather than assuming a completely random traders’ behavior, independent of the price model. As with FCE, the aim is to define a single, typical value for the long-term price behavior. To reiterate, the difference is that FCE presupposes totally random trading by buyers and sellers, while LTCE is a model of rational traders who maximize their expected profit/loss.

To see whether our simple model with rational behavior might be consistent with trading of individuals, we now calibrate the model to the experimental data from the experiment in Alton and Plott (2010). In that paper, the authors report on experiments in which participants (college students) receive random private values at random times that last for a certain lifetime, after which the values are no longer available. During those lifetime intervals, if a buyer buys a unit of the asset, she can sell it later to the experimenter at the guaranteed private value, and analogously for the seller. The participants trade in a standard limit order market, using a continuous double auction mechanism. That part is not directly modeled in our optimization framework, that can be thought of as a stylized way to depict the actual experimental market. However, let us mention that, effectively, our traders behave as submitting limit orders, because they trade only when the price reaches a certain level. The only difference is that they also have an option to submit a market order at the end of their trading lifetime.

Even though it is unlikely that the participants will individually estimate the price process as a mean-reverting process and then try to find the optimal exercise time as in our model, our hope is that on an average the result of their trading would not be far away from the aggregate theoretical predictions.⁶

The aim of our exercise is to compute the LTCE price, denoted $\tilde{\theta }$. The following are the steps we use for this computation.

• We set the discount rate to zero, because our time interval is short: two hours.

• We observe transacted prices. We use these observations to estimate the parameters $\kappa ,\,\sigma$ and $\theta$ of the Ornstein–Uhlenbeck process, to get estimates $\hat{\kappa },\,\hat{\sigma }$, and $\hat{\theta }$, using the maximum likelihood procedure.⁷

• We pick an initial value $\tilde{\theta }_0$ for the LTCE.

• We discretize the range of the private values (whose distribution is uniform in those experiments), and use the discrete values as the strike prices.

• For each private value as the strike price, we compute critical exercise values $\underline{X}$ and $\overline{X}$.

• Assuming the initial asset price is equal to the initially chosen $\tilde{\theta }_0$, we compute the probabilities of buys and sells for different private values, using the formulas from the previous section.

• We estimate the expected number of buys by the number of buyers multiplied by the average of buy probabilities. If the expected number of buys is not sufficiently close to that of the sells, we change the value of $\tilde{\theta }_0$ in the appropriate direction and repeat the procedure, until those numbers become close to each other. The final value $\tilde{\theta }$ so obtained is our LTCE price.

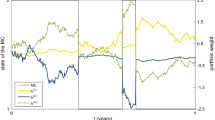
The results of this procedure are illustrated in Fig. 1. The figure shows the data generated by an experiment from Alton and Plott (2010) in which the distribution of the orders changed in the middle, which made the typical price values move up in the second part of the experiment. Also shown are the FCE and the LTCE for the two parts of the experiment. We see that those values, which make the expected number of buys and sells equal in the corresponding models, are not very different for this data set. That is, assuming no strategical behavior on the part of the participants (resulting in the FCE value) results in a competitive equilibrium value similar to that value when assuming that they optimally time the exercise of the option to trade using the OU model (resulting in the LTCE value). This is also confirmed by computing the root mean squared errors (rms) for LTCE and FCE: In the first period, rms is 30.65 for FCE and 30.16 for FTCE, and in the second period, rms is 62.34 for FCE and 64.86 for LTCE.

Fig. 1

Transaction prices from an Alton and Plott (2010) experiment and the corresponding FCE and LTCE. Duration of the experiment is 2 h, with first part lasting 71 min and the second 49 min. Buyer and seller arrival rates are 4/min. Lifetime of private values is 6 min, and their distribution is $U(52,451)$ for the first part and $U(273,672)$ for the second part

When computing the LTCE computed in Fig. 1, we used all the data points from the experiment (except for thirty initial trades for each part). We then computed the LTCE using only the first quarter of the data points, as well as using a half and three quarters of the data points. Remarkably, the LTCE value does not change much with the length of the sample, even though the statistical estimates of the parameters of the OU process change more significantly. See Tables 1 and 2 for more information. Here, $p=1/4$ means we only use the first quarter of data points (excluding the first thirty data points from the sample), and so on.

Table 1 Statistical estimates of the parameters of the OU process and the LTCE for the first part of the experiment

Table 2 Statistical estimates of the parameters of the OU process and the LTCE for the second part of the experiment

To reiterate, even though statistical estimation of the OU process parameters is somewhat unstable, the resulting LTCE value, which depends on that estimation, is quite robust. Combining with the fact that FCE is not that different from LTCE, one is tempted to infer that the notion of equilibrium based on the expected number of buys being equal to the expected number of sells is not very sensitive to the choice of the model. Whenever this is true for the trading venue at hand, then the question of how to decide whether to use FCE or LTCE (or LTCE based on some other model for the price process) becomes less important for estimation of the long-term price level. If this is generally correct, it is a good news for applications, but bad news in terms of deciding what exactly drives the traders’ behavior, at least when considering only the long-term price average.

5 Conclusions

We propose a model for trading an asset in a market with private reservation values, in which the traders decide optimally on the trade execution time. Assuming the market price follows a mean-reverting diffusion process, we find the equation for the optimal buy and sell levels, and expressions for the corresponding execution probabilities during a random interval of time. We then define long-term competitive equilibrium, LTCE, to be the value of the long-term stationary mean that makes the expected number of buys equal to the expected number of sells. The model is then fitted to the experimental data of Alton and Plott (2010). The data calibration results in a good fit of the model, with the prices in the experiment fluctuating around LTCE. Moreover, and somewhat surprisingly, unlike statistically estimated parameters of the price process, LTCE value is not very sensitive to the fraction of the sample we use to compute it.

While it would also be desirable to test the approach on real-market data, we cannot do such a calibration, because of the dependence on unknown private values. Let us mention that Lo et al. (2002), while performing a statistical analysis of the timing of limit orders, show that modeling trade execution times as passage times of a GBM process at a fixed level does not fit the market data well. In contrast, our price process is not a GBM process, but a mean-reverting process, and the trades are executed at varying passage times that are optimally decided by individual traders depending on their private values. Thus, it is a significantly richer model and might not be necessarily rejected by the actual market data.

In future research, it would be of interest to do “reverse engineering”—taking the observed orders as given, and finding the implied distribution of private values. The procedure would give a measure of the overall market sentiment during a chosen period of time, and this measure could be tested to see how well it depicts the actual mood changes over a sequence of time periods (assuming that the chosen model is a good fit to the market data).

Appendix

Proof of Proposition 3.1

As in Carr (1998), $P(X)$ is the Laplace transform of the standard American put price, and thus satisfies the ordinary differential equation (ODE)

$$\begin{aligned} \frac{\sigma ^2}{2}P''(X)+\kappa (\theta -X)P'(X)-rP(X)=\lambda \left[ P(X)-\left( K-e^X\right) ^+\right] ,\quad X>\underline{X}\nonumber \\ \end{aligned}$$

(6.1)

subject to the boundary conditions

$$\begin{aligned} \lim _{X\rightarrow \infty }P(X)=0,\quad \lim _{X\rightarrow \underline{X}}P(X)=K-e^{\underline{X}},\quad \lim _{X\rightarrow \underline{X}}P'(X)=-e^{\underline{X}} \end{aligned}$$

(6.2)

In the region $X>\log K\equiv \underline{X_0}$, the ODE is reduced to homogenous ODE

$$\begin{aligned} \frac{\sigma ^2}{2}P''(X)+\kappa (\theta -X)P'(X)-(r+\lambda )P(X)=0,\quad X>\underline{X_0} \end{aligned}$$

(6.3)

Introducing the change in variables

$$\begin{aligned} z=\dfrac{\sqrt{2\kappa }}{\sigma }(X-\theta ) \end{aligned}$$

and letting $P(X)=e^{z^2/4}\omega (z)$, Eq. (6.3) becomes

$$\begin{aligned} \omega ''(z)+\left( \frac{1}{2}-\nu -\frac{z^2}{4}\right) \omega (z)=0 \end{aligned}$$

(6.4)

with

$$\begin{aligned} \nu =(r+\lambda )/\kappa . \end{aligned}$$

The general solution of (6.4) can be represented as the linear combination of the so-called parabolic cylinder functions:⁸

$$\begin{aligned} \omega (z)=CD_{-\nu }(z)+ED_{-\nu }(-z). \end{aligned}$$

(6.5)

From $\lim _{X\rightarrow \infty }P(X)=0$, we get $E=0$. Therefore,

$$\begin{aligned} P(X)=Ce^{z^2/4}D_{-\nu }(z),\quad X>\underline{X_0}\equiv \log K \end{aligned}$$

(6.6)

In the region $\underline{X}<X<\underline{X_0}$, the solution can be written as the general solution plus a particular solution,

$$\begin{aligned} P(X)=A\phi (X)+B\psi (X)+Q(X), \end{aligned}$$

(6.7)

where $Q(X)$ is a particular solution that can be taken as in (3.8) (see, e.g., Johnson (2006)). From the boundary conditions Eq. (6.2) at $X=\underline{X}$ and using the continuity of $P(X)$ and $P'(X)$ at $X=\underline{X_0}$, it is not difficult to obtain $B=0$, and $A,\,C$, and $\underline{X}$ as in the statement of the proposition.

Proof of Proposition 3.2

Because the maturity date is exponential and independent of process $X$, we have

$$\begin{aligned} P_{min}(x~|~{\underline{X}},\lambda )&= \lambda \int \limits _0^\infty e^{-\lambda t} F_{\underline{X}}(x~|~t)~\hbox {d}t\end{aligned}$$

(6.8)

$$\begin{aligned}&= -\left[ F_{\underline{X}}(x~|~t) e^{-\lambda t}|_0^\infty -\int \limits _0^\infty e^{-\lambda t}f_{\underline{X}}(x~|~t)~\hbox {d}t\right] \end{aligned}$$

(6.9)

$$\begin{aligned}&= \int \limits _0^\infty e^{-\lambda t}f_{\underline{X}}(x~|~t)~dt\end{aligned}$$

(6.10)

$$\begin{aligned}&= \hat{f}_{\underline{X}}(x~|~\lambda ) \end{aligned}$$

(6.11)

Similarly,

$$\begin{aligned} P_{\mathrm{max}}(x~|~{\overline{X}},\lambda )=\hat{f}_{\overline{X}}(x~|~\lambda ). \end{aligned}$$

(6.12)

For our Ornstein–Uhlenbeck process $X$, function $p(x~|~y,t)$ satisfies the PDE

$$\begin{aligned} \frac{\partial p}{\partial t}=\kappa (\theta -x)\frac{\partial p}{\partial x}+\frac{\sigma ^2}{2}\frac{\partial ^2 p}{\partial x^2} \end{aligned}$$

(6.13)

with initial and boundary conditions $p(\infty ~|~y,t)=p(-\infty ~|~y,t)=0,\,p(x~|~y,0)=\delta (x-y)$. Taking the Laplace transform of Eq. (6.13), we get

$$\begin{aligned} \lambda \hat{p} -\delta (x-y)=\kappa (\theta -x)\frac{\mathrm{d}\hat{p}}{\mathrm{d} x}+\frac{\sigma ^2}{2}\frac{\mathrm{d}^2\hat{p}}{\mathrm{d}x^2} \end{aligned}$$

(6.14)

Therefore, we have

$$\begin{aligned} \hat{p}(x~|~y,\lambda )=\left\{ \begin{array}{l@{\quad }l} \psi (x)\phi (y), &{} y\ge x\\ \phi (x)\psi (y), &{} y\le x \end{array}\right. \end{aligned}$$

(6.15)

up to a constant factor. The result follows now from Theorem 3.1 in Darling and Siegert (1953).

Proof of Proposition 3.3

Note that we can write our Ornstein–Uhlenbeck process $X$ in the form

$$\begin{aligned} X(t)=xe^{-\kappa t}+\theta (1-e^{-\kappa t})+\sigma \int \limits _0^t e^{-\kappa (t-u)}~\mathrm{d}W(u) \end{aligned}$$

(6.16)

and that there is a Brownian motion $B(t)$ such that

$$\begin{aligned} \int \limits _0^t e^{\kappa u}\mathrm{d}W(u) = \frac{1}{\sqrt{2\kappa }}B(e^{2\kappa t}-1). \end{aligned}$$

(6.17)

Therefore, we have

$$\begin{aligned} X(t)=xe^{-\kappa t}+\theta (1-e^{-\kappa t})+\frac{\sigma }{\sqrt{2\kappa }}e^{-\kappa t}B(e^{2\kappa t}-1),~~X(0)=x \end{aligned}$$

(6.18)

It is then not difficult to show that the transition density is given by

$$\begin{aligned} p(x~|~y,t)=\sqrt{\frac{\kappa }{\pi \sigma ^2}\frac{1}{(1-e^{-2\kappa t)}}}\exp {\left\{ -\frac{\kappa }{\sigma ^2}\frac{\left[ y-xe^{-\kappa t}-\theta (1-e^{-\kappa t})\right] ^2}{1-e^{-2\kappa t}}\right\} }\nonumber \\ \end{aligned}$$

(6.19)

Buyer $i$ lives during random interval $[\tau ^B_i,\tau ^B_i+\Delta \tau ^B_i]$ with

$$\begin{aligned} Pr\{\tau _i^B\in \mathrm{d}t\}=\lambda _B e^{-\lambda _B t}\mathrm{d}t,\quad \quad Pr\{\Delta \tau ^B_i\in \mathrm{d}t\}=\rho _B e^{-\rho _B t}\mathrm{d}t \end{aligned}$$

(6.20)

Then, the probability that the minimum of $X(t)$ is less than $\underline{X}$ during a buyer’s lifetime is

$$\begin{aligned} \mathbf {P}_{\mathrm{min}}(x~|~\underline{X},\lambda _B,\rho _B)&= \int \limits _0^\infty \lambda _B e^{-\lambda _B\tau }~\hbox {d}\tau \nonumber \\&\times \left[ \int \limits _{\underline{X}}^\infty P_{\mathrm{min}}(y~|~\underline{X},\rho _B) p(x~|~y,\tau )~\mathrm{d}y+\int \limits _{-\infty }^{\underline{X}} p(x~|~y,\tau )~\mathrm{d}y\right] \nonumber \\&= \int \limits _{\underline{X}}^\infty \lambda _BP_{\mathrm{min}}(y~|~\underline{X},\rho _B)\hat{p}(x~|~y,\lambda _B)~\mathrm{d}y\nonumber \\&+\int \limits _{-\infty }^{\underline{X}}\lambda _B\hat{p}(x~|~y,\lambda _B)~\mathrm{d}y, \end{aligned}$$

(6.21)

where we use the fact that if $X(\tau _i^B)\le \underline{X}$, the buyer will make a transaction immediately after she enters the market, and if $X(\tau _i^B)\ge \underline{X}$, there is probability $P_{\mathrm{min}}(y~|~{\underline{X}},\rho _B)$ that $X(t)$ will hit $\underline{X}$ during the random period. The expression for $P_{\mathrm{min}}(y~|~{\underline{X}},\rho _B)$ follows from the previous section. The corresponding expression for the seller follows using the same method.

Next, we calculate the Laplace Transform of $p(x~|~y,t)$,

$$\begin{aligned} \hat{p}(x~|~y,\lambda )=\int \limits _0^\infty e^{-\lambda t}p(x~|~y,t)~\mathrm{d}t \end{aligned}$$

(6.22)

We know that $p(x~|~y,t)$ satisfies Kolmogorov equation

$$\begin{aligned} \frac{\partial f}{\partial t}=\kappa (\theta -x)\frac{\partial f}{\partial x}+\frac{\sigma ^2}{2}\frac{\partial ^2 f}{\partial x^2} \end{aligned}$$

(6.23)

subject to $f(\infty ~|~y,t)=f(-\infty ~|~y,t)=0$ and $f(x~|~y,0)=\delta (x-y)$. Taking Laplace transform on both sides of Eq. (6.23), we get

$$\begin{aligned} \lambda \hat{p}-\delta (x-y)=\kappa (\theta -x)\frac{\mathrm{d}\hat{p}}{\mathrm{d}x}+\frac{\sigma ^2}{2}\frac{\mathrm{d}^2\hat{p}}{\mathrm{d}x^2} \end{aligned}$$

(6.24)

Letting $z\equiv \dfrac{\sqrt{2\kappa }(x-\theta )}{\sigma }$ and $z_y\equiv \dfrac{\sqrt{2\kappa }(y-\theta )}{\sigma }$, Eq. (6.24) becomes

$$\begin{aligned} \frac{\mathrm{d}^2\hat{p}}{\mathrm{d}z^2}-z\frac{\mathrm{d}\hat{p}}{\mathrm{d}z}-\frac{\lambda }{k}\hat{p}=-\sqrt{\frac{2}{\kappa \sigma ^2}}~\delta (z-z_y) \end{aligned}$$

(6.25)

Imposing the boundary conditions, we get

$$\begin{aligned} \hat{p}=\left\{ \begin{array}{ll} Ae^{z^2/4}D_{-\nu }(z),\quad z\ge z_y\\ Be^{z^2/4}D_{-\nu }(-z),\quad z\le z_y \end{array}\right. \end{aligned}$$

(6.26)

From Eq. (6.25), we know that $\dfrac{d\hat{p}}{dz}$ cannot be continuous. Integrating both sides of Eq. (6.25) from $z_y^-$ to $z_y^+$, and because $\hat{p}$ is continuous, it is straightforward to get

$$\begin{aligned} \frac{\mathrm{d}\hat{p}}{\mathrm{d}z}({z_y^+})-\frac{\mathrm{d}\hat{p}}{\mathrm{d}z}({z_y^-})=-\sqrt{\frac{2}{\kappa \sigma ^2}} \end{aligned}$$

(6.27)

With Eq. (6.27) and $\hat{p}$ continuous, we get

$$\begin{aligned} \hat{p}(x~|~y,\lambda )=\left\{ \begin{array}{ll} \sqrt{\frac{2}{\kappa \sigma ^2}}e^{-z_y^2/4}\frac{D_{-\nu }(-z_y)}{D_{1-\nu }(z_y)D_{-\nu }(-z_y)+D_{1-\nu }(-z_y)D_{-\nu }(z_y)}e^{z^2/4}D_{-\nu }(z), \quad z\ge z_y\\ \sqrt{\frac{2}{\kappa \sigma ^2}}e^{-z_y^2/4}\frac{D_{-\nu }(z_y)}{D_{1-\nu }(z_y)D_{-\nu }(-z_y)+D_{1-\nu }(-z_y)D_{-\nu }(z_y)}e^{z^2/4}D_{-\nu }(-z), \quad z\le z_y \end{array}\right. \nonumber \\ \end{aligned}$$

(6.28)

with $\nu =\lambda /\kappa$. We can further simplify the answer by calculating $T(\nu ,z)\equiv D_{1-\nu }(z)D_{-\nu }(-z)+D_{1-\nu }(-z)D_{-\nu }(z)$. First, we prove $T(\nu ,z)$ is independent of $z$:

$$\begin{aligned} \frac{\mathrm{d} T(\nu ,z)}{\mathrm{d}z}&= D'_{1-\nu }(z)D_{-\nu }(-z)-D_{1-\nu }(z)D'_{-\nu }(-z)\nonumber \\&-D'_{1-\nu }(-z)D_{-\nu }(z)+D_{1-\nu }(-z)D'_{-\nu }(z)\nonumber \\&= D_{1-\nu }(z)\left[ -zD_{-\nu }(-z)+\nu D_{-\nu -1}(-z)\right] \nonumber \\&-D_{1-\nu }(-z)\left[ zD_{-\nu }(z)+\nu D_{-\nu -1}(z)\right] \nonumber \\&= D_{1-\nu }(z)D_{1-\nu }(-z)-D_{1-\nu }(-z)D_{1-\nu }(z)=0 \end{aligned}$$

(6.29)

Here, we use the recursion relation for parabolic cylinder functions,

$$\begin{aligned} D_{\nu +1}(z)-zD_{\nu }(z)+\nu D_{\nu -1}(z)&= 0\end{aligned}$$

(6.30)

$$\begin{aligned} D'_{\nu }(z)+\frac{1}{2} zD_{\nu }(z)-\nu D_{\nu -1}(z)&= 0 \end{aligned}$$

(6.31)

From these, it is also not difficult to get

$$\begin{aligned} T(\nu )=\nu T(\nu +1) \end{aligned}$$

(6.32)

(Note we dropped dependence on $z$ here.) Then, we have

$$\begin{aligned} T(\nu )=\frac{T(1)}{\Gamma (\nu )},\quad \nu >0, \end{aligned}$$

(6.33)

where $T(1)=\sqrt{2\pi }$. Plugging this result into Eq. (6.28), we get the stated expression for $\hat{p}$.