1 Introduction

It is well known that the count data show overdispersion (underdispersion) relative to the Poisson distribution for which variance equals the mean, although the phenomenon of underdispersion is uncommon. The overdispersion means that the variance is greater than the mean of a Poisson random variable having the same mean. The overdispersion can be caused due to various situations, for instance, due to having the heterogeneity in the data or due to having extra zeros than produced by the model. Mullahay (1997) has demonstrated that the unobserved heterogeneity commonly assumed to be the source of overdispersion in the count data models, have predictable implications for the probability structures of such models. One way to take care of the heterogeneity, is by way of mixture models. In the case of the Poisson distribution, the mean \(\theta \) of the Poisson distribution is considered as a random variable with an appropriate probability structure. The simplest choice of the distribution of \(\theta \) is the gamma density resulting in a negative binomial (NBD) distribution. Some generalizations of this concept have been studied by applying a generalized gamma distribution resulting in a generalized form of NBD, see Gupta and Ong (2004). Another choice of the distribution of \(\theta \) is taken as the inverse Gaussian or the generalized inverse Gaussian giving rise to Sichel distribution, see Ord and Whitmore (1986) and Atkinson and Yeh (1982). It is a long-tailed distribution that is suitable for highly skewed data. In addition to the choices mentioned above, various other mixing distributions have been used in the literature; see Gupta and Ong (2005) for more examples and illustrations.

Another way to analyze such data sets is to model with more general models having more than one parameter. For example, Consul (1989) had proposed a generalized Poisson distribution having two parameters and Gupta et al. (2004) have considered the zero-inflated generalized Poisson distribution with three parameters, one of which pertains to the extra zeros in the data than predicted by the generalized Poisson distribution.

More recently, the Conway–Maxwell Poisson (CMP) distribution is revived by Shmueli et al. (2005). This distribution is a two parameter extension of the Poisson distribution that generalizes some well- known discrete distributions (i.e., the binomial and the negative binomial distributions). The CMP distribution was originally proposed to handle queueing systems with state-dependent service rates.

The CMP distribution generalizes the Poisson distribution, allowing for overdispersion or underdispersion. Its probability function is given by

$$\begin{aligned} P(X=x)=\frac{\theta ^{x}}{(x!)^{\nu }} \cdot \frac{1}{Z(\theta ,\nu )},\quad x=0,1,2,\ldots , \end{aligned}$$
(1)

where

$$\begin{aligned} Z(\theta ,\nu )=\sum _{j=0}^{\infty }\frac{\theta ^{j}}{(j!)^{\nu }},\quad \theta >0,\nu >0. \end{aligned}$$
  1. 1.

    When \(\nu =1,\ Z(\theta ,\nu )=\exp (\theta ),\) an ordinary Poisson distribution.

  2. 2.

    As \(\nu \rightarrow \infty ,\ Z(\theta ,\nu )\rightarrow 1+\theta \), and the CMP distribution approaches a Bernoulli distribution with \(P(X=1)=\theta /(1+\theta ).\)

  3. 3.

    When \(\nu =0\) and \(0<\theta <1,\ Z(\theta ,\nu )\) is a geometric sum given by

    $$\begin{aligned} Z(\theta ,\nu )=\sum _{j=0}^{\infty }\theta ^{j}=\frac{1}{1-\theta }, \end{aligned}$$

    and the distribution is geometric with

    $$\begin{aligned} P(X=x)=\theta ^{x}(1-\theta ),\quad x=0,1,2,\ldots . \end{aligned}$$
  4. 4.

    When \(\nu =0\), and \(\theta \ge 1,\ Z(\theta ,\nu )\) does not converge and the distribution is undefined.

Shmueli et al. (2005) note that this distribution is appealing from a theoretical point of view as well because it belongs to the class of two parameter power series distribution. As a result, it allows for sufficient statistics and other elegant properties. Usually, many count tables correspond to the same sufficient statistics. Kadane et al. (2006a) investigated the number of solutions which give rise to the same sufficient statistics. Rodrigues et al. (2009) develop a flexible cure rate model assuming the number of competing causes of events of interest to follow CMP distribution. The Markov Chain Monte Carlo (MCMC) methods are used by Cancho et al. (2010) to develop Bayesian procedure for the CMP model. Bayesian analysis of the CMP distribution was also studied by Kadane et al. (2006b).

Although the CMP distribution is quite well researched, there are other aspects which have not been studied. Therefore, we shall develop some structural properties of (1) and study the monotonicity of its failure rate together with stochastic comparisons with the Poisson distribution in this paper. Since the additional parameter \(\nu \) controls the overdispersion or underdispersion, we develop the likelihood ratio test and the score test to test the importance of this additional parameter. The model (1) has overdispersion if \(\nu <1\) and underdispersion if \(\nu >1\). This fact can be checked using Theorem 3 of Kokonendji et al. (2008). The organization of this paper is as follows: In Sect. 2, we present some structural properties including the moments and the probability generating function. Section 3 deals with the reliability properties and some stochastic comparisons. In Sect. 4, we present the computation of moments and score equations to test the hypothesis that \(\nu =1\). Test for equidispersion and simulation study of power for the score and likelihood ratio tests are developed in Sect. 5. Two examples are presented in Sect. 6, one having overdispersion \((\nu <1)\) and the other having underdispersion \((\nu >1)\), to illustrate the procedure. In both the examples, it is shown that the CMP model fits slightly better than the generalized Poisson distribution. Finally, some conclusions and comments are presented in Sect. 7. Thus, the purpose of this paper is to present another versatile model which takes care of the overdispersion or underdispersion compared to the Poisson distribution, in analyzing discrete data.

2 Structural properties of the CMP model

2.1 Moments

To study the moments of our model, we notice that CMP distribution is a special case of the modified power series distribution introduced by Gupta (1974, 1975), as follows:

$$\begin{aligned} P(X=x)=\frac{A(x))(g(\theta ))^{x}}{f(\theta )},x\in B, \end{aligned}$$

where \(B\) is a subset of the set of non-negative integers, \(A(x)>0; \) \(f(\theta )\) and \(g(\theta )\) are positive, finite and differentiable functions of \(\theta .\)

In our case, \(g(\theta )=\theta ,\) \(f(\theta )=Z(\theta ,\nu )\) and \(A(x)=[(x!)^{\nu }]^{-1}.\) It can be verified that

$$\begin{aligned} E(X)&= \frac{g(\theta )f^{\prime }(\theta )}{f(\theta )g^{\prime }(\theta )}\\&= \theta \cdot \frac{\partial }{\partial \theta }[\ln Z(\theta ,\nu )]. \end{aligned}$$

2.2 Recurrence relations between the moments

Let \(\mu _{r}^{\prime }=E(X^{r}),\mu _{r}=E(X-\mu )^{r}\) and \(E(X^{[r]})=\mu ^{[r]},\) where \(\mu ^{[1]}=\mu _{1}^{\prime }=\mu \) and \(\mu ^{[r]}=E(X(X-1)(X-2)\ldots (X-r+1)).\)Gupta (1974) has shown that

$$\begin{aligned} \mu _{r+1}^{\prime }&= \frac{g(\theta )}{g^{\prime }(\theta )}\frac{d\mu _{r}^{\prime }}{d\theta } +\mu _{r}^{\prime }\mu _{1},\quad r=1,2,3,\ldots ,\end{aligned}$$
(2)
$$\begin{aligned} \mu _{r+1}&= \frac{g(\theta )}{g^{\prime }(\theta )}\frac{d\mu _{r}^{{}}}{d\theta }+r\mu _{2}\mu _{r-1},\quad r=1,2,3,\ldots ,\end{aligned}$$
(3)
$$\begin{aligned} \mu ^{[r+1]}&= \frac{g(\theta )}{g^{\prime }(\theta )}\frac{d\mu _{{}}^{[r]}}{d\theta }+\mu ^{[r]}\mu ^{[1]}-r\mu ^{[r]},\quad r=1,2,3,\ldots . \end{aligned}$$
(4)

As a special case, for our model

$$\begin{aligned} \mathrm{variance}&= \mu _{2}=\theta \frac{d\mu }{d\theta }\\&= \theta \cdot \frac{\partial ^{2}}{\partial \theta ^{2}}[\ln Z(\theta ,\nu )]. \end{aligned}$$

The recurrence relations given above can be used to obtain higher moments of the model.

2.3 Mode

To find the mode, we notice that for \(k\ge 2,\)

$$\begin{aligned} \frac{P(X=k)}{P(X=k-1)}=\frac{\theta }{k^{\nu }}. \end{aligned}$$

This means that as \(k\rightarrow \infty \), the above ratio \(\rightarrow 0.\) It has only one mode at the point \(k=1.\)

2.4 Probability generating function

$$\begin{aligned} \psi (t)=E(t^{X})=\frac{Z(\theta t,\nu )}{Z(\theta ,\nu )},0<t\le 1. \end{aligned}$$

The other generating functions viz. the characteristic function, the moment generating function, the factorial moment generating function and the cumulate generating function can be obtained using the probability generating function. Apart from the usefulness of the pgf in summarizing the probabilities or moments of the distribution, and in convergence results, the pgf has been applied in statistical inference; see, for instance, Rueda and O’Reilly (1999), Sim and Ong (2010) and Ng et al. (2013) and references therein.

3 Stochastic comparisons and reliability functions

3.1 Reliability functions

Let \(X\) be a discrete random variable whose mass is concentrated on the non-negative integers. Let \(p(t)=P(X=t).\) Then, the failure rate \(r(t),\) the survival function \(S(t)\) and the mean residual life function (MRLF) \(\mu (t)\) are given by

$$\begin{aligned} r(t)&= \frac{P(X=t)}{P(X\ge t)}=\frac{p(t)}{\sum _{i\ge t}p(i)},\quad t=0,1,2,\ldots ,\\ S(t)&= P(X\ge t)=\sum _{i\ge t}p(i),\quad t=0,1,2,\ldots , \end{aligned}$$

and

$$\begin{aligned} \mu (t)&= E(X-t|X\ge t)\\&= \frac{\sum _{i\ge t}ip(i)}{\sum _{i\ge t}p(i)}-t=\frac{\sum _{i>t} S(i)}{S(t)},\quad t=0,1,2,\ldots . \end{aligned}$$

The above functions \(p(t),r(t),S(t)\) and \(\mu (t)\) are equivalent in the sense that knowing one, others can be determined. This can be seen by the following relations.

$$\begin{aligned} r(t)=\frac{p(t)}{\sum _{i\ge t}p(i)}=\frac{S(t)-S(t+1)}{S(t)}=1-\frac{\mu (t)}{1+\mu (t+1)},\\ S(t)=\sum _{i\ge t}p(i)=\Pi _{i=0}^{t-1}(1-r(i))=\Pi _{i=0}^{t-1}\left[ \frac{\mu (i)}{1+\mu (i+1)}\right] , \end{aligned}$$

and

$$\begin{aligned} \mu (t)=\frac{\sum _{i\ge t}ip(i)}{\sum _{i\ge t}p(i)}-t=\sum _{i>t}\frac{S(i)}{S(t)}=\sum _{i>t}\Pi _{j=t}^{i-1}(1-r(j)). \end{aligned}$$

We now present the following definitions

Definition 1

A discrete life distribution has log-concave/log-convex probability mass function (pmf) if

$$\begin{aligned} \frac{p(t+2)p(t)}{[p(t+1)]^{2}}\le (\ge )1,\quad t\ge 0. \end{aligned}$$

Definition 2

A discrete life distribution has increasing failure rate/decreasing failure rate (IFR/DFR) if the failure rate is non-decreasing/non-increasing.

The following result, due to Gupta et al. (1997), establishes a relation between log-concavity (log-convexity) of the pmf and IFR (DFR) distributions.

Theorem 1

Let \(\eta (t)=1-P(X=t+1)/P(X=t)\) and \(\Delta \eta (t)=\eta (t+1)-\eta (t)=[p(t+1)/p(t)-p(t+2)/p(t+1)].\) Then,

  1. (i)

    If \(\Delta \eta (t)>0\) (log-concavity), then \(r(t)\) is non-decreasing (\(IFR).\)

  2. (ii)

    If \(\Delta \eta (t)<0\) (log-convex), then \(r(t)\) is non-increasing \((DFR)\).

  3. (iii)

    If \(\Delta \eta (t)=0\) for all \(t,\) then constant hazard rate.

In addition to the above, the following implications hold (for proofs, see Kemp (2004) and Gupta et al (2008)).

IFR (DFR) \(\Rightarrow \) DMRL (IMRL) where DMRL means decreasing mean residual life and IMRL means increasing mean residual life.

We now show that CMP distribution is log-concave.

Theorem 2

The CMP distribution has a log-concave pmf.

Proof

In this case

$$\begin{aligned} \Delta \eta (k)&= \frac{\theta }{(k+1)^{\nu }}-\frac{\theta }{(k+2)^{\nu }}\\&= \theta \left[ \frac{(k+2)^{\nu }-(k+1)^{\nu }}{(k+1)^{\nu }(k+2)^{\nu }}\right] >0. \end{aligned}$$

Thus, CMP distribution has a log-concave pmf and hence strongly unimodal, see Steutel (1985). \(\square \)

Using the relationships established above, we can say that CMP distribution is IFR and DMRL.

Remark 1

Kokonendji et al. (2008) showed the log-concavity of the CMP distribution for \(\nu \ge 1\) as a consequence of it being a weighted Poisson distribution where the weight function is log-concave only for \(\nu \ge 1\) (refer to Theorem 5 in their paper).

3.2 Stochastic comparisons

We present some definitions for stochastic orderings in the case of discrete distributions.

Definition 3

Let \(X\)and \(Y\) be two discrete random variables with probability mass functions \(\ f(x)\) and \(g(x).\) Then,

  1. 1.

    \(X\) is said to be smaller than \(Y\) in the likelihood ratio order (denoted by \(X\le _{lr}Y\)) if \(g(x)/f(x)\) increases in \(x\) over the union of the supports of \(X\) and \(Y.\)

  2. 2.

    \(X\) is smaller than \(Y\) in the hazard rate order (denoted by \(X\le _{hr}Y)\) if \(r_{X}(n)\ge r_{Y}(n)\) for all \(n.\)

  3. 3.

    \(X\) is smaller than \(Y\) in the mean residual life order (denoted by \(X\le _{MRL}Y)\) if \(\mu _{X}(n)\le \mu _{Y}(n)\) for all \(n.\)

See Shaked and Shanthikumar (2007) for more details and explanations.

The following theorem establishes the relationships between the above orderings.

Theorem 3

Suppose \(X\) and \(Y\) are two discrete random variables. Then, \(X\le _{lr}Y \Rightarrow X\le _{hr}Y\Rightarrow X\le _{MRL}Y\)

To compare the CMP distribution with the Poisson distribution, we let \(Y\) denote the Poisson variable and \(X\) denote the CMP variable. Then,

$$\begin{aligned} \frac{P(Y=n)}{P(X=n)}=\frac{(n!)^{\nu -1}Z(\theta ,\nu )}{e^{\theta }}, \end{aligned}$$

which is increasing in \(n.\) Thus, \(X\le _\mathrm{lr}Y.\) Using the above Theorem, we conclude that \(X\le _\mathrm{hr}Y\) and \(X\le _\mathrm{MRL}Y\)

4 Computation of moments and score equations

4.1 Computation of moments

The infinite sum \(Z(\theta ,\nu )\) is the normalization constant in the CMP probability mass function given by (1). The computation of \(Z(\theta ,\nu )\) for small \(\nu \) can be difficult. To overcome this difficulty, Minka et al. (2003) suggested a numerical approximation by truncating the series, that is,

$$\begin{aligned} Z(\theta ,\nu )\approx \sum _{j=0}^{k}{\frac{\theta ^{j} }{(j!)^{\nu } }}. \end{aligned}$$

Minka et al. (2003) also derived an asymptotic approximation of \(Z(\theta ,\nu )\) given as

$$\begin{aligned} Z(\theta ,\nu )={\frac{\exp (\nu \theta ^{1/\nu } )}{\theta ^{{\frac{\nu -1}{2\nu }} } (2\pi )^{{\frac{\nu -1}{2}} } \sqrt{\nu } }} (1+O(\theta ^{-{\frac{1}{\nu }} } )). \end{aligned}$$
(5)

The approximation expression for the moments, obtained from the asymptotic approximation of (5), is given by

$$\begin{aligned} E[X]&= \theta {\frac{\partial \log Z(\theta ,\nu )}{\partial \theta }} \approx \theta ^{{\frac{1}{\nu }} } -{\frac{\nu -1}{2\nu }},\end{aligned}$$
(6)
$$\begin{aligned} E[\log (X!)]&= -{\frac{\partial \log Z(\theta ,\nu )}{\partial \nu }} \approx {\frac{1}{2\nu ^{2} }} \log \theta +\theta ^{{\frac{1}{\nu }} } \left( {\frac{\log \theta }{\nu }} -1\right) . \end{aligned}$$
(7)

According to Minka et al. (2003), these approximations are good for \(\nu \le 1\) or \(\theta >10^{\nu }\), and they suggested a truncation approach to get more precise values. The accuracy of (7) can be improved by adding extra terms to get

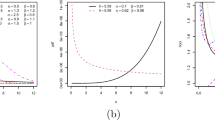
$$\begin{aligned} E[\log (X!)] \approx \frac{1}{2\nu ^2}\log \theta +\theta ^{\frac{1}{\nu }} \left( \frac{\log \theta }{\nu } -1\right) +\frac{1}{2\nu } +\frac{\log 2\pi }{2}. \end{aligned}$$
(8)

As no comparison of accuracy has been done, we examine the accuracy in the computation of (5), (7) and (8), with and without using the asymptotic approximation of \(Z(\theta ,\nu )\). This is presented in Table 1. The differences between the two quantities are given in italics. The partial derivatives of the infinite series \(Z(\theta ,\nu )\) are as follows:

$$\begin{aligned} \theta \frac{\partial \log Z(\theta ,\nu )}{\partial \theta } = \theta \frac{\displaystyle \sum \nolimits _{j=1}^{\infty } \frac{j\theta ^{j-1}}{(j!)^{\nu }} }{\displaystyle \sum \nolimits _{j=0}^{\infty } \frac{\theta ^{j}}{(j!)^{\nu }}},\end{aligned}$$
(9)
$$\begin{aligned} -\frac{\partial \log Z(\theta ,\nu )}{\partial \nu } = - \frac{\displaystyle \sum \nolimits _{j=2}^{\infty } \frac{-\theta ^{j}}{(j!)^{\nu }} \ln (j!)}{\displaystyle \sum \nolimits _{j=0}^{\infty } \frac{\theta ^{j}}{(j!)^{\nu }}}. \end{aligned}$$
(10)
Table 1 Comparison between moments obtained from asymptotic approximation (Asym) and infinite series (InfS) of \(Z(\theta ,\nu )\)
Full size table

Table 1 illustrates the discrepancy between the asymptotic approximation and infinite series for \(Z(\theta ,\nu )\). For \(E[X]\), the difference decreases when \(\nu \) increases for any \(\theta \). When \(\nu =1\), Eqs. (5) and (8) achieve the same value. On the other hand, for \(E[\log (X!)]\) Eq. (8) showed great improvement in accuracy over Eq. (7). Since the extra two terms in (8) are easily computed, the use of (8) over (7) is recommended.

4.2 Score equations

The log-likelihood function is given by

$$\begin{aligned} L=\, \sum _{x=0}^{\infty }\pi _{x} \ln P(X=x) , \end{aligned}$$

where \(\pi _{x}\) = observed frequency and \(\ln P(X=x) =x\ln \theta -\nu \ln (x!)- \ln {\displaystyle \sum \nolimits _{j=0}^{\infty } \frac{\theta ^{j}}{(j!)^{\nu } } }\).

The likelihood score equations of \(\theta \) and \(\nu \) are found to be

$$\begin{aligned} {\frac{\partial \ln P(X=x) }{\partial \theta }}&= \frac{x}{\theta } - \frac{\displaystyle \sum \nolimits _{j=1}^{\infty } \frac{j\theta ^{j-1}}{(j!)^{\nu }} }{\displaystyle \sum \nolimits _{j=0}^{\infty } \frac{\theta ^{j}}{(j!)^{\nu }}},\end{aligned}$$
(11)
$$\begin{aligned} \frac{\partial \ln P(X=x)}{\partial \nu }&= -\ln (x!) - \frac{\displaystyle \sum \nolimits _{j=2}^{\infty } \frac{-\theta ^{j}}{(j!)^{\nu }}\ln (j!) }{\displaystyle \sum \nolimits _{j=0}^{\infty }\frac{\theta ^{j}}{(j!)^{\nu }}}. \end{aligned}$$
(12)

The infinite sum under the CMP distribution, \(Z(\theta ,\nu )\) is calculated recursively with double precision and truncation of the series, that is, \(Z(\theta ,\nu )\le 1\times 10^{50} \). The recursive computation adopts the approach given in Lee et al. (2001). The simulated annealing (SA) algorithm (Metropolis et al. 1953) is used in the numerical optimization to obtain the maximum likelihood estimates required in the log-likelihood ratio test.

5 Test for dispersion

The CMP distribution reduces to the ordinary Poisson distribution with parameter \(\theta \) when \(\nu =1\). Since the parameter controls the under, equi and overdispersion of the distribution, we derive the Rao’s score test and the likelihood ratio test (LRT) to test the null hypothesis \(H_{0}{:\,}\nu =1\) against the alternative hypothesis \(H_{1} :\nu \ne 1\). The study of the statistical power of these two tests is developed and presented in this section. The brief introduction to Rao’s score test and LRT is given in Appendix.

In the simulation study of the power of the score and likelihood ratio tests, we consider the significance level \(\alpha \) at 5 and 10 % and samples of \(N =100\) (small), 500 (moderate) and 1,000 (large). The effect size (\(\left| \nu -1\right| \)) which serves as the index of departure from the null hypothesis, is set at 0.2, 0.5, 1.0, 3.0 and 4.0. It is found that 1,000 simulation runs give results of sufficient accuracy.

The results of the simulation study are presented in Tables 3, 4, 5 for \(\theta \) \(=\) 5 (short-tailed data), 10 (moderate-tailed data) and 20 (long-tailed data). Furthermore, the estimated empirical level for \(\theta \) \(=\) 1, 5, 7, 10 and 20 is studied and the results are presented in Table 6. In the tables, the power is number of rejection divided by number of repetitions.

The results in Tables 2, 3 and 4 are similar. The powers of the Rao’s score test and LRT are very close to each other when the sample size \(N\) is large enough (\(N\ge \mathrm {500}\)), for overdispersion (\(\nu <1\)) and underdispersion (\(\nu >1\)). For the case of equidispersion (Table 5, \(\nu =1\)), both tests have estimated empirical levels close to the specified significance levels of 5 and 10 %.

Table 2 Simulated power of Rao’s score and LR tests (\({\theta }=5\))
Full size table
Table 3 Simulated power of Rao’s score and LR tests (\({\theta }=10\))
Full size table
Table 4 Simulated power of Rao’s score and LR tests (\(\theta \)=20)
Full size table
Table 5 Estimated Empirical level of Rao’s score and LR tests (effect size = 0)
Full size table

The statistical power as shown in Tables 2, 3, 4 and 5 greatly depends upon the sample size and the effect size. As expected, the larger the sample size, the higher is the statistical power and the power increases with the deviation from \(\nu =1\). For overdispersion data, when the effect size is 0.5, a 100 % detection is achieved even for a small sample size of 100. When the sample size increases (\(N\ge \mathrm {500}\)), an effect size of 0.2 can be easily detected with a power close to 1. However, for underdispersion, a higher value of effect size and sample sizes is needed to achieve 100% detection. When \(N=100\), an effect size larger than 1.0 is required to detect the deviation from \(\nu =1\).

6 Application

To illustrate the application of the CMP distribution to data modeling, we consider the goodness-of-fit to data sets exhibiting under and overdispersion.

6.1 Example 1 (death notice data of London times)

The data consist of the number of death notices of women 80 years of age and older, appearing in the London Times on each day for three consecutive years. Hasselblad (1969) analyzed this data by mixture of two Poisson distributions. The counts are given below

$$\begin{aligned} \begin{array}{lllllllllll} \mathrm{Observed} &{}\quad 0 &{}\quad 1 &{}\quad 2 &{}\quad 3 &{}\quad 4 &{}\quad 5 &{}\quad 6 &{}\quad 7 &{}\quad 8 &{}\quad 9\\ \mathrm{Frequency} &{}\quad 162 &{}\quad 267 &{}\quad 271 &{}\quad 185 &{}\quad 111 &{}\quad 61 &{}\quad 27 &{}\quad 8 &{}\quad 3 &{}\quad 1\\ \end{array} \end{aligned}$$

The above data set was also analyzed by Gupta et al. (1996) by adjusting Poisson distribution for extra zeros. We have analyzed this data by CMP distribution and compared with the generalized Poisson distribution of Consul and Jain (1973). The results are given in the following Table 6. As can be seen, the index of dispersion is 1.21 and the estimated value of \(\nu \) using CMP distribution is 0.75 showing overdispersion relative to the Poisson distribution. The fit by the CMP distribution is much better than the generalized Poisson distribution in terms of Chi-square values. Using the CMP model, the hypothesis is rejected both by the LR test and the score test.

Table 6 Frequency distribution of death notice data of London times.
Full size table

6.2 Example 2

(Consul 1989, p. 131, Table 5.13) considers the number of discentrics per cell for 8 different doses and fitted GPD. We consider the following data (Dose 1200).

$$\begin{aligned} \begin{array}{lllllllllll} \mathrm{Observed} &{}\quad 0 &{}\quad 1 &{}\quad 2 &{}\quad 3 &{}\quad 4 &{}\quad 5 &{}\quad 6 &{}\quad 7 &{}\quad 8 &{}\quad 9\\ \mathrm{Frequency} &{}\quad 0 &{}\quad 4 &{}\quad 5 &{}\quad 23 &{}\quad 24 &{}\quad 38 &{}\quad 21 &{}\quad 10 &{}\quad 1 &{}\quad 4 \end{array} \end{aligned}$$

We have analyzed this data by the CMP and GPD distributions. The results are given in Table 7. As can be seen, the index of dispersion is 0.57 showing the underdispersion and the estimated value of for the CMP distribution is 1.813. Based upon the Chi-square values, the fit by the CMP distribution is better than the GPD distribution. Using the CMP model, the hypothesis is rejected both by the LR test and the score test.

Table 7 Frequency distribution of dicentrics for dose 1200
Full size table

7 Conclusion and comments

This paper deals with the problem of overdispersion (underdispersion) relative to Poisson distribution in analyzing discrete data. There are various ways of modeling such data sets including models having more than one parameter (for example, generalized Poisson distribution) or mixture models (negative binomial and their generalized forms). In this paper, we have presented another alternative, a CMP distribution which has one additional parameter \(\nu \), allowing for overdispersion \((\nu <1)\) and underdispersion \((\nu >1)\). Likelihood ratio test and score test are developed for testing \(H{:\,}\nu =1\). Simulation studies are carried out to examine the performance of these tests. Two examples are presented, one showing overdispersion and the other showing underdispersion. We hope that our investigation will be helpful to researchers modeling discrete data.