Introduction

Species diversity of phytoplankton is usually very high in natural aquatic ecosystems. Coexistence of many competitive species is extremely common in natural aquatic ecosystems (Hutchinson 1961 ; Ogawa and Ichimura 1984; Ogawa 1988). In spatially competitive communities, the coexistence of species is highly limited unless interspecific competition is weaker than intraspecific competition. Simulation studies usually exhibit the dominance of a single species, leading to the exclusion of all the rest (inferior species). At equilibrium, all but one species is persistent. This theoretical prediction (competitive exclusion) is often supported by the experimental results using chemostats (Tilman 1977, 1982; Takeya et al. 2004; Kuwata and Miyazaki 2000). Thus, local coexistence of multiple species is usually impossible without additional extrinsic factors. Many studies, therefore, proposed to include some extrinsic factors such as climatic changes, immigration, dormancy and spatial heterogeneity of habitats, and chaotic dynamics (Richerson et al. 1970; Levins 1979; Sommer 1985; Padisák et al. 1993; Huisman and Welssing 1999). Certainly the coexistence of two to three species has been shown in the systems with extrinsic factors. However, coexistence of four or more species is practically impossible due to the extremely sensitive tradeoffs between species. Thus, the coexistence of 10 or 100 species is totally out of question in these systems. Furthermore, such extrinsic factors seem to be not always applicable to aquatic systems. For example, spatial heterogeneity of microhabitats is difficult to imagine in aquatic ecosystems, because aquatic environment is homogeneous and the niches of phytoplankton are almost identical.

We build a lattice explicit model of multi-species competition with local interaction (“lattice Lotka–Volterra model or LLVM”; Tainaka 1988; Matsuda et al. 1992) and global interaction (Lotka–Volterra model, also called mean-field theory; Hofbauer and Sigmund 1988). In our model, competitive exclusion of all but one species is expected at the equilibrium state both in regards to local (Neuhauser 1992) and global interactions (Harris 1974). However, we only focus on the transient temporal dynamics in ecological time scales. We investigate the persistence of population in terms of spatial competition avoidance.

Methods

Lattice model

We consider a competitive ecosystem of ten planktonic algal species (i=1, ..., N=10); we apply a two-dimensional lattice (500×500), since phytoplankton distribute near the surface of the body of water and compete for light. Each lattice site is either occupied by i species (X i ) or empty (O). Overall reactions are as follows:

$${\text{X}}_{i} {\text{ }} + {\text{O}} \to 2{\text{X}}_{i} ,\quad {\text{rate: }}b_{i}$$
(1)
$${\text{X}}_{i} \to {\text{O,}}\quad {\text{rate: }}m_{i}$$
(2)

where X i is an individual (site) of species i of N species. The parameters b i and m i denote the rates of birth and death, respectively. The death rate is kept constant (m i =0.3) for all simulation runs. The simulation is carried out according to the contact process where interaction occurs between adjoining lattice sites (Harris 1974; Tainaka 1988; Marro and Dickman 1999).

When interactions are global, the two sites are chosen randomly from the whole lattice. In this case, the population dynamics of our system is given by the mean-field theory. Let x i be the overall density of species i. Since the probability of finding X i point becomes equal to overall density of X i , we have the following dynamics:

$$\frac{{{\text{d}}x_{i} }} {{{\text{d}}t}} = - m_{i} x_{i} + b_{i} x_{i} e$$
(3)

where i=1, ..., N, and e is the density of empty site (O). Note that \(e = 1 - {\sum\nolimits_i {x_{i} } }.\)

The first and second terms on the right-hand side of Eq. 3 denote death and birth processes, respectively. For example, we consider the cases of N=1 and N=2. When N=1, Eq. 3 becomes the logistic equation:

$$\frac{{{\text{d}}x_{1} }} {{{\text{d}}t}} = - m_{1} x_{1} + b_{1} x_{1} (1 - x_{1} ).$$
(4)

The non-zero steady-state density for this equation is given by; \(x_{1} = 1 - m_{1} /b_{1} .\)

In the two-species system (N=2), Eq. 3 can be rewritten as (i, j=1 or 2 and i≠j)

$$\frac{{{\text{d}}x_{i} }} {{{\text{d}}t}} = R_{i} x_{i} (K_{i} - x_{i} - a_{{ij}} x_{j} )/K_{i} .$$
(5)

Here the parameters satisfy the following relations:

$$R_{i} = b_{i} - m_{i} ,\quad K_{i} = \frac{{b_{i} - m_{i} }} {{b_{i} }},\quad a_{{ij}} = 1.$$
(6)

Equation 5 is called the Lotka–Volterra competition model, and its result is well known. Final stationary states are classified into four classes, depending on the values of parameters. Namely, (1) both X and Y coexist, (2) only X survives, (3) only Y survives, and (4) both become extinct. The condition for the coexistence is given by

$$K_{1} > a_{{12}} K_{2} \quad {\text{and}}\quad a_{{21}} K_{1} < K_{2} .$$
(7)

The above relations are not satisfied in our case (a=b=1). Hence, at least one species becomes extinct. In general, in the case of N>2, we can show that coexistence of two or more species is impossible.

Simulation procedure

The simulation procedures of local interaction are as follows:

  1. 1.

    Algal cells are distributed randomly over some of the square-lattice points in such a way that each point is occupied by only one species, if the point is occupied.

  2. 2.

    Each reaction process is performed in the following two steps.

    1. a.

      We perform the single body reaction (2). Choose one square-lattice point randomly. Let change the point to O with probability m i , if it is occupied by the species i.

    2. b.

      Next, we perform the two-body reaction (1). Select one point randomly and specify one of adjacent points. Here the adjacent site is set as the Neumann neighbors (four sites: up, down, left and right). If the selected pair is X i and O, then the latter point will become X i with probability b i . Here we employ periodic boundary conditions.

  3. 3.

    Repeat step 2 L×L times, where L×L is the total number of the square-lattice sites. Here we set L=500. This step is called a Monte Carlo step.

  4. 4.

    Repeat step 3 for a specific length (100,000 Monte Carlo steps).

The simulation procedures of global interaction are almost the same as those of local interaction. However, in the two-body reaction, step b in step 2, we select two lattice points randomly and independently.

Results

We first measure the steady-state density of a single species against birth rate (Fig. 1). For comparison, we determine the values of birth rates so that the steady-state densities (Fig. 1) become equal between local and global interactions.

Fig. 1
figure 1

Steady-state density vs. birth rate (b i ) in a single-species lattice ecosystem with local and global interactions. Death rate is kept at m=0.3. For local interaction, the steady-state density is estimated at around 20,000 Monte Carlo steps. The lattice size is 500×500 cells. The threshold value for positive density was b1≈0.49 for local interaction (b1=0.3 for global interaction). Below this value, the population becomes extinct. For global interaction, the density is calculated analytically. The two horizontal arrows indicate the comparative parameter conditions between local and global interactions under poor and rich nutritional conditions. When conditions are poor, b(local)=0.5, while b(global)=0.322. When conditions are rich, b(local)=0.9, while b(global)=0.786

Full size image

We simulate both low and high nutrient conditions (Fig. 2). In the low nutrient conditions (near extinction thresholds), the difference in the birth rates is kept small, since algal growth in natural oligotrophic waters is slow and the difference in the growth rates between species is considered small. In the high nutrient concentrations (high productivity), these differences are proportionally increased. In eutrophicated waters, we expect a high variation in species-specific growth rates.

Fig. 2
figure 2

Temporal dynamics of ten competitive species in the lattice competition model in ecological timescale under low and high growth rates. Low variable birth rates are assumed (b i =b+0.0001(i-1), where b=0.5 for local interaction and 0.322 for global interaction). High variable birth rates are assumed (b i =b+0.00018(i-1), where b=0.9 for local interaction and 0.786 for global interaction). The death rate is constant at m i =0.3. The density of each species is plotted for 20,000 Monte Carlo steps. a Local interaction with low growth rates. b Global interaction with low growth rates. c Local interaction with high growth rates. d Global interaction with high growth rates

Full size image

In low nutrient conditions, when interactions are local (Fig. 2a), the two most superior species (S10, S9) increase their density only slightly more than all of the rest of the species. In contrast, when interactions are global (Fig. 2b), the most superior species (S10) grows out of other species, followed by the second most superior species (S9). The average density of the surviving species is very low regarding local interaction, while it is relatively higher regarding global interaction (Fig. 2a, b).

Similarly, in high nutrient conditions, species stay together when interactions are local (Fig. 2c). Furthermore, the difference in birth rates is not exactly reflected in the order of species. From the third species, the order in density does not correspond with the order in growth rates. When interactions are global (Fig. 2d), the most superior species (S10) flourishes, reaching nearly 0.5 in density, while others move toward extinction. Thus the density profiles are almost similar in both high and low nutrient conditions (Fig. 2). When interactions are local, species stay together: none stand out (Fig. 2a, c). In contrast, when interactions are global, one species thrives while the others move toward extinction (Fig. 2b, d).

The extinction process of these dynamics is plotted as the number of species (Fig. 3). Extinction processes show that relatively inferior species become extinct when interactions are global (Fig. 3b, d). In contrast, when interactions are local with high birth rates, all ten species persisted during simulation runs. Even with low birth rates, nine species persisted and only one species became accidentally extinct, because low birth rates are close to the extinction boundary (Fig. 1). Thus, the persistence of species is extremely strengthened by local interactions.

Fig. 3
figure 3

Temporal changes in the number of persisting species with low and high growth rates in Fig. 2. a Local interaction with low growth rates. b Global interaction with low growth rates. c Local interaction with high growth rates. d Global interaction with high growth rates. Below local interaction (a and c), almost all species persist up to 20,000 time steps. When interactions are global (b and d), many inferior species become extinct in a short time

Full size image

To evaluate the species differences in birth rates, the densities of all ten species at 20,000 time steps are plotted for ten simulation runs under both local and global conditions in low nutrient conditions (Fig. 4). When interactions are local, most species persist with similar densities in all ten runs with slightly higher tendencies with superior species (Fig. 4a). In contrast, the superior species stands out from the others in all ten runs and all inferior species (S1 to S7) become extinct (Fig. 4b).

Fig. 4
figure 4

Densities of ten species at 20,000 Monte Carlo steps in regards to both local (a) and global (b) interactions. Parameter settings and simulation conditions are the same as in Fig. 2 for all ten simulation runs

Full size image

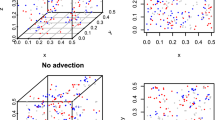
The spatial patterns in regards to local interactions exhibit strong clumping (Fig. 5). In high birth rates, species clumps are almost touching other species’ clumps (Fig. 5b), while, in low birth rates, species clumps are isolated/separated by a wide area of open cells (Fig. 5a). No competitive interactions are possible in low birth rates because of spatial separation.

Fig. 5
figure 5

Snapshots of a temporal pattern at 20,000 time steps in Fig.  2 . a Low growth rates. b High growth rates

Full size image

Discussion

The population dynamics in regards to local interaction are different from those when interactions are global (Figs. 2, 3). Regarding global interaction, a superior species “wins out” at the expense of the other species (Figs. 2b, d, 4b). However, when interactions are local, species tends to stay at almost similar densities: no single species stands out among the others (Figs. 2a, c, 4a). This means that the effective time scale is elongated by many orders of magnitude. This condition seems further elongated when the growth rates are lower. The temporal dynamics in regards to local interaction with low growth rates becomes extremely slow. Thus, in the ecological time scale, the coexistence of species is achieved when interactions are local with low growth rate conditions, even though the mathematical expectation (with infinite time horizon) is the exclusion of all but one superior species. With this system, coexistence of hundreds of species is easily achieved by simulation as long as the size of the lattice is large enough. This finite aspect of coexistence is markedly different from the traditional studies of coexistence based on equilibrium analysis (Marro and Dickman 1999).

It is well known that it is easy for a low density with a finite lattice to become extinct (Marro and Dickman 1999). However, our results show that extinction seems delayed considerably, due to the lack of actual competition (Fig. 2a). The snapshot of pattern indicates extreme clumping, resulting in a lack of competition (Fig. 5). One of the most important results of LLVM is the “divergence of the clumping degree” in a low density limit (Tainaka and Fukazawa 1992; Tainaka et al. 2004). Namely, the degree of clumping is universally inverse proportional to the density in lattice models.

Many models of coexistence have been suggested since the paradox of plankton was proposed (Hutchinson 1961). The current model is markedly different in terms of the following two points: (1) persistence based on the finite ecological time scale instead of the infinite mathematical equilibrium state, and (2) focus on the local interaction in contrast to global (random) interaction. These two features are very basic to communities and ecosystems. We also do not include specific external factors or a detailed kinetics such as chaotic fluid dynamics. From the natural observation (Ogawa and Ichimura 1984; Ogawa 1988), the biodiversity feature of phytoplankton is common and universal. Therefore, the mechanism for coexistence should not rely on highly specific factors such as chaotic flows or disturbance patterns. Rather, it is based on very common features which we have missed. In this sense, our model does not have any specific factors, but is based solely on very common features of any organisms. The only main difference is the combination of shifting the viewpoint of coexistence (transient vs. equilibrium states) and the realistic spatial nature of community—local (lattice) vs. global (random) interactions.

We should also note that the current model is also more advantageous than the previous models from the aspect of the number of coexisting species. In previous models, only a few (2–4) species are shown to coexist. It is almost definitely impossible for ten species to coexist in these systems. In our system, however, virtually 100 species can coexist for a long time, depending on the lattice size. Thus, there seems to be almost no limit to the biodiversity of plankton as observed in nature (Hutchinson 1961).

The mechanism of competition avoidance is very simple; the enhancement in the clumping degree originates in the fact that “offspring are located near their mother.” Our idea in this paper is based on the divergence behavior. If the nutritional conditions of a system is very poor, or if densities of species are very low, then segregation of habitats may occur. Therefore, in poor conditions, species can coexist for a very long period without actual competitive interactions (Liggett 1999). The poor nutritional condition when interactions are local maintains at least a high species diversity of phytoplankton. It may result in the paradox of enrichment (Rosenzweig 1971). The coexistence of plankton (Hutchinson 1961) thus becomes possible if the interactions are local as is expected in many natural aquatic systems.