HICC: an entropy splitting-based framework for hierarchical co-clustering

Abstract

Two-dimensional contingency tables or co-occurrence matrices arise frequently in various important applications such as text analysis and web-log mining. As a fundamental research topic, co-clustering aims to generate a meaningful partition of the contingency table to reveal hidden relationships between rows and columns. Traditional co-clustering algorithms usually produce a predefined number of flat partition of both rows and columns, which do not reveal relationship among clusters. To address this limitation, hierarchical co-clustering algorithms have attracted a lot of research interests recently. Although successful in various applications, the existing hierarchical co-clustering algorithms are usually based on certain heuristics and do not have solid theoretical background. In this paper, we present a new co-clustering algorithm, HICC, with solid theoretical background. It simultaneously constructs a hierarchical structure of both row and column clusters, which retains sufficient mutual information between rows and columns of the contingency table. An efficient and effective greedy algorithm is developed, which grows a co-cluster hierarchy by successively performing row-wise or column-wise splits that lead to the maximal mutual information gain. Extensive experiments on both synthetic and real datasets demonstrate that our algorithm can reveal essential relationships of row (and column) clusters and has better clustering precision than existing algorithms. Moreover, the experiments on real dataset show that HICC can effectively reveal hidden relationships between rows and columns in the contingency table.

1 Introduction

Two-dimensional contingency table arises frequently in various applications such as text analysis and web-log mining. Co-clustering algorithms have been developed to perform two-way clustering on both rows and columns of the contingency table. Traditional co-clustering algorithms usually generate a strict partition of the table [11, 12, 22]. This flat structure is insufficient to describe relationships between clusters. Such relationships are essential for data exploring in many applications related to document analysis.

To combine the advantages of both co-clustering and hierarchical clustering, various hierarchical co-clustering algorithms have been recently proposed [16, 17, 20, 33, 39]. However, existing hierarchical co-clustering algorithms are usually based on certain heuristic criteria or measurements for agglomerating or dividing clusters of rows and columns. Such criteria may be domain specific and lack of generality. Another limitation of many existing hierarchical co-clustering algorithms is that they often require the number of clusters (for both rows and columns) as an input. However, accurate estimation of the number of clusters may be a trivial task in many applications.

To overcome these limitations, we propose a hierarchical co-clustering algorithm with solid information-theoretic background. Our approach aims to generate the simplest co-cluster hierarchy that retains sufficient mutual information between rows and columns in the contingency table. More specifically, the mutual information between resulting row clusters and column clusters should not differ from the mutual information between the original rows and columns by more than a small fraction (specified by the user). Finding the optimal solution for this criterion, however, would take exponential time. Thus, we devise an efficient greedy algorithm that grows a co-cluster hierarchy by successively performing row-wise or column-wise splits that lead to the maximal mutual information gain at each step. This procedure starts with a single row cluster and a single column cluster and terminates when the mutual information reaches a threshold (defined as a certain percentage of the mutual information between the original rows and columns). Other termination criteria (such as the desired number of row/column clusters) can be easily incorporated.

In principle, we can construct a co-cluster hierarchy in either agglomerative (i.e. recursive grouping) or divisive (i.e. recursive splitting) manner. The rationale of having a divisive clustering algorithm is that a simple hierarchy with a small number of clusters is usually able to effectively retain most mutual information in the original contingency table in practice (as confirmed in our experiments). Thus, it is much more efficient to generate such hierarchy through recursive divisions.

The proposed hierarchical co-clustering algorithm has several desired properties.

• It builds cluster hierarchies on both rows and columns simultaneously. The relationships between clusters are explicitly revealed by the hierarchies. The hierarchical structures inferred by our approach are useful for indexing and visualizing data, exploring the parent–child relationships and deriving generation/specialization concepts.

• It uses an uniform framework to model the hierarchical co-clustering problem. The optimality of splitting the clusters is guaranteed by rigorous proofs.

• It does not require the prior knowledge of the number of row and column clusters. Instead, it uses a single input, the minimum percentage of mutual information retained, and automatically derives a co-cluster hierarchy. On the other hand, the proposed method can also incorporate optional constraints such as the desired number of clusters.

• It can explore the inherent hierarchy for both features and objects, which is very helpful for users to understand the inner, existing relationships among objects and features.

Experiments on both synthetic and real datasets show that our algorithm performs better than the existing co-clustering algorithms: (1) the leaf clusters of our hierarchies have better precision than co-clusters produced by previous algorithms and (2) our co-cluster hierarchies can effectively reveal hidden relationships between rows and columns in the contingency table, which cannot be achieved by any previous co-clustering algorithm.

2 Related work

Co-clustering methods aim to cluster both rows and columns of a data matrix simultaneously [2, 5, 8, 9, 15, 23, 27, 29, 32, 35, 37, 38, 40]. It has been studied extensively in recent years. These clustering algorithms usually generate flat partitions of rows and columns. However, a taxonomy structure can be more beneficial than a flat partition for many applications. In this section, we present a brief discussion of the recent co-clustering algorithms.

A pioneering co-clustering algorithm based on information theory was proposed in [12]. Taking the numbers of row and column clusters as input, the algorithm generates a flat partition of data matrix into row clusters and column clusters, which maximizes the mutual information between row and column clusters. In each iteration, the row clusters are adjusted to maximize the mutual information between row and column clusters followed by adjusting the column clusters in a similar fashion. It continues until there is no significant improvement in mutual information. The idea is further generalized into a meta algorithm [4]. It can be proven that any Bregman divergence can be used in the objective function, and the two-step iteration algorithm can always find a co-cluster by converging the objective function to a local minimum. A key difference between these methods and our method is that our method generates hierarchical cluster structures, which entails different objective functions and optimization techniques.

Linear algebra methods have also been applied to derive co-clusters. In [11], a co-clustering algorithm based on bipartite spectral graph partitioning was developed. Co-clustering is performed by singular value decomposition. A k-means algorithm is then applied on the calculated singular vectors to form $k$ clusters, where $k$ is pre-specified by the user. A co-clustering algorithm based on block value decomposition was proposed in [22]. It factorizes the data matrix into three components: row-coefficient matrix, column-coefficient matrix, and block value matrix. The final co-cluster is established according to the decomposed matrices.

Although these methods are different in the criteria employed in decomposing matrices, they all need the number of clusters as input. The conjunctive clustering method proposed in [24] does not require the number of clusters as input. However, the minimum size of the co-clusters is required, which is also hard to set. Moreover, when there are too many qualified co-clusters, only the best $k$ of them are reported. These $k$ best co-clusters cover the remaining qualified co-clusters but have little overlap with each other.

The clustering scheme of fully crossed association proposed in [7] adopts a data compression technique and does not require any input parameters. Because it favours lossy compression, the algorithm usually terminates with considerably more row (column) clusters than the actual number of clusters. Although they use a similar splitting procedure in order to approach the optimal number of clusters, the clusters are formed by reassignment of each individual row and column, which is analogous to the reassignment step in k-means clustering (rather than hierarchical clustering). A similar approach is also used in divisive information-theoretic clustering [10]. However, this method cannot be applied to cluster rows and columns simultaneously.

Hierarchical clustering [1, 3, 14, 18, 25, 26, 30, 31, 36] on one side of the matrix has been studied extensively and become a popular data analysis technique in many applications. In the following, we review several hierarchical clustering techniques that are closely related to our work.

The double clustering method in [34] is an agglomerative method. It considers the word–document dataset as a joint probability distribution. In the first stage, it clusters the columns into $k$ clusters by an agglomerative information bottleneck algorithm. Then, in the second stage, it clusters the rows while considering each generated column cluster as a single column. This method has been shown to be able to increase clustering accuracy in a number of challenging cases such as the noisy datasets. However, it has high computation cost due to the bottom-up approach in constructing the hierarchy. In [13], an extended algorithm, iterative double clustering (IDC), was presented, which performs iterations of double clustering. The first iteration of IDC is just a DC procedure. And starting from the second iteration, when columns are being clustered, the row clusters generated in the previous iteration are used as new rows. Both DC and IDC do not generate the row and column clusters simultaneously and rely on heuristic procedures with no guarantee on approximation ratio. Even though DC and IDC generate clusters using hierarchical method, the final clusters are still presented as flat partitions. It has been shown that co-clustering algorithms outperformed DC and IDC on word–document datasets [12, 22].

By integrating hierarchical clustering and co-clustering, hierarchical co-clustering aims at simultaneously constructing hierarchical structures for two or more data types [16, 17, 28]. A hierarchical divisive co-clustering algorithm is proposed in [39] to simultaneously find document clusters and the associated word clusters. Another hierarchical divisive co-clustering using n-Ary splits is proposed in [17, 28]. It has been incorporated into a novel artist similarity quantifying framework for the purpose of assisting artist similarity quantification by utilizing the style and mood clusters information [33]. Both hierarchical agglomerative and divisive co-clustering methods have been applied to organize the music data [20].

3 Preliminary

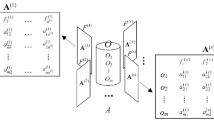
We denote the two-dimensional contingency table as $T$. $R=\{r_1,r_2,\ldots ,r_n\}$ represents the set of rows of $T$, where $r_i$ is the $i$th row. $C=\{c_1,c_2,\ldots ,c_m\}$ represents the set of columns, where $c_j$ is the $j$th column. The element at the $i$th row and $j$th column is denoted by $T_{ij}$. For instance, in a word–document table, each document is represented by a row and each word maps to a column. Each element stores the frequency of a word in a document. An example table consisting of four rows and four columns is shown in Table 1 on the left.

Table 1 (a): Example table, (b): normalized example table

We can compute a joint probability distribution by normalizing elements in the table. Let $X$ and $Y$ be two discrete random variables that take values in $R$ and $C$, respectively. The normalized table can be considered as a joint probability distribution of $X$ and $Y$. The table on the right in Fig. 1 shows the result of normalizing the example table on the left. We denote $p(X=r_i,Y=c_j)$ by $p(r_i,c_j)$ for convenience in the remainder of this paper.

Fig. 1

Left: synthetic contingency table. right:$I(\hat{X},\hat{Y})$ for each splitting step

A co-cluster consists of a set of row clusters and a set of column clusters. We denote the set of row clusters as $\hat{R}$,

$$\begin{aligned} \hat{R}=\left\{ \hat{r}_1,\hat{r}_2,\ldots ,\hat{r}_l|\hat{r}_i\subseteq {R},\hat{r}_i\cap \hat{r}_j=\emptyset , i\ne {j}\right\} \end{aligned}$$

where $\hat{r}_i$ represents the $i$th row cluster.

Similarly, we denote the set of column clusters as $\hat{C}$,

$$\begin{aligned} \hat{C}=\left\{ \hat{c}_1,\hat{c}_2,\ldots ,\hat{c}_k|\hat{c}_j\subseteq {C}, \hat{c}_j\cap \hat{c}_i=\emptyset , j\ne {i}\right\} \end{aligned}$$

where $\hat{c}_j$ represents the $j$th row cluster.

We denote the number of clusters in $\hat{R}$ as $L_{\hat{R}}=|\hat{R}|$, and the number of clusters in $\hat{C}$ as $L_{\hat{C}}=|\hat{C}|$.

Given the sets of row and column clusters, a co-cluster can be considered as a “reduced” table $\hat{T}$ from $T$. Each row (column) in $\hat{T}$ represents a row (column) cluster. Each element in $\hat{T}$ is the aggregation of the corresponding elements in $T$,

$$\begin{aligned} \hat{T}_{ij}=\sum \left\{ T_{uv}|r_u\in {\hat{r}_i}, c_u\in {\hat{c}_j}\right\} \end{aligned}$$

Let $\hat{X}$ and $\hat{Y}$ be two discrete random variables that take values in $\hat{R}$ and $\hat{C}$, respectively. A normalized reduced table can be considered as a joint probability distribution of $\hat{X}$ and $\hat{Y}$. We will denote $p(\hat{X}=\hat{r}_i,\hat{Y}=\hat{c}_j)$ by $p(\hat{r}_i,\hat{c}_j)$ for convenience. Using the above example (shown in Fig. 1), Table 2 shows the reduced table and normalized reduced table for the following co-cluster.

$$\begin{aligned} \hat{R}&= \left\{ \hat{r}_1,\hat{r}_2,\hat{r}_3\right\} \!, \hbox {where} \qquad \hat{r}_1=\{r_1\},\hat{r}_2=\{r_2,r_3\},\hat{r}_3=\{r_4\}\\ \hat{C}&= \left\{ \hat{c}_1,\hat{c}_2,\hat{c}_3\right\} \!, \hbox {where} \qquad \hat{c}_1=\{c_1\},\hat{c}_2=\{c_2,c_3\},\hat{c}_3=\{c_4\} \end{aligned}$$

Note that the original contingency table can be viewed as a co-cluster by regarding each single row (column) as a row (column) cluster. Given any co-cluster $(\hat{R}, \hat{C})$ on a contingency table, we employ the mutual information between $\hat{X}$ and $\hat{Y}$ to measure the relationship between row clusters and column clusters.

$$\begin{aligned} I(\hat{X}, \hat{Y})=\sum _{\hat{r}\in {\hat{R}}}\sum _{\hat{c}\in {\hat{C}}}p(\hat{r},\hat{c})\log _2\frac{p(\hat{r},\hat{c})}{p(\hat{r})p(\hat{c})} \end{aligned}$$

As we may observe, the mutual information of the original table $I(X, Y)$ is larger than the mutual information of the aggregated table $I(\hat{X},\hat{Y})$, due to clustering. This is in fact a property held by co-clustering described in Theorem 3.1.

Table 2 (a): Reduced table of a co-cluster, (b): normalized reduced table

In order to prove Theorem 3.1, we first prove the following lemmas based on the theorems proven by Dhillon et al [12].

Lemma 3.1

Given two co-clusters, $\{\hat{R}^{(1)},\hat{C}^{(1)}\}$ and $\{\hat{R}^{(2)},\hat{C}^{(1)}\}$, where $\hat{R}^{(2)}$ is generated by splitting a row cluster in $\hat{R}^{(1)}$. Then $I(\hat{X}^{(1)},\hat{Y}^{(1)})\le {I}(\hat{X}^{(2)},\hat{Y}^{(1)})$

Proof

Assume that $\hat{R}^{(2)}$ is generated by splitting $\hat{r}_1^{(1)}\in \hat{R}^{(1)}$ into $\hat{r}_1^{(2)}$ and $\hat{r}_2^{(2)}$. We have

$$\begin{aligned} I\left( \hat{X}^{(2)},\hat{Y}^{(1)}\right) -{I}\left( \hat{X}^{(1)},\hat{Y}^{(1)}\right)&= H\left( \hat{Y}^{(1)}|\hat{X}^{(1)}\right) -H\left( \hat{Y}^{(1)}|\hat{X}^{(2)}\right) \\&= -\,\sum _{\hat{c}^{(1)}\in \hat{Y}^{(1)}}p\left( \hat{r}_1^{(1)},\hat{c}^{(1)}\right) \log {p}\left( \hat{c}^{(1)}|\hat{r}_1^{(1)}\right) \\&\quad +\,\sum _{\hat{c}^{(1)}\in \hat{Y}^{(1)}} p\left( \hat{r}_1^{(2)},\hat{c}^{(1)}\right) \log {p}\left( \hat{c}^{(1)}|\hat{r}_1^{(2)}\right) \\&\quad +\,\sum _{\hat{c}^{(1)}\in \hat{Y}^{(1)}}p\left( \hat{r}_2^{(2)},\hat{c}^{(1)}\right) \log {p}\left( \hat{c}^{(1)}|\hat{r}_2^{(2)}\right) \end{aligned}$$

Because $\hat{r}_1^{(2)}\cup {\hat{r}_2^{(2)}}=\hat{r}_1^{(1)}$, we have

$$\begin{aligned} p\left( \hat{r}_1^{(1)},\hat{c}^{(1)}\right) =p\left( \hat{r}_1^{(2)},\hat{c}^{(1)}\right) +p\left( \hat{r}_2^{(2)},\hat{c}^{(1)}\right) \!, \forall {\hat{c}^{(1)}\in \hat{Y}^{(1)}} \end{aligned}$$

Therefore,

$$\begin{aligned} I\left( \hat{X}^{(2)},\hat{Y}^{(1)}\right) -{I}\left( \hat{X}^{(1)},\hat{Y}^{(1)}\right)&= \sum _{\hat{c}^{(1)}\in \hat{Y}^{(1)}}p\left( \hat{r}_1^{(2)},\hat{c}^{(1)}\right) \log \frac{p\left( \hat{c}^{(1)}|\hat{r}_1^{(2)}\right) }{p\left( \hat{c}^{(1)}|\hat{r}_1^{(1)}\right) }\nonumber \\&\quad +\,\sum _{\hat{c}^{(1)}\in \hat{Y}^{(1)}}p\left( \hat{r}_2^{(2)},\hat{c}^{(1)}\right) \log \frac{p\left( \hat{c}^{(1)}|\hat{r}_2^{(2)}\right) }{p\left( \hat{c}^{(1)}|\hat{r}_1^{(1)}\right) }\nonumber \\&= p\left( \hat{r}_1^{(2)}\right) D\left( p\left( \hat{c}^{(1)}|\hat{r}_1^{(2)}\right) ||p\left( \hat{c}^{(1)}|\hat{r}_1^{(1)}\right) \right) \nonumber \\&\quad +\,p\left( \hat{r}_2^{(2)}\right) D\left( p\left( \hat{c}^{(1)}|\hat{r}_2^{(2)}\right) ||p\left( \hat{c}^{(1)}|\hat{r}_1^{(1)}\right) \right) \nonumber \\ \end{aligned}$$

(1)

where $D(p(\hat{r}_1^{(2)},\hat{c}^{(1)})||p(\hat{r}_1^{(1)},\hat{c}^{(1)}))$ is the relative entropy (KL-divergence) between $p(\hat{c}^{(1)}|\hat{r}_1^{(2)})$ and $p(\hat{c}^{(1)}|\hat{r}_1^{(1)})$, which is always non-negative (by definition). Therefore,

$$\begin{aligned} I(\hat{X}^{(2)},\hat{Y}^{(1)})-{I}(\hat{X}^{(1)},\hat{Y}^{(1)})\ge {0} \end{aligned}$$

$\square$

Similarly, we have the following lemma.

Lemma 3.2

Given two co-clusters, $\{{\hat{R}}^{(1)},{\hat{C}}^{(1)}\}$ and $\{{\hat{R}}^{(1)},{\hat{C}}^{(2)}\}$, and ${\hat{C}}^{(2)}$ is generated by splitting one column cluster in $\hat{C}^{(1)}$. Then,

$$\begin{aligned} I\left( \hat{X}^{(1)},\hat{Y}^{(1)}\right) \le {I}\left( \hat{X}^{(1)},\hat{Y}^{(2)}\right) \end{aligned}$$

The above two lemmas state that splitting either row- or column-wise clusters increases the mutual information between the two sets of clusters. Hence, we can obtain the original contingency table (i.e. each row/column itself is a row/column cluster) by performing a sequence of row-wise splits or column-wise splits on a co-cluster. By Lemmas 3.1 and 3.2, the mutual information monotonically increases after each split, which leads to the following theorem.

Theorem 3.1

The mutual information of a co-clustering, $I(\hat{X},\hat{Y})$, always increases when any one of its row or column clusters is split, until the mutual information reaches its maximal value, $I(X,Y)$, where each row and column is considered as a single cluster.

Based on the previous results, we design a greedy algorithm that starts by considering the rows and columns as two clusters. In each iteration, the cluster that can increase $I(\hat{X},\hat{Y})$ most is split until $\frac{I(\hat{X},\hat{Y})}{I(X,Y)}$ is larger than a user-defined threshold or there are enough (row or column) clusters generated as user required. The monotonicity property of mutual information leads to the following problem definition.

Problem Definition Given a normalized two-dimensional contingency table, $T$, and a threshold $\theta (0< \theta < 1)$, find a hierarchical co-clustering containing a minimum number of the leaf row clusters $\hat{R}$ and leaf column clusters $\hat{C}$, such that the mutual information corresponding to co-clustering $\{\hat{R},\hat{C}\}$ satisfies $\frac{I(\hat{X},\hat{Y})}{I(X,Y)}\ge \theta$. Optionally, a user can specify desired number of row or column clusters ($L_{\hat{R}} = \hbox {max}_r$ or $L_{\hat{C}} = \hbox {max}_c$) and ask for a co-cluster with maximal mutual information.

4 The co-clustering algorithm

In this section, we present the details of our co-clustering algorithm. The monotonicity property of mutual information stated in Lemmas 3.1 and  3.2 inspires us to develop a greedy divisive algorithm that optimizes the objective function $I(\hat{X},\hat{Y})$ at each step. Our algorithm starts from a single row cluster (containing all rows) and a single column cluster (containing all columns). At each subsequent step, we perform the split that maximizes the mutual information $I(\hat{X},\hat{Y})$. Our algorithm takes local greedy partitioning strategy. The algorithm finds a co-cluster $\{\hat{R},\hat{C}\}$ by splitting one row or column cluster, which maximizes the increase in objective function in each iteration. The main routine is presented in Sect. 4.1. The method of finding a proper split of a cluster to maximize gain in $I(\hat{X},\hat{Y})$ will be discussed in Sect. 4.3.

Our co-clustering algorithm starts by considering all rows and all columns as two clusters. In each iteration, one of the clusters gets split into two sub-clusters. The method of splitting one cluster will be discussed in Sect. 4.3.

4.1 The main algorithm

The pseudocode of the algorithm is shown in Algorithm 1. In Step 1 of the main function Co-Clustering(), function InitialSplit() is called to generate the initial co-cluster $\{\hat{R}^{(0)},\hat{C}^{(0)}\}$ with two row clusters and two column clusters. In Step 2, the joint distribution $p(\hat{X},\hat{Y})$ of this initial co-cluster is calculated. Then, the algorithm goes through iterations. During each iteration, a split is performed to maximize the mutual information of the co-cluster. In Steps 5 and 6, each row or column cluster $s_i$ is examined by function SplitCluster() to determine the highest gain in mutual information, $\delta {I^{(k)}_i}$, which can be brought by an optimal split on $s_i$. ($s_{i1}$ and $s_{i2}$ denote the resulting clusters after split.) Steps 7 to 9 select the row or column cluster, whose split gives the highest gain $\delta {I^{(k)}_i}$, and perform the split. In Step 10, the joint distribution $p(\hat{X},\hat{Y})$ is updated according to the new co-cluster $\{\hat{R}^{(k+1)},\hat{C}^{(k+1)}\}$. The algorithm continues until the mutual information ratio $\frac{I(\hat{X},\hat{Y})}{I(X,Y)}$ reaches the threshold, $\theta$, and/or the number of clusters (row or column) reaches the number of desired clusters, denoted by $\hbox {max}_c$ and $\hbox {max}_r$. Note that the termination condition can be easily modified to suit users’ needs.

Before we discuss $\textit{InitialSplit}()$ and $\textit{SplitCluster}()$ in detail, we first illustrate the general procedure by an example. Given the normalized table in Table 3, InitialSplit() splits it into two row clusters and two column clusters:

Table 3 Normalized table $T$

$$\begin{aligned}&\hat{R}^{(0)}=\left\{ \hat{r}^{(0)}_1,\hat{r}^{(0)}_2\right\} ,\hat{r}^{(0)}_1=\{r_1,r_4\}, \hat{r}^{(0)}_2=\{r_2,r_3\}\\&\hat{C}^{(0)}=\left\{ \hat{c}^{(0)}_1,\hat{c}^{(0)}_2\right\} ,\hat{c}^{(0)}_1=\{c_1,c_4\}, \hat{c}^{(0)}_2=\{c_2,c_3\}\\&I^{(0)}\left( \hat{X}^{(0)},\hat{Y}^{(0)}\right) =0.722 \end{aligned}$$

During the first iteration, row cluster $\hat{r}^{(0)}_1$ is split

$$\begin{aligned}&\hat{R}^{(1)}=\left\{ \hat{r}^{(1)}_1,\hat{r}^{(1)}_2,\hat{r}^{(1)}_3\right\} \\&\hat{r}^{(1)}_1=\{r_1\},\hat{r}^{(1)}_2=\{r_4\},\hat{r}^{(1)}_3=\{r_2,r_3\}\\&\hat{C}^{(1)}=\hat{C}^{(0)}\\&I^{(1)}\left( \hat{X}^{(1)},\hat{Y}^{(1)}\right) =0.722 \end{aligned}$$

Note that $I(\hat{X},\hat{Y})$ remains the same. This is because it happens to be the case where no splits can increase $I(\hat{X},\hat{Y})$.

During the second iteration, column cluster $\hat{c}^{(1)}_1$ is split

$$\begin{aligned}&\hat{R}^{(2)}=\hat{R}^{(1)}\\&\hat{C}^{(2)}=\left\{ \hat{c}^{(2)}_1,\hat{c}^{(2)}_2,\hat{c}^{(2)}_3\right\} \\&\hat{c}^{(2)}_1=\{c_1\},\hat{c}^{(2)}_2=\{c_4\},\hat{c}^{(2)}_3=\{c_2,c_3\}\\&I^{(2)}\left( \hat{X}^{(2)},\hat{Y}^{(2)}\right) =0.923 \end{aligned}$$

The mutual information of the original table (Table 3) is $I(X,Y)=0.923$, which is equal to $I^{(2)}(\hat{X}^{(2)},\hat{Y}^{(2)})$. Therefore, co-cluster $\{\hat{R}^{(2)},\hat{C}^{(2)}\}$ retains 100 % of mutual information in the original table. The algorithm terminates.

4.2 Convergence of mutual information

A larger example may better demonstrate the trend of mutual information after each iteration. A synthetic contingency table is shown on the left side of Fig. 1. We plot $I(\hat{X},\hat{Y})$ after each step on its right side. $I(X,Y)$ of the original table (plotted with a dashed line) has the maximal value and serves as the upper bound of $I(\hat{X},\hat{Y})$ (plotted in solid line). As shown in Fig. 1, the mutual information $I(\hat{X},\hat{Y})$ approaches $I(X,Y)$ after our algorithm splits both rows and columns into four clusters. Note that in Step 1, the InitialSplit() function splits both rows and columns into two clusters as we will discuss in the next section.

4.3 Initial split

Function InitialSplit() splits the contingency table into two row clusters and two column clusters. In Step 1, the joint distribution is set to the normalized table $T$. In Step 2, all rows are considered as in a single row cluster $s_1$, and all columns are considered as in a single column cluster $s_2$. They are then split in Steps 3 and 4 by calling the function SplitCluster(). The initial co-cluster $\{\hat{R}^{(0)},\hat{C}^{(0)}\}$ and the corresponding mutual information $I^{(0)}=I(\hat{X}^{(0)},\hat{Y}^{(0)})$ are calculated accordingly in Steps 5 and 6.

Note that we split both row clusters and column clusters in this initial step. To ensure a good initial split, when the function SplitCluster() is called, we tentatively treat each row as an individual cluster so that the initial column clusters are created by taking into account the row distribution. By the same token, we also tentatively treat each column as an individual cluster when we create the initial row clusters.

The algorithm starts with one row cluster and one column cluster, and in the first iteration, one of the clusters gets split. However, it is easy to see that at the end of the first iteration, with a single cluster on one side and two clusters on the other side, objective function $I(\hat{X},\hat{Y})$ is always 0. Therefore, in order to get a proper initial splitting, in the initial step, when splitting the row cluster, each column is considered as a cluster itself and vice versa. In the algorithm, the initial splitting is separated from others, and it splits both columns and rows into two clusters to form the initial four clusters.

4.4 Cluster splitting

According to Lemmas 3.1 and 3.2, a split will never cause $I(\hat{X},\hat{Y})$ decrease. In addition, only the split cluster may contribute to the increase in $I(\hat{X},\hat{Y})$. Therefore, in each iteration in the main algorithm, all current clusters are tried to be properly split to maximize the increase in $I(\hat{X},\hat{Y})$ and the cluster that can achieve the maximal increase in $I(\hat{X},\hat{Y})$ by splitting is finally split. We will explain the details of function SplitCluster() in this section. As we proved in Theorem 3.1, the increase in $I(\hat{X},\hat{Y})$ only relates to the cluster being split. Suppose that a row cluster $\hat{r}^{(1)}$ is split into $\hat{r}^{(2)}_1$ and $\hat{r}^{(2)}_2$, the increase in $I(\hat{X},\hat{Y})$ is

$$\begin{aligned} \delta {I}&= I\left( \hat{X}^{(2)},\hat{Y}^{(1)}\right) -{I}\left( \hat{X}^{(1)},\hat{Y}^{(1)}\right) \\&= p\left( \hat{r}_1^{(2)}\right) D\left( p\left( \hat{c}^{(1)}|\hat{r}_1^{(2)}\right) ||p\left( \hat{c}^{(1)}|\hat{r}_1^{(1)}\right) \right) \!+\!p\left( \hat{r}_2^{(2)}\right) D\left( p\left( \hat{c}^{(1)}|\hat{r}_2^{(2)}\right) ||p\left( \hat{c}^{(1)}|\hat{r}_1^{(1)}\right) \right) \end{aligned}$$

Therefore, SplitCluster() can calculate the maximal value of $\delta {I}$ by examining each cluster to be split separately. However, it may still take exponential time (with respect to the cluster size) to find the optimal split. Therefore, SplitCluster() adopts a greedy algorithm that can effectively produce a good split achieving a local maximum in $\delta {I}$. Elements in the cluster are initially randomly grouped into two sub-clusters. For each sub-cluster, a weighted mean distribution is calculated to represent it by aggregating the distributions in the sub-cluster in an weighted way. A sequence of iterations is taken to re-assign each element to its closer sub-cluster according to KL-divergence until $\delta {I}$ converges.

The details of function SplitCluster() are shown in Algorithm 3. In Step 1, the joint probability distribution $p(\hat{X},\hat{Y})$ is transposed if the input cluster $s$ is a column cluster so that column clusters can be split into the same way as row clusters. In Step 2, cluster $s$ is randomly split into two clusters. In Step 3, $\delta {I}$ is calculated according to Eq. 1, and the weighted mean conditional distributions of $\hat{Y}$ for both clusters $s_1$ and $s_2$ ($p(\hat{Y}|s_1)$ and $p(\hat{Y}|s_2)$) are calculated according to Eq. 2.

$$\begin{aligned} p(\hat{X}=s_i)&= \sum _{x_j\in {s_i}}p(X=x_j)\nonumber \\ p(\hat{Y}|s_i)&= \sum _{x_j\in {s_i}}\frac{p(X=x_j)}{p(\hat{X}=s_i)}\cdot {p(\hat{Y}|x_j)} \end{aligned}$$

(2)

From Step 5 to Step 7, each element $x_i$ in cluster $s$ is re-assigned to the cluster ($s_1$ or $s_2$), which can minimize the KL-Divergence between $p(\hat{Y}|x_i)$ and $p(\hat{Y}|s_j)$. $p(\hat{Y}|s_1), p(\hat{Y}|s_2)$ and $\delta {I}$ are updated at the end of each iteration. The procedure repeats until $\delta {I}$ converges. In Step 9, the two sub-clusters, $s_1$ and $s_2$, and $\delta {I}$ are returned.

In order to prove that function SplitCluster() can find a split that achieves local maximum in $\delta {I}$, we need to prove that the re-assignment of element $x_i$ in Steps 4–8 can monotonically increase $\delta {I}$. Since the same principle is used to split row clusters and column clusters, without loss of generality, we only prove the case of splitting row clusters.

A similar cluster split algorithm was used in [10], which re-assigns elements among $k$ clusters. It is proven that such re-assignment can monotonically decrease the sum of within-cluster JS-divergence of all clusters which is

$$\begin{aligned} Q(\{s_1,s_2,\ldots ,s_k\})=\sum _{i=1}^k\sum _{x_j\in {s_i}}p(X=x_j)*{D\left( p(\hat{Y}|x_j)||p(\hat{Y}|s_i)\right) } \end{aligned}$$

In our function SplitCluster(), we only need to split the cluster into two sub-clusters. Therefore, we show the proof for a special case where $k=2$. The following lemma was proven in [10].

Lemma 4.1

Given cluster $s$ containing $n$ elements ($(\hat{Y}|x_i)$), the weighted mean distribution of the cluster ($(\hat{Y}|s)$) has the lowest weighted sum of KL-divergence of $p(\hat{Y}|s)$ and $p(\hat{Y}|x_i)$. That is, $\forall {q(\hat{Y})}$, we have

$$\begin{aligned} \sum _{i=1}^{n}p(x_i)\cdot {D}\left( p(\hat{Y}|x_i)||q(\hat{Y})\right) \ge {\sum _{i=1}^{n}p(x_i)\cdot {D}\left( p(\hat{Y}|x_i)||p(\hat{Y}|s)\right) } \end{aligned}$$

Theorem 4.1

When splitting cluster $s$ into two sub-clusters, $s_1$ and $s_2$, the re-assignment of elements in $s$ as shown in Steps 5–7 of function SplitCluster() can monotonically decrease the sum of within-cluster JS-divergence of the two sub-clusters $s_1$ and $s_2$.

Proof

Let $Q_{l}\{s_1,s_2\}$ and $Q_{l+1}\{s_1,s_2\}$ be the sum of within-cluster JS-divergence of the two clusters before and after the $l$th re-assignment of elements, respectively. And let $p_l(\hat{Y}|s_i)$ and $p_{l+1}(\hat{Y}|s_i)$ be the corresponding weighted mean conditional distributions of sub-clusters before and after the $l$th re-assignment. We will prove that $Q_{l+1}\{s_1,s_2\}\le {Q_{l}\{s_1,s_2\}}$. Assume that the two clusters after reassignment are $s^{*}_1$ and $s^{*}_2$.

$$\begin{aligned} Q_{l}\{s_1,s_2\}&= \sum _{i=1}^2\sum _{x_j\in {s_i}}p(X=x_j)\cdot {D\left( p(\hat{Y}|x_j)||p_l(\hat{Y}|s_i)\right) }\\&\ge \sum _{i=1}^2\sum _{x_j\in {s_i}}p(X=x_j)\cdot {D\left( p(\hat{Y}|x_j)||p_l(\hat{Y}|s^{*}_i)\right) }\\&= \sum _{i=1}^2\sum _{x_j\in {s^{*}_i}}p(X=x_j)\cdot {D\left( p(\hat{Y}|x_j)||p_l(\hat{Y}|s^{*}_i)\right) }\\&\ge \sum _{i=1}^2\sum _{x_j\in {s^{*}_i}}p(X=x_j)\cdot {D\left( p(\hat{Y}|x_j)||p_{l+1}(\hat{Y}|s^{*}_i)\right) }\\&= Q_{l+1}\{s_1,s_2\} \end{aligned}$$

The first inequality is a result of Step 6 in SplitCluster(), and the second inequality is due to Step 7 in SplitCluster() and Lemma 4.1. Therefore, we prove that the re-assignment of elements in $s$ can monotonically decrease $Q(\{s_1,s_2\})$.$\square$

Note that the sum of $\delta {I}$ and $Q(\{s_1,s_2\})$ is a constant, which is shown in Eq. 3.

$$\begin{aligned} \sum _{x_j\in {s}}p(x_j)D\left( p(\hat{Y}|x_j)||p(\hat{Y}|s)\right)&= \sum _{i=1}^2\sum _{x_j\in {s_i}}p(x_j)D\left( p(\hat{Y}|x_j)||p(\hat{Y}|s_i)\right) \nonumber \\&\quad +\,\sum _{i=1}^2p(s_1)D\left( p(\hat{Y}|s_i)||p(\hat{Y}|s)\right) \nonumber \\&= Q(\{s_1,s_2\})+\delta {I} \end{aligned}$$

(3)

Since the re-assignment process monotonically decreases $Q(\{s_1,s_2\})$, it will monotonically increase $\delta {I}$ as a result. Thus, function SplitCluster() can find a split that achieves local maximum in $\delta {I}$.

We now illustrate the function SplitCluster() with an example. The table in Table. 4 represents a row cluster to be split. Assume that the initial random split creates sub-clusters $s_1=\{x_1\}$ and $s_2=\{x_2,x_3,x_4\}$, then the weighted mean distributions of these two sub-clusters are

Table 4 A row cluster to be split

$$\begin{aligned} p(\hat{Y}|s_1)=[1, 0, 0, 0], p(\hat{Y}|s_2)=[0.1, 0.45, 0.45, 0] \end{aligned}$$

Then, for each element $x_i$, we calculate its KL-divergence with these two weighted mean distributions and re-assign it to the sub-cluster having the smaller value of KL-divergence.

$$\begin{aligned}&D\left( p(\hat{Y}|x_1)||p(\hat{Y}|s_1)\right) =0, D\left( p(\hat{Y}|x_1)||p(\hat{Y}|s_2)\right) =3.3\\&D\left( p(\hat{Y}|x_2)||p(\hat{Y}|s_1)\right) =28, D\left( p(\hat{Y}|x_2)||p(\hat{Y}|s_2)\right) =0.15\\&D\left( p(\hat{Y}|x_3)||p(\hat{Y}|s_1)\right) =28, D\left( p(\hat{Y}|x_3)||p(\hat{Y}|s_2)\right) =0.15\\&D\left( p(\hat{Y}|x_4)||p(\hat{Y}|s_1)\right) =0, D\left( p(\hat{Y}|x_4)||p(\hat{Y}|s_2)\right) =3.3 \end{aligned}$$

Only element $x_4$ is re-assigned to cluster $s_1$. The new sub-clusters are $s_1=\{x_1,x_4\}$ and $s_2=\{x_2,x_3\}$. If we repeat the process, the sub-clusters will not change any more.

4.5 Finding optimal $\theta$

Basically, the setting of $\theta$ is a non-trivial problem. A mechanism by which an appropriate value of $\theta$ can be determined within the capability of a clustering algorithm can be very useful. In this section, we provide a model selection method to determine an appropriate value of $\theta$ in the dataset due to Brunet et al. [6]. We emphasize that the consistency of the clustering algorithm with respect to random initial splitting is critical in successful application of this model selection method. In order to measure the consistency, a connectivity matrix is defined as follows. The connectivity matrix, $C_{\theta }\in {\mathbf {R}}^{n\times n}$ for $n$ data points, is constructed from each execution of a clustering algorithm. $C_{\theta }(i,j)=1$ if $i$-th data point and $j$-th data point are assigned to the same cluster, and 0 otherwise. Then, for given $\theta$, we can run the co-clustering algorithm several times and calculate the average connectivity matrix $\hat{C}_{\theta }$. Ideally, if each run obtains similar clustering assignments, elements of $\hat{C}_{\theta }$ should be close to either 0 or 1. Thus, we can define a general quality of the consistency by

$$\begin{aligned} \rho _{\theta }=\frac{1}{n^2}\sum _{i=1}^{n}\sum _{j=1}^{n}4\left( \hat{C}_{\theta }(i,j)-\frac{1}{2}\right) ^2 \end{aligned}$$

(4)

where $0\le \rho _{\theta }\le 1, \rho _{\theta }$=1 represents the perfectly consistent assignment. Hence, we can get value of $\rho _{\theta }$ for various $\theta$’s. Then, the appropriate value of $\theta$ could be determined by the value $\theta$ where $\rho _{\theta }$ drops.

5 Experimental study

In this section, we perform extensive experiments on both synthetic and real data to evaluate the effectiveness of our co-clustering algorithm. In Sect. 5.1, we run our co-clustering algorithm on a synthetic dataset with a hidden cluster structure to see whether our algorithm is able to reveal the clusters. In Sects. 5.3 and 5.4, we use real datasets for to evaluate our method. We compare the quality of the clusters generated by our method with those generated by previous co-clustering algorithms in Sect. 5.3. We use micro-averaged precision [12, 22] as the quality measurement. Besides the precision of the clusters, we also show the hierarchical structure of the discovered clusters in Sect. 5.4. Since we use a document-word dataset consisting of documents from different newsgroups, we demonstrate how the hierarchical structure reveals the relationships in document clusters and word clusters.

5.1 Experimental evaluation on synthetic data

We generated a $1{,}000\times 1{,}000$ matrix, which has value 1 for three matrices along the diagonal, each of which contains a sub-matrix of value 1.4, and 0 for the rest elements as shown in Fig. 2a. Then, we add noise into the matrix by flipping the value of each element with probability $p=0.3$ as shown in Fig. 2b. Before we run our algorithm, we permute the rows and columns randomly to hide the cluster structure, and the final synthetic data are shown in Fig. 2c. We run our co-clustering algorithm on the data with $\theta =0.7$ and get seven row clusters and eight column clusters as shown in Fig. 2d, which resemble the original co-cluster structure. The dendrogram of row and column clusters is shown along the axis.

Fig. 2

Experiment on synthetic data

5.2 Experimental settings on real dataset

In this section, we describe the experimental settings, which include the structure of the real data and the quality measurement.

Table 5 Subsets of 20 newsgroups used in Sect. 5.3

5.3 Real dataset

We downloaded the 20 Newsgroup dataset from UCI website.¹ The package consists of 20,000 documents from 20 major newsgroups. Each document is labelled by the major newsgroup in which it is involved. However, according to the detailed labels in the head section of each document, a document can also be involved in several minor newsgroups, which are not described in the 20 major newsgroups. Therefore, even for documents labelled by one newsgroup, they can be further divided by their minor newsgroups. These relationships can not be revealed by previous co-clustering algorithms that generate clusters in flat structure. We will see in Sect. 5.4 that, with the hierarchical co-clustering, documents in the same major newsgroup are further clustered into meaningful subgroups, which turn out to be consistent with their minor newsgroup labels.

We pre-process the 20 Newsgroup dataset to build the corresponding two-dimensional contingency table. Each document is represented by a row in the table, and 2,000 distinct words are selected to form 2,000 columns. Words are selected using the same method as in [34].

In order to compare the quality of clusters generated by our method with those of previous algorithms, we generate several subsets of the 20 Newsgroup dataset using the method in [12, 22, 34]. Each subset consists of several major newsgroups and a subset of the documents in each selected newsgroups. The details are listed in Table 5. As in [12, 22, 34], each of these subsets has two versions, one includes the subject lines of all documents and the other does not. We use $dataset_{s}$ and $dataset$ to denote these two versions, respectively.

In order to illustrate the effectiveness of the hierarchical structure of our clusters, we use two subsets of the 20 Newsgroup dataset in Sect. 5.4. The details are reported in Table 6. Subset Multi$5_1$ consists of the same newsgroups as in Multi5. However, Multi$5_1$ contains all documents in each newsgroup so that documents involved in different minor newsgroups can be included. All experiments are performed on a PC with 2.20 GHz Intel i7 eight-core CPU, and 8 GB memory. The running time of the proposed algorithm is 2.16 and 4.72 s on dataset $\textit{Multi}5$ and $\textit{Multi}5$, respectively.

Table 6 Subsets of 20 newsgroups used in Sect. 5.4

5.4 Quality measurement

To compare our algorithm with previous algorithms in [12, 22], we use the same quality measurement, micro-averaged precision, used by those algorithms.

For each generated row (document) cluster, its cluster label is decided by the majority documents in the cluster from the same major newsgroup. And a document is correctly clustered if it has the same label as the cluster. Assume that the total number of rows (documents) is $N$ and the total number of correctly clustered rows (documents) is $M$. The value of micro-averaged precision is $\frac{M}{N}$.

5.5 Comparison with previous algorithms

In this section, we compare our co-clustering algorithm with several previous algorithms. We use micro-averaged precision on the document clusters to measure the cluster quality since only documents are properly labelled in the dataset. For all the datasets, we set $\theta =0.7$ in our algorithm. Using $\textit{Multi}5_1$ dataset, we compare the results of different $\theta$’s in Fig. 3. We observed $\theta =0.7$ obtains the best clustering result.

Fig. 3

Comparison of the clustering results using different $\theta$’s on $\textit{Multi}5_1$

The state of the art hierarchical co-clustering algorithms used for comparison are as follows:

• NBVD [22]: Co-clustering by block value decomposition. This algorithm solves the co-clustering problem by matrix decomposition. It sets the number of row clusters to be the number of major newsgroups in datasets. The resulting clusters form a strict partition.

• ICC [12]: Information-theoretic co-clustering. This algorithm is also based on information-theoretic measurements and considers the contingency table as a joint probability distribution. It is a k-means clustering algorithm that generates exact $k$ disjoint row clusters and $l$ disjoint column clusters for given parameters $k$ and $l$.

• HCC [21]: a hierarchical co-clustering algorithm. HCC brings together two interrelated but distinct themes from clustering: hierarchical clustering and co-clustering. The former theme organizes clusters into a hierarchy that facilitates browsing and navigation, and the latter theme clusters different types of data simultaneously by making use of the relationship information between two heterogenous data.

• HiCC [17]: a hierarchical co-clustering algorithm produce compact hierarchies because it produces n-ary splits in the hierarchy instead of the usual binary splits. Thus, it is able to simultaneously produces two hierarchies of clusters: one on the objects and the other one on the features.

• Linkage [25]: a set of agglomerative hierarchical clustering algorithms based on linkage metrics. Four different linkage metrics were used in our experiments, i.e. Single-Link, Complete-link, UPGMA (average), WPGMA (weighted average). We used its build-in version in MatLab 7 to conduct the experiments.

There are other existing co-clustering/clustering algorithms, such as [13, 19, 34], which conducted experiments on the same subsets in Table 5. Since NVBD and ICC outperform these algorithms in terms of micro-averaged precision, we will not furnish a direct comparison with them. The fully crossed association co-clustering algorithm in [7] is not used in the comparison because its experiments were conducted on other datasets.

Both NVBD and ICC set the number of document clusters as the number of major newsgroups in the dataset, while our algorithm terminates when $I\{\hat{X},\hat{Y}\}$ is big enough ($I\{\hat{X},\hat{Y}\}/I\{X,Y\}\ge \theta$), which may generate slightly more clusters. Therefore, in addition to measuring the quality of the original clusters output by our algorithm, we also merge the document clusters into the same number of clusters as that from NVBD and ICC so that they can also be compared directly with each other. We consider each document cluster as a probability distribution over the word clusters. And we merge the clusters by calculating the relative entropy (KL-divergence) between them. In each step, we merge two document clusters, which have the minimal relative entropy of their distributions over word clusters. It is repeated until the remaining number of document clusters is equal to that in NVBD and ICC. For the Linkage algorithms, we set their number of clusters as same as the number of document clusters generated by our algorithm since both of them are hierarchical clustering algorithms.

For convenience, we use HICC to represent our algorithm and use m-pre to represent micro-averaged precision. For the number of word clusters, ICC generates about 60–100 word clusters as reported in [12], while our algorithm HICC generates about 50–80 word clusters. The number of word clusters generated by NVBD is not reported in [22]. While in the Linkage algorithms, since they only cluster the rows, each column can be considered as a column cluster.

The comparison of micro-averaged precision on all datasets in Table 5 is shown in Table 7. The average value of micro-averaged precision is computed based on 10 repeatedly runs of each experiment. In the table, the micro-averaged precision decreases slightly after we merge our original clusters into the same number of clusters as NVBD and ICC. This is because cluster merge may over-penalize the incorrectly labelled documents. Nevertheless, our algorithm is still the winner in all cases.

Table 7 Micro-averaged precision on subsets of 20 Newsgroup

The single-linkage metric has a very low precision comparing with all other algorithms. The reason may be that using the shortest distance between two clusters as the inter-cluster distance suffers from the high dimensionality and the noise in the dataset. Note that we so far only examine the leaf clusters of the rich hierarchy that our algorithm is able to generate. In the next section, we will show that, besides the cluster quality, our hierarchical structure reveals more information which previous algorithms cannot find.

5.6 Analysing hierarchical structure of clusters

In this section, we show that the hierarchical structure built by our algorithm provides more information than previous algorithms. Generally, there are two kinds of extra information in the hierarchical structure of document clusters.

• The relationship between major newsgroups. The major newsgroups of the 20 Newsgroup dataset can be organized in a tree structure according to their naming convention. The flat cluster structure in [12, 22] cannot reveal the information about the tree structure of newsgroups while our algorithm can capture these relationships.

• The relationship between documents in the same major newsgroup. As we mentioned, besides the major newsgroup label, each document can have several minor newsgroup labels. Therefore, documents in a major newsgroup can be further divided into several subgroups according to their minor labels. Our algorithm can partition the documents in one major newsgroup into meaningful subgroups.

In addition to the hierarchical structure of document clusters, our algorithm builds a hierarchical structure of word clusters at the same time. The relationships between word clusters, which were not found by previous co-clustering algorithms, are also provided in the hierarchical structure. We will use the two datasets in Table 6 for experiments in this section. Note that, although Linkage algorithms also generate a hierarchy of the row clusters, the structure is much larger and does not reveal the relationships correctly. Therefore, we do not present the hierarchy from Linkage algorithms in this section.

5.6.1 Hierarchical structure of multi$5_1$

The first dataset Multi$5_1$ consists of five major newsgroups. Our algorithm generates 30 document clusters and 39 word clusters. We represent the hierarchical structure in a tree format. Each final cluster corresponds to a leaf node in the tree, while intermediate clusters correspond to intermediate tree nodes. The root node corresponds to the cluster consisting of all documents. Each final cluster has an ID $c_i$, and the number in the circle underneath the node represents its label of major newsgroups. For each intermediate node, the newsgroup label is also given in the circle if majority of the documents in its sub-tree come from the same major newsgroup. The hierarchical structure of document clusters for Multi5$_1$ is shown in Fig. 4.

Fig. 4

Hierarchical structure of document clusters on Multi$5_1$. Each leaf node represents a cluster. Intermediate nodes represent the hierarchical structure. The label below the node represents the newsgroup that the cluster belongs to

We observe that (1) clusters labelled by 1 (talk.politics.mideast) are contained in two separate sub-trees; (2) clusters labelled by 3 and 4 (rec.motocycle and rec.sports.baseball) are contained in one sub-tree and are separated further down the tree; (3) clusters labelled by 2 and 5 (comp.graphics and sci.space) are contained in one sub-tree and are also separated later. This cluster separation makes sense. Newsgroups rec.motocycle and rec.sports.baseball are certainly close to each other since they share one keyword rec. For the rest newsgroups, both comp.graphics and sci.space relate to scientific techniques so that they are contained in one sub-tree. The newsgroup talk.politics.mideast is obviously most distant from the other four newsgroups. Figure 4 clearly demonstrates that the hierarchical structure of document clusters reveals relationships between the five major newsgroups.

Furthermore, the structure also reveals relationships of documents within a major newsgroup. Document clusters belonging to newsgroup talk.politics.mideast are separated into two sub-trees, each of which contains documents with different minor newsgroup labels. Note that all documents in this newsgroup share the same major newsgroup label talk.politics.mideast. Consider the following 3 clusters: $c8, c24$, and $c21$. Cluster $c21$ is far from $c8$ and $c24$, while $c8$ and $c24$ are more similar to each other. After checking the minor newsgroup labels for documents in these clusters, labels soc.culture.turkish and soc.culture.greek are found to play roles in this separation. Table 8 shows the number and the corresponding percentage of documents having these two minor newsgroup labels in each cluster.

Table 8 Absolute number and percentage of documents having the minor newsgroup label in each cluster

We observed soc.culture.turkish makes cluster $c21$ separated from $c8$ and $c24$, while soc.culture.greek makes $c8$ and $c24$ separated. This indicates that the hierarchical structure of document clusters reveals the relationship between documents in one major newsgroup via meaningful sub-clusters.

In addition to document clusters, our algorithm also builds hierarchical structure for word clusters. Since words do not have labels, we label each word cluster manually according to the five major newsgroups in the dataset. For those word clusters containing only general words, they are unlabelled. Table 9 lists nine of the word clusters. The words are sorted according to the scoring function in [34], and the top five words of each of these nine clusters are shown. The first row of each column contains word cluster ID, and the second row contains the cluster label which corresponds to the five major newsgroups.

Table 9 Labelled word clusters of Multi$5_1$

The word clusters appear to be meaningful. Word clusters $c6$ and $c11$ also correlate with the separation of document clusters $c8, c24$ and $c21$. Word cluster $c11$ has higher occurrence in both document clusters $c8$ and $c24$, while word cluster $c6$ has higher occurrence only in $c8$. Word clusters $c12$ and $c20$ have label $2 \& 5$ because the words in these two clusters are common scientific words, which could be used in both sci.space and comp.graphics newsgroups.

A truncated hierarchical structure of word clusters is shown by the left tree in Fig. 5 due to space limitation. In this structure, sub-trees in which majority of nodes sharing a single cluster label are represented by its top intermediate node and labelled by the dominating cluster. Nodes without a label represent sub-trees consisting of un-labelled (general) word clusters. We can make similar observations on the word cluster hierarchy as we did on document cluster hierarchy: (1) word clusters labelled by 1 are separated from other clusters, (2) word clusters labelled by 3 and 4 are in the same sub-tree, and (3) word clusters labelled by 2 and 5 are in another sub-tree.

For those word clusters containing general words, their positions in the hierarchical structure are also expected. For example, node 9 of the left tree in Fig. 5 represents word clusters related to talk.politics.mideast. Its sibling node contains general words related to politic topics, such as “national,” “human,” and “military”. Node 17 contains some general words, which are related to the labels of its sibling node 25, such as “driver”, “point,” and “time”.

5.6.2 Hierarchical structure of multi$4_1$

In the Multi5$_1$ dataset, two of the newsgroups share one keyword “rec” in the label. In Multi4$_1$, we add one newsgroup rec.sport.hockey so that three of the newsgroups share one keyword “rec” and furthermore, two of them share two keywords “rec.sport” in the label. With these more complicated relationships between newsgroups, the effectiveness of our algorithm can be seen in the hierarchical structure of clusters.

Because of space limitation, we only show a truncated hierarchical structure of document clusters by the tree on the right in Fig. 5, which is sufficient to show the effectiveness of our algorithm. The word clusters are similar to those of Multi5$_1$ and thus are omitted here.

Fig. 5

Left tree: a truncated hierarchical structure of word clusters on Multi$5_1$. Right tree: a truncated hierarchical structure of document clusters on Multi$4_1$

We observe in the right tree in Fig. 5 that clusters with label 4 are separated from others, while clusters with labels 1, 2, and 3 are in the same sub-tree. In the sub-tree under node 1, clusters with label 1 are separated from clusters with labels 2 and 3. This hierarchical structure correctly reveals the relationships between the four newsgroups.

The experiments in this section demonstrate that our hierarchical co-clustering algorithm reveals much more information including relationships between different newsgroups and relationships between documents in one newsgroup. This information cannot be found by previous algorithms such as NVBD and ICC. This advantage is in addition to the higher cluster quality than all competing algorithms.

6 Conclusions

In this paper, we present a hierarchical co-clustering algorithm based on entropy splitting to analyse two-dimensional contingency tables. Taking advantage of the monotonicity of the mutual information of co-cluster, our algorithm uses a greedy approach to look for simplest co-cluster hierarchy that retains sufficient mutual information in the original contingency table. The cluster hierarchy captures rich information on relationships between clusters and relationships between elements in one cluster. Extensive experiments demonstrate that our algorithm can generate clusters with better precision quality than previous algorithms and can effectively reveal hidden relationships between rows and columns in the contingency table.