High utility K-anonymization for social network publishing

Abstract

Privacy and utility are two main desiderata of good sensitive information publishing schemes. For publishing social networks, many existing algorithms rely on $k$-anonymity as a criterion to guarantee privacy protection. They reduce the utility loss by first using the degree sequence to model the structural properties of the original social network and then minimizing the changes on the degree sequence caused by the anonymization process. However, the degree sequence-based graph model is simple, and it fails to capture many important graph topological properties. Consequently, the existing anonymization algorithms that rely on this simple graph model to measure utility cannot guarantee generating anonymized social networks of high utility. In this paper, we propose novel utility measurements that are based on more complex community-based graph models. We also design a general $k$-anonymization framework, which can be used with various utility measurements to achieve $k$-anonymity with small utility loss on given social networks. Finally, we conduct extensive experimental evaluation on real datasets to evaluate the effectiveness of the new utility measurements proposed. The results demonstrate that our scheme achieves significant improvement on the utility of the anonymized social networks compared with the existing anonymization algorithms. The utility losses of many social network statistics of the anonymized social networks generated by our scheme are under 1 % in most cases.

1 Introduction

Social networks have been growing rapidly in recent years. More and more people start using online social network applications to communicate with their families, friends, and colleagues, etc.. The popularity of social networking is undeniable. Statistical studies show that social networking sites now reach 82 % of the worldwide online population, representing 1.2 billion users around the world. In October 2011, social networking ranked as the most popular content category in worldwide engagement, accounting for 19 % of all time spent online [7]. As people constantly share information through social networks, social networks have became important data sources of various domains, e.g., marketing, social psychology, and homeland security. On the one hand, it is beneficial to release social network data to the public for data mining and analysis activities. On the other hand, most real-world social network data contain sensitive information about the users. How to publish social network data without disclosing the privacy of the users becomes a realistic concern [2, 3, 18, 19, 31, 36, 39].

Among many social network-related privacy problems, the re-identification attack [19] is one of the most concerned. Given a social network modeled as an undirected graph $G$ with vertices representing individuals and edges representing connections among the individuals, a published (modified) version of $G$, denoted as $G^*$, suffers from the re-identification attack if any vertex $v$ in $G^*$ can be mapped to an individual in $G$. Existing researches have demonstrated that even though all unique identities (e.g., names, social security numbers) were removed, adversaries could still re-identify a vertex in a published social network with high confidence based on the topological structure around it, such as vertex degree (i.e., the number of connections), neighborhood, and subgraph.

To resist the structure-based re-identification attack, the notion of k-anonymity [29] has been widely adopted. By $k$-anonymity, every vertex in $G^*$ is made indistinguishable from at least $k-1$ other vertices. For example, if the degree of each vertex is considered to be known to the adversary, by inserting some fake edges and/or deleting some existing edges, we make at least $k$ vertices of the published social network share the same degree (i.e., $k$-anonymity in terms of the vertex degree). Thereafter, the probability that the adversary successfully re-identifies one vertex based only on the degree information will not exceed $1/k$.

Logically, a larger $k$ provides a stronger privacy protection, but it does come with a price. In an extreme case, a social network $G$ could be anonymized into a fully connected graph $G^*$, in which each vertex is connected to all the other vertices and all the vertices appear identical. However, $G^*$ actually loses all the structural properties of $G$ and hence is useless for data mining and analysis activities. The cost of the anonymization is quantified by the utility loss. Ideally, we prefer that the anonymized social network protects the privacy with the smallest utility loss, so that the data mining and analysis results derived from the anonymized social network are very similar to those from the original one. Although the utility issue in publishing tabular data has been well addressed [17, 18, 25], it is not fully studied in social network publishing.

1.1 Motivation and challenges

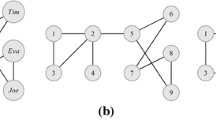
Most existing works anonymize a social network by performing edge insertion and/or deletion operations. They reduce the utility loss by minimizing the changes on the graph degree sequence (i.e., minimizing the $L_1$ distance). However, the degree sequence is a fairly simple graph model. It only captures limited structural properties of the graph. Thus, the utility model that solely aims at preserving the graph degree sequence in the anonymization algorithm may fail to safeguard many valuable graph properties. We demonstrate this observation using a simple example. Given a social network $G$ in Fig. 1a, three graphs $G^*_1, G^*_2$, and $G^*_3$ are formed that all satisfy 2-degree anonymity (i.e., there are at least two vertices sharing the same degree), as illustrated in Fig. 1b–d, respectively. $G^*_1$ and $G^*_2$ are formed by inserting an edge between vertices $f, h$ and vertices $c, h$, respectively, while $G^*_3$ is formed by deleting the edge between vertices $d$ and $e$. Existing works adopt the $L_1$ distance between the degree sequences (DSs) of the anonymized graph and the original graph as the measurement of the utility loss. With the degree sequences of $G, G^*_1, G^*_2$, and $G^*_3$ illustrated in the figures, respectively, we can easily observe that based on this common measurement, $G^*_1, G^*_2$, and $G^*_3$ cause the same utility loss. However, if considering other important graph structural properties, such as average path length (APL), average betweenness (BTW), clustering coefficient (CC), and average closeness (CLN), we find that these anonymized graphs actually have very different structural properties, as illustrated in Table 1. Among the three anonymized graphs, $G^*_1$ is the most similar one with the original graph $G$ in terms of APL, BTW, CC, and CLN, while $G^*_2$ and $G^*_3$ are much more different from $G$. Consequently, the simple graph degree sequence-based utility model cannot capture the utility differences among $G^*_1, G^*_2$, and $G^*_3$, and naturally the $k$-anonymization algorithms developed based on the simple graph degree sequence-based utility model might not be able to generate anonymized social networks with high utility.

Fig. 1

Examples of the 2-degree anonymity achieved by adding or deleting edges. a Social network $G$. b Published $G^*_1$. c Published $G^*_2$. d Published $G^*_3$

Table 1 Properties of the original and anonymized graphs

Motivated by the fact that most existing $k$-anonymization algorithms for social network publishing are mainly developed based on the simple degree sequence utility model and may cause significant utility loss, we want to design a new utility measurement based on more complex graph models to guide the anonymization process, then to generate high utility anonymized social networks. However, this is a challenging task due to the following issues. The first issue is that the usage of the published anonymized social network is unknown. The social network is a complex data structure and has many topological properties (utility), such as degree distribution, eigenvector, and clustering coefficient. Different applications may have different preferences toward which network properties should be preserved in the published network data. Moreover, there are many data mining tasks focusing on discovering unknown network properties. Therefore, we want to find an efficient measurement to capture many important network structural properties in general. The second issue is that the utility loss measurement needs to be quantitative and easy to calculate. In order to search for an optimal anonymized social network $G^*$ “closest” to the original social network $G$ in terms of the utility, we need to quantitatively evaluate the difference (utility loss) between $G$ and $G^*$ with high efficiency. There are some well-known metrics that represent the general structural features of $G$ to some degree, but they are difficult to calculate. For example, the average path length reflects the small-world properties of social networks, but the calculation is based on the expensive all-pair shortest path operation. Another example is the eigenvector, which has been proved to be strongly correlated with many network topological features. However, it requires expensive matrix decomposition to calculate the eigenvector, and re-calculation is necessary when edge operations are performed. The third issue is that the existing anonymization algorithms designed to minimize the utility loss based on the simple graph degree sequence model are not directly applicable to optimize the utility loss based on other new utility measurements, and new algorithms need to be developed accordingly.

1.2 Contributions

Optimizing the utility during the social network anonymization process is a challenging problem, and it cannot be perfectly solved in one effort. We take the initiative to explore this problem in this paper. We propose to build the utility loss measurement based on the community-based graph model instead of the simple degree sequence-based graph model. The community structure reflects locally inhomogeneous edge distribution among the vertices of the network, with high density of edges between vertices within communities and low density of edges between vertices from different communities. It is a central organizing principle of complex social networks and has strong correlation with many other important social network topological features such as betweenness, eigenvector, and clustering coefficient [27]. Thus, it captures the main topological features of a social network better than the simple degree sequence model. In addition, we try to minimize the impact of the edge operations to this community-based graph model during the anonymization process, so that we can generate an anonymized $G^*$ that is structurally similar to $G$ with respect to many important graph properties. The influence of the edge insertion or deletion operations during the anonymization process can be easily reflected by the changes on the edge distribution within or between communities, thus can be quantitatively evaluated.

To sum up, the main contributions of this work are fourfolded as listed in the following:

• 1. We identify the ineffectiveness of the common utility measurement adopted by many existing $k$-anonymization algorithms on preserving the structural features (i.e., utility) of the published social networks;

• 2. We propose new utility loss measurements built on the community-based graph models to better capture the impact of the anonymization process on the social network topology. We consider both the flat community model and the hierarchical community model.

• 3. We design a general framework to anonymize social networks and minimize the utility loss evaluated by our new measurements. This framework is general and can potentially be used with other utility models.

• 4. We conduct extensive experiments to verify the effectiveness and efficiency of our proposed approach. The results show that our scheme achieves significant improvement on the utility of the anonymized social networks compared with the existing anonymization algorithms. In most cases, our algorithm generates anonymized social networks with utility loss less than 1 % on many important network statistics.

The rest of the paper is organized as follows. Section 2 presents preliminaries. Section 3 details the community structure-based utility models, including a flat community model and a hierarchical community model. Section 4 presents a $k$-anonymization framework based on the described utility models. Section 5 provides privacy analysis of our scheme against the minimality attack and reviews-related works. Section 6 reports the experimental results. Finally, Sect. 7 concludes the paper.

2 Preliminaries

We model the social network as an undirected graph $G(V,E)$, where a vertex set $V$ represents entities (e.g., persons and organizations) and an edge set $E$ represents relationships between entities (e.g., friendship and collaboration). Notation $e(v_i,v_j)\in E$ represents an edge between two connected vertices $v_i$ and $v_j$. We use the notation $|S|$ to refer to the cardinality of a set $S$. For ease of presentation, we use “graph” and “social network” interchangeably in our discussion.

2.1 Structural re-identification attack

Social network publishing faces various challenges in privacy protection, and we only focus on the identity disclosure problem in this work. We assume that the entities’ identities in the original social network $G$ are sensitive, and hence, they should be hidden in a published social network $G^*$, as specified in Definition 1. An attacker, on the other hand, aims to identify some target entities as vertices in $G^*$ by using her background knowledge about the targets. We use $F$ to denote a background knowledge function that an attacker uses to determine the characteristics of an entity and $F(v)$ to represent the characteristics of an entity $v$ with respect to $F$. If $F$ is performed based on the graph structure, such as the number of connections of a vertex (called degree), neighborhood, and subgraph, we call this kind of attack structural re-identification attack, which is formally defined in Definition 2.¹

Definition 1

(Published social network) The published version $G^*(V^*, E^*)$ of a social network $G(V, E)$ is obtained by removing all the vertex identity information of $G$ and with possible structural modifications (e.g., edge and/or vertex insertion and/or deletion) ). $G^*(V^*, E^*)$ is published and used as $G$ for data mining and analysis activities.

Definition 2

(Structural re-identification attack) Given a social network $G(V,E)$, its published version $G^*(V^*, E^*)$, the background knowledge function $F$, and a target entity $v_t \in V$, the structural re-identification attack searches for all the vertices in $G^*$ that could provide the same result for $F$ as $v_t$, i.e., $V_{F(v_t)}=\{v\in V^*|F(v)=F(v_t)\}$. If $|V_{F(v_t)}|\ll |V^*|$, then $v_t$ has a high probability to be re-identified.

2.2 K-Anonymity and utility loss

$K$-anonymity is a widely adopted notion to prevent the structural re-identification attack on social networks [19, 31, 36, 38, 39], as formally defined in Definition 3.

Definition 3

($K$-Anonymity) Given a published social network $G^*(V^*, E^*)$ and the attacker’s background knowledge $F, G^*$ satisfy $k$-anonymity with respect to $F$, iff for each $v\in V^*$, there are at least $k-1$ other vertices $v^{\prime } \in V^*$ with $F(v^{\prime })=F(v)$.

Given a published $k$-anonymized graph with respect to the background knowledge $F$, assume that an attacker knows that there is an entity $v_t$ in the social network with the background knowledge $F(v_t)$. She performs the re-identification attack and finds $x$ vertices with the same $F$ value of $F(v_t)$. According to the $k$-anonymity notion, $x\ge k$. Without further information, the attack could not differentiate these $x$ vertices and the probability for her to identify $v_t$ among these vertices is $\frac{1}{x} \le \frac{1}{k}$. Therefore, the $k$-anonymity notion prevents the re-identification attack by providing an upper bound (i.e., $\frac{1}{k}$) to the re-identification probability. The higher the $k$ value is, the smaller the upper bound is and hence the lower the risk to the users privacy is. Please note that we need to specify the type of background knowledge $F$ that an attacker has in order to formally define $k$-anonymity (e.g., $k$-degree anonymity [19], $k$-neighborhood anonymity [36]). However, when the meaning of $F$ is clear in the context, we use $k$-anonymity in this paper for the brevity of presentation.

Various approaches have been proposed to anonymize a social network. In this work, we focus on the approaches based on edge modification, that is, to anonymize a graph via inserting and/or deleting edges. It is expected that an anonymized social network is structurally different from the original one, and hence it loses some utility compared with the original one. Ideally, social network publishing should take both the privacy and utility into consideration. In other words, $k$-anonymity-based social network publishing should publish social network $G^*$ that satisfies $k$-anonymity and meanwhile has as small utility loss as possible.

3 Utility measurement

Our goal in this work is to design a high utility social network anonymization scheme. Therefore, the key issue to address first is how to properly measure the utility loss of a published social network. As discussed in Sect. 1, the utility measurement based on the simple graph degree sequence model cannot capture many important social network topology changes. Hence, we want to design a more proper utility model that can better capture the complex social network structure properties.

In this work, we propose to build our utility loss measurement based on the community-based graph models. The community structure is a central organizing principle of many real social networks. Generally, it reflects locally inhomogeneous edge distribution among the vertices of a network, with high density of edges (i.e., strong connections) between vertices within one community and low density of edges (i.e., weak connections) between vertices from different communities. Given a fixed community organization, the influence of an edge insertion or deletion can be reflected by the changes on the edge distribution within or between communities. In addition, many researches have demonstrated that the community structure has a strong correlation with many other important topological features of social networks such as betweenness, eigenvector, and clustering coefficient [27]. Therefore, we believe that the impact of an anonymization process on the community organization also reflects its influence on other social network topological features. Our experimental study to be presented in Sect. 6 will further verify this point.

There are various ways to model social network communities [27]. In this paper, we consider both the flat community model and the hierarchical community model, and our utility loss measurement is built around the idea of measuring the edge distribution changes within and among the communities. Therefore, the anonymization algorithm designed to minimize the utility loss preserves the graph community structure via preserving the edge distribution among fixed community partitions. In the following subsections, we will introduce our utility models in detail.

3.1 Flat community-based utility model

First, we introduce a utility measurement based on the flat community model. The flat community model is defined as a non-overlapping partition of graph vertices, so that the vertices within one partition (community) are connected with edges of high density and the vertices from different communities are connected with edges of low density. Given a graph $G(V, E)$, we assume that the graph is divided into $m$ disjoint communities, denoted as $\mathcal C _G=\{C_1, C_2, \ldots , C_m\}$, such that $\forall v\in V$, there is one community $C_i$ containing $v$. For example, in Fig. 2, the social network $G$ is divided into 2 communities as indicated by the dash circles. Community $C_1$ contains vertices $\{a,b,c\}$, and $C_2$ contains $\{d,e,f,g,h\}$.

Fig. 2

An example of the flat community model

Here, we explain how to quantitatively measure the utility loss of a given modified (anonymized) graph $G^{\prime }(V^{\prime }, E^{\prime })$ based on the community model compared with the original graph $G(V,E)$. The algorithm used to generate communities will be introduced later. Suppose the community structure of a graph $G(V,E)$ is available, we can quantitatively capture the edge distribution within and among the communities via an edge distribution sequence, denoted as $ES$. To be more specific, we first count, i) for any community $C_i$, the number of edges that connect vertices within $C_i$, denoted as $n_{ii}$, and ii) for any pair of communities $C_i$ and $C_j$ $(i\ne j)$, the number of edges that connect vertices from $C_i$ to vertices from $C_j$, denoted as $n_{ij}$. Thereafter, the percentage of edges distributed within community $C_i$ is $\frac{n_{ii}}{|E|}$, and the percentage of edges distributed across $C_i$ and $C_j$ is $\frac{n_{ij}}{|E|}$. The edge distribution sequence $ES$ is then defined as $\left\langle \frac{n_{11}}{|E|}, \frac{n_{12}}{|E|},\ldots ,\frac{n_{ij}}{|E|}, \ldots , \frac{n_{mm}}{|E|} \right\rangle$, ($1\le i\le j\le m$). For instance, based on the community model of $G$ depicted in Fig. 2, there are 3 and 6 edges lying within community $C_1$ and community $C_2$, respectively, and one edge lying across them. Since the total number of edges in $G$ is $10, ES_G=\left\langle \frac{3}{10}, \frac{1}{10}, \frac{6}{10}\right\rangle$. Table 2 lists the $ES$s of the original graph $G$ and its three anonymized counterparts.

Table 2 Edge distribution sequence and utility loss based on the flat community model

Given an original graph $G$ and its modified (anonymized) version $G^{\prime }$, we assume their corresponding edge distribution sequences are $ES_G$ and $ES_{G^{\prime }}$, respectively. Compared with $G$, the utility loss caused by $G^{\prime }$, denoted as $UL(G,G^{\prime })$, is measured by the $L_1$ distance between $ES_G$ and $ES_{G^{\prime }}$, as defined in Equation (1). Using this utility loss measurement, we list the utility loss of all three anonymized graphs in Table 2. We observe that the anonymized graph $G^*_1$ causes the smallest utility loss. This is consistent with our observations made in Sect. 1.

$$\begin{aligned} UL(G,G^{\prime })=||ES_G - ES_{G^{\prime }}||_1=\sum _{1\le i \le m}{|ES_G[i]-ES_{G^{\prime }}[i]|} \end{aligned}$$

(1)

There are various community detection algorithms proposed in the literature. In this paper, we adopt the modularity-based method, one of the most popular community detection methods, to generate the flat community model. Modularity is a quality function defined based on null model to express the “strength” of the communities. By assumption, high values of modularity indicate good community partitions. To the interests of running time, we implement the greedy modularity maximization algorithm proposed by Newman [24]. It is an agglomerative clustering method, where groups of vertices (partitions) are successively joined to form larger communities. It starts with every vertex as one partition. Then, at each step, an edge is added to join the partition such that the maximum increase or minimum decrease in modularity w.r.t. the previous configuration can be achieved. The algorithm terminates until one unified partition is formed. Among all partition configurations generated at each step of this process, the one with the largest value of modularity is returned as the result. The complexity of the algorithm is $O((|V|+|E|)\times |V|)$, and it has been demonstrated to perform well on large social networks. However, we want to emphasize that our utility model is independent of the algorithm used for generating communities and any algorithm that can generate good community partitions is applicable.

3.2 Hierarchical community-based utility model

Besides the well-studied flat community structure, some recent studies suggest that the communities of social networks often exhibit hierarchical organization (i.e., large communities in a social network may contain small communities). The hierarchical communities capture the structure information of a social network from coarse to fine scale. Presumably, the graph model based on the hierarchical community organization provides more structure information of a graph. As a result, the utility measurement built upon the hierarchical community model is more sensitive to the small graph structure change caused by an anonymization process, thus provides a better control on the utility loss. In the following, we discuss how to measure the utility loss based on the hierarchical community model.

In this paper, we use the hierarchical random graph (HRG) model proposed in Clauset et al. [5, 6] to capture the hierarchical organization of the social network communities. An HRG of a graph $G(V, E)$ is a binary tree, denoted as $\mathcal{H }_G$. Its leaf nodes correspond to the vertices in $V$, and each of the non-leaf nodes $r$ roots a subtree denoted as $T_r$. The vertices in the subtree $T_r$ are regarded as a community $C_r$. Thus, $\mathcal H _G$ organizes the communities hierarchically.

Each non-leaf node $r$ of $\mathcal{H }_G$ is associated with a connection probability $p_r$. Here, $p_r$ is the probability that a vertex in the left subtree $T^L_r$ linked by an edge with a vertex in the right subtree $T^R_r$. The larger the $p_r$ is, the stronger the connection between $r$’s two subtrees is. Mathematically, the connection probability $p_r$ is defined in Equation (2).

$$\begin{aligned} p_r=\frac{|E_r|}{|T^L_r| \cdot |T^R_r|} \end{aligned}$$

(2)

where $|E_r|$ is the number of edges $e(v_i, v_j)\in E$ with $v_i \in T^L_r$ and $v_j \in T^R_r$, and $|T^L_r|$ and $|T^R_r|$ represent the numbers of vertices in $r$’s left and right subtrees, respectively. An HRG of the graph shown in Fig. 1a is depicted in Fig. 3. The connection probability $p_{r_4}$ of node $r_4$ is 1 as all the nodes in the left subtree (i.e., node $a$ and node $b$) connect to all the nodes in the right subtree (i.e., node $c$). On the other hand, the connection probability $p_{r_6}$ of node $r_6$ is $\frac{1}{3}$ as $|E_{r_6}|=|\{e(g,d), e(g,f)\}|=2, |T^L_{r_6}| = |\{e, d, f\}|=3$, and $|T^R_{r_6}|=|\{g,h\}|=2$.

Fig. 3

An example of the hierarchical community model

Given the HRG model of a graph, we observe that the edges of the graph actually distribute on all the non-leaf nodes $r_i$, i.e., $\cup _{r_i}E_{r_i}=E$. We then generate the edge distribution sequence $ES$ based on the edge distribution on these non-leaf nodes. Thus, $ES=\left\langle \frac{|E_{r_1}|}{|E|}, \frac{|E_{r_2}|}{|E|}, \ldots , \frac{|E_{r_m}|}{|E|}\right\rangle$, where $m$ is the total number of non-leaf nodes on $\mathcal H _G$. Again, we define the utility loss based on the $L_1$ distance of the $ES$s of the original and anonymized graphs. Table 3 lists the $ES$s of the original graph $G$ and its three anonymized versions based on the HRG model together with their corresponding utility loss. Consistent with our expectation, we find that $G^*_1$ causes the smallest utility loss. This simple example used in this paper is only able to demonstrate that the utility measurements based on the flat community model and the HRG model both have the potential to help to identify good anonymization options. We will conduct comprehensive experiments on real social networks to evaluate the performance of both community models in Sect. 6.

Table 3 Edge distribution sequence and utility loss based on the HRG model

Given a social network $G$, the optimal HRG that fits it can be determined using the Markov chain Monte Carlo method (MCMC) proposed in Clauset et al. [6]. It first defines a likelihood function $\mathcal{L }$ to evaluate the fitness of a given HRG $\mathcal H _G$ to $G$, with $\mathcal{L }(\mathcal H _G)$ $=$ $\prod _{r\in \mathcal H _G}\left[ p_r^{p_r}(1-p_r)^{1-p_r}\right] ^{|T^L_r| \cdot |T^R_r|}$. The higher this likelihood score is, the better the $\mathcal H _G$ captures the topological structure of $G$. Then, the MCMC method samples the space of all possible HRGs with the probability proportional to $\mathcal{L }$ and returns the one having the maximum $\mathcal{L }$ value. The MCMC method creates Markov chain by defining several transitions to transfer an HRG $\mathcal H _G$ to a new $\mathcal H ^{\prime }_G$. It calculates the logarithm of $\mathcal{L }$ of each HRG during sampling and accepts a transaction $\mathcal H _G\rightarrow \mathcal H ^{\prime }_G$ if $\Delta \log \mathcal{L } = \log \mathcal{L }(\mathcal H ^{\prime }_G) - \log \mathcal{L }(\mathcal H _G) \ge 0$. Otherwise, the transaction is accepted with probability $exp(\log \mathcal{L }(\mathcal H ^{\prime }_G) - \log \mathcal{L }(\mathcal H _G))$. In the worst case, the time complexity of the MCMC method is exponential. However, it is stated in Clauset et al. [6] that in practice, MCMC converges to plateau roughly after $O(|V|^2)$ steps.

4 HRG-based $K$-anonymization

After introducing the community-based graph models and the corresponding utility loss measurements, we are ready to present our high utility $k$-anonymization algorithm that anonymizes a given social network via edge operations with the utility loss as small as possible. In the following, we first present the basic idea of the algorithm and then detail its three main components, i.e., estimating local structure information, generating candidate edge operations, and refining the graph. Notice that although we only focus on $k$-degree anonymity in this section, our approach is general and it is applicable to other $k$-anonymity-based privacy protection schemes on social networks (e.g., $k$-neighborhood anonymity). We will briefly discuss how to adjust this approach to support $k$-neighborhood anonymity in Sect. 4.6.

4.1 Basic idea and algorithm framework

The $k$-anonymization problem on social networks is NP-hard.² Instead of searching for an optimal solution (i.e., a $k$-anonymized graph with the smallest utility loss) which is computationally expensive, in the paper, we design a greedy strategy that may derive suboptimal results. Following the works in the literature, we only consider achieving $k$-anonymity via performing a sequence of edge operations on the social network. As a result, the utility loss is affected by both the number of edge operations performed and the impact of each edge operation on the utility loss. Consequently, our greedy strategy is trying to approach the optimal solution by finding a short edge operation sequence to anonymize the social network with each edge operation causing a small utility loss. The basic idea of our algorithm is as follows. Given a graph $G$, the attack model $F$, and the privacy requirement $k$, we carefully perform one edge operation at a time on $G$ to approach $k$-anonymity against the attacks under $F$. On the one hand, to make the number of performed edge operations as small as possible, we choose the edge operation that directs the current $G$ toward its “nearest” $k$-anonymized graph. Here, “nearest” $k$-anonymized graph refers to the graph that satisfies $k$-anonymity with the smallest number of edge operations, which is denoted as $G^*$ to facilitate our explanation. On the other hand, among all the possible edge operations that can direct $G$ toward $G^*$, at each time, we perform the one which causes the smallest utility loss based on our utility loss measurement introduced in Sect. 3.

In this process, the knowledge of $G^*$ is essential, which, however, is unknown and hard to locate. Given the fact that forming $G^*$ directly is not always possible, we try to estimate $G^*$ to derive the local structure information of its vertices (e.g., the vertex degree and/or the neighbor degree of each vertex), which, based on the given graph $G, F$ and $k$, is possible. Then, according to the local structure information of $G^*$, a set of candidate edge operations leading $G$ toward $G^*$ can be generated and we always perform the one that causes the smallest utility loss first.

Algorithm 1 sketches a high-level outline of our high utility $k$-anonymization algorithm. It takes a graph $G$, the attacker’s background knowledge $F$, and the privacy parameter $k$ as inputs, and outputs a modified graph $G^{\prime }$ that is $k$-anonymized and meanwhile has small utility loss. Initially, the algorithm constructs and maintains a flat/hierarchical community model of $G$ as $M_G$ (line 1). Then, it sets $G^{\prime }$ to $G$ and sets the local structure information $LS^*$ as an estimation of $G^*$ based on $G, F$ and $k$ (lines 2–3). Thereafter, it generates a set of candidate edge operations (i.e., edge insertion operations or edge deletion operations) based on current $G^{\prime }$ and the estimated target $LS^*$. The candidate operations are maintained by a set $S_{op}$ together with the utility loss caused by each edge operation that is calculated based on the community model $M_G$ (line 5). At each step, our algorithm performs the edge operation, which causes the smallest utility loss on $G^{\prime }$, and then regenerates the candidate operation set based on the updated $G^{\prime }$ (lines 7–9). This process continues until $S_{op}$ becomes empty (lines 6–9). After performing all the identified candidate edge operations, there are two possible outcomes depending on whether the current $G^{\prime }$ is $k$-anonymized. If $G^{\prime }$ is $k$-anonymized, the algorithm terminates and returns $G^{\prime }$ as the result (line 12). Otherwise, $G^{\prime }$ does not satisfy the privacy requirement, i.e., the $k$-anonymized graph with the local structure information $LS^*$ is not achievable. We need to refine the target $LS^*$ via small adjustments and continue the previous process (line 11). We would like to point out that when refining the target $LS^*$, we only consider additive adjustment, which makes $LS^*$ changing toward the local structure of a complete graph. Thus, in the worst case, $G^{\prime }$ will be modified toward the complete graph, which always satisfies the privacy requirement (if $|V|\ge k$).³ Therefore, our algorithm is convergent.

In the following, we detail the three key components involved in Algorithm 1, i.e., estimating local structure information, generating candidate edge operations, and refining local structure information.

4.2 Estimating local structure information

Deriving local structure information of $G^*$ (i.e., the $k$-anonymized graph with the smallest number of edge operations) is essential as it sets up the target for our anonymization algorithm. In this section, we explain how this task is performed. As stated earlier, we only focus on the $k$-degree anonymity for presentation simplicity. Since the privacy requirement sets constraint on the vertex degree of the target anonymized graph, we estimate the degree sequence $DS^*$ as the local structure information of $G^*$. Degree sequence $DS$ of a graph $G(V, E)$ is a vector of size $|V|$ with each element $DS[i]\in DS$ representing the degree of vertex $v_i$ in $G$. We further assume the degree sequence is sorted by the non-ascending order of its elements (i.e., $DS[1]\ge DS[2]\ge \ldots \ge DS[|V|]$). There are some observations that can guide the estimation. First, $DS^*$ shares equal size with $DS$, because we only consider graph modification via edge operations but not vertex operations. Second, $DS^*$ must be $k$-anonymized since $DS^*$ is the degree sequence of a $k$-degree anonymized graph $G^*$. In other words, for each element $DS^*[i]\in DS^*$, there are at least $k-1$ other elements sharing the same value as $DS^*[i]$. Third, because that $DS^*$ is the degree sequence of the “nearest” $k$-anonymized graph $G^*$, the $L_1$ distance between $DS^*$ and $DS$ should be minimized. Based on the above observations, we employ the dynamic programming method proposed in Liu and Terzi [19] to find optimal $DS^*$ in $O(|V|^2)$ times. A greedy algorithm is also available in Liu and Terzi [19] with time complexity $O(k|V|)$. We ignore the detail because they are not the focus of our work.

4.3 Generating candidate edge operation set

Once $DS^*$ that represents the target local structure information is ready, we need to find candidate edge operations that can convert $G^{\prime }$ to a $k$-anonymized graph with its degree sequence matching $DS^*$. Before we introduce the detailed algorithm, we first define three basic types of edge operations, i.e., edge insertion, edge deletion, and edge shift, denoted as $ins(v_i, v_j), del(v_i, v_j)$, and $shift((v_i, v_j), (v_i,v_k))$. As suggested by their names, $ins(v_i, v_j)$ is to insert a new edge that links vertex $v_i$ to vertex $v_j$, and $del(v_i, v_j)$ is to remove the edge between $v_i$ and $v_j$. Operation $shift((v_i, v_j), (v_i,v_k))$ is to replace the edge $e(v_i, v_j)$ with edge $e(v_i, v_k)$. Notice that edges $e(v_i, v_j)$ and $e(v_i, v_k)$ of any edge shift operation are carefully selected so that the edge shift operation does not change the edge distribution of the constructed community model, thus causes zero change to the utility loss. For example, as shown in Fig. 2, $G$ is partitioned into two communities. Edge $e(c, d)$ is the crossing edge between these two communities. An edge shift operation $shift((c,d), (c,h))$ shifts the end point $d$ of this edge to vertex $h$. Since $d$ and $h$ are in the same community, there is still one edge lying between these two communities; thus, it does not change the edge distribution on the flat community model. The edge shift operation based on the flat community model is formally expressed in Definition 4. Similarly, the edge shift operation can also be defined on the hierarchical community model, as defined in Definition 5. Due to this unique feature, edge shift operations should receive a higher priority when modifying the graph to achieve $k$-anonymity.

Definition 4

(Edge shift on flat community model) Given a graph $G(V, E)$, the corresponding flat community model $\mathcal C _G$, an edge $e(v_i, v_j)\in E$, and a vertex $v_k\in V$ such that $e(v_i, v_k)\not \in E$, if $v_j$ and $v_k$ are in the same community, an edge shift $shift((v_i, v_j), (v_i,v_k))$ could be performed to replace $e(v_i, v_j)$ with $e(v_i, v_k)$.

Definition 5

(Edge shift on HRG) Given a graph $G(V, E)$, the corresponding HRG $\mathcal H _G$, an edge $e(v_i, v_j)\in E$, and a vertex $v_k\in V$ such that $e(v_i, v_k)\not \in E$, let $r$ be the lowest common ancestor of $v_j$ and $v_k$ on $\mathcal H _G$. If $v_i$ is not in the subtree of $r$, an edge shift operation $shift((v_i, v_j), (v_i,v_k))$ could be performed to replace $e(v_i, v_j)$ with $e(v_i, v_k)$.

The goal of the edge operations is to modify the graph, such that its new degree sequence $DS^{\prime }$ matches the target degree sequence $DS^*$. Consequently, the degree difference sequence $\delta =(DS^*-DS^{\prime })$ can give some guidance. Each element $\delta [i] \in \delta$ with $\delta [i]>0$ (i.e., $DS^{\prime }[i]<DS^*[i]$) indicates that a vertex in $G^{\prime }(V^{\prime },E^{\prime })$ with degree $DS^{\prime }[i]$ needs to increase its degree, i.e., it should have more edges connected to. We maintain $DS^{\prime }[i]$s with $\delta [i]>0$ via a set $DS^{+}$ and maintain all vertices $v \in V^{\prime }$ that have degree $DS^{\prime }[i]$ via a set $VS^+$, which includes all the vertices that may require edge insertion operation. Similarly, each element $\delta [j] \in \delta$ with $\delta [j]<0$ (i.e., $DS^{\prime }[j]<DS^*[j]$) indicates that a vertex in $G^{\prime }$ with degree $DS^{\prime }[j]$ needs to decrease its degree, i.e., it should have less edges connected to. We maintain $D^{\prime }[j]$s with $\delta [j]<0$ via a set $DS^-$ and maintain all the vertices $v \in V^{\prime }$ that have degree $DS^{\prime }[j]$ via a set $VS^-$, which includes all vertices that may require edge deletion operation. Notice that a degree value of $DS^{\prime }[i]$ or $DS^{\prime }[j]$ may correspond to multiple vertices in $G^{\prime }$, and we treat them equally in our work. In addition, if the degree $DS^{\prime }[i]$ ($DS^{\prime }[j]$) only appears once in $DS^+$ ($DS^-$), we cannot perform edge insertion (deletion) to connect (disconnect) two vertices $v_l, v_k$ both with the degree of $DS^{\prime }[i]$ ($DS^{\prime }[j]$), and hence, we mark these vertices mutual exclusive, denoted as $EX(v_l, v_k)=True$. The mutual exclusive set is formally defined in Definition 6.

Definition 6

(Mutual exclusive set) Given a difference sequence $\delta =(DS^*-DS^{\prime })$ of the target degree sequence $DS^*$ and the degree sequence $DS^{\prime }$ of the current graph $G^{\prime }(V^{\prime },E^{\prime })$, we define the degree set $DS^+=\{DS^{\prime }[i]\in DS^{\prime } | \delta [i]>0\}$ and the vertex set $VS^+=\{v_j\in V^{\prime } | \exists DS^{\prime }[i] \in DS^+, d(v_j)=DS^{\prime }[i]\}$ with $d(v_j)$ referring to the degree of the vertex $v_j$. Let $G_d =\{v_j|v_j \in VS^+ \wedge d(v_j) = d\}$ and $D_d=\{DS^{\prime }[i]|DS^{\prime }[i]\in DS^+\wedge DS^{\prime }[i]=d\}$. If $|D_d| = 1$, the set $G_d=\{v_1,v_2,\ldots , v_t\}$ is a mutual exclusive set, denoted as $\{v_1,v_2,\ldots , v_t\}_{EX}$ and each pair of vertices $v_l,v_k \in G_d$ is mutual exclusive to each other, denoted as $EX(v_l, v_k)=True$. The mutual exclusive set on $DS^-$ can be defined analogously.

Back to the graph $G$ depicted in Fig. 1a. Its degree sequence $DS$ and the target 2-degree anonymized degree sequence $DS^*$ are shown in Fig. 4. We derive $\delta =(DS^*-DS)=(0, 1, 0, 0, 0, 0, 0, 1)$ and find $\delta [2]=\delta [8]=1>0$. Hence, $DS[2] (=3)$ and $DS[8] (=1)$ are inserted into $DS^+$. Then, all the vertices in $G$ with degree being 3 or 1 are inserted into $VS^+$ ( $VS^+=\{c, f, g\, h$}). Notice that {$c, f, g$} is a mutual exclusive set. As there is no element of $\delta$ with its value smaller than 0, $DS^- = VS^- = \emptyset$.

Fig. 4

The degree sequence of $G$ and candidate operations

The reason that we form the $VS^+$ set and the $VS^-$ set is to facilitate the generation of candidate edge operations. As $VS^+$ contains those vertices that need larger degree, $ins(v_i, v_j)$ is a candidate operation, if $v_i, v_j (i\ne j)\in VS^+ \wedge e(v_i, v_j)\not \in E^{\prime } \wedge EX(v_i, v_j) \ne True$. We enumerate all the candidate edge insertion operations based on $VS^+$ and preserve them in a set $Op^{ins}$. Similarly, $del(v_i, v_j)$ is an candidate edge deletion operation, if $e(v_i, v_j)\in E^{\prime } \wedge v_i, v_j(i\ne j)\in VS^- \wedge EX(v_i, v_j) \ne True$. Again, we explore all the candidate edge deletion operations and preserve them in a set $Op^{del}$. We also consider the candidate edge shift operation. For a pair of vertices ($v_j, v_k$) ($j \ne k$) with $v_j\in VS^-\wedge v_k\in VS^+$, if there is a vertex $v_i, (i\ne j, k)$ such that $v_i, v_j$ and $v_k$ satisfy the condition in Definition 4 (or Definition 5 if the HRG model but not the flat community model is used), $shift((v_i, v_j),(v_i, v_k))$ is a candidate. All possible edge shift operations form another set $Op^{shift}$. We continue the above example shown in Fig. 4. As $VS^-=\emptyset$, we only need to consider possible edge insertion operations, i.e., $Op^{del}=Op^{shift}=\emptyset$. Based on $VS^+=\{c, f, g, h\}$ and the mutual exclusive set, we have $Op^{ins}=\{ins(c, h), ins(f, h)\}$.

Given all the candidate edge operations maintained in the operation sets $Op^{ins}, Op^{del}$, and $Op^{shift}$, respectively, we insert them into the candidate operation set $S_{op}$, which is used by the high utility $k$-anonymization algorithm (i.e., Algorithm 1). Before inserting the edge operations into $S_{op}$, we need to calculate the utility loss caused by each of them, so that the edge operation causing smaller utility loss will be performed earlier. Continue our example depicted in Fig. 4 with the utility loss calculated based on the flat community model in Fig. 3. The corresponding candidate edge operation set $S_{op}$ is set to $\{\langle ins(f, h), 0.0727 \rangle , \langle ins(c, h), 0.1636\rangle \}$. Algorithm 2 presents the pseudocode of finding candidate operations.

4.4 Refining target local structure information

As mentioned above, our high utility $k$-anonymization algorithm generates $DS^*$ that estimates the local structure information of the “nearest” $k$-anonymized graph as the target and performs edge operations to change the current graph toward $DS^*$. However, it is possible that the $k$-anonymized graph with degree sequence $DS^*$ is not achievable by the current executed operation sequence. If this happens, we fine-tune $DS^*$ and start another round of attempt. We prefer that the new target degree sequence is close to the old $DS^*$, and we only consider additive adjustments on $DS^*$ to ensure the convergence of our algorithm. Hopefully, the new target $DS^*$ will be achievable through our anonymization process.

In order to decide how to adjust $DS^*$, we first consider $VS^+$, which contains the vertices that have not been $k$-anonymized and need to increase their degrees. For any vertex $v_i$ in $VS^+$, we cannot find a vertex $v_j$ to form a valid $ins(v_i,v_j)$ operation to increase its degree according to the current $DS^*$. Therefore, we want to find an element on $DS^*$ to increase its value, so that later we could find the candidate operation that increases $v_i$’s degree. For each $v_i\in VS^+$, we find some vertices $v_j\in V$ $(i\ne j)$ that $e(v_i,v_j)\not \in E^{\prime }$, and $EX(v_i,v_j)\ne True$. These $v_j$s form the candidates of which we could increase the target degree on $DS^*$. We could randomly choose one among the candidate $v_j$s to increase its target degree by a small value (e.g., 1) on $DS^*$, but it may break the $k$-anonymity of $DS^*$. Therefore, instead of directly increasing the target degree of $v_j$ on $DS^*$, we increase the degree of $v_j$ on $DS$ and then we regenerate $DS^*$ based on the updated $DS$. As the changes made to $DS$ are very small, the new $DS^*$ should be very similar to the old one.

We only consider $VS^+$ above because we want to make additive change to $DS^*$. However, when $VS^+$ is empty, we have to utilize $VS^-$ that contains the vertices that have not been $k$-anonymized and need to decrease their degrees. Similar to above, for a vertex $v_i\in VS^-$, we could find a vertex $v_j$ to reduce its target degree to make a valid candidate operation $del(v_i, v_j)$. However, this is against our goal of only making additive change. Alternatively, for a vertex $v_i\in VS^-$, we increase the degree of another vertex $v_j$ on $DS$ whose degree value is the closest to that of $v_i$ in $G$ and then regenerates $DS^*$ based on the updated $DS$. The rationale is that because $v_j$ and its corresponding $v_i\in VS^-$ have similar degrees, they are very likely to be anonymized to have the same degree in the anonymized graph. After the degree of $v_j$ has been increased, $v_i$ may not need to decrease its degree any more.

4.5 Computational complexity

In this subsection, we briefly discuss the time complexity of our algorithm by analyzing the time complexity of each step in the $k$-anonymization process.

Based on Sect. 4.2, estimating local structure information can be processed in $O(k|V|)$ time. Then, the following step is generating candidate operations. In this step, firstly, a one-time scan on the difference sequence $\delta$ is performed to generate the vertex sets $VS^+$ and $VS^-$, which takes time $O(|V|)$. Given $t=\max \{|VS^+|, |VS^-|\}$, it takes $O(t^2)$ time to generate all candidate operations and the total number of candidate operations generated is at most $O(t^2)$. For each candidate operation, we need to calculate the utility loss caused based on the given community model, which is the $L_1$ distance of the edge distribution sequence $ES$. Usually, the time complexity of calculating $L_1$ distance is linear to the length of $ES$, denoted as $l$. However, we observe that each edge operation only affects the number of edges corresponding to at most one element of $ES$, as well as the total number of edges. For example, if we add one edge $e(c,h)$ in the example graph shown in Fig. 1a, then it will only affect $n_{12}$ (i.e., the number of the edges distributed between communities $C_1$ and $C_2$) of the flat community model shown in Fig. 2 and increase the total number of edges by 1. Suppose $ES$ and $ES^{\prime }$ are the edge distribution sequence of the original graph and that of the modified graph via adding $e(c,h)$, the $L_1$ distance between them is calculated as following: $||ES-ES^{\prime }||_1=\sum _{ij}\left( \frac{n_{ij}}{|E|}-\frac{n_{ij}}{|E|+1}\right) -\left( \frac{n_{12}}{|E|}-\frac{n_{12}}{|E|+1})+(|\frac{n_{12}}{|E|}- \frac{n^{\prime }_{12}}{|E|+1}|\right) =\left( \frac{1}{|E|}-\frac{1}{|E|+1}\right) \sum _{ij}n_{ij} -\left( \frac{n_{12}}{|E|}-\frac{n_{12}}{|E|+1}\right) +\left( |\frac{n_{12}}{|E|} -\frac{n^{\prime }_{12}}{|E|+1}|\right)$. With $\sum _{ij}n_{ij}$ being calculated only once within $O(l)$ time, the utility loss of every candidate operation can be easily calculated in constant time. This observation also applies to the HRG model. Consequently, calculating the utility loss scores of all candidate operations can be proceed in $O(l+t^2)$ time including spotting the operation with the lowest utility loss score. To sum up, the overall computation time of the second step is $O(|V|)+O(l+t^2)$. In the worst case, when all vertices need to increase or decrease their degree, $t=\max \{|VS^+|, |VS^-|\}=|V|$. For the flat community model, $l=m^2$ with $m$ being the number of communities in the model. For the HRG model, $l=|V|-1$. Therefore, the upper bound of the value of $l$ is $|V|^2$. Consequently, the worst-case time complexity of generating candidate operations is $O(|V|^2)$. However, in the real cases, the degree sequence of a social network usually follows power-law distribution, resulting in low frequencies of the vertices sharing large degree and high frequencies of the vertices having small degree. In other words, in a social network, it is very likely that a large amount of low-degree vertices already satisfy $k$-degree anonymity and hence do not need to change their degrees, i.e., $t<<|V|$. And then, the number of communities $m$ is also far smaller than $|V|$. Therefore, the running time of the candidate operation generation process most likely will be much smaller than that in the worst case.

The running time of the refinement process depends on the size of the remaining $VS^+$ or $VS^-$ sets. Suppose the size is $t$, then the time complexity of this process is $O(t|V|)$. Generally, $t<<|V|$, thus $t|V|<<|V|^2$.

Based on the above analysis, the worst-case computational complexity of one iteration of the $k$-anonymization process is $O(|V|^2)$, but the real running time of this process in most cases is much shorter. As it is hard to anticipate the number of iterations the algorithm will run before convergence, we will conduct experiments to further test the time performance of our algorithm in Sect. 6.

4.6 Discussion

As mentioned before, the proposed high utility anonymization framework is general and it is applicable to other $k$-anonymity schemes besides $k$-degree anonymity. In the following, we briefly explain how to extend the framework (as defined in Algorithm 1) to support $k$-neighborhood anonymity. Due to the focus of this work, we only present how to estimate the local structure information and how to generate candidate edge operations in the context of $k$-neighborhood anonymity.

A $k$-neighborhood anonymized graph $G^{\prime }(V^{\prime },E^{\prime })$ requires that for any vertex $v\in V^{\prime }$, there are at least $k-1$ other vertices sharing isomorphic neighborhood with $v$. The neighborhood $NB(v)$ of $v$ is a subgraph containing all the vertices within a certain distance $d$ to $v$ and the edges among these vertices. The diameter $d$ decides the size of the neighborhood. To simplify our discussion, we only consider the neighborhood within distance of 1, which is also a common practice assumed by other works [36]. Unless otherwise noted, the term neighborhood only refers to the neighborhood with $d=1$.

The local structure information used by $k$-neighborhood anonymization is the neighborhood subgraph of every vertex. Like using the degree sequence to capture the local degree information of graphs in the $k$-degree anonymization process, we use the neighborhood set $NS$ to record the local neighborhood $NB(v_i)$ of every vertex $v_i$ of a graph and we try to generate the neighborhood set $NS^*$ of the “nearest” anonymized graph $G^*$. Again, for a given graph $G$, its “nearest” anonymized graph $G^*$ refers to an anonymized graph that satisfies $k$-neighborhood anonymity and meanwhile is generated via the smallest number of edge operations. As the generation of $G^*$ is not always possible, we use the neighborhood set $NS^*$ of $G^*$ as the estimation of the local structure information of $G^*$.

Given $G$ and the privacy parameter $k, NS^*$ has the following properties. First, $NS^*$ has the same size as $NS$. Second, $NS^*$ is $k$-anonymized, meaning that for each $NB^*(v_i)\in NS^*$, it has at least $k-1$ other isomorphic subgraphs in $NS^*$. Third, the sum of the graph edit distance from each $NB^*(v_i)$ to its corresponding $NB(v_i)$ is minimized (i.e., the number of edge operations of changing $G$ to $G^*$ is minimized). Again, take the graph shown in Fig. 1a as an example. Assume parameter $k=2$, the neighborhood $NS(v_i)$ and its corresponding target neighborhood $NS^*(v_i)$ of every vertex $v_i$ are depicted in Fig. 5. We group all the vertices $v_i$ sharing the same isomorphic neighborhood in the target anonymized graph into one equivalent group $EG$, i.e., $\forall v_i, v_j \in EG, NS^*(v_i)=NS^*(v_j)$. As shown in the figure, the vertices $\{a, b\}$ are in the same equivalent group, so as the vertices $\{c, g\}, \{e, h\}$, and $\{d, f\}$.

Fig. 5

An example of the vertices’ neighborhoods and the estimated target neighborhoods

After obtaining the $NS^*$, we need to find candidate operations that can direct the current graph to a $k$-neighborhood anonymized graph with its neighborhood set captured by $NS^*$. In order to do this, we first identify the vertices whose neighborhoods do not match their target neighborhoods and store them in a set $VS$. And then, for each of these vertices $v_i\in VS$, all the viable edge operations that can lead $NB(v_i)$ toward $NB^*(v_i)$ are added into the candidate operation set. Continue the previous example. It is observed that, to transform their current neighborhoods to the target neighborhoods, both vertex $e$ and vertex $d$ need to delete one edge(vertex) from their neighborhoods, respectively. Consequently, the edge deletion operation $del(e, d)$ qualifies as a candidate operation. Given a set of candidate operations, we calculate the utility loss for each of them and perform the one with the smallest utility loss. Then, we update $VS$ and regenerate the candidate operation set.

Obviously, each candidate edge operation serves at least one vertex $v_i$ by converting the neighborhood of $v_i$ to its target neighborhood $NS^*(v_i)$. For example, operation $del(e, d)$ serves vertex $e$ and vertex $d$. However, we want to highlight that an edge operation may affect the neighborhoods of some vertices $v_j$, which it does not mean to affect, and hence the corresponding target neighborhoods $NS^*(v_j)$ might no long be applicable after the candidate edge operation is performed. For instance, $del(e,d)$ will also affect the neighborhood of $f$. Notice that this issue does not exist in $k$-degree anonymity as a given edge operation only changes the degrees of the two vertices of the edge. In order to make the target neighborhoods consistent in an iteration of the algorithm, we identify all the vertices whose neighborhoods are not supposed to be affected but are changed, as well as the vertices in the same equivalent groups with them, and then exclude them from the updated set $VS$ when we regenerate the candidate operations. The process repeats until no candidate operation is generated. If the obtained graph $G^{\prime }$ is $k$-anonymized, the algorithm stops. If not, we regenerate the target $NS^*$ based on the current obtained $G^{\prime }$. In this step, the previously excluded vertices in the above iteration are considered and their new target neighborhoods are regenerated. To ensure the convergence of the algorithm, we could slightly bias toward choosing edge insertion operations among the candidate operations.

Continue the above example. Since there is only one candidate operation $del(e, d)$, we have no other choices but perform it. All the neighborhoods affected by this operation are illustrated in Fig. 6a including vertices $e, d$ and $f$. As this edge deletion operation is to serve vertices $e$ and $d$, the vertex that it does not mean to affect but is actually affected is $f$. Consequently, all the vertices that are within the same equivalent group as $f$ (i.e., vertex $d$) should be excluded when we regenerate the candidate edge operations after performing $del(e,d)$. However, we find that after performing this operation, no candidate operations can be found. As the graph is already 2-anonymized, the algorithm completes. The generated 2-neighborhood anonymized graph is shown in Fig. 6b.

Fig. 6

An example of 2-neighborhood anonymization. a $del(e, d)$ changes $NB(d), NB(e), NB(f)$. b An example output

5 Privacy analysis and related works

In this section, we analyze the privacy of our $k$-degree anonymity scheme against the minimality attacks and then review related works.

5.1 Privacy analysis

The minimality attack first discussed in Wong et al. [30] is a well-known attack on the $k$-anonymity schemes on tabular data. As stated in Wong et al. [30], in order to preserve the utility of the published data, the $k$-anonymity mechanisms all have the underlying principle of minimizing the distortion to the original data. In other words, the $k$-anonymity algorithms only distort the data when necessary. Sometimes, this information can be used by the adversary to launch the minimality attack to the published data to infer the sensitive values of some individuals and jeopardize the privacy. In the following, we discuss the minimality notions defined in our $k$-degree anonymity algorithm and show that these notions will not lead to a minimality attack.

The first minimality notion used in our algorithm is minimizing the distortion on the degree sequence (i.e., minimize the number of edges modified). We use this notion to generate the objective degree sequence (i.e., the degree sequence of the published graph). We assume that in the worst case, the adversary has the background knowledge of both the identity and the degree of every individual in the social network. Figure 7a shows the adversary’s worst-case background knowledge of the social network depicted in Figs. 1a and 7b lists the degree of the vertices in the published 2-degree anonymized graph in Fig. 1c. The adversary’s goal is to map the real identities of the individuals to the vertex IDs of the published graph. With the notion of minimality in anonymization, the adversary reasons that there must be only one vertex of degree 3 and one vertex of degree 1 having their degrees increased, and the degrees of other vertices remain. Therefore, the adversary infers that $Alice$ with degree 4 must be mapped to a vertex also with degree 4 in the published graph. Since there are 2 vertices $c$ and $d$ with degree 4, without any extra information, the probability of $Alice$ mapped to any of them is equal (i.e., $\frac{1}{2}$). However, $Bob$ with degree 3 can be mapped to either a vertex with degree 4 or a vertex with degree 3. Because that there are totally 3 individuals with degree 3 in the original social network, the probability of $Bob$ being the one that has the degree increased (i.e., mapped to a vertex with degree 4) is $\frac{1}{3}$, and the probability that his degree is unchanged is $\frac{2}{3}$. Therefore, the probability of $Bob$ mapped to vertex $c$ or $d$ is $\frac{1}{3}\times \frac{1}{2}=\frac{1}{6}$, and the probability of him mapped to vertex $g$ or $f$ is $\frac{2}{3}\times \frac{1}{2}=\frac{1}{3}$. Similarly, the mapping probability of every individual is inferred as shown in Fig. 7c. Lemma 1 proofs that the mapping probabilities inferred by the adversary with the minimality notion will not exceed $\frac{1}{k}$.

Fig. 7

Minimality attack: attacker’s worst-case background knowledge, vertex degree of the published graph, and inference probability

Lemma 1

Given a published $k$-degree anonymized social network, which is constructed by minimizing the distortion on the degree sequence, we assume that in the worst case, an attacker knows the real identity and degree of every individual in the social network, and she is also aware of the minimality notion. The attacker cannot map an individual to any vertex with probability larger than $\frac{1}{k}$.

Proof

We denote the inferred mapping probability of an individual $x$ to a vertex $v$ in the published graph with degree $d$ as $p^{x}_{v}$. $p^{x}_{v}=p_1\times p_2$, where $p_1$ is the probability that $x$ is mapped to a vertex with degree $d$, and $p_2$ equals to the probability that among all the vertices with degree $d, x$ is mapped to the vertex $v$. In the worst case, with the minimality notion, the attacker can infer $p_1$ with the maximum probability 1. According to the $k$-anonymity condition, there must be at least $k$ vertices in the published graph sharing the degree $d$. Without any extra information, the attacker can only infer the mapping from $x$ to every one of these vertices with equal probabilities. Therefore, the maximum value of $p_2$ is $\frac{1}{k}$. Therefore, $p^{x}_{v} \le 1\times \frac{1}{k}=\frac{1}{k}$.$\square$

The second minimality notion used in our algorithm is modifying the vertices degree to achieve the desired anonymity by adding and deleting edges that make the smallest changes to the community-based utility model, which is captured by the flat or hierarchical community model of the graph and represented by the edge distribution sequence. For the adversary to utilize this notion to infer the details of the edge modification (anonymization) process, and then, possibly to further infer the user identities, she has to know the utility loss caused by the possible edge operations. However, in order to calculate the utility loss, she has to know the community model based on which the utility measurement is generated. Without the exact community model, the attacker could not utilize this minimality notion to make inferences and perform attack. Therefore, in order to prevent the adversary to make use of the second minimality notion, when publishing the anonymized graph, the community model constructed should be kept in secret. Moreover, revealing the community model will also provide the adversary extra information about the original graph besides the vertex degree, which is against the worst-case assumption of our privacy scheme that the adversary only knows the degree information of the vertices. This further convinces that the community model should not be disclosed. However, we do not mind whether the adversary knows the algorithm used to construct the community model. This is because that the adversary, based on the construction algorithm and the vertex degree, cannot reconstruct the community model.

We need to point out that the above analysis is based on the assumption that the attacker only has the background knowledge of the vertex degree. If the attacker has some extra information about the edges among certain individuals, she might be able to infer the identities of some vertices with a higher chance. We reserve this topic as one of the interesting problems to be studied in the near future.

5.2 Related works

Preserving the private information in data publishing and analysis has been well recognized in the area of data mining and data management [1]. Many works in this area focus on tabular data publishing [18, 25], and there are some works focusing on privately publishing transactional data [13] and survey rating data [28]. A comprehensive survey is provided in Fung et al. [11].

With the increasing popularity of social network applications, the privacy problem in publishing social networks starts to gain a lot of attentions [20]. Structural re-identification is one of the major privacy concerns in social network publishing. It was first addressed in Backstrom et al. [2]. The initial study demonstrates that simply removing the identification information of entities is not sufficient to protect privacy. The identities of vertices can be inferred by the attacker due to the structural uniqueness of some small embedded subgraphs. The main work in Backstrom et al. [2] proves that subgraphs, which are maliciously planted by the attacker (i.e., active attack) and naturally exist in the social network (i.e., passive attack), can be used to identify entities. However, it does not provide any effective solution to defend these attacks. Later, work presented in Hay et al. [15] further points out that the re-identification power of an attacker depends on both the descriptive power of her background knowledge and the structural similarity of vertices. Various classes of structural attacks are thereafter proposed based on different types of attackers’ background knowledge, including vertex refinement queries, subgraph queries, and hub-fingerprint queries.

To conquer structural re-identification attacks, various protection schemes have been proposed [3, 14, 15]. For example, the random permutation approach protects privacy by randomly deleting and inserting $m$ edges [14]. Although the method is simple, it does not provide any quantified guarantee on both privacy and utility. Graph generalization-based approach [15] partitions vertices of a social network into small blocks. Then, it abstracts the social network into a super graph, in which super nodes represent blocks of vertices and super edges between super nodes represent the connections between vertices within corresponding blocks. The super graph is then released with the statistical information of the super nodes and super edges (e.g., the number of vertices and edges covered by a super node, and the number of edges represented by a super edge). To guarantee privacy, this method requires partitions of size at least $k$. However, the structural uncertainty introduced by the generalization significantly tampers the utility of the released graph. Work presented in Bhagat et al. [3] also considers using graph partitioning to protect privacy, but it focuses on labeled bipartite graphs.

The notion of $k$-anonymity [29], which has been widely used as a criterion for tabular data privacy protection, has also been applied to social network publishing. Based on the types of attackers’ background knowledge, various $k$-anonymity schemes and the corresponding $k$-anonymization algorithms have been proposed [19, 31, 36, 38, 39] (see [38] for a brief survey). All these algorithms try to modify graphs to achieve $k$-anonymity based on edge/node modifications (i.e., addition and/or deletion) and try to preserve the utility of the released social network data. The $k$-degree anonymity scheme is developed against the attackers with knowledge of entity degree [19]. It requires that for a vertex $v$, there are at least $k-1$ other vertices having the same degree as $v$. Scheme proposed in Zhou and Pei [36] considers the attackers with vertex neighborhood information and a graph is $k$-anonymous; if for any vertex $v$, there are at least $k-1$ other vertices having isomorphic neighborhoods. Due to the unpredictability of attackers’ background knowledge, techniques against multiple structural attacks have also been proposed. For instance, $k$-automorphism modifies the graph such that for each vertex, there exists at least $k-1$ other structurally equivalent vertices [39] and $k$-symmetry utilizes the social network structure symmetry to make changes to the graph [31]. Generally speaking, most, if not all, of these algorithms employ the number of edge/node changes as the only measurement to quantify the utility loss, which is not effective, as explained in Sect. 1. The focus of this work is to design a more effective utility measurement.

Recently, researchers also try to protect the identity privacy and link privacy in a unified anonymization model [4]. They present the $k$-security model, by which the attacker should not be able to map any vertex to an entity with probability larger than $1/k$ based only on the published social network, and not be able to determine two entities linked by a path of certain length with a probability of more than $1/k$. They solve this problem by forming $k$ pairwise isomorphic subgraphs via edge addition and deletion. Yet, it still counts the number of edges modified to measure the utility loss, only with an additional condition that requires the number of added edges to be almost same as the number of deleted edges. This utility measure still purely relies on the degree sequence model, which might not be directly related to other graph properties.

In addition to the structural re-identification problem, some other privacy concerns in publishing social network have been considered as well. For example, the problem of protecting sensitive relationships between entities in social networks is addressed in Zheleva and Getoor [35]. The main idea is to use edge deletion or graph generalization methods to reduce the probability of predicting sensitive edges in the published graph. Along the same line, some works propose random edge permutation methods to provide link obfuscation [32, 33]. Ying and Wu [33] study the impact of the edge permutation techniques on the eigenvalues, while [32] designs a randomization scheme named LORA to obfuscate edge existence based on the HRG model to preserve critical graph statistical properties of released graphs. Although we also utilize the HRG model to design our utility measurement in this paper, the purpose and the solution are very different. The purpose of our work is to protect the node identity privacy while LORA protects the link privacy. And then, LORA obfuscates edge existence by performing random edge permutation. The HRG model is used to capture the link probabilities among the nodes in the graph. It permutes the existing edge randomly with some equivalent edges so that the link probabilities on the HRG model will not be changed. However, our work protects node identity by performing targeted edge addition and deletion to achieve $k$-anonymity. We use the HRG model to capture the hierarchical community structure of the graph. The selected edges are added or deleted to achieve $k$-anonymity while minimizing the changes to the edge distribution within and among the captured hierarchical communities. The study in Ying and Wu [34] shows that various similarity metrics can be exploited to improve the accuracy of sensitive link prediction in a randomized graph. However, no effective solutions are given to counter this attack. Liu et al. [21] present edge weight perturbing techniques to protect private edge weight information in the published graph and to retain the shortest paths and the approximate cost of the paths between certain pairs of entities. The techniques proposed in above works for link privacy protection are not directly applicable to protect the node identity privacy.

Unlike the works introduced above which protect privacy by transforming the social networks prior publishing and releasing the altered or generalized graphs, some other works consider only releasing answers to specific queries. To ensure privacy, random noise is added to the true answer before releasing. Many recent works on private query answering use the notion of differential privacy [9], which is a very strong privacy notion. It injects controlled level of noise to the output result to guarantee that the query results on two “neighboring” input datasets are indistinguishable. The neighboring datasets are defined as the insertion or removal of a single record on tabular data. The query sensitivity is defined to measure the maximum difference between the query results on two neighboring inputs. It decides how much noise should be injected. Differential privacy works best with insensitive queries since it introduces low level of errors. High-sensitivity queries require so much noise that the results are useless. A comprehensive survey of results on tabular data is presented in Dwork [8].

Generally, there are two adaptations of differential privacy on graphs, namely edge-differential privacy and node-differential privacy according to their definition on neighboring graphs and their protections on the privacy of graph edges and nodes, respectively. How to accurately estimate the degree distribution of a social network under $k$-edge-differential privacy is studied in Hay et al. [16]. [23, 26] propose the methods to publish differentially private graph models, based on which synthetic graphs that mimic important properties of the original graph can be generated. These works focus on protecting the edge-differential privacy, which is less sensitive with guaranteed results accuracy. On the other hand, under the definition of the node-differential privacy, many graph queries, including those simple ones (e.g., average node degree and graph diameter), are highly sensitive. As no meaningful results can be derived, the privacy can be guaranteed. Different from edge-differential privacy, our work focuses on protecting node privacy. That is why we still follow the notion of $k$-anonymity in this work, and our objective is to improve the utility of the published graph.

Another line of research deals with the distributed graph reconstruction problem [10]. It assumes a group of authorities with each owning a local piece of a graph and wants to reassemble these pieces privately. A set of cryptographic protocols have been designed to solve the problem [10]. And then, Gao et al. [12] study a problem of preventing outsourced graphs from neighborhood attacks. It transforms the original graph into a link graph stored locally at the client side and a set of outsourced graphs at the server side. Its objective is to process the shortest distance query efficiently with low costs on the client side and to guarantee that the data stored at the server side do not leak private information. However, in this paper, we consider the centralized graph publishing problem. Therefore, our discussion is orthogonal to these works.

6 Experimental evaluation

In this section, we present our comprehensive experimental study to demonstrate the advantages of the newly proposed high utility $k$-anonymization scheme. We focus on the $k$-degree anonymity and implement the anonymization algorithms based on both the flat community model and the hierarchical community model, referred as ${\mathsf{Flat}}$ and ${\mathsf{HRG}}$, respectively. Meanwhile, we implement two existing $k$-degree anonymization algorithms proposed in Liu and Terzi [19] as competitors. Note that [19] is the only work in the literature focusing on $k$-degree anonymity, and the algorithms are designed to preserve the graph utility based on the simple degree sequence model. The first probing method only considers edge addition operations, and the second greedy swap method considers both edge addition and deletion operations. We refer them as ${\mathsf{Prob.}}$ and ${\mathsf{Swap}}$, respectively.

We use utility loss and time efficiency as the main performance metrics. The former evaluates the utility loss caused by various $k$-anonymization algorithms, and the latter evaluates the running time of these algorithms. Following the works in the literature, we evaluate the utility loss of different algorithms by the changes caused on a set of common graph metrics, including average path length (APL), clustering coefficient (CC), average betweenness (BTW), and average closeness (CLN). As these metrics of different graphs have different scales, we report the normalized change ratio of each graph metric.

Two real datasets are used in our simulation, namely dblp and dogster. The former is extracted from dblp (http://dblp.uni-trier.de/xml), and the latter is crawled from a dog-theme online social network (http://www.dogster.com). We sample different-sized subgraphs from these datasets. To ensure that the general structural properties, especially the community structure, of the sampled subgraphs are consistent with the original graph, we adopt the snowball algorithm [22] to sample the graph. The properties of the sampled subgraphs are summarized in Table 4. In general, dblp contains sparse graphs with average vertex degree within the range of 2–3, and dogster contains dense graphs with average degree within the range of 10–20.

Table 4 Properties of the datasets

6.1 Utility loss versus graph size

In the first set of experiments, we evaluate the graph utility loss of different-sized graphs under different $k$-anonymization methods. We set the anonymity requirement as $k = 25$. We will evaluate the utility loss with different $k$ values in the next subsection.

First, we report the change ratio of different structural properties of graphs with various sizes in Figs. 8 and 9. As observed, in most of the cases, both ${\mathsf{Flat}}$ and ${\mathsf{HRG}}$ perform very well on preserving the graph utility in terms of the four common graph metrics. In general, the graph property change ratio caused by our methods is within the range of $(0.01\,\%,1\,\%)$, which is around 10–100 times better than that of the existing ${\mathsf{Swap}}$ and ${\mathsf{Prob.}}$ methods.⁴ Only with a few exceptions, the ${\mathsf{Prob.}}$ method performs better than our methods. For instance, on the dblp graphs with 1,000 and 2,000 vertices and the dogster graph with 5,000 vertices, it provides better results than our methods on the CC metric. However, we could not figure out the exact reason that explains these exceptions. One possibility is that it happens that the community models constructed on these graphs do not capture the CC property very well. It may be interesting to study the bias of each anonymization scheme toward different graph structural properties in the future works. In addition, we observe that ${\mathsf{Swap}}$ performs better than ${\mathsf{Prob.}}$ on the sparse dblp graphs. Oppositely, ${\mathsf{Prob.}}$ performs better than ${\mathsf{Swap}}$ on the dense dogster graphs. However, the performance of our methods is stable on both datasets. Finally, we find that the ${\mathsf{HRG}}$ algorithm that runs based on the hierarchical community model generally generates graphs with higher utility than the ${\mathsf{Flat}}$ algorithm that is developed based on the flat community model. The reason is that the complex HRG model captures more information of the graph structure, and it is more sensitive to the small number of edge modifications. Therefore, the anonymization algorithm that evaluates the utility loss of the possible edge operations based on this model is more accurate, thus generates the graphs that better represent the features of the original graphs.

Fig. 8

Graph property change ratio versus graph size on dblp graphs ($k=25$). a APL. b CC. c BTN. d CLN

Fig. 9

Graph property change ratio versus graph size on dogster graphs($k=25$). a APL. b CC. c BTN. d CLN

6.2 Utility loss versus $k$

In the second set of experiments, we evaluate the impact of the privacy requirement $k$ on the graph property change ratio of different methods. Here, the size of the graph is fixed to 5,000 vertices.

Figures 10 and 11 present the results on both datasets. As observed, the privacy requirement (i.e., $k$) has no obvious impact on the performance of ${\mathsf{Swap}}$. This is because, ${\mathsf{Swap}}$ method has to perform a large number of edge operations even for a small $k$. When $k$ increases, the number of newly performed edge operations, compared with the total number of edge operations, is very small. On the other hand, the impact of $k$ on ${\mathsf{Flat}}$, ${\mathsf{HRG}}$, and ${\mathsf{Prob.}}$ is much more significant. Their utility losses increase as $k$ increases. This is because that all these methods need to perform more edge operations to achieve $k$-anonymity with larger $k$. Similar with the observation in the above subsection, in most of the cases, our ${\mathsf{Flat}}$ and ${\mathsf{HRG}}$ approaches outperform the others in terms of the utility loss on every evaluated graph metrics.

Fig. 10

Graph property change ratio versus $k$ on dblp graphs ($|V|=5000$). a APL. b CC. c BTN. d CLN

Fig. 11

Graph property change ratio versus $k$ on dogster graphs($|V|=5000$). a APL. b CC. c BTN. d CLN

6.3 Running time

In our last set of experiments, we investigate the time performance of our ${\mathsf{Flat}}$ and ${\mathsf{HRG}}$ anonymization processes and compare it with that of the existing ${\mathsf{Prob.}}$ and ${\mathsf{Swap}}$ algorithms. First, we report the running time of the algorithms with graphs of different sizes in Fig. 12 with $k$ set to 25. Generally, the running time increases as the graph size increases, and the ${\mathsf{Prob.}}$ approach achieves the best time performance, while the ${\mathsf{Swap}}$ method performs the worst. The time performance of our community model-based approaches is in between of the ${\mathsf{Prob.}}$ and ${\mathsf{Swap}}$ methods. Meanwhile, we find that the running time is sensitive to the graph density. For the sparse dblp graphs (see Fig. 12a), the running time of all the algorithms is short (e.g., under 140 s) and our community model-based algorithms definitely can find a $k$-anonymized graph within 40 s. However, for the dense dogster graphs, all the algorithms have to spend much longer time (e.g., up to thousands of seconds). The reason is that in the sparse dblp graphs, there are many vertices with the same low degree (e.g., 1 and 2), which already satisfy $k$-anonymity, while the vertices in the dense dogster graphs tend to have more diverse degrees. Therefore, the dogster graphs have more vertices whose degree need to be changed to achieve $k$-anonymity compared with the dblp graphs of the same size, thus cause more candidate edge operations. Moreover, we find that ${\mathsf{HRG}}$ runs slower than ${\mathsf{Flat}}$ in most of the cases. This is probably because that the ${\mathsf{HRG}}$ method which is developed based on the more complex hierarchical community model is more sensitive to every single edge operation.

Fig. 12

The running time versus graph size. a dblp. b dogster

Next, we evaluate the time performance of different algorithms with graph size fixed to 5,000 vertices and the privacy parameter $k$ varying. The results are depicted in Fig. 13. We observe that for both datasets, the running time of ${\mathsf{Swap}}$ is not sensitive to the changes of the privacy parameter $k$ and it always remains on a high level. This is because that the ${\mathsf{Swap}}$ method always performs large number of edge modifications even with small $k$. While for the other three algorithms, the running time shows an increasing trend as $k$ increases. This is because that in order to achieve anonymity with larger $k$, usually more edges need to be modified. Generally, the running time of our community model-based methods lies in between the running time of ${\mathsf{Prob.}}$ and that of ${\mathsf{Swap}}$. We believe that the great increase in running time of our community model-based algorithms with very large $k$ (e.g., 50, 100) is caused by the greatly increased number of candidate operations.

Fig. 13

The running time versus $k$ ($|V|=5000$). a dblp. b dogster

6.4 Discussion

To sum up, our experiments use different graph metrics to evaluate the utility loss of the proposed community model-based methods. The experimental results clearly verify that the community structure has high correlation with other key structure features of social networks. The flat and HRG models developed based on the community structure successfully capture most, if not all, core features of the social networks, and our anonymization algorithms which employ these models are the most effective for preserving the graph utility. In addition, we also evaluate the running time of different algorithms. The results demonstrate that with a relatively small but reasonable privacy parameter $k$, our community model-based methods show acceptable convergence time compared with the existing algorithms. However, the running time may increase rapidly when $k$ is very large (e.g., 50) due to the sharp increase in the number of candidate operations.

We also compare the anonymization algorithms based on the flat and hierarchical community models, respectively. According to the experimental results, the hierarchical community model-based method is able to generate anonymized graphs with higher utility but longer convergence time.

7 Conclusion

Privacy and utility are two main components of a good privacy protection scheme. Existing $k$-anonymization approaches on social networks provide good protection for entities’ identity privacy. However, with a simple graph degree sequence-based utility model, they fail to generate anonymized graphs with high utility. Motivated by this issue, in this paper, we propose novel high utility social network anonymization approaches to achieve good privacy protection with low utility loss. In our approaches, the utility measurement is designed based on more complex graph community models, including the flat community model and the hierarchical community model. Experimental evaluations on real datasets show that our approaches outperform the existing approaches in terms of the utility with comparable running time.

In the near future, we would like to further improve the time performance of our approaches and meanwhile evaluate them on larger social networks and for other k-anonymization models (e.g., $k$-neighborhood anonymity). In addition, instead of developing the anonymization approaches to preserve general graph structure properties, we would like to study privacy preserving methods that could provide high utility for particular graph mining applications.