Hubness-aware shared neighbor distances for high-dimensional $k$-nearest neighbor classification

Abstract

Learning from high-dimensional data is usually quite challenging, as captured by the well-known phrase curse of dimensionality. Data analysis often involves measuring the similarity between different examples. This sometimes becomes a problem, as many widely used metrics tend to concentrate in high-dimensional feature spaces. The reduced contrast makes it more difficult to distinguish between close and distant points, which renders many traditional distance-based learning methods ineffective. Secondary distances based on shared neighbor similarities have recently been proposed as one possible solution to this problem. However, these initial metrics failed to take hubness into account. Hubness is a recently described aspect of the dimensionality curse, and it affects all sorts of $k$-nearest neighbor learning methods in severely negative ways. This paper is the first to discuss the impact of hubs on forming the shared neighbor similarity scores. We propose a novel, hubness-aware secondary similarity measure $simhub_s$ and an extensive experimental evaluation shows it to be much more appropriate for high-dimensional data classification than the standard $simcos_s$ measure. The proposed similarity changes the underlying $k$NN graph in such a way that it reduces the overall frequency of label mismatches in $k$-neighbor sets and increases the purity of occurrence profiles, which improves classifier performance. It is a hybrid measure, which takes into account both the supervised and the unsupervised hubness information. The analysis shows that both components are useful in their own ways and that the measure is therefore properly defined. This new similarity does not increase the overall computational cost, and the improvement is essentially ‘free’.

1 Introduction

Machine learning in many dimensions is often rendered very difficult by an interplay of several detrimental factors, commonly referred to as the curse of dimensionality. In high-dimensional spaces, all data is sparse, as the requirements for proper density estimates rise exponentially with the number of features. Empty space predominates [2] and data lies approximately on the surface of hyper-spheres around cluster means, that is, in distribution tails. Relative contrast between distances on sample data is known to decrease with increasing dimensionality, as the distances concentrate [3, 4]. The expectation of the distance value increases, but the variance remains constant. It is therefore much more difficult to distinguish between close and distant points. This has a profound impact on nearest neighbor methods, where inference is done based on the $k$ examples most similar (relevant) to the point of interest. The very concept of a nearest neighbor was said to be much less meaningful in high-dimensional data [5].

Difficulty in distinguishing between relevant and irrelevant points is, however, not the only aspect of the dimensionality curse which burdens $k$-nearest neighbor–based inference. The recently described phenomenon of hubness is also considered to be highly detrimental. The term was coined after hubs, very frequent neighbor points which dominate among allthe occurrences in the $k$-neighbor sets of inherently high-dimensional data [6, 7]. Most other points either never appear as neighbors or do so very rarely. They are referred to as anti-hubs.

The skewness of the $k$-occurrence distribution has a geometric interpretation and does not reflect the underlying semantics of the data. This was first noticed in music retrieval applications [8, 9] and is still an unresolved issue [10–14]. Some songs were very frequently retrieved by the recommendation systems, but were in fact irrelevant for the considered queries. Their occurrences were simply an artifact of the employed similarity measures, when applied to high-dimensional audio data.

There is no easy way out, as demonstrated in [15], since dimensionality reduction techniques fail to eliminate the neighbor occurrence distribution skewness for any reasonable dimensionality of the projection space. The skewness decreases only when the data are projected onto spaces below the intrinsic dimensionality of the data, where some potentially relevant information is irretrievably lost. It is therefore necessary to work under the assumption of hubness when using nearest neighbor methods for analyzing high-dimensional data.

Different metric spaces exhibit different degrees of hubness, so choosing a proper distance measure becomes a non-trivial task. The apparent inadequacy of many common metrics (Manhattan, Euclidean, etc.) in high-dimensional data has motivated some researchers to start using higher-order secondary distances based on shared nearest neighbor similarity scores. This approach has frequently been used in clustering applications [16–21]. The basic idea is that the similarity between two points can be measured by the number of $k$-nearest neighbors that they have in common. This is somewhat similar to collaborative filtering, where the purchase set intersections are used to determine similarity between different customers.

Turning a similarity score into a distance is a trivial task. We will address the details in Sect. 2.1. Shared neighbor distances are considered by some as a potential cure for the curse of dimensionality [22].

Even though the shared neighbor distances have mostly been considered in the context of clustering, we will focus on the supervised learning case and show their usefulness in $k$-nearest neighbor ($k$NN) classification.

Hubness exhibits a dual influence on shared neighbor distances. As the secondary metric is introduced, the overall hubness in the data must also change. We will show that even though the skewness in the $k$-occurrence distribution is somewhat reduced, some non-negligible hubness still remains and using the hubness-aware classification methods yields definite improvements. More importantly, the hubness in the original metric space has a profound impact on how the shared neighbor similarity scores are formed in the first place. Hubs are very frequent neighbors so they become very frequently shared neighbors as well. As we have already mentioned, hubs are usually points where the semantics of the similarity measure is most severely compromised, so relying on them when defining a secondary distance is not a very wise choice. This is why we have proposed a new hubness-aware method for calculating shared neighbor similarities/distances [1].

The paper is structured as follows. In Sect. 2, we outline the basic concepts in defining the shared neighbor distances and discuss some recent findings in learning under the assumption of hubness. We proceed by considering how the two might be successfully combined and propose a new way to define shared neighbor similarities in Sect. 3. In Sect. 4, we test our hypothesis on several high-dimensional synthetic and image datasets and examine the findings.

2 Related work

2.1 Shared neighbor distances

Regardless of the skepticism expressed in [5], nearest neighbor queries have been shown to be meaningful in high-dimensional data under some natural assumptions [23], at least when it comes to distinguishing between different clusters of data points. If the clusters are pairwise stable, that is, inter-cluster distances dominate intra-cluster distances, the neighbors will tend to belong to the same cluster as the original point. An obvious issue with this line of reasoning is that cluster assumption violation is present to different degrees in real-world data, so that sometimes the categories do not correspond well to the aforementioned clusters. Nevertheless, this observation motivated the researchers to consider using secondary distances based on the ranking induced by the original similarity measure [22]. A common approach is to count the number of shared nearest neighbors (SNN) between pairs of points for a given, fixed neighborhood size.

Let $D = {(x_1, y_1), (x_2, y_2), \ldots (x_n, y_n)}$ be the data set, where each $x_i \in \mathbb R ^{d}$. The $x_i$ are feature vectors which reside in some high-dimensional Euclidean space, and $y_i \in {c_1,c_2,\ldots c_C}$ are the labels. Denote by $D_k(x_i)$ the $k$-neighborhood of $x_i$. A shared neighbor similarity between two points is then usually defined as:

$$\begin{aligned} simcos_s(x_i,x_j) = \frac{|D_s(x_i) \cap D_s(x_j)|}{s} \end{aligned}$$

(1)

where we have used $s$ to denote the neighborhood size, since we will use these similarity measures to perform $k$-nearest neighbor classification and the neighborhood sizes in these two cases will be different. The $simcos_s$ similarity can easily be transformed into a distance measure in one of the following ways [22]:

$$\begin{aligned} dinv_s(x_i,x_j)&= 1 - simcos_s(x_i,x_j)\nonumber \\ dacos_s(x_i,x_j)&= \arccos (simcos_s(x_i,x_j))\nonumber \\ dln_s(x_i,x_j)&= -\ln (simcos_s(x_i,x_j)) \end{aligned}$$

(2)

All three of the above given distance measures produce the same ranking, so they are essentially equivalent when being used for $k$-nearest neighbor inference. We based all our subsequent experiments on $dinv_s(x_i,x_j)$.

In shared neighbor distances, all neighbors are treated as being equally relevant. We argue that this view is inherently flawed and that its deficiencies become more pronounced when the dimensionality of the data is increased. Admittedly, there have been some previous experiments on including weights into the SNN framework for clustering [24], but these weights were associated with the positions in the neighbor list, not with neighbor objects themselves. In Sect. 3, we will discuss the role of hubness in SNN measures.

2.2 Hubs: very frequent nearest neighbors

High dimensionality gives rise to hubs, influential objects which frequently occur as neighbors to other points. Most instances, on the other hand, are very rarely included in $k$-neighbor sets, thereby having little or no influence on subsequent classification. What this change in the $k$-occurrence distribution entails is that potential errors, if present in the hub points, can easily propagate and compromise many $k$-neighbor sets. Furthermore, hubness is a geometric property of inherently high-dimensional data, as the points closer to the centers of hyper-spheres where most of the data lies tend to become very similar to many data points and are hence often included as neighbors [7]. This means that hubness of a particular point has little to do with its semantics. Hubs are often not only neighbors to objects of their own category, but also neighbors to many points from other categories as well. In such cases, they exhibit a highly detrimental influence and this is why hubness of the data usually hampers $k$-nearest neighbor classification.

Hubness has only recently come into focus, but some hubness-aware algorithms have already been proposed for clustering [25], instance selection [26], outlier and anomaly detection [15, 27] and classification [6, 28–32], which we will discuss below.

Let us introduce some notation. Denote by $R_k(x_i)$ the reverse neighbor set of $x_i$, so the number of $k$-occurrences is then $N_k(x_i) = |R_k(x_i)|$. This total number of neighbor occurrences includes both the good occurrences, where the labels of points and their neighbors match and the bad occurrences where there is a mismatch between them. Formally, $N_k(x_i) = GN_k(x_i) + BN_k(x_i)$, the former being referred to as the good hubness and the latter as the bad hubness of $x_i$. The bad hubness itself can be viewed as a composite quantity, comprising all the class-specific $k$-occurrences where label mismatch occurs. Let $N_{k,c}(x_i) = |x \in R_k(x_i): y = c|$ denote such class-specific hubness. The total occurrence frequency is then simply $N_k(x_i) = \sum _{c \in C}{N_{k,c}(x_i)}$. Calculating all the $N_k(x_i)$ equals building an occurrence model, which can be used to somehow estimate all the implied posterior class probabilities in the point of interest $p(y=c|x_i \in D_k(x))$. This observation served as the basis for several recent hubness-aware approaches [28–31].

2.3 Hubness-aware classification methods

The basic $k$-nearest neighbor method [33] is very simple, but has nevertheless been proven to exhibit certain beneficial asymptotic properties [34–37]. A label in the point of interest is decided upon by a majority vote of its nearest neighbors. Many extensions of the basic algorithm have been developed over the years, improving the original approach in various ways. [38–45] The $k$-nearest neighbor classification is still widely used in many practical applications, with a recent focus on time series analysis [46, 47] and imbalanced data classification [48–53].

Hubness in high-dimensional data, nevertheless, affects $k$NN in some severely negative ways [6, 7, 15]. This is why several hubness-aware classification algorithms have recently been proposed. An effective vote weighting scheme was first introduced in [6], assigning to each neighbor a weight inversely correlated with its bad hubness. More specifically, $w_k(x_i) = e^{-h_b(x_i,k)}$, where $h_b(x_i,k) = (BN_k(x_i)-\mu _{BN_k})/\sigma _{BN_k}$ is the standardized bad hubness. We will refer to this approach as hubness-weighted $k$-nearest neighbor (hw-$k$NN).

Fuzzy measures based on $N_{k,c}(x_i)$ have been introduced in [28], where the fuzzy $k$-nearest neighbor voting framework was extended to include hubness information (h-FNN). This was further refined in [30] by considering the self-information of each individual occurrence. Anti-hubs were therefore treated as more informative. Intuitively, such neighbor points are more local to the point of interest, as they are not frequent neighbors. The algorithm was named hubness information $k$-nearest neighbor (HIKNN).

Along with the fuzzy approaches, a naive Bayesian model was desribed in [29], where the algorithm naive hubness-Bayesian $k$NN (NHBNN) was proposed for probabilistic $k$-nearest neighbor classification in high-dimensional data.

We will see in Sect. 4.3 that these hubness-aware algorithms are in fact well suited for dealing with the secondary SNN distances.

3 Hubness-aware shared neighbor distances

Since hubness affects the distribution of neighbors, it must also affect the distribution of neighbors shared between different points. Each $x_i$ is shared between $N_s(x_i)$ data points and participates in $\genfrac(){0.0pt}{}{N_s(x_i)}{2}$ similarity scores. Hub points, by the virtue of being very frequent neighbors, are expected to arise quite frequently as shared neighbors in pairwise object comparisons. What this means, however, is that sharing a hub $s$-neighbor is quite common and not very informative. This is consistent with observations in [30]. Rarely shared neighbors (anti-hubs), on the other hand, carry information more local to the points of interest and should be given preference when calculating similarities. Figure 1 outlines this observation.

Fig. 1

An illustrative example. $x_1$ and $x_2$ share two neighbors, $D_s(x_1) \cap D_s(x_2) = \{x_a, x_b\}$. The two shared neighbors are not indicative of the same level of similarity, as $x_b$ is a neighbor only to $x_1$, $x_2$ and one other point, while $x_a$ is a more frequently shared neighbor

Each neighbor point can, depending on its hubness, contribute to many pairwise similarities. Some of these similarities will be between the elements from the same class and some between the elements from different classes. Therefore, we can expect some neighbors to contribute more to the intra-class similarities and some more to the inter-class similarities, depending on the class distribution in their occurrence profiles. Clearly, hubs which occur almost exclusively as neighbors to points from a single category ought to be preferred to those which occur inconsistently among various categories in the data. This is illustrated in Fig. 2. The purity of the reverse neighbor sets can clearly be exploited for improving class separation.

Fig. 2

A binary example where the shared neighbors have significantly different occurrence profiles. $x_a$ is equally often present as a neighbor to objects from both categories, while $x_b$ is almost exclusively in $s$-neighbor sets of the second class. By favoring $x_b$ over $x_a$ in the similarity score, the average intra-class similarity is expected to increase and the inter-class similarity decreases

In order to refine the basic shared neighbor similarity, we will give preference to less frequent and good neighbor points and reduce the influence of bad hubs. We propose a new SNN similarity measure:

$$\begin{aligned} simhub_s(x_i,x_j)&= \frac{\sum _{x \in D_s(x_i) \cup D_s(x_j)}{I_n(x) \cdot (\max {H_s} - H(R_s(x)))}}{s \cdot \max {H_s} \cdot \max {I_n}}\end{aligned}$$

(3)

$$\begin{aligned} I_n(x)&= \log {\frac{n}{(N_s(x))}}; \max {I_n} = \log {n}\end{aligned}$$

(4)

$$\begin{aligned} H(R_s(x))&= H(Y|x \in D_s) = -\sum _{c \in C}{\frac{N_{s,c}(x)}{N_s(x)}\log {\frac{N_{s,c}(x)}{N_s(x)}}}; \max {H_s} = \log {c}\quad \end{aligned}$$

(5)

Though it may seem slightly complicated, $simhub_s$ is in fact very simple and intuitive. The denominator merely serves the purpose of normalization to the $[0,1]$ range. Each shared neighbor is assigned a weight which is a product of two quantities. Occurrence informativeness ($I_n(x)$) increases the voting weights of rare neighbors. The reverse neighbor set entropy ($H(R_s(x))$) measures the non-homogeneity (inconsistency) in occurrences. When subtracted from the maximum entropy ($\max {H_s}$), it represents the information gain from observing the occurrence of $x$, under the uniform label assumption. The labels are, of course, not uniformly distributed, but it is convenient to have $(\max {H_s} - H(R_s(x))) \ge 0$. For the purposes of calculating $I_n(x)$ and $H(R_s(x))$, $x$ is treated as its own $0$th nearest neighbor, in order to avoid zero divisions for points which have not previously occurred as neighbors on the training data. In other words, $N_s(x) := N_s(x)+1$, $N_{s,y}(x) := N_{s,y}(x)+1$, where $y$ is the label of x. The $simhub_s$ similarity can be turned into a distance measure in the same way as the $simcos_s$, as previously demonstrated in Eq. 2.

What is great about this new way of defining similarity is that the extra computational cost is negligible, since all the $s$-neighbor sets need to be calculated anyway. One only has to count the occurrences, which is done in $O(s \cdot n)$ time. Calculating all the $D_s(x)$ neighbor sets accurately takes $\Theta (d \cdot n^2)$ time in high-dimensional data, where $d$ is the number of features (since usually $d > s$), which is the time required to compute the distance matrix in the original metric. An approximate algorithm exists, however, which does the same in $\Theta (d \cdot n^{1+t})$, $t \in [0,1]$ [54]. It is a divide and conquer method based on recursive Lanczos bisection. In our initial experiments, very good estimates are obtained even for $t=0$ (so, in linear time!), provided that the stop criterion for subset division is set high enough, since the accurate $s$-neighborhoods are computed in the leaves of the split.

It is possible to observe the $simhub_s$ similarity in terms of its constituents, as it is jointly based on two different quantities—neighbor informativeness and neighbor occurrence purity. These factors can be considered separately, as given in Eqs. 6 and 7.

$$\begin{aligned} simhub_s^{\mathrm{IN}}&= \frac{\sum _{x \in D_s(x_i) \cup D_s(x_j)}{I_n(x)}}{s \cdot \max {I_n}}\end{aligned}$$

(6)

$$\begin{aligned} simhub_s^{\mathrm{PUR}}&= \frac{\sum _{x \in D_s(x_i) \cup D_s(x_j)}{(\max {H_s} - H(R_s(x)))}}{s \cdot \max {H_s}} \end{aligned}$$

(7)

In some of the experiments, we will examine the influence of each of the two constituent measures on the final $simhub_s$ similarity score and the overall classification performance.

4 Experiments and discussion

4.1 Overview of the data

The analysis was performed on both synthetic and real-world data. In synthetic data, we were interested only in such datasets that would pose significant difficulties for $k$NN-based methods, as this fits well with the analysis of hubness and the rest of the experimental setup. To that purpose, we have generated 10 difficult 100-dimensional Gaussian mixtures with a significant class overlap, each comprising 10 different categories. The overlap was achieved by randomly placing each distribution center for each feature within a certain range of another already generated center, constraining the distance between them to a certain multiple of their standard deviations. This is well reflected in Table 1, where we can see that these datasets ($DS_1$–$DS_{10}$) exhibit substantial bad hubness.

Table 1 The summary of high-hubness datasets

Most of the analysis was done on high-dimensional image representations, but some brief comparisons were also performed on relatively low-dimensional data, in order to gain further insights into the potential applicability of the similarity measures (Table 2, Sect. 4.9).

Table 2 The summary of low-to-medium-dimensional datasets from the UCI repository

Ten image datasets were selected for the basic high-dimensional experiments, as the image data are known to exhibit significant hubness [55]. They represent different subsets of the public ImageNet repository (http://www.image-net.org/). We have selected the same subsets that were used in classification benchmarks in previous papers on hubness-aware classification [1, 28, 30, 55], to simplify the comparisons.

The images in these ten datasets (iNet3-iNet7, iNet3Imb-iNet7Imb) were represented as 400-dimensional quantized SIFT feature vectors [56, 57] extended by 16-bin color histograms. SIFT features are commonly used in object recognition systems, as they exhibit invariance to scale, rotation and translation. Each part of the representation was normalized separately. This particular image representation may not be the best choice for the given datasets [55], but is nevertheless a natural choice and quite challenging for $k$NN classification, which makes it a good benchmark. It can be seen in Table 1 that these image datasets exhibit substantial bad hubness.

As implied by the names, there is a correspondence between the first (iNet3..iNet7) and the second five datasets (iNet3Imb..iNet7Imb). The latter have been obtained from the former via random sub-sampling of the minority classes in order to increase the imbalance in the data. The difference is easily seen in Table 1 by considering the relative imbalance factor: $\text{ RImb} = \sqrt{(\sum _{c \in C}{(p(c) - 1/C)^2})/((C-1)/C)}$, which is merely the normalized standard deviation of the class probabilities from the absolutely homogenous mean value of $1/c$.

We will not focus on class imbalance in this paper, as this is addressed in detail in [58]. We will, however, use one recently proposed framework for imbalanced data analysis [59] to outline the most important differences between the analyzed metrics. This will be discussed in Sect. 4.6.

Additionally, three partially faulty quantized Haar feature representations [60] of iNet3 (iNet3Err:100, iNet3Err:150, iNet3Err:1000) were presented in Sect. 4.7 as a pathological special case where erroneous hub points rendered the $k$-nearest neighbor classification completely ineffective. It will be shown that the secondary shared neighbor similarities are able to reduce the negative consequences of hubness in the data and that the proposed $simhub_s$ measure does so more effectively than $simcos_s$.

Table 1 shows the properties of the data when the primary metrics are used. Since the images have been represented in a form of coupled probability distributions, Manhattan distance ($L_1$) is used in experiments on image data, as it represents the integral of the absolute difference between the distributions. The Euclidean distance ($L_2$) was used when analyzing Gaussian data, as it induces hyper-spherical neighborhoods, which are well suited for modeling Gaussian clusters. In our initial experiments, the difference between the two metrics ($L_1$,$L_2$) was not so big, but we have nevertheless opted for the more natural choice in both cases.

The reason why Table 1 shows the statistics for several different neighborhood sizes ($k=5$ and $k=50$ for the image data and $k=10$ and $k=50$ for the synthetic data) is that we will be performing $5-NN$ classification of the image data and $10-NN$ classification of the synthetic data, while using the shared neighbor distances based on $50$-neighbor sets. The neighborhood size for the image data is chosen for comparison with previous work, while a larger $k$ is beneficial in Gaussian mixtures, as it allows for better estimates in the borderline regions. In Sect. 4.4, we will show that the difference between the examined metrics actually holds regardless of the particular choice of $k$.

An increase in neighborhood size somewhat reduces the skewness of the occurrence distribution, since more points become hubs. Bad hubness increases, as well as the non-homogeneity of reverse neighbors sets. This is illustrated in Fig. 3 for iNet5Imb dataset. The increase is not always smooth as in the given figure, but the same general trend exists in all the datasets that we have analyzed in our experiments.

Fig. 3

$s$-occurrence skewness and reverse neighbor set entropy over a range of neighborhood sizes for iNetImb5 dataset

The degree of major hubs is quite high for $s=50$ neighborhood size which will be used to calculate the secondary SNN distances. In some of the datasets, the major hub appears in approximately 20 % of all neighbor lists. This shows why it might be important to take the hubness into account when deducing the secondary distances for high-dimensional data. Likewise, high reverse neighbor set entropies indicate that good hubs are a rarity when using large neighborhoods, so their influence on similarity should be emphasized, whenever possible.

Even though both $simcos_s$ and $simhub_s$ were designed primarily for high-dimensional data, it is prudent to perform some comparisons on low-to-medium-dimensional data as well. We have selected 10 such datasets from the UCI repository (http://archive.ics.uci.edu/ml/). The summary of low dimensional datasets is given in Table 2. We see that the skewness of the occurrence distribution is even negative in some datasets, so there is no hubness to speak of. The comparisons on this data are given in Sect. 4.9.

4.2 Hubness in the shared neighbor metric space

Switching to secondary distances induces a change in the hubness of the data. As the similarities are recalculated, so are the $k$-nearest neighbor sets and this affects the structure of the $k$NN graph. The change can be either beneficial or detrimental to the following classification process. The impact on the $k$NN classification can already be estimated by observing the change in the total number of bad occurrences on the data. This is summarized in Fig. 4, for both the synthetic and the ImageNet data.

Fig. 4

Bad occurrence percentages in each of the examined metrics. The standard shared neighbor similarity measure $simcos$ manages to reduce the overall bad hubness in the data, but the proposed hubness-aware $simhub$ similarity reduces the frequency of bad occurrences even more, on all of the analyzed datasets

As mentioned in Sect. 2.1, we are using the $dinv_s(x_i,x_j)$ method of converting a similarity into a distance measure, which essentially means that we are subtracting the normalized similarity score from 1 to obtain the normalized distance score. Therefore, the primary distances in Fig. 4 are compared to the $dinv_s(x_i,x_j)$ distances based on the $simcos_s$ and $simhub_s$ similarity scores. To simplify the notation in Figures and Tables, we will be using the $simcos_s$ and $simhub_s$ interchangeably throughout the following sections to denote either similarity or the implied dissimilarity, depending on the context.

The comparison between the bad occurrence percentages in Fig. 4 reveals that both secondary distances achieve a significant reduction in the overall bad hubness of the data. The proposed hubness-aware $simhub_{50}$ similarity score clearly outperforms the standard $simcos_{50}$ similarity, as it produces fewer bad occurrences on every single analyzed dataset. The reduction in both similarity measures is more pronounced in the synthetic data, both for $k=5$ and $k=10$ (though only the latter is shown in Fig. 4). As mentioned before, two different neighborhood sizes will be used for classifying the image data and the Gaussian mixtures, so the analysis here is also aligned with the following classification experiments in Sect. 4.3.

Both similarity measures significantly reduce the skewness in $k$-occurrences on the analyzed data, which is shown in Fig. 5. The reduction rates are similar, though the $simcos_{50}$ induces somewhat less hubness in the secondary metric space. This is an important property of both shared neighbor similarity scores. Reducing the hubness in the data partly resolves the implications of the curse of dimensionality in $k$-nearest neighbor inference. This result reaffirms the previous claims regarding the usefulness of shared neighbor distances [22]. Nevertheless, it should be noted that the remaining occurrence skewness is non-negligible. On synthetic data, it amounts to 1.62 and 1.75 on average for $simcos_{50}$ and $simhub_{50}$, respectively. This remaining hubness implies that even though the shared neighbor similarities are doubtlessly helpful in redefining the metric space, the subsequent classification should probably be performed in a hubness-aware way as well. In other words, these similarity scores reduce but do not entirely eliminate the consequences of the dimensionality curse.

Fig. 5

Overall hubness ($k$-occurrence skewness) in each of the examined metrics. Both secondary similarity measures significantly reduce the hubness of the data, which should be beneficial for the ensuing classification

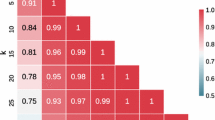
Figures 4 and 5 have shown us how $simcos_{50}$ and $simhub_{50}$ change the overall nature of hubness in the data. However, the average occurrence skewness and the average bad occurrence percentage cannot tell us everything about the change in the $k$NN graph structure. What needs to be seen is if the good/bad hub points are invariant to this particular change of metric. Figure 6 gives the pointwise Pearson correlations in the total occurrence frequencies ($N_k(x)$) and bad occurrence frequencies ($BN_k(x)$) between the $k$NN graphs in the primary and secondary metric spaces, on synthetic data. Similar trends are present in the ImageNet data as well.

Fig. 6

The Pearson correlation in point hubness ($N_k(x)$) and point bad hubness ($BN_k(x)$) between the primary metric space and the secondary metric spaces induced by $simcos_{50}$ and the proposed $simhub_{50}$ shared neighbor similarity

The two comparisons in Fig. 6 reveal a major difference between the standard $simcos_{50}$ and the proposed $simhub_{50}$ similarity measure. Namely, there exists low-to-moderate positive correlation between hubs and bad hubs in the primary metric space and the metric space induced by $simcos_{50}$. Some primary hubs remain secondary hubs and even more importantly—some primary bad hubs remain secondary bad hubs. On the other hand, $simhub_{50}$ changes the $k$NN graph structure more drastically, as there is nearly no correlation in bad hubness between the two metric spaces. The correlation in $N_k(x)$ is even slightly negative both in Gaussian mixtures and in ImageNet data. This may be a part of the reason why $simhub_{50}$ succeeds in reducing the overall bad occurrence percentage much more effectively than $simcos_{50}$—as it is able to reconfigure the $k$NN graph enough to rectify most of the semantic similarity breaches.

An illustrative example is given in Fig. 7, showing how the neighbor occurrence profile of a particular image changes when the secondary similarities are introduced. The number of the reverse $5$-nearest neighbors of $X_{14}$ in each category is written above the arrow connecting it to the image. This example is taken from the iNet3 dataset, the simplest among the examined ImageNet subsets. It consists of three different categories: sea moss, fire and industrial plant. Not surprisingly, most misclassifications occur between the fire and sea moss image categories. Many images of fire were taken in the dark, and most sea moss images taken at considerable depth also have a dark background. Some sea mosses are yellow or reddish in color. Also, it is clear from the selected photograph in Fig. 7 how sometimes the shape of the flames could be confused with leaf-like organic objects.

Fig. 7

The change in the neighbor occurrence profile of point $X_{14}$ in iNet3 dataset, as the secondary similarities are introduced. The iNet3 data contain three image categories: sea moss, fire and industrial plant. In the primary metric space, image $X_{14}$ is above average in terms of its occurrence frequency. However, 90 % (18/20) of its occurrences are bad, it acts as a neighbor to points in other categories. We see how the secondary similarity scores gradually resolve this issue

The example in Fig. 7 nicely illustrates both properties of the secondary similarity measures that were discussed in this Section. Due to a reduction in the overall hubness of the iNet3 data, a hub point $X_{14}$ is reduced to being slightly above average in number of occurrences under $simcos_{50}$ and below average under the proposed $simhub_{50}$ similarity score. Both secondary measures significantly reduce its number of bad occurrences $BN_5(X_{14})$, but $simhub_{50}$ performs better than $simcos_{50}$ by allowing only one remaining $X_{14}$ bad occurrence into the $k$NN graph.

4.3 Classification with the secondary metrics

The analysis outlined in Sect. 4.2 suggests that the hubness-aware definition of shared neighbor similarities might prove more useful for the $k$NN classification when compared to the standard approach. In order to test this hypothesis, we have compared $simhub_{50}$ with $simcos_{50}$ in the context of $k$-nearest neighbor classification both on synthetic and image data.

The choice of parameters was the same as before: The shared neighbor similarities were derived from the $50$-neighbor sets and the values of $k=5$ and $k=10$ were used for ImageNet data and the Gaussian mixtures, respectively. Other parametrizations are certainly possible and Sect. 4.4 deals precisely with the impact of different neighborhood sizes on the classification process.

As some hubness remains even in the shared neighbor metric space, the similarity measures were compared both in the basic $k$NN and across a range of hubness-aware $k$-nearest neighbor classification methods (hw-$k$NN [6], h-FNN [28], NHBNN [29], HIKNN [31]).

All experiments were run as 10-times 10-fold cross-validation, and the corrected re-sampled $t$-test was used to check for statistical significance. The features in ImageNet data were normalized prior to classification. No normalization was performed on the Gaussian mixtures, as it was noticed that it actually harms the classification performance. For example, the average $k$NN accuracy drops from 59.2 to 41.78 % when the Euclidean distance is applied to the normalized feature vectors.

The classification accuracy under the primary metrics ($L_1$,$L_2$) is given in Table 3. These results were already discussed from the perspective of classification in presence of class imbalance [58], so we will merely use them here as a baseline for comparisons with the classifier performance on the secondary metrics. Both the synthetic and the image data exhibit high hubness, so it is no surprise that the hubness-aware classification methods clearly outperform the basic $k$NN. In ImageNet data, all hubness-aware algorithms perform similarly, but NHBNN achieves the best result in the synthetic experiments.

Table 3 Algorithm performance when using the primary metrics

Classification performance on the image datasets when using the secondary shared neighbor similarities is given in Table 4. The use of $simcos_{50}$ increases the average $k$NN accuracy by about 5 % when compared to the $L_1$ distance case. However, the proposed $simhub_{50}$ similarity performs even better and further improves the observed accuracy by another 5 %. This is consistent with the observed difference in induced bad occurrence percentages which was shown in Fig. 4. Both secondary measures improve not only the basic $k$NN method, but all the examined hubness-aware approaches as well. The hubness-aware $simhub_{50}$ is clearly to be preferred, since it leads to equal or higher accuracies for all the algorithms on all the datasets.

In both secondary metric spaces, the hubness-aware methods still perform favorably when compared to $k$NN. On the other hand, when the $k$NN is coupled with $simhub_{50}$, it performs better than some of the hubness-aware approaches in the primary metric space. Nevertheless, the best results are obtained by combining the hubness-aware metric learning with the hubness-aware classification (Fig. 8).

Fig. 8

The average accuracy for each algorithm and similarity measure, when taken over all the analyzed datasets (both ImageNet and the Gaussian mixtures). The increase in performance when using the shared neighbor similarities is most pronounced in $kNN$, which was to be expected, as the hubness-aware methods are less affected by the dimensionality curse and the hubness phenomenon. The proposed $simhub_{50}$ similarity measure leads to better accuracy in each examined algorithm

Table 4 Experiments with $simhub_{50}$ and $simcos_{50}$ on ImageNet data

The results on the synthetic data (Table 5) are even more convincing. The standard $simcos_{50}$ raises the average $k$NN classification accuracy from 59.2 to 76.25 %. Using the $simhub_{50}$ similarity gives 86.3 % instead, which is a substantial further increase. As in the ImageNet data, the hubness-aware methods outperform the basic $k$NN in both secondary metric spaces and $simhub_{50}$ outperforms $simcos_{50}$ on every algorithm and for every dataset. The major difference is that here we see that using the $simcos_{50}$ similarity actually reduced the accuracy of NHBNN, which was the single best approach in the primary metric space. A decrease was observed on each examined synthetic dataset. Furthermore, the best obtained average result when using the $simcos_{50}$ measure equals to 83.85 % (by hw-$k$NN, Table 5), which is still less than the best result obtained in the primary $L_2$ metric space (86.18 %, shown in Table 3). This shows that the use of $simcos_{50}$ is not always beneficial to hubness-aware $k$NN classification.

Table 5 Experiments with $simhub_{50}$ and $simcos_{50}$ on Gaussian mixture data

4.4 The influence of neighborhood size

All the previously discussed experiments depended on two neighborhood size parameters ($k$,$s$). The choice of $s$ affects the overall quality of the induced secondary $k$NN graph, and the choice of $k$ affects the algorithm performance in the secondary metric space. This is why it is very important to test the shared neighbor similarities over a range of different parameter values, in order to determine whether the previously discussed results are relevant and not merely an artifact of a particular ($k$,$s$) choice. Figures 9 and 10 show that the $k$NN and h-FNN classification performance on $DS_1$ and $DS_2$ is not greatly affected by a change in $k$. The same holds on other datasets as well.

Fig. 9

$k$NN accuracy over a range of $k$-neighbor set sizes. The hubness-aware $simhub_{50}$ similarity leads to better results in all cases

Fig. 10

h-FNN accuracy over a range of $k$-neighbor set sizes

Figure 10 shows a peculiar trend, especially when compared to Fig. 9. The secondary $simcos_{50}$ similarity reduces the overall bad hubness in the data, which improves the classification accuracy of $k$NN. On the other hand, there is a very small improvement in h-FNN and the other hubness-aware methods for $k=10$ and it seems that even this is lost as the $k$ is further increased. As all algorithms are operating in the same metric space, we would expect the decrease in bad hubness to affect them in similar ways and yet this is not the case when using $simcos_{50}$. This result suggests that there has to be another, more subtle difference between $simcos_{50}$ and $simhub_{50}$.

It turns out that the $k$NN graphs induced by $simhub_{50}$ have a significantly lower reverse neighbor set entropy, as shown in Fig. 11. The reverse neighbor set entropy is defined as $H(R_k(x))=\sum _{c \in C}{\frac{N_{k,c}(x)}{N_k(x)} \cdot \log {\frac{N_k(x)}{N_{k,c}(x)}}}$. Anti-hubs with no previous occurrences are assigned a $0$ reverse neighbor set entropy by default. The observed difference between the entropies induced by $simcos_{50}$ and $simhub_{50}$ increases with $k$. In other words, $simhub_{50}$ increases the average purity of neighbor occurrence profiles, which increases the quality and the reliability of occurrence models inferred by the hubness-aware classification methods. This is precisely the reason why the $simhub_{50}$ measure turns out to be more useful than $simcos_{50}$ when used in conjunction with the hubness-aware classifiers. Even though it reduces the overall bad occurrence frequency, $simcos_{50}$ reduces the purity of the secondary neighbor occurrence profiles, especially when considering larger neighborhoods. These two factors cancel each other out, so in the end no significant change in the hubness-aware classification performance remains.

Fig. 11

The normalized reverse neighbor set entropies over a range of neighborhood sizes ($k$) for $L_2$, $simcos_{50}$ and $simhub_{50}$, averaged over all the synthetic datasets ($DS_1$–$DS_{10}$). The hubness-aware $simhub_{50}$ increases the purity of reverse neighbor sets, while $simcos_{50}$ decreases it

The other neighborhood parameter, $s$, which is used to determine the size of the neighbor set from which the shared neighbor counts will be taken, is directly involved in the quality of the resulting secondary metric spaces. The use of relatively large $s$ values was advocated for $simcos_{s}$ [22], as it was argued that it leads to a better similarity score. The proper $s$-size was said to be of the same order as the cluster size. In our synthetic Gaussian mixtures, that would amount to anywhere between $50$ and $200$, depending on the dataset. Indeed, in $DS_1$ and $DS_2$, the optimum for $simcos_{s}$ in terms of bad occurrence frequencies is reached around $s=150$, as shown in Fig. 12. The hubness-aware $simhubs_{s}$ seems to behave differently, as it reaches its optimum for $s$ values between $50$ and $100$ in these two datasets. After reaching the optimum, the performance of $simhub_{s}$ slowly deteriorates if $s$ is further increased. Nevertheless, its bad hubness optimum seems to be well below the $simcos_{s}$ optimum. Also, for every $s \in [10,200]$, $BN_{10}^{simhub_s} < BN_{10}^{simcos_s}$ in all the examined cases. It is actually beneficial to reach the optimum for lower $s$ values, if possible, since it entails less computations and a shorter execution time.

Fig. 12

Bad occurrence frequencies for $k=10$ in the secondary metric space as the $s$ parameter is varied in $simcos_s$ and $simhub_s$ similarity measures

The trends involving the reverse neighbor set entropy are somewhat different. Unlike bad hubness, $H(R_{10}(x))$ monotonously decreases both for $simcos_{s}$ and $simhub_{s}$. This is shown in Fig. 13, for $DS_1$ and $DS_2$. The difference between the two measures seems to be constant, regardless of the choice of $s$-value. This reaffirms the previously stated observation that $simhub_{s}$ seems to generate metric spaces where the hubness-aware occurrence models yield greater improvements. Very small $s$-neighborhoods are not well suited for this task, as the improvement in $H(R_{10}(x))$ over $L_2$ is achieved by $simhub_{s}$ only for $s \ge 50$. On the other hand, $simcos_{s}$ requires at least $s=150$ to produce equally pure neighbor occurrence profiles as the primary metric.

We can conclude that the proposed $simhub_{s}$ similarity measure outperforms $simcos_{s}$ not only for $s=50$ as confirmed above, but also over the entire range of different $s$ values. Additionally, $simhub_{s}$ seems to reach its optimum sooner and it seems to be somewhere in the range $s \in [50,100]$ on the synthetic datasets that we have examined.

Fig. 13

Normalized reverse neighbor set entropy for $k=10$ in the secondary metric space as the $s$ parameter is varied in $simcos_s$ and $simhub_s$ similarity measures

4.5 Individual contributions of the two hubness-aware weighting terms

The hubness-aware $simhub_{s}$ similarity measure is based on the occurrence weighting which incorporates both the unsupervised hubness-aware component ($simhub_s^{\mathrm{IN}}$) and the supervised occurrence profile homogeneity term ($simhub_s^{\mathrm{PUR}}$). Here, we will analyze how each of these individual weights affects the properties of the final $simhub_{s}$ similarity score.

Since bad hubness has been a focal point of the previous discussion, it is important to see how each of these weighting terms helps in reducing the overall bad hubness in the data. Figure 14 shows the reduction rates on two representative ImageNet datasets, iNet5Imb and iNet6Imb. Naturally, as $simhub_s^{\mathrm{IN}}$ is an unsupervised weighting term and $simhub_s^{\mathrm{PUR}}$ a supervised one, $simhub_s^{\mathrm{PUR}}$ induces less bad hubness in the secondary metric space. Nevertheless, as Fig. 14 suggests, the unsupervised term also slightly decreases the overall bad hubness. More importantly, it contributes to the overall bad hubness reduction in the final $simhub_{s}$ measure, as we see that the $simhub_{s}$ similarity induces less bad hubness than $simhub_s^{\mathrm{PUR}}$ on these image datasets.

Fig. 14

The induced bad occurrence frequencies in two ImageNet datasets, given over a range of neighborhood sizes for $simcos_{50}$, $simhub_{50}$, $simhub_{50}^{\mathrm{IN}}$ and $simhub_{50}^{\mathrm{PUR}}$

Figure 14 shows that both hubness-aware terms are relevant in reducing the overall bad hubness of the data, but it also wrongly suggests that $simhub_s^{\mathrm{IN}}$ a minor role in the final similarity measure. Even though the bad hubness is a good indicator of the difficulty of the data, it needs not be very strongly correlated with the actual $k$NN classification performance for $k > 1$. Indeed, as shown in Fig. 15, $simhub_{50}^{\mathrm{IN}}$ is the single best similarity measure on the iNet5Imb dataset when $k > 3$, in terms of both the accuracy and the macro-averaged $F_1$ score. The difference in $F_1^M$ is more pronounced than in the overall accuracy, which implies that $simhub_{50}^{\mathrm{IN}}$ better improves the minority class recall under the class imbalance in the iNet5Imb data. This makes sense, as $simhub_{50}^{\mathrm{IN}}$ gives preference to those neighbors which are judged to be more local to the points of interest. The observation is confirmed in Fig. 16, where the recall for each class in the iNet5Imb dataset is shown. Similar trends can also be seen in the other examined imbalanced ImageNet datasets. On the other hand, both weighting terms perform more or less equally on the examined Gaussian mixtures, which is not surprising, as this data is not so highly imbalanced.

Fig. 15

The accuracy and the macro-averaged $F_1$ score on INet5Imb for $k$NN when using some of the different secondary similarities: $simcos_{50}$, $simhub_{50}$, $simhub_{50}^{\mathrm{IN}}$ and $simhub_{50}^{\mathrm{PUR}}$

Fig. 16

The class-specific recall given for $simcos_{50}$, $simhub_{50}^{\mathrm{IN}}$ and $simhub_{50}^{\mathrm{PUR}}$ on the iNet5Imb dataset for $k=5$. The unsupervised hubness-aware term $simhub_{50}^{\mathrm{IN}}$ outperforms the supervised $simhub_{50}^{\mathrm{PUR}}$ on all the minority classes in the data. The recall of $simhub_{50}^{\mathrm{PUR}}$ is higher only for the majority class

Whether it turns out that the stated conclusions hold in general or not, it is already clear that $simhub_{s}^{\mathrm{IN}}$ and $simhub_{s}^{\mathrm{PUR}}$ affect the final $simhub_{s}$ similarity measure in different ways. Therefore, it makes sense to consider a parametrized extension of the $simhub_{s}$ weighting by introducing regulating exponents to the individual hubness-aware terms.

$$\begin{aligned} simhub_s^{\alpha ,\beta }(x_i,x_j) = \frac{\sum _{x \in D_s(x_i) \cup D_s(x_j)}{I_n(x)^\alpha \cdot (\max {H_s} - H(R_s(x)))^\beta }}{s \cdot \max {H_s}^\beta \cdot \max {I_n}^\alpha } \end{aligned}$$

(8)

However, it remains rather unclear how one should go about determining the optimal $(\alpha ,\beta )$ combination for a given dataset without over-fitting on the training split. The parameter values could also be derived from the misclassification cost matrix in unbalanced classification scenarios. A thorough analysis of this idea is beyond the scope of this paper, but it is something that will definitely be carefully investigated in the future work.

4.6 Handling of the difficult points

Some points are more difficult to properly classify than others and each individual dataset is composed of a variety of different point types with respect to the difficulty they pose for certain classification algorithms. A point characterization scheme based on the nearest neighbor interpretation of classification difficulty has recently been proposed for determining types of minority class points in imbalanced data [59]. As the method is limited to imbalanced data, it can be used to characterize points in any class and on any dataset. It is the most natural approach to adopt in our analysis, as the point difficulty is expressed in terms of the number of label mismatches among its 5-NN set. Points with at most one mismatch are termed safe, points with 2-3 mismatches are referred to as being borderline examples, points with 4 mismatches are considered rare among their class and points with all neighbors from different classes are said to be outliers.

As the SNN similarity measures induce a change in the $k$NN structure of the data, we can expect that a change in metric might lead to a change in the overall point type distribution. Reducing the overall difficulty of points can be directly correlated with the improvement in the $k$NN classification performance. This is precisely what happens when the SNN measures are used, as shown in Fig. 17 for the synthetic datasets. Both the standard $simcos_{50}$ and the proposed $simhub_{50}$, $simhub_{50}^{\mathrm{IN}}$ and $simhub_{50}^{\mathrm{PUR}}$ significantly increase the number of safe points when compared to the primary $L_2$ metric. The hubness-aware shared neighbor similarities improve the point difficulty distribution more than $simcos_{50}$, which explains the classification accuracy increase discussed in Sect. 4.3.

Fig. 17

Distribution of point types on synthetic data under several employed metrics. The hubness-aware secondary similarity measures significantly increase the proportion of safe points which leads to an increase in $k$NN classification performance

The two hubness-aware weighting terms lead to an approximately equal classification accuracy on the examined Gaussian mixtures, so it is somewhat surprising that they induce different distributions of point difficulty. The purity term, $simhub_{50}^{\mathrm{PUR}}$, is better at increasing the number of safe points than the occurrence self-information term, $simhub_{50}^{\mathrm{IN}}$. This is compensated by the fact that the difference in the number of borderline points is in favor of $simhub_{50}^{\mathrm{IN}}$ by a slightly larger margin. As borderline points are correctly classified approximately 50 % of the time, the two distributions exhibit similar overall difficulties for the $k$NN classification methods.

The difference between the examined similarities/metrics is present in each examined dataset. The proportion of safe points is shown in Fig. 18 for each of the Gaussian mixtures. ImageNet data exhibit the same properties. The increase in the proportion of safe points is yet another desirable property of the proposed hubness-aware SNN measures.

Fig. 18

The percentage of safe points on each of the examined Gaussian mixtures. The proposed $simhub_{50}$ measure induces a larger proportion of safe points in each dataset, when compared to the standard $simcos_{50}$

4.7 Reducing the error propagation

Data processing and preparation sometimes introduces additional errors in the feature values, and these errors can more easily propagate and negatively affect the learning process under the assumption of hubness. We will briefly discuss three such datasets (iNet3Err:100, iNet3Err:150, iNet3Err:1000) described in [55]. The three datasets contain the 100-, 150- and 1,000-dimensional quantized representations, respectively. While the system was extracting the Haar feature representations for the dataset, some I/O errors occurred which left a few images as zero vectors, without having been assigned a proper representation. Surely, this particular error type can easily be prevented by proper error-checking within the system, but we will nevertheless use it as an illustrative example for a more general case of data being compromised by faulty examples. In a practical application, obvious errors such as these would either be removed or their representations recalculated. In general, the errors in the data are not always so easy to detect and correct. This is why the subsequent data analysis ought to be somewhat robust to errors and noise.

Even though errors in the data are certainly undesirable, a few zero vectors among 2,731, which is the size of iNet3 data, should not affect the overall classifier performance too much, as long as the classifier has good generalization capabilities. The $k$NN classifier, however, suffers from a high specificity bias, and this is further emphasized by the curse of dimensionality under the assumption of hubness. Namely, the employed metric ($L_1$) induced an unusually high hubness of zero vectors. It can easily be shown that the expected $L_1$ dissimilarity between any two quantized image representations increases with increasing dimensionality. On the other hand, the distance to the zero-vector remains constant for each image. Eventually, when $d=1{,}000$, the few zero vectors in the data infiltrated and dominated all the $k$-neighbor sets and caused the 5-NN to perform worse than zero rule, as they were, incidentally, of the minority class. The increasing bad hubness of the top 5 bad hubs is shown in Fig. 19.

Fig. 19

The increasing bad hubness of the top 5 erroneous bad hubs in the quantized iNet3 Haar feature representations. All the bad hubs were in fact zero vectors generated by a faulty feature extraction system, and all of them were of the minority class. These zero vectors became dominant bad hubs as the dimensionality of the data representation was increased. Such a pathological case clearly illustrates how even a few noisy examples are enough to compromise all $k$-nearest neighbor inference in high-hubness data

Such pathological cases are rare, but clearly indicate the dangers in disregarding the skewness of the underlying occurrence distribution. As this example is quite extreme, it is a good test case to examine the robustness of the secondary similarity measures to such a high violation of semantics in the $k$-nearest neighbor graph. The comparisons were performed as 10-times 10-fold cross-validation, and the results for $k$NN are summarized in Fig. 20. The neighborhood size $k=5$ was used.

Fig. 20

The $k$NN accuracy on high-hubness erroneous image data under $L_1$, $simcos_{50}$, $simhub_{50}$, $simcos_{200}$, $simhub_{200}$. The secondary similarity measures reduce the impact of faulty and inaccurate examples

For the 1,000-dimensional faulty representation, the secondary $simcos_{200}$ and $simhub_{200}$ similarities improved the overall $k$NN accuracy from 20 to 94 %, which is undeniably impressive. Both the $simcos_{s}$ and $simhub_{s}$ reached their optimum for $s=200$, but for $s \in [50,200]$ the hubness-aware similarity measure outperformed its counterpart, as it converges to the correct $k$NN graph configuration faster than $simcos_{s}$, which was previously discussed in Sect. 4.4. This is shown in Fig. 20 for $s=50$.

What this example shows is that the hubness-aware shared neighbor distances are able to significantly reduce the impact of errors on high-hubness data classification. Such robustness is of high importance, as real-world data are often inaccurate and noisy. This particular example might have been extreme, but such extreme cases are likely to occur whenever errors end up being hubs in the data, which depends on the choice of feature representation and the primary metric.

4.8 Class separation

Ensuring a good separation between classes is what a good metric should ideally be able to achieve. This is not always possible, as the cluster assumption is sometimes severely violated. Even so, we would expect the examples from the same class to be, on average, closer to each other than the pairs of examples taken from different classes. Increasing the contrast between the average intra-class and inter-class distance is one way to make the classification task somewhat easier. The improvement is not, however, guaranteed, especially when the $k$NN methods are used. Unless the $k$NN structure changes in such a way that the ensuing distribution of point difficulty becomes favorable, the contrast is of secondary importance.

The proposed $simhub_{s}^{\mathrm{PUR}}$ measure was designed in such a way that the neighbors with higher occurrence profile purity are valued more, as they usually contribute more to the intra-class similarities. However, note that this is only guaranteed in binary classification. If there are only two classes in the data, $H(R_s(x_1)) < H(R_s(x_2))$ directly follows from the fact that $x_1$ has a higher relative contribution to the contrast than $x_2$.

There is also a downside to using the occurrence entropies for determining neighbor occurrence weights. The entropies measure the relative purity which reflects the relative positive contribution of the neighbor point. However, if we are interested specifically in increasing the contrast, we are interested in rewarding the absolute positive contributions, not the relative ones. In other words, even if two points $x_1$ and $x_2$ have the same reverse neighbor set purity, $x_1$ has a higher contribution to the overall similarity if $N_s(x_1) > N_s(x_2)$. Within the $simhub_{s}$ measure, this problem is even more pronounced because $N_s(x_1) > N_s(x_2) \Rightarrow I_n(x_1) < I_n(x_2)$.

This is very interesting, as we have seen in Sect. 4.5 that reducing the weight of hubs by $simhub_{s}^{\mathrm{IN}}$ is highly beneficial. It increases the reverse neighbor set purity, reduces bad hubness and improves the $k$NN classification as much as $simhub_{s}^{\mathrm{PUR}}$. However, it seems that it actually reduces the contrast between the intra-class and inter-class similarities, especially when used in conjunction with $simhub_{s}^{\mathrm{PUR}}$.

In multi-class data, things get even more complicated. Each neighbor point $x_i$ contributes to $\genfrac(){0.0pt}{}{N_s(x_i)}{2} = GS(x_i) + BS(x_i)$ shared neighbor similarity scores, where $GS(x_i)$ and $BS(x_i)$ represent the number of intra-class and inter-class similarities, respectively. Denote by $CS(x_i) = GS(x_i) - BS(x_i)$ the contribution of each $x_i$ to the total difference between the two similarity sums.

$$\begin{aligned} GS(x_i)&= \sum _{c \in C}{\genfrac(){0.0pt}{}{N_{s,c}(x_i)}{2}}\nonumber \\ BS(x_i)&= \sum _{c_1,c_2 \in C, c_1 \ne c_2}{N_{s,c_1}(x_i) \cdot N_{s,c_2}(x_i)} \end{aligned}$$

(9)

The occurrence purity $OP(x_i) = \max {H_s} - H(R_s(x_i))$ is tightly correlated with $CS(x_i)$. Nevertheless, in non-binary classification, some occurrence profiles exist such that $OP(x_i) < OP(x_j)$, but $CS(x_i) > CS(x_j)$ or vice versa. Consider the following 4-class example:

$$\begin{aligned} C&= 4, \qquad \max H_s = \log 4 = 2\nonumber \\ N_s(x_i)&= N_s(x_j) = 100\nonumber \\ N_{s,1}(x_i)&= 5,\quad N_{s,2}(x_i) = 15,\quad N_{s,3}(x_i) = 25,\quad N_{s,4}(x_i) = 55\nonumber \\ N_{s,1}(x_j)&= 6,\quad N_{s,2}(x_j) = 10,\quad N_{s,3}(x_j) = 34,\quad N_{s,4}(x_j) = 50\nonumber \\ CS(x_i)&= GS(x_i) - BS(x_i) \quad =\quad 1900 - 3050 \quad =\quad -1150\nonumber \\ CS(x_j)&= GS(x_j) - BS(x_j) \quad =\quad 1846 - 3104 \quad =\quad -1258\nonumber \\ OP(x_i)&= 2 - H(R_s(x_i)) \quad \approx \quad 2 - 1.6010 \quad =\quad 0.3990\nonumber \\ OP(x_j)&= 2 - H(R_s(x_j)) \quad \approx \quad 2 - 1.5989 \quad =\quad 0.4011\nonumber \\ OP(x_i)&< OP(x_j) \quad \wedge \quad CS(x_i) > CS(x_j) \end{aligned}$$

(10)

This example shows that the reverse neighbor set purity is not monotonous with respect to the difference between the intra-class and inter-class similarity contributions of a neighbor point.

Note, however, that maximizing the sum total of $CS_D = \sum _{x \in D} CS(x)$ is not equivalent to maximizing the contrast between the inter- and intra-class distances, as that quantity requires normalization. Let $C_D = \frac{\text{ AVG}_{y_i \ne y_j}(dist(x_i,x_j)) - \text{ AVG}_{y_i = y_j}(dist(x_i,x_j))}{\max _{x_i,x_j \in D}dist(x_i,x_j) - \min _{x_i,x_j \in D}dist(x_i,x_j)}$ quantify the contrast. The denominator is necessary, as it would otherwise be possible to increase the contrast arbitrarily simply by scaling up all the distances. In practice, this means that the contrast also depends on the maximum/minimum pairwise distances on the data—and these quantities also change while we are changing the instance weights when trying to increase $CS_D$. Nevertheless, increasing $CS_D$ seems like a sensible approach to improving class separation, slightly more natural than increasing the overall purity $OP_D = \sum _{x \in D} OP(x)$. To see if this is really the case, we defined two additional hubness-aware similarity measures.

$$\begin{aligned} simhub_s^{01}&= \frac{\sum _{x \in D_s(x_i) \cup D_s(x_j)}{1\!\!\!\!\text{ I}_{\{\bar{x}:CS(\bar{x}) > 0\}}(x)}}{s}\end{aligned}$$

(11)

$$\begin{aligned} simhub_s^{\mathrm{REL}}&= \frac{\sum _{x \in D_s(x_i) \cup D_s(x_j)}{(CS(x) - \min _{\bar{x}\in D}(CS(\bar{x}))})}{s \cdot {(\max _{\bar{x}\in D}CS(\bar{x}) - \min _{\bar{x}\in D}CS(\bar{x})})} \end{aligned}$$

(12)

If we limit the weight of each shared neighbor point to the interval $w(x) \in [0,1]$, it is not difficult to see that the $CS_D$ is trivially maximized if and only if $w(x) = 1$ when $CS(x) > 0$ and $w(x) = 0$ when $CS(x) \le 0$. This weighting in embodied in $simhub_s^{\mathrm{01}}$, defined in Eq. 11 above. Even though the total difference between the contributions to inter- and intra-class distances is maximized, it is clear that this measure has some very undesirable properties. First of all, it is not impossible to construct a dataset with a severe cluster assumption violation where $\forall x \in D: CS(x) \le 0$. All the $simhub_s^{\mathrm{01}}$ similarities would then equal zero, and this is certainly not what we want. In less extreme, real-world data, this measure could similarly annul some of the pairwise similarities when all the shared neighbors have $CS(x) \le 0$. What this example clearly shows is that even though we would like to increase $CS_D$ and improve the contrast, not only does the global optimum for $CS_D$ not guarantee the best class separation, it also involves having a similarity measure which has many practical weaknesses.

The $simhub_s^{\mathrm{REL}}$ similarity score is a far less radical approach than $simhub_s^{\mathrm{01}}$. The neighbor occurrence weights are proportional to the normalized neighbor contributions $CS(x)$ to the $CS_D$ total. Even though this measure is in a sense similar to $simhub_s^{\mathrm{PUR}}$, there are no more problems with monotonicity of $w(x)$ with respect to $CS(x)$. This ought to help improve the class separation. Also, $w(x) \ge 0$ for points with $CS(x) < 0$, so there is no risk of having many zero similarities, as was the case with $simhub_{s}^{\mathrm{01}}$.

Figure 21 shows the class separation induced by each of the mentioned similarity measures, on the Gaussian mixture datasets. The standard $simcos_{50}$ measure achieves better class separation than the previously considered hubness-aware SNN measures: $simhub_{50}$, $simhub_{50}^{\mathrm{IN}}$ and $simhub_{50}^{\mathrm{PUR}}$. This is somewhat surprising, given that it was shown to be clearly inferior in terms of $k$NN classification accuracy, bad hubness, as well as the inverse neighbor set purity. However, this is 10-class data and, as was explained above, there is no guarantee that any of the three hubness-aware measures would improve the separation, as defined by $C_D$. On the other hand, the newly proposed $simhub_{50}^{\mathrm{REL}}$ measure does manage to increase the separation, unlike the initial choice $simhub_{50}^{\mathrm{01}}$, which fails for reasons already discussed.

The difference between the $simcos_{50}$ and $simhub_{50}^{\mathrm{REL}}$ is present in all datasets. The comparisons were also performed in terms of the widely used Silhouette coefficient [61], which is shown in Fig. 22. The Silhouette coefficient is used for evaluating cluster configurations. If we observe each class as a cluster, a higher Silhouette score means that the classes in the data conform better to the cluster assumption. If the index value is low, it means that the classes are not really compact and either overlap or are composed of several small clusters, scattered around a larger volume of space. The Silhouette values for the considered overlapping Gaussian mixtures are still rather low, but the original ones (in the $L_2$ metric) were even negative in some datasets, meaning that the points from some different class are on average closer than the points from the same class. So, both $simcos_{50}$ and $simhub_{50}^{\mathrm{REL}}$ improve the cluster structure of the data, but the $simhub_{50}^{\mathrm{REL}}$ does it better.

Fig. 21

The average class separation induced by different metrics on the Gaussian mixtures ($DS_1$-$DS_{10}$). Even though the $simcos_{50}$ measure has been shown to be inferior in $k$NN classification, it achieves better class separation than the previously considered $simhub_{50}$, $simhub_{50}^{\mathrm{IN}}$ and $simhub_{50}^{\mathrm{PUR}}$ similarities. On the other hand, the newly proposed $simhub_{50}^{\mathrm{REL}}$ measure gives the best separation between the classes

Fig. 22

The comparison in terms of the Silhouette index on the Gaussian mixtures ($DS_1$-$DS_{10}$) between $simcos_{50}$ and $simhub_{50}^{\mathrm{REL}}$. The newly proposed hubness-aware SNN measure makes the class-clusters more compact in all considered datasets

Regardless of the fact that it improves class separation, $simhub_{s}^{\mathrm{REL}}$ turns out to be not nearly as good as $simhub_{s}$ when it comes to reducing bad hubness and improving the classification performance. This is why we would not recommend it for $k$NN classification purposes. Regardless, as it raises the Silhouette coefficient, $simhub_{s}^{\mathrm{REL}}$ could be used in some clustering applications. Admittedly, it is a supervised measure (it requires the data points to have labels), but these labels could either be deduced by an initial clustering run or already present in the data. Namely, a considerable amount of research was done in the field of semi-supervised clustering [62], where some labeled/known examples are used to help improve the clustering process. This was done either by introducing constraints [63] or precisely by some forms of metric learning [62, 64].

To conclude, we can say that not increasing the class separation as much as $simcos_{s}$ is the only apparent downside of using $simhub_{s}$, but one which can be tolerated, as we have seen that the proposed hubness-aware shared neighbor similarity measure helps where it matters the most—in improving the classifier performance and reducing bad hubness, which is a very important aspect of the curse of dimensionality. Nevertheless, $simhub_{s}$ still significantly improves the class separation when compared to the primary metric, and if the class separation and the cluster structure of the data is of highest importance in a given application, $simhub_{s}^{\mathrm{REL}}$ is still preferable to the standard $simcos_{s}$.

4.9 Low-dimensional data

Low-dimensional data does not exhibit hubness and is usually easier to handle as it does not suffer from the curse of dimensionality. We have analyzed 10 such low-dimensional datasets. The detailed data description was given in Table 2. Some datasets even exhibited negative skewness of the neighbor occurrence distribution, which might even be interpreted as anti-hubness, an opposite of what we have been analyzing up until now.

We have compared the $simcos_{50}$ and $simhub_{50}$ with the primary Euclidean distance on this data, by observing the $k$NN accuracy in 10-times 10-fold cross-validation for $k=5$. All features were standardized by subtracting the mean and dividing by standard deviation prior to classification. The results are shown in Fig. 23.

Fig. 23

The accuracy of the $k$-nearest neighbor classifier on low-dimensional data under different distance measures. As there is no hubness in this data, there are no visible improvements

Apparently, both shared neighbor similarities seem to be somewhat inadequate in this case. They offer no significant improvements over the primary metric, sometimes being slightly better, sometimes slightly worse. The average accuracy over the ten considered low-dimensional datasets is 85.17 for $L_2$, 84.55 for $simcos_{50}$ and 85.1 for $simhub_{50}$.

This comparison shows that the shared neighbor similarities ought to be used primarily when the data are high dimensional and exhibits noticeable hubness. In low-dimensional data, other approaches might be preferable.

5 Conclusions and future work

In this paper, we proposed a new secondary shared neighbor similarity measure $simhub_{s}$, in order to improve the $k$-nearest neighbor classification in high-dimensional data. Unlike the previously used $simcos_{s}$ score, $simhub_{s}$ takes hubness into account, which is important as hubness is a known aspect of the curse of dimensionality which can have severe negative effects on all nearest neighbor methods. Nevertheless, it has only recently come into focus, and this is the first attempt at incorporating hubness information into some form of metric learning.

An experimental evaluation was performed both on synthetic high-dimensional overlapping Gaussian mixtures and quantized SIFT representations of multi-class image data. The experiments have verified our hypothesis by showing that the proposed $simhub_{s}$ similarity measure clearly and significantly outperforms $simcos_{s}$ in terms of the associated classification performance. This improvement can be attributed to a reduce in the bad hubness of the data and the increased purity of the neighbor occurrence profiles. The $k$NN graphs induced by the $simhub_{s}$ measure are less correlated to the primary metric $k$NN structure, which shows that the hubness-aware measure changes the $k$NN structure much more radically than $simcos_{s}$.

As $simhub_{s}$ was defined in a hybrid way, by exploiting both the supervised and the unsupervised hubness information, we have thoroughly analyzed the influence of both constituents ($simhub_{s}^{\mathrm{PUR}}$ and $simhub_{s}^{\mathrm{IN}}$, respectively) on the final similarity score. It was shown that both factors decrease the bad hubness of the data and that they do it best when combined, as in $simhub_{s}$. On the other hand, $simhub_{s}^{\mathrm{IN}}$ seems to be somewhat better in dealing with imbalanced datasets.

All secondary metrics change the overall distribution of point types in the data. The hubness-aware measures excel in increasing the proportion of safe points, which are the ones that are least likely to be misclassified in $k$-nearest neighbor classification. This is closely linked to the improved classifier performance.

The only notable downside to the $simhub_{s}$ measure is that it does not increase the class separation as much as the standard $simcos_{s}$. This has been thoroughly discussed in Sect. 4.8, where we have tried to overcome this difficulty by proposing an additional two hubness-aware SNN measures: $simhub_{s}^{\mathrm{01}}$ and $simhub_{s}^{\mathrm{REL}}$. The experiments have shown that $simhub_{s}^{\mathrm{REL}}$ does indeed improve the class separation better than both $simcos_{s}$ and $simhub_{s}$. The proposed $simhub_{s}$ is still to be preferred for classification purposes, but $simhub_{s}^{\mathrm{REL}}$ might be used in some other applications, as for instance the semi-supervised clustering.

In our future work, we would like to compare the outlined approaches to other forms of metric learning, both theoretically under the assumption of hubness, as well is various practical applications. As for the possible extensions, it would be interesting to include position-based weighting, as was done before in some shared nearest neighbor clustering algorithms. In this paper, we focused mostly on the supervised case, but we intend also to explore in detail the use of hubness-aware SNN similarity measures in unsupervised data mining tasks.